Teoretyczne podstawy analizy termicznej
dynamicznych właściwości mechanicznych
(DMTA). Stosowane aparaty i metodyka
prowadzenia pomiarów.

dr hab. inż. Józef T. Haponiuk, prof. nadzw. PG
Politechnika Gdańska , Wydział Chemiczny, Katedra
Technologii Polimerów, [e-mail]

Analiza termiczna dynamicznych właściwości mechanicznych (DMTA)
charakteryzuje właściwości lepkosprężyste materiałów i pozwala na
określenie zależności temperaturowych dynamicznego modułu sprężystości
E* i jego składowych: modułu zachowawczego E’ i modułu stratności E”.

Zmiany tangensa kąta stratności mechanicznej (tgd = E”/E’) w funkcji
temperatury charakteryzują zmiany ruchliwości molekularnej badanego układu
w zależności od temperatury.

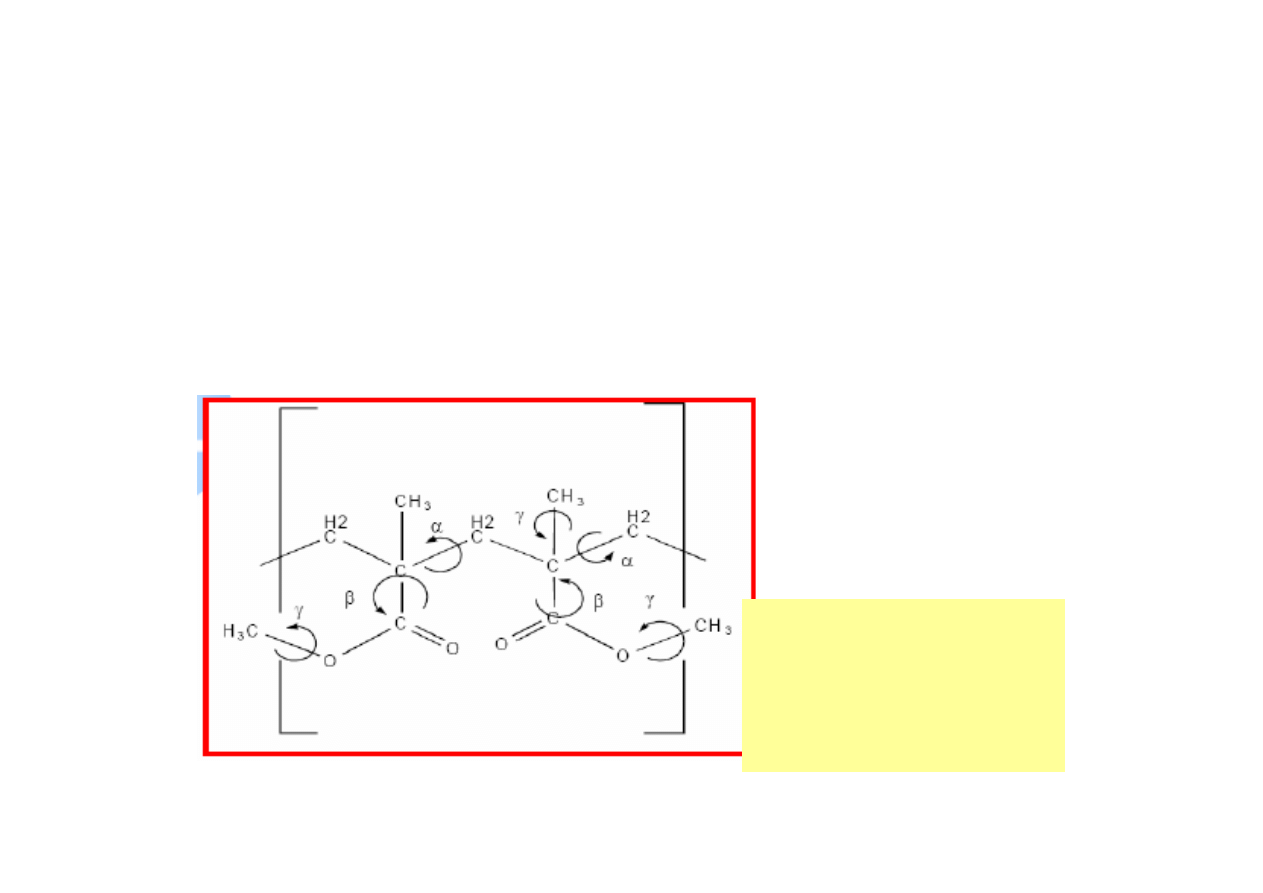
Ruchliwość
molekularna
fragmentów struktury
poli(metakrylanu
metylu)

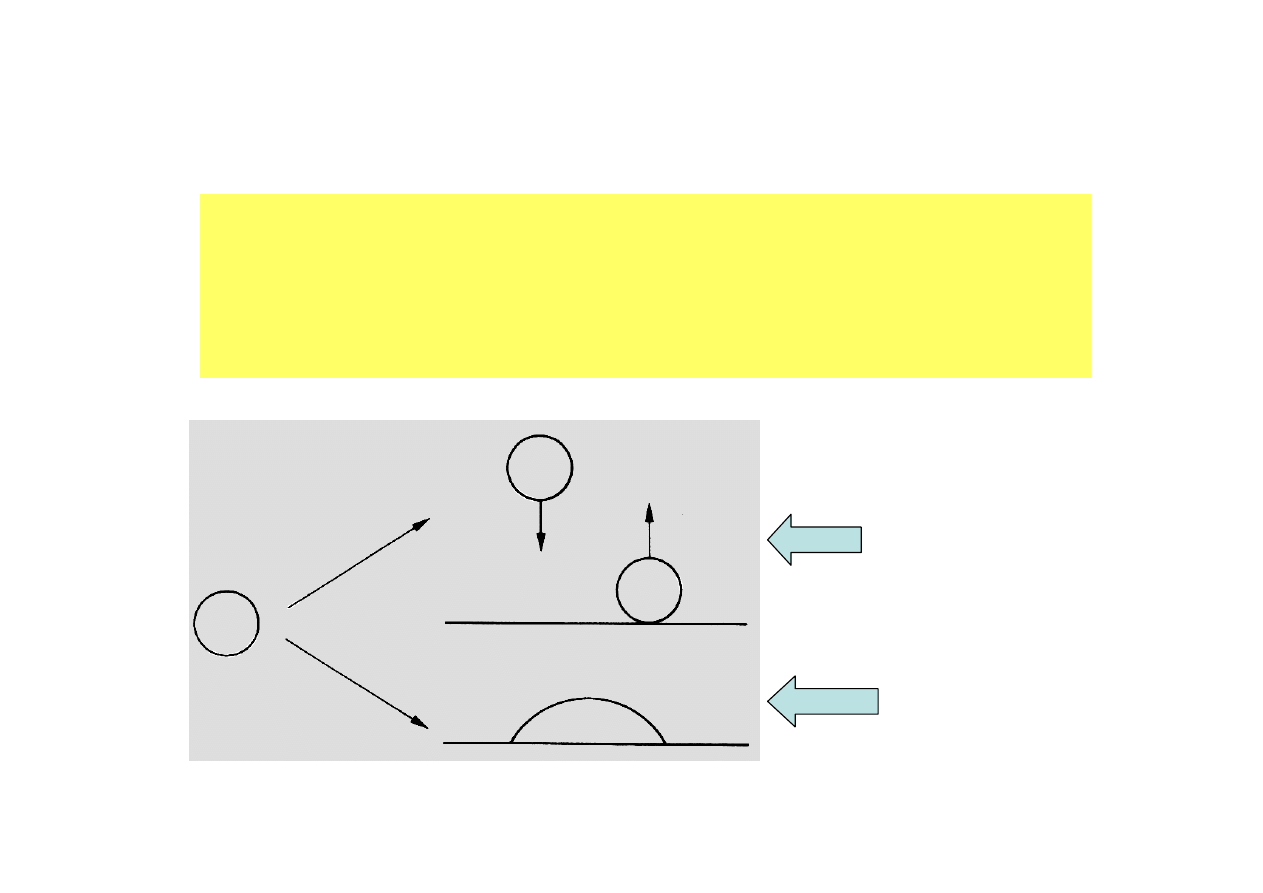
WŁAŚCIWOŚCI LEPKOSPRĘŻYSTE POLIMERÓW

Polimery mają właściwości ciała lepkosprężystego, tzn. że
pod wpływem sił zewnętrznych odkształcają się sprężyście
(odwracalnie) i niesprężyście (nieodwracalnie), zależnie od
czasu - płynięcie.

Zachowanie
sprężyste

Zachowanie
lepkie

WŁAŚCIWOŚCI LEPKOSPRĘŻYSTE POLIMERÓW

Mikroreologia zajmuje się poznaniem zależności między
mikroskopową strukturą materiału a właściwościami
reologicznymi zarówno w stanie stałym, jak i stopionym.

Polimery (materiały) są ciałami stałymi o właściwościach
lepkosprężystych

(tj.ciałami stałymi, które podczas odkształcenia mają

właściwości lepkie w wyniku rozproszenia energii)

lub cieczami lepkosprężystymi

(tj. lepkimi płynami-cieczami, które mają właściwości
sprężyste).

Właściwości lepkosprężyste polimerów

Odkształcenia polimerów pod wpływem naprężeń mogą
być:

sprężyste,

plastyczne

lub lepkie (przepływ).

W realnych ciałach procesy odkształcania są bardzo złożone
i zależą od takich czynników, jak rodzaj naprężenia,
szybkość obciążania lub czas działania obciążenia.

Do ich opisu służą różne modele, np. mechaniczne,

elektryczne itp., które symulują układy lepkosprężyste.

Zasada równoważności temperaturowo-czasowej

Jeżeli polimer poddamy (powyżej jego Tg) działaniu
naprężenia lub będzie odkształcany, łańcuchy jego dążą do
przyjęcia nowych konformacji.

Szybkość zmian konformacji zależy od oporów

napotykanych przez łańcuchy. Opór ten reprezentowany
jest przez współczynnik tarcia lepkiego, który równa się sile
potrzebnej na przesuwanie łańcucha w jego otoczeniu z
jednostkową prędkością.

Tak więc im szybsze wymagane jest przesunięcie łańcucha,

tym większą siłę trzeba zastosować. Podobnie większej siły
na przesunięcie łańcucha wymaga układ, gdy obniżymy
temperaturę. Wynika stąd, że powinien istnieć pewien
związek pomiędzy czasową i temperaturową zależnością
własności lepkosprężystych.

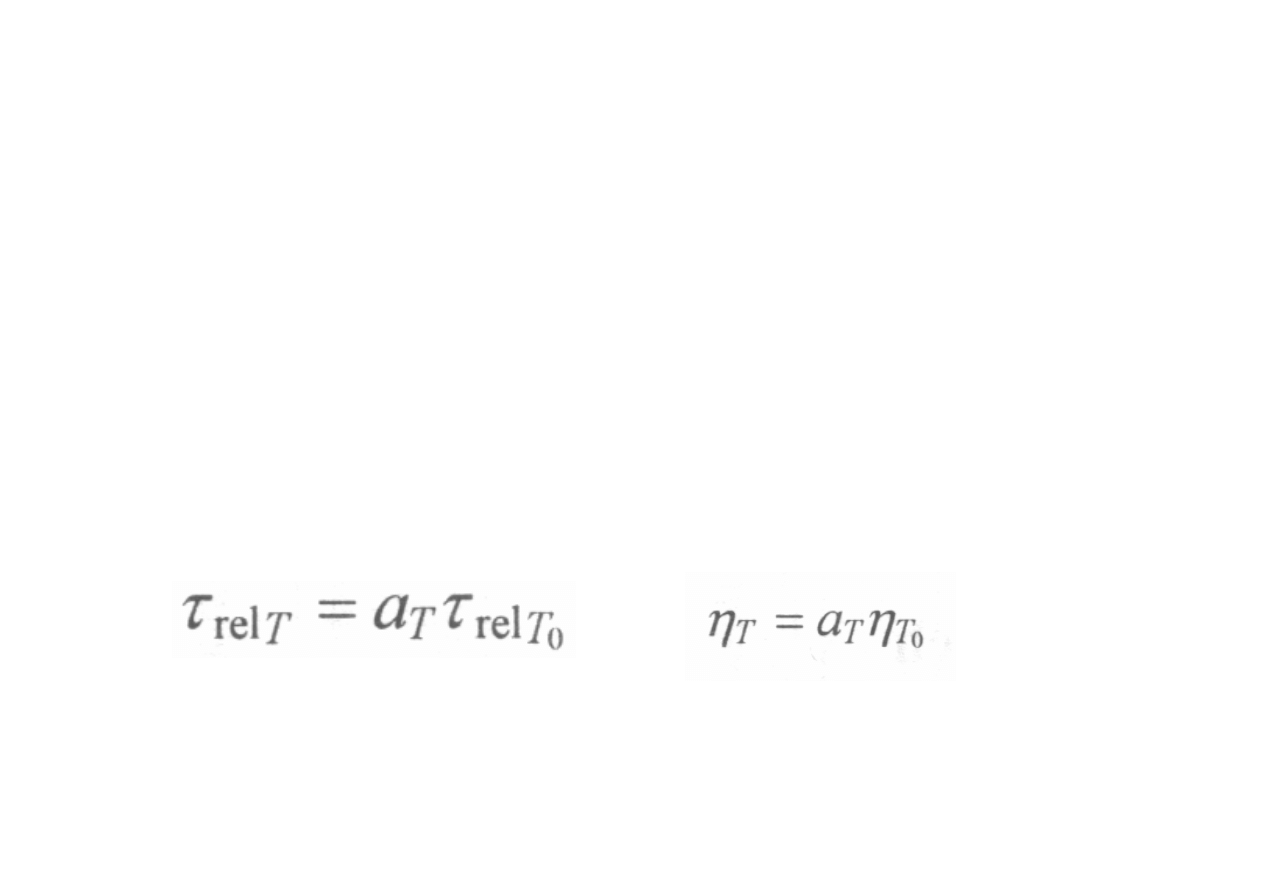
Zasada równoważności temperaturowo-czasowej

Właściwości układów lepkosprężystych zależą od
ruchliwości segmentów łańcucha, którą obrazuje
czas relaksacji lub lepkość zmieniająca się wraz z
temperaturą w sposób wykładniczy.

Na podstawie zachowania się

polimeru

relaksacyjnego w danej temperaturze można
przewidzieć zachowanie się polimeru w innej
temperaturze jedynie przez zmianę czasu. Zasadę tę
opisuje równanie

gdzie: a

T

- współczynnik przesunięcia (redukcji), - czas

relaksacji w temperaturze T i T

0

,

η

- lepkość w

temperaturze T i T

0

.

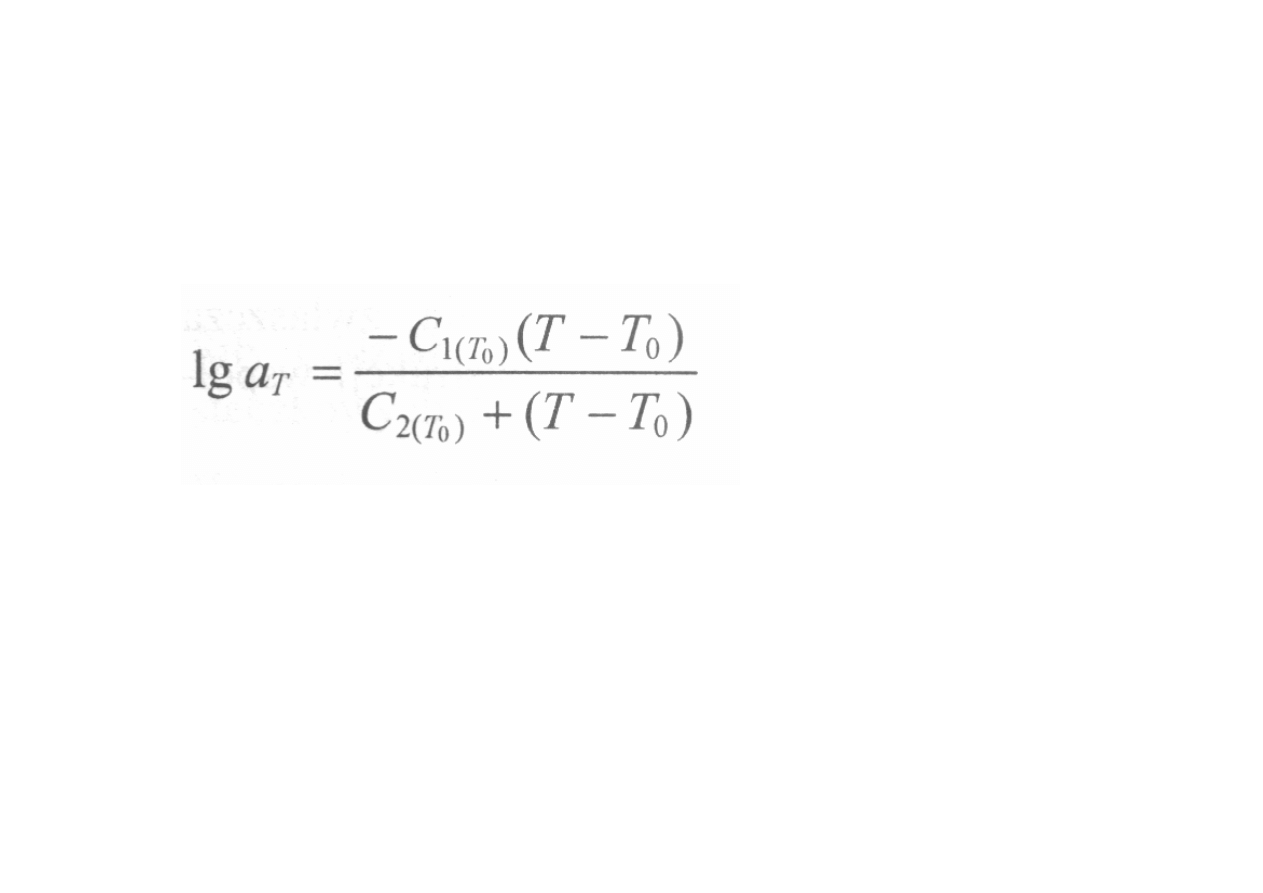
Współczynnik przesunięcia a

T

zależy wykładniczo

od temperatury i jest opisany równaniem WLF
(Williamsa, Landela, Ferry)

gdzie: T

0

- temperatura odniesienia,

T

0

= T

g

+ 50 K,

C

1

, C

2

- stałe (C

1

= 8,86; C

2

= 101,6).

Dla T

0

= T

g

wartość stałych C

1

= 17, C

2

= 52.

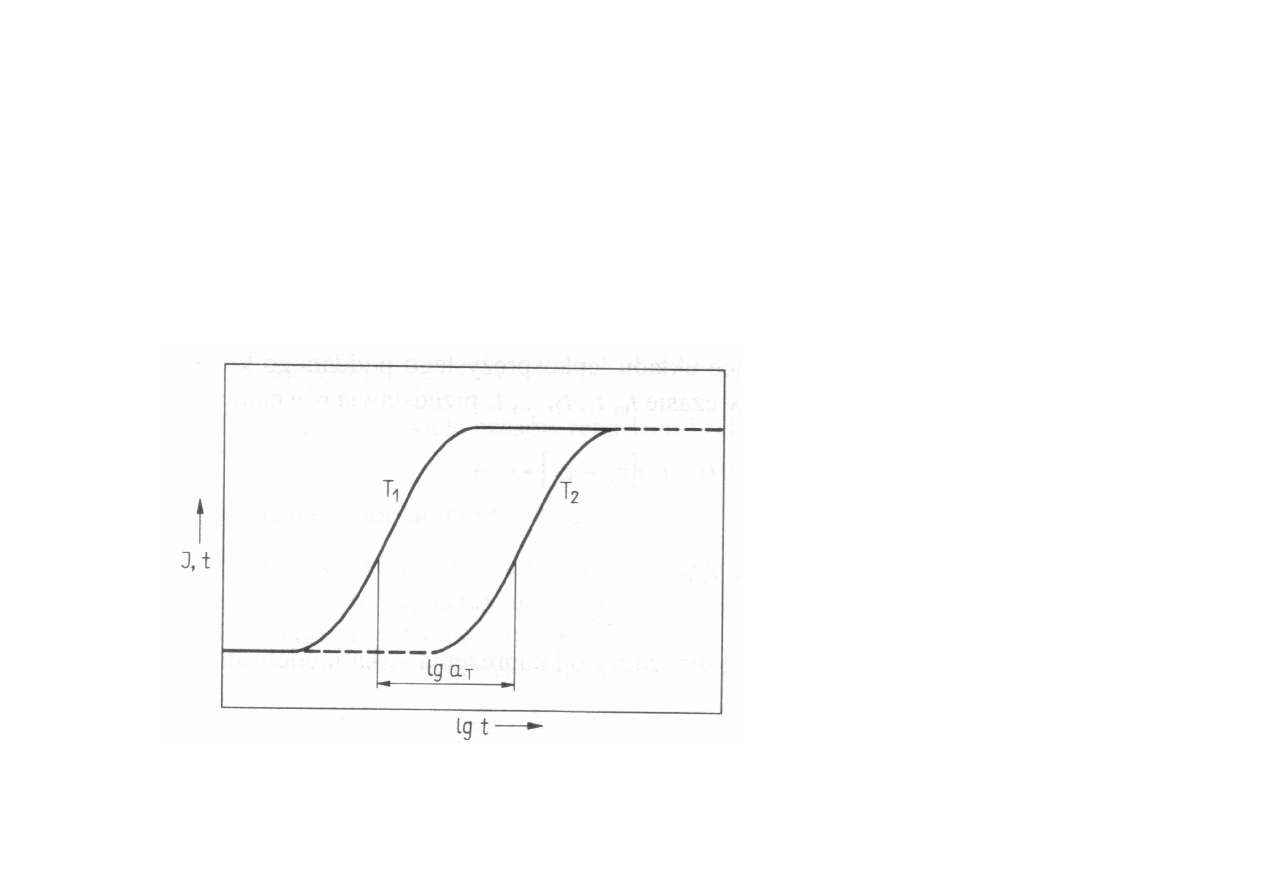
Zgodnie z zasadą równoważności temperaturowo-
czasowej krzywe, np. rozkładu czasów relaksacji lub
modułów dla poszczególnych temperatur, można
przesunąć równolegle wzdłuż osi czasu (t) do zetknięcia z
krzywą

obowiązującą

dla dowolnej temperatury

odniesienia.

R

R

ó

ó

wnowa

wnowa

ż

ż

no

no

ść

ść

temperaturowo

temperaturowo

-

-

czasowa, podatno

czasowa, podatno

ś

ś

ci na pe

ci na pe

ł

ł

zanie

zanie

J(t)

J(t)

Cechy szczeg

Cechy szczeg

ó

ó

lne

lne

Polimery amorficzne wykazują duże, a

polimery krystaliczne i usieciowane małe

relaksacje naprężeń i małe pełzanie.

W temperaturze pokojowej dla większości

metali i stopów pełzanie jest pomijalnie małe

- obserwuje się je dopiero w wysokich

temperaturach i pod dużym naprężeniem.

Procesy relaksacyjne zachodzą w odpowiednich warunkach i są
wynikiem termicznej ruchliwości i orientacji cząsteczek polimeru. Pod
wpływem naprężenia mechanicznego następuje deformacja łańcuchów,
co powoduje zmniejszenie entropii układu i odpowiednio zwiększenie
swobodnej energii. Jeżeli odkształcenie jest stałe, to ruchliwość
termiczna łańcuchów powoduje relaksację naprężeń, w wyniku której
deformacja cząstek zanika, a nadmiar energii zostaje rozproszony jako
ciepło.

Czas relaksacji t

rel

określa się jako czas, po którym początkowe

naprężenie w materiale zmienia się o wartość e (tzn. ok. 2, 7-krotnie). W
stanie szklistym procesy relaksacyjne zachodzą w bardzo długim czasie
natomiast w stanie plastycznym w bardzo krótkim, rzędu ułamków
sekundy.

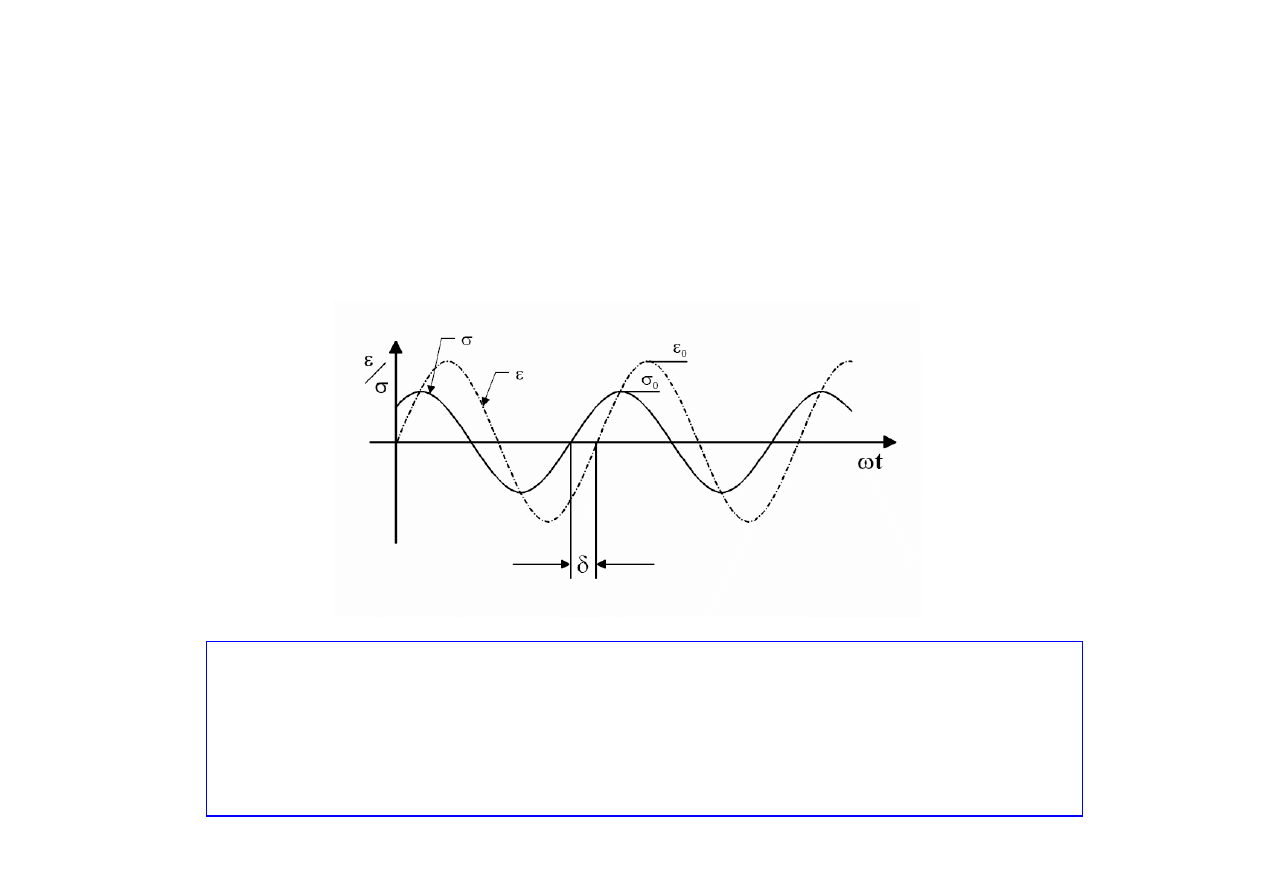
Podczas badań DMTA próbka poddawana jest sinusoidalnym
odkształceniom, a mierzone jest powodowane przez nie naprężenie.
Sprzężony dynamiczny moduł sprężystości ( E* przy zginaniu, G* przy
ścinaniu) wyznaczany jest na podstawie zależności naprężenia i
odkształcenia.

Właściwości lepkosprężyste polimerów uwidaczniają się tym, że jeśli
próbkę podda się drganiom sinusoidalnym zmiennym w czasie, to
powstające naprężenie jest przesunięte w fazie w stosunku do
wywołanego odkształcenia o pewien kąt delta (δ) zwany
przesunięciem fazowym

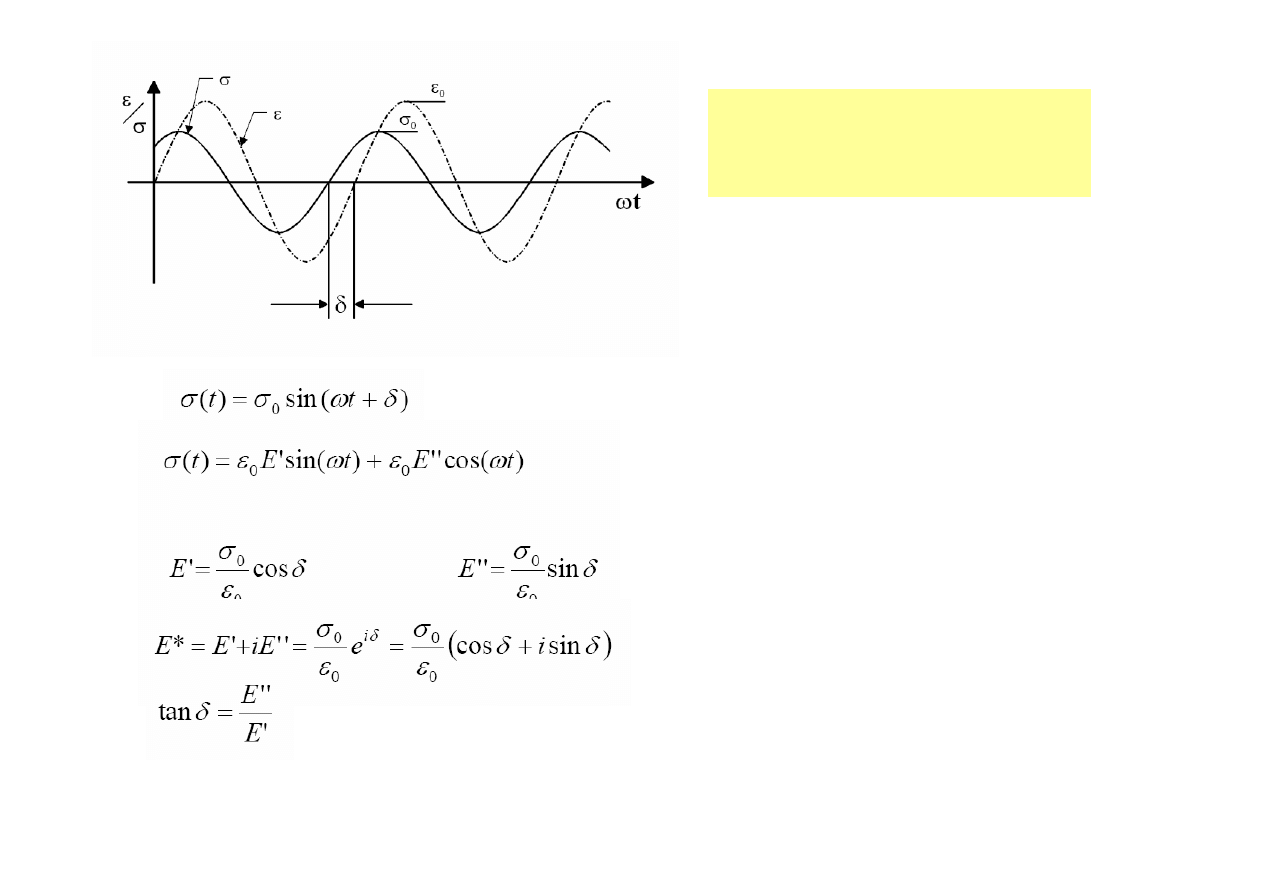
Dynamiczny moduł
sprężystości w badaniach
dynamicznych

Sprzężony moduł dynamiczny obliczany jest ze stosunku :

E* = amplituda naprężenia (b) / amplituda odkształcenia (a)

Moduł ten wyznaczony metodą dynamiczną jest modułem zespolonym:

E*= E’ + E”

złożonym z dwu części,

rzeczywistej E’

(występującej zgodnie z fazą odkształcenia)

urojonej E”

(przesuniętej względem odkształcenia o kąt

π/2).

Moduł części rzeczywistej E’ jest związany z zachowaniem i oddawaniem

energii podczas odkształceń i jest modułem zachowawczym

lub dynamicznym modułem sprężystości.

Moduł części urojonej E” jest modułem stratności lud dynamicznym

modułem lepkości i określa rozproszenie energii podczas odkształcenia.

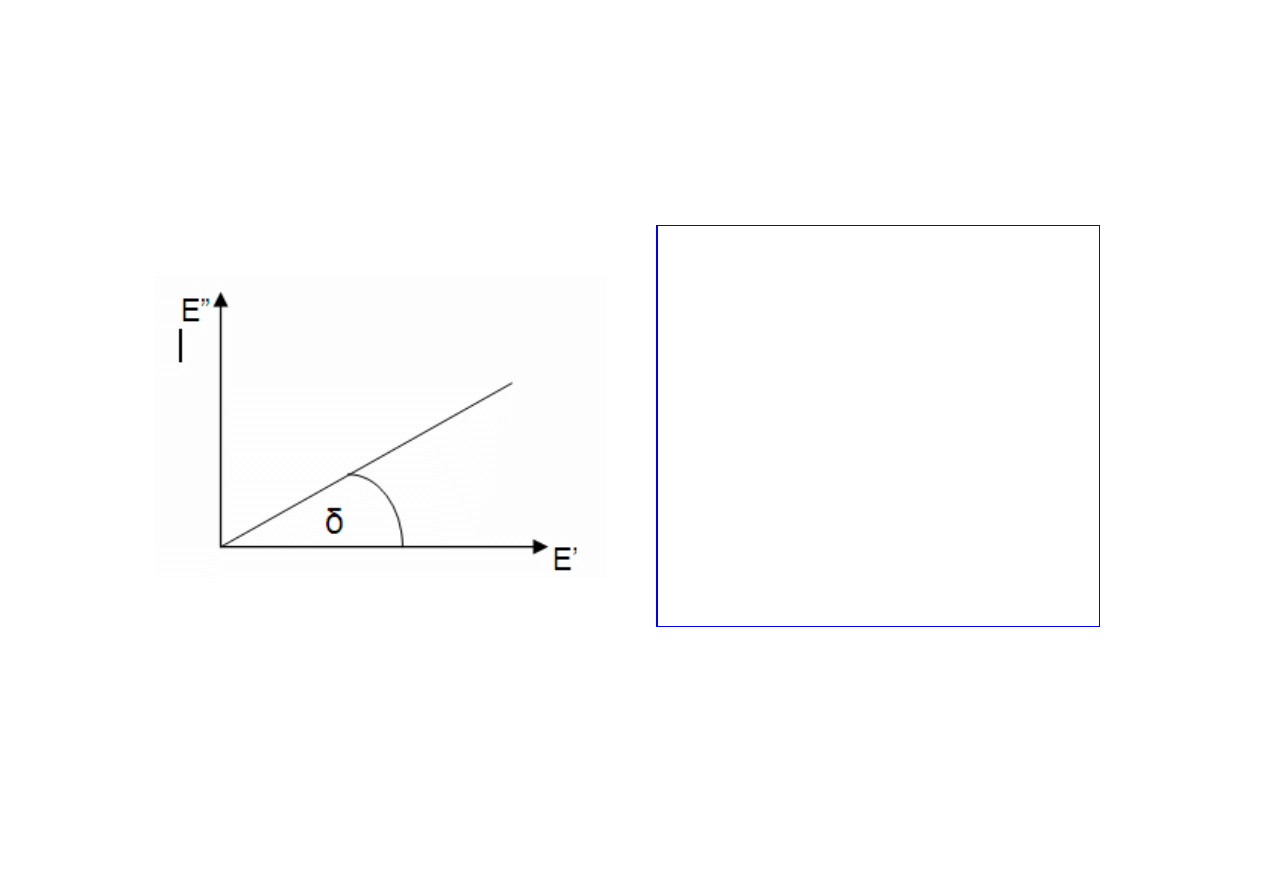
Stosunek E’ do E” odpowiada tangensowi kąta przesunięcia fazowego δ
(współczynnika strat mechanicznych) i wyznaczany jest z diagramu Arganda

W większości przypadków E” jest
mały w porównaniu z E’. E* jest
więc w przybliżeniu równy E’.
Zwykle definiuje się dynamiczne,
mechaniczne zachowanie się
polimeru wyrażeniami: modułem
E~E’ oraz kątem przesunięcia
fazowego δ lub też często tg δ =
E”/E’.
Z dobrym przybliżeniem można
założyć, że δ= tg δ, gdy moduł
strat E” jest mały.

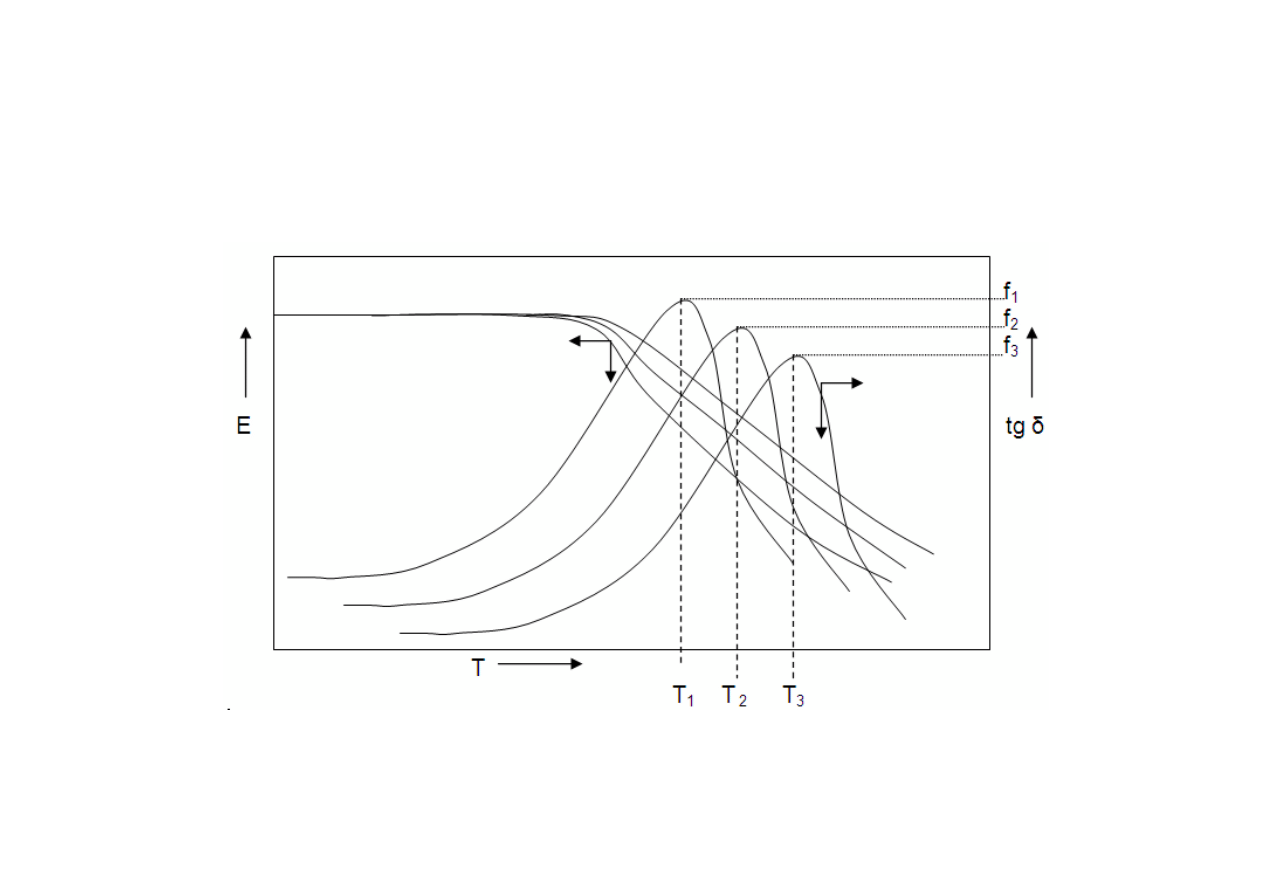
W badaniach DMTA moduł E’ i tg δ mierzone są w zalezności od

temperatury i częstotliwości zmiany odkształcenia.

Mając jako dane rożne częstotliwości i odpowiadające tym
częstotliwościom temperatury w maksimum piku tangensa delta,
można obliczyć energię aktywacji danej przemiany.

Energię aktywacji przemiany wyznacza się korzystając z wykresu
logarytmu częstotliwości w funkcji odwrotności absolutnej temperatury
maksimum piku krzywej tangensa delta (obliczony współczynnik
kierunkowy krzywej odpowiada wartości energii aktywacji),

Dla dwóch częstotliwości wartość energii aktywacji określa równanie:

E

akt

= R log ( f2 -f1 ) / ( 1/T1 – 1/ T2 )

ENERGIA AKTYWACJI

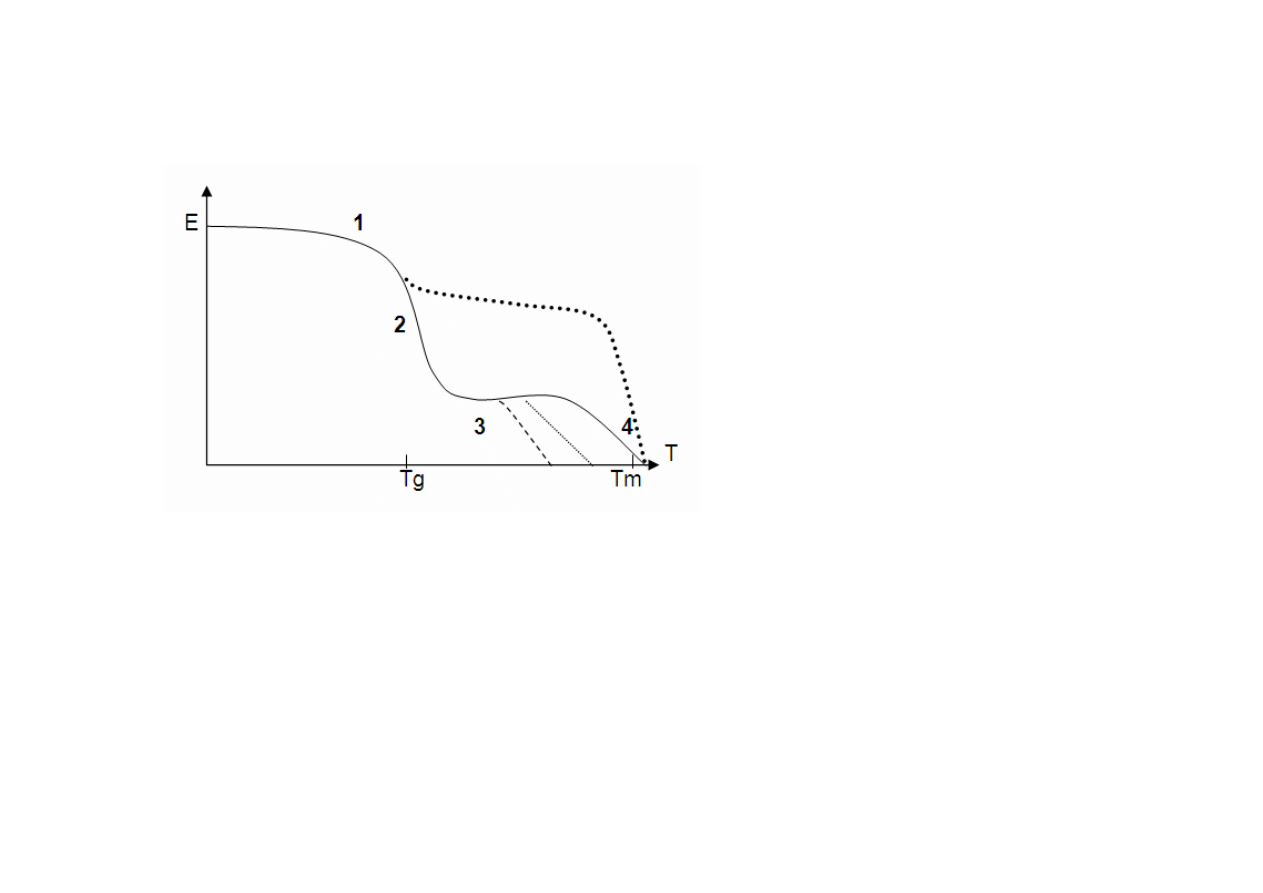
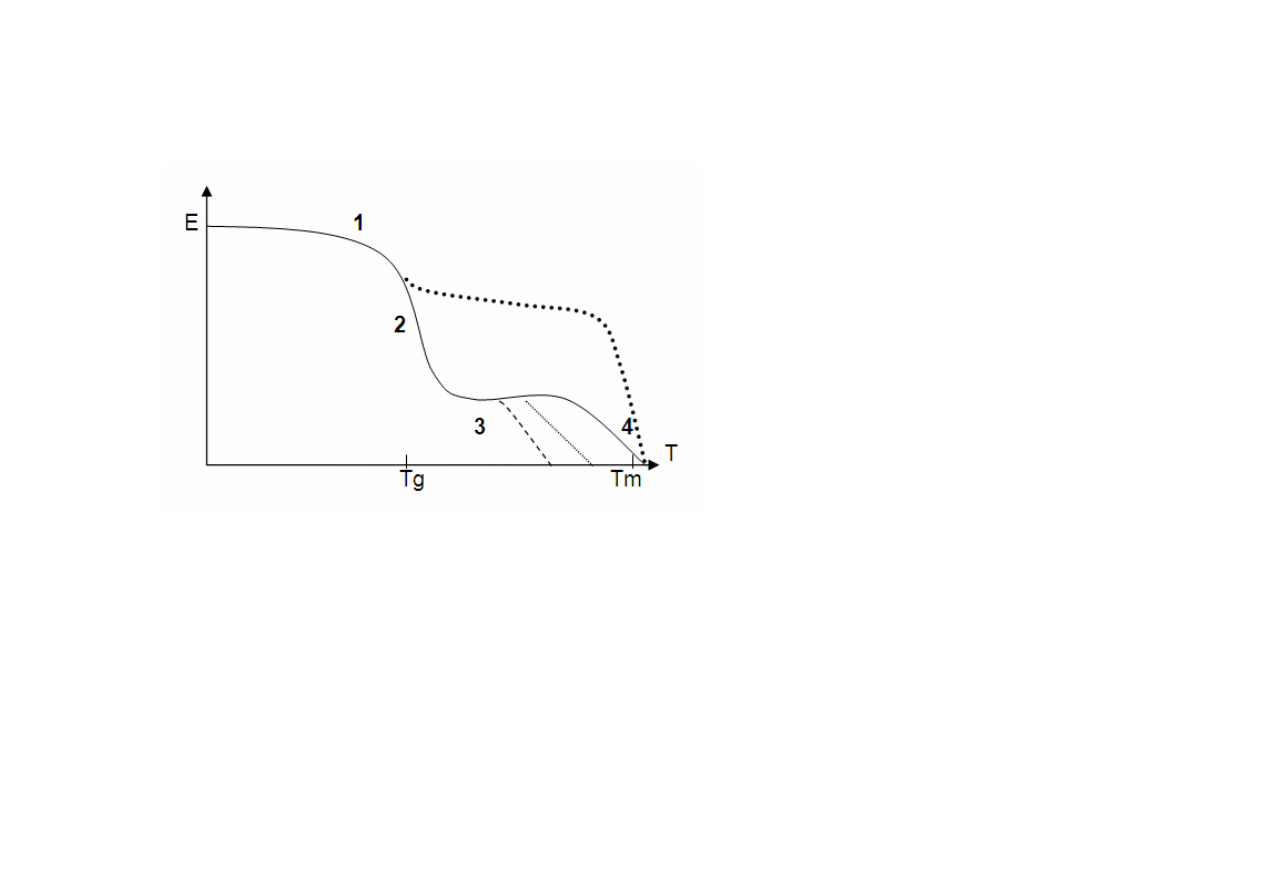
ZALEŻNOŚĆ MODUŁU OD TEMPERATURY PODCZAS BADAŃ
METODĄ DMTA.

1-obszar ten określa zakres temperatury, w którym polimer jest w stanie
szklistym. Polimer w tym obszarze jest materiałem kruchym i sztywnym.
Polimer amorficzny ma w tym zakresie cechy szkliwa lub przechłodzonej
cieczy. Każda makrocząsteczka jest uwięziona w sztywnej matrycy
utworzonej przez inne cząsteczki – jest unieruchomiona. Podobnie jak w
ciele stałym, krystalicznym ruchy termiczne atomów lub fragmentów
cząsteczek ograniczają się do drgań. Amplituda i wielkość drgającego
fragmentu cząsteczki zależą od temperatury.

ZALEŻNOŚĆ MODUŁU OD TEMPERATURY PODCZAS BADAŃ
METODĄ DMTA.

2-obszar ten odpowiada przemianie polimeru ze stanu szklistego w stan
lepkosprężysty. Przemiana ta jest określana jako przejście szkliste. W
badaniach DMTA przyjmuje się, że punkt najszybszego zmniejszania się
modułu przypada na temperaturę przejścia szklistego Tg.
W obszarze przejścia szklistego polimer staje się elastyczny, choć
zachowuje jeszcze pewną twardość i stabilność wymiarów.

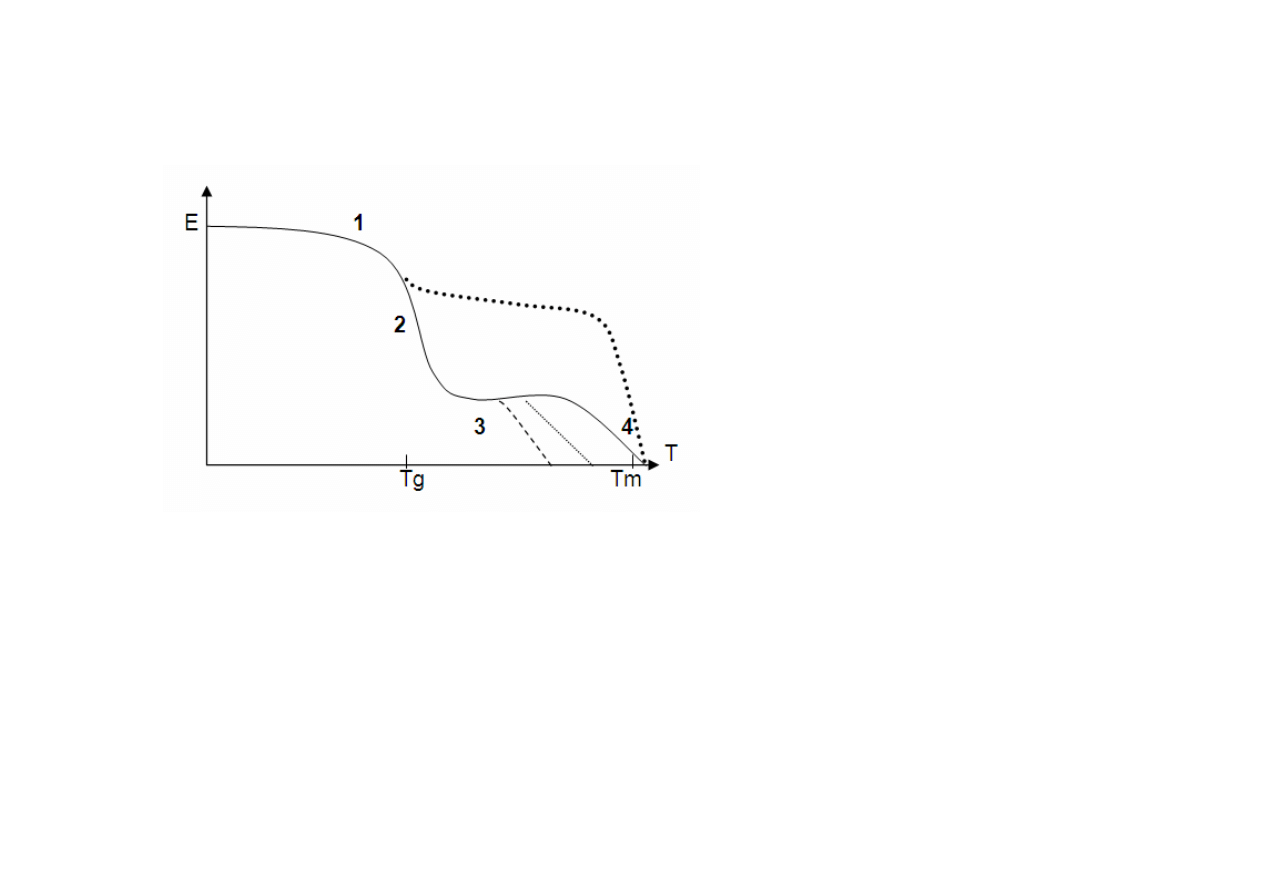
ZALEŻNOŚĆ MODUŁU OD TEMPERATURY PODCZAS BADAŃ
METODĄ DMTA.

3-w temperaturze odpowiadającej temu położeniu rozpoczyna się tzw.
plateau elastyczności kauczukowej.
Zakres temperatury obszaru elastyczności kauczukowej zależy od
rodzaju i stopnia usieciowania polimeru.

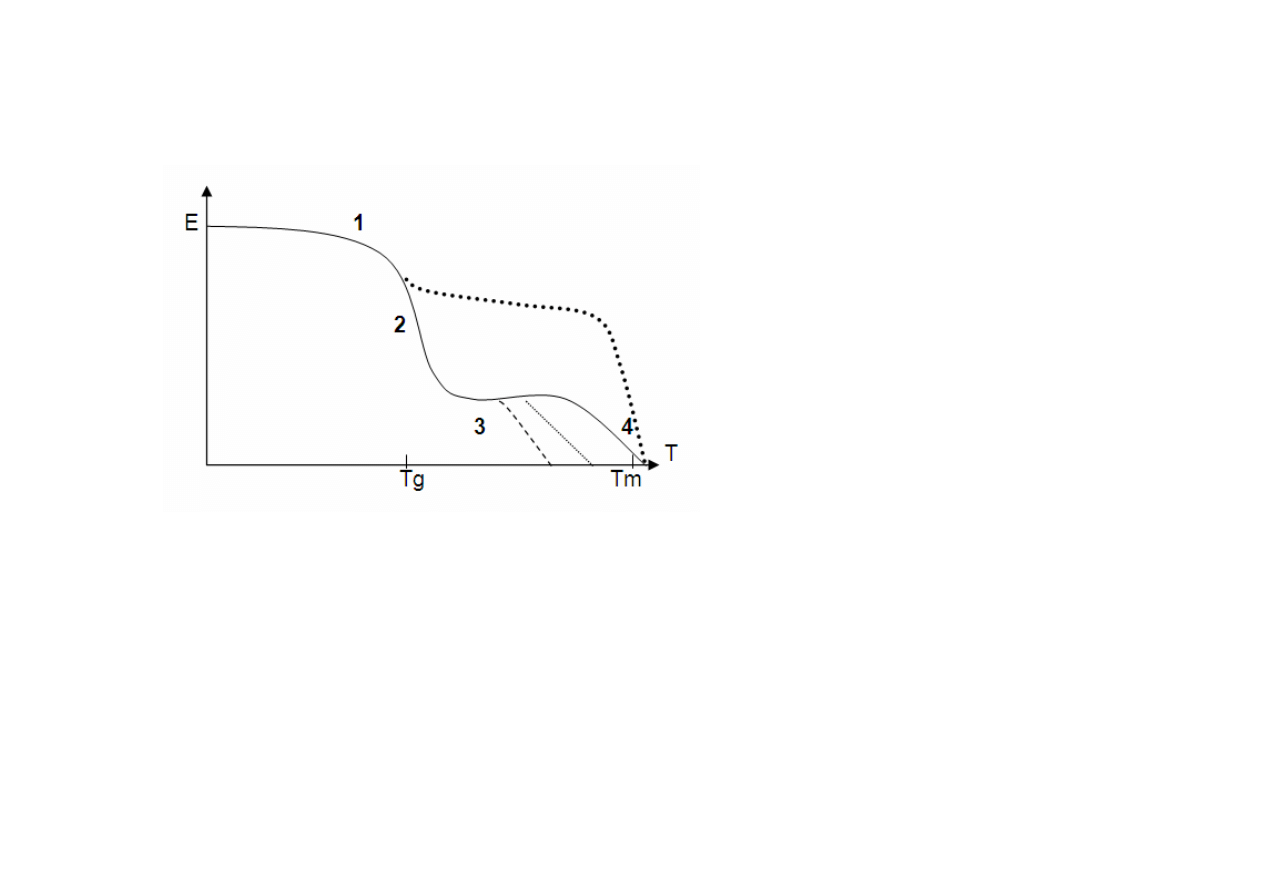
ZALEŻNOŚĆ MODUŁU OD TEMPERATURY PODCZAS BADAŃ
METODĄ DMTA.

4- punkt ten określa zapoczątkowanie przejścia ze stanu dużej
elastyczności w stan elastoplastyczny, oznaczany jako Tm (temperatura
mięknięcia).
Pod niewielkim obciążeniem polimer płynie, ma więc cechy lepkiej cieczy.
W stanie elastoplastycznym przetwarza się większość polimerów
termoplastycznych.

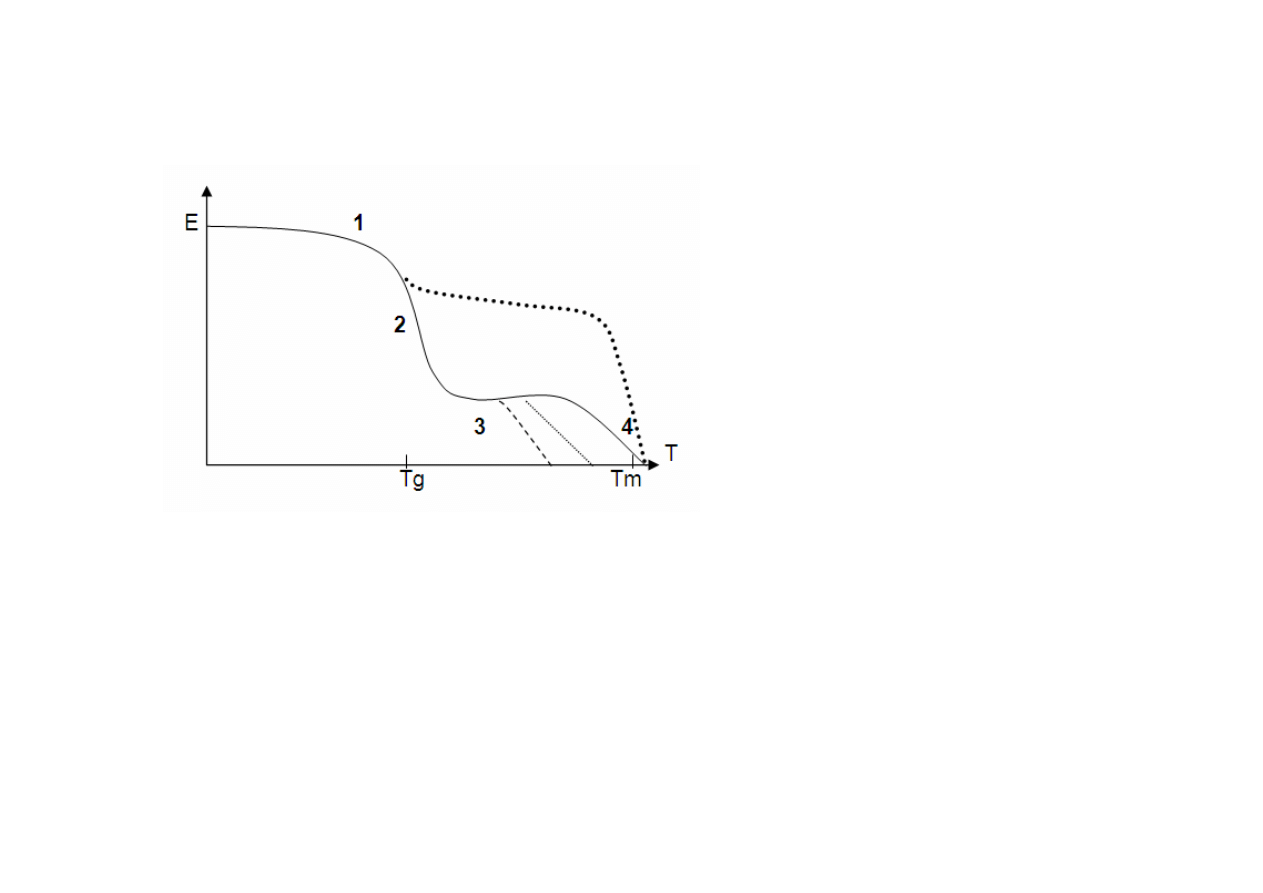
ZALEŻNOŚĆ MODUŁU OD TEMPERATURY PODCZAS BADAŃ
METODĄ DMTA.

Linia kropkowana na przedstawia z kolei zależność moduł-temperatura
dla polimeru częściowo krystalicznego, w odniesieniu do którego
obserwuje się mniejszy spadek modułu podczas przejścia szklistego.
Zakres zmiany modułu zależy w tym przypadku od zawartości fazy
krystalicznej polimeru. Obserwuje się natomiast duży spadek modułu
występujący w temperaturze topnienia krystalitów Tm.
Linie przerywane odnoszą się do polimerów o różnej masie
cząsteczkowej. Im mniejsza jest masa cząsteczkowa tworzywa, tym jest
krótsze plateau obszaru elastyczności kauczukowej.

TEMPERATURA ZESZKLENIA POLIMERÓW AMORFICZNYCH

W polimerach amorficznych w stanie lepkosprężystym są możliwe jedynie
ruchy cieplne segmentów łańcucha oraz swobodnych końców łańcuchów, a nie
całych makrocząsteczek. Ze zwiększeniem się ciężaru cząsteczkowego
zmniejsza się udział swobodnych końców łańcucha, których ruchliwość w
istotny sposób wpływa na wartość temperatury zeszklenia. Struktura głównego
łańcucha także może mieć wpływ na wartość Tg. Występowanie grup
ułatwiających zmiany konformacji, np. zawierających wiązanie eterowe,
najczęściej obniża temperaturę

przemiany zeszklenia, podczas gdy

wprowadzanie grup usztywniających łańcuch główny podwyższa wartość
temperatury zeszklenia.

Analiza wpływu grup bocznych wykazuje, iż wzrost ich długości obniża

temperaturę przejścia szklistego. Jest to zrozumiałe jako wzrost objętości
swobodnej w danej temperaturze.

Chemiczne wiązania sieciujące podwyższają temperaturę zeszklenia oraz
rozszerzają obszar przemiany. W tworzywach bardzo wysoko usieciowanych
temperatura Tg nie występuje.

TEMPERATURA ZESZKLENIA POLIMERÓW AMORFICZNYCH

Przemiany relaksacyjne w polimerach amorficznych zwykle oznacza się w
alfabetycznym porządku α, β, γ, δ, .. z obniżającą się temperaturą.

Relaksacja α, w temperaturze, jest przemianą zeszklenia i sprzężona jest
podczas analizy DMTA z dużymi zmianami modułu.
Relaksacja β związana jest najczęściej z ruchami łańcuchów bocznych grup
estrowych.
Natomiast relaksacje γ i δ obejmują ruchy grup metylowych, przyłączonych do
głównego albo bocznego łańcucha. Dodatkowo relaksacja γ powstaje na
zasadzie mechanizmu korbowego.
Mechanizm ten polega na równoczesnych obrotach ogniw wokół dwóch
wiązań, to jest pierwszego i siódmego, grup -CH2- w liniowej części łańcucha.

POLIMERY KRYSTALICZNE

Polimery krystaliczne są to polimery o regularnej, liniowej budowie
łańcucha lub zawierające grupy silnie polarne, które tworzą struktury
trójwymiarowe, uporządkowane na poziomie wymiarów atomów.
Te uporządkowania struktury powstają na skutek ruchów termicznych i
oddziaływań międzycząsteczkowych chaotycznie skłębionych łańcuchów
polimerów, ale nie w całej jego masie, lecz w pewnych obszarach.
Tak więc polimery krystaliczne zawierają obszary uporządkowane –
krystaliczne oraz obszary bezpostaciowe – amorficzne.
Te polimery, w których udział fazy krystalicznej jest mały są nazywane
polimerami semikrystalicznymi.
Polimery krystaliczne, oprócz temperatury zeszklenia odpowiadającej fazie
amorficznej, mają wyraźnie zaznaczoną temperaturę topnienia obszarów
krystalicznych Tt. Podczas ogrzewania zmniejsza się stopień
krystaliczności polimerów, gdyż część fazy krystalicznej przemienia się w
fazę bezpostaciową.
W badaniach DMTA ze zwiększeniem się stopnia krystaliczności zmienia
się charakter zależności modułu zespolonego od temperatury.

POLIMERY KRYSTALICZNE

W polimerach krystalicznych wyróżnia się następujące relaksacje:

Relaksacje, które występują w fazie amorficznej, będą obejmowały

przemianę zeszklenia, są to najczęściej relaksacje α, rzadziej γ.

Relaksacje β, które zachodzą w fazie krystalicznej, mogą być dwu

rodzajów:

zawierające współdziałające ruchy łańcuchów wzdłuż długości krystalitu;
sprzężone z takimi defektami struktury, jak grupy końcowe w krysztale –

takie relaksacje mogą również obejmować ruchy łańcuchów.

Relaksacje, które występują zarówno w fazie krystalicznej jak i

amorficznej, z pewnymi, szczegółowymi różnicami, w zależności od
fazy, którą obejmują, będą zawierały ruchy ograniczonych długości
łańcucha głównego, bądź grup bocznych. Są to najczęściej relaksacje
typu γ.

Relaksacje związane z różnymi energiami aktywacji, lub związane ze

słabym ruchem fałdy łańcucha głównego. Do tego typu relaksacji
zaliczane są relaksacje α’.

MIESZANINY I KOPOLIMERY

Mieszalność pomiędzy dwoma polimerami, w fazie amorficznej, jest
określona przez obecność pojedynczej temperatury zeszklenia (Tg),
pośredniej pomiędzy temperaturami zeszklenia poszczególnych składników
mieszaniny polimerowej.
Niemieszalność dwóch polimerów określona jest przez wystąpienie dwóch
odrębnych temperatur zeszklenia dla poszczególnych składników. Należy
tu jednak zaznaczyć, że częściowo mieszalne układy również wykazują
dwie odrębne temperatury zeszklenia, ale obniża się różnica temperatur
zeszklenia pomiędzy nimi, w stosunku do różnicy temperatur zeszklenia
czystych składników.
Analiza termiczna dynamicznych właściwości mechanicznych pozwala
także na określenie morfologii domen (matryca, wtrącenia, spójność
bardziej sztywnej fazy). Ponadto przy pomocy DMTA w pewnych
przypadkach można wykryć fazę pośrednią.

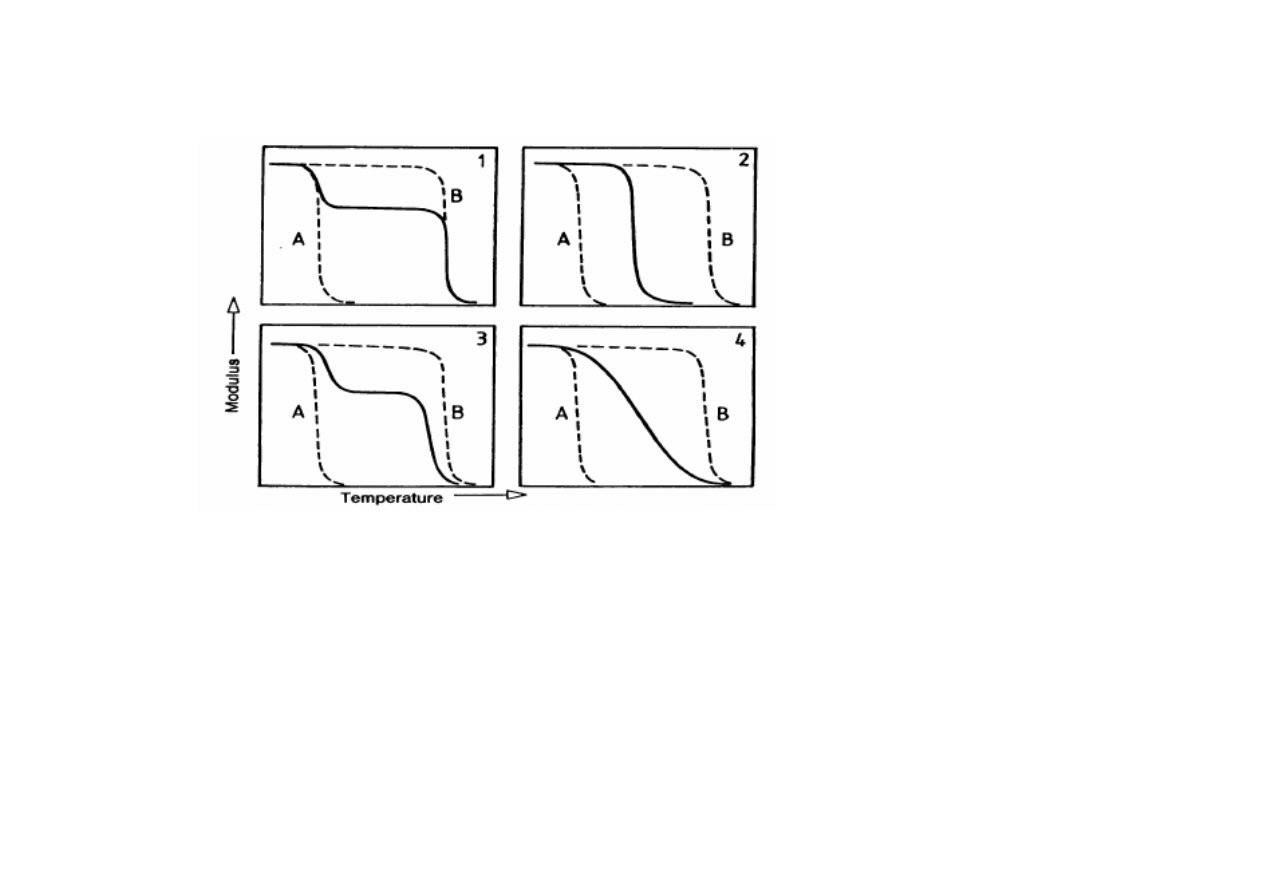
1. Polimery niemieszalne

2. Polimery całkowicie mieszalne

3. Polimery częściowo mieszalne

4. Polimery tworzące układy o złożonych

morfologiach

Rodzaje mieszanin polimerowych według badań DMTA

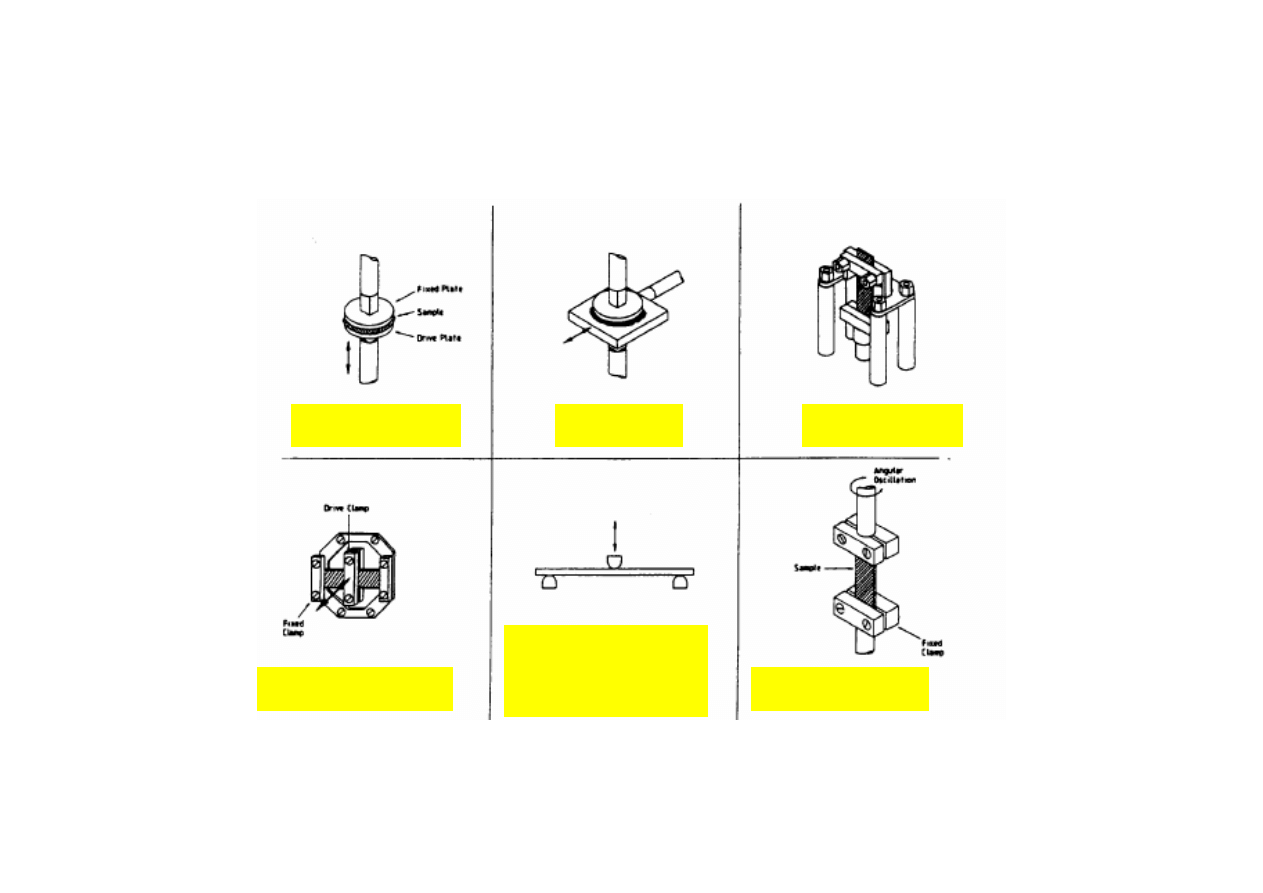
Możliwości prowadzenia badań DMTA

ściskanie

ścinanie

rozciąganie

zginanie

Zginanie

3-punktowe

skręcanie

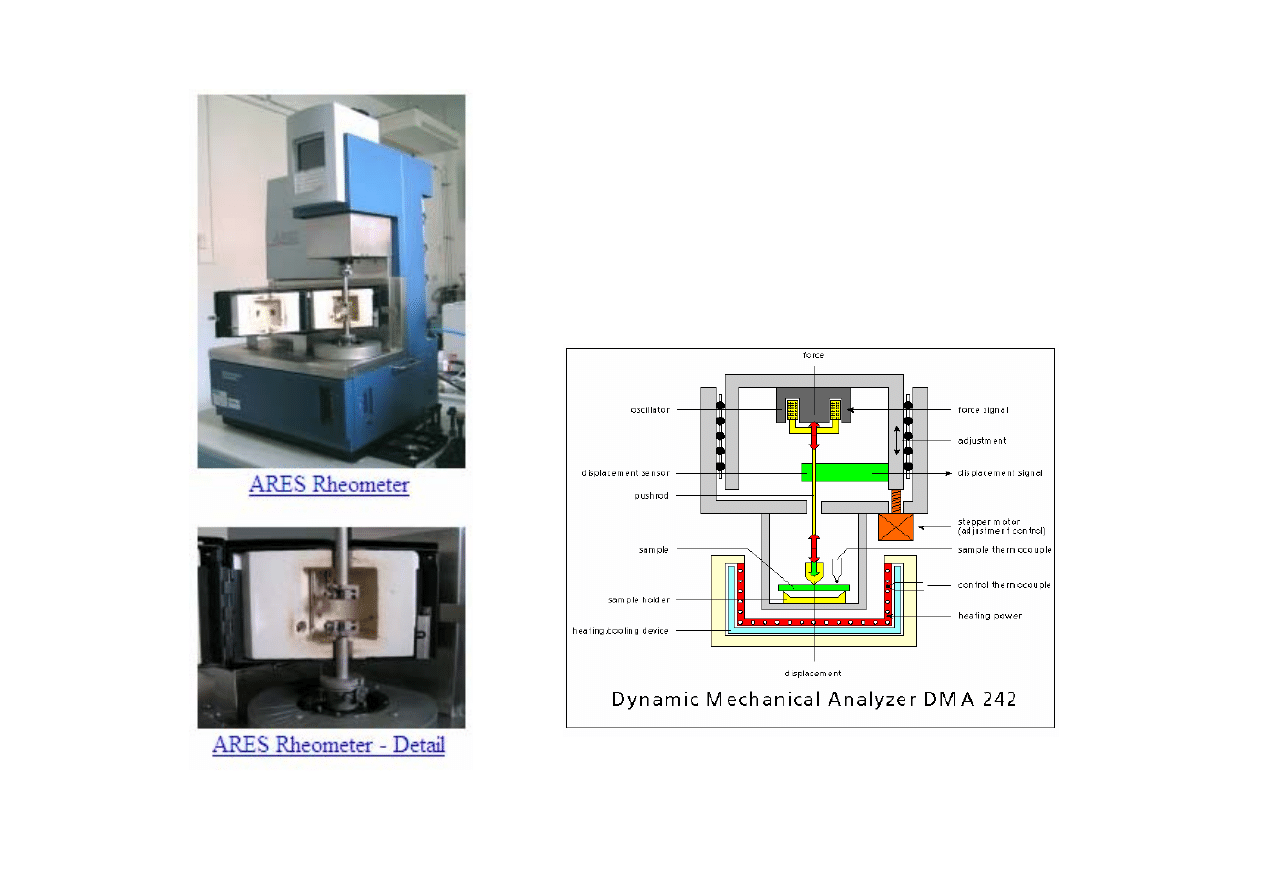
Aparaty do pomiarów DMTA