Zapis i Podstawy Konstrukcji Mechanicznych. Wybrane zagadnienia wytrzymałości materiałów

Opracowali: J. Felis, H. Jaworowski str. 1

Przyczyna
Siły zewnętrzne
działające na ciało
odkształcalne

Skutek pierwotny
Powstanie sił
wewnętrznych w
elemencie (naprężeń)

Temat: WYBRANE ZAGADNIENIA WYTRZYMAŁOŚCI MATERIAŁÓW

Wprowadzenie

Wytrzymałość materiałów (stereomechanika techniczna) jest nauką o metodach
obliczeń i projektowania konstrukcji odkształcalnych.
Do problemów wytrzymałości należy ustalanie zależności między siłami działającymi na
ciało odkształcalne (przyczynami) a odkształceniami tego ciała (skutkami).
Efektem obliczeń jest taki dobór materiałów i wymiarów poszczególnych elementów
konstrukcji, aby były zdolne do przeniesienia działających na nie obciążeń zewnętrznych z
dostatecznym zapasem bezpieczeństwa

.

Związek przyczynowo-skutkowy między siłami zewnętrznymi, wewnętrznymi
i odkształceniami

WYZNACZANIE SIŁ WEWNĘTRZNYCH (NAPRĘŻEŃ)
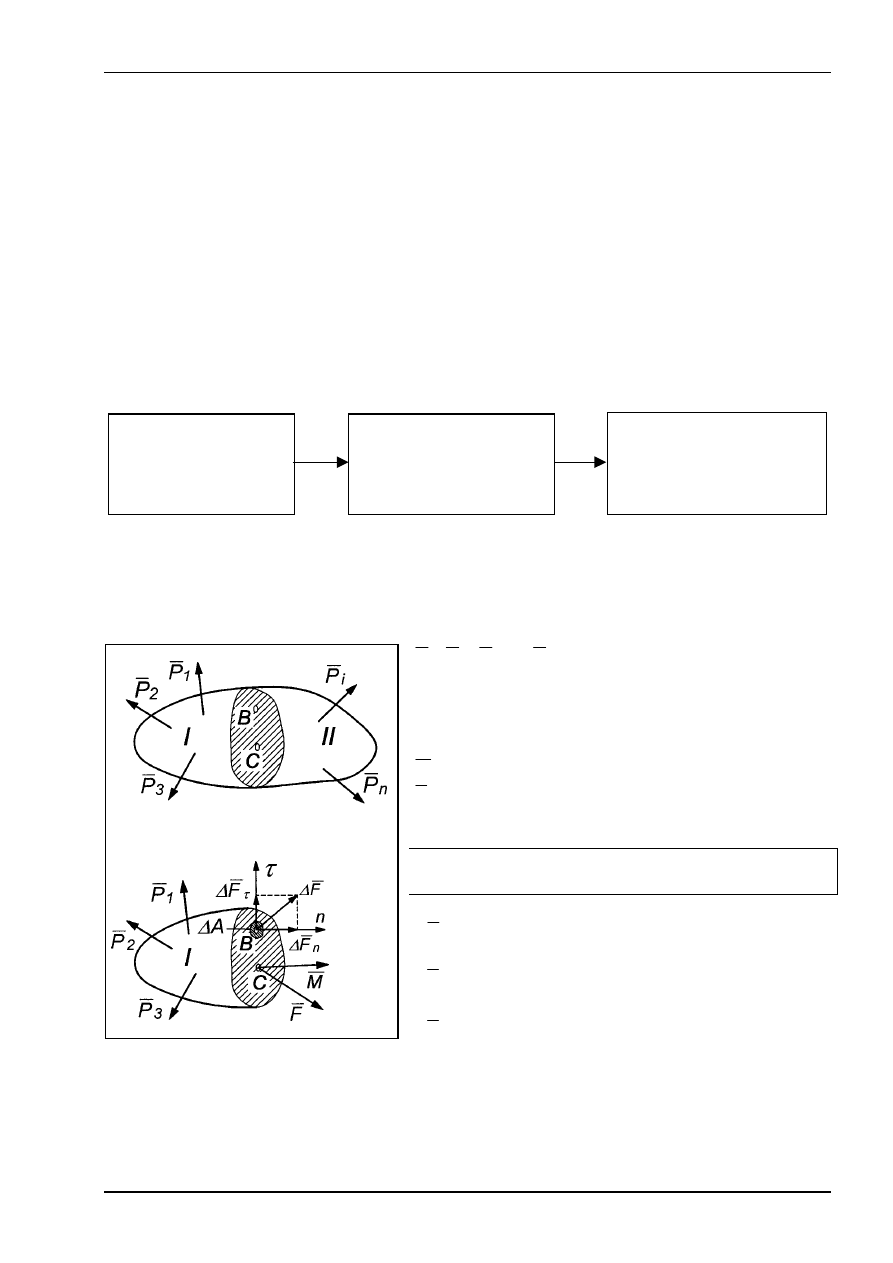
Wyznaczanie sił wewnętrznych można przeprowadzić po przecięciu ciała i odrzuceniu
jednego z elementów. Zachodzi wówczas równowaga układów sił zewnętrznych i sił
wewnętrznych działających na analizowane elementy.

P

,...,

P

,

P

,

P

n

3

2

1

- obciążenie zewnętrzne

C – biegun redukcji sił wewnętrznych
B – dowolny punkt

A – całkowita powierzchnia przekroju

M

- moment główny sił wewnętrznych

F - wektor główny sił wewnętrznych

Twierdzenie:
Siły zewnętrzne są w równowadze z siłami
wewnętrznymi działającymi na element I

A

∆

- element powierzchni, zawierający punkt B

F

∆

– elementarna siła działająca na powierzchnię

A

∆

n

F

∆

– składowa normalna elementarnej siły

wewnętrznej

τ

∆

F – składowa styczna elementarnej siły
wewnętrznej

Rys. 1

Skutek wtórny
Powstanie odkształceń
(zmian geometrycznych
elementu)

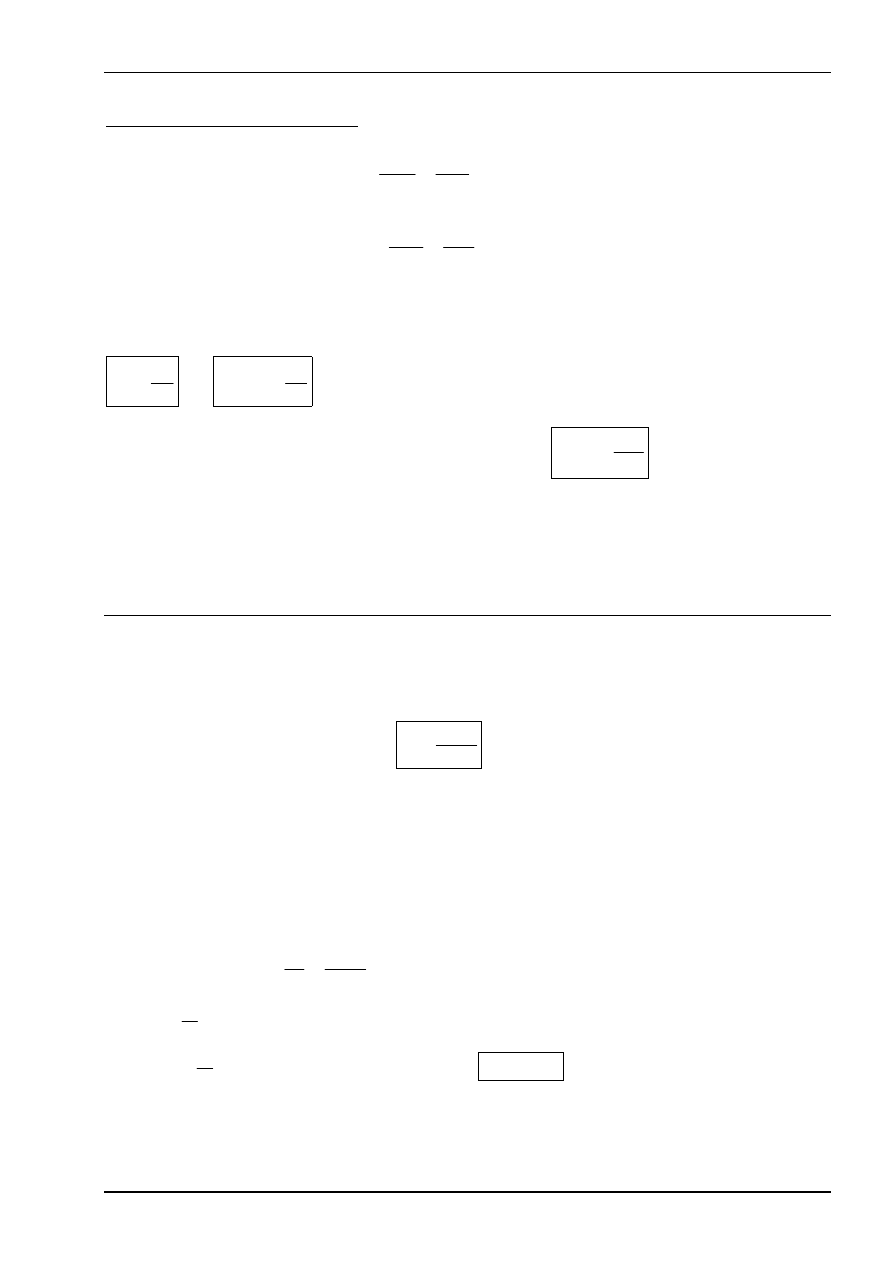
Zapis i Podstawy Konstrukcji Mechanicznych. Wybrane zagadnienia wytrzymałości materiałów

Opracowali: J. Felis, H. Jaworowski str. 2

Definicje naprężeń w punkcie

Naprężenie normalne:

dA

dF

A

F

lim

n

n

0

A

n

=

=

→

∆

∆

σ

∆

Naprężenie styczne:

dA

dF

A

F

lim

0

A

τ

τ

∆

τ

∆

∆

τ

σ

=

=

=

→

Jeżeli rozkład elementarnych sił wewnętrznych jest równomierny, naprężenia liczymy ze
wzorów:

A

F

n

n

=

σ

A

F

τ

τ

τ

σ

=

=

Jednostką naprężenia w układzie SI jest pascal (Pa):

2

m

N

1

Pa

1

=

Stosuje się również jednostki:

Pa

10

81

,

9

mm

/

KG

1

Pa

10

81

,

9

cm

/

KG

1

Pa

10

m

/

N

10

MPa

1

6

2

4

2

6

2

6

⋅

=

⋅

=

=

=

Zależność pomiędzy naprężeniami i odkształceniami dla jednoosiowego rozciągania

PRAWO HOOKE’A. Materiały pod wpływem obciążeń wydłużają się lub skracają
proporcjonalnie do działającej siły o ile wartość siły nie przekroczy pewnej granicy (granicy
proporcjonalności).

Prawo Hooke’a wyraża się wzorem:

A

E

l

P

l

o

⋅

⋅

=

∆

gdzie: l

∆

- wydłużenie pręta [m],

P

- wartość działającej siły [N],

l

o

- początkowa długość pręta [m] (przed wydłużeniem),

A

- pole przekroju poprzecznego [m

2

],

E - moduł sprężystości wzdłużnej materiału (moduł Younga), wielkość stała dla

danego materiału [MPa].

Jeżeli zapiszemy:

l

l

l

l

l

0

0

0

−

=

= ∆

ε

- wydłużenie jednostkowe,

oraz

A

P

=

σ

- naprężenia normalne

wtedy:

E

σ

ε =

Można też zapisać:

ε

σ

⋅

=

E

Zapis i Podstawy Konstrukcji Mechanicznych. Wybrane zagadnienia wytrzymałości materiałów

Opracowali: J. Felis, H. Jaworowski str. 3

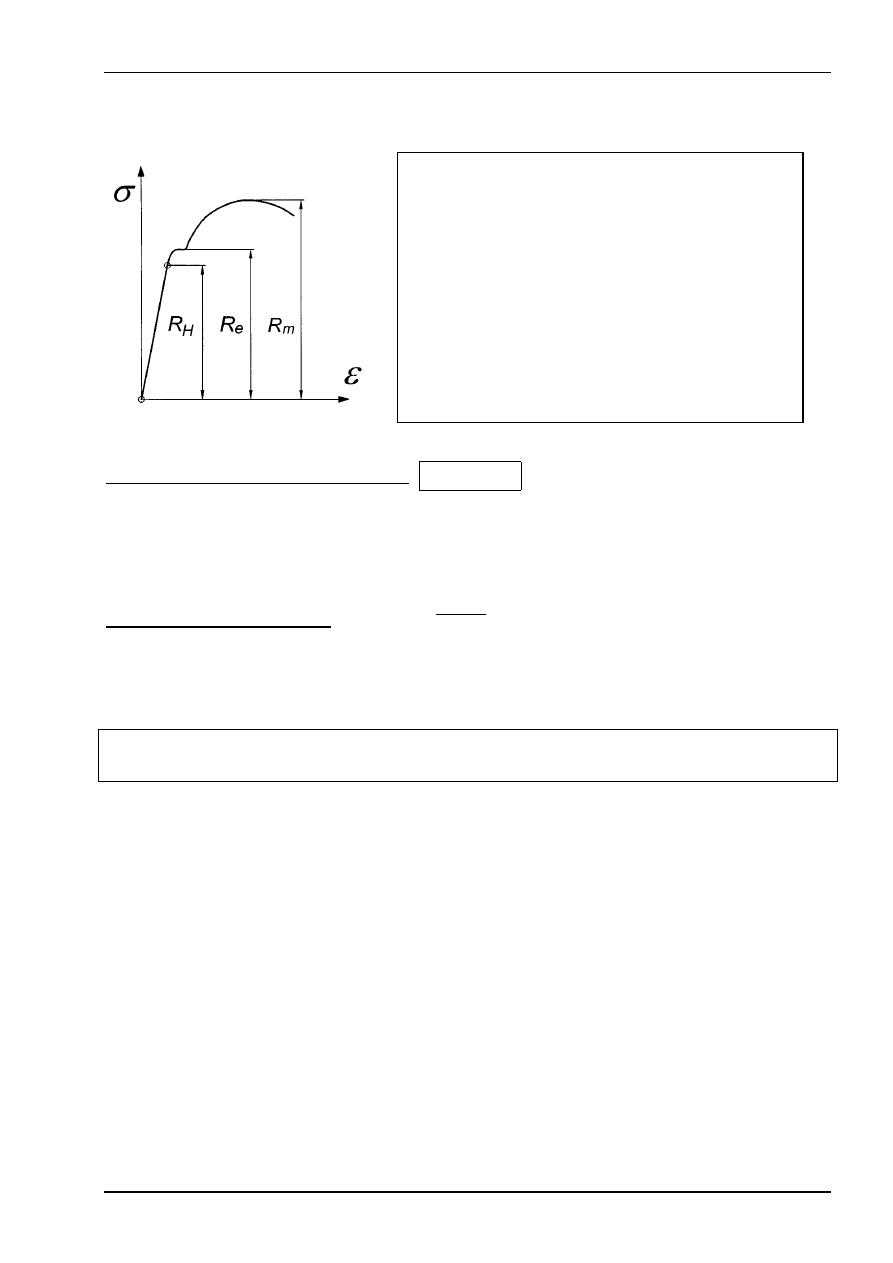
Dobrą ilustracją prawa Hooke’a jest wykres rozciągania próbki stalowej w zakresie granicy
proporcjonalności R

H

Rys. 2

Ogólny warunek wytrzymałościowy

σ

σ

dop

red

≤

gdzie:

σ

red

- naprężenie zastępcze w danym punkcie wyznaczone na podstawie odpowiedniej

hipotezy wytężenia,

σ

dop

- naprężenie dopuszczalne dla danego materiału i danego stanu naprężenia.

Naprężenie dopuszczalne

x

nieb

dop

σ

σ

=

gdzie:

σ

nieb

- naprężenie niebezpieczne dla danego materiału,

x – współczynnik bezpieczeństwa , x>1

Współczynnik bezpieczeństwa określony ze względu na

R

e

oznacza sie symbolem

x

e

,

jeżeli natomiast określony jest ze względu na

R

m

oznacza się symbolem

x

m

.

TYPOWE PRZYPADKI WYTRZYMAŁOŚCIOWE DLA OBCIĄŻEŃ STATYCZNYCH

I. Wytrzymałość prosta. Obciążenia statyczne

•

rozciąganie i ściskanie

•

ścinanie

•

docisk powierzchniowy

•

skręcanie

•

zginanie,

•

wyboczenie

II. Wytrzymałość złożona. Obciążenia statyczne.

•

zginanie i ściskanie (rozciąganie),

•

zginanie i ścinanie,

•

zginanie i skręcanie.

R

H

– granica proporcjonalności (granica

stosowania prawa Hooke’a),
R

e

– granica plastyczności,

R

m

– wytrzymałość na rozciąganie

Naprężenia określone symbolami R

e

i R

m

są

naprężeniami niebezpiecznymi dla materiału
ponieważ powodują trwałe, bezpowrotne
odkształcenia próbki lub jej zerwanie.
Dlatego też po przyjęciu współczynnika
bezpieczeństwa stanowią podstawę określenia
tzw. naprężeń dopuszczalnych

Zapis i Podstawy Konstrukcji Mechanicznych. Wybrane zagadnienia wytrzymałości materiałów

Opracowali: J. Felis, H. Jaworowski str. 4

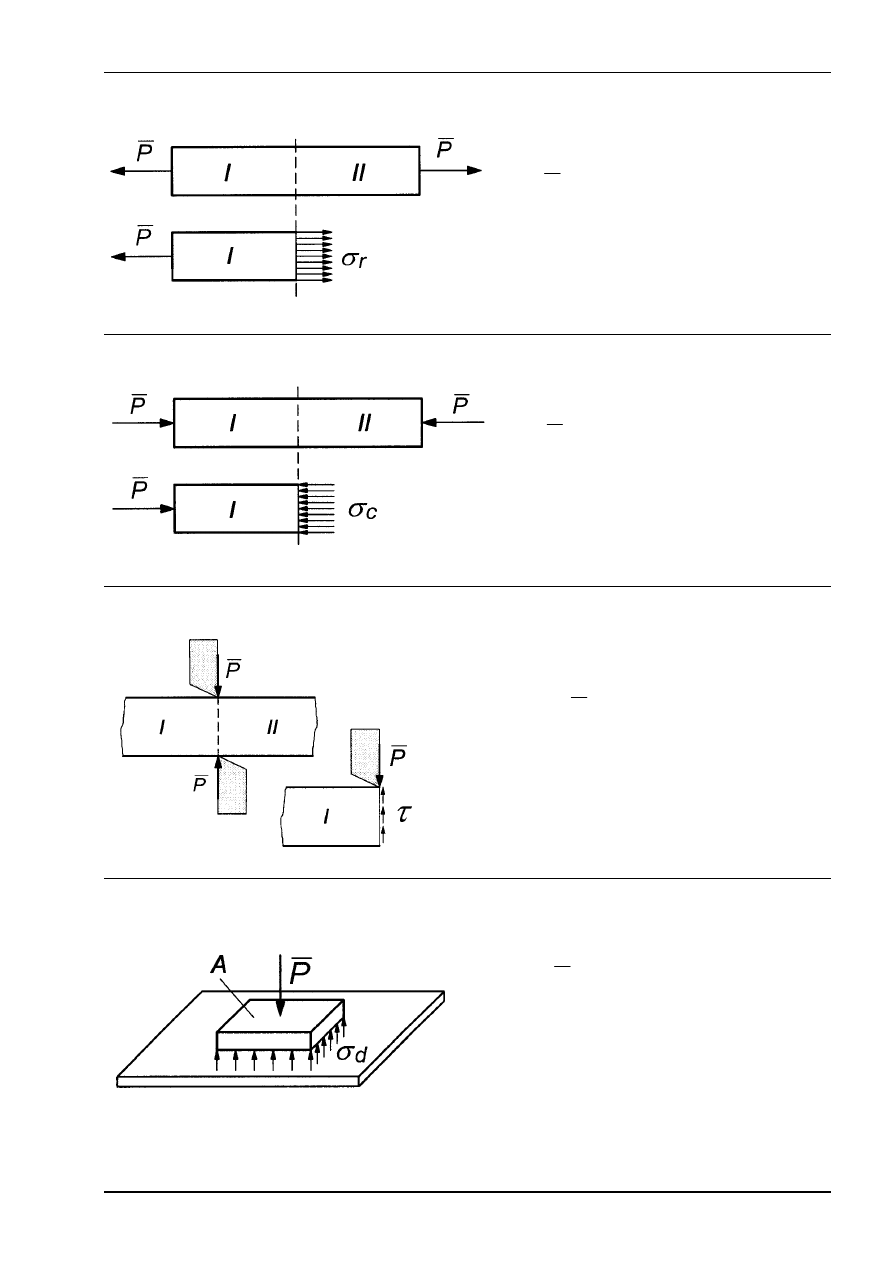
ROZCIĄGANIE

Warunek wytrzymałościowy

k

A

P

r

dop

r

=

≤

=

σ

σ

σ

r

- naprężenia rozciągające

P - osiowa siła rozciągająca

A - przekrój poprzeczny

k

r

dop

=

σ

- naprężenia dopuszczalne

na rozciąganie

Rys. 3

ŚCISKANIE

Warunek wytrzymałościowy

k

A

P

c

dop

c

=

≤

=

σ

σ

σ

c

- naprężenia ściskające

P

- osiowa siła ściskająca

A - przekrój poprzeczny

k

c

dop

=

σ

- naprężenia dopuszczalne

na ściskanie

Rys. 4

ŚCINANIE

Warunek wytrzymałościowy

k

A

P

t

≤

=

=

σ

τ

τ

σ

τ

τ

=

- naprężenia ścinające

P

- siła poprzeczna tnąca

A - przekrój poprzeczny

k

t

- naprężenia dopuszczalne na

ścinanie

Rys. 5

DOCISK POWIERZCHNIOWY

Warunek wytrzymałościowy

k

A

P

d

d

≤

=

σ

σ

d

- naprężenia między dociskanymi

elementami (ciśnienie)

P

- siła docisku

A - umowna powierzchnia docisku

k

d

- naprężenia dopuszczalne na

docisk powierzchniowy
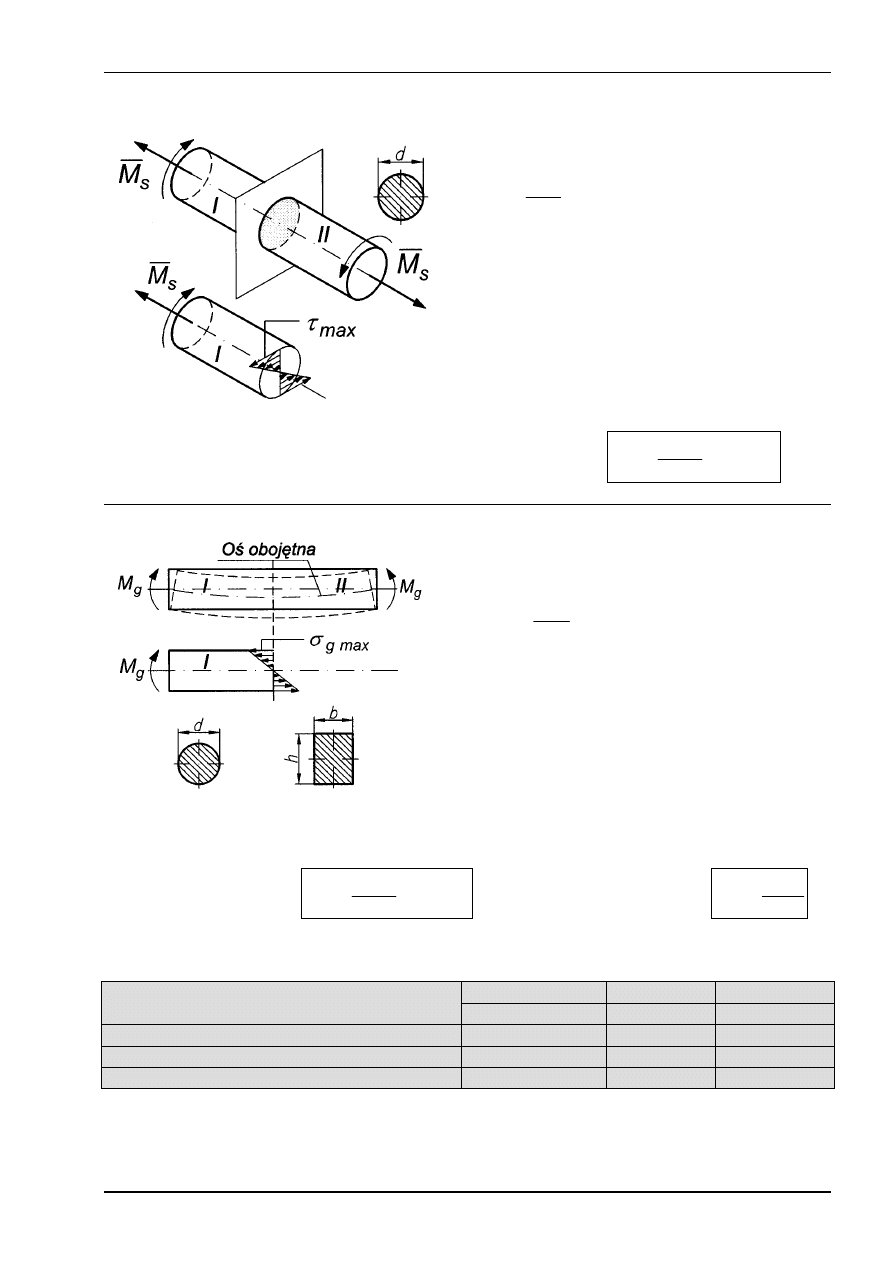
SKRĘCANIE

Rys. 6

Zapis i Podstawy Konstrukcji Mechanicznych. Wybrane zagadnienia wytrzymałości materiałów

Opracowali: J. Felis, H. Jaworowski str. 5

Warunek wytrzymałościowy

k

W

M

s

o

s

max

≤

=

τ

τ

max

- max naprężenie styczne skręcanego

elementu

M

s

- moment skręcający

W

o

- wskaźnik wytrzymałości na skręcanie

k

s

- naprężenia dopuszczalne na skręcanie

Rys. 7

Wskaźnik wytrzymałości na skręcanie dla przekroju kołowego:

d

2

,

0

16

d

W

3

3

o

⋅

≈

⋅

= π

ZGINANIE

Warunek wytrzymałościowy

k

W

M

g

g

g

max

g

≤

=

σ

σ

max

g

- max naprężenie gnące (normalne)

zginanego elementu

M

g

- moment zginający

W

g

- wskaźnik wytrzymałości na zginanie

k

g

- naprężenia dopuszczalne na zginanie

Rys. 8

Wskaźniki wytrzymałości na zginanie wynoszą odpowiednio:

dla przekroju kołowego:

d

1

,

0

32

d

W

3

3

g

⋅

≈

⋅

= π

dla przekroju prostokątnego:

6

h

b

W

2

g

⋅

=

Tabela 1. Orientacyjne wartości naprężeń dopuszczalnych w Mpa

Rozciąganie

Zginanie

Skręcanie

Materiał

k

r

k

g

k

s

Stal węglowa St5

130-150

160-185

78-90

Stal niskostopowa 18G2

148-170

174-200

96-110

Stop aluminium PA6

104-120

113-130

61-70

Uwaga: naprężenia k

r

obliczone zostały dla współ. bezpiecz. x

e

o wartościach 2 i 2,3.

Zapis i Podstawy Konstrukcji Mechanicznych. Wybrane zagadnienia wytrzymałości materiałów

Opracowali: J. Felis, H. Jaworowski str. 6

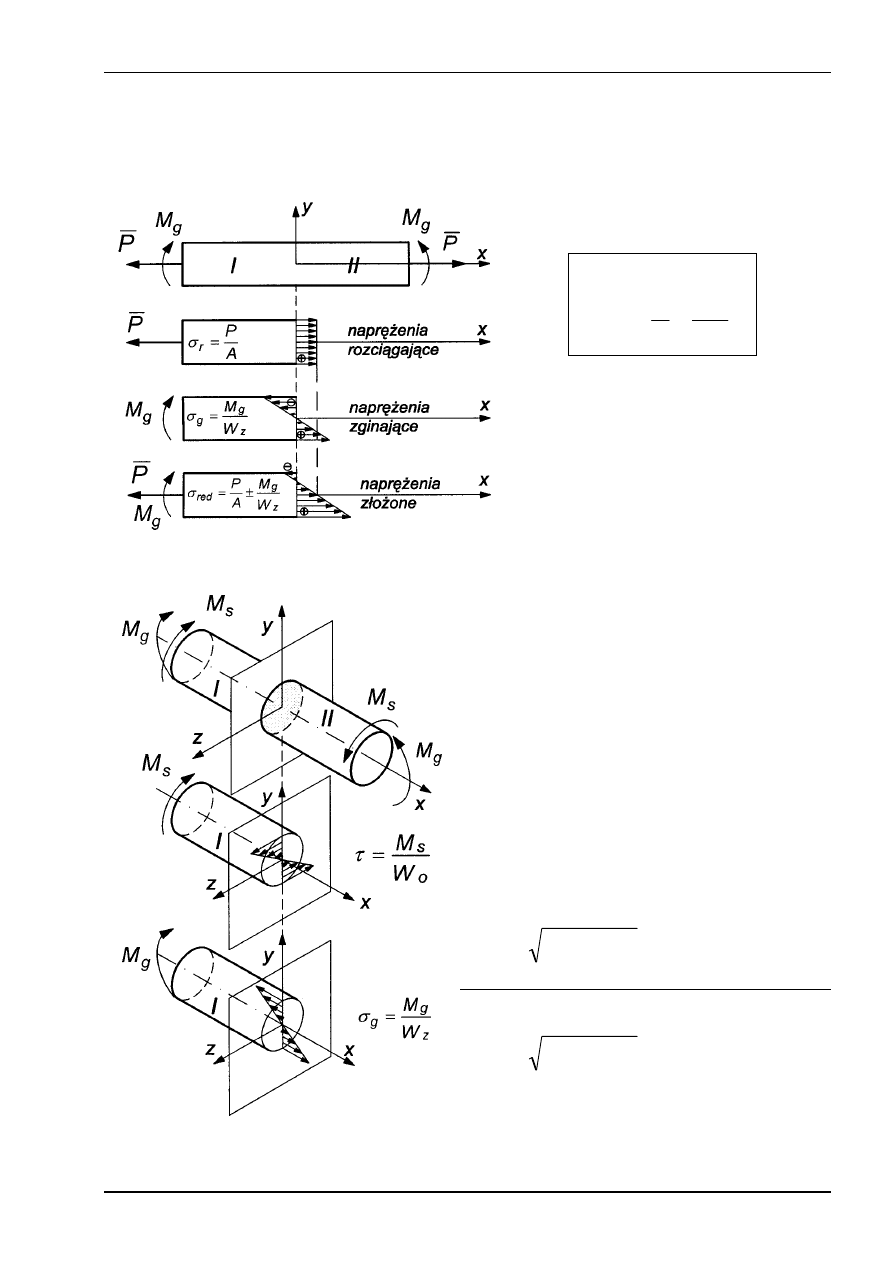
WYTRZYMAŁOŚĆ ZŁOŻONA. OBCIĄŻENIA STATYCZNE.

ZGINANIE I ROZCIĄGANIE, (ŚCISKANIE)

Naprężenia zastępcze:

W

M

A

P

)

(

g

g

red

g

c

r

red

±

±

=

+

=

σ

σ

σ

σ

σ

gdzie:

W

W

z

g

=

- wskaźnik

wytrzymałości na zginanie

)

k

(

k

c

r

red

≤

σ

Rys. 9

ZGINANIE I SKRĘCANIE

W przekroju poprzecznym występuje
równocześnie:
moment zginający: M

g

moment skręcający: M

s

Ponieważ mamy do czynienia ze złożonym
stanem naprężeń, ocenę stopnia wytężenia
materiału należy oprzeć na odpowiedniej
hipotezie wytrzymałościowej.
Dla materiałów plastycznych np. stale
walcowane, kute stopy miedzi i aluminium
naprężenia zredukowane można obliczyć wg
wzorów:

1) hipoteza

τ

max

k

4

r

2

2

g

red

≤

⋅

+

=

τ

σ

σ

2) hipoteza Hubera

k

3

r

2

2

g

red

≤

⋅

+

=

τ

σ

σ

Rys. 10

Zapis i Podstawy Konstrukcji Mechanicznych. Wybrane zagadnienia wytrzymałości materiałów

Opracowali: J. Felis, H. Jaworowski str. 7

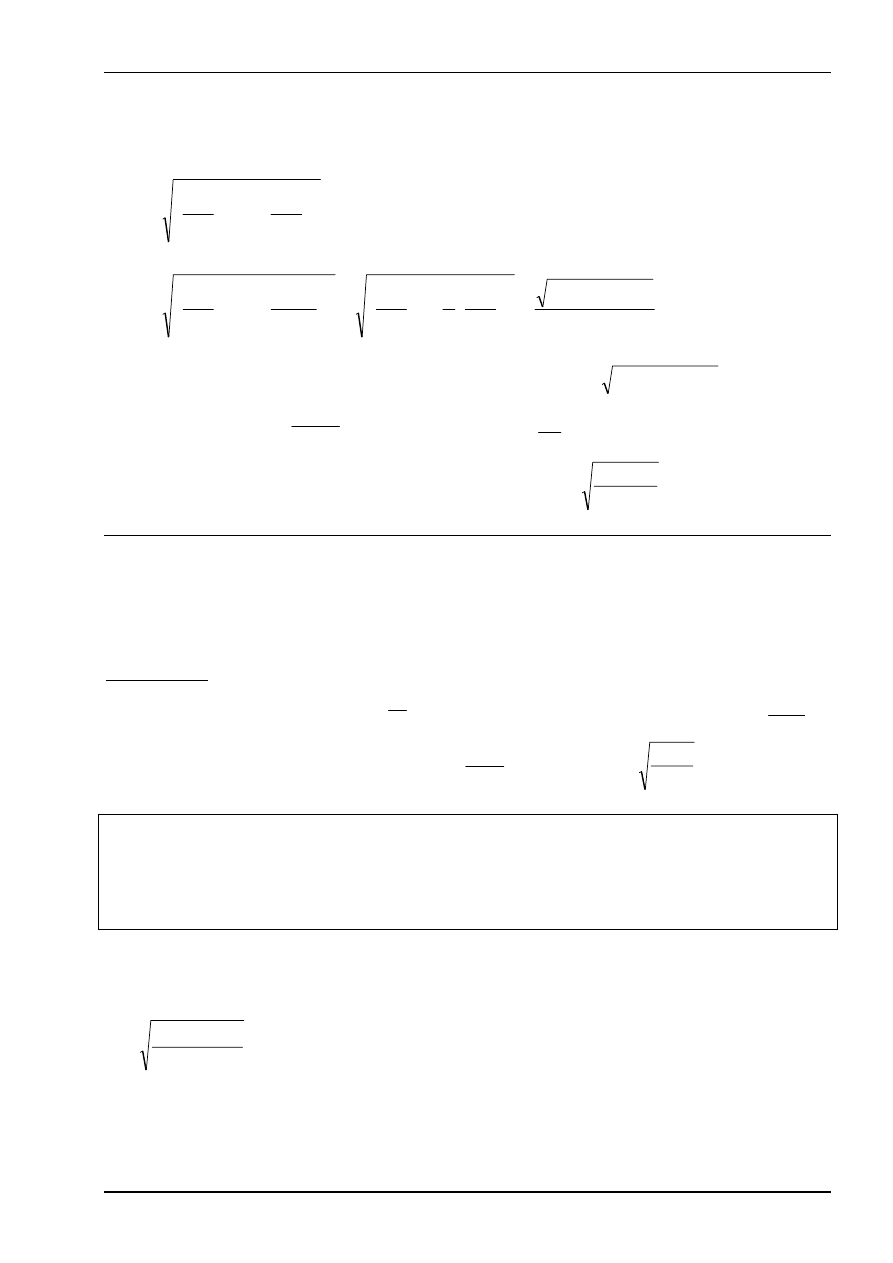
W przypadku zginania ze skręcaniem wzory na naprężenia zredukowane można wyrazić
jako funkcję momentów gnącego M

g

i skręcającego M

s

.

Przy zastosowaniu hipotezy Hubera:

k

W o

Ms

3

W z

Mg

r

2

2

red

≤









+









=

σ

Dla przekroju kołowego zachodzi :

W

2

W

z

o

=

(patrz strona 5), otrzymamy:

k

W

M

75

,

0

M

W z

Ms

4

3

W z

Mg

W

2

z

Ms

3

W z

M g

r

z

2

s

2

g

2

2

2

2

red

≤

+

=









+

















=









⋅

+

















=

σ

po wprowadzeniu pojęcia tzw. momentu zastępczego:

M

75

,

0

M

M

2

s

2

g

red

+

=

, naprężenia

zredukowane:

k

W

M

r

z

red

red

≤

=

σ

, ponieważ

d

32

W

3

z

π

=

,

wymaganą średnicę wału pełnego obliczymy ze wzoru:

3

r

red

k

M

32

d

π

≥

Przykład 1

Obliczyć średnicę pręta rozciąganego sił osiową P=20 kN.
Pręt wykonany jest ze stali St 5.

Rozwiązanie

Warunek wytrzymałościowy:

k

A

P

r

dop

r

=

≤

=

σ

σ

, przekrój pręta wynosi:

4

d

A

2

π

=

Z warunku wytrzymałościowego otrzymamy:

k

d

P

4

r

2

≤

⋅

π

oraz

k

P

4

d

r

⋅

≥

π

Wartość k

r

dla stali St 5 obliczamy na podstawie R

m

lub R

e

zakładając współczynnik

bezpieczeństwa lub przyjmujemy gotowe wartości na podstawie tablic z Poradnika
Mechanika.

R

m

, R

e

- również znajdujemy w tablicach własności mechanicznych materiałów

w Poradniku Mechanika.

Przyjmując do obliczeń dolną wartość k

r

=130 MPa ( Tabl. 1 str. 5), obliczymy wymaganą

średnice rozciąganego pręta.

mm

14

m

014

,

0

01399

,

0

10

130

10

20

4

d

6

3

=

≅

=

⋅

⋅

⋅

⋅

≥

π

Do wykonania konstrukcji można przyjąć pręt o średnicy 14 mm lub większej z tablic
wyrobów hutniczych.

Zapis i Podstawy Konstrukcji Mechanicznych. Wybrane zagadnienia wytrzymałości materiałów

Opracowali: J. Felis, H. Jaworowski str. 8

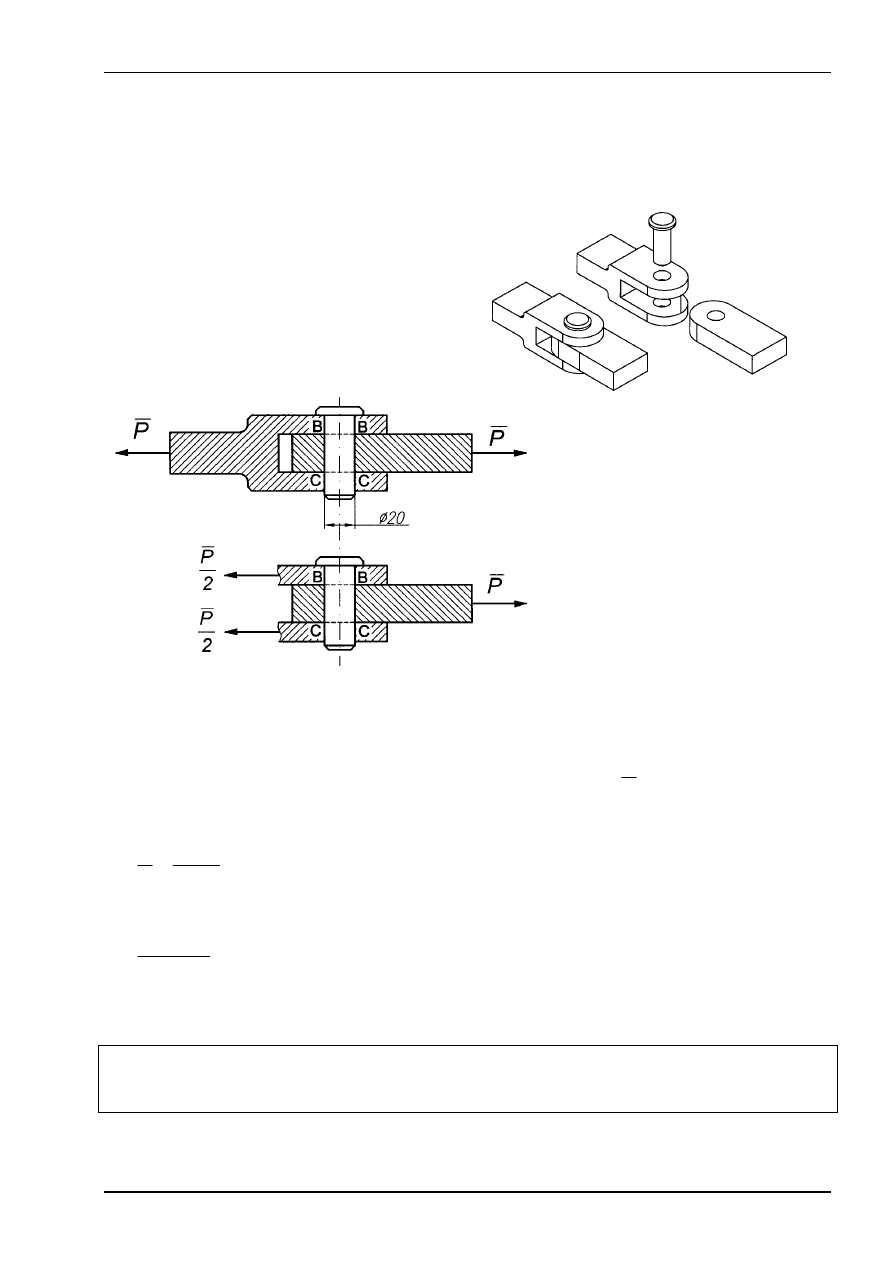
Przykład 2
Sprawdzić naprężenia ścinające w połączeniu sworzniowym wykonanym ze stali St3,
jeżeli siła obciążająca złącze wynosi 10000 N, średnica sworznia wynosi 20 mm,
natomiast naprężenia dopuszczalne na ścinanie

MPa

54

k

t

=

.

Naprężenia ścinające występują w dwóch przekrojach połączenia B-B oraz C-C.
Jeżeli założyć symetrię obciążenia to płaskownik górny i dolny przenoszą połowę siły
przyłożonej do złącza.

Zatem siła tnąca występująca w jednym przekroju wyniesie:

2

P

T

=

Zakładając równomierny rozkład naprężeń w każdym przekroju kołowym sworznia
otrzymamy naprężenia ścinające:

d

2

P

4

A

T

2

π

τ

=

=

,

po podstawieniu wartości liczbowych jest:

MPa

54

k

MPa

16

Pa

3

,

15915494

02

,

0

2

10000

4

t

2

=

<

≅

=

⋅

=

π

τ

Obliczenia wykazały, że złącze spełnia warunek wytrzymałości na ścinanie z dużym
zapasem bezpieczeństwa.

W celu uzyskania pewności bezpiecznej pracy połączenia należałoby ponadto sprawdzić
sworzeń na zginanie, naciski powierzchniowe oraz sprawdzić naprężenia rozrywające w
niebezpiecznych przekrojach płaskowników.

Rys. 11

Zapis i Podstawy Konstrukcji Mechanicznych. Wybrane zagadnienia wytrzymałości materiałów

Opracowali: J. Felis, H. Jaworowski str. 9

Przykład 3
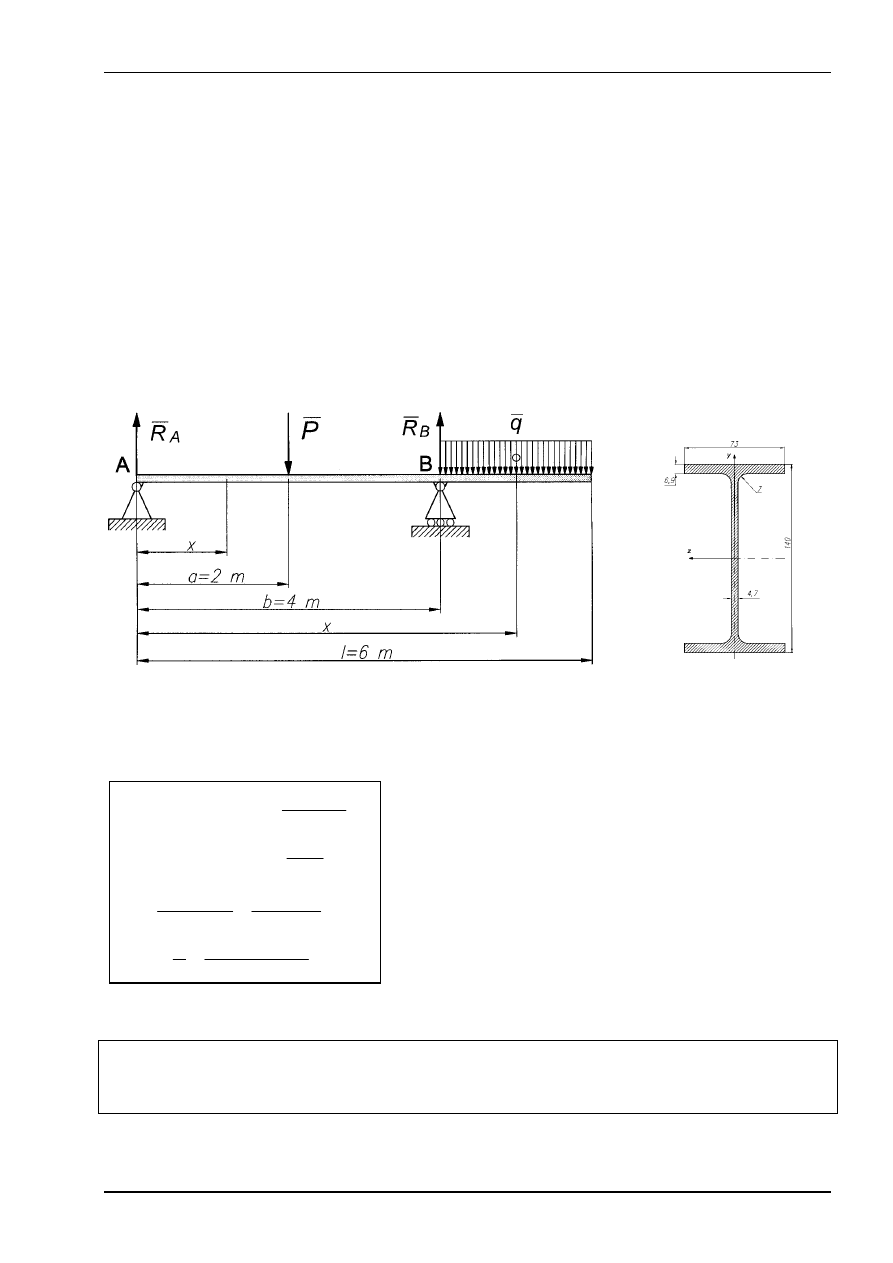
Przeprowadzić analizę wytrzymałościową belki prostej dwupodporowej o jednorodnym
przekroju dwuteownika 140PE (wymiary na rys.12), wykonanej ze stali 18G2 , obciążonej
siłą skupioną P i obciążeniem ciągłym q jak na rys. 12.
Dane: l=6 m, a=2 m, b=4 m, P=10 kN, q=2 kN/m, W

z

=77,3 cm

3

, k

g

=174 MPa

W ramach analizy wytrzymałościowej belki należy:
1. obliczyć reakcje w podporach A i B,
2. przebieg momentu gnącego

)

x

(

M

g

,

3. określić przebieg siły tnącej

)

x

(

T

,

4. wskazać wartość maksymalną momentu gnącego,
5. sprawdzić naprężenia gnące

σ

g

.

Rys. 12

Ad 1). Reakcje w podporach

R

,

R

A

A

wyznaczamy na podstawie warunków równowagi

belki.

Po podstawieniu wartości liczbowych otrzymamy:

Ad 2). Przebieg momentu gnącego określimy przesuwając się wraz z myślowym
przekrojem poprzecznym od lewego do prawego końca belki lub odwrotnie.
Moment gnący M

g

w dowolnym przekroju poprzecznym belki jest równy sumie

algebraicznej momentów wszystkich sił działających na część belki odciętą tym
przekrojem względem jego środka ciężkości.

(

) ( )

(

)

(

) (

)

(

)(

)

0

b

2

b

l

b

l

q

b

a

P

R

0

b

2

b

l

q

b

a

b

P

R

0

2

b

l

b

l

q

a

P

b

R

0

2

b

l

q

a

b

P

b

R

B

2

A

B

2

A

=

+

−

+

=

=

−

−

−

⋅

=

=

+

−

−

⋅

−

⋅

=

−

−

−

⋅

+

⋅

−

kN

10

R

kN

4

R

B

A

=

=

Zapis i Podstawy Konstrukcji Mechanicznych. Wybrane zagadnienia wytrzymałości materiałów

Opracowali: J. Felis, H. Jaworowski str. 10

Ad 3). Przebieg sił tnących określimy przesuwając się wraz z myślowym przekrojem
poprzecznym od lewego do prawego końca belki lub odwrotnie.

Siła tnąca T w dowolnym przekroju belki jest równa sumie współrzędnych wszystkich sił
działających na część belki odciętą tym przekrojem na kierunku prostopadłym do osi belki.


Między momentem gnącym, siłą tnącą i obciążeniem ciągłym zachodzą związki :

T

dx

M

d

g

=

,

q

dx

dT

−

=

,

q

dx

M

d

2

g

2

−

=

Związki te można wykorzystać przy sprawdzeniu poprawności zapisu i wykresów
momentów gnących i sił tnących.


Tablica 2

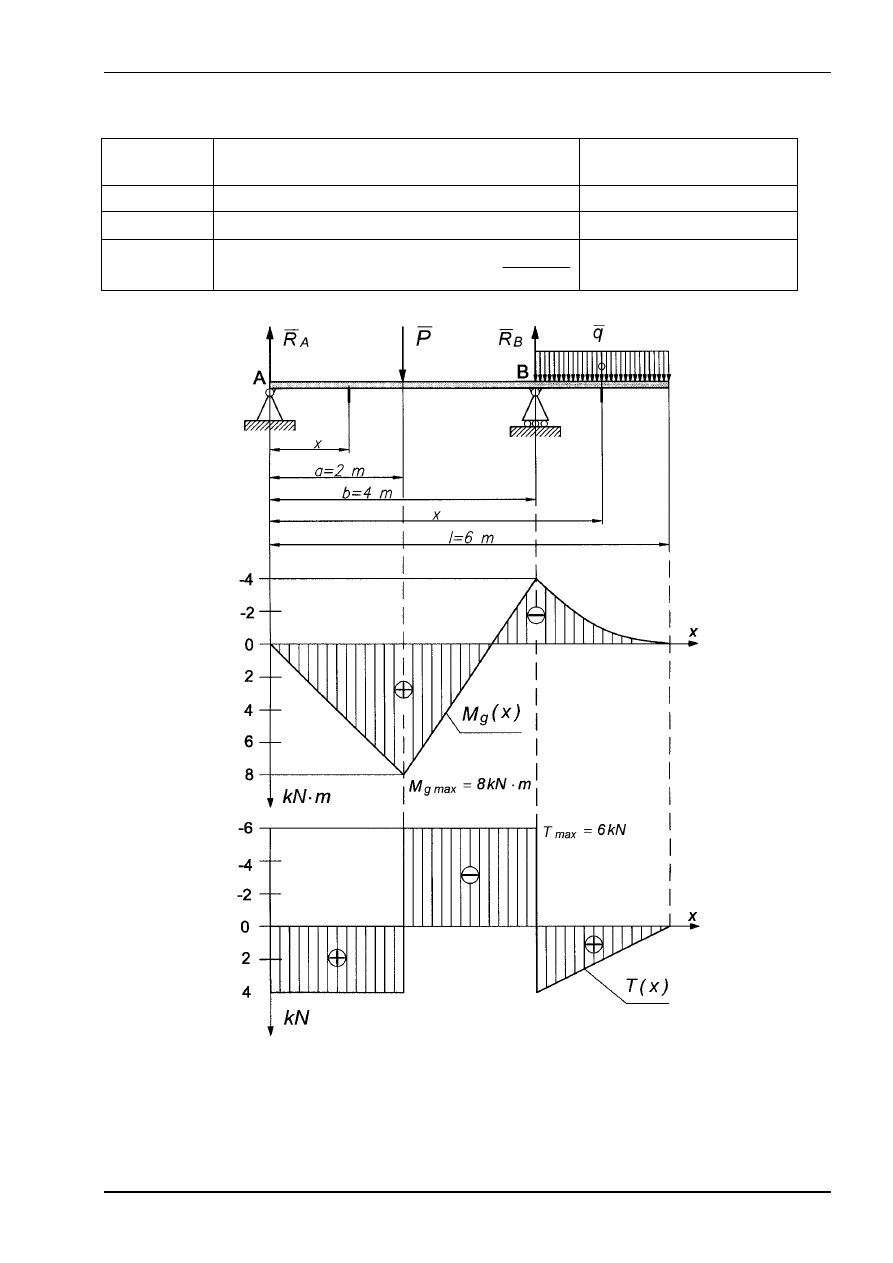
Równania momentów gnących i sił tnących analizowanej belki zostały przedstawione w
Tablicy 3, natomiast wykresy momentów gnących i sił tnących przedstawia rys. 13.

Ad 4). Maksymalna wartość momentu zginającego wynosi

m

N

8000

m

kN

8

M

max

g

⋅

=

⋅

=

( na podstawie wykresu rys. 13)

Ad 5). Sprawdzenie naprężeń gnących w belce:

W

z

=77,3 cm

3

, k

g

=174 MPa

k

MPa

5

,

103

Pa

10

5

,

103

10

3

,

77

8000

W

M

g

6

6

z

max

g

max

g

<

=

⋅

≅

⋅

=

=

−

σ

Przekrój belki spełnia warunek wytrzymałości na zginanie.

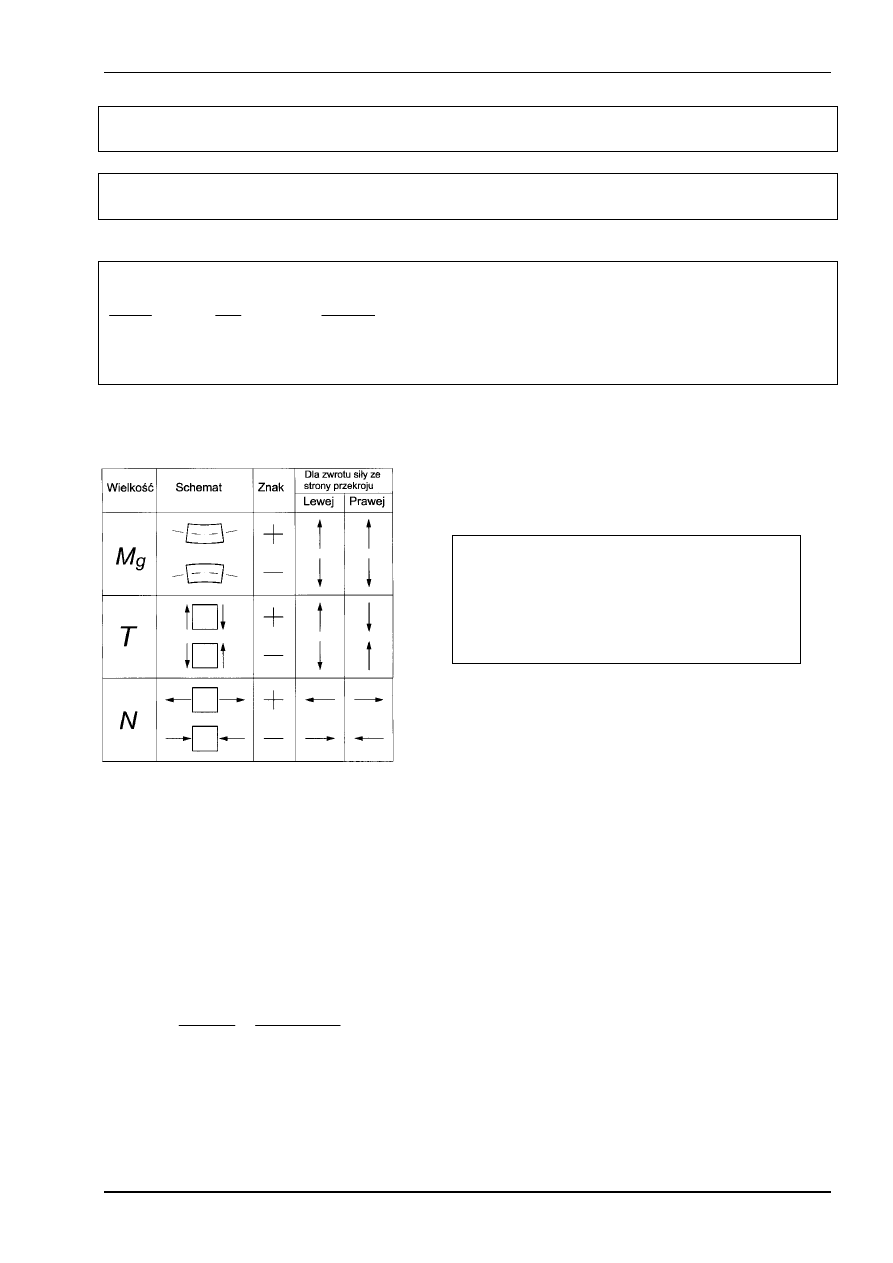
Uwaga: W celu analitycznego zapisu
momentów gnących i sił tnących i
następnie ich prezentacji graficznej,
przyjęte zostały reguły określania
znaków momentów gnących, sił tnących.
Reguły te przedstawia Tablica 2.

Zapis i Podstawy Konstrukcji Mechanicznych. Wybrane zagadnienia wytrzymałości materiałów

Opracowali: J. Felis, H. Jaworowski str. 11

Tablica 3

Rys. 13

Przedział x

Moment gnący

M

g

Siła tnąca

T

a

x

0

<

≤

x

R

M

A

g

⋅

=

R

T

A

=

b

x

a

<

≤

)

a

x

(

P

x

R

M

A

g

−

−

⋅

=

P

R

T

A

−

=

l

x

b

<

≤

(

)

(

) (

)

2

b

x

q

b

x

R

a

x

P

x

R

M

2

B

A

g

−

−

−

+

−

−

⋅

=

(

)

b

x

q

R

P

R

T

B

A

−

−

+

−

=

Zapis i Podstawy Konstrukcji Mechanicznych. Wybrane zagadnienia wytrzymałości materiałów

Opracowali: J. Felis, H. Jaworowski str. 12

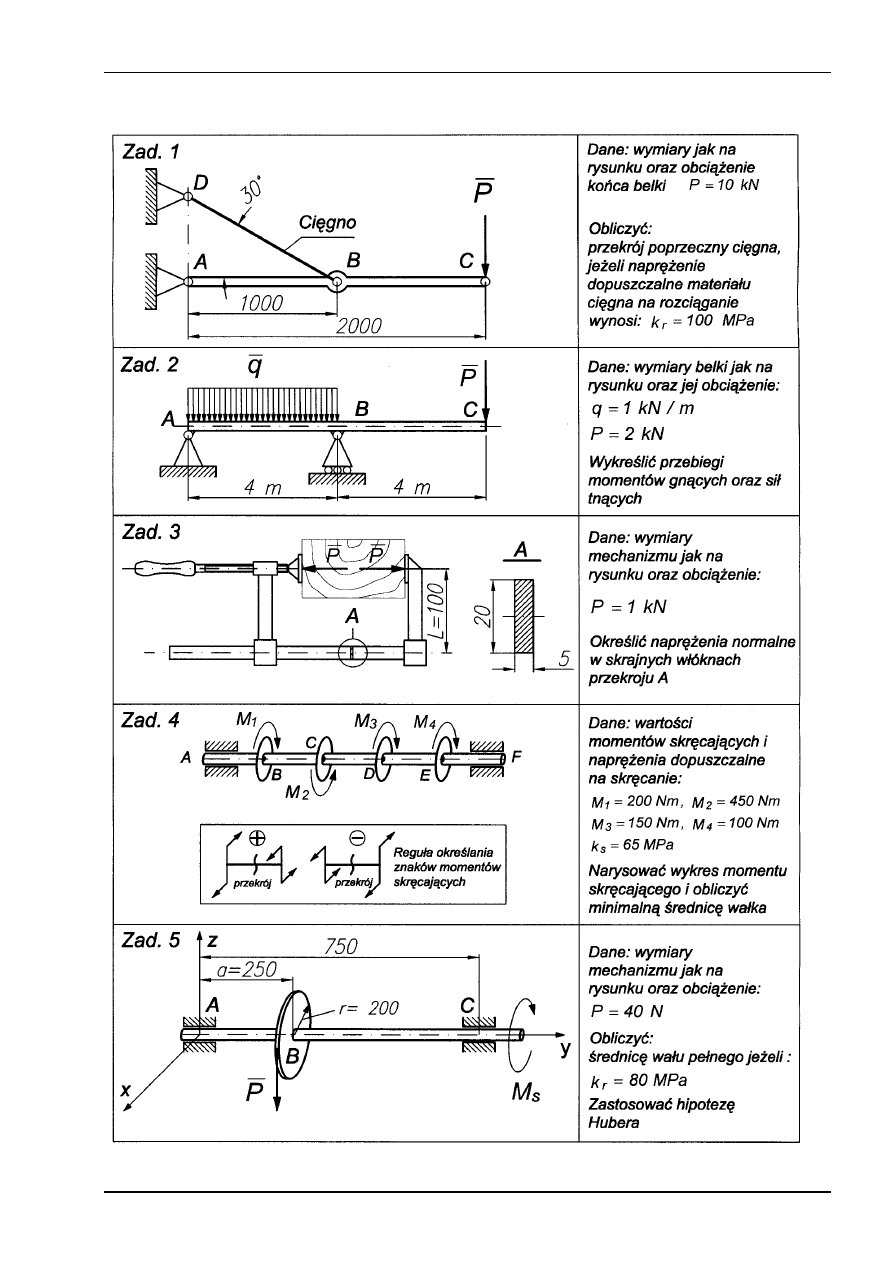
ZADANIA DO ROZWIĄZANIA NA ĆWICZENIACH