10 Stany naprężenia i odkształcenia. Hipotezy wytrzymałosciowe

111

STANY NAPRĘŻENIA I ODKSZTAŁCENIA

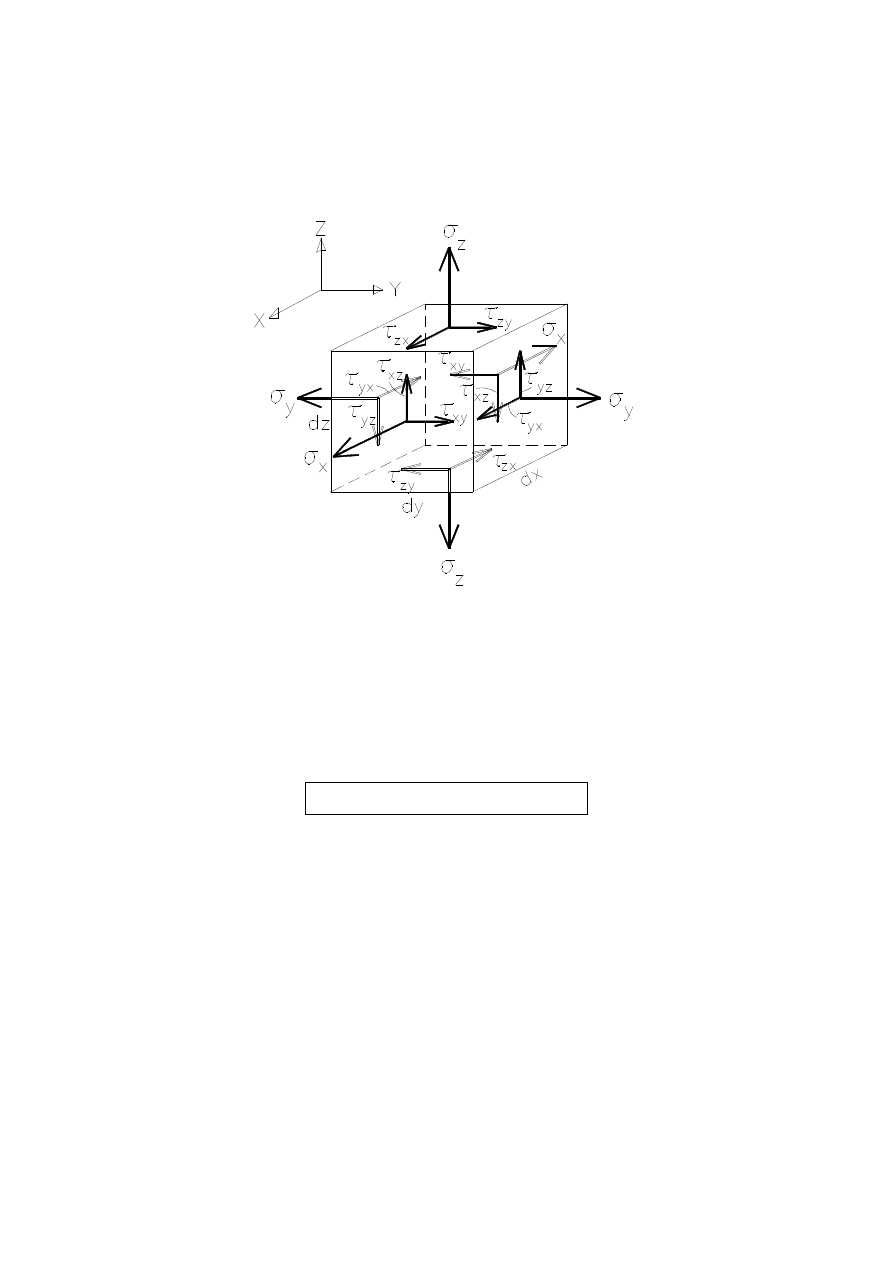
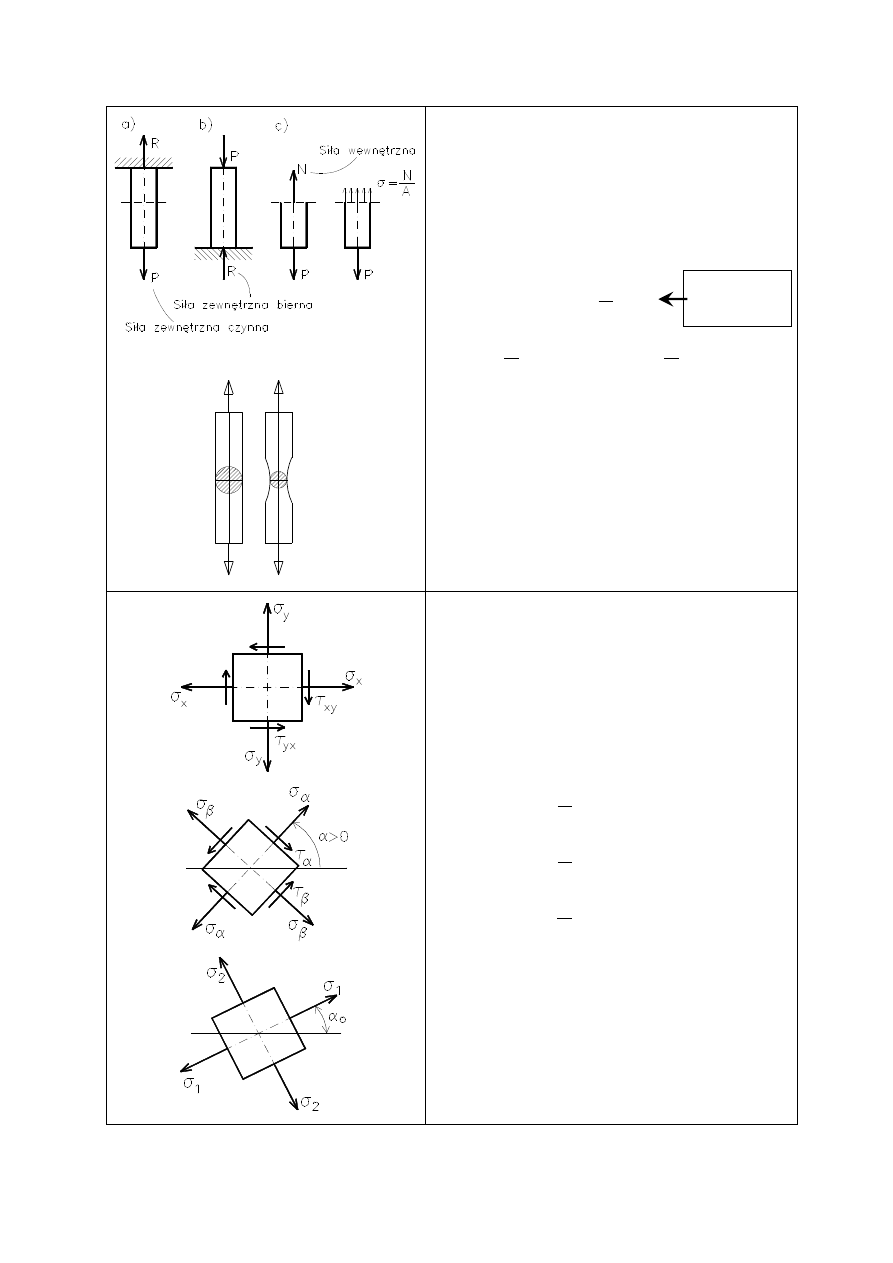
Analiza stanu naprężenia:

Stan naprężenia jest określony sześcioma składowymi:

naprężenia normalne:

,

,

,

z

y

x







naprężenia styczne:

.

,

,

zx

y z

xy







W celu zachowania równowagi sześciennej kostki, naprężenia styczne

na wzajemnie prostopadłych płaszczyznach są sobie równe (twierdze-
nie o równości naprężeń stycznych):

.

,

,

xz

zx

zy

y z

y x

xy



















STANY NAPRĘŻENIA:



Jednoosiowy stan naprężenia:



x



0,



y

=



z

=



xy

=



zx

=



zy

= 0.



Płaski stan naprężenia:



x



0,



y



0,



xy



0,



z

=



zx

=



zy

= 0.



Przestrzenny stan naprężenia.

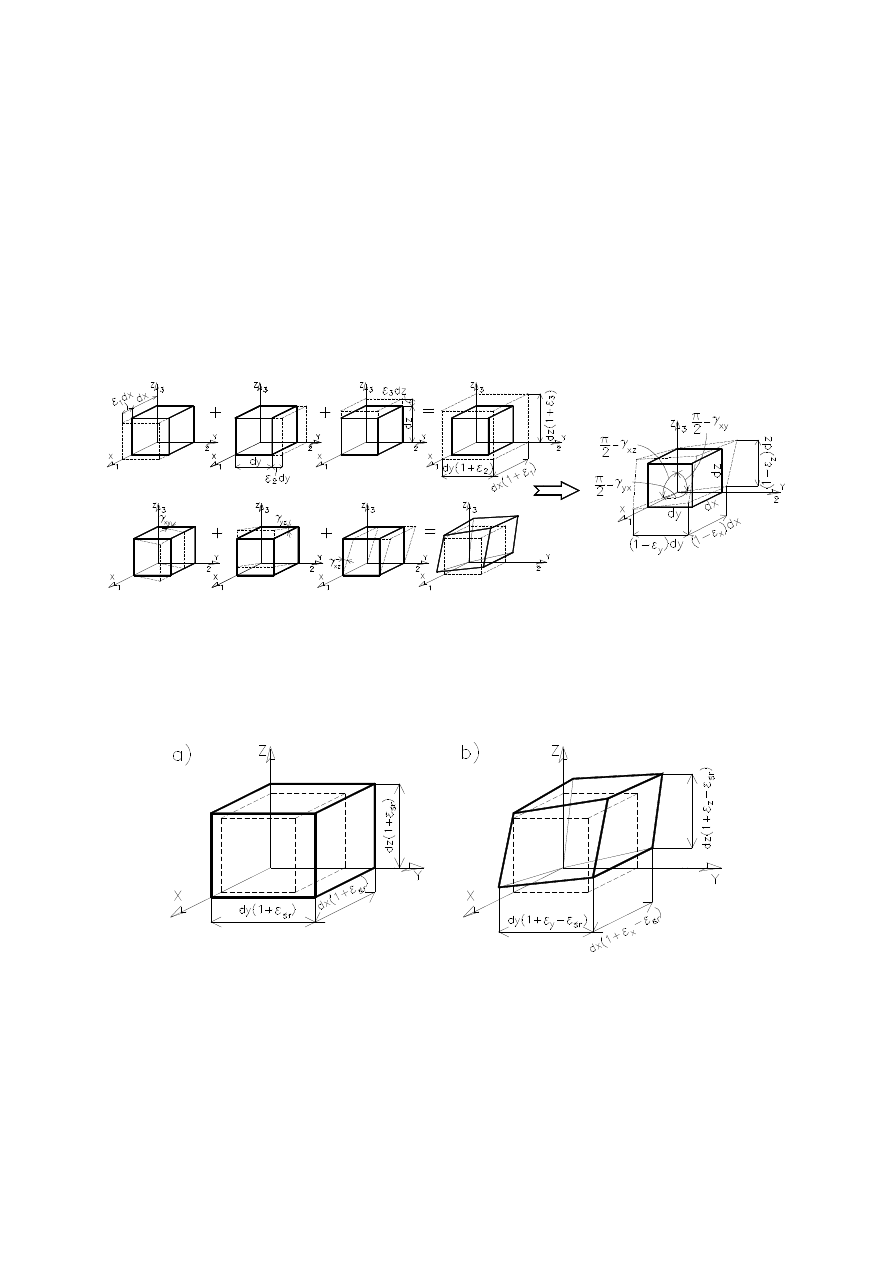
10 Stany naprężenia i odkształcenia. Hipotezy wytrzymałosciowe

112

Analiza stanu odkształcenia

St

an odkształcenia jest określony sześcioma składowymi:

wydłużenia liniowe:



x

,



y

,



z

kąty odkształcenia postaciowego:



xy

,



xz

,



zx

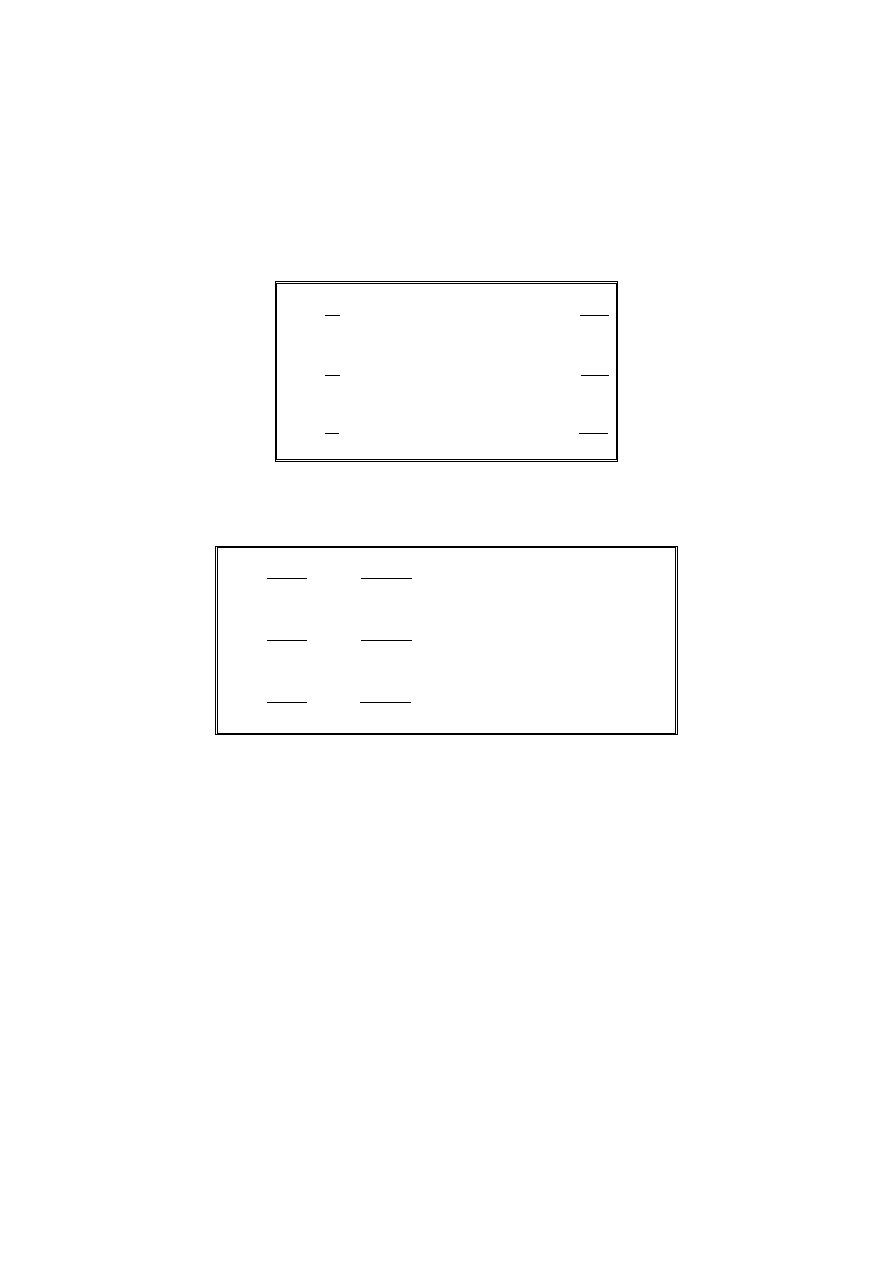
Poniższy rysunek pokazuje odkształcenia sześciennej kostki pod dzia-
łaniem wydłużeń liniowych



1

,



2

,



3

(indeksy 1, 2 i 3 oznaczają pominię-

cie odkształceń kątowych) oraz w dolnym wierszu odkształceń posta-
ciowych



w trzech płaszczyznach..

STANY ODKSZTAŁCENIA:



Odkształcenia czysto objętościowe.



Odkształcenia czysto postaciowe.

Odkształcenie: a) czysto objętościowe, b) czysto postaciowe

10 Stany naprężenia i odkształcenia. Hipotezy wytrzymałosciowe

113

Związki między stanem odkształcenia

i stanem na

prężenia

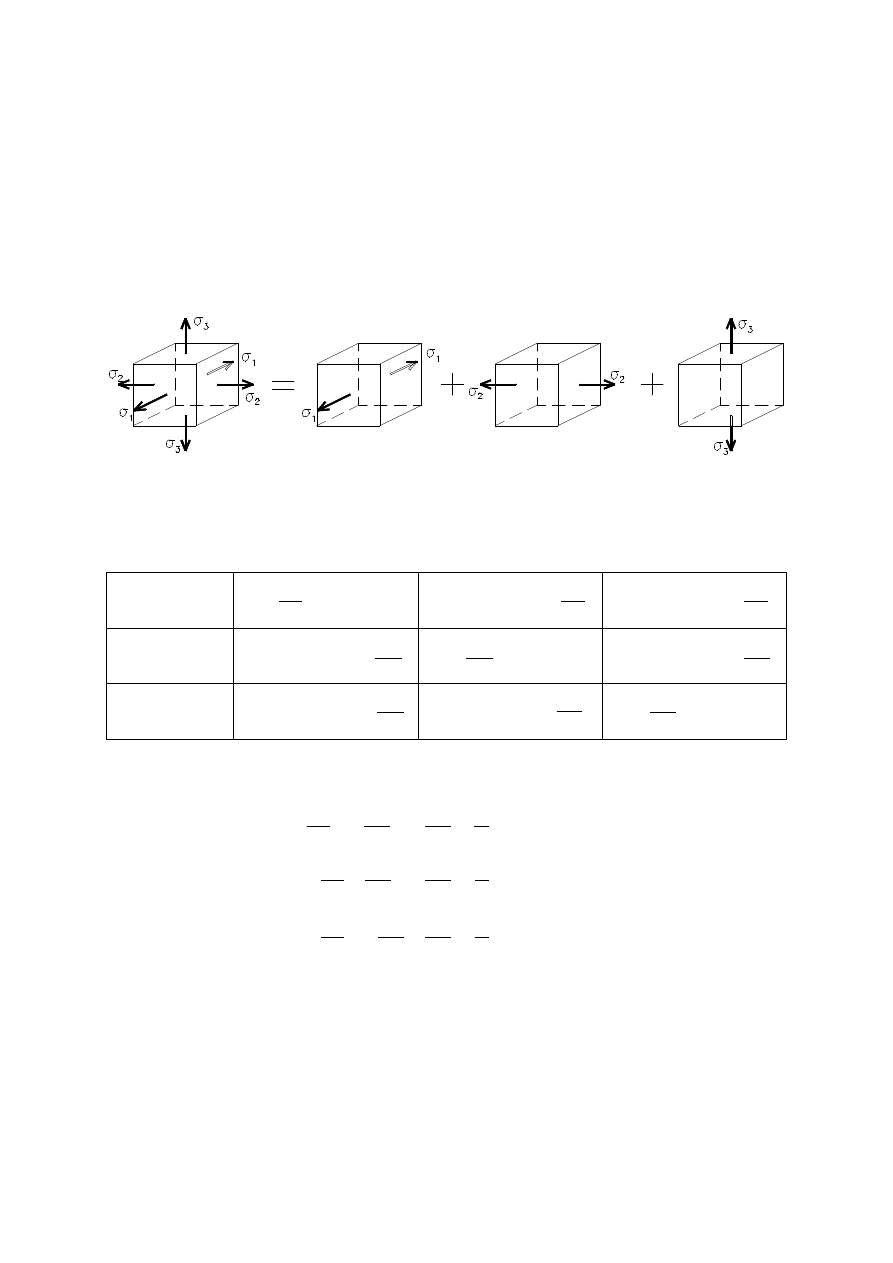
Dla sześcianu na który działają tylko naprężenia normalne (zwane na-
prężenia głównymi



1

,



2

,



3

dla podkreślenia, że pomija się wszystkie

naprężenia styczne



i

stan odkształceń jest czysto objętościowy), wy-

dłużenia liniowe w kierunku trzech osi XYZ wynoszą:

Trójwymiarowy stan naprężeń głównych

Zgodnie z zasadą superpozycji i prawem Hooke'a wydłużenia liniowe

w poszczególnych kierunkach wynoszą:

– kierunek 1:

,

E

1

1







,

E

1

1

2

















,

E

1

1

3

















– kierunek 2:

,

E

2

2

1

















,

E

2

2







,

E

2

2

3

















– kierunek 3:

,

E

3

3

1

















,

E

3

3

2

















.

E

3

3







Po zastosowaniu zasady superpozycji, wydłużenia liniowe wynoszą:









,

E

1

E

E

E

3

2

1

3

2

1

1



















































.

E

1

E

E

E

,

E

1

E

E

E

2

1

3

3

2

1

3

3

1

2

3

2

1

2





































































Ponieważ odkształcenia kątowe nie mają wpływu na wydłużenia linio-

we, powy

ższe zależności można uogólnić dla dowolnego stanu:

10 Stany naprężenia i odkształcenia. Hipotezy wytrzymałosciowe

114

























.

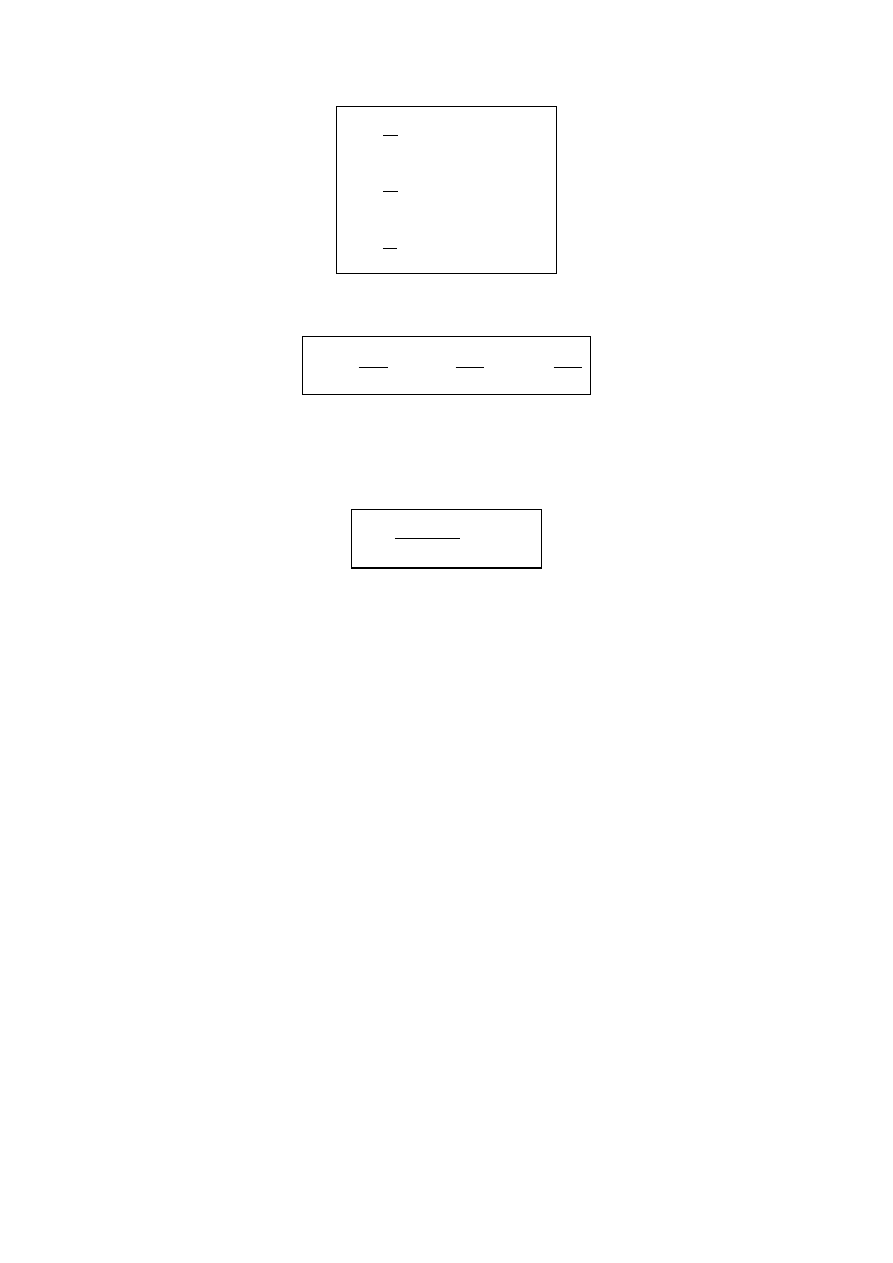
E

1

,

E

1

,

E

1

y

x

z

z

z

x

y

y

z

y

x

x

















































Dla odkształceń czysto postaciowych można wyprowadzić kolejne za-

leżności pomiędzy składowymi stanu naprężenia i stanu odkształcenia:

.

G

,

G

,

G

zx

zx

y z

y z

xy

xy



















Powyższe zależności określają prawo Hooke'a dla czystego ścina-

nia.

Współczynnik G nosi nazwę modułu ścinania (modułu odkształcenia

postaciowe

go, modułu Kirchhoffa):





.

[MPa]

1

2

E

G







Moduł ścinania G jest obok modułu Younga E i liczby Poissona

trzecią stałą sprężystą opisującą właściwości materiału.

10 Stany naprężenia i odkształcenia. Hipotezy wytrzymałosciowe

115

UOGÓLNIONE PRAWO HOOKE’A

Dla idealnie sprężystego materiału izotropowego zależności między

składowymi stanu odkształcenia i składowymi stanu naprężenia noszą
nazwę uogólnionego prawa Hooke'a. Składowe stanu odkształcenia
jako funkcje składowych stanu naprężenia wyrażone są zależnościami:

























.

G

,

E

1

,

G

,

E

1

,

G

,

E

1

zx

zx

y

x

z

z

y z

y z

z

x

y

y

xy

xy

z

y

x

x



































































Rozwiązując ten układ równań, można określić składowe stanu naprę-

żenia jako funkcje składowych stanu odkształcenia:













.

G

,

2

1

1

E

,

G

,

2

1

1

E

,

G

,

2

1

1

E

zx

zx

z

y

x

z

z

y z

y z

z

y

x

y

y

xy

xy

z

y

x

x

x































































































































Przedstawione wyżej zależności znajdują zastosowanie przede

wszystkim w tensometrii,

doświadczalnym dziale wytrzymałości mate-

ria

łów, zajmującym się pomiarem składowych stanu odkształcenia i obli-

czaniem na tej podstawie wartości składowych stanu naprężenia.

Składowe stanu naprężenia są stosowane w warunku wytrzymało-

ściowym, wykorzystując hipotezę wytrzymałościową, umożliwiającą
analizę złożonych stanów naprężenia (tzn. na projektowanie i obliczenia
wytrzymałościowe dominujących w wytrzymałości materiałów przypad-
ków wytrzymałości złożonej).

Uogólnione prawo Hooke’a pozwala zrozumieć szereg zjawisk zwią-

zanych z od

kształceniami elementów konstrukcyjnych. Odkształcenia

próbki podczas statycznej próby rozciągania oraz płaski stan naprężenia
przedstawiono w poniższej tabeli.

10 Stany naprężenia i odkształcenia. Hipotezy wytrzymałosciowe

116

Statyczna próba rozciągania:

P

P

P

P

Szyjka

Jednoosiowe rozciąganie

(statyczna próba rozciągania):



x



0,



y

=



z

=



xy

=



zx

=



zy

= 0.

Z uogólnionego prawa Hooke’a:

 









.

E

1

,

E

1

,

E

1

x

z

x

y

x

x























Jednoosiowemu rozciąganiu towarzy-
szy trójwymiarowy stan odkształceń –
stąd można wyjaśnić powstawanie
szyjki w rozciąganej próbce po prze-
kroczeniu granicy plastycz

ności.

Płaski stan naprężenia:



x



0,



y



0,



xy



0,



z

=



zx

=



zy

= 0.

Z uogólnionego prawa Hooke’a:

















.

E

1

,

E

1

,

E

1

y

x

z

x

y

y

y

x

x





































Płaski stan naprężenia tworzy trój-
wymiarowy stanu odk

ształcenia (po-

dobnie

– płaski stan odkształcenia

tworzy trójwymiarowy stan napręże-
nia).

Klasyczna

po

stać

prawa Ho

oke’a

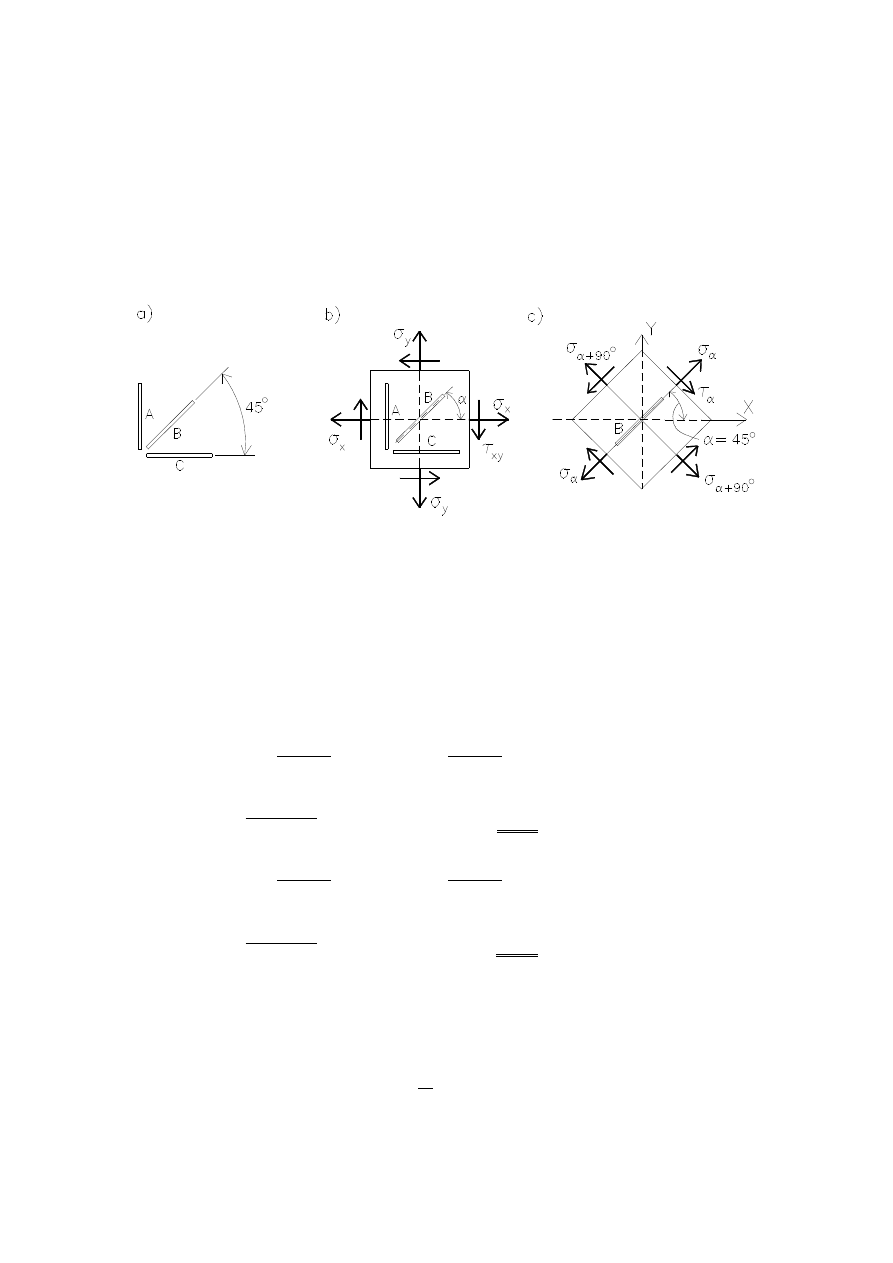
10 Stany naprężenia i odkształcenia. Hipotezy wytrzymałosciowe

117

ZASTOSOWANIE

UOGÓLNIONEGO

PRAWA

HOOKE’A

W

TENSOMETRII

Na powierzchni sprężystego ciała (E = 2,1



10

5

MPa,



= 0,3) dokonano

tensometrycznego p

omiaru wydłużeń względnych w kierunkach A, B, C i

uzyskano:



A

= 1,36

o

/

oo

,



B

= 0,24

o

/

oo

,



C

=

–0,85

o

/

oo

. Wyznaczyć składowe

stanu naprężenia oraz wartości i kierunki naprężeń głównych.

Ro

zeta tensometryczna, płaski stan naprężenia

Na powierzchni ciała występuje płaski stan naprężenia. Rysunek

przedstawia typową rozetę tensometryczną, umożliwiającą pomiar od-
kształceń liniowych w trzech kierunkach (kąt



= 45



). Po prz

yjęciu ukła-

du osi XY i określeniu składowych stanu naprężenia dla tego układu (rys.
b) można z uogólnionego prawa Hooke’a dla płaskiego stanu określić
war

tości naprężeń normalnych:





























.

MPa

255

10

85

,

0

3

,

0

36

,

1

3

,

0

1

10

1

,

2

1

E

1

E

,

MPa

102

10

36

,

1

3

,

0

85

,

0

3

,

0

1

10

1

,

2

1

E

1

E

3

2

5

C

A

2

x

y

2

y

3

2

5

A

C

2

y

x

2

x





























































































W celu wyznaczenia naprężenia stycznego należy skorzystać ze

schematu przedstawionego na rys. c. Wydłużenie w kierunku tensometru
B wynosi





.

E

1

90

B

























Naprężenia normalne dla kierunku



= 45



określa się następująco:

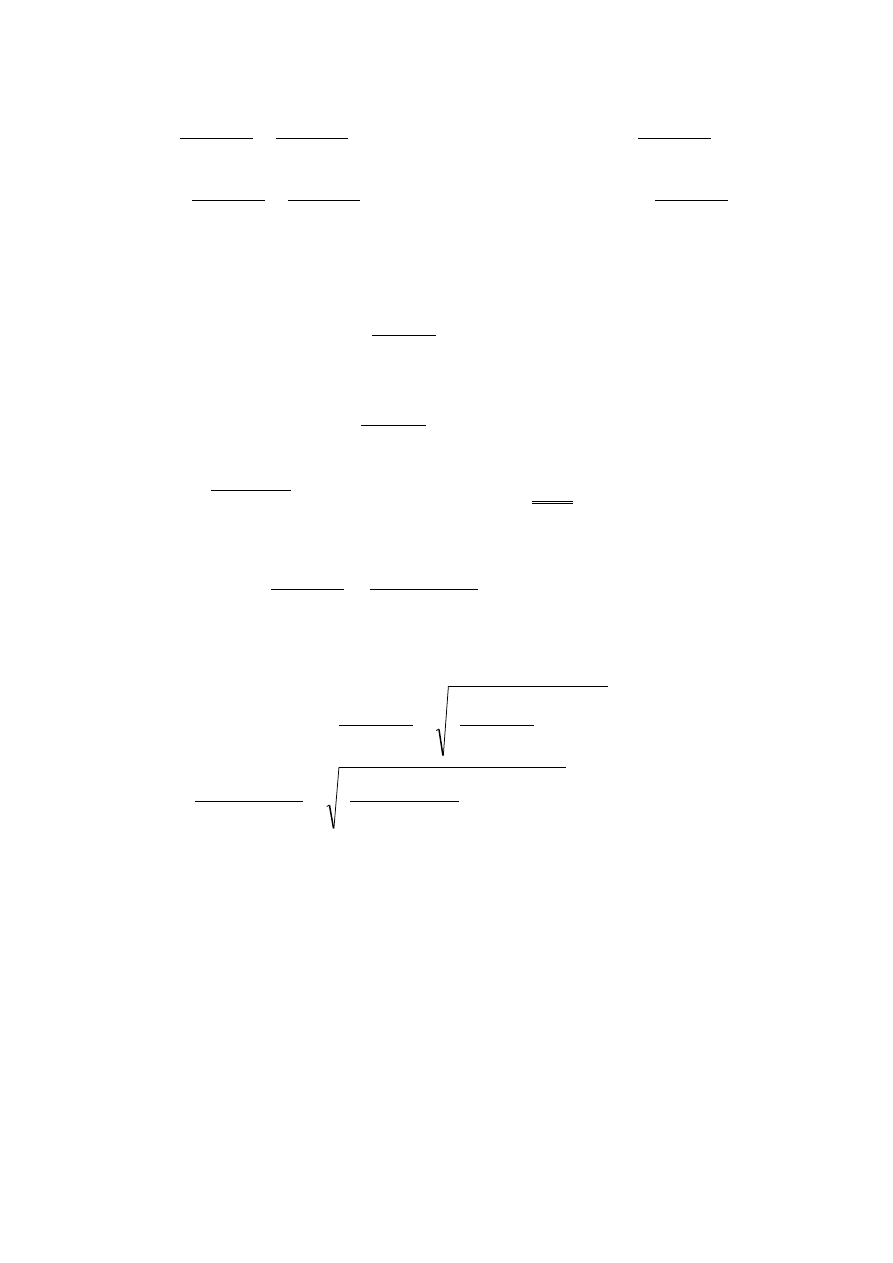
10 Stany naprężenia i odkształcenia. Hipotezy wytrzymałosciowe

118

,

2

)

45

2

sin(

)

45

2

cos(

2

2

xy

y

x

o

xy

o

y

x

y

x









































.

2

)

45

2

sin(

)

45

2

cos(

2

2

xy

y

x

o

xy

o

y

x

y

x

90

o











































Po wprowadzeniu tych

zależności do wzoru na



B

i po uporządkowaniu

otrzymuje się zależność pozwalającą obliczyć wartość naprężeń stycz-
nych:









.

2

1

2

E

y

x

xy





















Po wstawieniu danych liczbowych



















.

MPa

5

,

148

10

24

,

0

2

36

,

1

85

,

0

3

,

0

1

2

10

1

,

2

2

1

2

E

3

5

B

A

C

xy









































Kierunki naprężeń głównych oblicza się ze wzoru:

.

20

8319

,

0

255

102

5

,

148

2

2

tg

o

o

y

x

xy

0

































Ponieważ



x

<



y

, kąt



o

wyznacza kierunek naprężenia



2

. Napręże-

nia główne wynoszą:

.

MPa

2

,

232

5

,

76

5

,

148

2

255

102

2

255

102

,

2

2

2

2

2

,

1

2

xy

2

y

x

y

x

2

,

1



































































Zgodnie z umową



1

= 308,7 MPa,



2

=

–155,7 MPa. Do sprawdzenia

poprawności wyników można wykorzystać związki

.

MPa

153

2

1

y

x

















Przedstawiony przykład ma znaczenie praktyczne – dzięki pomiarom

tensometrycznym odkształceń można określić doświadczalnie wartości
naprężeń w niebezpiecznych punktach konstrukcji i porównać je z wyni-
kami obli

czeń numerycznych.

10 Stany naprężenia i odkształcenia. Hipotezy wytrzymałosciowe

119

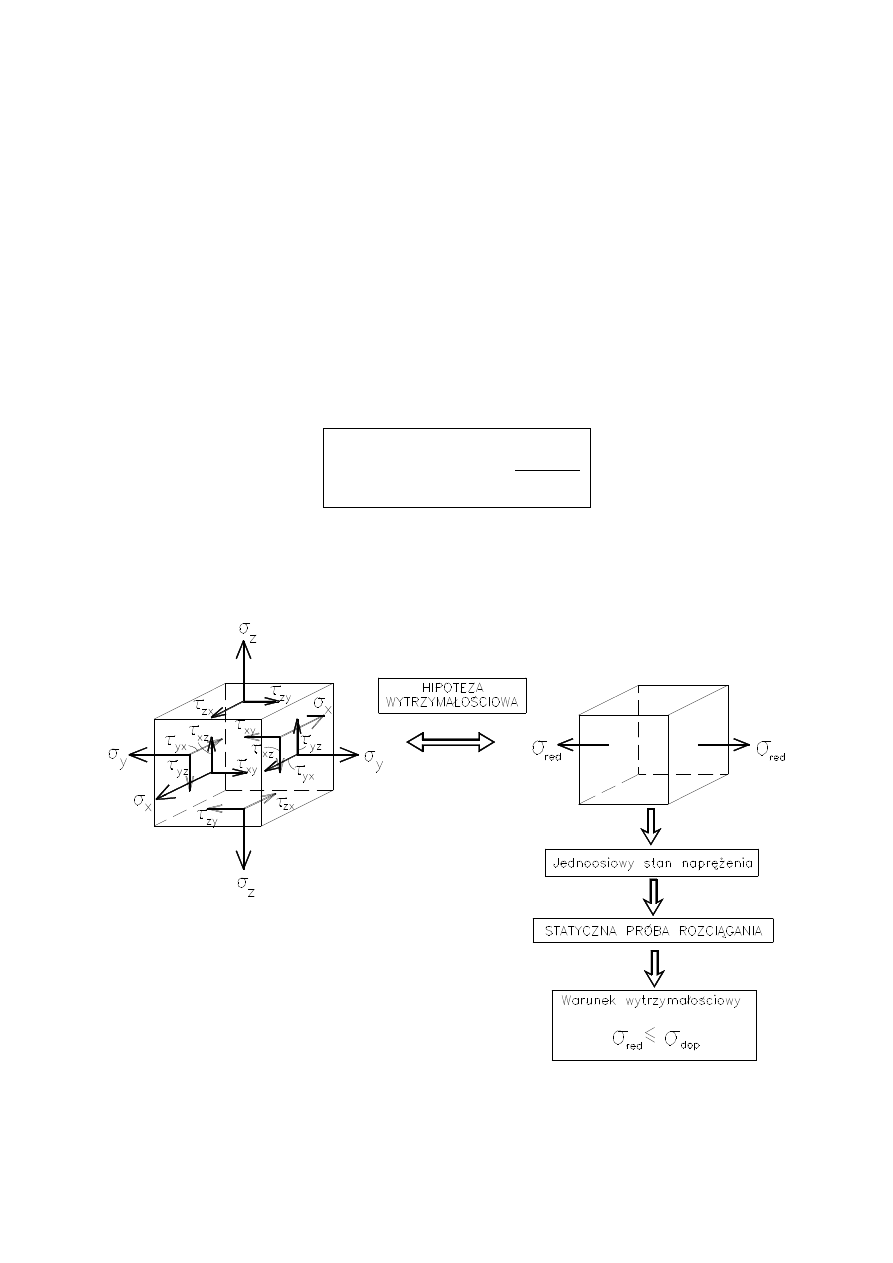
HIPOTEZY WYTRZYMAŁOŚCIOWE

W praktyce inżynierskiej występują złożone stany napręże-

nia, będące kombinacją naprężeń normalnych i stycznych.
Przy

jęcie hipotezy wytrzymałościowej umożliwia znalezienie

matema

tycznej funkcji pozwalającej na zastąpienie złożonego,

przestrzennego stanu naprężenia przez stan jednoosiowego
rozciągania, dokładnie opisany przez statyczną próbę rozcią-
gania

. Dzięki temu w obliczeniach wytrzymałościowych można

wyko

rzystać warunek wytrzymałościowy:

.

n

nieb

dop

red











Ideę obliczeń wytrzymałościowych opartą na

naprężeniach zredukowanych pokazano na rysunku.

10 Stany naprężenia i odkształcenia. Hipotezy wytrzymałosciowe

120

Obecnie znanych jest kilkadziesiąt hipotez wytrzymałościo-

wych. Niektóre z nich mają już tylko znaczenie historyczne, inne
nie są dostatecznie potwierdzone przez doświadczenie, jeszcze
inne są bardzo wyspecjalizowane i przeznaczone do wąskiej
klasy zagadnień wytrzymałościowych.

Spośród hipotez ogólnych, dających wyniki zgodne z do-

świadczeniem, należy wymienić hipotezę energii odkształce-
nia postaciowego (hipo

tezę Hubera).

Maksymilian Tytus Huber (1872-1950) polski uczony,

współtwórca współczesnej mechaniki teoretycznej,

profesor Politechniki Lwowskiej, Politechniki Warszawskiej

i po II Wojnie Światowej Politechniki Gdańskiej.

Hipoteza ta należy do licznej grupy tzw. hipotez energetycz-

nych. Twórcy hipotezy (Huber 1904, Mises 1913, Hencky 1925)
przyjęli, że miarą wytężenia materiału jest wartość energii
sprężystej odkształcenia postaciowego.

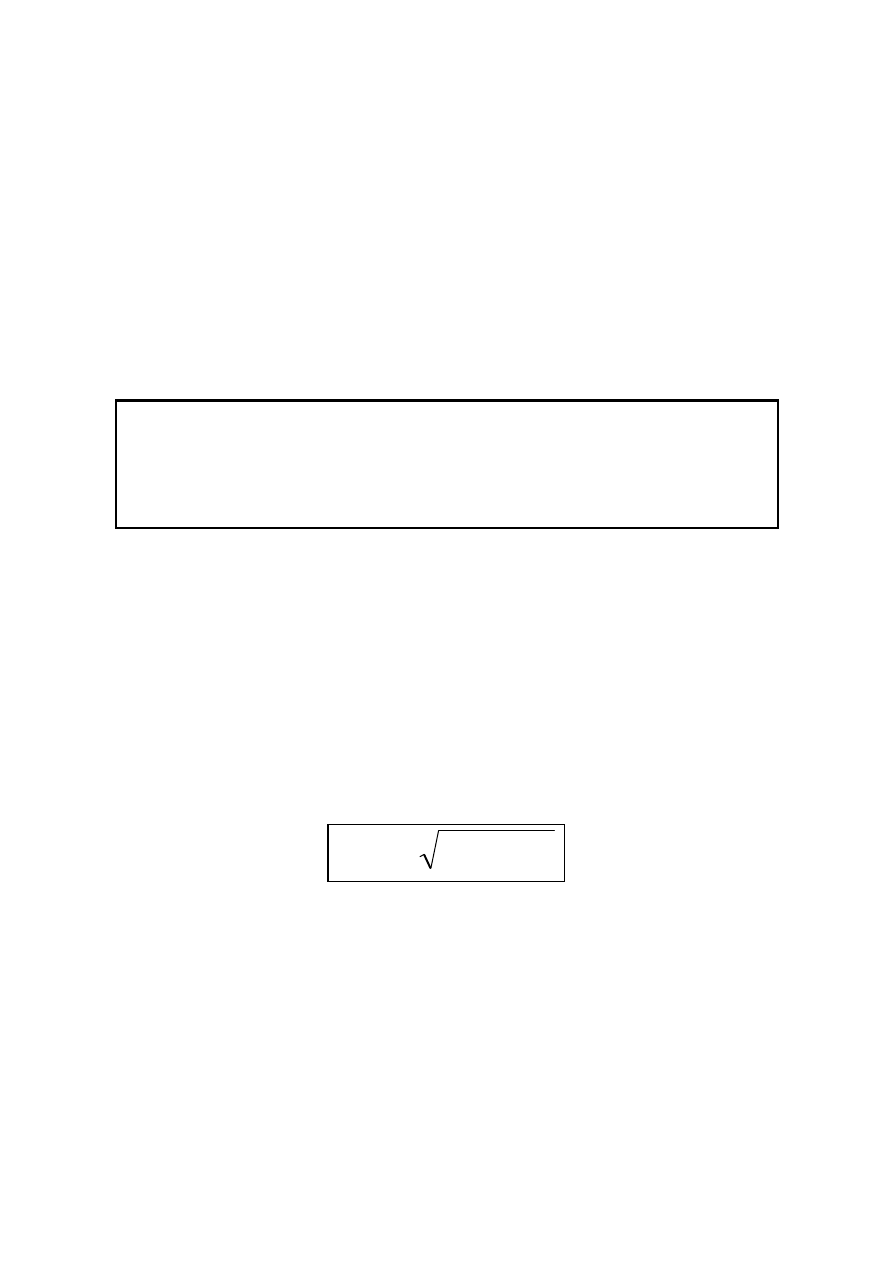
Dla przypadku jednoczesnego występowania naprężeń nor-

malnych i stycznych (zginanie belek), naprężenia zredukowane
zastępujące ten złożony stan naprężenia oblicza się z zależno-
ści:

.

3

2

2

red











Hipoteza Hubera (Hubera

– Misesa – Hencky’go) jest po-

twierdzona doświadczalnie i jest obecnie bardzo szeroko sto-
sowana w praktyce inżynierskiej.