71
Rozdział 5
WYBRANE ZAGADNIENIA Z WYTRZYMAŁOŚCI MATERIAŁÓW W ODNIESIENIU DO
TKANEK CZŁOWIEKA
Aktywność komórek wpływa na ich kształtowanie, rozmiary oraz skład chemiczny. Kość posiada
również zdolność dostosowania się do zewnętrznego środowiska. Według teorii Funga [10], wszelkie
zmiany w strukturach tkankowych organizmów żywych są związane z przemianą materii. Dla dobrego
zrozumienia procesów wzrostu oraz zmian struktur kostnych niezbędna jest ocena stanów naprężeń i
odkształceń w okresie przemian w danym organizmie.
5.1. Terminologia
W biomechanice niekiedy występują problemy w znalezieniu wspólnej terminologii określającej
własności materiałów tkankowych oraz implantów. Własności mechaniczne opisują dany materiał,
gdy poddany jest on określonym obciążeniom, co umożliwia analizę porównawczą wybranych
materiałów. Dla zdefiniowania niektórych własności mechanicznych materiałów używa się określeń
[25]:
Wytrzymałość – zdolność materiału do przenoszenia obciążeń bez jego zniszczenia;
Twardość – odporność materiału na odkształcenia trwałe pod wpływem sił skupionych działających na
małą powierzchnię tego materiału;
Sprężystość – zdolność materiału do odzyskania pierwotnego kształtu i wymiarów po usunięciu
obciążeń, wywołujących odkształcenie;
Plastyczność – zdolność materiału do osiągania nowych kształtów oraz zachowania tych kształtów po
zdjęciu obciążenia, bez naruszania spójności (pęknięć);
Ciągliwość – zdolność materiału do ulegania dużym odkształceniom trwałym pod działaniem sił bez
pęknięć;
Kruchość – właściwość materiału polegająca na jego pękaniu bez uprzednich znaczniejszych
odkształceń plastycznych.
Najczęściej stosowane określenia:
-
- naprężenie – rozkład siły na danej powierzchni (F/A) [N/m
2
];
-
- wydłużenie (skrócenie) - bezwymiarowa wielkość miary zmiany długości ((l-l
0
)/l
0
);
- E - moduł Younga (współczynnik proporcjonalności) - zmiana naprężenia wymagana dla zmiany
wydłużenia (E=
/
) [N/m
2
];
- ciągliwość - energia na jednostkę wielkości wymagana do pęknięcia materiału (T =
d
) [m].
72
5.2. Przypadki wytrzymałościowe
W celu określenia własności mechanicznych materiałów poddanych określonym stanom
naprężenia, prowadzi się badania wytrzymałościowe. Elementarne przypadki wytrzymałości próbki, o
kształcie pręta, to zginanie, rozciąganie, ściskanie, skręcanie i ścinanie [4,8].
Wiedza związana ze znajomością własności mechanicznych i strukturalnych tkanek miękkich oraz
kostnych jest podstawowym warunkiem wstępnym dla teoretycznych, numerycznych oraz
eksperymentalnych przybliżeń w analizie fizjologicznych funkcji ciała. Wszelkie uszkodzenia
narządów zależą od własności materiałów, kości oraz tkanek miękkich. Dotyczy to zarówno urazów,
jak i zmian chorobowych, wynikających z patologii. W literaturze istnieje wiele opracowań
dotyczących badań własności omawianych struktur (tkanki miękkie i kostne) [1,18,24]. Zwykle
badania te przeprowadza się na małych próbkach wypreparowanych z kości lub całych więzadłach,
ścięgnach, itd. Badania na próbkach odbywają się w ściśle określonych warunkach obciążeń, przy
znanych kierunkach i wartościach naprężeń oraz odkształceń. Z reguły, badania własności materiałów
tkanek określane są z prób rozciągania oraz skręcania (czasami również ścinania). Jednocześnie należy
uwzględnić, czy są to tkanki świeże, balsamowane czy też wysuszone. Ważne jest miejsce pobrania i
opis dawcy, czyli wiek, waga, płeć, itd., jak też warunki realizacji badania, np. szybkość odkształcania
i temperatura.
5.2.1. Zginanie
W układzie mięśniowo-szkieletowym człowieka dominują w zasadzie obciążenia ściskające i
rozciągające. Wynika to z geometrycznego ukształtowania oraz obciążenia (np. stawy, przyczepy
mięśni) [1]. Układ szkieletowy znajduje się zwykle w warunkach złożonego stanu obciążeń. W
analizie własności mechanicznych kości, biomechanika posługuje się analogiami wziętymi z
mechaniki klasycznej. Podczas zginania (czystego), górne włókna belki są rozciągane, a dolne
ściskane (rys. 5.1)
Rys. 5.1. Zginanie pręta [92]
Rys. 5.2. Zginanie wskutek wywierania siły na głowę kości udowej [92]
73
W wyniku analizy przypadku zginania kości zauważono, że kość łamie się po stronie rozciągania
(wypukłej) i jest dość odporna na ściskanie (rys. 5.2). W cienkich kościach występują większe
naprężenia niż w kościach grubych. W analizie różnych stanów naprężeń, ich wartości w istotny
sposób zależą od przekroju poprzecznego, momentu bezwładności względem osi (podczas zginania)
oraz momentu biegunowego przekroju względem środka ciężkości (podczas skręcania).
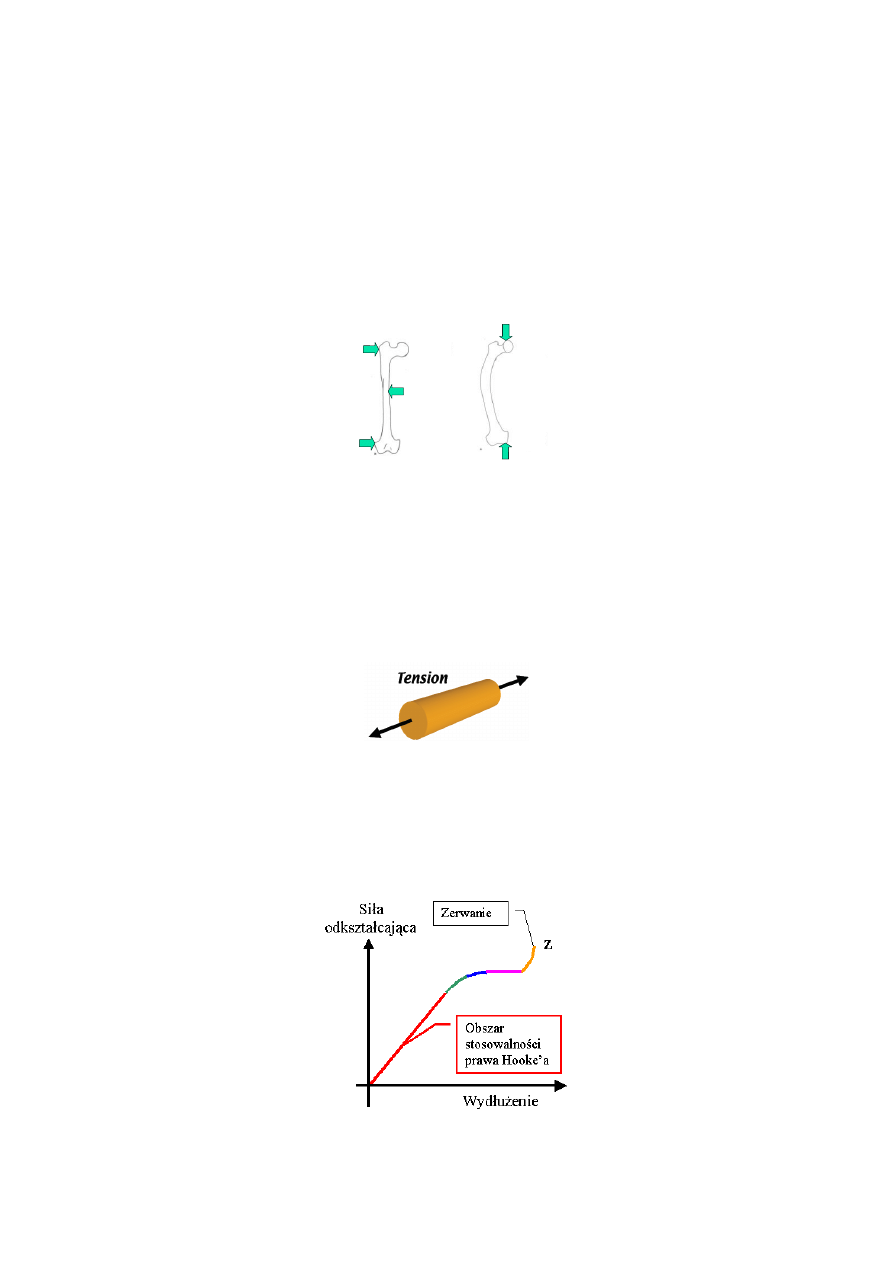
W ciele ludzkim można zauważyć dwa rodzaje obciążenia, które powodują zginanie kości: pod
wpływem obciążenia bocznego oraz naprężenia osiowego na końcach kości (rys. 5.3)
a)
b)
Rys. 5.3. Zginanie kości pod wpływem obciążenia: a) bocznego, b) osiowego
5.2.2. Rozciąganie
Rozciąganie powoduje wydłużenie i pocienienie kości, a jego źródłem są przeważnie mięśnie.
Rozciąganie jest zjawiskiem typowym dla kości gąbczastych (rys. 5.4) [1]. Zachowanie struktury
zależy tylko od własności materiału i płaszczyzny przecięcia a nie zależy od kształtu.
Rys. 5.4. Rozciąganie pręta [92]
Zachowanie różnych materiałów poddanych siłom rozciągającym lub ściskającym określa prawo
Hooke’a: „naprężenie pojawiające się w ciele odkształcanym jest proporcjonalne do względnego
odkształcenia ciała, czyli odkształcenie ciała pod wpływem działającej nań siły jest wprost
proporcjonalne do tej siły (prawdziwe dla odkształceń sprężystych)” (rys. 5.5) [8].
Rys. 5.5. Prawo Hooke’a [93]
74
Prawo Hooke’a można opisać wzorem (1):
(1)
gdzie: l
0
– początkowa (bez działania siły) długość pręta (w układzie SI w metrach: m),
l –
wydłużenie (ogólnie odkształcenie), czyli zmiana długości pręta (w układzie SI w metrach: m), F –
siła powodująca odkształcenie (w układzie SI w niutonach: N = kg·m/s
2
), S – pole przekroju
poprzecznego (w układzie SI w metrach kwadratowych: m
2
), K – współczynnik charakteryzujący
materiał (w układzie SI w jednostkach: m·s
2
/kg) [8].
Prawo Hooke’a nie jest prawem stuprocentowo ścisłym. Dla materiałów sprężystych (np. guma)
stosuje się ono do stosunkowo największych odkształceń. Jednak, prędzej czy później, zwiększenie
siły wyprowadzi odkształcane ciało z obszaru proporcjonalności, czyli z obszaru stosowalności tego
prawa. Typowy przebieg rozciągania ciała przedstawiony jest na rys. 5.5. Zawiera on kilka obszarów
zachowania, w których zjawisko odkształcenia przebiega w odmienny sposób [8,93]:
1. obszar stosowalności prawa Hooke’a - w obszarze tym zwiększenie siły np. o 50% spowoduje
przyrost wydłużenia w tym samym stosunku – czyli też 50%;
2. obszar sprężystości – obszar, w którym ciało nie odkształca się trwale, co oznacza, że po ustaniu
działania siły ciało wraca do pierwotnego kształtu. Jednak w obszarze tym zwiększenie siły o
10% może spowodować zwiększenie wydłużenia np. o 12%, czy 15%, czyli wzór na prawo
Hooke’a już nie obowiązuje;
3. początkowy obszar odkształceń trwałych - dalsze zwiększanie siły wiąże się z postępującym
rozciąganiem materiału, jednak w obszarze tym ciało zatraca swój pierwotny kształt, co
oznacza, że ustąpienie siły nie spowoduje skurczenia się rozciąganego materiału do początkowej
długości;
4. obszar plastyczności – w obszarze tym zwiększanie odkształcenia nie wiąże się ze zwiększeniem
siły – siła o stałej wartości można „wyciągać” ciało i kształtować je w szerokim zakresie
wydłużeń;
5. obszar poprzedzający zerwanie – całkowite zerwanie ciała następuje w punkcie Z. Jednak aby do
niego dojść, trzeba jeszcze nieco zwiększyć siłę w stosunku do tej, która wystarczała w obszarze
plastyczności.
Proporcje obszarów przedstawionych na rys. 5.5 mogą różnić się w zależności od materiału, np.
wykres dla materiałów twardych i kruchych będzie bardzo stromy (duży moduł Younga), a obszar
sprężystości będzie krótki: plastelina ma długi obszar plastyczności (mały moduł Younga), natomiast
materiały sprężyste mają stosunkowo duże dwa początkowe obszary.
75
5.2.3. Ściskanie
Wskutek ściskania kość staje się krótsza i grubsza, przy czym następuje złamanie osteonów,
jednostek morfologicznych kości zbitej (rys. 5.6). To zjawisko jest typowe dla kręgów. Podczas
ściskania znaczenie ma kształt oraz rozmiar kości.
Rys. 5.6. Ściskanie pręta [92]
W kościach występuje złożony stan naprężeń, jak wynika z układu sił działających w stawach oraz
budowy geometrycznej ukształtowania stawów, jak również całej kości (rys. 5.7). Najczęstszym
przypadkiem w kościach długich kończyn dolnych jest kombinacja obciążeń ściskających oraz
rozciągających. Stan naprężenia w dowolnym przekroju wynika z sumowania naprężeń pochodzących
od obciążeń osiowych oraz gnących.
ściskanie
rozciąganie
ściskanie
rozciąganie
Rys. 5.7. Złożony stan naprężeń kości udowej bliższej [94]
5.2.4. Skręcanie
Jeżeli pręt o długości l poddany zostanie działaniu momentu skręcającego (przyłożenie pary sił),
przyłożonego w płaszczyźnie prostopadłej do jego osi w jednym końcu, a drugi koniec zostanie
obciążony podobnym momentem, lecz przeciwnie skierowanym, nastąpi zrotowanie, czyli skręcenie
płaszczyzn (zrotowanie jednego końca względem drugiego) (rys. 5.8).
Rys. 5.8. Skręcanie pręta [92]
Zastosowane siły powodują wewnętrzne, kątowe przemieszczenie w kierunkach przeciwnych i
możliwe jest pękanie kości gąbczastej. Wytrzymałość na skręcanie zależy zarówno od własności
materiałowych, jak i własności strukturalnych. Skręcanie powoduje trzy rodzaje naprężeń:
rozciągające, ściskające oraz ścinające.
76
5.2.5. Ścinanie
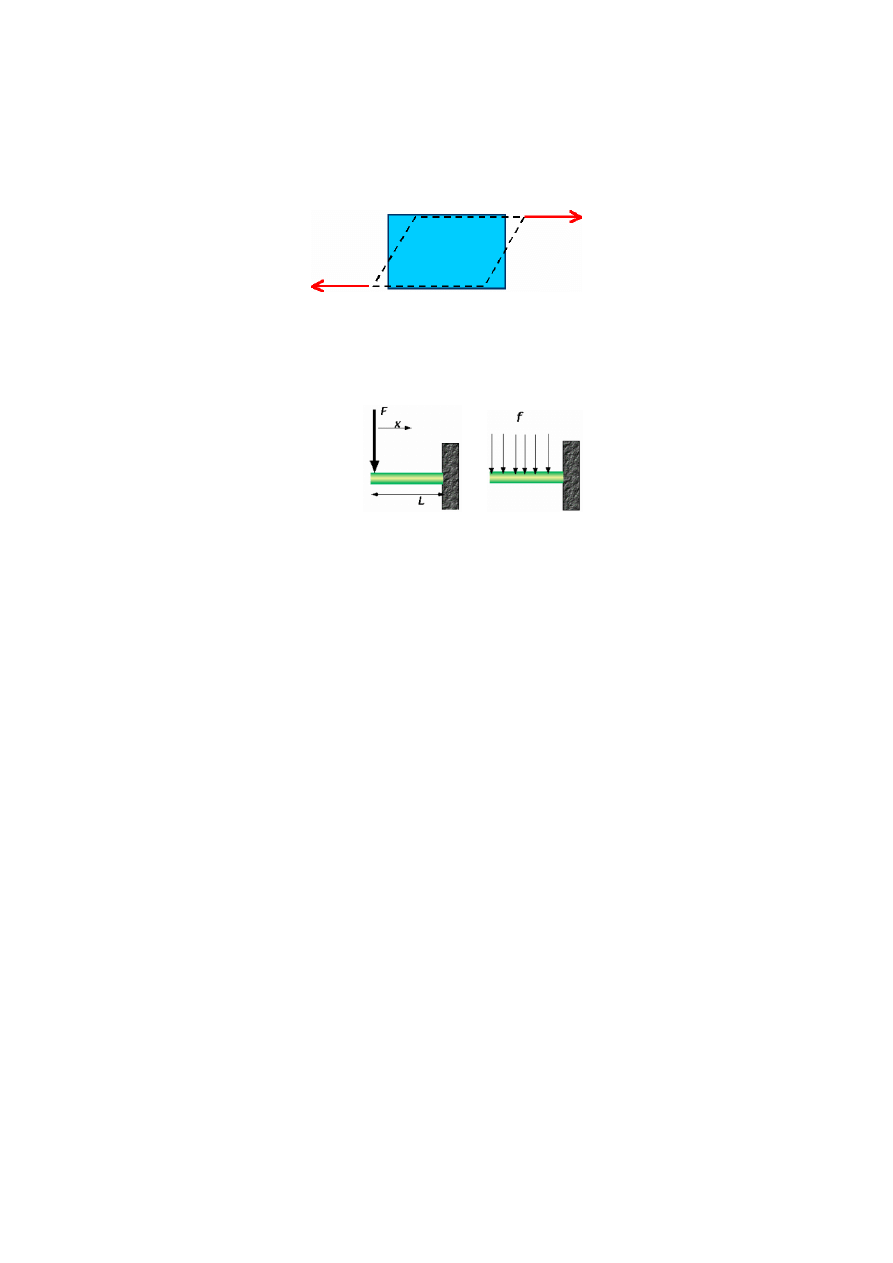
Ścinanie powoduje zmianę kształtu, lecz wielkość pozostaje taka sama (rys. 5.9). Kość jest
najmniej wytrzymała na ścinanie.
Rys. 5.9. Ścinanie
Istnieją różne rodzaje obciążeń: jednoosiowe, dwuosiowe i trójosiowe oraz punktowe i
równomiernie rozłożone (rys. 5.10)
a)
b)
Rys. 5.10. Obciążenie: a) punktowe, b) równomiernie rozłożone [92]
5.3. Wytrzymałość zmęczeniowa
Elementy kostne, mięśniowe i więzadłowe, generalnie tkanki człowieka, są narażone na obciążenia
zmienne w czasie. Organizm praktycznie cały czas pozostaje w ruchu, w związku z czym elementy
ciała człowieka są stale obciążone. Wartości tych obciążeń oraz ich amplituda ulegają ciągłym
zmianom. Z badań doświadczalnych wynika, że powtarzające się obciążenia zmienne mogą
doprowadzić do zniszczenia danego elementu nawet wówczas, gdy naprężenia wywołane tymi
obciążeniami są znacznie mniejsze od doraźnej wytrzymałości danego elementu. Zjawisko
zmniejszenia wytrzymałości elementów pod obciążeniami zmiennymi wiąże się ze zmęczeniem
materiału [1,8,18,24].
Podczas zmęczenia struktur kostnych pod wpływem cyklicznych obciążeń, obserwuje się
pojawienie progresywnie rosnących mikropęknięć, które mogą się kumulować w postaci pęknięć lub
całkowitych złamań, jeśli wartość odkształceń lub liczba cykli będzie odpowiednio duża. Analizując
badania kliniczne wynika, że najczęściej urazy spowodowane przekroczeniem wytrzymałości
zmęczeniowej obserwowane są wśród zawodowych sportowców, rekrutów w wojsku, uprawiających
jogging oraz biegaczy-amatorów [18].
Wyznaczenie granicy własności zmęczeniowych materiałów tkankowych jest praktycznie
niemożliwe. Kości są zabudowane tkankami miękkimi i w ciele człowieka mogą wykazywać wyższą
wytrzymałość zmęczeniową niż podczas badań na preparatach, na co może mieć wpływ przesycenie
płynami ustrojowymi żywej kości. Ponadto, w zależności od wieku człowieka, kości posiadają
odmienne zakresy wytrzymałości zmęczeniowej. Kości dzieci wykazują większe odkształcenia przed
77
momentem zerwania lub pęknięcia, ponieważ są mniej zmineralizowane i ich rekonstrukcja jest
znacznie szybsza. Pod działaniem zmiennych obciążeń następuje tzw. polaryzacja kości i masa kostna
powiększa się po stronie potencjału ujemnego, a zmniejsza się po stronie potencjału dodatniego.
Efekty te są widoczne np. podczas zginania kości, które powoduje odpowiednie przeformowanie jej
struktury. Po stronie większych krzywizn kości znajdują się ładunki dodatnie, a tam, gdzie są mniejsze
krzywizny, ładunki ujemne, które działają pobudzająco na tworzenie się nowej tkanki kostnej.
Występujące napięcia, zwłaszcza w kościach długich, osiągają wartości rzędu 3 mV/N [1,20].
Związki pomiędzy naprężeniami i odkształceniami dla kości są zupełnie inne, niż dla większości
materiałów konstrukcyjnych, ponieważ z punktu widzenia biomechaniki tkanka kostna stanowi
materiał anizotropowy. Kości są zdolne do przystosowywania swojej struktury wewnętrznej, geometrii
i własności materiałowych do przenoszonych obciążeń tak, aby zachować korzystny dla struktur
kostnych stan naprężeń i odkształceń, o czym mówi prawo Wolffa [42]. Własności materiałowe tkanki
kostnej są również związane z wiekiem. Okazuje się, że co 10 lat, pomiędzy 20 a 30 rokiem życia,
następuje spadek 2% wytrzymałości na rozciąganie, tj. odpowiednio od wartości 120 MPa, do 105
MPa w trzeciej dekadzie życia. Jednocześnie spadek modułu Younga z 17 GPa do 15.6 GPa [1].
Zmniejszenie odporności tkanki kostnej na obciążenia zewnętrzne jest także związane ze spadkiem
fizycznej gęstości kości, a tym samym ze wzrostem jej porowatości.
Podsumowując, kości długie, dzięki warstwie korowej zbudowanej na kształt współosiowych rur,
posiadają dużo większą odporność niż analogiczny lity walec o tej samej średnicy. Istota gąbczasta
nasad posiada taki rozkład beleczek kostnych, aby efektywnie przenosić obciążenia z powierzchni
stawowych. Istota międzykomórkowa, złożona z części niezmineralizowanej (białkowej), tzw.
osceiny, to 35% masy kośćca. Złożona jest głównie z włókien kolagenowych przypominających
spirale. Część mineralna masy kostnej jest zbudowana w 65% z hydroksyapatytów. Taka budowa
kości zapewnia jej następujące własności:
1. plastyczność – kość ulega modelowaniu zgodnie z prawem Wolff’a-Delpecha, czyli w reakcji
na ściskanie zanika, a w reakcji na rozciąganie – powstaje [42]. Plastyczność kości zmienia się
w funkcji czasu;
2. sprężystość – kość posiada pamięć kształtu w związku z własnościami kolagenu
umożliwiającemu powrót do kształtu wyjściowego. Po ustąpieniu bodźca, występuje sprężyste
ugięcie łuku kości udowej;
3. odkształcenie fazowe – kość podlega cyklicznym zmianom kształtu, zgodnie z teorią
Sutherlanda, która zakłada, że kość będąca zmodyfikowaną tkanką łączną, zachowuje się w
swej istocie, jak ciecz [91].
Własności tkanki kostnej, jako materiału lepkosprężystego, zależą od prędkości obciążeń i czasu ich
trwania. Poznanie dynamicznych własności kości ma istotne znaczenie, w szczególności, dla
prawidłowego doboru materiału na implanty kostne, których charakterystyki powinny być zbliżone do
charakterystyk kości.