Prof. Edmund Wittbrodt
Tarcie cięgien
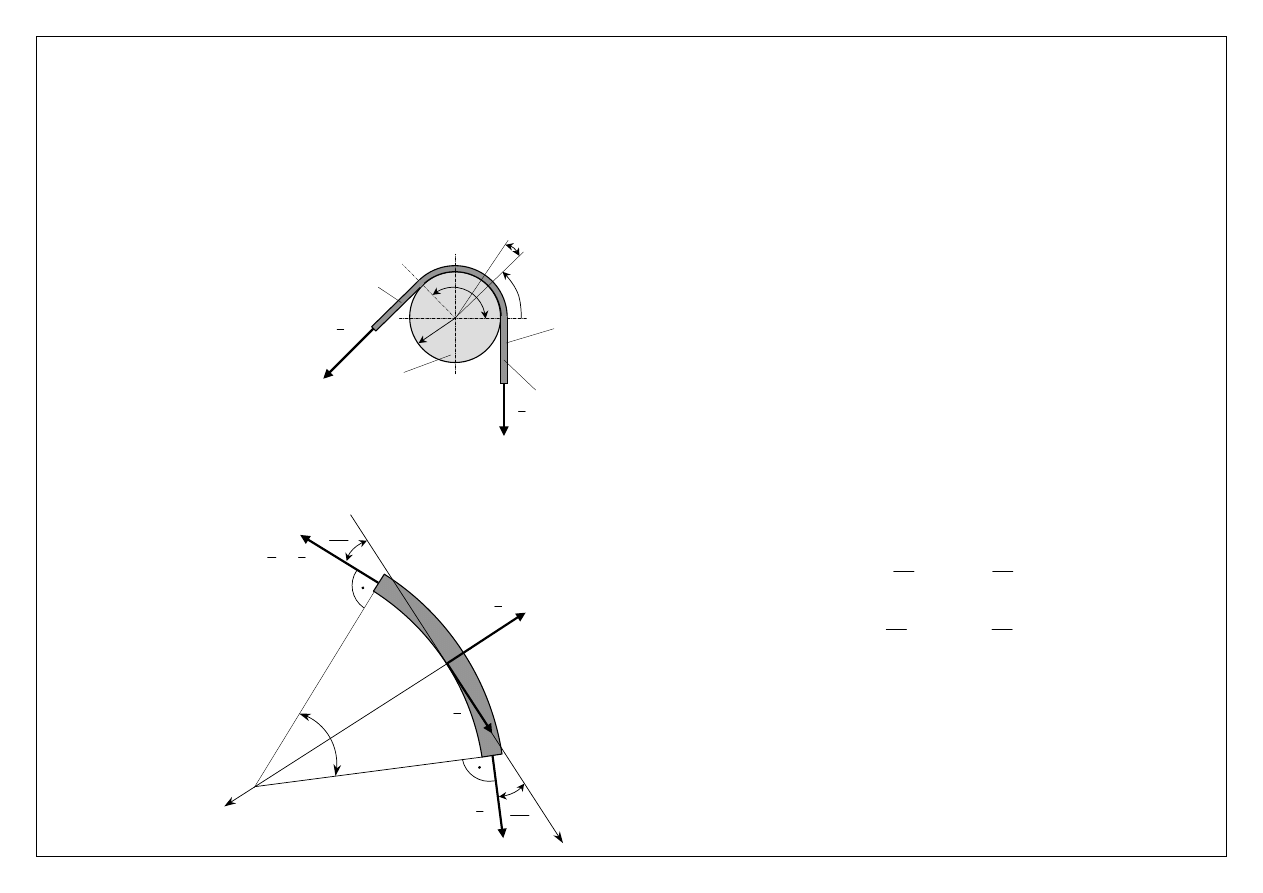
Rozważmy sytuację, w której cięgno przerzucone jest przez bęben. Dane są: R – promień bębna,
ϕ
– kąt opasania,
µ
–
współczynnik tarcia pomiędzy cięgnem a bębnem.
Siły działające na cięgno
Określić chcemy zależność pomiędzy siłami przyłożonymi do końców cięgna tak, aby nie nastąpił poślizg cięgna
względem bębna. W tym celu rozważamy wycinek bębna z zaznaczeniem sił działających na cięgno. Z warunków
równowagi sił na kierunek styczny i normalny mamy:
(
) cos
cos
0
2
2
t
d
d
W
S
dS
dT
S
α
α
= − +
+
+
=
,
(2.32a)
sin
(
) sin
0
2
2
n
d
d
W
dN
S
S
dS
α
α
= −
+
+
+
=
.
(2.32b)
Rozkład sił działających na elementarny fragment cięgna
α
d
2
α
d
2
S
t
α
d
dT
dN
n
+
S
dS
bęben
(cięgno czynne)
α
d
ϕ
α
cięgno
R
O
S
S
(cięgno bierne)
Prof. Edmund Wittbrodt
Przy założeniu małych kątów
d
α
możemy przyjąć uproszczenia:
sin
2
2
d
d
α
α
≈
,
cos
1
2
d
α
≈
,
0
2
d
dS
α
≈
, co po podstawieniu do
(2.32) daje układ równań:
0
dT
dS
−
=
,
0
α
−
=
dN
Sd
(2.33)
Aby rozwiązać ten układ, który zawiera trzy niewiadome, przyjmujemy graniczny stan równowagi, a zatem
dT
dN
µ
=
.
(2.34)
Z układu trzech równań (2.33a, 2.33b) i (2.34) otrzymujemy
µ α
=
dS
d
S
,
(2.35)
co po scałkowaniu daje
µα
=
S
Ae
,
(2.36)
gdzie A jest stałą całkowania.
Stałą całkowania A określimy z następujących warunków brzegowych (rys.): gdy:
α
= 0, S = S
0
;
α
=
ϕ
, S = S, które po
podstawieniu do (2.36) dają:
A = S
0
,
α
=
ϕ
.
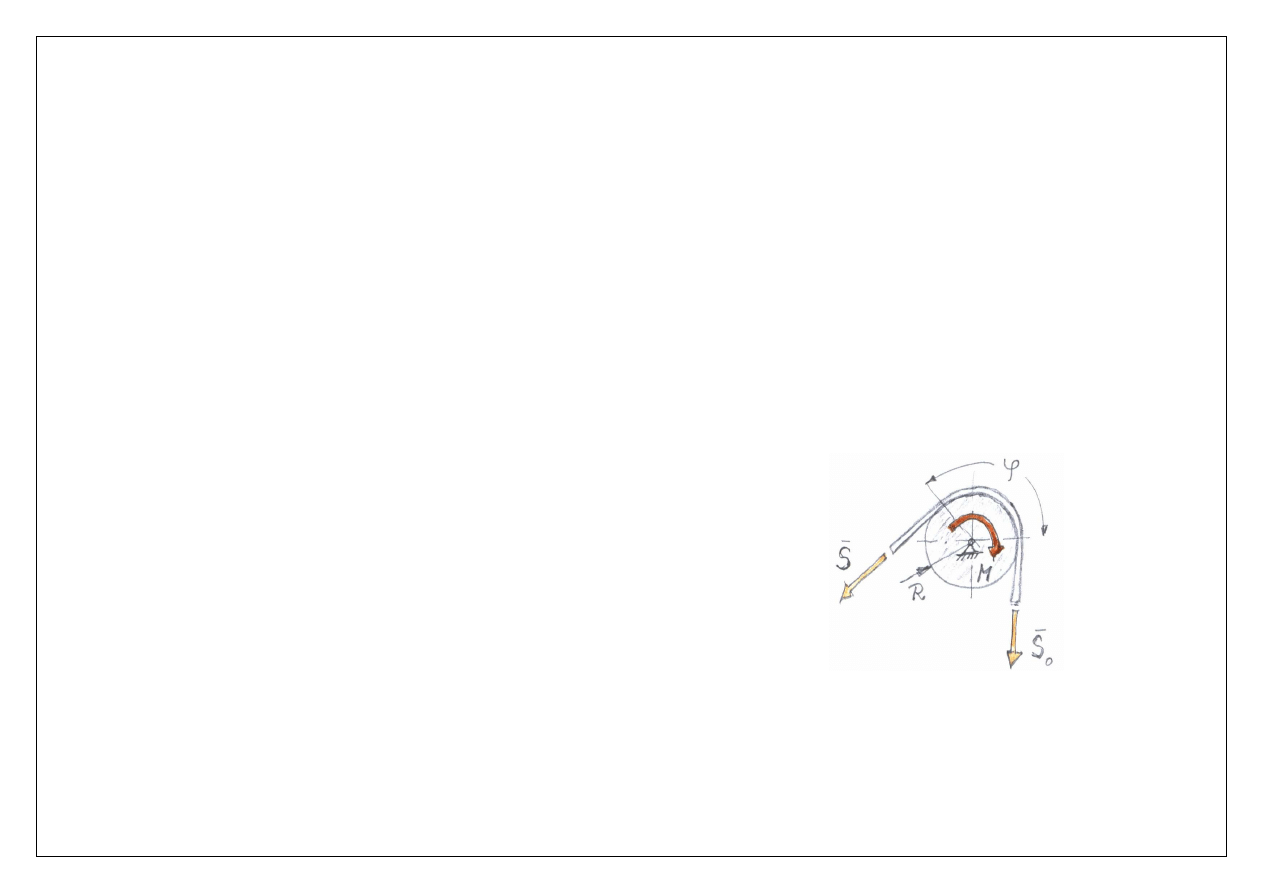
Prof. Edmund Wittbrodt
Zatem wzór (2.36) przyjmuje ostateczną postać (dla
tarcia granicznego
)
0
µϕ
=
S
S e
,
(2.37)
gdzie:
S
– siła przyłożona do cięgna czynnego (ciągnącego),
S = S
0
– siła przyłożona do cięgna biernego (ciągnionego),
µ
– współczynnik tarcia,
ϕ
– kąt opasania bębna.
Moment przenoszony przez przekładnię pasową obliczamy (dla tarcia granicznego,
maksymalny
):
)
1
(
−
=
µϕ
e
R
S
M
o
Prof. Edmund Wittbrodt
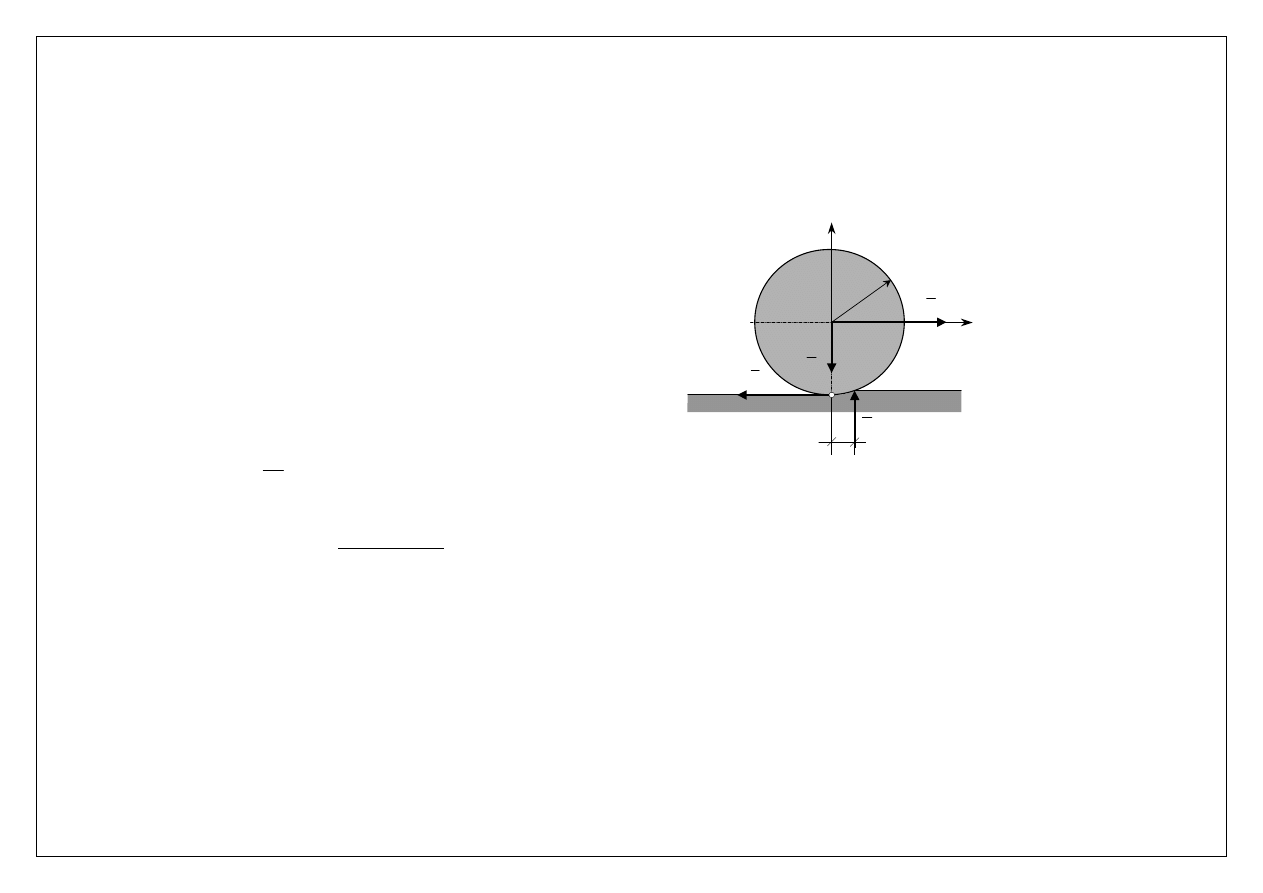
Opory toczenia
Podczas toczenia walca po płaszczyźnie mamy do czynienia z innym rodzajem oporów. Tłumaczymy je odkształcalnością
podłoża i samego walca. W związku z powyższym reakcja normalna podłoża jest przesunięta o wielkość f.
Siły działające na toczący się walec
Z sumy momentów względem punktu O mamy
0
− +
=
Pr
Nf
,
skąd
f
P
N
r
=
.
(2.38)
Jeżeli toczenie odbywa się bez poślizgu, to suma rzutów sił na kierunek osi x równa jest
0
x
W
P T
= − =
,
a zatem
T
P
=
.
(2.39)
Toczenie odbywa się bez poślizgu dopóki siła tarcia spełnia warunek
µ
≤
T
N
.
(2.40)
Z sumy rzutów na kierunek osi y mamy
N
Q
=
.
(2.41)
f
T
N
Q
P
r
y
x
O
Prof. Edmund Wittbrodt
Po podstawieniu (2.41), (2.39), (2.38) do (2.40), otrzymujemy warunek toczenia się walca bez poślizgu w postaci
µ
≤
f
r
.
(2.42)
W tabeli podano wartości współczynników oporu toczenia f dla niektórych par materiałów.
Wartości współczynników oporu toczenia f dla niektórych par materiałów
rodzaje materiałów
f [mm]
koło żeliwne po żeliwie
0,05
koło stalowe po stali
0,05
koło drewniane po drewnie
0,5–1,5
koło drewniane po kamieniu
1,3
koło ze stali hartowanej po
stali hartowanej
0,005–0,01
koło samochodowe po asfalcie
2,4
koło samochodowe po gruncie
trawy
10–15