Dariusz Sobala, dr inż. Materiał dydaktyczny
P
P
r
r
a
a
k
k
t
t
y
y
c
c
z
z
n
n
a
a
m
m
e
e
t
t
o
o
d
d
a
a
w
w
y
y
z
z
n
n
a
a
c
c
z
z
a
a
n
n
i
i
a
a
o
o
d
d
k
k
s
s
z
z
t
t
a
a
ł
ł
c
c
e
e
ń
ń
/
/
n
n
a
a
p
p
r
r
ę
ę
ż
ż
e
e
ń
ń
t
t
e
e
r
r
m
m
i
i
c
c
z
z
n
n
y
y
c
c
h
h
w
w
d
d
o
o
w
w
o
o
l
l
n
n
y
y
m
m
p
p
r
r
z
z
e
e
k
k
r
r
o
o
j
j
u
u
p
p
r
r
z
z
y
y
d
d
o
o
w
w
o
o
l
l
n
n
y
y
m
m
r
r
o
o
z
z
k
k
ł
ł
a
a
d
d
z
z
i
i
e
e
t
t
e
e
m
m
p
p
e
e
r
r
a
a
t
t
u
u
r
r
y
y
n
n
a
a
j
j
e
e
g
g
o
o
w
w
y
y
s
s
o
o
k
k
o
o
ś
ś
c
c
i
i
/
/
s
s
z
z
e
e
r
r
o
o
k
k
o
o
ś
ś
c
c
i
i
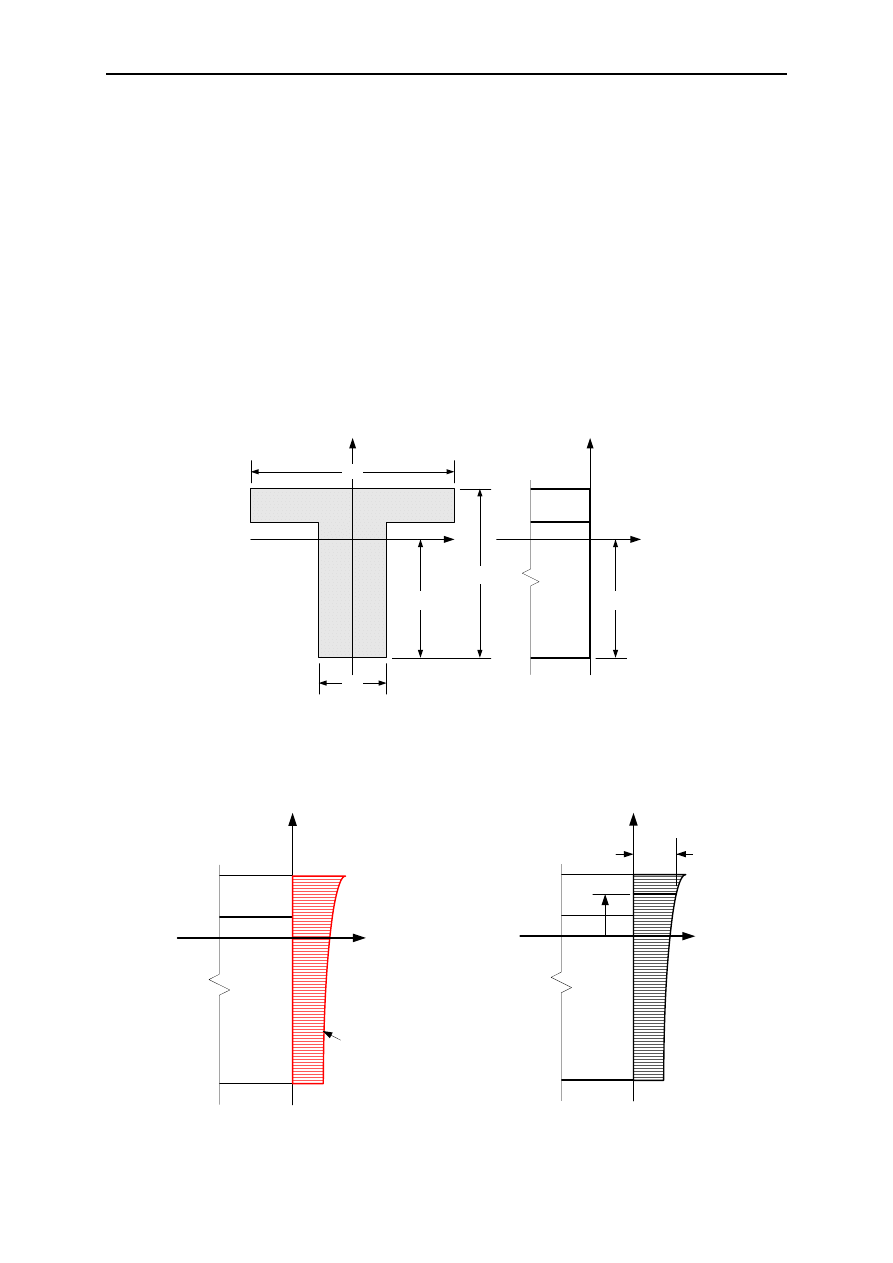
W najogólniejszym przypadku na przekrój poprzeczny elementu działa rozkład nieliniowy
temperatury. Przy zachowaniu założenia płaskich przekrojów odkształcenia termiczne mogą
występować w postaci wydłużenia, skrócenia lub/i obrotu przekroju. Każdy rozkład
nieliniowy temperatury można rozłożyć na składowe: stałą, liniowo zmienną po
wysokości/szerokości przekroju oraz składową nieliniową po wysokości/szerokości
przekroju. Każdą z ww. składowych można poddać odrębnej analizie, a obliczone wielkości
odpowiednio zsumować. Poniżej przedstawiono wygodną procedurę wyznaczania
odkształceń/naprężeń termicznych w dowolnym przekroju, który poddany jest oddziaływaniu
dowolnego rozkładu temperatury. Ze względu na jej praktyczny charakter przedstawiono
procedurę obliczeń dla rozkładu po wysokości przekroju,. Analogiczny tok postępowania
można zastosować w poprzek przekroju znając kształt występującego tam rozkładu
temperatury i charakterystykę elementu w tym kierunku.
Z
Y
b(z)
b(z)
z
0
H
z
X
Z
z
0
Rys. 1. Schemat przekroju poprzecznego i widok z boku elementu
Gdyby włókna przekroju nie były ze sobą powiązane, każde z nich odkształciłoby się
swobodnie zgodnie z (1.1)
X
Z
T(z)
X
Z
z
ε
s
(z)
Rys. 2. Rozkład temperatury T(z) na wysokości przekroju i jego odkształcenia swobodne
ε
s
(z)
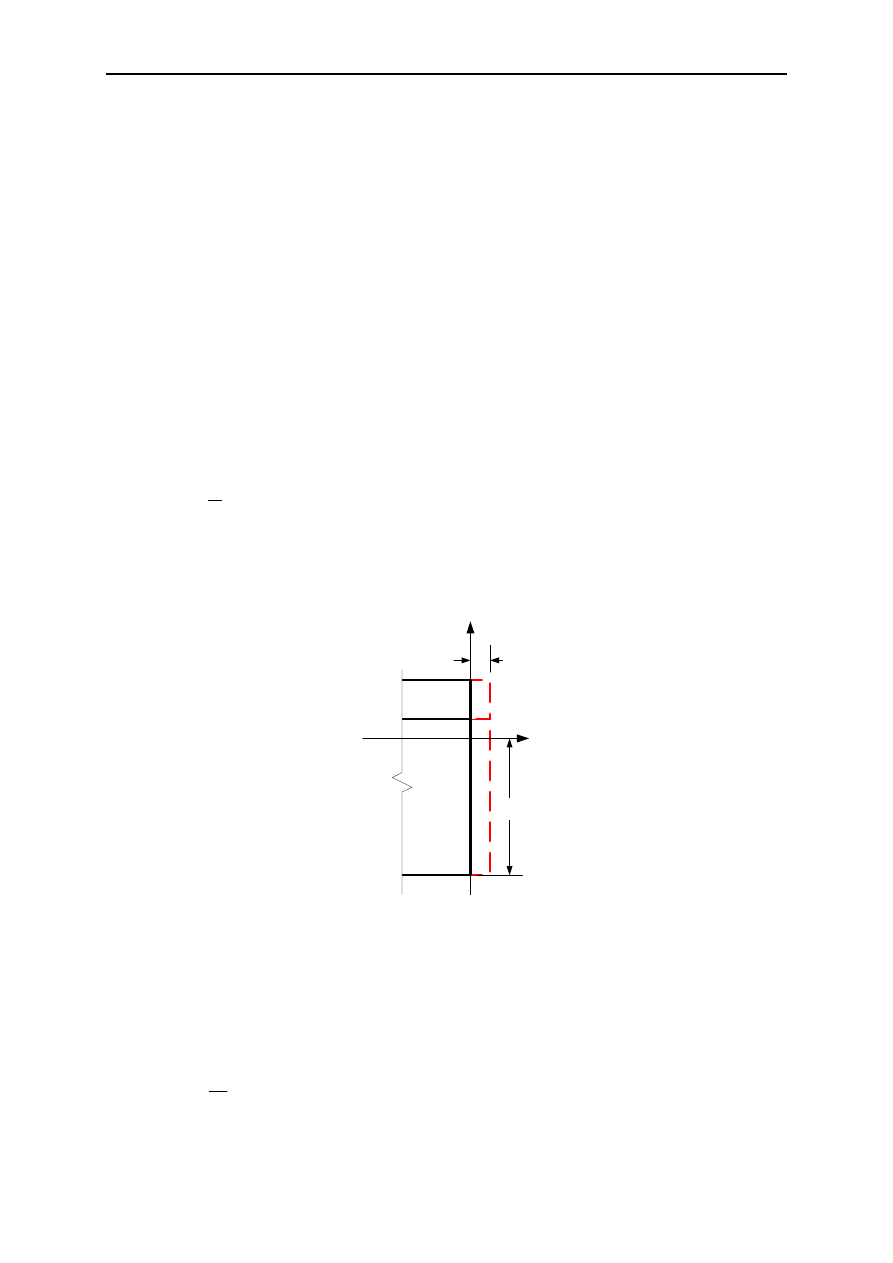
Dariusz Sobala, dr inż. Materiał dydaktyczny
(1.1)
)
(
)
(
)
(
z
T
z
z
s
⋅
=
α
ε
gdzie
ε
s
(z) – odkształcenie swobodne włókna przekroju o współrzędnej z;
α
(z) – współczynnik rozszerzalności termicznej włókna o współrzędnej z;
T(z) – temperatura włókna o współrzędnej z lub jej przyrost w stosunku do stanu
początkowego (rozkład temperatury po wysokości);
z – współrzędna (odległość) rozpatrywanego włókna od osi X w kierunku osi Z, która
zmienia się od wartości -z
0
do H
z
-z
0
;
H
z
– wysokość przekroju wzdłuż osi Z (Rys. 1)
(1.2)
)
(
)
(
)
(
z
E
z
z
P
s
⋅
=
ε
gdzie E(z) – moduł sprężystości dla włókna przekroju o współrzędnej z;
P(z) – uogólniona zastępcza siła zewnętrzna przywracająca rzeczywisty
kształt/wymiary elementu i powodująca powstanie naprężeń w przekroju.
Część równomierną odkształcenia w przekroju (wydłużenie/skrócenie) można wyznaczyć z
zależności (1.3).
(1.3)
∫
−
−
=
0
0
)
(
)
(
)
(
1
z
H
z
u
z
dz
z
b
z
z
T
A
α
ε
gdzie
ε
u
– składowa równomierna odkształcenia na wysokości przekroju;
A – sprowadzone pole przekroju poprzecznego elementu;
b(z) – szerokość przekroju na poziomie z.
X
Z
z
0
ε
u
Rys. 1. Składowa równomierna odkształcenie przekroju
Zachowanie zasady płaskich przekrojów Bernoulli’ego-Navier’a wymaga, aby przekrój płaski
po obciążeniu pozostał nadal płaski. Ten stan osiąga poprzez przesunięcie przekroju po osi
lub obrót przekroju wokół osi, np. osi poziomej Y. Krzywiznę (nachylenie) przekroju
φ
y
można wyznaczyć na podstawie zależności (1.4) sformułowanej przez Priestley’a [Pristley,
1978]. Odkształcenia spowodowane obrotem są równe
ε
φ
(z)=
φ
y
⋅
z.
(1.4)
∫
−
−
=
0
0
)
(
)
(
)
(
1
z
H
z
y
y
z
dz
z
z
b
z
z
T
I
α
φ
gdzie I
y
- sprowadzony moment bezwładności przekroju względem osi Y.
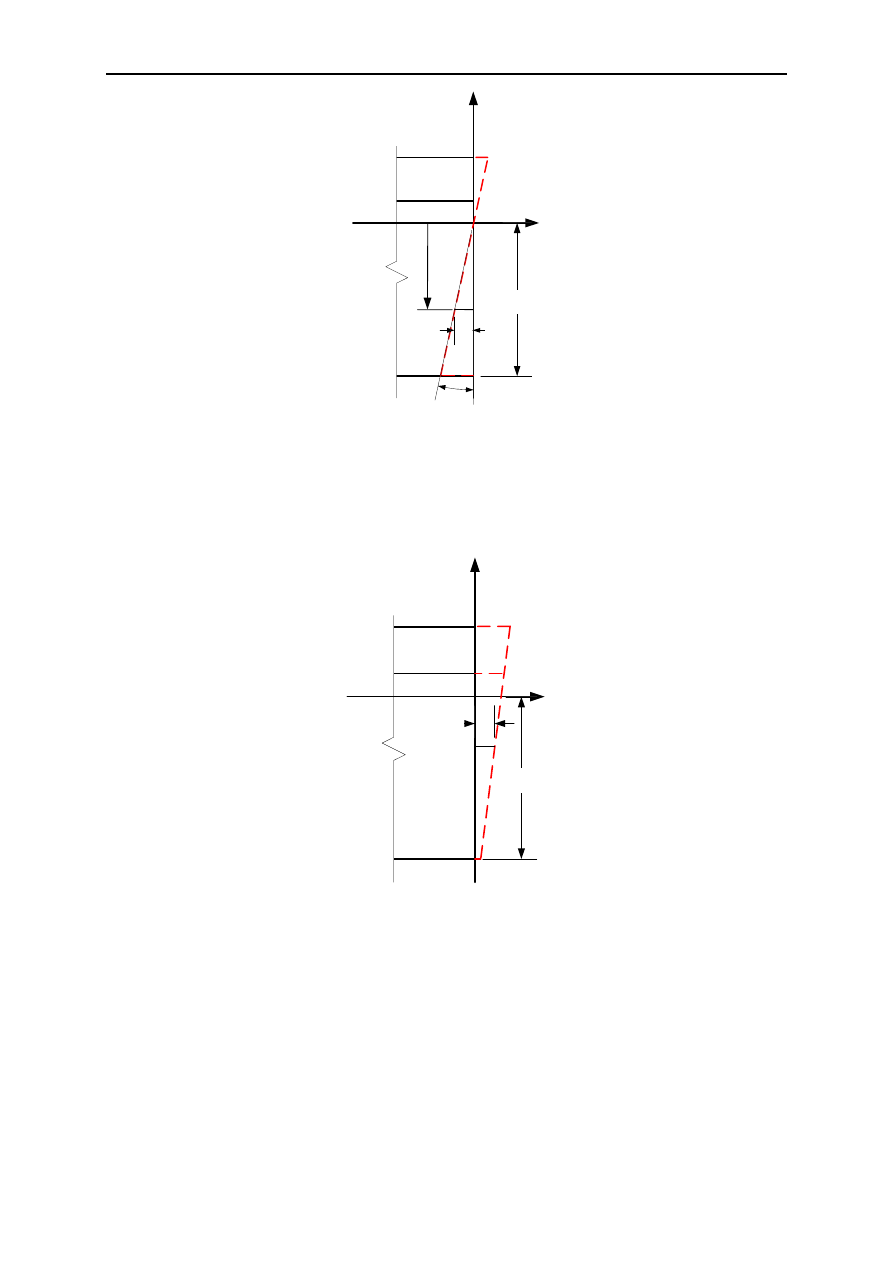
Dariusz Sobala, dr inż. Materiał dydaktyczny
X
Z
z
0
ε
φ
(z)
z
φ
y
z
Rys. 2. Obrót przekroju
φ
y
spowodowany liniowym rozkładem temperatury na wysokości przekroju
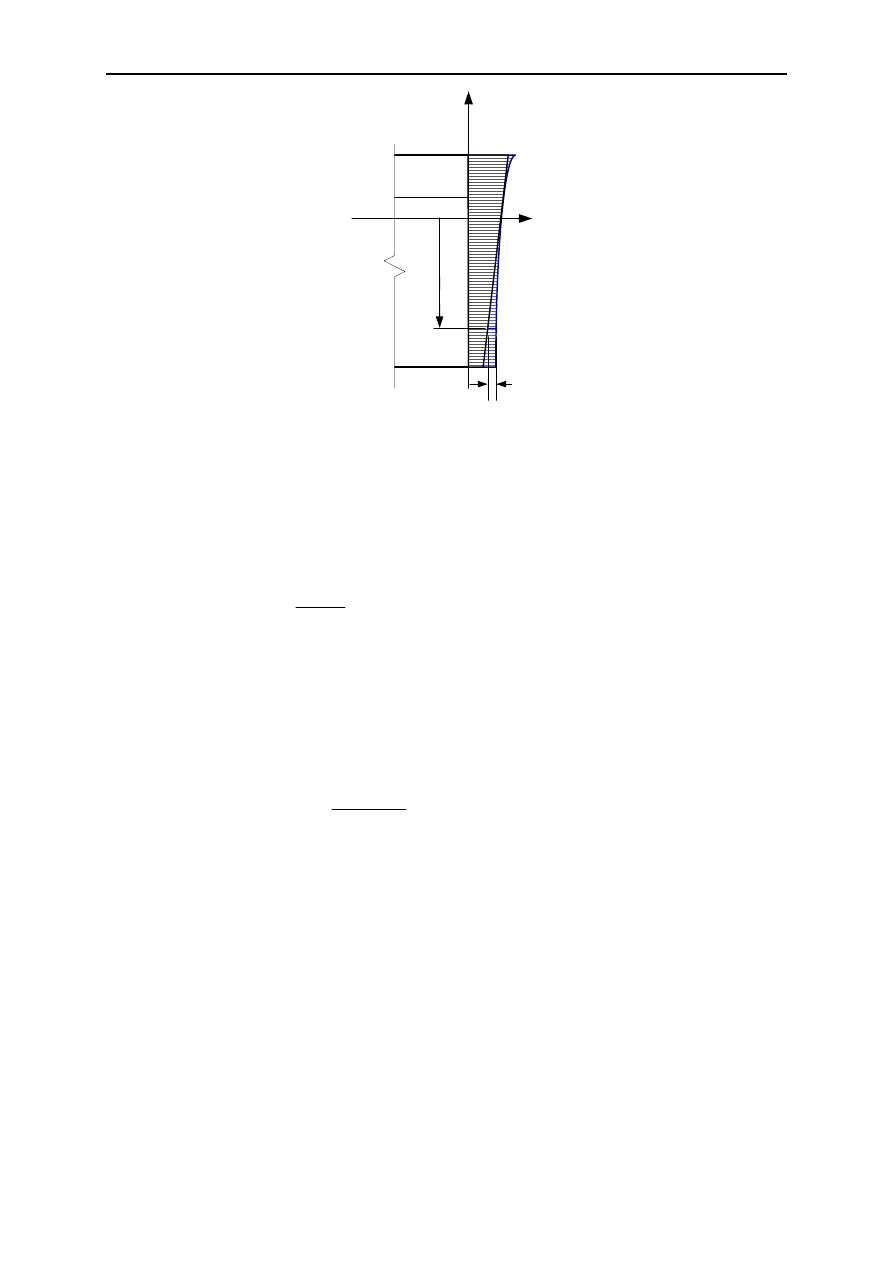
Odkształcenie całkowite przekroju składać się będzie z odkształcenia równomiernego oraz
odkształcenia wywołanego obrotem (1.5).
(1.5)
z
z
z
y
u
u
c
⋅
+
=
+
=
φ
ε
ε
ε
ε
φ
)
(
)
(
X
Z
z
0
ε
c
(z)
Rys. 3. Odkształcenia całkowite przekroju
ε
c
(z)
Zatem naprężenia termiczne, do których wyznaczenia ostatecznie dążymy, pochodzić będą od
odkształcenia wymuszonego (1.6), które stanowić będzie różnicę odkształcenia całkowitego i
swobodnego.
(1.6)
)
(
)
(
)
(
z
z
z
s
c
w
ε
ε
ε
−
=
gdzie
ε
w
(z) – odkształcenie włókna o współrzędnej z wymuszone więzami wewnętrznymi
istniejącymi w przekroju
Dariusz Sobala, dr inż. Materiał dydaktyczny
X
Z
z
ε
w
(z)
Rys. 4.. Odkształcenia wymuszone w przekroju
(1.7)
)
(
)
(
)
(
z
z
E
z
w
T
ε
σ
⋅
=
gdzie
σ
T
(z) – naprężenie w przekroju na poziomie włókna z;
E(z) – moduł sprężystości włókna z przekroju.
Przemieszczenie punktu leżącego na osi przekroju można wyznaczyć z zależności (1.8).
(1.8)
∫
−
−
⋅
⋅
⋅
Δ
=
⋅
=
Δ
0
0
)
(
)
(
)
(
z
H
z
T
u
u
x
z
dz
z
b
z
A
L
T
L
z
L
α
ε
gdzie
L
x
– odległość przekroju od podpory stałej mierzona wzdłuż osi X.
Dla dowolnego punktu przekroju należy wprowadzić korektę wartości przemieszczenia
wynikającą z obrotu przekroju w postaci (1.9).
(1.9)
∫
−
⋅
⋅
⋅
⋅
⋅
Δ
=
⋅
⋅
=
ΔΔ
0
0
)
(
)
(
)
(
z
H
z
T
y
x
u
x
y
x
z
dz
z
z
b
z
I
z
L
T
L
z
z
L
α
φ