1

MATERIAŁY DLA STUDENTÓW

Przedmiot:

Higiena i Epidemiologia

Ć

wiczenie:

Podstawy biostatystyki

Prowadzący:

Prof. dr hab. med. Jan E. Zejda

Cel (wynik) zajęć:

Poznanie podstawowych pojęć i terminów stosowanych w biostatystyce
i zrozumienie znaczenia pojęcia „efekt”. Poznanie metody szacowania oraz
stosowania podstawowych testów statystycznej znamienności różnic
i zależności

Przeznaczenie materiałów:

Przygotowanie studenta do aktywnego udziału w ćwiczeniu

Program ćwiczenia:

Szacowanie parametrów populacyjnych (zmienne ilościowe i jakościowe)

Zastosowanie testu t-Studenta, testu chi-kwadrat i analizy korelacji

……………………………………………………………………………………………….

1.0

Definicje

1.1

Zmienna (ang: variable)

Cecha poddawana obserwacji i mierzona w sposób zgodny z jej właściwościami lub protokołem badania jest w
terminologii biostatystycznej określana jako zmienna. Przykładami zmiennych są m.in. ‘wysokość ciała’,
‘poziom wykształcenia’, ‘kreatyninemia’, ‘duszność’, ‘cień okrągły w obrazie rtg płuc’.

Nazwa wywodzi się z faktu, że badana cecha w naturalny sposób przyjmuje różną (zmienną) wartość (ang.
value) u różnych badanych (lub szerzej obiektów badania). Na przykład zmienna ‘wysokość ciała’ przyjmuje
różne wartości u poszczególnych badanych, w określonym przedziale, wyrażane w centymetrach (wartością
zmiennej jest w tym przypadku wynik pomiaru w cm). Z kolei zmienna ‘cień okrągły w obrazie rtg płuc’ – w
najprostszym ujęciu – przyjmuje dwie wartości; albo cień jest obecny (wartość = „tak”), albo cień jest nieobecny
(wartość = „nie”). W ostatnim przykładzie można sobie wyobrazić więcej wartości, na przykład: cień nieobecny
(„-”), cień prawdopodobnie obecny („+/-”), cień obecny („+”). Niezależnie od sposobu prezentacji każdy
badany posiada sobie właściwą wartość analizowanej zmiennej (w danym stanie). Na przykład dla badanego
J.E.Z. wartość zmiennej ‘wysokość ciała’ wynosi 178 cm, a wartość zmiennej ‘cień okrągły w rtg płuc’ wynosi
„-” (należy przynajmniej mieć taką nadzieję).

1.2

Klasyfikacja zmiennych

Prosty podział zmiennych uwzględnia ich postać lub funkcję.

1.2.1

Postać zmiennej

Postać zmiennej jest zależna od sposobu prezentacji jej wartości. Najprostszy podział wyróżnia zmienne
ilościowe, zmienne półilościowe i zmienne jakościowe.

W przypadku zmiennych ilościowych wartość ma charakter ilościowy. Przykładem może być ‘wysokość ciała’
wyrażona w cm (dla danego badanego wartość tej zmiennej to „ilość centymetrów”, np. 164 cm). Innym
przykładem tego typu zmiennej może być ‘glikemia’ (wartość to ilość wyrażona w mg/100 ml).

W przypadku zmiennych jakościowych wartość ma charakter jakościowy. Przykładem może być ‘remisja bólu’.
Jest ona albo obecna (wartość „tak”), albo nieobecna (wartość „nie”). U jednego badanego te wartości
wzajemnie się wykluczają (remisja nie może być jednocześnie obecna i nieobecna). Sposób zapisu wartości
zmiennej jakościowej ma charakter umowny. Można np. zapisać obecność remisji symbolem „tak” lub „+” lub
„1”, a brak remisji symbolem „nie” lub „-” lub „2”).

2

W przypadku zmiennych półilościowych wartość zmiennej ma charakter pośredni pomiędzy zmienną ilościową i
jakościową. Na przykład wartość zmiennej ‘remisja bólu’ może przyjmować jeden z następujących poziomów:
„całkowita”, „prawie całkowita”, „częściowa”, „ledwo zauważalna”, „brak”. Innym przykładem tego typu
zmiennej jest tzw. ‘kliniczny stopień duszności’. Wartość tej zmiennej waha się w przedziale od 1 do 5, w
zależności od natężenia aktywności fizycznej, podczas której pojawia się uczucie duszności.

Zmienne ilościowe można poddawać transformacji. Jej rezultatem mogą być zmienne jakościowe lub
półilościowe. Przykładem może być transformacja zmiennej ‘wskaźnik masa ciała’ (w.m.c.). W oryginalnej
postaci jest to zmienna ilościowa (wartością jest ilość kilogramów w odniesieniu do kwadratu wysokości, na
przykład 23 kg/m

2

). Wartości w.m.c. w zakresie 20-25 kg/m

2

traktowane są jako prawidłowe, większe jako

przejaw nadwagi lub otyłości. W tej postaci zmienna w.m.c. jest traktowana jako zmienna jakościowa z dwiema
wartościami: prawidłowy w.m.c / zwiększony w.m.c. Wiadomo, że ma biologiczny sens dalsze zróżnicowanie
wartości w.m.c., co prowadzi do uzyskania zmiennej półilościowej o następujących wartościach: niedożywienie
(<18,0 kg/m

2

), szczupłość (18,0-20,0 kg/m

2

), prawidłowa masa (20,1-25,0 kg/m

2

), nadwaga (25,1-27,0 kg/m

2

),

otyłość (>27 kg/m

2

). W tym przypadku zmienna półilościowa ma pięć wartości. Transformacja zmiennych jest

powszechnie wykorzystywana w diagnostyce – hiperbilirubinemię (zmienna jakościowa o wartościach tak lub
nie) rozpoznaje się na podstawie zmierzonej wartości bilirubinemii (zmienna ilościowa), podwyższone ryzyko
zgonu sercowo-naczyniowego (tak/nie) na podstawie obliczonej wartości liczbowego wskaźnika (np. SCORE),
itp.

Sposób przekształcenia zmiennej ilościowej w jakościową (wybór wartości decyzyjnej) może mieć charakter
standardowy lub umowny (autorski). W praktyce klinicznej dominuje pierwszy sposób – ustalone są np. górne
wartości stężeń tzw. parametrów biochemicznych w płynach ustrojowych (np. stężenie kreatyniny w krwi,
stężenie mikroglobulin w moczu itd.). W badaniach naukowych wykorzystuje się także drugi sposób.

Przedstawiony powyżej podział zmiennych ma charakter uproszczony, aczkolwiek wystarczający w większości
sytuacji. Kompletny podział uwzględnia cztery klasy:

zmienne ilościowe:

ciągłe (wartością jest liczba – np. masa ciała w kg)

dyskretne (wartością jest liczebność – np. liczba zgonów w ciągu doby)

zmienne jakościowe:

nominalne (wartością jest kategoria – np. płeć; obie płci są jednakowo ważne)

porządkowe (wartością jest hierarchiczna kategoria – np. kliniczny stopień duszności)

1.2.2

Funkcja zmiennej

Pomiar zmiennych jest prowadzony w dwóch celach. Pierwszym jest cel opisowy, drugim jest cel analityczny.

Cel opisowy jest jednoznaczny – jest nim opis stanu faktycznego. Na przykład przedmiotem badania może być
poznanie ilorazu inteligencji epidemiologów lub poznanie przyrostu masy ciała kobiet w drugim trymestrze
ciąży. W tego typu sytuacjach opis może mieć mniej lub bardziej rozbudowany charakter, ale w najprostszym
wydaniu polega na obliczeniu średniej wartości zmiennej ilościowej lub częstości poszczególnych wartości
zmiennej jakościowej. W pierwszym przypadku będzie to średni iloraz inteligencji (zmienna ilościowa) i średni
przyrost masy ciała (zmienna ilościowa); w drugim przypadku odsetek niskich i wysokich ilorazów inteligencji
(zmienna jakościowa) lub odsetek prawidłowych i nadmiernych przyrostów masy ciała (zmienna jakościowa).

Cel analityczny wiąże się z badaniem uwarunkowań obserwowanych zjawisk (analiza uwarunkowań). W tym
przypadku osią dociekań jest ustalenie zależności pomiędzy dwiema (lub więcej niż dwiema) zmiennymi.
Można np. analizować zależność pomiędzy wartością energetyczną posiłków i wskaźnikiem masy ciała.
Naturalnym założeniem w tym przypadku jest oczekiwanie, że w.m.c zależy od podaży kalorii. W związku z
tym w.m.c. jest traktowany jako zmienna zależna (ang. dependent variable) a podaż kalorii jako zmienna
niezależna (ang. independent variable). To badanie może uwzględniać także inne okoliczności, np. płeć
(możliwość innych relacji „podaż kalorii – masa ciała” u kobiet i mężczyzn), wiek i pochodzenie etniczne. W
tym przypadku jednej zmiennej zależnej (w.m.c.) towarzyszą cztery zmienne niezależne: podaż kalorii, płeć,
wiek, etniczność. Należy przy tym zwrócić uwagę, że w każdej analizie występuje tylko jedna zmienna zależna i
musi być ona w sposób jednoznaczny zdefiniowana. Zadanie to nie zawsze jest łatwe. W podanym przykładzie
kierunek dociekań jest uzasadniony na gruncie wiedzy medycznej i znajduje potwierdzenie etiopatogenetyczne.
Można jednakże wyobrazić sobie sytuację, w której sprecyzowanie kierunku dociekań jest trudne. Można np. się
zastanawiać, czy częstość napadów duszności astmatycznej zależy od częstości stosowania inhalatora
broncholitycznego czy też ma miejsce sytuacja odwrotna – chorzy z cięższym przebiegiem astmy częściej

3

sięgają po inhalator. W takiej sytuacji obowiązek jednoznacznego określenia co jest zmienną zależną a co jest
zmienną niezależną spoczywa na prowadzącym badanie. Może być przecież przedmiotem zainteresowania
pytanie, czy np. pobór kalorii w posiłkach jest zależny od masy ciała.

Zmienna zależna odzwierciedla – w założeniu – skutek oddziaływań zmiennych niezależnych. Te ostatnie, w
zależności od rodzaju badania, mogą być także nazywane zmiennymi objaśniającymi, predykatorami,
determinantami. Termin „zmienna niezależna” ma jednakże ogólny charakter i wystarczająco tłumaczy funkcję
zmiennej.

1.3

Obserwacja

W terminologii biostatystycznej obserwacja (czasem zwana rekordem) jest zbiorem wartości zmiennych
pozyskanych w wyniku pomiarów zaplanowanych i przeprowadzonych w obiekcie (jednostce) badania. W
epidemiologii obiektem (jednostką) badania jest najczęściej pojedynczy człowiek, ale inne sytuacje są częste.
Na przykład obiektem badania może być „anonimowa” próbka krwi (celem pracy może być ustalenie wyłącznie
współwystępowania niedoboru żelaza z obrazem morfologicznym erytrocytów, bez zamiarów powiązania tej
cechy z innymi cechami dawcy krwi). Obiektem badania może być powiat (celem pracy może być ustalenie
zależności pomiędzy poziomem bezrobocia w powiecie i zachorowalnością na gruźlicę) – w tym przypadku
pojedynczy powiat jest pojedynczą obserwacją składającą się z dwóch zmiennych: bezrobocie i zachorowalność
na gruźlicę.

W epidemiologii zwykle i najczęściej badany człowiek jest – w terminologii biostatystycznej – pojedynczą
obserwacją. Każda obserwacja (każdy badany) posiada swój unikalny identyfikator (najczęściej numer). W
przypadku, gdy grupa objęta badaniem liczy 70 osób tego typu badanie zawiera 70 obserwacji,
ponumerowanych od 1 do 70. Jest niezmiernie istotne, aby każdy badany był zbadany w ten sam sposób, w
takim samym zakresie. Innymi słowy, dla każdego badanego konieczne jest pozyskanie pomiarów w zakresie
wszystkich zmiennych zaplanowanych w protokole badawczym. Odstępstwa od tego kanonu nie są niespotykane
w przypadku badań na tzw. materiale klinicznym, ale konsekwencje tego odstępstwa są poważne. Ich uniknięcie
jest możliwe, gdy pierwszym etapem badania jest opracowanie i spisanie szczegółowego protokołu badawczego,
rygorystycznie przestrzeganego podczas wszystkich faz realizacji badania.

Zbiór wszystkich obserwacji pozyskanych w ramach jednego badania stanowi bazę danych. Ze względów
praktycznych, także związanych z wymogami programów statystycznych, nazwy zmiennych w bazie danych są
kodowane (np., skrót oryginalnej nazwy lub inny sposób kodowania), a dla identyfikacji tych kodów (pamięć
epidemiologa a nawet biostatystyka bywa zawodna) konieczne jest przygotowanie czytelnego słowniczka.
Dotyczy to także kodowania wartości zmiennych. Na przykład obecność ‘przewlekłego kaszlu’ może być
kodowana jako „tak” lub „+” lub „1”, a jego brak jako „nie” lub „-” lub „2”. Przykład bazy danych jest
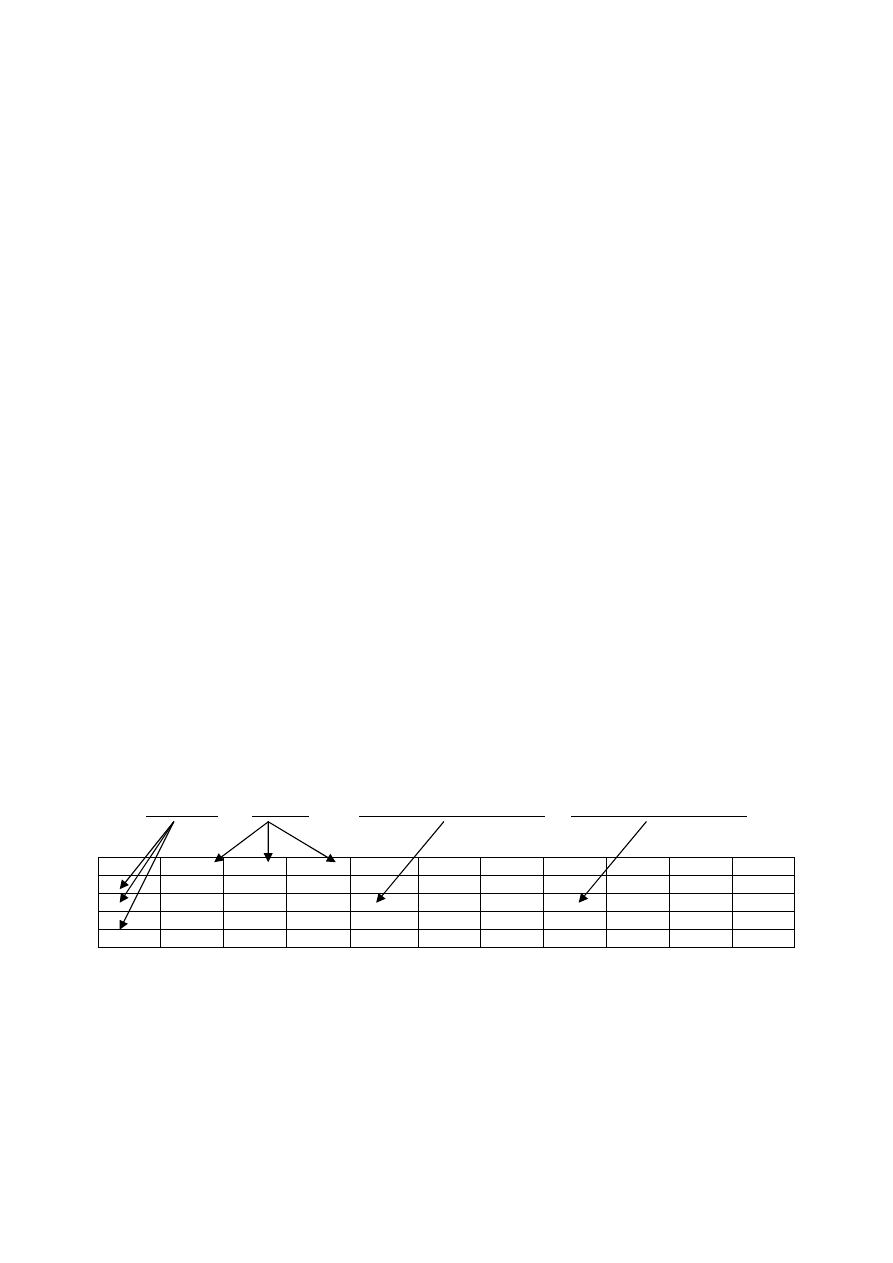
przedstawiony poniżej (każda obserwacja zawiera 10 zmiennych).

obserwacje

zmienne

wartość zmiennej jakościowej

wartość zmiennej ilościowej

NR

WIEK

PLEC

PKASZ ODKRZ KSD

FVC

FEV1

PAL

KRW

RTG

1

37

1

1

2

2

4,37

4,00

1

2

1

2

54

1

2

2

4

2,78

2,11

1

2

2

…

70

40

2

1

1

1

5,34

4,87

2

2

1

Słowniczek: NR – numer badanego; WIEK – wiek w latach; PLEC – płeć (1=mężczyzna, 2=kobieta); PKASZ –
przewlekły kaszel (1 = tak, 2 = nie); ODKRZ – przewlekłe odkrztuszanie (1=tak, 2=nie); KSD – kliniczny
stopień duszności (według skali 0-5); FVC – natężona pojemność życiowa (w litrach) ……


2.0

Rozkład zmiennych

Ze względu na zjawisko biologicznej zmienności międzyosobniczej żadna pojedyncza wartość analizowanej
zmiennej nie charakteryzuje badanej cechy. Nie istnieje przecież jedna „sztywna” wartość wysokości ciała
zdrowych dwudziestolatków; nie istnieje jedna, prawidłowa wartość tętna typowa dla zdrowych noworodków.

4

Zróżnicowanie wartości zmiennej jest zatem naturalnym zjawiskiem, a opis tego zróżnicowania jest – w
terminologii biostatystycznej – opisem rozkładu tej zmiennej. Opis rozkładu zmiennej jest konieczny dla
prezentacji i zrozumienia właściwości badanej cechy. Opis rozkładu jest inny w przypadku zmiennej ilościowej i
inny w przypadku zmiennej jakościowej.

2.1

Rozkład zmiennych ilościowych

Pomiar jednej zmiennej ilościowej u kilkunastu, a na pewno u kilkudziesięciu badanych prowadzi do otrzymania
serii liczb, które trudno ogarnąć bez zastosowania technik upraszczających, identyfikujących sedno rozkładu.
Przykładem może być zamieszczona poniżej seria wyników pomiaru masy ciała u pięćdziesięciu noworodków:
2,21 2,24 2,33 2,33 2,45 2,47 2,49 2,50 2,52 2,55 2,55 2,74 2,76 2,79 2,80 2,81 2,83 2,89 2,93 3,00 3,13 3,14
3,14 3,23 3,24 3,24 3,24 3,25 3,28 3,28 3,55 3,56 3,56 3,65 3,67 3,68 3,69 3,71 3,72 3,84 3,84 3,86 3,87 3,93
3,94 4,03 4,04 4,11 4,20 4,63 (seria ta została wtórnie uporządkowana zgodnie z rosnącymi wartościami).
Rozkład zmiennej w podanym przykładzie można przedstawić w formie graficznej lub matematycznej.

Podstawową graficzną prezentacją rozkładu zmiennej ilościowej jest histogram. Histogram ujawnia, z jaką
częstością występują poszczególne wartości zmiennych. W podanej powyżej serii można odnaleźć dwa pomiary
w przedziale 2,20 – 2,29 kg, dwa pomiary o wartościach 2,30-2,39 kg, trzy pomiary o wartościach 2,40-2,49 kg,
i.t.d. Szerokość przedziałów nie powinna być zbyt duża, aby ujawnić obserwowane zróżnicowane, ale decyzja w
tej sprawie jest zwykle zależna od liczby obserwacji i należy do osoby analizującej uzyskane dane. Rezultatem
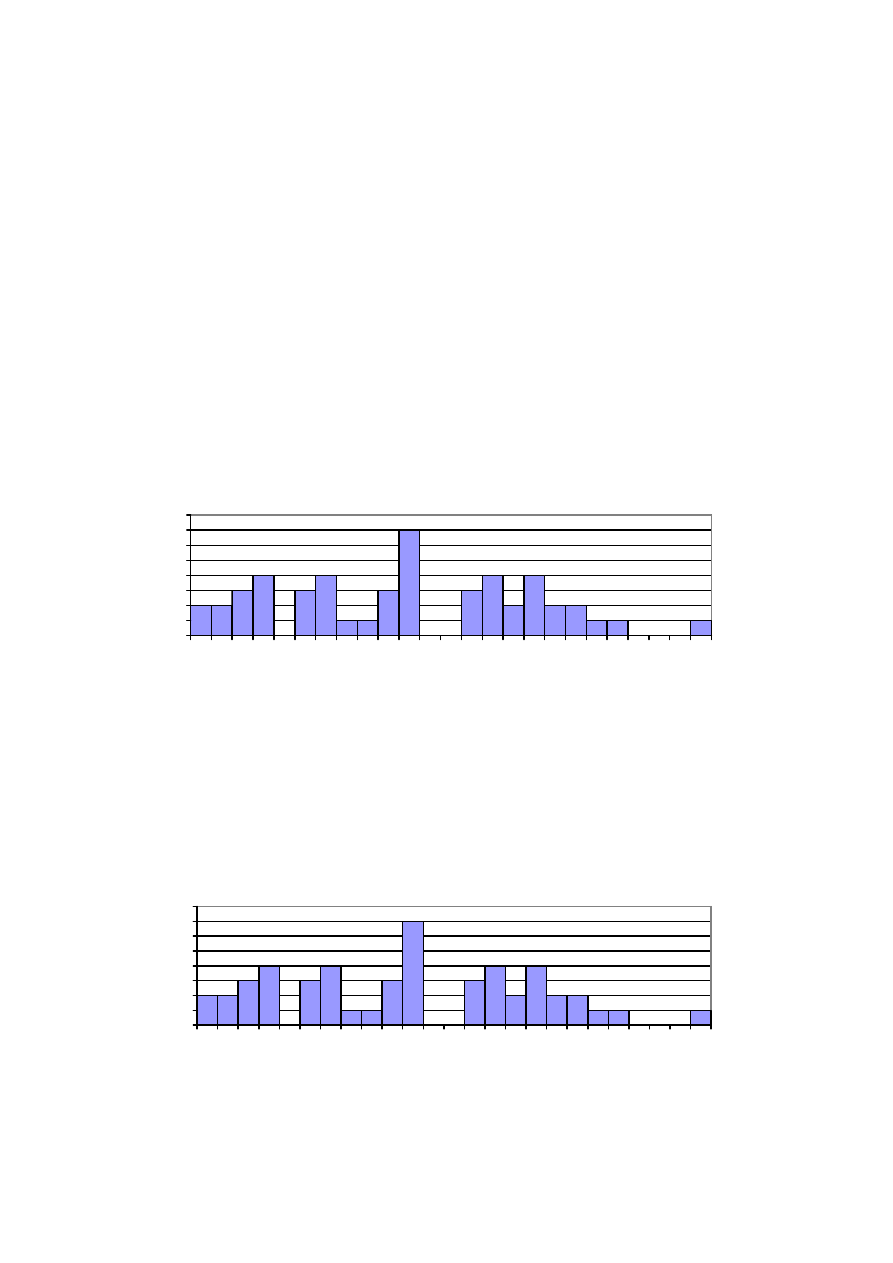
analizy jest histogram, w przypadku przytoczonego przykładu zamieszczony poniżej:















Ogląd histogramu ujawnia, że w serii wyników pomiaru masy ciała (w rozkładzie zmiennej masa) najwięcej jest
wartości lokowanych w środku rozkładu, mniej w jego krańcowych obszarach. Taki profil rozkładu jest znany
jako tzw. rozkład normalny („gaussowski”), znajdujący zastosowanie w opisie („pasujący do”) wielu zmiennych
reprezentujących cechy biologiczne. Powyższy histogram pokazuje bezwzględną częstość poszczególnych
wartości. Przydatne, dla porównań rozkładów tej samej zmiennej w różnych grupach, jest zastosowanie tzw.
względnej częstości (%). W tym przypadku liczba obserwacji (n=50) stanowi 100%, a zatem dwie obserwacje z
przedziału 2,20 – 2,29 kg stanowią 4,0% (2/50 * 100% = 4,0%). Histogram przekształcony do wartości
względnych jest przedstawiony poniżej:














Poza profilem rozkładu i częstością poszczególnych wartości histogram ujawnia wartość najmniejszą i
największą, czyli zakres wartości badanej zmiennej.

0

1

2

3

4

5

6

7

8

2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 4 4,1 4,2 4,3 4,4 4,5 4,6

Masa (kg)

n

0

2

4

6

8

10

12

14

16

2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 4 4,1 4,2 4,3 4,4 4,5 4,6

Masa (kg)

%

5

Matematyczna prezentacja rozkładu zmiennej ilościowej polega na podaniu zakresu wartości (najniższa i
najwyższa wartość), wartości występującej najczęściej (modalna lub moda), wartości środkowej dzielącej zbiór
na dwie równe połowy, po uszeregowaniu wyników od najmniejszego do największego (mediana), a wreszcie na
obliczeniu wartości średniej arytmetycznej i wartości odchylenia standardowego. Wystarczająca informacja na
temat rozkładu zmiennej ilościowej, w analizowanym przykładzie rozkładu masy ciała, przedstawia się
następująco:

Nazwa Zmiennej

i Jednostka Pomiaru

Ś

rednia

arytmetyczna

Ochylenie

standardowe

Mediana

Modalna

Zakres

Masa (kg)

3,12

0,62

3,24

3,24

2,21 - 4,63

Wypowiedź na temat cech charakterystycznych rozkładu powinna uwzględniać zarówno wartość przeciętną, jak
i rozrzut wartości wokół wartości przeciętnej. Wartość przeciętna, zwykle średnia arytmetyczna jest podstawową
miarą położenia centralnego. Rozrzut wartości, dobrze widoczny na histogramie, jest określany jako
rozproszenie i podstawową miarą rozproszenia jest tzw. wariancja (miara zmienności zmiennej; ang. variance)
oraz jej wystandaryzowana dla oryginalnych jednostek pomiaru pochodna czyli odchylenie standardowe.
Odchylenie standardowe (ang. standard deviation) informuje jak gęsto, wokół wartości średniej, rozmieszczone
są wszystkie wartości zmiennej w opisywanym zbiorze. Gdy rozkład (wartości) zmiennej ma charakter normalny
wówczas 95% wartości mieści się w przedziale wyznaczonym przez dolny i górny limit. Dolny limit dla
rozkładu normalnego oblicza się odejmując 1,96 odchylenia standardowego od średniej arytmetycznej, górny
limit oblicza się dodając 1,96 odchylenia standardowego do wartości średniej. W związku z tym znajomość
wartości średniej (X) i odchylenia standardowego (OS) jest zwykle wystarczająca dla opisu rozkładu zmiennej
ilościowej, a obie wartości stanowią „tablicę rejestracyjną” rozkładu: „X ± OS”. Dodatkową zaletą wynikającą
ze znajomości X i OS jest możliwość obliczenia tzw. współczynnika zmienności (ang. coefficient of variation),
zgodnie z formułą: WZ = OS/X * 100%. W podanym powyżej przykładzie współczynnik zmienności wynosi
19,8% (WZ=0,62/3,12*100%).

2.2

Rozkład zmiennych jakościowych

Podobnie, jak to ma miejsce w przypadku zmiennej ilościowej, również opis rozkładu zmiennej jakościowej
może mieć charakter graficzny lub matematyczny.

Graficzna prezentacja polega na sporządzeniu wykresu, na którym zamieszczone są częstości poszczególnych
wartości danej zmiennej. Częstości mogą być przedstawione w formie bezwzględnej (liczba poszczególnych
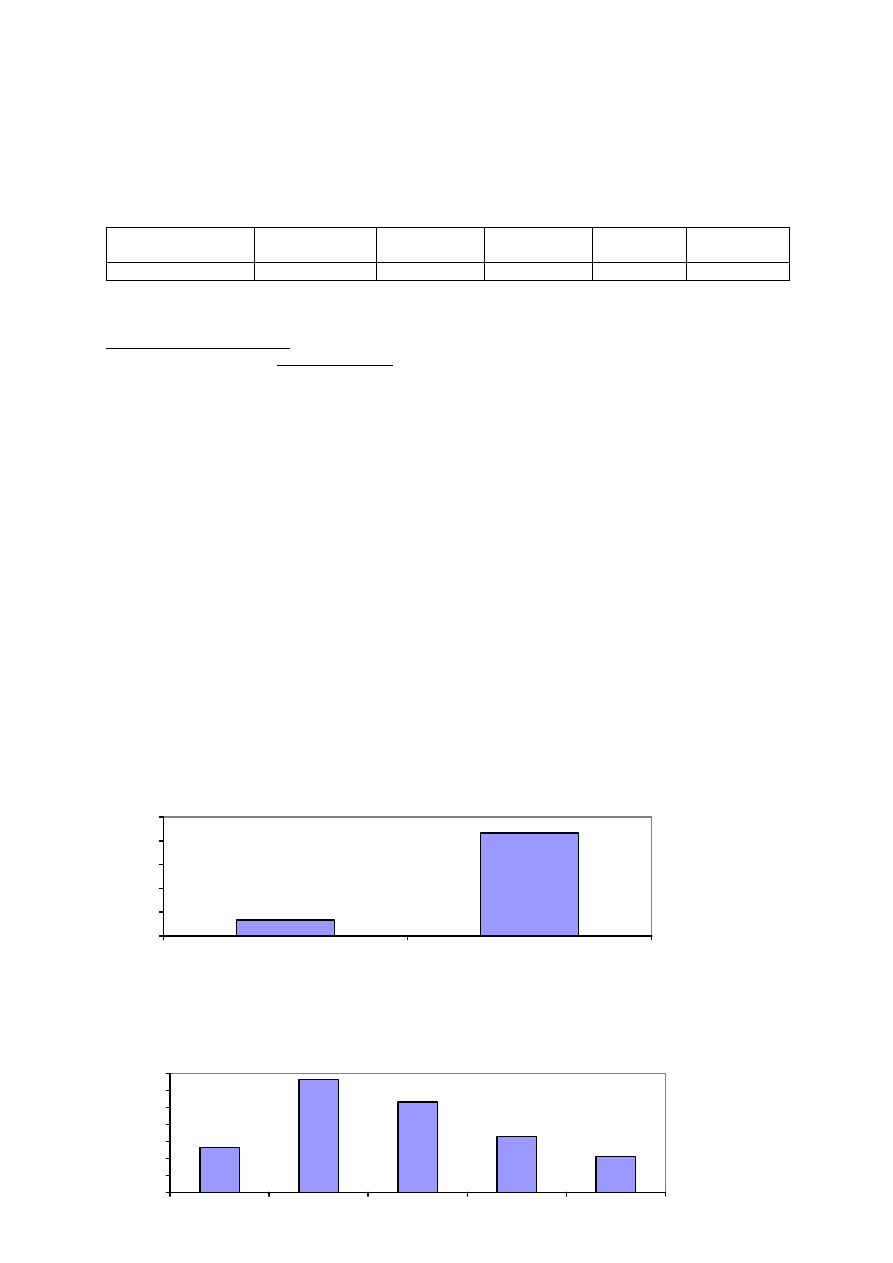
wartości) lub względnej (odsetek poszczególnych wartości). Poniższa rycina przedstawia rozkład zmiennej
objaw uboczny, posiadającej dwie wartości: objaw obecny lub objaw nieobecny. Zmienną tę analizowano u 150
badanych, wśród których 20 osób nie miało objawu ubocznego (13,3%) a 130 osób miało objaw uboczny
(83,7%). Scenariusz dotyczy najprostszej postaci zmiennej jakościowej, posiadającej tylko dwie wzajemnie
wykluczające się wartości (badany ma albo nie ma objawu ubocznego), a poniższa rycina przedstawia rozkład
zmiennej ‘objaw uboczny’ u 150 badanych, w postaci wartości odsetkowych:












Wykres może prezentować rozkład zmiennej posiadającej więcej niż dwie wartości, w tym także rozkład
zmiennej półilościowej. Przedstawia to poniższa rycina:

0

5

10

15

20

25

30

35

Brak

Słabe

Ś

rednie

Du

ż

e

B. Du

ż

e

Nasilenie Objawu Ubocznego u 150 Badanych

%

0

20

40

60

80

100

Brak

Obecny

Objaw Uboczny u 150 Badanych

%

6

Matematyczny opis rozkładu zmiennej jakościowej jest analogiczny do opisu zmiennej ilościowej. Korzystając z
teorii prawdopodobieństwa możliwe jest obliczenie wartości średniej (oczekiwanej), mediany, modalnej a także
wariancji. Szczegółowa znajomość tych zagadnień nie jest bezwzględnie konieczna dla zrozumienia zasad
analizy zmiennych jakościowych. W praktyce, najprostsza prezentacja rozkładu uwzględnia podanie
bezwzględnych i względnych częstości poszczególnych wartości zmiennej jakościowej. Gdy zmienna ta ma
dwie wartości (np. objaw obecny / objaw nieobecny) podaje się częstość każdej z nich (np. w grupie 150
badanych objaw obecny: n = 130 t.j. 83,7%; objaw nieobecny: n=20 t.j. 13,3%). Przedstawiony przykład dotyczy
rozkładu dwumianowego („zero-jedynkowego”). Znane są inne typy rozkładów, stosowane w zależności od cech
charakterystycznych obserwowanego zjawiska (np. rozkład Poisson’a).


3.0

Efekt

W terminologii epidemiologicznej pojęcie ‘efekt’ oznacza nieprzypadkową relację pomiędzy zmiennymi,
widoczną w postaci różnicy, zależności lub np. ryzyka. Istotą tej relacji jest brak przypadkowości, a więc jest
ona przejawem związku przyczynowo-skutkowego (w szerokim rozumieniu tego pojęcia) pomiędzy zmiennymi.
Stwierdzenie różnicy w częstości występowania nadwagi pomiędzy osobami stosującymi dietę bogatokaloryczną
i osobami stosującymi dietę ubogokaloryczną ilustruje efekt kaloryczności diety w odniesieniu do ryzyka
wystąpienia nadwagi. Efekt ten będzie także widoczny, gdy bezpośrednio zbada się tę zależność (już nie różnicę)
analizując korelację pomiędzy dobową podażą kalorii a wskaźnikiem masy ciała. Widać zatem, że efekt jest
pojęciem ogólnym, a jego dokumentowanie jest możliwe przy użyciu różnych metod (tu albo ocena różnicy,
albo ocena zależności).

Ze względu na uniwersalne zjawisko zmienności międzyosobniczej obserwacja i pomiar efektu są możliwe
poprzez badanie grupy ludzi. Przy ocenie np. kancerogennego efektu palenia tytoniu znajdzie się namiętny
palacz, u którego nigdy nie dojdzie do zachorowania na raka płuc, a z drugiej strony są niepalacze chorujący na
tę chorobę. Ten sam lek hipotensyjny u jednego chorego obniży ciśnienie rozkurczowe krwi w stopniu
satysfakcjonującym, u innego – w analogicznym stanie klinicznym – okaże się nieskuteczny (wobec wartości
ciśnienia rozkurczowego).

Uwzględnienie zjawiska zmienności międzyosobniczej ma kluczowe znaczenie dla strategii dokumentowania
efektu (w wielu sytuacjach w grę wchodzi jeszcze zjawisko zmienności wewnątrzosobniczej – nie omawiane w
niniejszym materiale). Ilustracją zmienności międzyosobniczej danej zmiennej (cechy) jest rozkład wartości tej
zmiennej (rozkład zmiennej) w populacji. Nie istnieje np. jedna typowa wartość wysokości ciała u chłopców
dziesięcioletnich (rozkład zmiennej ‘wysokość ciała’ ma charakter normalny – większość dziesięcioletnich
chłopców ma wzrost plasujący się wokół wartości średniej, odpowiednio mniej chłopców ma wzrost niski lub
wysoki).

Znaczenie analizy rozkładu dla dokumentowania efektu ilustruje poniższy przykład. W poniższym scenariuszu
celem badania jest odpowiedź na pytanie, czy palenie papierosów ma wpływ na sprawność wentylacyjną płuc ?
To samo pytanie można zadać w inny sposób. Na przykład można spytać, czy osoby palące papierosy mają
gorszą sprawność wentylacyjną płuc niż niepalacze ? Można też spytać czy i jaki jest efekt nałogu palenia w
odniesieniu do sprawności wentylacyjnej płuc ? Wszystkie sformułowania są uprawnione, chociaż drugie
zawiera sugestię odnośnie kierunku efektu, czego na gruncie metodologii badań naukowych lepiej unikać.
Trzecie ma wymiar generalny – odpowiedź na to pytanie można uzyskać poprzez badanie różnicy (porównanie
sprawności wentylacyjnej; dwie grupy: palacze i niepalacze) lub poprzez badanie zależności (korelacja
sprawności wentylacyjnej z liczbą tzw. paczkolat).

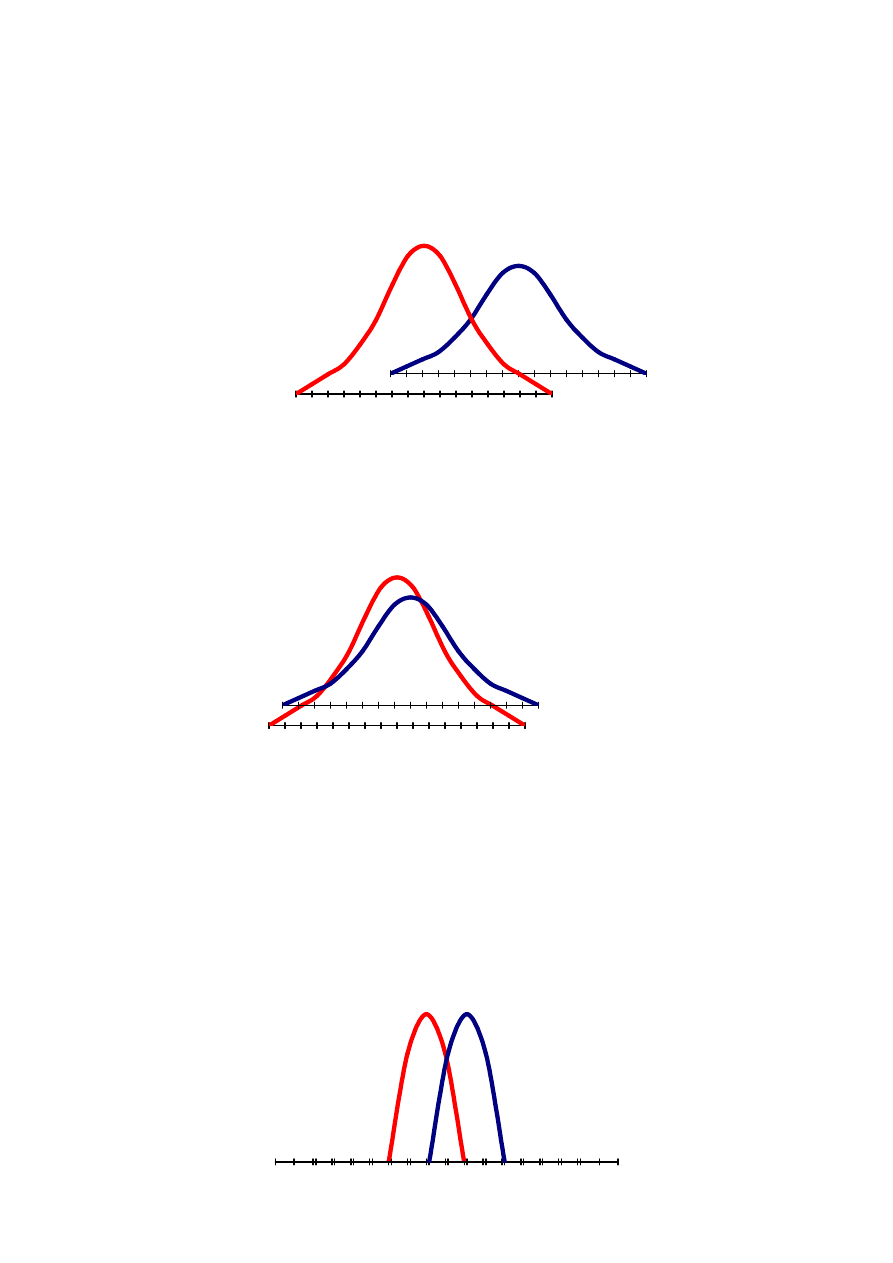
Poniższa rycina przedstawia rozkład wartości zmiennej FEV

1

(natężona pierwszosekundowa objętość

wydechowa – wskaźnik sprawności wentylacyjnej) u 100 zdrowych niepalaczy (P-), mężczyzn w wieku 40-49
lat. Zaznaczona jest wartość średnia (tu, wokół szczytu krzywej największy odsetek pomiarów), wartość
minimalna i wartość maksymalna.

P-

M

IN

W

.

Ś

R

E

D

N

IA

M

A

X

7

Analogiczny rozkład cechuje wartość FEV

1

u 100 nałogowych palaczy (P+), mężczyzn w wieku 40-49 lat.

Zestawienie obu rycin ujawnia jednakże, że w przypadku palaczy rozkład ma ten sam profil, ale lokuje się w
zakresie mniejszych wartości. Nie zaskakuje fakt, że niektórzy palacze mają większe wartości FEV

1

niż

niektórzy niepalacze.
















Interpretacja powyższej ryciny jest – intuicyjnie - stosunkowo prosta. Rozkład FEV

1

jest inny u palaczy i inny u

niepalaczy – są to zatem dwa różne rozkłady. Różne rozkłady reprezentują różne grupy (w kontekście wartości
FEV

1

) i ta różnica ma swoją przyczynę. Testowaną i potwierdzoną przyczyną jest nałóg palenia (ujawniony

został efekt nałogu palenia). Ale możliwe jest także uzyskanie następującego wyniku:
















Na powyższej rycinie dwa rozkłady prawie się pokrywają i można mieć uzasadnione wątpliwości, czy
rzeczywiście reprezentują one różne rozkłady. Może to być tak naprawdę jeden i ten sam rozkład, z nieco inną
prezentacją u palących i niepalących, związaną z przypadkowością wyników („rozkład P+ jest składową
rozkładu P- i odwrotnie; jest to jeden rozkład reprezentujący jedną grupę - populację). Gdyby taka sytuacja miała
miejsce nie można potwierdzić efektu nałogu palenia – ta okoliczność (nałóg palenia) nie różnicuje rozkładów,
ergo nałóg palenia nie ma znaczenia dla sprawności wentylacyjnej płuc.

Możliwy jest wreszcie inny wynik:

P-

M

IN

W

.

Ś

R

E

D

N

IA

M

A

X

P+

M

IN

W

.

Ś

R

E

D

N

IA

M

A

X

P+

M

IN

W

.

Ś

R

E

D

N

IA

M

A

X

P-

M

IN

W

.

Ś

R

E

D

N

IA

M

A

X

P+

P-

8

W pokazanym powyżej scenariuszu różnica pomiędzy wartościami średnimi FEV

1

w grupie P- i grupie P+ nadal

jest stosunkowo mała, ale przypuszczenie o różnych rozkładach wydaje się całkiem uzasadnione. Wynika to z
faktu, że w każdej grupie występuje małe rozproszenie wartości FEV

1

(„homogenne grupy”).

Ogląd wariantów przedstawionych na powyższych rycinach ujawnia zatem, że dla oceny czy wyniki badania
obejmującego dwie grupy reprezentują dwa różne czy tak naprawdę jeden rozkład (danej zmiennej) istotne
znaczenie posiada różnica pomiędzy wartościami średnimi (miarami położenia centralnego) i wielkość odchyleń
standardowych (rozproszenie rozkładów). Obie miary uwzględniane są w testach statystycznych.

Zgodnie z podaną prostą klasyfikacją efektu (albo różnica albo zależność) istnieją testy dotyczące różnic (np.
test t-Studenta dla zmiennych ilościowych i test chi-kwadrat dla zmiennych jakościowych) oraz testy dotyczące
zależności (np. analiza korelacji liniowej lub analiza regresji). Pozwalają one na ustalenie czy w analizowanym
zbiorze danych daje się zidentyfikować zakładany efekt, a jeżeli tak, to czy na gruncie teorii
prawdopodobieństwa efekt ten jest nieprzypadkowy (statystycznie znamienny). W związku z celami, dla których
opracowano metody testowania efektu wyróżnia się zatem testy statystycznej znamienności różnic i testy
statystycznej znamienności zależności.

Termin „test statystycznej znamienności różnicy” jest zwykle stosowany w zapisie „test statystycznej
znamienności różnicy pomiędzy średnimi” (lub częstościami). Takie sformułowanie nie jest błędne, jak długo
pamięta się, że tak naprawdę jest to test statystycznej znamienności różnicy pomiędzy rozkładami danej
zmiennej ilościowej (lub jakościowej).