05-01-21

Reinhard Kulessa

1

Wykład 27

11.12 Efekt Dopplera
11.12.1 Znaczenie ośrodka
11.12.2 Efekt Dopplera w relatywistyce
11.13 Prędkości naddźwiękowe

05-01-21

Reinhard Kulessa

2

11.12 Efekt Dopplera

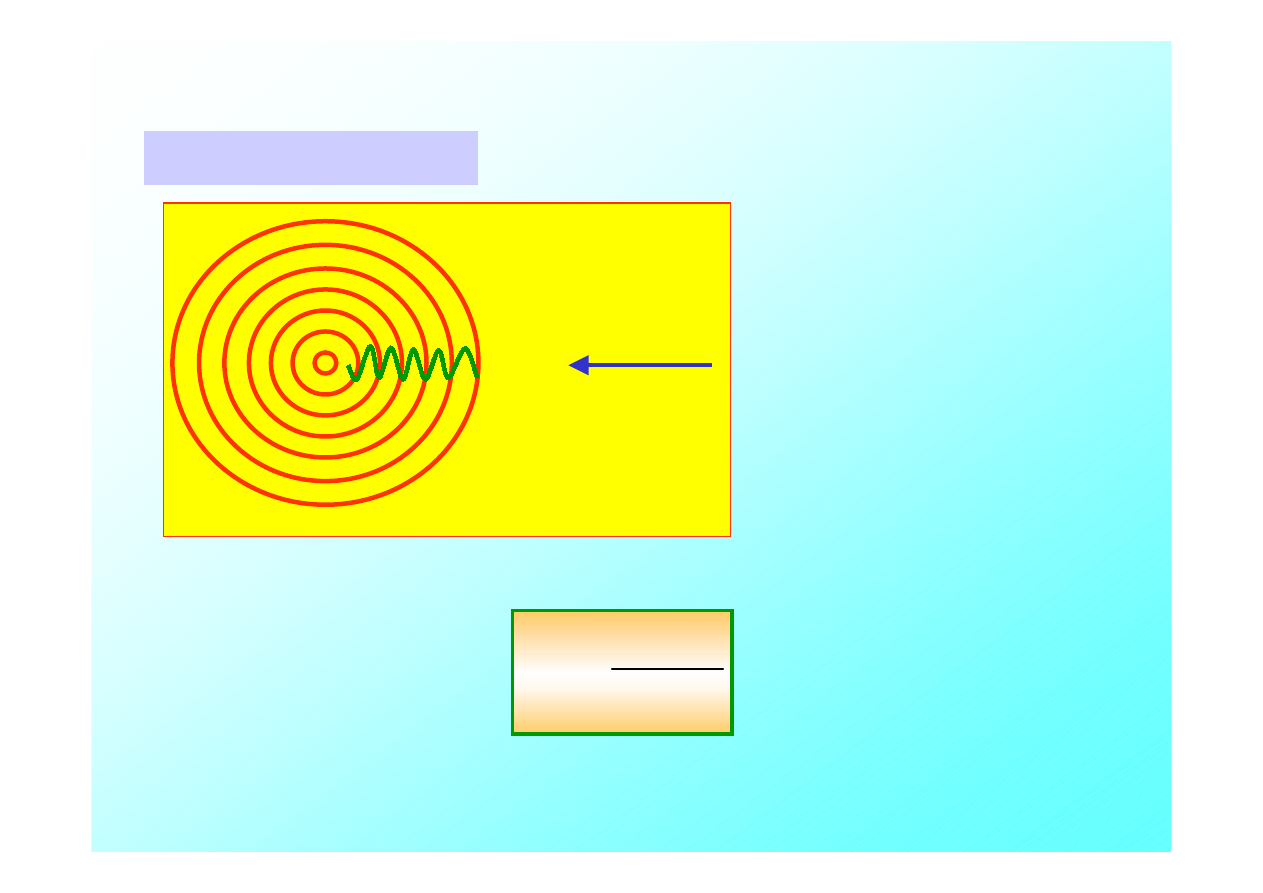
Jeżeli źródło emitujące falę oraz obserwator znajdują się
względem siebie w ruchu, obserwator zaobserwuje falę o
częstości zmienionej

ν

zm

w stosunki do częstości emitowanej

przez źródło

ν

z

. Taką zmianę częstości możemy często

zauważyć w ruchu ulicznym np. w czasie przejeżdżania obok
nas karetki na sygnale. Dla fal dźwiękowych efekt ten został
po raz pierwszy zauważony przez Christiana Dopplera 1842 r.

Doppler wynajął na dwa dni pociąg towarowy i grupę trębaczy z
wiedeńskiej orkiestry. Połowę muzyków umieścił w pociągu, a drugą na
stacji. Obydwie grupy trąbiły w tej samej tonacji. Muzycy byli oczywiście
w stanie określić wysokość słyszanego dźwięku.

05-01-21

Reinhard Kulessa

3

Przy obliczeniach różnicy częstości musimy rozróżnić
następujące przypadki;

ruch obserwatora

,

ruch źródła fal

,

oraz

równoczesny ruch źródła i obserwatora

.

Ruch oznacza tu w każdym przypadku ruch względem ośrodka
w którym rozchodzi się fala.

Przyjmijmy następujące oznaczenia,
u -- prędkość rozchodzenia się fali
v

zr

-- prędkość źródła,

v

ob

-- prędkość obserwatora,

f

0

--

częstość fali emitowanej przez źródło,

f

ob

-- częstość fali odbieranej przez obserwatora

λ

0

-- długość fali wysyłanej przez źródło

λ

ob

-- długość fali obserwowanej

Użyjmy dla częstości
oznaczenia f dla
lepszego odróżnienia
od prędkości v

05-01-21

Reinhard Kulessa

4

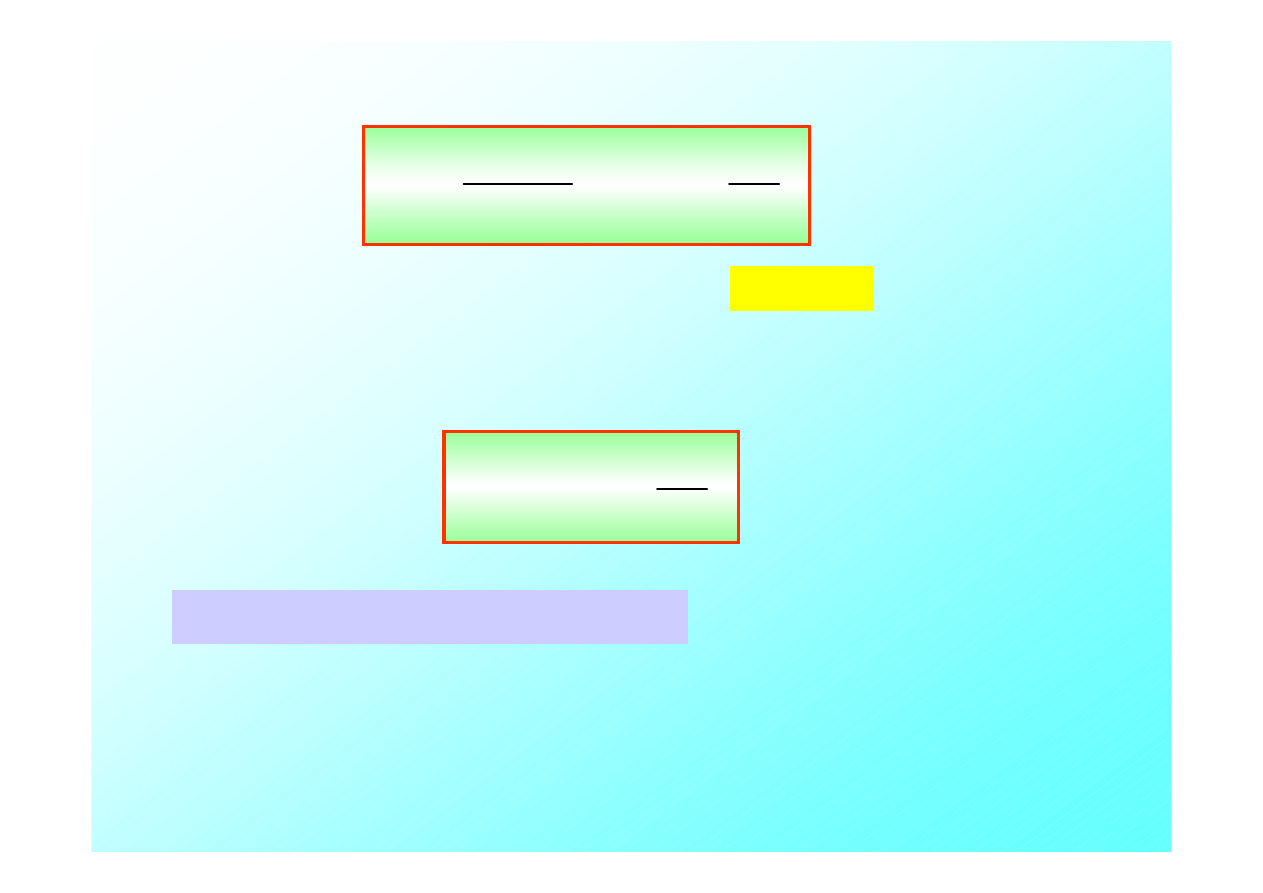
Rozważmy kilka przypadków:

I. v

zr

= 0, v

ob

≠

0

Fale będą dochodziły
do obserwatora z
prędkością równą
sumie prędkości
obserwatora i
prędkości fali. Czas
pomiędzy dwoma
kolejnymi

v

ob

wierzchołkami fal który zmierzy obserwator będzie równy;

0

ob

ob

T

u v

λ

=

+

.

05-01-21

Reinhard Kulessa

5

Częstość fali , którą odbiera obserwator wynosi więc;

0

0

1

ob

ob

ob

u v

v

f

f

u

λ

+





=

=

+









.

(11.34)

Wykorzystaliśmy tutaj zależność, że

λ

0

=u/f

0

.

Obserwatora, który oddala się od źródła zaobserwuje
częstość;

0

1

ob

ob

v

f

f

u





=

−









(11.35)

.

II. v

ob

= 0, v

zr

< 0, v

zr

> 0

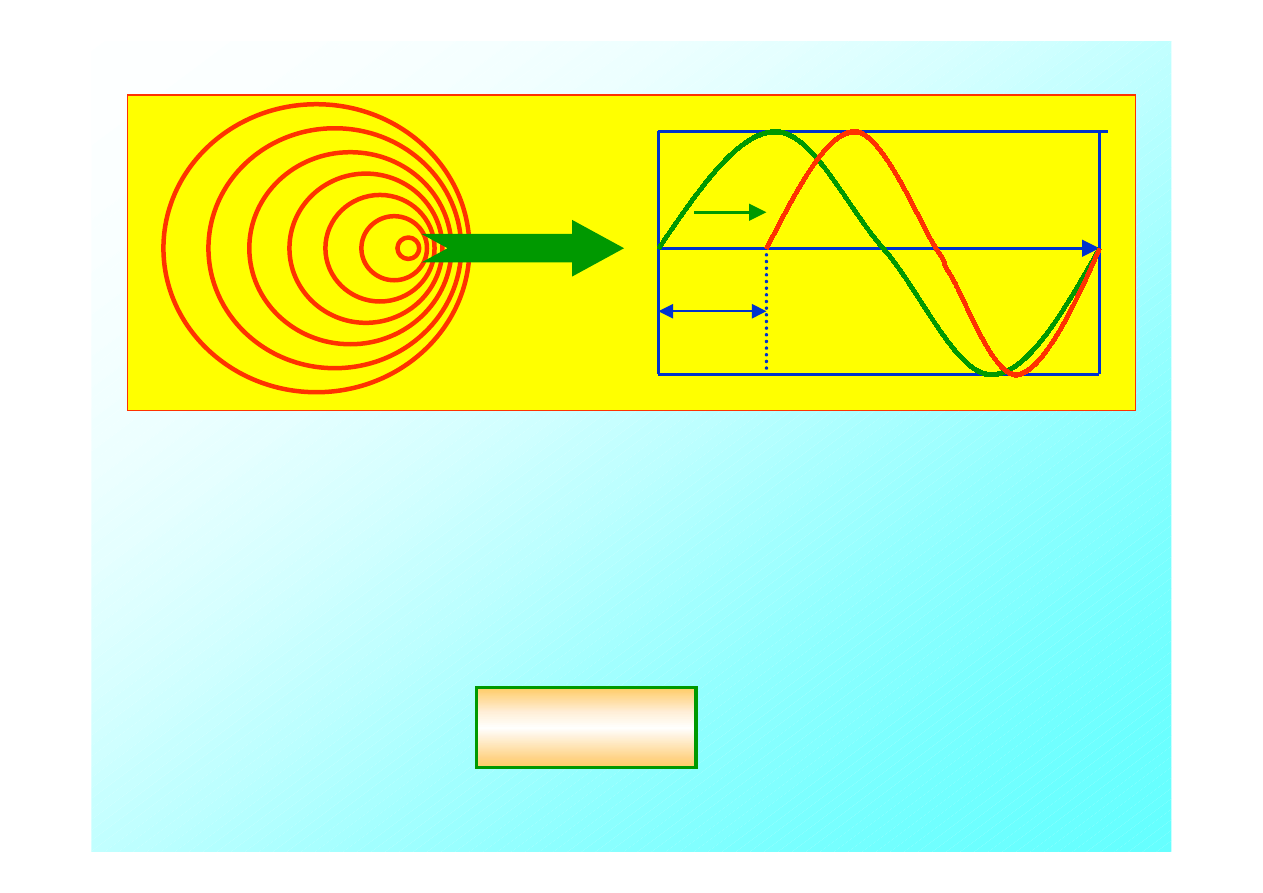
W tym przypadku obserwator spoczywa, a źródło fal
przybliża się do, lub oddala się od obserwatora.

05-01-21

Reinhard Kulessa

6

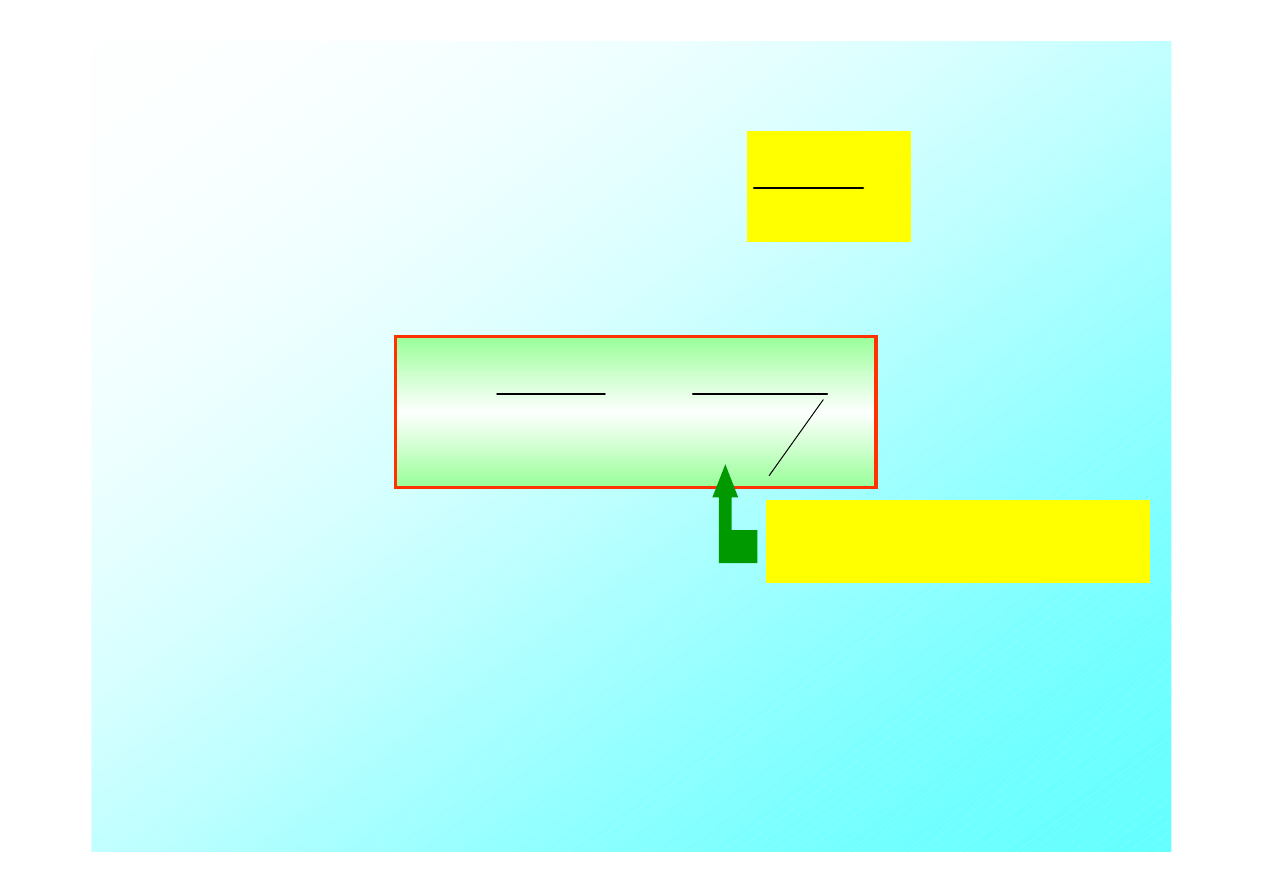
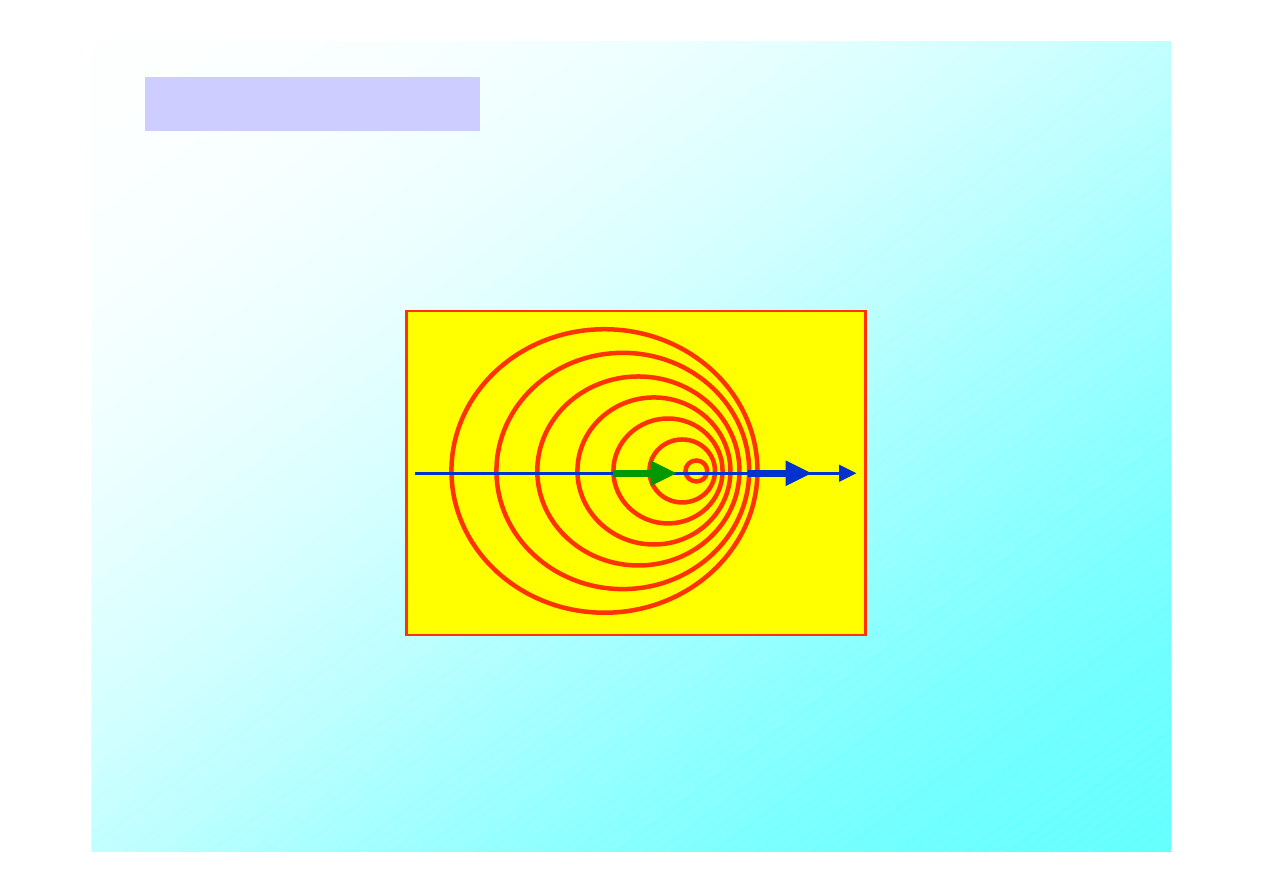
λ

0

λ

ob

v

zr

T

zr

u

v

zr

O

Źródło porusza się z prędkością

v

zr

,emituje falę pierwotną o

częstości

f

0

, która porusza się z prędkością

u

.

Dwa wierzchołki fali są generowane w odstępie czasowym

T

0

=1/ f

0

.

W międzyczasie źródło przebywa drogę

T

0

v

zr

.

Odległość pomiędzy dwoma wierzchołkami będzie więc

0

(

)

zr

u v T

∓

.

05-01-21

Reinhard Kulessa

7

obserwatora będzie więc różnił się o .

0

zr

T

u v

u

∓

Czas pomiędzy dwoma wierzchołkami fali docierającymi do

Otrzymamy więc na częstość odbieraną przez obserwatora
wyrażenie;

0

0

1

1

ob

zr

zr

u

f

f

f

v

u v

u

=

=

∓

∓

.

(11.36)

- ruch w stronę obserwatora
+ ruch od obserwatora

05-01-21

Reinhard Kulessa

8

III. v

ob

≠

0, v

zr

≠

0

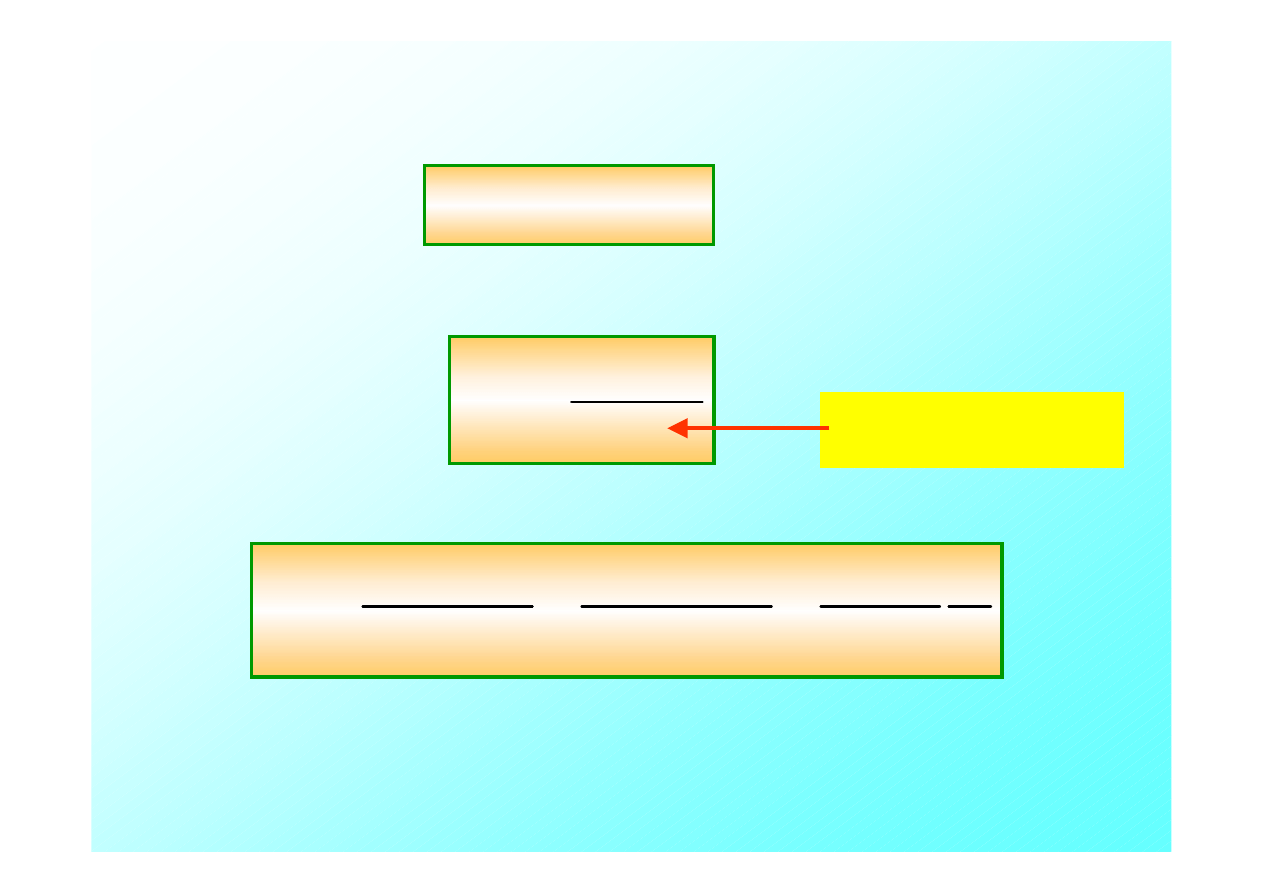
W tym przypadku mamy do czynienia z czterema
możliwościami. Załóżmy, że zarówno źródło fali, jak i obserwator
poruszają się w tum samym kierunku.

v

zr

v

ob

Możemy znaleźć częstość fal odbieranych przez obserwatora
bazując na dwóch już znanych przypadkach.

05-01-21

Reinhard Kulessa

9

Wskutek ruchu źródła długość emitowanej przez nie fali
zmienia się

0

0

zr

v T

λ

λ

′ =

−

.

ob

ob

u v

f

λ

−

=

′

Częstość fali widziana przez oddalającego się obserwatora
wynosi (patrz I);

.

długość zmieniona przez
ruch źródła

Otrzymamy więc;

0

0

0

0

0

1

ob

ob

ob

ob

zr

zr

zr

u v

u v

u v

f

v T

uT

v T

u v T

λ

−

−

−

=

=

=

−

−

−

.

Na obserwowaną w tym przypadku częstość otrzymujemy;

05-01-21

Reinhard Kulessa

10

0

ob

ob

zr

u v

f

f

u v

−

=

−

.

(11.37)

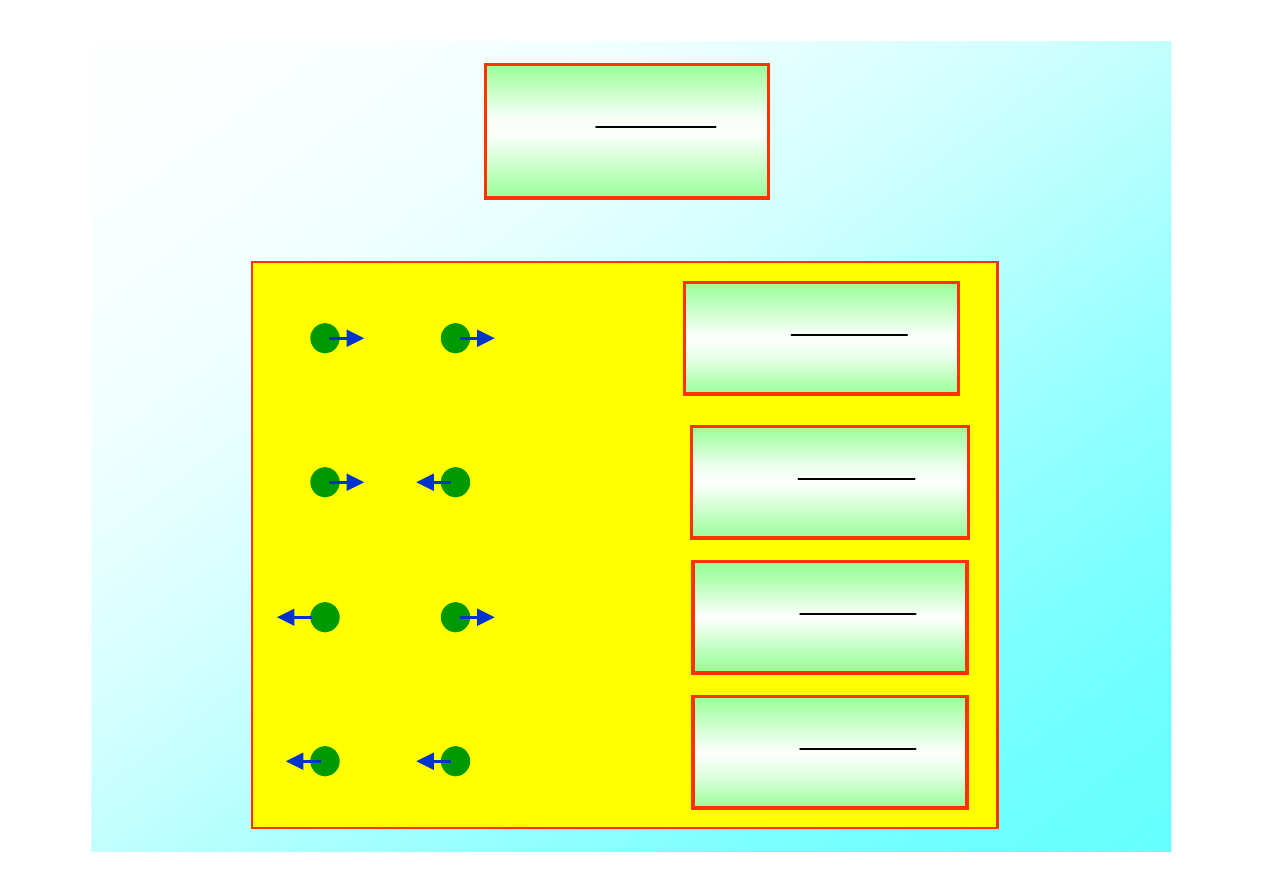
Poniższa tabela pokazuje wszystkie cztery możliwości.

0

ob

ob

zr

u

v

f

f

u

v

−

=

−

0

ob

ob

zr

u

v

f

f

u

v

+

=

−

0

ob

ob

zr

u

v

f

f

u

v

−

=

+

0

ob

ob

zr

u

v

f

f

u

v

−

=

−

źródło obserwator

05-01-21

Reinhard Kulessa

11

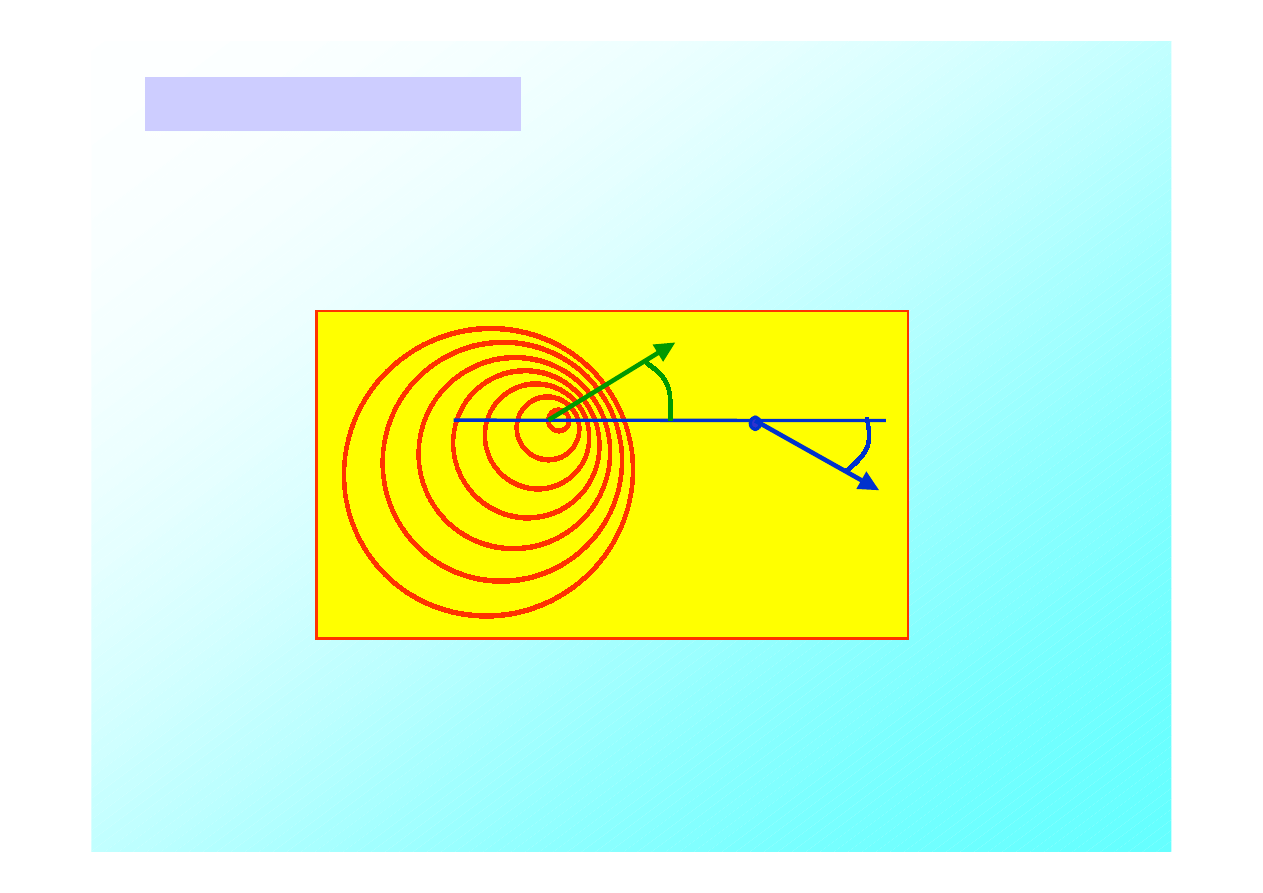
IV . Ruch pod kątem

Do tej pory rozważaliśmy przypadki, w których źródło fal i
obserwator poruszali się względem siebie po jednej prostej. Tak
jednak nie zawsze musi być.

v

zr

v

ob

θ

zr

θ

ob

W takim przypadku bierzemy składowe równoległe prędkości
do kierunku łączącego źródło z obserwatorem.

05-01-21

Reinhard Kulessa

12

0

cos

cos

ob

o

ob

zr

zr

u v

f

f

u v

θ

θ

−

=

−

(11.38)

.

11.12.1 Znaczenie ośrodka

Stwierdziliśmy w rozważanych przypadkach, że dla efektu
Dopplera istotne jest, czy porusza się źródło fal, czy
obserwator. Pamiętamy, że fale np.; głosowe rozchodzą się w
powietrzu. Powietrze to jest dla nas wzorcem względem
którego wyznaczamy prędkość źródła i obserwatora.
Jeżeli wieje wiatr, musimy to uwzględnić w naszych
rozważaniach.
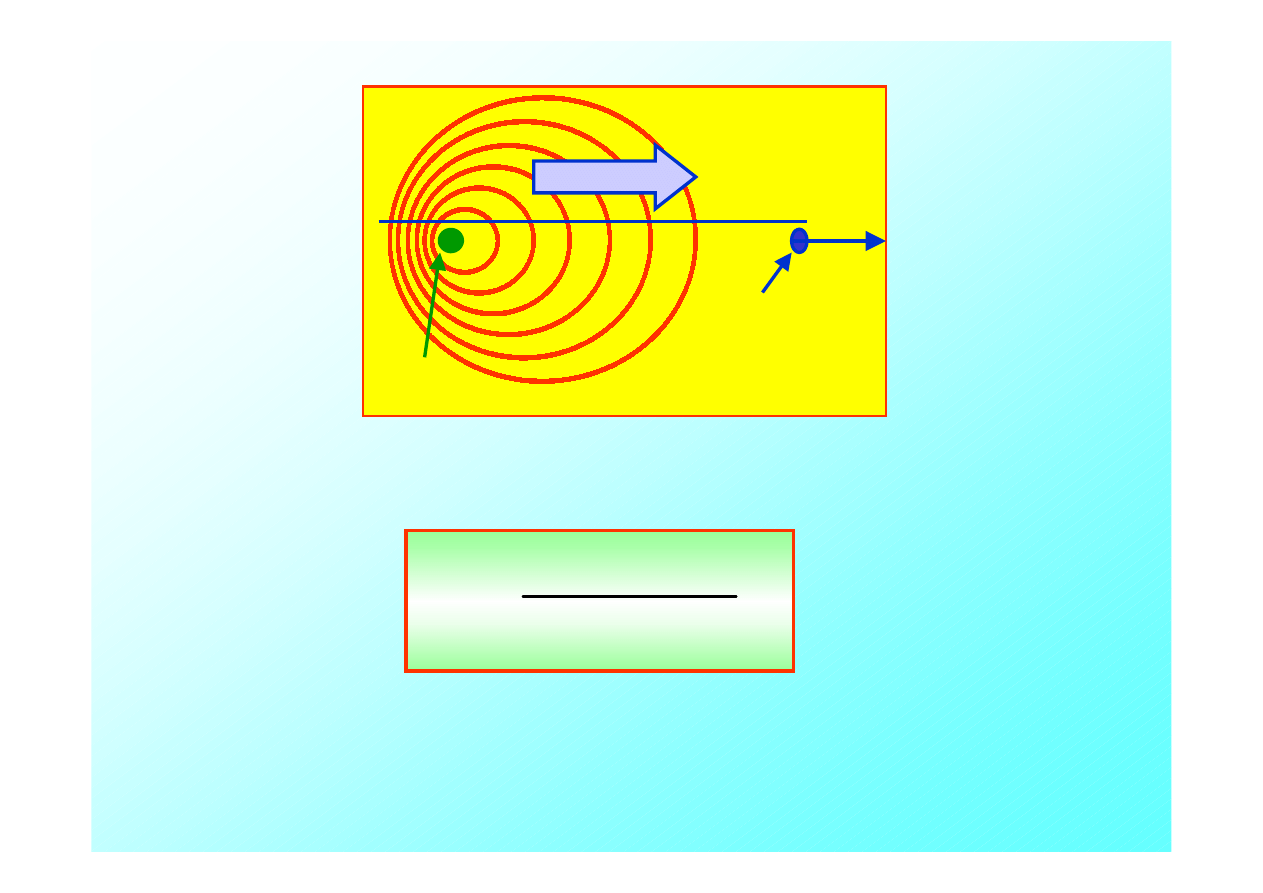
Rozważmy przypadek ruchomego obserwatora i stałego
wiatru.

05-01-21

Reinhard Kulessa

13

źródło

obserwator

v

ob

Wiatr v

w

Na częstość fali którą zarejestruje obserwator uzyskamy
wartość;

0

ob

w

ob

w

u v

v

f

f

u v

−

+

=

+

(11.39)

.

05-01-21

Reinhard Kulessa

14

11.12.2 Efekt Dopplera w relatywistyce

Wiemy, że dla fal elektromagnetycznych wzory

(11.34), (11.35)

i

(11.36)

nie mogą być zastosowane. Dla fal

elektromagnetycznych nie istnieje ośrodek w którym
rozprzestrzenia się fala (brak „eteru”). Wobec tego przypadki
ruchomego źródła i ruchomego obserwatora są
nierozróżnialne. Wymienione równania muszą zostać
zastąpione przez wyrażenie, w którym wystąpi jedynie
względna prędkość pomiędzy źródłem a obserwatorem.
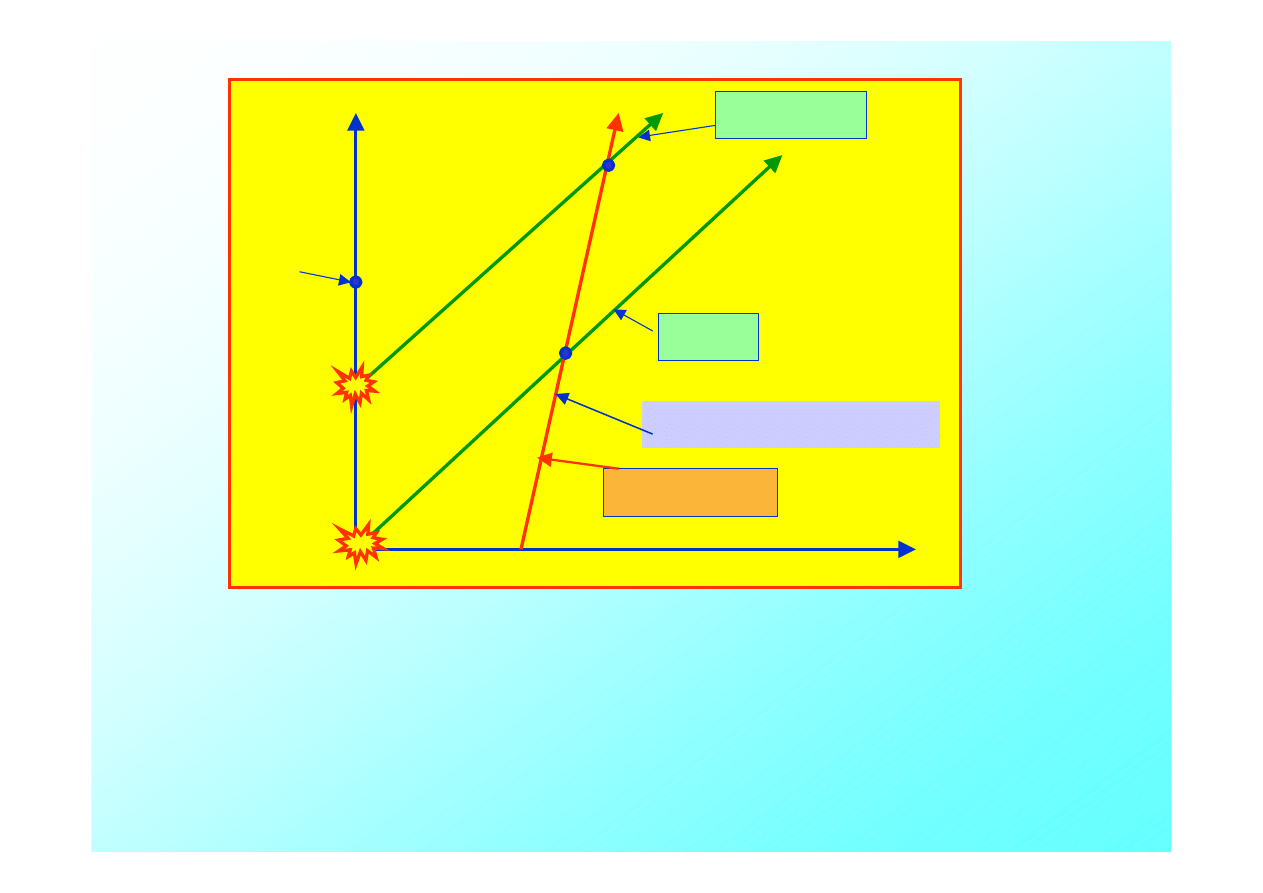
Rozpatrzmy następujący przykład.
Mamy źródło promieniowania elektromagnetycznego np.
nadajnik radarowy, który spoczywa w początku układu
współrzędnych

U

. Obserwator oddala się wzdłuż osi

x

z

prędkością

v

od tego źródła. Źródło, wysyła impulsy w

regularnych odstępach czasowych

τ

, które biegną z prędkością

światła

c

.

05-01-21

Reinhard Kulessa

15

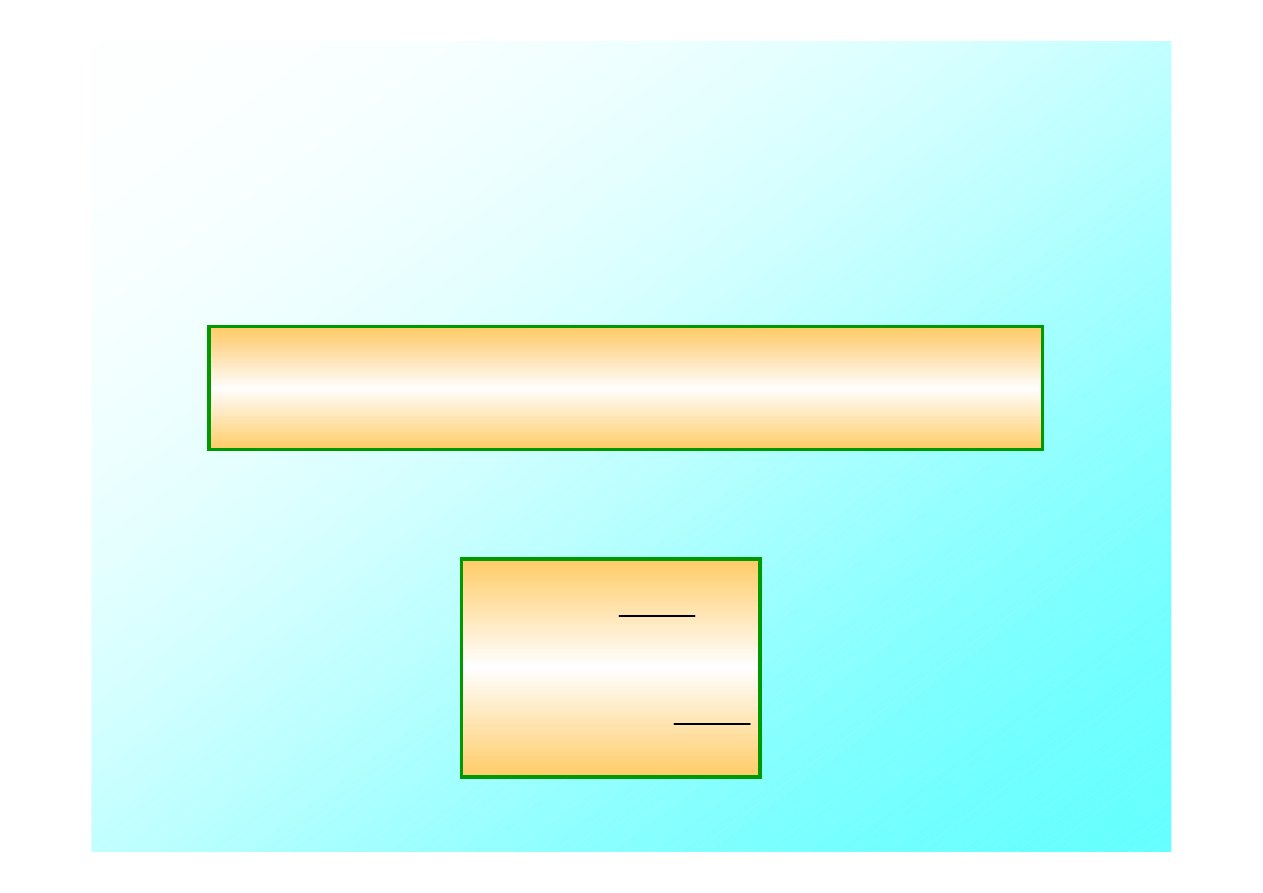
x

t

Impuls 1

Impuls 2

(x

1

, t

1

)

(x

2

, t

2

)

x=c · t

x = c(t -

τ

)

x = x

0

+ v · t

t =

τ

Obserwator ruchomy

Źródło

w czasie t

O

x

0

Obserwator spoczywający w układzie

U

zaobserwuje impulsy

radarowe w odstępach czasowych

τ

.

Jaką częstość obserwuje poruszający się obserwator?

05-01-21

Reinhard Kulessa

16

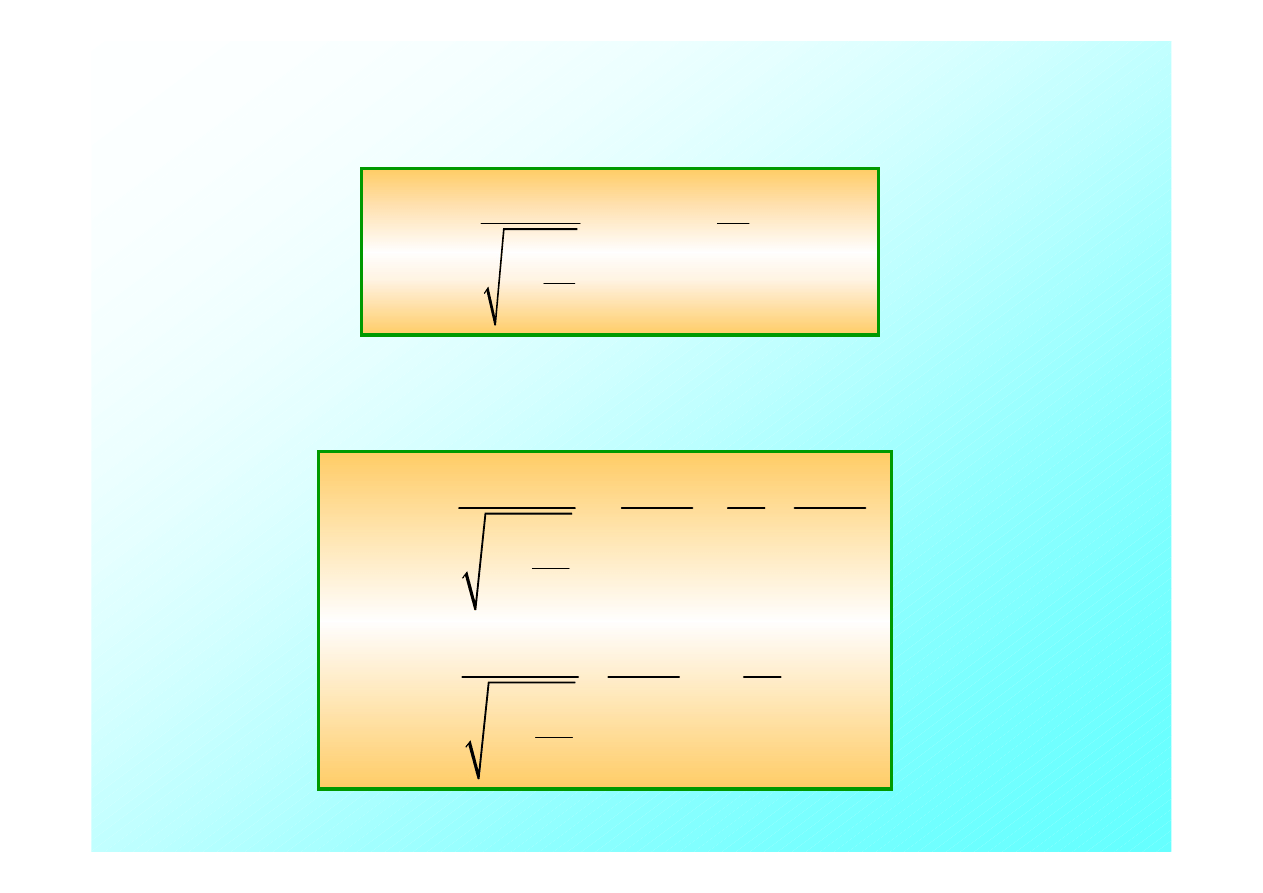
Otóż;
A) Różnica czasu pomiędzy obserwacją dwóch impulsów

przez obserwatora w układzie

U

jest równa

t

2

– t

1

.

Z matematycznych warunków na punkty przecięcia

(x

1

, t

1

)

i

(x

2

, t

2

)

mamy;

1

1

0

1

0

1

2

2

0

2

0

2

(

)

(

)

(

)

x

c t

x

v t

x

c v t

x

c t

x

v t

x

c

c v t

τ

τ

= ⋅ =

+ ⋅

⇒

= − ⋅

= ⋅

− =

+ ⋅

⇒

+ ⋅ = − ⋅

.

Z równań tych otrzymujemy;

2

1

2

1

c

t

t

c v

v

x

x

c

c v

τ

τ

− =

−

− = ⋅

−

.

05-01-21

Reinhard Kulessa

17

B. Tę samą różnicę czasową obserwator w układzie

ruchomym

U’

zmierzy jako;

2

1

2

1

2

1

2

2

2

1

(

)

(

)

1

v

t

t

t t

x x

c

v
c





′ ′

− =

− −

−









−

.

Po wstawieniu wyliczonych powyżej wartości,
otrzymujemy;

2

1

2

2

2

2

2

2

2

1

1

1

(1

)

1

c

v

c v

t

t

c v c

c v

v
c

c

v

c v

c

v
c

τ

τ

τ

⋅





′

′

− =

−





−

−





−

=

−

−

−

.

05-01-21

Reinhard Kulessa

18

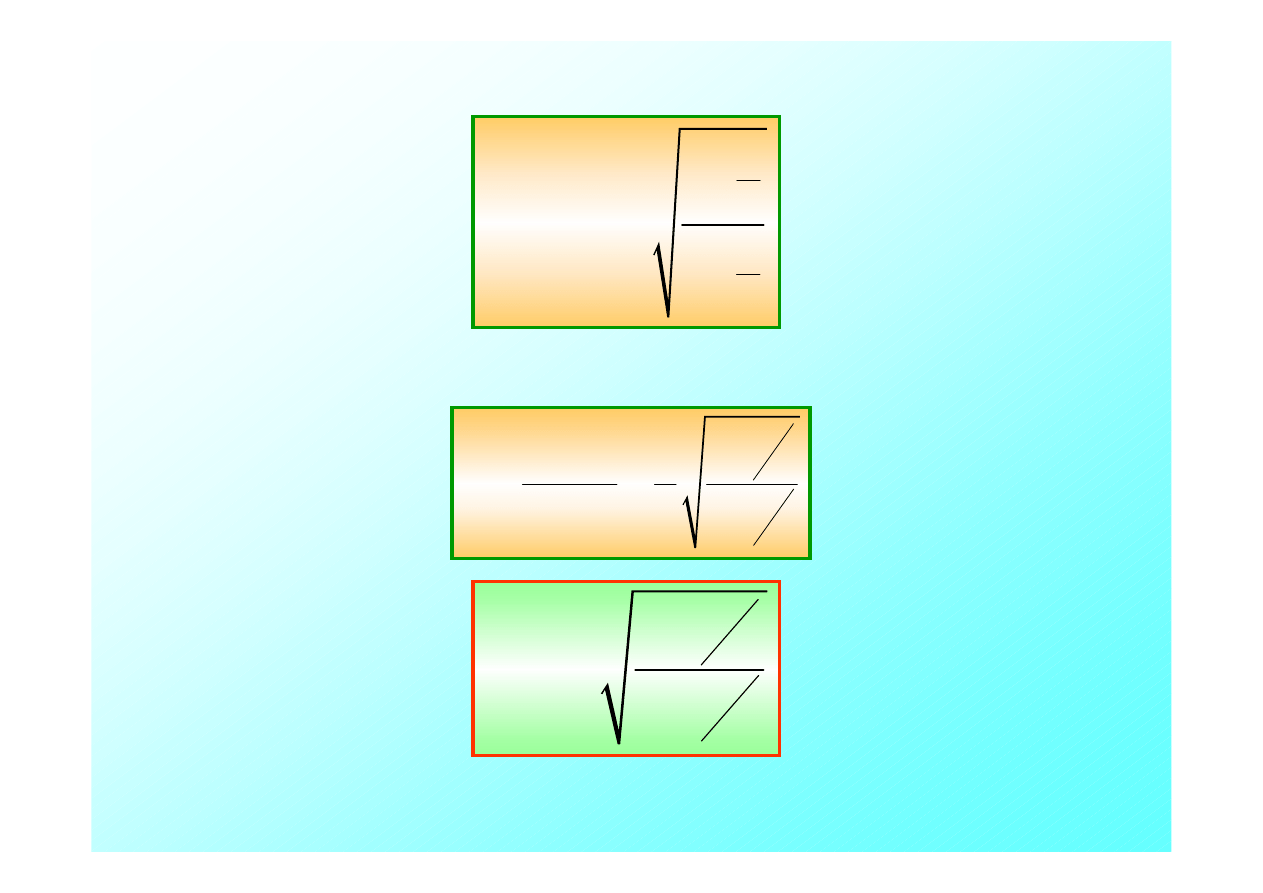
2

1

1

1

v
c

t

t

v
c

τ

+

′

′

−

=

−

Po krótkich przekształceniach otrzymujemy

.

Częstość, z którą ruchomy obserwator odbiera sygnały
jest równa;

2

1

1

1

1

1

v

c

v

t

t

c

ν

τ

−

′ =

=

′

′

+

−

,

czyli

1

1

v

c

v

c

ν

ν

−

′ =

+

.

(11.40)

05-01-21

Reinhard Kulessa

19

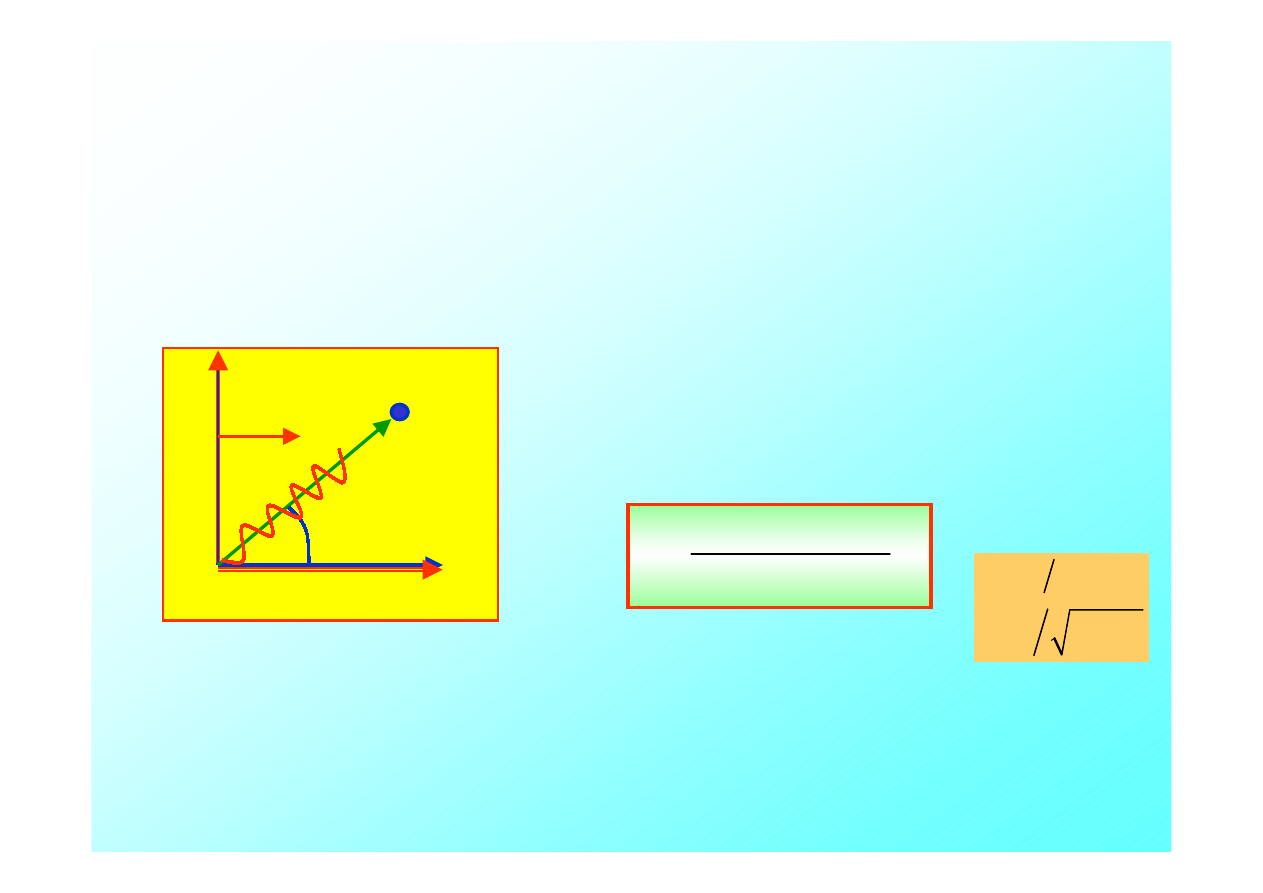
Rozważaliśmy szczególny przypadek efektu Dopplera, kiedy
obserwator odbiera falę ze źródła oddalającego się od niego wzdłuż osi

x

.

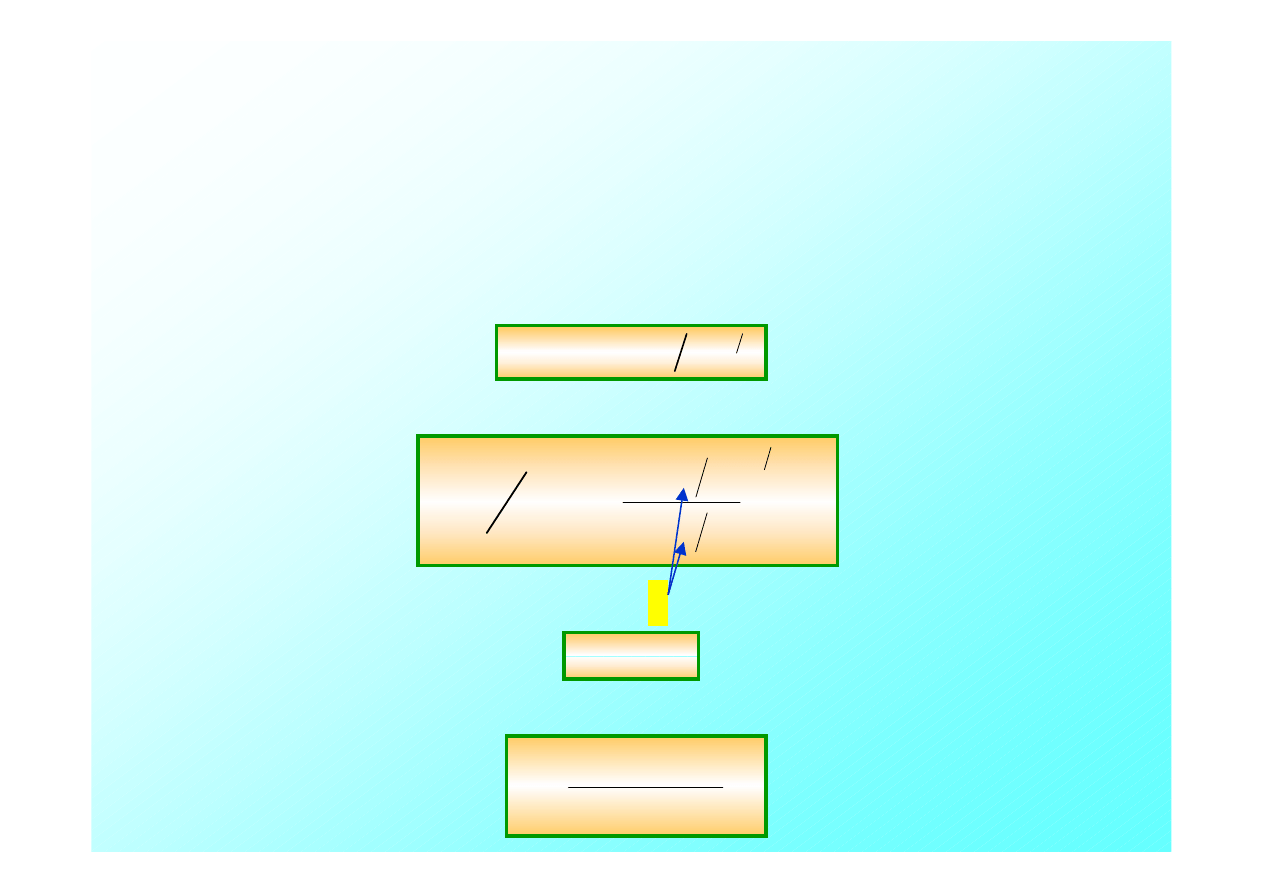
W ogólnym przypadku fala świetlna o częstości drgań

ν

’

wysłana ze źródła

O’

spoczywającego w układzie

U’

, który porusza się z prędkością

v

względem układu

U

wzdłuż osi

Ox

, może docierać do obserwatora

O

spoczywającego (w punkcie

P

) w układzie

U

pod kątem

α

względem

kierunku ruchu źródła

O’

.

Obserwator w punkcie

P

zmierzy następującą częstość

ν

’

fali świetlnej;

x

x’

y

y’

O

≡

O’

v

α

P

1

(1

cos )

ν

ν

γ

β

α

′

=

−

.

2

1 1

v c

β

γ

β

=

=

−

Prześledźmy krótko własności relatywistycznego przesunięcia
dopplerowskiego.

05-01-21

Reinhard Kulessa

20

1. Dla

α

= 0

0

źródło i obserwator zbliżają się do siebie. Częstość

obserwowanej fali ulega

przesunięciu ku fioletowi

.

2. Dla

α

=

π

źródło i obserwator oddalają się od siebie. Mamy wtedy do

czynienia z

przesunięciem ku czerwieni

.

3. Dla kątów

α

=

π

/2, 3

π

/2

mamy do czynienia z

poprzecznym

relatywistycznym efektem Dopplera

. Nie ma on odpowiednika w

mechanice klasycznej.

2

2 1 2

(1

)

v c

ν ν ′

= ⋅ −

.

1 2

1 (

)

1

1

1 (

)

v c

z

v c

ν

ν

+





′

=

− =

−





−





Zależność pomiędzy prędkością galaktyk

v

a ich odległością

r

jest następująca;

.

Przesunięcie ku czerwieni

widm odległych galaktyk definiujemy jako;

v H r

=

⋅

,

gdzie

H

jest

stałą Hubble’a

i

H

≤

(75 km/s)/Mpc, 1Mpc = 3.086·10

22

m.

2

2

(1

)

1

(1

)

1

z

v

c

z

+

−

=

⋅

+

+

Wiadomo również, że

.

05-01-21

Reinhard Kulessa

21

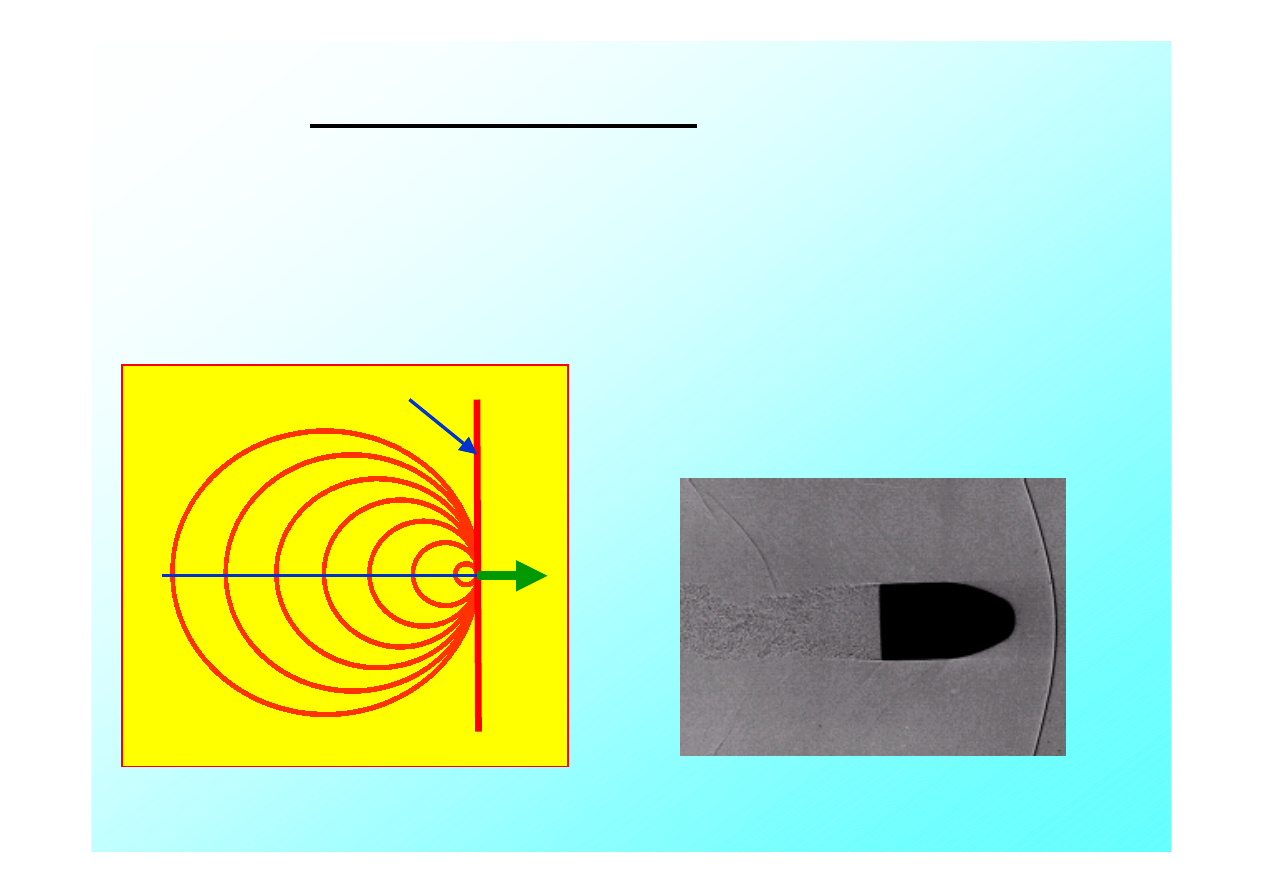
11.13 Prędkości naddźwiękowe

Powróćmy do rozchodzenia się dźwięku i zastanówmy się co
dzieje się gdy prędkość źródła dźwięku

v

zr

jest równa prędkości

dźwięku

u

. Powstaje wtedy fala uderzeniowa. Następuje

kumulacja energii na czole fali.

Natężenie rośnie do

∞

.

Czoło fali

v

zr

Przykład ---- lecący pocisk o
prędkości

v

zr

= 1.01 u

.

05-01-21

Reinhard Kulessa

22

F/A Hornet przekraczający
Barierę dźwięku

05-01-21

Reinhard Kulessa

23

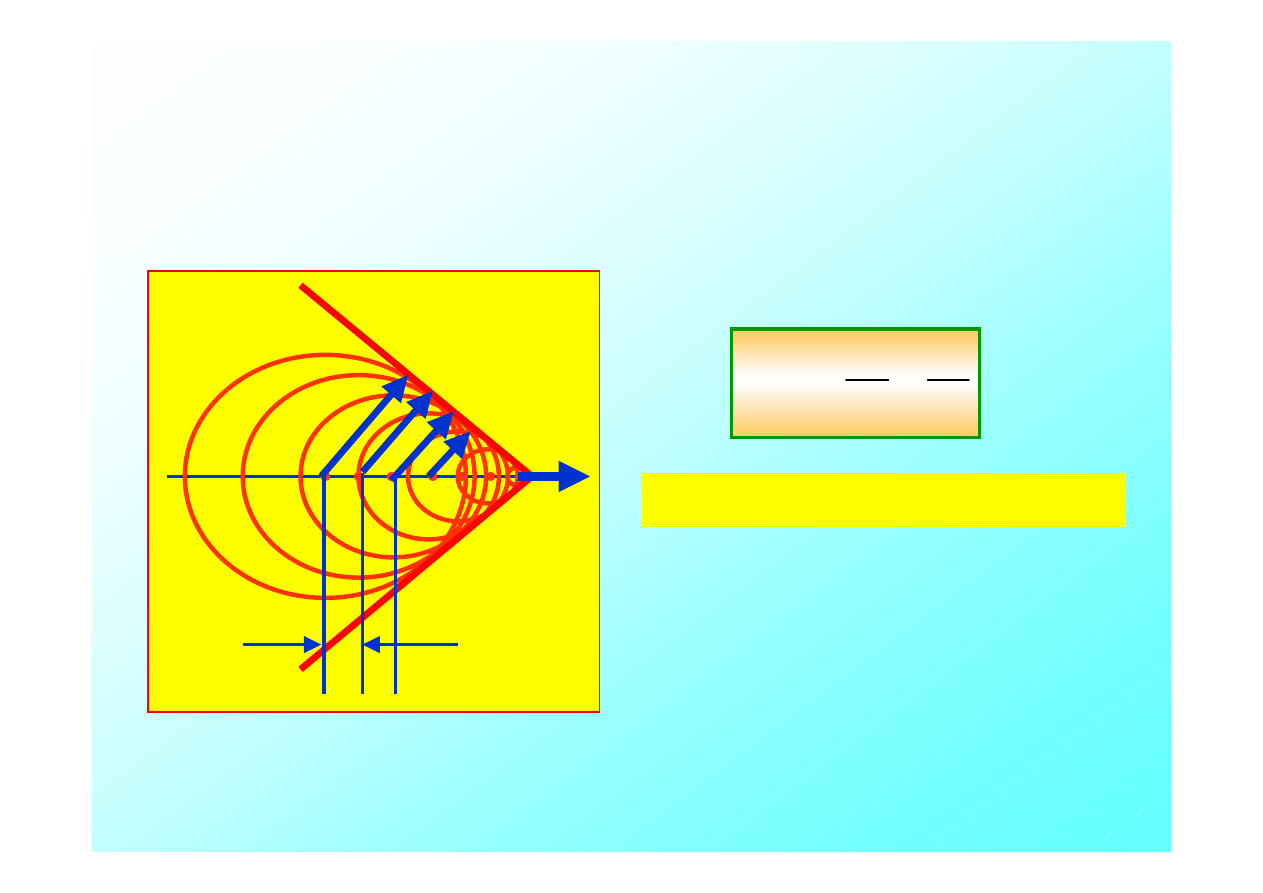
Kiedy obiekt emitujący dźwięk ma prędkość większą od prędkości
rozchodzenia się dźwięku, płaskie czoło fali uderzeniowej zmienia
się w stożek. Również energia koncentruje się na powierzchni
Stożka.

Połowa kąta rozwarcia stożka
jest dana przez;

v

zr

v

zr

T

1

sin

zr

u

v

M

θ =

=

.

M jest nazwane liczbą Macha.

Świetlne fale uderzeniowe również
istnieją w ośrodkach o współczynniku
załamania

n >1

co zmniejsza

prędkość światła w stosunku do tej

w próżni.

Powstające świetlne fale uderzeniowe nazywamy

promieniowaniem Cerenkova

.