Zwierciadło kuliste wklęsłe

W tym temacie omówimy

zwierciadło kuliste wklęsłe

.

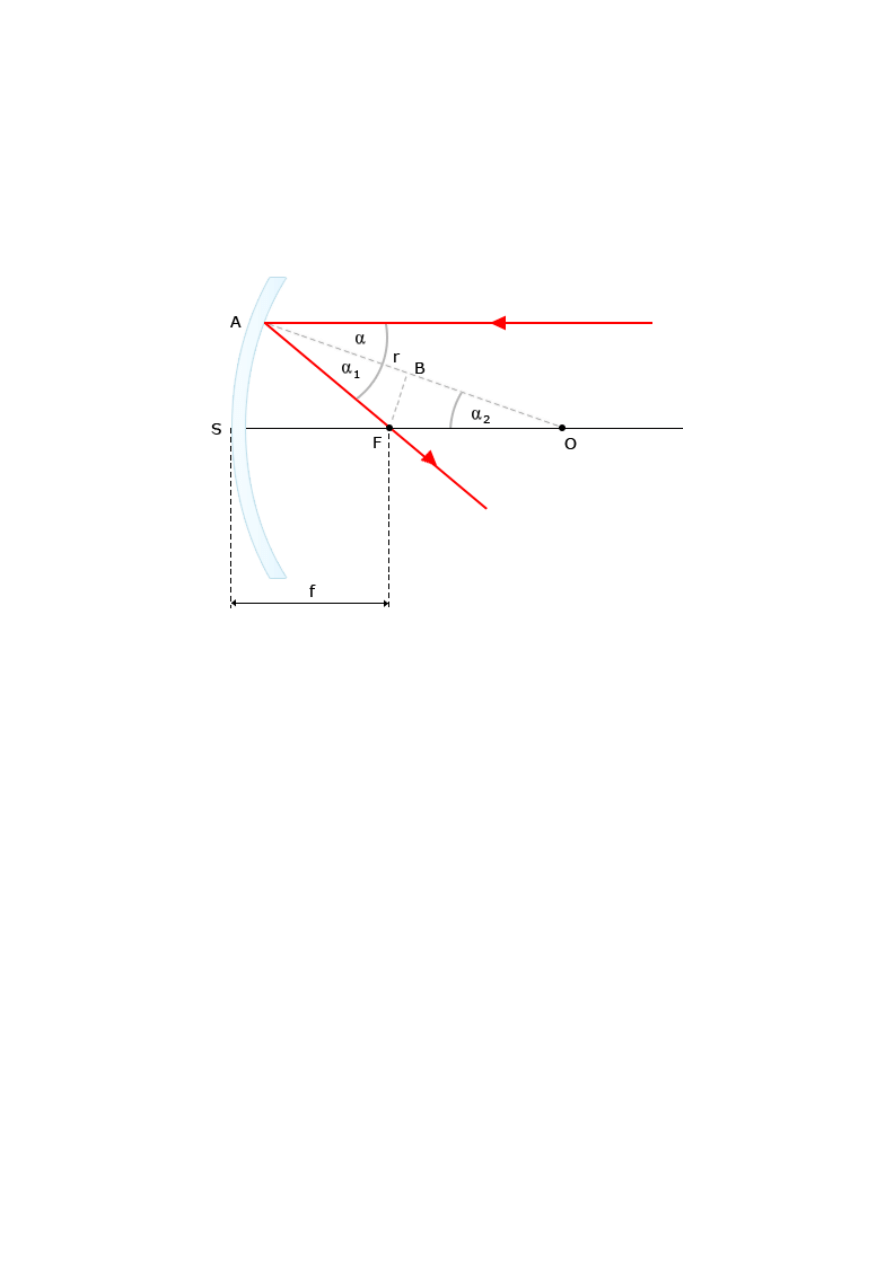
Prześledzimy bieg promienia, który odbija się od wewnętrznej strony zwierciadła.

Oś optyczna zwierciadła to prosta przechodząca przez środek kuli O oraz środek zwierciadła S.

Widzimy, że promień równoległy do osi optycznej odbija się od zwierciadła w punkcie A i przecina

oś w punkcie F. Wszystkie promienie, które biegną równolegle do osi optycznej, przecinają się w

tym samym punkcie F, zwanym

ogniskiem zwierciadła

. Odległość ogniska zwierciadła od

zwierciadła to

ogniskowa

i wynosi f=r/2.

Teraz przedstawimy konstrukcję przedmiotu, którego obraz odbija się od zwierciadła kulistego

wklęsłego. Niech ten przedmiot będzie strzałką ustawioną prostopadle do osi w odległości x>r

(czyli w odległości większej od promienia zwierciadła). Rysując bieg promieni, szukamy obrazu

końca tego przedmiotu, czyli punktu B (a szukamy punktu B’ – patrz animacja). A więc, podobnie

jak to czyniliśmy wcześniej, rysujemy bieg promienia, równoległy do osi optycznej, który po

odbiciu od zwierciadła przechodzi przez ognisko. Jednak, aby otrzymać obraz punktu B,

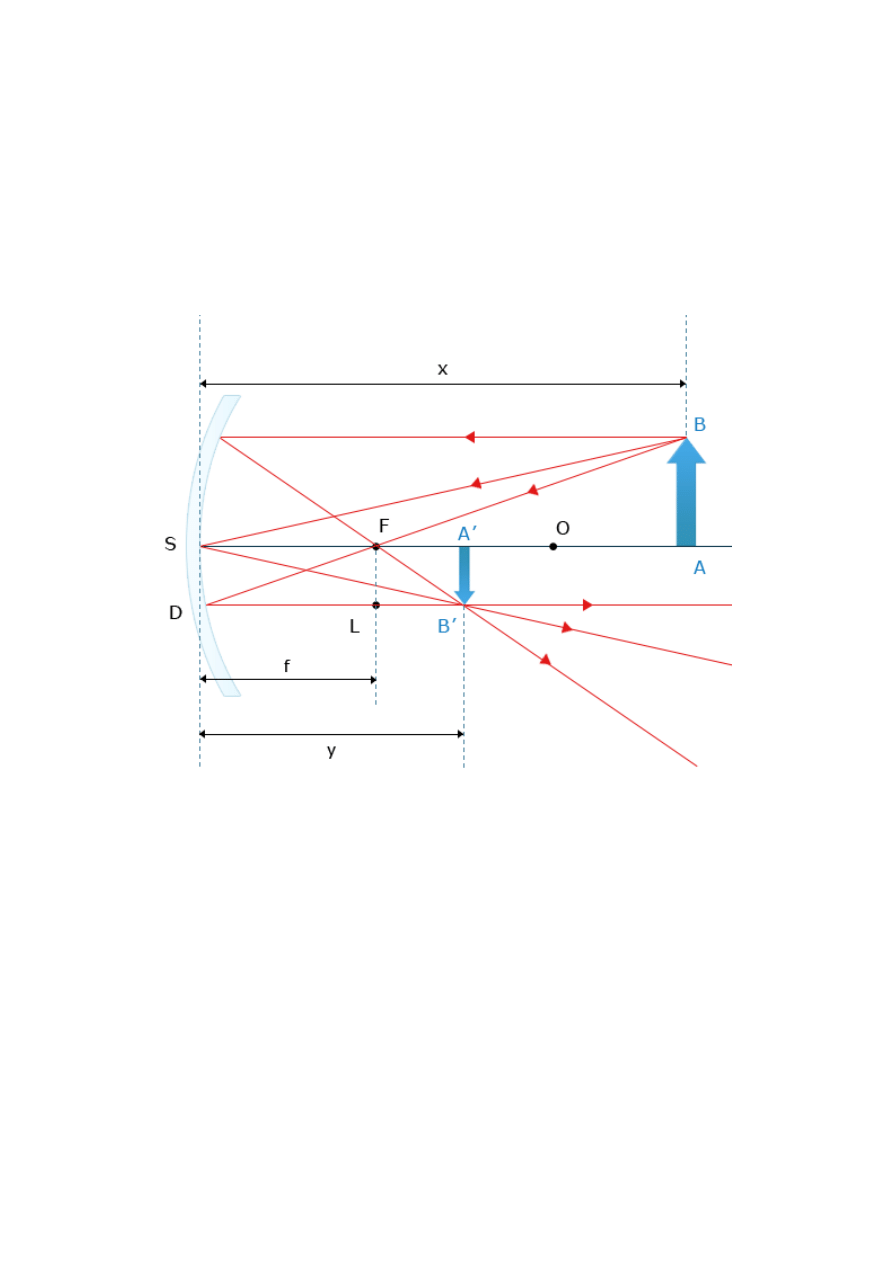
potrzebujemy jeszcze co najmniej jednego, innego, biegu promienia tego obrazu (może być ich

więcej). Tworzymy więc promień, który najpierw przechodzi przez ognisko, a później, po odbiciu

od zwierciadła, biegnie równolegle do osi optycznej. Punkt przecięcia tych promieni jest końcem

obrazu przedmiotu, a więc jest szukanym przez nas punktem B’. Tak więc otrzymaliśmy odcinek A’

B’ , który jest obrazem przedmiotu AB.

Powstały obraz jest

rzeczywisty

– można go obejrzeć na ekranie,

odwrócony

– punkt B jest po

przeciwnej stronie niż punkt B’ oraz

pomniejszony

- wysokość przedmiotu jest większa od

wysokości obrazu tego przedmiotu.

Gdy obraz znajduje się w odległości x=f (czyli w odległości równej ogniskowej), to obraz nie

powstaje, ponieważ promienie odbite od zwierciadła są równoodległe.

Dla f<x<2f obraz jest rzeczywisty, powiększony i odwrócony.

Teraz przedstawimy wzór, który będzie bardzo przydatny w rozwiązywaniu wielu problemów

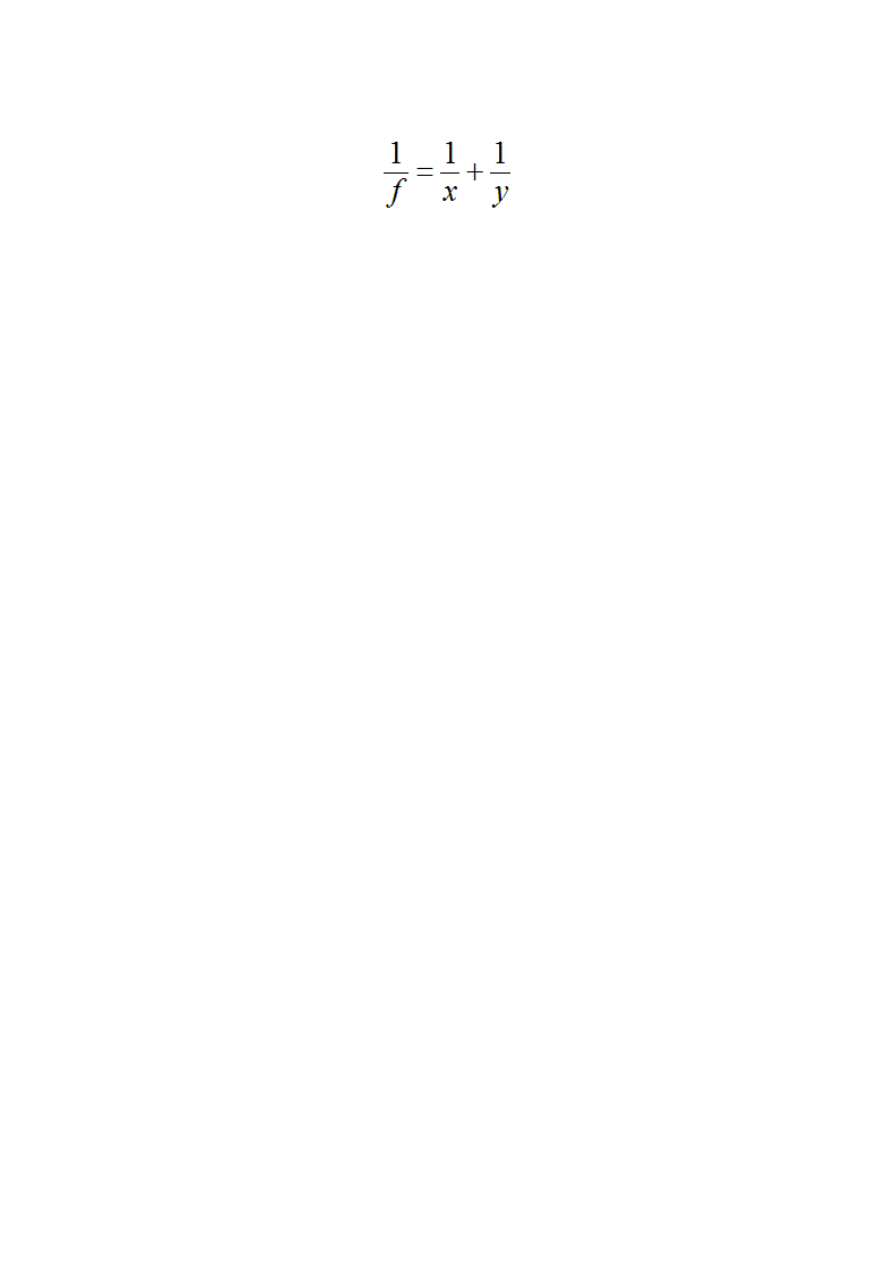
związanych z tym tematem.