PODSTAWY TELEDETEKCJI-ćwiczenia rachunkowe
Temat 1. Metody przeszukiwania przestrzeni oraz fizyczne zasady wykrywania obiektów.
Zadanie1.
Obliczyć okres obserwacji radaru realizującego dookólne przeszukiwanie przestrzeni oraz
liczbę impulsów oświetlających cel punktowy za jeden obrót anteny dla następujących
danych: częstotliwość obrotów anteny f = 12 obr/min, szerokość charakterystyki antenowej
w azymucie
= 2,7 , częstotliwość powtarzania impulsów sondujących F = 600 Hz.
A
α
Θ
0
p
T
obs
=
A
f
60
otrzymujemy
12
60
=5s
T
obs
otrzymujemy w [s] jeśli f
A
podstawiamy w [
]
min
/
obr
A
a
a
a
opr
f
t
6
θ
θ
=
Ω
=
otrzymujemy
min
/
12
6
7
,
2
0
obr
⋅
=0,037[s]
Liczbę impulsów w paczce znajdujemy z wyrażenia:
22
]
/
1
[
600
037
.
0
=
⋅
=
⋅
=
s
s
F
t
n
p
opr
Odp.22impulsy
Zadanie 2.
Antena radaru obraca się z prędkością 6obr/min. Szerokość charakterystyki antenowej
w płaszczyźnie azymutu
. Określić odległość R
0
1
=
a
θ
max
wynikającą z jednoznacznego
pomiaru odległości, przy której cel jest opromieniowany nie mniej niż 10-cioma impulsami.
Odp.416km
Zadanie3.
Obliczyć czas opromieniowania obiektu punktowego i liczbę odebranych impulsów jeśli radar
ma antenę o wiązce w kształcie symetrycznego cygara o szerokości
az
Θ =
= 3
el
Θ
0
i realizuje
przeszukiwanie sektorowe w strefie ograniczonej kątami: w azymucie
az
Φ = 90
0
, w elewacji
= 25
el
Φ
0
. Okres obserwacji T
obs
= 2[s] , a częstotliwość powtarzania radaru F
p
= 2000 Hz.
Korzystając z wyrażenia :
e
a
el
az
opr
obs
t
T
θ
θ
φ
φ
⋅
⋅
=
, otrzymujemy 16 impulsów.
Odp: 16 impulsów
Zadanie 4.
Radar realizujący metodę przeszukiwania przestrzeni typu rastru telewizyjnego posiada
następujące parametry techniczne: szerokość charakterystyki antenowej w azymucie
= 2,5
a
Θ
0
, w elewacji
=4
e
Θ
0
, sektor przeszukiwania w płaszczyźnie azymutu
a
α
=40
0
, w
płaszczyźnie elewacji
e
β
=30
0
, czas obserwacji sektora T
obs
= 5[s]. Obliczyć częstotliwość
1
powtarzania impulsów F
p
przy założeniu, że wykrywany obiekt powinien być
opromieniowany przynajmniej 10-cioma impulsami.
Zależności:
ilość linii w rastrze
e
e
N
θ
β
/
=
;
czas przeszukiwania jednej linii
N
T
T
obs
A
/
=
;
prędkość kątowa przeszukiwania w płaszczyźnie azymutu
A
A
a
T
/
α
=
Ω
;
czas
opromieniowania
a
a
opr
t
Ω
=
/
θ
Liczba impulsów w paczce
p
opr
F
t
n
⋅
=
Odp.257Hz.
Zadanie 5.
Radar realizuje przeszukiwanie metodą rastru telewizyjnego. Obliczyć szerokość sektora w
azymucie
A
α
przy następujących parametrach radaru: sektor przeszukiwania w płaszczyźnie
elewacji
e
β
= 24
0
, szerokość charakterystyki antenowej w płaszczyźnie azymutu
= 3
A
Θ
0
, w
płaszczyźnie elewacji
=3
e
Θ
0
, częstotliwość powtarzania radaru
Hz, czas
przeszukiwania rastrowego
s. Cel powinien być oświetlony przynajmniej 12-toma
impulsami.
400
=
p
F
10
=
obs
T
Odp.
A
α
= 125
0
Zadanie 6
Radar kontroli ruchu lotniczego ma płaską wiązkę antenową w azymucie o szerokości
. Antena obraca się z prędkością f
0
1
=
Θ
az
A
= 6obr/min. Obliczyć czas opromieniowania oraz
liczbę odebranych impulsów, jeśli częstotliwość ich powtarzania wynosi F
p
= 500Hz.
Odp: 14 impulsów
Zadanie 7.
Radar realizuje elektroniczne częstotliwościowe przeszukiwanie przestrzeni w płaszczyźnie
elewacji poprzez zmianę częstotliwości generowanych drgań według zależności :
t
T
f
f
t
f
Δ
+
=
0
)
(
dla
[ ]
T
t
,
0
∈
gdzie: f
0
= 3.10
9
Hz ;
= 3.10
f
Δ
7
Hz ; T = 1s.
Wyznaczyć czas promieniowania celu, jeżeli pasmo przenoszenia jednego kanału odbiornika
wynosi
= 3MHz.
k
F
Δ
Wyrażenia opisujące częstotliwościową metodę przeszukiwania przestrzeni:
- Szybkość zmian częstotliwości
( )
dt
t
df
v
f
=
;
2
- Czas opromieniowania obiektu
( )
( )
∫
Δ
+
=
k
F
f
f
f
opr
f
t
df
t
ν
przy zmiennej szybkości zmian f;
- Czas opromieniowania obiektu
f
k
opr
F
t
ν
Δ
=
przy stałej szybkości zmian częstotliwości
Odp. 0.1s
Zadanie 8.
W radarze zastosowano elektroniczną metodę przeszukiwania w płaszczyźnie elewacji,
natomiast mechaniczną w płaszczyźnie azymutu. Obliczyć czas opromieniowania obiektu,
jeśli przesunięcie fazy w dwóch kolejnych elementach promieniujących zmienia się z
prędkością
11
, odległość między elementami promieniującymi d=10cm,
długość fali
=
Φ dt
d /
s
rad /
λ
=10cm, szerokość wiązki w płaszczyźnie elewacji
e
Θ =1
0
, maksymalny. kąt
odchylenia wiązki ≤15
0
.
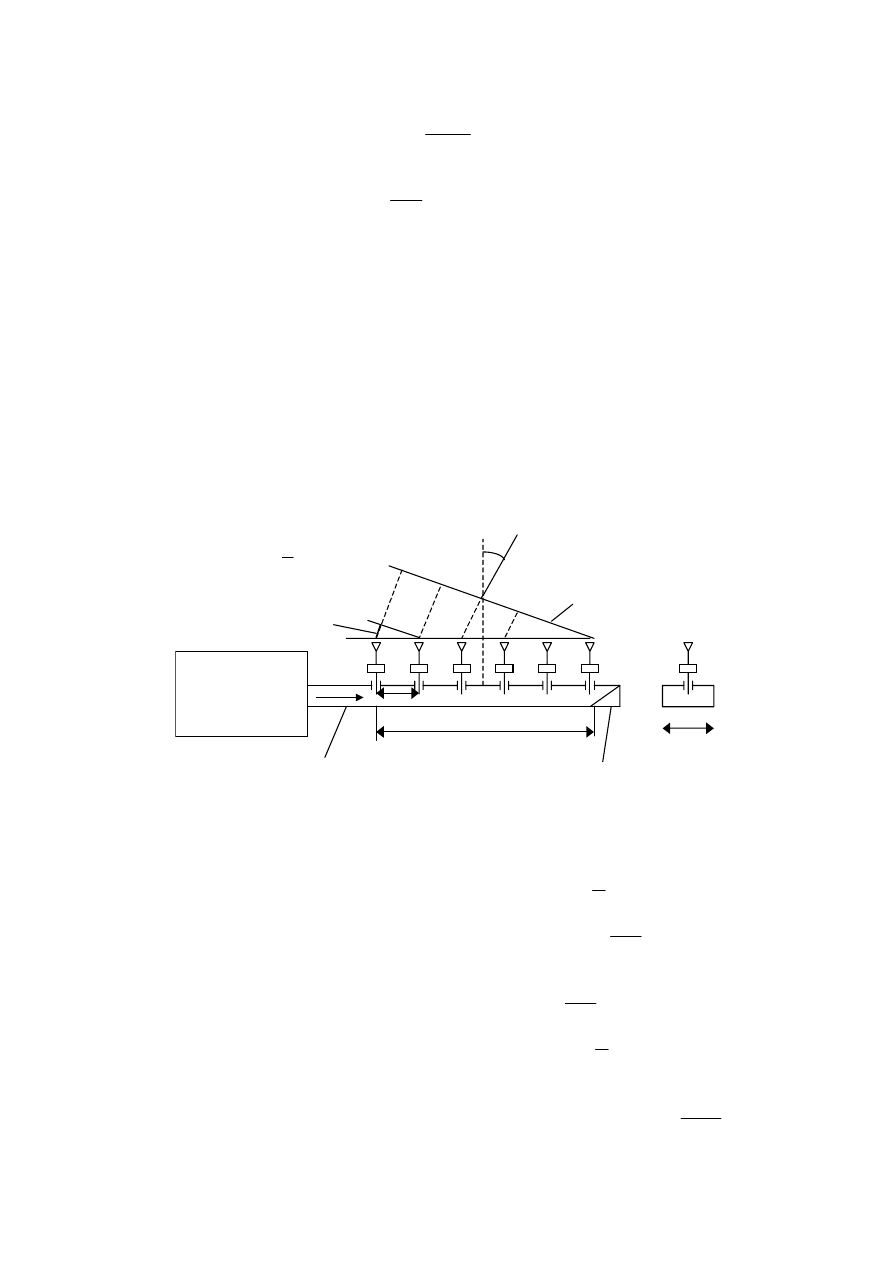
Opis metody przeszukiwania częstotliwościowego z liniowym szykiem antenowym w
płaszczyźnie elewacji.
Generator
bwcz
a
f(t)
Falowód zasilający
Sztuczne obciążenie
d
α
Front falowy
0
Φ
2
Φ
5
Φ
5
Φ
α
sin
d
Kierunek propagacji
L
α
λ
π
sin
2
d
=
Φ
Rys. Poziomy wiersz (lub pionowa kolumna) sieci antenowej
a – szerokość dłuższej ścianki falowodu
Zależności:
Liniowa rozróżnialność w danej współrzędnej kątowej
L
R
r
a
λ
=
Δ
Odchylenie wiązki od normalnej do apertury anteny
Φ
⋅
=
d
π
λ
α
2
arcsin
, gdzie
Φ -
fazowe przesunięcie drgań w sąsiednich elementach promieniujących.
Dla małych kątów odchylenia
α
≤ 15
0
Φ
≅
d
π
λ
α
2
.
Minimalna szerokość wiązki
(przy
e
Θ
α
= 0)
L
e
λ
=
Θ
min
.
[rad], gdzie
L
szerokość apertury anteny płaszczyźnie elewacji.
Przy rosnącym
α
szerokość
zmienia się zgodnie z zależnością
e
Θ
α
cos
min
Θ
≈
Θ
e
.
3
Kątowa prędkość przemieszczania wiązki w płaszczyźnie elewacji
dt
t
d
d
dt
d
)
(
2
Φ
⋅
=
=
Ω
π
λ
α
Czas opromieniowania celu punktowego
Ω
Θ
=
e
opr
t
.
Odp. 0.01s
Zadanie 9.
W pokładowym koherentno-impulsowym radarze z syntetyzowaną charakterystyką antenową
i obróbką nieoptymalną wymagany okres integracji winien wynosić
. Na jakiej
maksymalnej odległości można obserwować cele, jeśli
λ=3cm, v=2000km/godz?. Jaka winna
być częstotliwość powtarzania impulsów F
s
T
15
.
0
≤
p
jeśli sumowaniu winno podlegać 100 impulsów?
Czy w takich warunkach spełniony będzie warunek jednoznacznego pomiaru odległości?
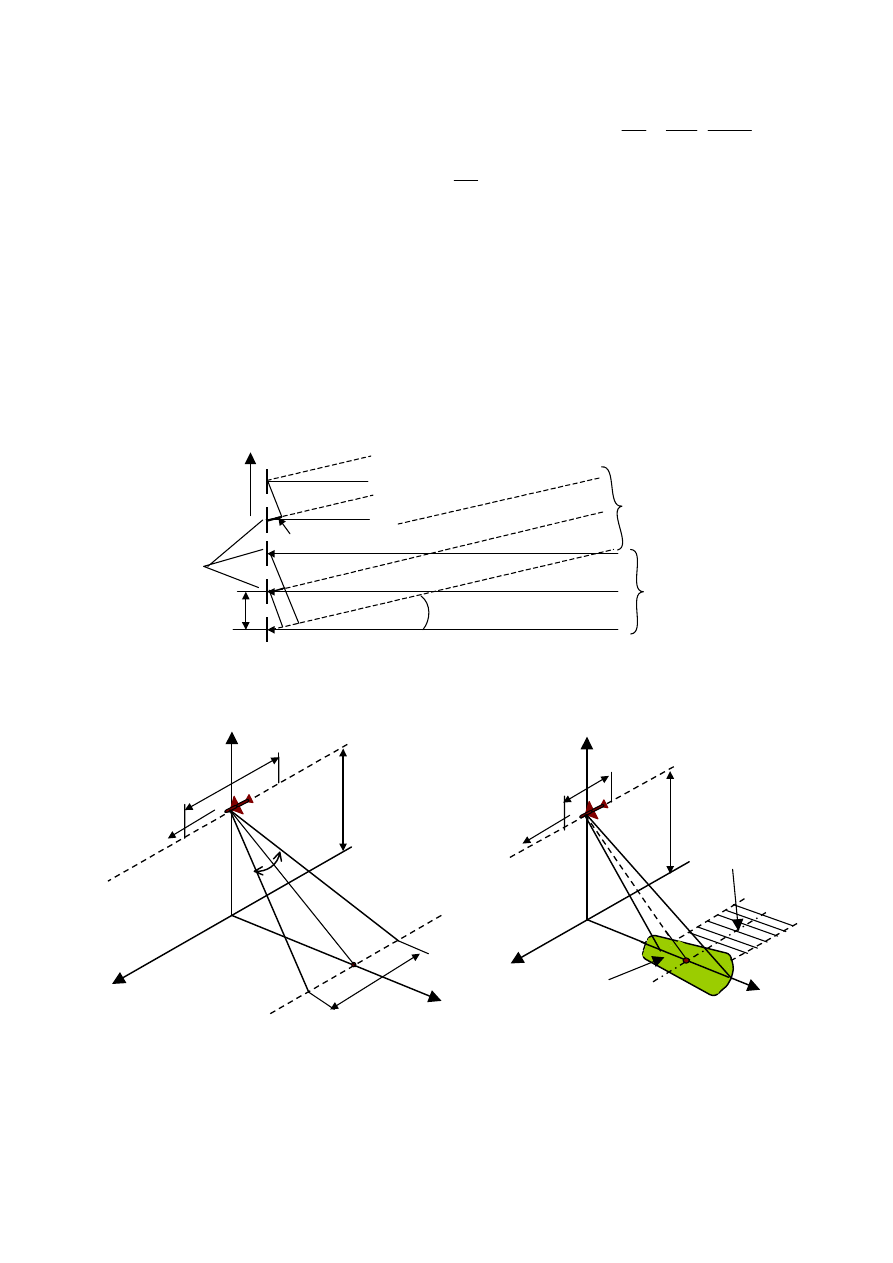
Opis metody obserwacji powierzchni ziemi z wykorzystaniem radaru typu SAR
Sygnał z kierunku
α
Sygnał od obiektów
na osi głównej
v
p
Położenia
anteny realnej
w kolejnych T
p
d
α
α
α
sin
sin
p
p
T
v
d
=
Rys.1 Sposób kształtowania syntetyzowanej apertury anteny
L
Z
d
X
d
Y
d
L
R
0
h
0
θ
a
v
p
L
Z
d
X
d
Y
d
h
0
v
p
Obserwowany
pas terenu
Ślad charakterystyki
anteny
Rys.2 Układ współrzędnych SAR
Rys.3 Schemat obserwacji bocznej
Zależności
Przesunięcia fazy
Φ w antenie odbieranego sygnału w kolejnych jej położeniach, czyli w
kolejnych okresach powtarzania impulsów sondujących wynoszą
4
α
λ
π
α
λ
π
sin
4
sin
4
p
p
T
v
d
=
=
Φ
dla
0
15
≤
α
α
λ
π
p
p
T
v
4
≅
Φ
SAR z obróbką optymalną
Dla SAR z anteną o szerokości na poziomie połowy mocy wynoszącej
5
.
0
θ
θ
=
a
czas
opromieniowania celu punktowego znajdującego się na odległości R
0
wynosi
v
R
T
t
opr
/
5
.
0
0
θ
=
=
na drodze samolotu
5
.
0
0
θ
R
L
=
, gdzie v jest prędkością samolotu, T–okres integracji impulsów
odebranych za czas przelotu drogi L.
Przyjmując, że
a
d
/
5
.
0
λ
θ
=
, gdzie d
a
stanowi wymiar apertury anteny radaru, otrzymujemy
a
d
R
L
/
0
λ
=
,
a czas opromieniowania
)
/(
0
a
opr
vd
R
T
t
λ
=
=
.
W czasie odbioru sygnałów w okresie T na skutek zmiany odległości zmienia się
częstotliwość Dopplera w zakresie
max
.
0
max
.
0
D
odb
D
F
f
f
F
f
+
≤
≤
−
a
D
d
v
v
F
/
/
5
.
0
max
.
=
=
λ
θ
Zatem przy ciągłym sygnale sondującym odbierany jest „impuls” o długości T i dewiacji
częstotliwości
a
D
M
d
v
F
f
/
2
2
max
=
=
Δ
.
Taki impuls podlega kompresji ze współczynnikiem
T
f
K
M
Δ
=
Długość impulsu po kompresji
v
d
f
t
a
M
wy
i
2
/
/
1
.
=
Δ
=
Rozróżnialność dwóch obiektów wynosi
s
a
R
r
.
5
.
0
0
θ
=
Δ
L
R
λ
0
2
1
=
, gdzie
s
5
.
0
θ
szerokość syntetyzowanej charakterystyki
na poziomie połowy mocy, L długość syntetyzowanej apertury anteny.
SAR z obróbką nieoptymalną (SAR niezogniskowany)
Czas opromieniowania celu punktowego (okres integracji T) w przypadku obróbki bez
ogniskowania wynosi
( )
2
/
/
1
0
λ
R
v
T
t
opr
=
=
.
Rozróżnialność dwóch obiektów wynosi
2
/
0
λ
R
r
a
=
Δ
Liczba odebranych w okresie integracji impulsów wynosi
p
p
TF
T
T
n
=
= /
.
Odpowiedzi:
,
km
R
460
max
≅
66
.
666
=
p
F
imp/s, Z jednoznacznego zakresu pomiaru
odległości wynika, że
a zatem warunek jednoznaczności nie jest spełniony.
km
R
225
max
≤
5
Zadanie 10.
W pokładowym koherentno-impulsowym radarze z syntetyzowaną charakterystyką antenową
i obróbką optymalną maksymalna odległość obserwacji wynosi R
max
=100km. Obliczyć czas
opromieniowania celu punktowego jeśli
λ=3cm, v=2000km/godz, długość apertury anteny
d
a
=1m. Jaka winna być częstotliwość powtarzania impulsów F
p
jeśli sumowaniu winno
podlegać 3000 impulsów? Czy w takich warunkach spełniony będzie warunek
jednoznacznego pomiaru odległości?
Odp
,
imp/s,
s
t
opr
4
.
5
=
556
=
p
F
270
max
=
R
km
Zadanie 11
Wyznaczyć czas opromieniowania celu punktowego z wykorzystaniem zogniskowanego
impulsowo-koherentnego radaru, jeśli
, R=300km, v=1000km/godz. Porównać czas
opromieniowania z czasem dla radaru niezogniskowanego przy fali o
λ=3cm.
0
5
.
0
1
=
Θ
s
t
opr
8
.
18
=
dla zogniskowanego,
s
t
opr
242
.
0
=
dla niezogniskowanego
Zadanie 12
Wymagane jest elektroniczne przeszukiwanie sektora azymutu. Dopuszczalne rozszerzenie
wiązki antenowej przy maksymalnym odchyleniu od normalnej do apertury anteny wynosi
1,5
.Określić rozwartość sektora przy którym spełniony będzie ten warunek.
min
Θ
Posługujemy się wyrażeniem
α
cos
min
Θ
≈
Θ
e
Odp.
0
max
5
,
48
≤
α
6
Document Outline