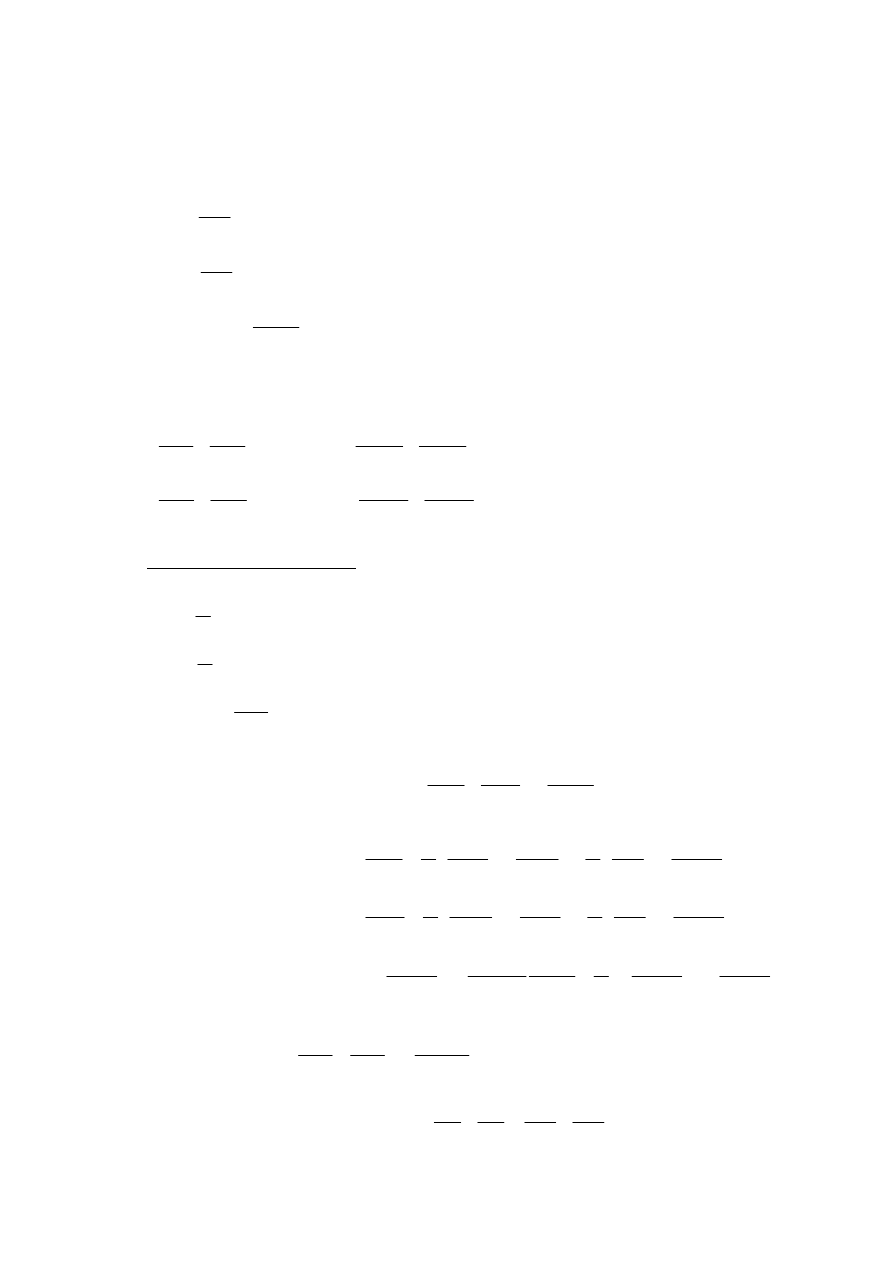
RÓWNANIE BIHARMONICZNE – wyprowadzenie
(
1
2
,
F x x
)
- funkcja naprężeń (funkcja Airy’ego) taka, że
2 2
1 1
1 2
2
11
,
2
2
2
22
,
2
1
2
12
21
2 1
1 2
,
2 1
1 2
1
2
x x
x x
x x
F
F
x
F
F
x
F
b x
b x
F
b x
b x
x x
σ
σ
σ
σ
ρ
ρ
ρ
ρ
⎧
∂
=
=
⎪
∂
⎪
⎪
∂
⎪
=
=
⎨
∂
⎪
⎪
∂
⎪
=
= −
−
−
= −
−
−
∂ ∂
⎪⎩
(1)
Funkcja ta automatycznie spełnia równania równowagi:
3
3
11
21
1
1
2
2
1
2
1
2
1
2
3
3
12
22
2
2
2
2
1
2
1
2
1
2
0
0
0
0
F
F
b
b
x
x
x x
x x
F
F
b
b
x
x
x x
x x
σ
σ
ρ
ρ
σ
σ
ρ
ρ
⎧∂
∂
∂
∂
+
+
=
⇒
−
−
+
=
⎪ ∂
∂
∂ ∂
∂ ∂
⎪
⎨
∂
∂
∂
∂
⎪
+
+
=
⇒
−
−
+
=
⎪ ∂
∂
∂ ∂
∂ ∂
⎩
1
2
b
b
ρ
ρ
Płaski stan naprężenia (PSN):
(
)
(
)
11
11
22
22
22
11
12
21
12
1
1
1
E
E
E
ε
σ
νσ
ε
σ
νσ
ν
ε
ε
σ
⎧
=
−
⎪
⎪
⎪
=
−
⎨
⎪
+
⎪
=
=
⎪⎩
Równanie nierozdzielności:
2
2
2
11
22
12
2
2
2
1
1
2
2
0
x
x
x x
ε
ε
ε
∂
∂
∂
+
−
=
∂
∂
∂ ∂
Wielkości pomocnicze:
(
)
2
2
2
4
4
11
11
22
2
2
2
4
2
2
2
2
2
2
1
2
2
2
2
4
4
22
22
11
2
2
2
4
2
2
1
1
1
1
1
2
2
2
4
4
12
12
2
2
2
2
2
2
1
2
1
2
1
2
1
2
1
1
1
1
2 1
1
2
2
F
F
x
E
x
x
E
x
x x
F
F
x
E
x
x
E
x
x x
F
F
2
x x
E
x x
E
x x
x
ε
σ
σ
ν
ν
ε
σ
σ
ν
ν
ν
ε
σ
ν
⎛
⎞
⎛
⎞
∂
∂
∂
∂
∂
=
−
=
−
⎜
⎟
⎜
⎟
∂
∂
∂
∂
∂ ∂
⎝
⎠
⎝
⎠
⎛
⎞
⎛
∂
∂
∂
∂
∂
=
−
=
−
⎜
⎟
⎜
∂
∂
∂
∂
∂ ∂
⎝
⎠
⎝
+
⎛
⎞
∂
∂
∂
−
= −
=
+
⎜
∂ ∂
∂ ∂
∂ ∂
∂ ∂
⎝
⎟
⎠
x
⎞
⎟
⎠
∂
Po podstawieniu:
4
4
4
4
4
2
2
1
2
1
2
2
0
F
F
F
x
x
x x
∂
∂
∂
+
+
=
∂
∂
∂ ∂
lub
,1111
,2222
,1122
2
0
F
F
F
+
+
=
lub:
(
)
(
)
2
2
2
2
1
2
2
2
2
2
1
2
1
2
,
0
F
F
F x x
x
x
x
x
⎛
⎞⎛
∂ ⋅ ∂ ⋅
∂
∂
∆ ∆
=
+
+
=
⎜
⎟⎜
∂
∂
∂
∂
⎝
⎠⎝
⎞
⎟
⎠

Płaski stan odkształcenia (PSO):
(
)
(
)
11
11
22
22
22
11
12
21
12
1
1
1
1
1
E
E
E
ν
ε
ν σ
ν
νσ
ε
ν σ
νσ
ν
ε
ε
σ
+
⎧
=
−
−
⎡
⎤
⎣
⎦
⎪
⎪
+
⎪
=
−
−
⎡
⎤
⎨
⎣
⎦
⎪
+
⎪
=
=
⎪⎩
Równanie nierozdzielności:
2
2
2
11
22
12
2
2
2
1
1
2
2
0
x
x
x x
ε
ε
ε
∂
∂
∂
+
−
=
∂
∂
∂ ∂
(
)
(
)
(
)
(
)
(
)
2
2
2
4
11
11
22
2
2
2
4
2
2
2
2
2
2
2
4
22
22
11
2
2
2
4
1
2
2
1
2
2
4
12
12
2
2
1
2
1
2
1
1
1
1
1
1
1
1
1
2 1
1
2
2
F
F
4
2
2
1
2
4
2
2
1
2
x
E
x
x
E
x
x
F
F
x
x
E
x
x
E
x
x
F
x x
E
x x
E
x
ε
σ
σ
ν
ν
ν
ν
ν
ν
ε
σ
σ
ν
ν
ν
ν
ν
ν
ν
ε
σ
ν
⎛
⎞
⎛
∂
∂
∂
+
+
∂
=
−
−
=
−
−
⎜
⎟
⎜
∂
∂
∂
∂
⎝
⎠
⎝
⎛
⎞
⎛
∂
∂
∂
+
+
∂
=
−
−
=
−
−
⎜
⎟
⎜
∂
∂
∂
∂
⎝
⎠
⎝
+
∂
∂
+
∂
−
= −
=
⋅
∂ ∂
∂ ∂
∂
x
⎞
∂
⎟
∂ ∂ ⎠
⎞
∂
⎟
∂ ∂ ⎠
2
2
2
x
∂
Po podstawieniu:
(
)
(
)
(
)
4
4
4
4
4
2
2
1
2
1
2
1
1
2 1
F
F
F
x
x
x x
ν
ν
ν
∂
∂
∂
−
+ −
+
−
=
∂
∂
∂ ∂
0
Stąd
4
4
4
4
4
2
2
1
2
1
2
2
0
F
F
F
x
x
x x
∂
∂
∂
+
+
=
∂
∂
∂ ∂
(
)
(
)
2
2
2
2
1
2
2
2
2
2
1
2
1
2
,
0
F
F
F x x
x
x
x
x
⎛
⎞⎛
∂ ⋅ ∂ ⋅
∂
∂
∆ ∆
=
+
+
=
⎜
⎟⎜
∂
∂
∂
∂
⎝
⎠⎝
⎞
⎟
⎠
- identyczna postać, jak w PSN
Wyszukiwarka
Podobne podstrony:
21 Równanie naturalne klotoidy
19-21, Rozwiązanie numeryczne równań różniczkowych przy rozwinięciu w szereg Taylora
Rozwiązywanie układów równań
W 21 Alkohole
Równanie Laplace’a
Rownanie Maxwella
21 02 2014 Wykład 1 Sala
21 Fundamnety przyklady z praktyki
BO I WYKLAD 01 3 2011 02 21
Rozwiązywanie układów równań metodą wyznaczników
więcej podobnych podstron