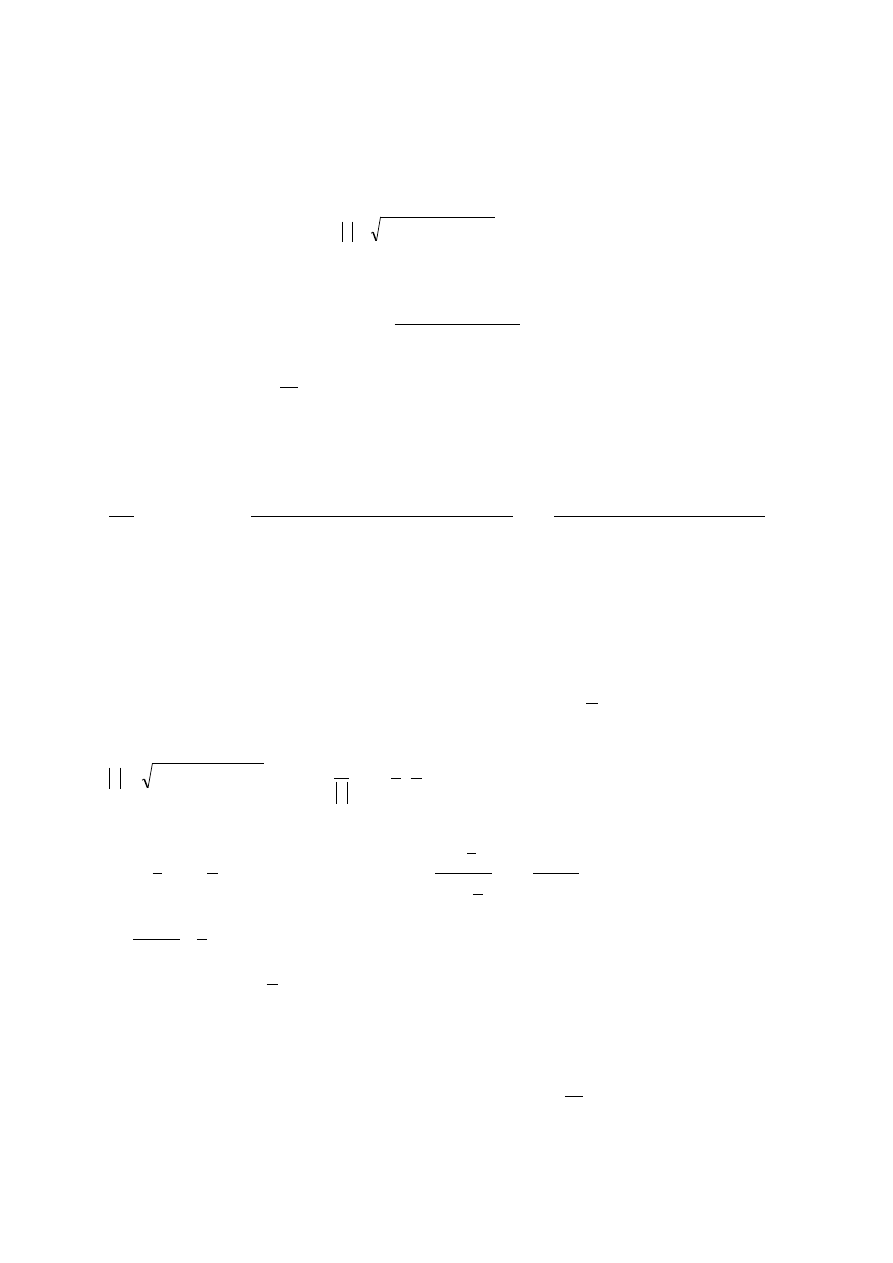
AM2 2011/ 12 w10

9.05.2012

P

OCHODNE

K

IERUNKOWA

(

UO GÓLNIENIE PO CHODNEJ CZASTKOWEJ

)

Niech

f będzie funkcją określoną w otoczeniu U punktu

)

,

,

,

,

,

,

,

(

0

0

1

0

0

1

0

2

0

1

0

n

i

i

i

x

x

x

x

x

x

x











,

v będzie wektorem jednostkowym

1

2

2

2

2

1











n

v

v

v

v



takim, że punkt

U

tv

x





0

.

D

EF

.

Jeżeli istnieje skończona granica

t

x

f

tv

x

f

t

)

(

)

(

lim

0

0

0







to nazywamy ją pochodną kierunkową funkcji f w punkcie x

0

w kierunku wektora v.

Oznaczamy ją symbolem

)

(

0

x

v

f





lub

)

(

0

x

f

v



.

Przykład

3



n

,

)

1

,

0

,

0

(

3





e

v





)

,

,

(

)

,

,

(

)

,

,

(

lim

)

,

,

(

)

1

,

0

,

0

(

)

,

,

(

lim

)

,

,

(

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

3

z

y

x

f

t

z

y

x

f

t

z

y

x

f

t

z

y

x

f

t

z

y

x

f

z

y

x

e

f

z

t

t

























W

NIOS EK

Pochodna kierunkowa funkcji f w punkcie x

0

w kierunku wektora

i

e jest równa pochodnej cząstkowej

funkcji f w punkcie x

0

względem i-tej zmiennej

)

(

)

(

0

0

x

f

x

f

i

i

x

e







.

Przykład

Obliczyć z definicji pochodną kierunkową funkcji

y

x

z

z

y

x

f





2

)

,

,

(

w punkcie

)

1

,

2

,

4

(





w

kierunku wektora

)

0

,

4

,

3

(





v

5

0

4

)

3

(

2

2

2











v

,

















0

,

5

4

,

5

3

v

v

i

v

3

)

1

,

2

,

4

(







f

t

t

t

t

f

t

t

f

4

10

5

3

5

4

2

5

3

4

)

1

(

)

1

,

2

,

4

(

0

1

,

5

4

2

,

5

3

4

2















































2

1

4

10

5

lim

0







t

t

odp.

2

1

)

1

,

2

,

4

(









f

v

i

T

WIERDZENIE

(

WZÓR DO OBLICZANIA POCHODNEJ KIERUNKOWEJ

,

UZASADNIENIE DLA N

=2)

Jeżeli funkcja f ma ciągłe pochodne cząstkowe pierwszego rzędu w punkcie

0

x

,

n

R

v



jest

dowolnym wektorem jednostkowym, to pochodna kierunkowa

)

(

0

x

v

f





jest iloczynem

skalarnym wektora gradientu i wektora v

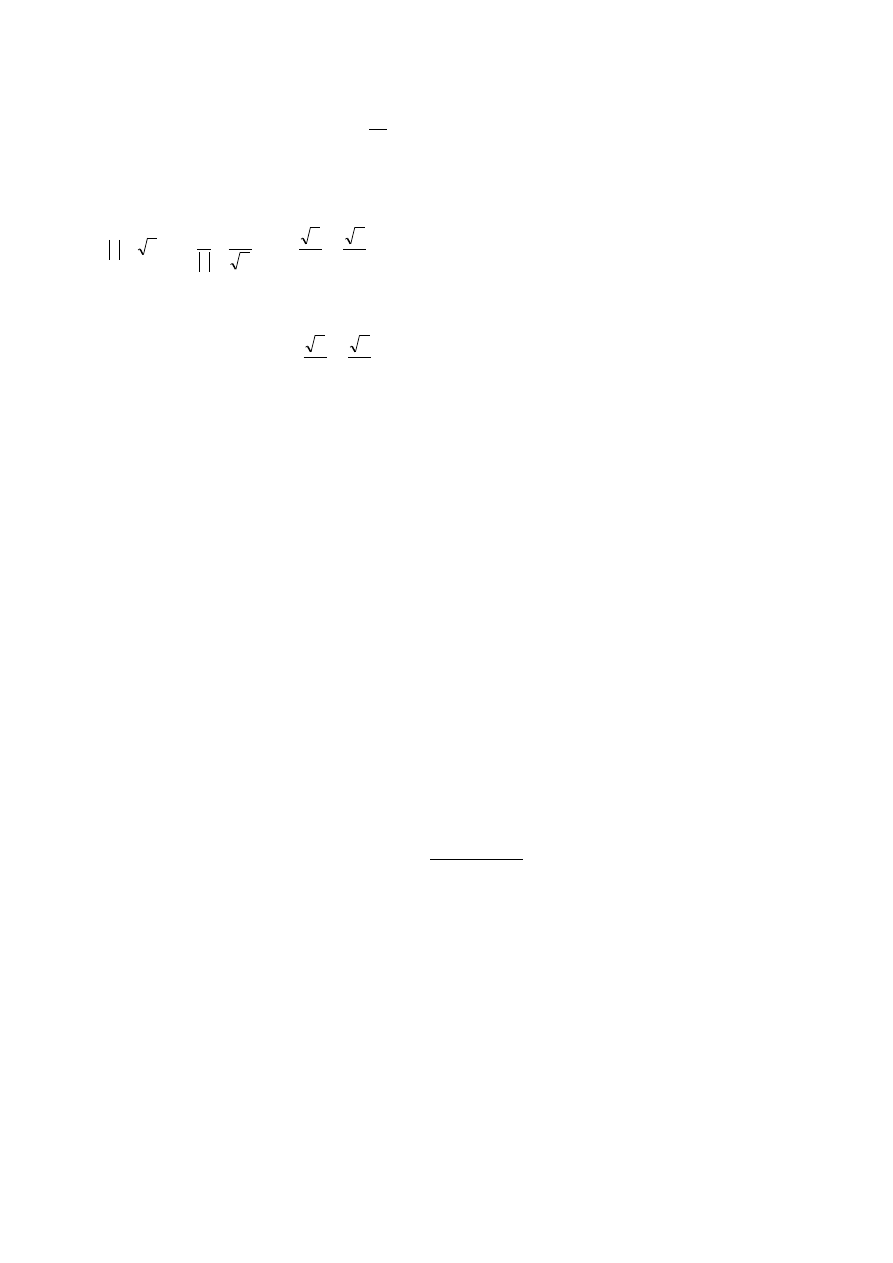
AM2 2011/ 12 w10

9.05.2012

v

x

gradf

x

v

f









)

(

)

(

0

0

.

P

RZYKŁAD

Obliczyć pochodną kierunkową funkcji

2

cos

)

,

,

(

yz

e

x

z

y

x

f





w punkcie

)

1

,

0

,

(





w kierunku

wektora





1

,

0

,

1



.

2



v

,























2

2

,

0

,

2

2

2

1

v

v

v

i

v





yz

xe

z

xe

xe

z

y

x

gradf

yz

yz

yz

2

2

2

cos

2

,

cos

,

sin

)

,

,

(

2









0

,

1

,

0

)

1

,

0

,

(









gradf

0

2

2

,

0

,

2

2

)

0

,

1

,

0

(

)

1

,

0

,

(































f

v

i

WNIOSKI
Jeżeli

0

)

(

0



x

gradf

, to

- pochodna kierunkowa przyjmuje największą wartość, gdy jest obliczana w kierunku
gradientu
- gradient wskazuje kierunek najszybszego wzrostu funkcji f w punkcie

0

x

- gradient jest wektorem, którego moduł jest równy maksymalnej wartości pochodnej
kierunkowej w danym punkcie.

P

ŁASZCZYZNA STYCZNA

Jeżeli funkcja f jest klasy

1

C

w punkcie

)

,

(

0

0

y

x

, to równanie

)

,

(

)

)(

,

(

)

)(

,

(

0

0

0

0

0

0

0

0

y

x

f

y

y

y

x

f

x

x

y

x

f

z

y

x















jest równaniem płaszczyzny stycznej do wykresu funkcji f w punkcie





)

,

(

,

,

0

0

0

0

y

x

f

y

x

.

C

AŁKA PODWÓJNA W PROSTOKĄCIE

Rozważmy prostokąt P





d

y

c

b

x

a

R

y

x

P













,

:

)

,

(

2

oraz funkcję dwóch zmiennych f określoną i ograniczoną w tym prostokącie.

Prostokąt P dzielimy na n prostokątów

k

P

o polach

k

s



n

k



,

2

,

1



. Prostokąty

k

P

n

k



,

2

,

1



mają rozłączne wnętrza i całkowicie wypełniają prostokąt P. Podział ten oznaczmy

n



.

Niech

k

d

oznacza długość przekątnej prostokąta

k

P

.

Liczbę

k

n

k

n

d







1

max



(długość najdłuższej z przekątnych) nazywamy średnicą podziału

n



.

Rozważmy ciąg podziałów

 

n



prostokąta P.

Ciąg podziałów

 

n



nazywamy ciągiem normalnym podziałów jeżeli odpowiadający mu ciąg

średnic dąży do zera tzn.

0

lim







n

n



.

W każdym z prostokątów wybieramy dowolnie punkt

)

,

(

k

k

k

y

x

A



, obliczamy

)

,

(

k

k

y

x

f

i

tworzymy sumę









n

k

k

k

k

n

s

y

x

f

S

1

)

,

(

.

AM2 2011/ 12 w10

9.05.2012

Sumę tę nazywamy sumą całkową funkcji f w prostokącie P.


D

EF

.

Jeżeli dla każdego normalnego ciągu podziałów prostokąta P ciąg sum całkowych

 

n

S

jest

zbieżny do tej samej granicy właściwej, niezależnej od wyboru punktów, to tę granicę
nazywamy całką podwójną funkcji f w prostokącie P i oznaczamy symbolem



P

dxdy

y

x

f

)

,

(

.

Definicję tę można zapisać krótko













n

k

k

k

k

def

P

s

y

x

f

dxdy

y

x

f

n

1

0

)

,

(

lim

)

,

(



.

PRZYPADEK SZCZEGÓLNY

Jeżeli

1

)

,

(



y

x

f

, to

P

s

s

y

x

f

S

n

k

k

n

k

k

k

k

n

prostokata

pole

1

)

,

(

1

1



















(ciąg sum całkowych jest stały)
zatem

P

dxdy

P

prostokata

pole

1





.

TW:

W

ARUNEK WYSTARCZAJĄCY ISTNIENIA CAŁKI PODWÓJNEJ W PROSTOKĄCIE

Jeżeli funkcja f jest ciągła w prostokącie P, to jest w nim całkowalna.

I

NTERPRETACJA

G

EOMETRYCZNA

Jeżeli funkcja f jest ciągła w prostokącie P i przyjmuje wartości nieujemne

P

x,y

y

x

f





)

(

dla

0

)

,

(

,

to całka podwójna



P

dxdy

y

x

f

)

,

(

jest równa objętości bryły ograniczonej płaszczyznami

0

,

,

,

,











z

d

y

c

y

b

x

a

x

oraz powierzchnią o równaniu

)

,

(

y

x

f

z



.

TW:

LINIOWOŚĆ CAŁKI

Jeżeli funkcje f i g są całkowalne na prostokącie P, to
1. funkcja

g

f



jest całkowalna na prostokącie P oraz

















P

P

P

dxdy

y

x

g

dxdy

y

x

f

dxdy

y

x

g

y

x

f

)

,

(

)

,

(

)

,

(

)

,

(

2. funkcja

cf

dla

R

c



jest całkowalna na P oraz







P

P

dxdy

y

x

f

c

dxdy

y

x

cf

)

,

(

)

,

(

.

T

W

:

O

BLICZANIE CAŁKI PODWÓJNEJ NA PROSTOKĄCIE

P

ZA POMOCĄ CAŁKI ITEROWANEJ

Jeżeli funkcja f jest ciągła w prostokącie P,





d

y

c

b

x

a

R

y

x

P













,

:

)

,

(

2

,

to

 

 





















b

a

d

c

b

a

d

c

P

dy

y

x

f

dx

dx

dy

y

x

f

dxdy

y

x

f

)

,

(

)

,

(

)

,

(

oraz

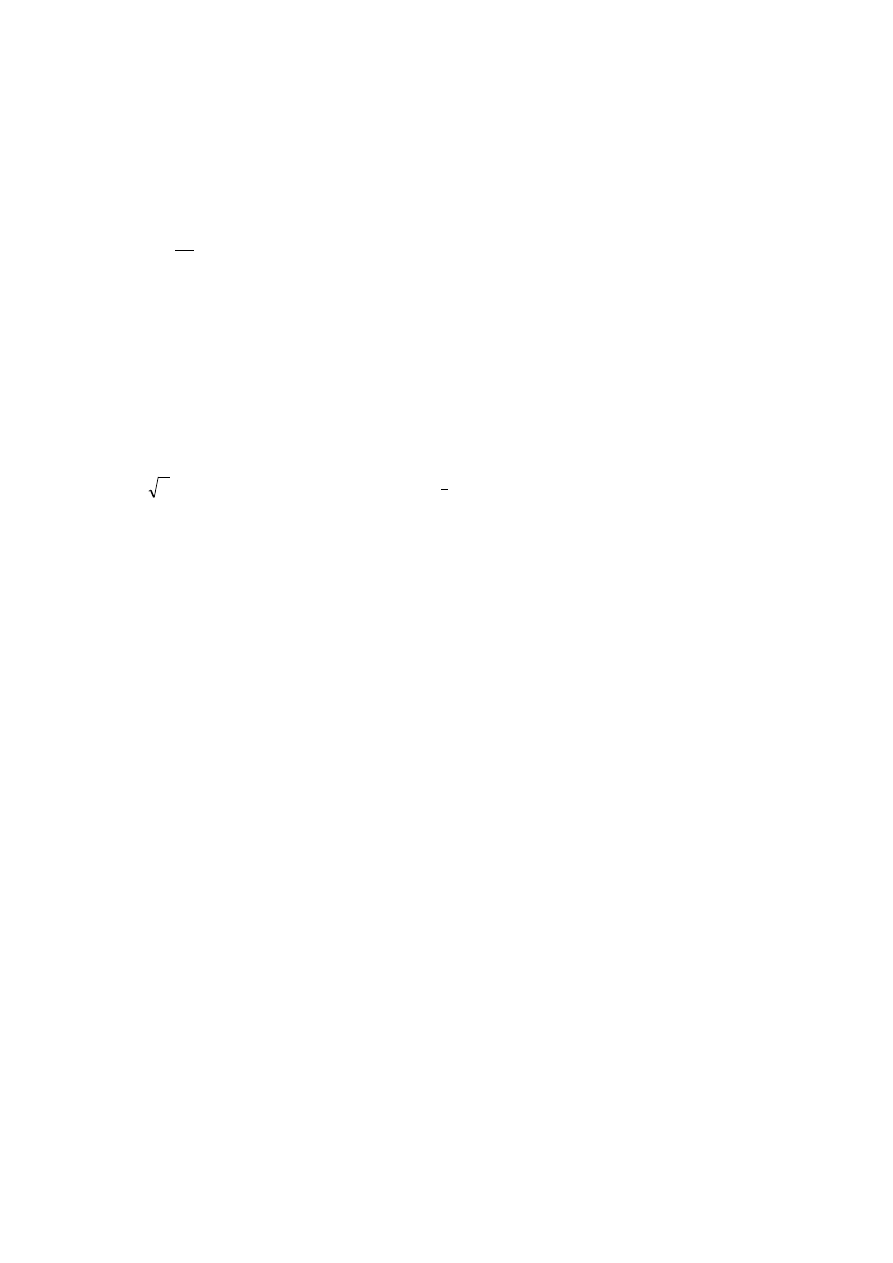
AM2 2011/ 12 w10

9.05.2012

 

 





















d

c

b

a

d

c

b

a

P

dx

y

x

f

dy

dy

dx

y

x

f

dxdy

y

x

f

)

,

(

)

,

(

)

,

(

.

Przykład
Obliczyć całkę podwójną na podanym prostokącie

a)

















P

dxdy

x

y

2

1

gdzie













3

,

2

2

,

1

P

odp:

3

b)









P

dxdy

x

y

x

2

gdzie













3

,

0

2

,

1

P

Uwaga
Jeżeli funkcja f ma postać

)

(

)

(

)

,

(

y

h

x

g

y

x

f



gdzie g, h są ciągłe na przedziałach odpowiednio





b

a,

,





d

c,

, to















 





d

c

d

c

b

a

P

b

a

dy

y

h

dx

x

g

dxdy

y

h

x

g

)

(

)

(

)

(

)

(

,

,

.

c)









P

x

dxdy

e

y

gdzie













4

,

1

1

,

0

P

odp:

e

3

3

5



C

AŁKA PODWÓJNA W OBSZARZE NORMALNYM

Niech f będzie funkcją określoną i ograniczoną na zbiorze ograniczonym D,

2

R

D



.

Całkę podwójną funkcji f na zbiorze D definiujemy wzorem









D

P

dxdy

y

x

f

dxdy

y

x

f

)

,

(

)

,

(

gdzie P jest dowolnym prostokątem zawierającym zbiór D, zaś funkcja



f

jest określona

wzorem















D

P

y

x

D

y

x

y

x

f

y

x

f

\

)

,

(

dla

0

)

,

(

dla

)

,

(

)

,

(

.

PRZYPADEK SZCZEGÓLNY

Jeżeli

1

)

,

(



y

x

f

, to

D

bioru

dxdy

D

z

pole

1





D

EF

.

Obszarem normalnym względem osi 0x nazywamy obszar





)

(

)

(

,

:

)

,

(

2

x

h

y

x

g

b

x

a

R

y

x

D













gdzie g, h są funkcjami ciągłymi w przedziale





b

a,

.

Obszarem normalnym względem osi 0y nazywamy obszar





)

(

)

(

,

:

)

,

(

2

y

q

x

y

p

d

y

c

R

y

x

D













gdzie p, q są funkcjami ciągłymi w przedziale





d

c,

.

D

EF

.

Obszar regularny

Obszarem regularnym na płaszczyźnie nazywamy sumę skończonej liczby obszarów normalnych
(względem osi 0x lub 0y) o parami rozłącznych wnętrzach.

Przykład
Naszkicować obszary ograniczone podanymi krzywymi. Który z nich jest normalny względem osi 0x,

a który względem osi 0y.

AM2 2011/ 12 w10

9.05.2012

a)

4

,

2

,







x

x

y

x

y

b)

4

,

2

,







y

x

y

x

y

c)

0

,

6

,

2









y

x

y

x

y

d)

4

2

2





y

x

TW:

ZAMIANA CAŁKI PODWÓJNEJ PO OBS ZARZE NORMALNYM NA CAŁKI ITEROWANE

Jeżeli funkcja f jest ciągła na obszarze





)

(

)

(

,

:

)

,

(

2

x

h

y

x

g

b

x

a

R

y

x

D













normalnym względem osi 0x , to



 























b

a

b

a

x

h

x

g

x

h

x

g

D

dy

y

x

f

dx

dx

dy

y

x

f

dxdy

y

x

f

)

(

)

(

)

(

)

(

)

,

(

)

,

(

)

,

(

Jeżeli funkcja f jest ciągła na obszarze





)

(

)

(

,

:

)

,

(

2

y

q

x

y

p

d

y

c

R

y

x

D













normalnym względem osi 0y , to

 

 





















d

c

y

q

y

p

d

c

y

q

y

p

D

dx

y

x

f

dy

dy

dx

y

x

f

dxdy

y

x

f

)

(

)

(

)

(

)

(

)

,

(

)

,

(

)

,

(

.

I

NTERPRETACJA

G

EOMETRYCZNA

Jeżeli funkcja f jest ciągła na obszarze normalnym D

2

R

D



i przyjmuje wartości nieujemne, to całka

podwójna jest równa objętości bryły o podstawie D ograniczonej powierzchnią o równaniu

)

,

(

y

x

f

z



oraz powierzchnią walcową utworzoną z prostych równoległych do osi 0z i

przechodzących przez brzeg obszaru D.

Przykład
Obliczyć całkę podwójną

;

)

4

2

24

(







D

dxdy

y

x

po obszarze ograniczonym przez krzywe o

podanych równaniach:

2

,

2

,

1







x

y

xy

odp:

4

ln

24

58

2

1



Podać interpretację geometryczną.

TW (o wartości średniej dla całki podwójnej)
Jeżeli funkcji f jest ciągła na obszarze normalnym D, to istnieje punkt

D

y

x



)

,

(

, taki,że

D

y

x

f

dxdy

y

x

f

D







)

,

(

)

,

(

.

Liczbę



D

dxdy

y

x

f

D

)

,

(

1

nazywamy wartością średnią funkcji f na obszarze D.

TW:

Jeżeli obszar regularny D jest sumą obszarów normalnych D

1

, D

2

o rozłącznych wnętrzach,

2

1

D

D

D





, funkcja f jest ciągła na D, to

AM2 2011/ 12 w10

9.05.2012

C

AŁKA POTRÓJNA W PROSTOPADŁOŚCIANIE

Rozważmy prostopadłościan P





q

z

p

d

y

c

b

x

a

R

z

y

x

P

















,

,

:

)

,

,

(

3

oraz funkcję trzech zmiennych f określoną i ograniczoną w tym prostopadłościanie.
Oznaczmy przez V objętość prostopadłościanu P.
Prostopadłościan P dzielimy na n prostopadłościanów

k

P

o objętościach

k

V



n

k



,

2

,

1



.

Prostopadłościany

k

P

n

k



,

2

,

1



mają rozłączne wnętrza i całkowicie wypełniają

prostopadłościan P. Podział ten oznaczmy

n



.

Niech

k

d

oznacza długość przekątnej prostopadłościanu

k

P

o wymiarach

k

k

k

z

y

x







,

,

2

2

2

k

k

k

k

z

y

x

d













.

Liczbę

k

n

k

n

d







1

max



(długość najdłuższej z przekątnych) nazywamy średnicą podziału

n



.

Rozważmy ciąg podziałów

 

n



prostopadłościanu P.

Ciąg podziałów

 

n



nazywamy ciągiem normalnym podziałów jeżeli odpowiadający mu ciąg

średnic dąży do zera tzn.

0

lim







n

n



.

W każdym prostopadłościanie wybieramy dowolnie punkt

)

,

,

(

k

k

k

k

z

y

x

A



, obliczamy

wartość funkcji f w tym punkcie

)

,

,

(

k

k

k

z

y

x

f

i tworzymy sumę









n

k

k

k

k

k

n

V

z

y

x

f

S

1

)

,

,

(

.

Sumę tę nazywamy sumą całkową funkcji f w prostopadłościanie P.

D

EF

.

Jeżeli dla każdego normalnego ciągu podziałów prostopadłościanu P ciąg sum całkowych

 

n

S

jest zbieżny do tej samej granicy właściwej, niezależnej od wyboru punktów, to tę

granicę nazywamy całką potrójną funkcji f w prostopadłościanie P i oznaczamy symbolem



P

dxdydz

z

y

x

f

)

,

,

(

.

Definicję tę można zapisać krótko













n

k

k

k

k

k

def

P

V

z

y

x

f

dxdydz

z

y

x

f

n

1

0

)

,

,

(

lim

)

,

,

(



.

PRZYPADEK SZCZEGÓLNY

Jeżeli

1

)

,

,

(



z

y

x

f

, to

V

V

V

z

y

x

f

S

n

k

k

n

k

k

k

k

k

n



















1

1

1

)

,

,

(

,

Ciąg sum całkowych jest w tym przypadku ciągiem stałym o wyrazach

V

S

n



.

V

V

V

dxdydz

n

n

n

k

k

def

P



















0

1

0

lim

lim

1





.

V

- objętość prostopadłościanu P.

TW:

W

ARUNEK WYSTARCZAJĄCY ISTNIENIA CAŁKI POTRÓJNEJ W PROSTOPADŁOŚCIANIE

Jeżeli funkcja f jest ciągła w prostopadłościanie P, to jest w nim całkowalna.

AM2 2011/ 12 w10

9.05.2012

I

NTERPRETACJA

F

IZYCZNA

Jeżeli funkcja



jest gęstością objętościową masy prostopadłościanu P, to całka potrójna



V

dxdydz

z

y

x

)

,

,

(



jest równa masie prostopadłościanu.

TW:

LINIOWOŚĆ CAŁKI

Jeżeli funkcje f i g są całkowalne w prostopadłościanie P, to
1. funkcja

g

f



jest całkowalna w prostopadłościanie P oraz

















P

P

P

dxdydz

z

y

x

g

dxdydz

z

y

x

f

dxdydz

z

y

x

g

z

y

x

f

)

,

,

(

)

,

,

(

)

,

,

(

)

,

,

(

2. funkcja

cf

dla

R

c



jest całkowalna na P oraz







P

P

dxdydz

z

y

x

f

c

dxdydz

z

y

x

cf

)

,

,

(

)

,

,

(

T

W

:

O

BLICZANIE CAŁKI POTRÓJNEJ W PROSTOPADŁOŚCIANIE

P

ZA POMOCĄ CAŁKI

ITEROWANEJ

Jeżeli funkcja f jest ciągła w prostopadłościanie P,





q

z

p

d

y

c

b

x

a

R

z

y

x

P

















,

,

:

)

,

,

(

3

,

to

  

  





































b

a

d

c

q

p

b

a

d

c

q

p

P

dz

z

y

x

f

dy

dx

dx

dy

dz

z

y

x

f

dxdydz

z

y

x

f

)

,

,

(

)

,

,

(

)

,

,

(

Uwaga
Kolejność iteracji po prawej stronie wzoru może być dowolna. Istnieje sześć możliwych
ustaleń kolejności całkowania.

Przykład
Obliczyć całkę potrójną w podanym prostopadłościanie
a)







P

dxdydz

z

y

x

)

(

2

3

gdzie



















3

,

1

2

,

0

2

,

1

P

b)



P

dxdydz

z

y

x

3

gdzie



















e

P

,

1

2

,

1

1

,

0

Uwaga
Jeżeli funkcja f ma postać

)

(

)

(

)

(

)

,

,

(

z

k

y

h

x

g

z

y

x

f



gdzie g, h, k są ciągłe na przedziałach

odpowiednio





b

a,

,





d

c,

,





q

p,

, to



















 



 



q

p

d

c

q

p

d

c

b

a

b

a

dz

z

k

dy

y

h

dx

x

g

dxdydz

z

k

y

h

x

g

)

(

)

(

)

(

)

(

)

(

)

(

,

,

,

.

C

AŁKA POTRÓJNA W OBSZARZE NORMALNYM

Niech f będzie funkcją określoną i ograniczoną na zbiorze ograniczonym D,

3

R

D



.

Całkę podwójną funkcji f na zbiorze D definiujemy wzorem









D

P

dxdydz

z

y

x

f

dxdydz

z

y

x

f

)

,

,

(

)

,

,

(

gdzie P jest dowolnym prostopadłościanem zawierającym zbiór D, zaś funkcja



f

jest

określona wzorem

AM2 2011/ 12 w10

9.05.2012















D

P

z

y

x

D

z

y

x

z

y

x

f

y

x

f

\

)

,

,

(

dla

0

)

,

,

(

dla

)

,

,

(

)

,

(

.

PRZYPADEK SZCZEGÓLNY

Jeżeli

1

)

,

,

(



z

y

x

f

, to

V

dxdydz

D





1

gdzie jest objętością zbioru D.

D

EF

.

Obszarem normalnym względem płaszczyzny 0xy nazywamy obszar





)

,

(

)

,

(

,

)

,

(

:

)

,

,

(

3

y

x

h

z

y

x

g

D

y

x

R

z

y

x

D

xy











gdzie

xy

D

jest obszarem regularnym na płaszczyźnie 0xy zaś funkcje g, h są w nim ciągłe.

Analogicznie definujemy obszary normalne względem płaszczyzn 0yz, 0xz.

Obszarem normalnym względem płaszczyzny 0yz nazywamy obszar





)

,

(

)

,

(

,

)

,

(

:

)

,

,

(

3

z

y

x

z

y

D

z

y

R

z

y

x

D

yz















gdzie





,

p, są funkcjami ciągłymi w zbiorze

.

yz

D

Przykład
Naszkicować i opisać obszar ograniczony podanymi powierzchniami.

0

12

3

4

6

,

0

,

0

,

0















z

y

x

z

y

x

TW:

ZAMIANA CAŁKI POTRÓJNEJ PO OBSZARZE NORMALNYM NA CAŁKI ITEROWANE

Jeżeli funkcja f jest ciągła na obszarze





)

,

(

)

,

(

,

)

,

(

:

)

,

,

(

3

y

x

h

z

y

x

g

D

y

x

R

z

y

x

D

xy











normalnym względem płaszczyzny 0xy , to



 

















D

D

y

x

h

y

x

g

xy

dxdy

dz

z

y

x

f

dxdydz

z

y

x

f

)

,

(

)

,

(

)

,

,

(

)

,

,

(

.

Jeżeli funkcja f jest ciągła na obszarze





)

,

(

)

,

(

,

)

,

(

:

)

,

,

(

3

z

y

x

z

y

D

z

y

R

z

y

x

D

yz















normalnym względem płaszczyzny 0yz , to



 

















D

D

z

y

z

y

yz

dydz

dx

z

y

x

f

dxdydz

z

y

x

f

)

,

(

)

,

(

)

,

,

(

)

,

,

(





Jeżeli funkcja f jest ciągła na obszarze





)

,

(

)

,

(

,

)

,

(

:

)

,

,

(

3

z

x

y

z

x

D

z

x

R

z

y

x

D

xz















normalnym względem płaszczyzny 0xz , to



 

















D

D

z

x

z

x

xz

dxdz

dy

z

y

x

f

dxdydz

z

y

x

f

)

,

(

)

,

(

)

,

,

(

)

,

,

(





Przykład
Obliczyć objętość obszaru ograniczonego powierzchniami

6

3

2

,

0

,

0

,

4

,

0













z

y

z

y

x

x

.