Obliczanie odległości X

m

występowania stężenia maksymalnego

zanieczyszczenia powietrza S

m

na podstawie:

Rozporządzenia Ministra Środowiska

z dnia 26 stycznia 2010 roku

w sprawie wartości odniesienia dla

niektórych substancji w powietrzu

Dziennik Ustaw nr 16 z 2010 roku, Poz. 87

http://isap.sejm.gov.pl/search.jsp

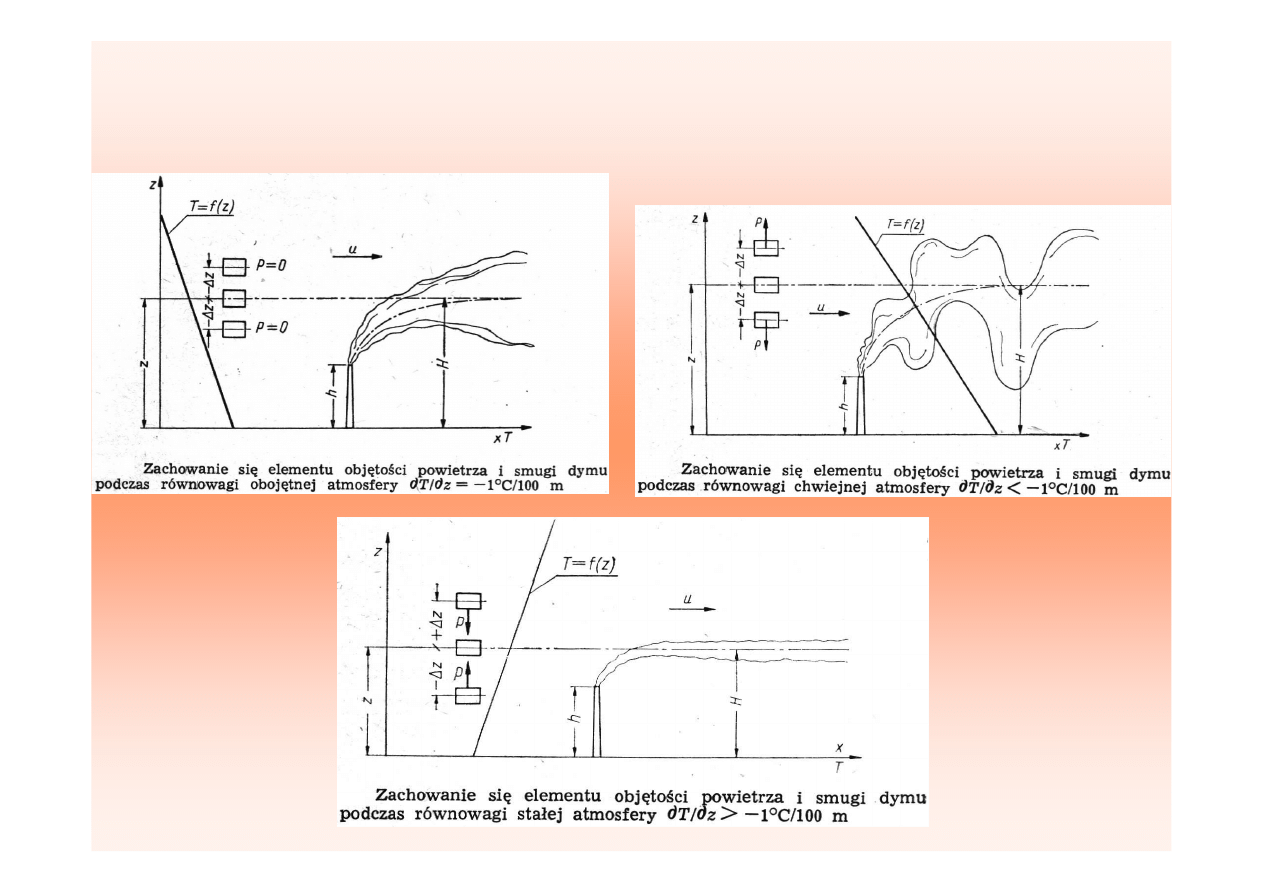
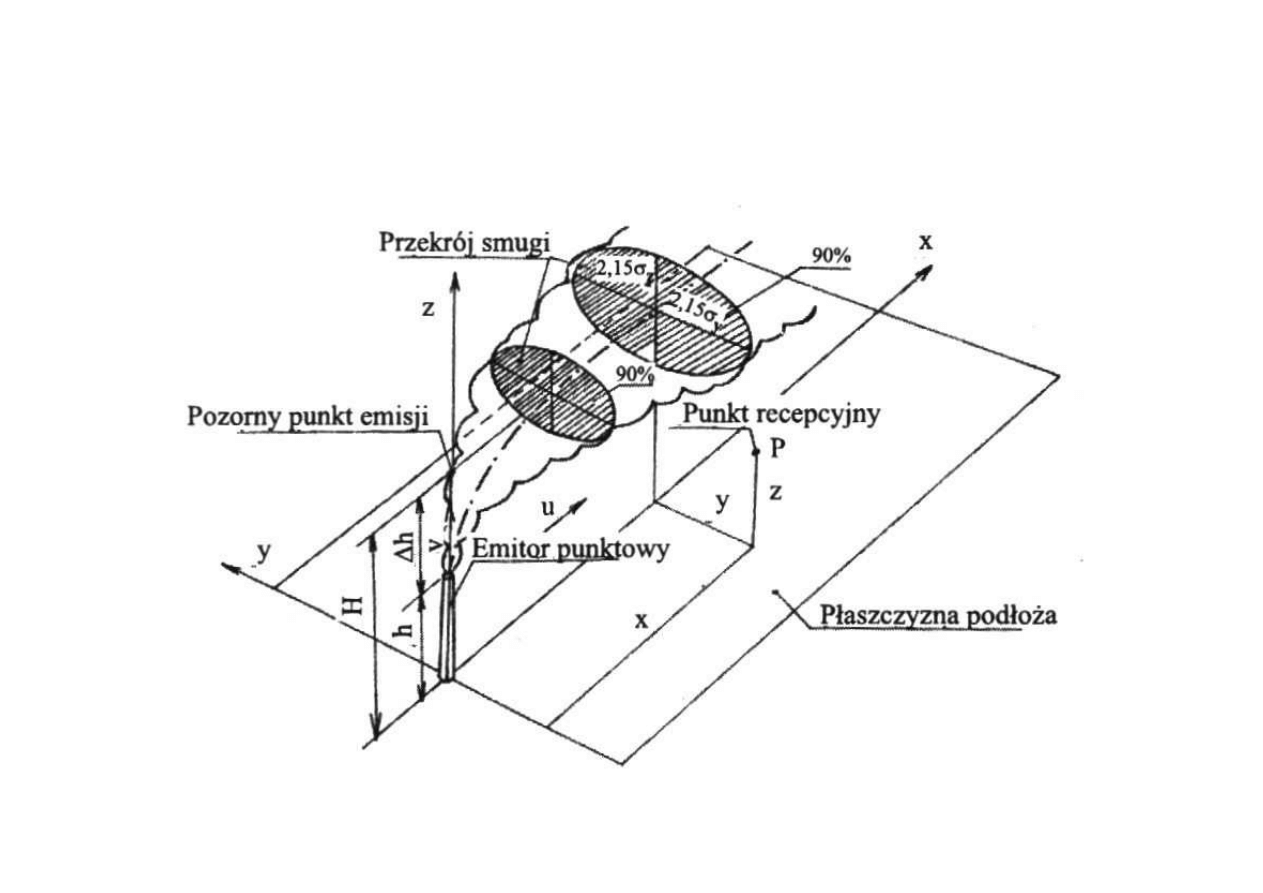
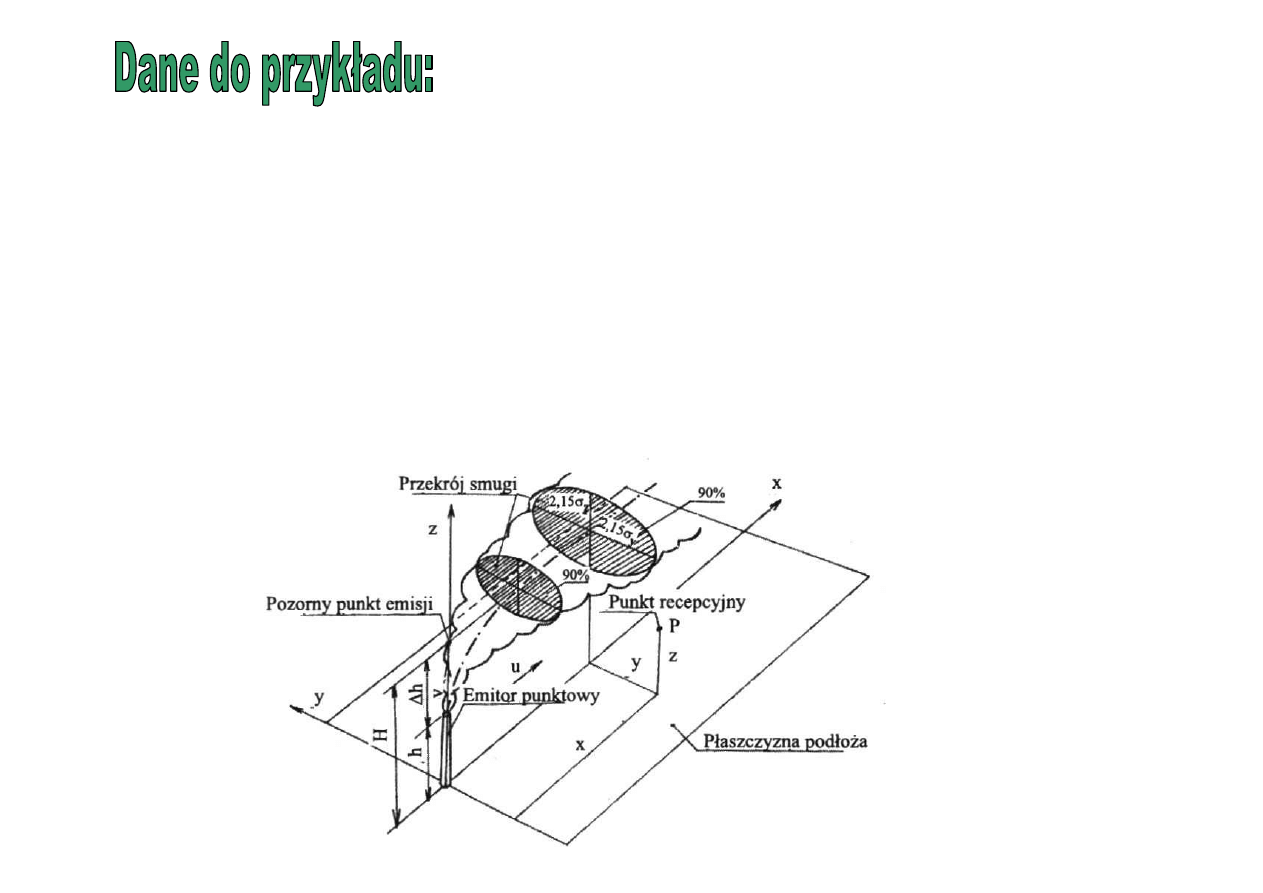
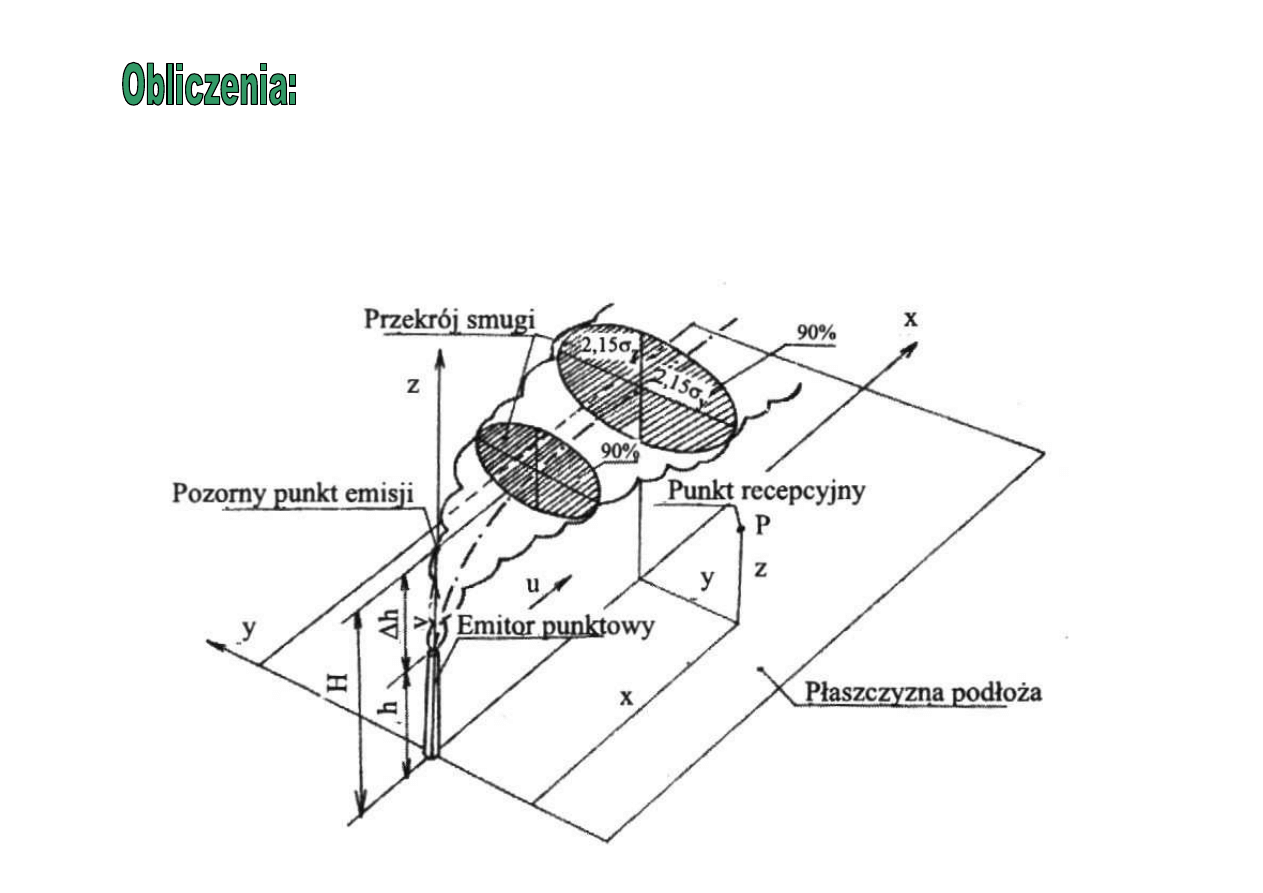
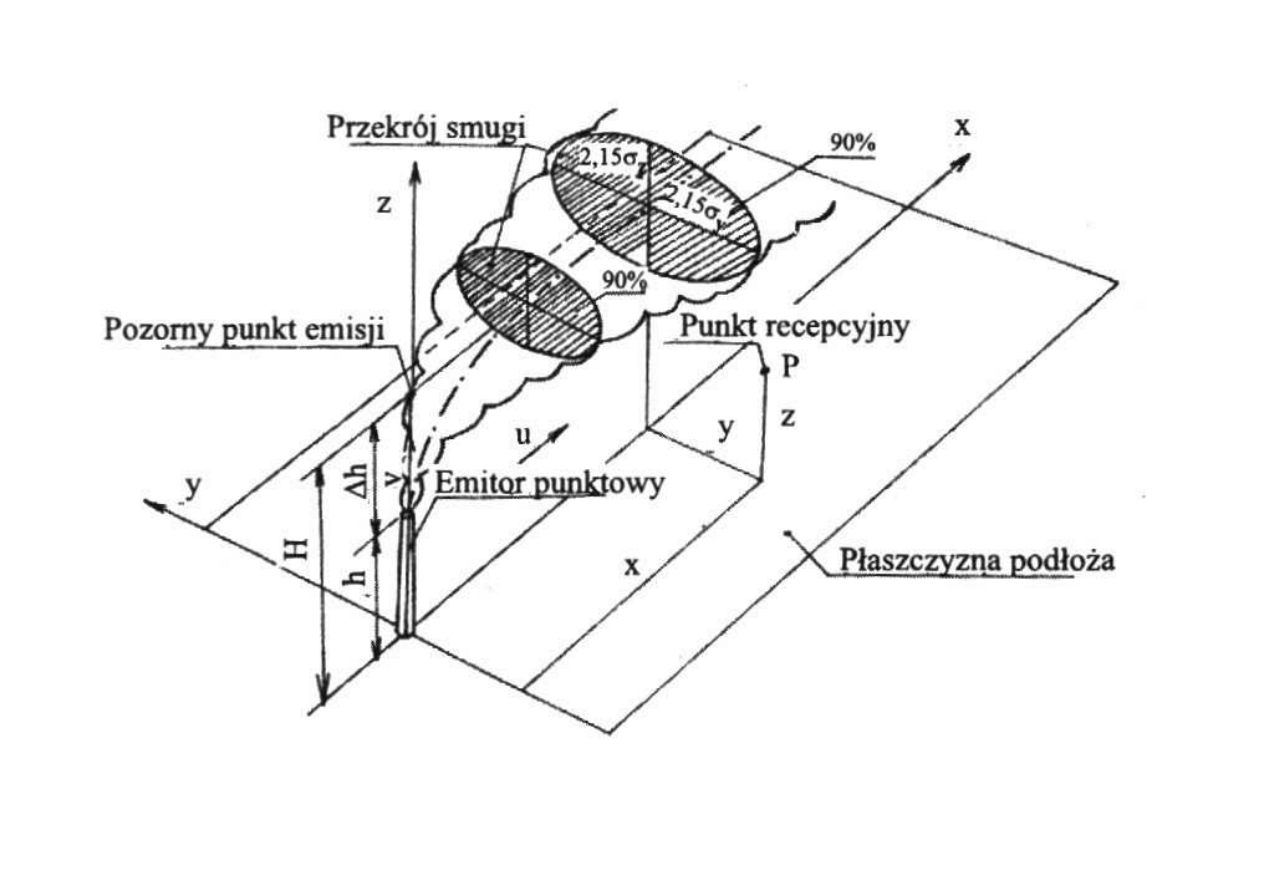
Zachowanie się smugi dymu

w różnych stanach równowagi atmosfery

Jednym z zada

ń

dotycz

ą

cych ochrony

powietrza atmosferycznego jest

sprawdzenie, czy st

ęż

enie

zanieczyszczenia w danym miejscu nie

przekracza st

ęż

enia dopuszczalnego.

Zagadnienie to rozpatrzone jest na podstawie

równania Pasquilla, b

ę

d

ą

cego rozwi

ą

zaniem

problemu dyfuzji zanieczyszcze

ń

w poruszaj

ą

cym si

ę

o

ś

rodku gazowym. Równanie zostało zweryfikowane

empirycznie i dla poszczególnych stanów równowagi

dobrano odpowiednie współczynniki.

Równanie Pasquilla dyfuzji

zanieczyszczenia gazowego

w poruszającym się ośrodku gazowym,

dla zagadnień rozprzestrzeniania się

zanieczyszczeń

wyrzucanych do atmosfery z emitorów

punktowych (kominów)

2

2

2
z

2

2

2

y

z

S

2

S

dt

d

y

S

2

S

dt

d

t

S

∂

∂

⋅













+

∂

∂

⋅















=

∂

∂

gdzie:

S – stężenie zanieczyszczenia w punkcie recepcyjnym,

t – czas wędrówki zanieczyszczenia od chwili wyrzutu do

osiągnięcia punktu recepcyjnego,

S

y

– współczynnik dyfuzji Pasquilla wzdłuż osi 0Y w układzie

współrzędnych t,y,z

S

z

– współczynnik dyfuzji Pasquilla wzdłuż osi 0Z w układzie

współrzędnych t,y,z

S

y

, S

z

– zależne od x

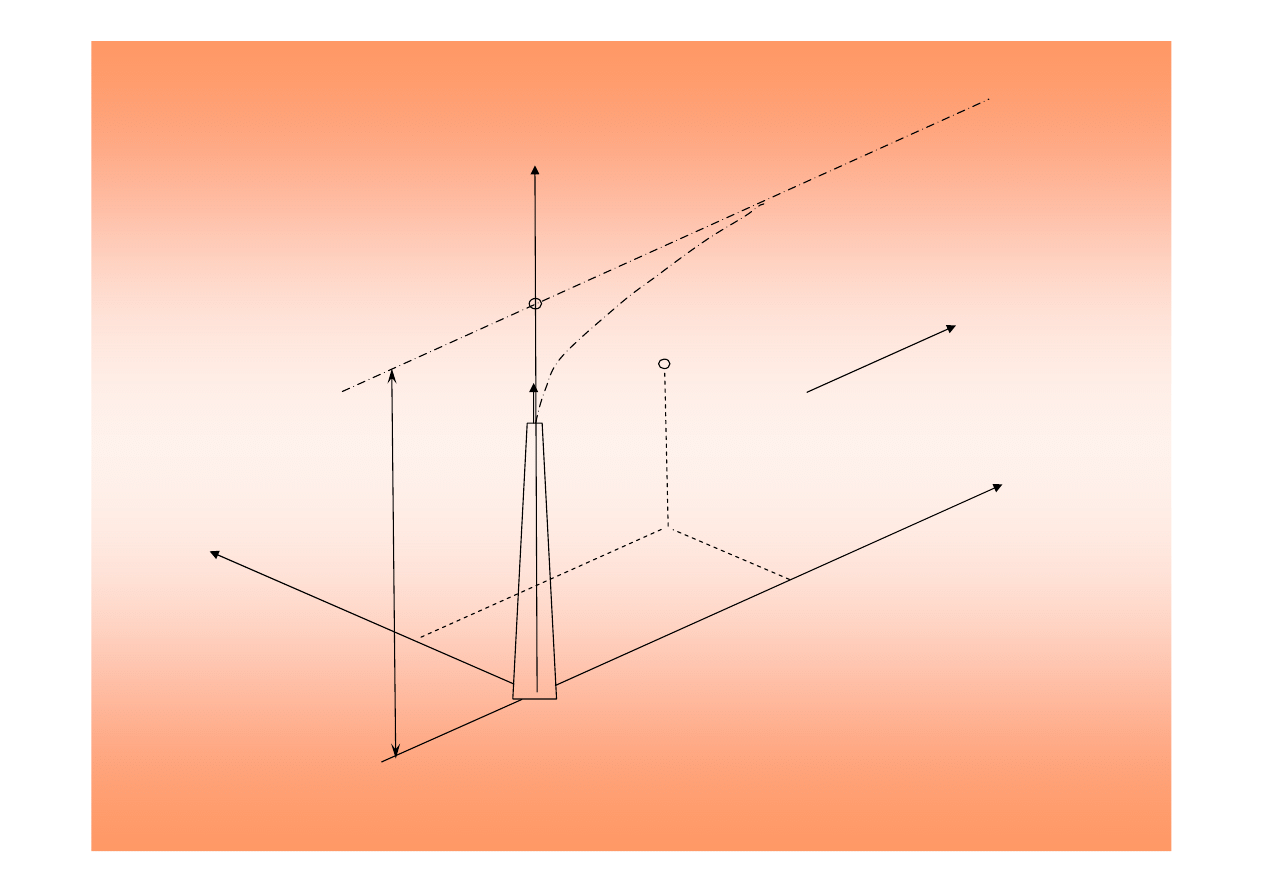
X

Y

Z

u

Xe=Ye=0, Ze=H

H

P

(xyz)

x

y

z

0

v

Równanie opisuje rozprzestrzenianie się zanieczyszczeń dla

dowolnego punktu emisji, ustalonego w czasie.

Warunki brzegowe:

-źródło emisji o masowym natężeniu E jest umieszczone w punkcie

(źródło punktowe) o współrzędnych t = 0, y

e

=x

e

= 0 i z

e

= H,

-na powierzchni podłoża nie zachodzi pochłanianie zanieczyszczeń, tj.

dla z = 0 strumień zanieczyszczeń jest zerowy (ilość zanieczyszczeń

docierających do podłoża jest równa ilości zanieczyszczenia od

podłoża),

-stężenie zanieczyszczeń w odległości nieskończenie dużej od źródła

(tzn. t, y oraz z =∞) ma wartość zerową.

( )

( )









































































































+

−

+

−

−

−

=

2

z

2

σ

2

H

z

exp

2

z

2

σ

2

H

z

exp

2

y

2

σ

2

y

exp

z

σ

y

σ

u

2

π

g

E

xyz

S

Przy powyższych warunkach brzegowych i ogólnie

przyjętych oznaczeniach współczynników dyfuzji

jako σ

y

i σ

z

otrzymujemy rozwiązanie równania

Pasquilla określające stężenie zanieczyszczenia,

w postaci:

Dane do oblicze

ń

poziomów substancji

w powietrzu:

Parametry emitora

-geometryczna wysoko

ść

emitora liczona

od poziomu terenu –

h [m]

-

ś

rednica wewn

ę

trzna wylotu emitora –

d [m]

-pr

ę

dko

ść

gazów odlotowych na wylocie

emitora –

v [m/s]

-temperatura gazów odlotowych na wylocie

emitora –

T [K]

Emisja
-maksymalna emisja u

ś

redniona dla 1 godziny –

E

g

, E

p

[mg/s]

Dane meteorologiczne
-

ś

rednia temperatura powietrza dla okresu obliczeniowego (roku,

sezonu, podokresu) –

T

o

[K]

-statystyka stanów równowagi atmosfery, pr

ę

dko

ś

ci i kierunków

wiatru (ró

ż

a wiatru).

Wyró

ż

nionych jest 36 ro

ż

nych sytuacji meteorologicznych

wynikaj

ą

cych z 6 stanów równowagi atmosfery, którym

odpowiadaj

ą

zakresy pr

ę

dko

ś

ci wiatru na wysoko

ś

ci h

a

=14 m, ze

skokiem co 1 m/s (tablica1)

Dane do oblicze

ń

poziomów substancji w powietrzu cd:

1 – 4

6 - stała

1 – 5

5 - lekko stała

1 – 11

4 – oboj

ę

tna

1 – 8

3 - lekko chwiejna

1 – 5

2 – chwiejna

1 – 3

1 - silnie chwiejna

Zakres pr

ę

dko

ś

ci

wiatru u

a

[m/s]

Stan równowagi

atmosfery

Tablica 1. Sytuacje meteorologiczne

0,457

0,553

0,657

0,727

0,771

0,815

C

2

0,271

0,251

0,234

0,224

0,218

0,213

C

1

2,372

2,188

1,995

1,864

1,781

1,692

g

0,551

0,660

0,822

0,978

1,108

1,284

b

0,756

0,784

0,818

0,845

0,865

0,888

a

0,440

0,363

0,270

0,196

0,143

0,080

m

6

5

4

3

2

1

Stan równowagi atmosfery

Stała

Tablica 2. Stałe zale

ż

na od stanów równowagi

1.Obliczy

ć

wielko

ść

st

ęż

enia maksymalnego S

mm

dwutlenku siarki

oraz odległo

ść

jego wyst

ę

powania X

m

od miejsca emisji.

2.Sprawdzi

ć

czy nie zostało przekroczone st

ęż

enie dopuszczalne

D

1

dla 1 godzinnego czasu u

ś

redniania.

Nale

ż

y obliczy

ć

st

ęż

enia S

m

dla 36 sytuacji meteorologicznych

(6 stanów równowagi atmosfery i zwi

ą

zanych z nimi pr

ę

dko

ś

ciami

wiatru, co 1m/s). Wybra

ć

spo

ś

ród st

ęż

e

ń

, maksymalne – S

mm

i porówna

ć

z warto

ś

ci

ą

st

ęż

enia dopuszczalnego (zał

ą

cznik nr 1

do ustawy jw.).

-geometryczna wysoko

ść

emitora

h=20 m

-

ś

rednica wewn

ę

trzna wylotu emitora

d=0,8 m

-pr

ę

dko

ść

gazów odlotowych na wylocie emitora

v=4 m/s

-temperatura gazów odlotowych na wylocie emitora

T=373 K

-maksymalna emisja u

ś

redniona dla 1 godziny

E

g

=1200 mg/s SO

2

-

ś

rednia temperatura powietrza

dla okresu obliczeniowego (rok)

T

o

=278,5 K

-wysoko

ść

pomiaru pr

ę

dko

ś

ci wiatru

h

a

=14 m

-miasto do 10 000 mieszka

ń

ców

z

o

=1,0 (z tablicy 3)

5,0

-zabudowa wysoka

10.3

2,0

-zabudowa

ś

rednia

10.2

0,5

-zabudowa niska

10.1

Miasto powy

ż

ej 500 tys.

Mieszka

ń

ców

10

3,0

-zabudowa wysoka

9.3

2,0

-zabudowa

ś

rednia

9.2

0,5

-zabudowa niska

9.1

Miasto 100-500 tys. mieszka

ń

ców

9

2,0

-zabudowa

ś

rednia

8.2

0,5

-zabudowa niska

8.1

miasto 10-100 tys. Mieszka

ń

ców

8

1,0

miasto do 10 tys. mieszka

ń

ców

7

0,5

zwarta zabudowa wiejska

6

2,0

Lasy

5

0,4

Sady, zaro

ś

la, zagajniki

4

0,035

Pola uprawne

3

0,02

ł

ą

ki, pastwiska

2

0,00008

Woda

1

Współczynnik z

o

Typ pokrycia terenu

Lp.

Tablica 3. Warto

ść

współczynnika aerodynamicznej szorstko

ś

ci

terenu z

o

1. Obliczamy efektywn

ą

wysoko

ść

emitora (wysoko

ść

pozornego

pkt-u emisji) wg wzoru:

H=h+

∆

h

(1)

- obliczamy emisj

ę

ciepła wg wzoru:





















−

⋅

⋅

⋅

⋅

=

kJ/s

o

T

T

v

1,3

T

273,16

4

2

π

d

Q

(2)

(

)

[ ]

kJ/s

180,8

278,5

373

4

1,3

373

273,16

4

2

0,8

3,14

Q

=

−

⋅

⋅

⋅

⋅

⋅

=

Wysoko

ść

efektywna zale

ż

y od pr

ę

dko

ś

ci wylotowej

gazów v, emisji ciepła Q i pr

ę

dko

ś

ci wiatru na wysoko

ś

ci

wylotu z emitora u

h

.

Pr

ę

dko

ść

wiatru na wysoko

ś

ci wylotu emitora u

h

dla h

≤

300m

oblicza si

ę

wg wzoru:

[ ]

m/s

m

14

h

a

u

h

u

















⋅

=

(3)

gdzie: u

a

– pr

ę

dko

ść

wiatru na wysoko

ś

ci anemometru (jedna z 36)

m – stała zale

ż

na od stanu równowagi atmosfery, tablica 2.

Dla równowagi silnie chwiejnej, u

a

=1m/s otrzymujemy:

[ ]

m/s

1,03

0,08

14

20

1

h

u

=

⋅

=





















Wykonujemy obliczenia dla pozostałych 35 przypadków.

Wyniesienie gazów odlotowych

∆

h oblicza si

ę

wg formuły Hollanda lub

CONCAWE.

Obliczone Q jest z przedziału 0

≤

Q

≤

16 000 kJ/s, a ponadto v

≥

u

h

wi

ę

c

u

ż

yjemy formuły Hollanda:

h

u

Q

0,00974

d

v

1,5

H

∆

h

∆

h

⋅

+

⋅

⋅

=

=









=

⋅

+

⋅

⋅

=

m

6,4

1,03

180,8

0,00974

0,8

4

1,5

∆

h

Zatem efektywna wysoko

ść

emitora zgodnie z (1) wynosi:

H=26,4 [m]

(4)









=

m/s

1,04

u

2. Parametry meteorologiczne:

Ś

redni

ą

pr

ę

dko

ść

wiatru w warstwie od geometrycznej wysoko

ś

ci emitora do

efektywnej wysoko

ś

ci emitora dla H

≤

300m i H

≠

h obliczamy wg wzoru:

(

)(

)















+

−

+

⋅

⋅

+

⋅

−

=

m

1

h

m

1

H

m

14

m

1

h

H

a

u

u

(5)

współczynnik poziomej dyfuzji atmosferycznej:

















−

+

−

⋅

=

⋅

=

o

z

H

ln

1

0,3

6m

0,088

A

gdzie

a

x

A

y

σ

(6)

(7)

współczynnik pionowej dyfuzji atmosferycznej:





















−

⋅

=

⋅

=

o

z

H

ln

8,7

1,3

0,38m

B

gdzie

b

x

B

z

σ

(8)

(9)

Warto

ś

ci stałych – m, a, b podane s

ą

w tablicy 2.

Wyst

ę

puj

ą

one w równaniu Pasquilla, b

ę

d

ą

cym

rozwi

ą

zaniem równania dyfuzji zanieczyszcze

ń

w poruszaj

ą

cym si

ę

o

ś

rodku gazowym.

( )

( )









































































































+

−

+

−

−

−

=

2

z

2

σ

2

H

z

exp

2

z

2

σ

2

H

z

exp

2

y

2

σ

2

y

exp

z

σ

y

σ

u

2

π

g

E

xyz

S

Współczynniki pionowej i poziomej dyfuzji atmosferycznej

σ

z

i

σ

y

maj

ą

wymiar długo

ś

ci i s

ą

proporcjonalne do wymiarów poprzecznych

rozszerzaj

ą

cej si

ę

i niezakłóconej powierzchni

ą

ziemi smugi.

Współczynnik pionowej dyfuzji atmosferycznej wynosi:

Współczynnik poziomej dyfuzji atmosferycznej wynosi:





















−

+

−

⋅

⋅

=

1

26,4

ln

1

0,3

0,08

6

0,088

A

A=0,93

0,888

0,93x

y

σ

=

















−

⋅

⋅

=

1

26,4

ln

8,7

1,3

0,08

0,38

B

B=0,077

1,284

0,077x

z

σ

=

St

ęż

enie maksymalne subst. gazowej u

ś

rednione dla 1 godziny S

m

w okre

ś

lonej sytuacji meteorologicznej oblicza si

ę

wg wzoru:



































⋅

=

3

µ

g/m

1000

g

H

B

AB

u

g

E

1

C

m

S

(10)

gdzie stałe zale

ż

ne od stanu równowagi atmosfery C

1

i g podano

w tablicy 2, a współczynniki A i B oblicza si

ę

wg wzorów 7 i 9.

3. Najwy

ż

sze ze st

ęż

e

ń

maksymalnych substancji w powietrzu S

mm

dla pojedynczego emitora



































=

⋅

⋅

⋅

⋅

=

3

µ

g/m

177,6

1000

1,692

26,4

0,077

0,077

0,93

1,03

1200

0,213

m

S

St

ęż

enia S

m

wyst

ę

puj

ą

w stosunku do emitora w odległo

ś

ci x

m

wyra

ż

onej wzorem:

1/b

B

H

2

C

m

x

















=

(11)

gdzie stałe C

2

oraz b podano w tablicy 2.

[ ]

m

76,5

0,077

26,4

0,815

x

1/1,284

m

=













⋅

=

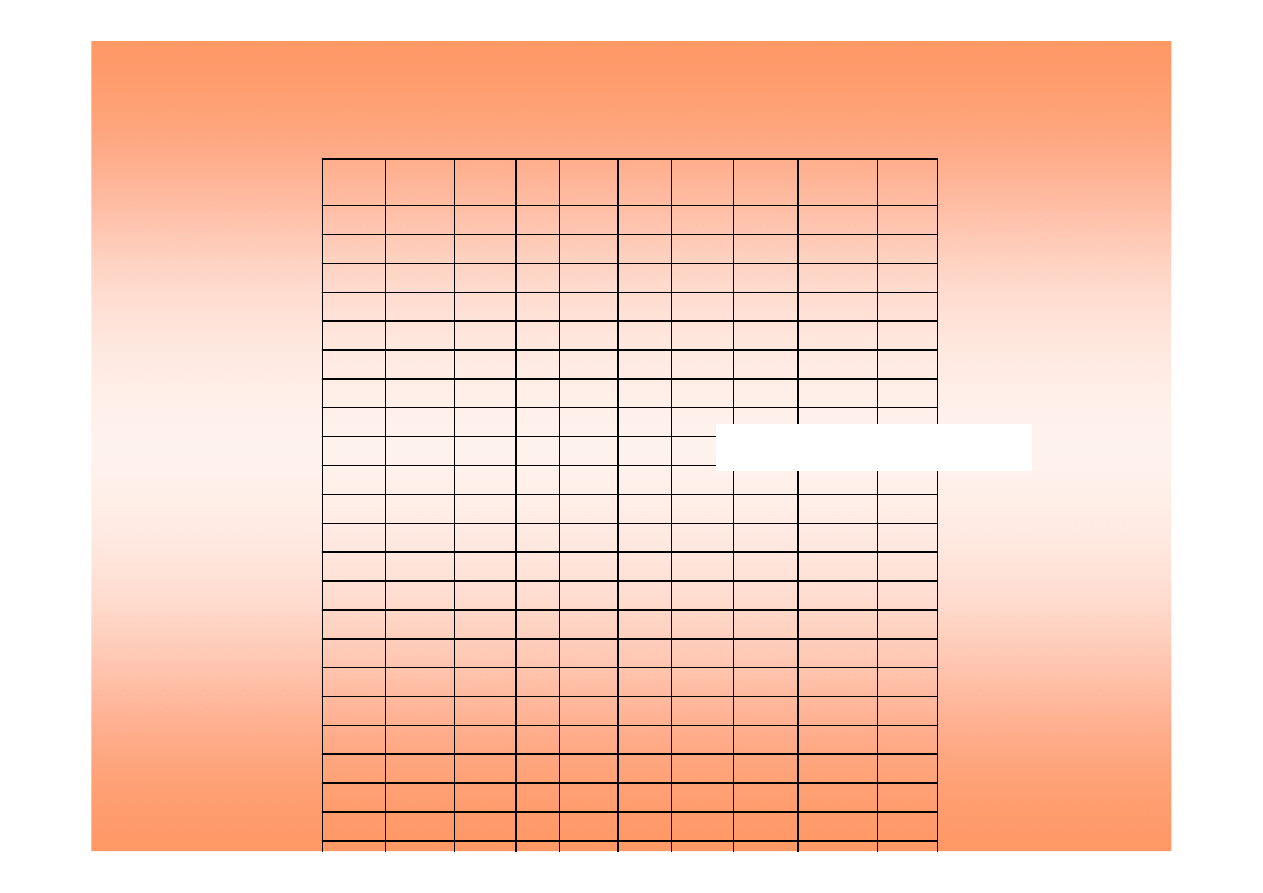
Zestawienie wyników st

ęż

e

ń

maksymalnych S

m

i ich odległo

ś

ci od

ź

ródła emisji.

Spo

ś

ród nich wybieramy st

ęż

enie maksymalne i oznaczamy je S

mm

.

78,0

60,3

0,395

0,606

7,71

20,0

0,0

7,71

180,8

7

79,0

69,0

0,394

0,605

6,62

20,2

0,2

6,61

180,8

6

80,8

80,0

0,393

0,604

5,53

20,5

0,5

5,51

180,8

5

84,6

93,2

0,391

0,601

4,44

21,2

1,2

4,40

180,8

4

89,1

115,1

0,389

0,598

3,35

22,0

2,0

3,30

180,8

3

94,9

156,9

0,386

0,594

2,24

23,0

3,0

2,20

180,8

2

113,1

240,8

0,377

0,583

1,14

26,0

6,0

1,10

180,8

1

61,5

53,7

0,261

0,685

8,58

20,0

0,0

8,58

180,8

8

61,7

61,1

0,260

0,685

7,51

20,1

0,1

7,51

180,8

7

62,4

69,9

0,260

0,684

6,44

20,2

0,2

6,43

180,8

6

63,8

81,1

0,259

0,683

5,38

20,6

0,6

5,36

180,8

5

66,5

94,6

0,258

0,680

4,32

21,3

1,3

4,29

180,8

4

69,2

118,2

0,256

0,677

3,25

22,0

2,0

3,22

180,8

3

73,0

162,0

0,254

0,673

2,18

23,1

3,1

2,14

180,8

2

84,9

252,7

0,248

0,662

1,10

26,1

6,1

1,07

180,8

1

58,0

76,1

0,172

0,768

5,15

20,6

0,6

5,26

180,8

5

60,3

89,1

0,171

0,765

4,13

21,4

1,4

4,21

180,8

4

62,3

112,1

0,170

0,762

3,10

22,1

2,1

3,16

180,8

3

65,5

154,5

0,169

0,758

2,07

23,1

3,1

2,10

180,8

2

74,9

244,6

0,165

0,747

1,04

26,2

6,2

1,05

180,8

1

65,1

80,7

0,080

0,942

3,10

22,1

2,1

3,09

180,8

3

68,0

111,5

0,079

0,938

2,07

23,2

3,2

2,06

180,8

2

76,5

177,6

0,077

0,926

1,04

26,4

6,4

1,03

180,8

1

X

m

[m]

S

m

[

µ

g/m

3

]

B

A

ū

H

∆

h

u

h

Q

[kJ/s]

u

a

[m/s]

L

e

k

k

o

c

h

w

ie

jn

a

S

mm

=252,7 X

m

=84,9

S

il

n

ie

c

h

w

ie

jn

a

C

h

w

ie

jn

a

O

b

o

j

ę

tn

a

S

ta

n

y

r

ó

w

n

o

w

a

g

i

a

tm

o

s

fe

ry

:

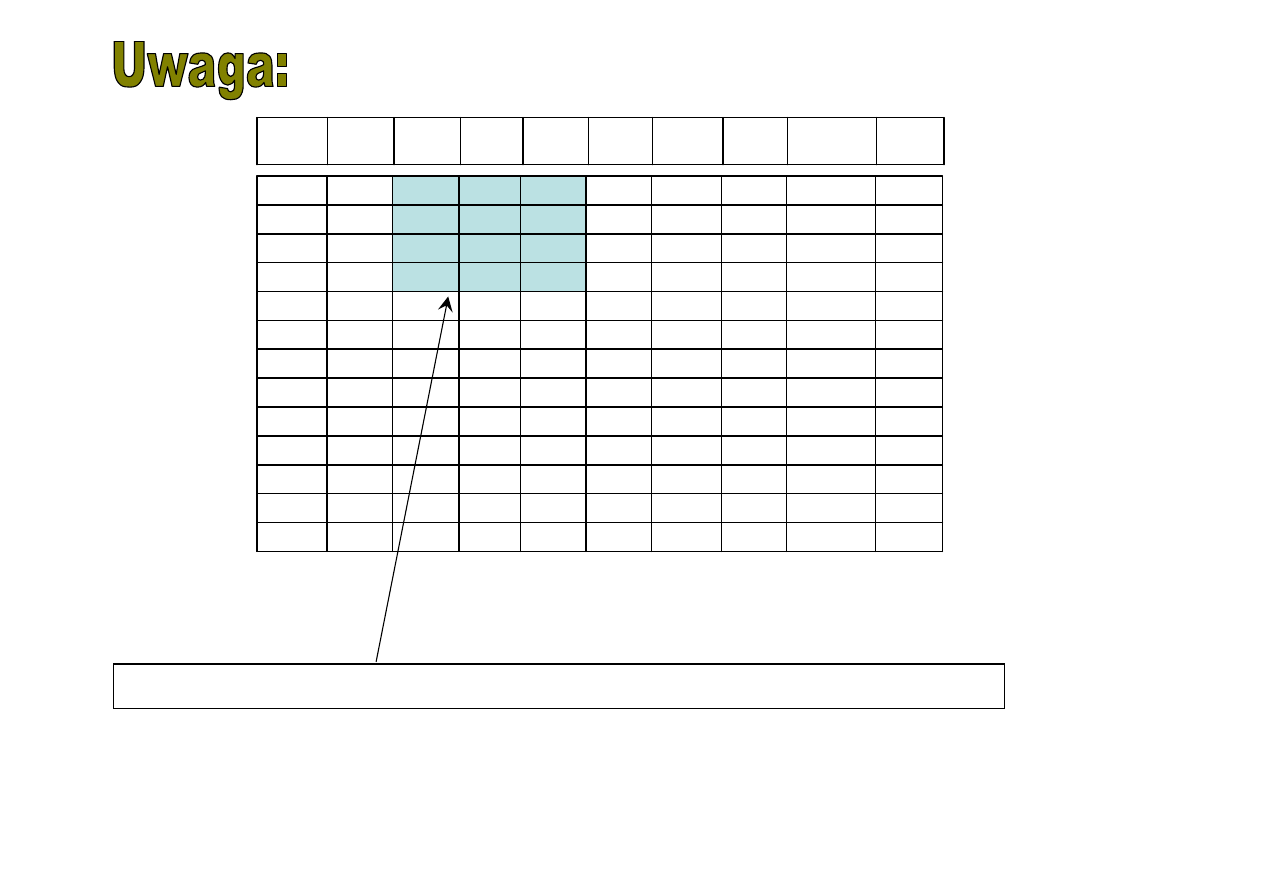
198,4

67,0

0,739

0,496

4,73

21,0

1,0

4,68

180,8

4

216,5

80,1

0,734

0,492

3,58

21,9

1,9

3,51

180,8

3

236,8

107,5

0,728

0,488

2,41

22,8

2,8

2,34

180,8

2

303,6

157,6

0,713

0,478

1,24

25,6

5,6

1,17

180,8

1

122,9

69,2

0,578

0,538

5,72

20,5

0,5

5,69

180,8

5

129,7

80,4

0,575

0,535

4,60

21,1

1,1

4,55

180,8

4

138,9

97,6

0,571

0,532

3,47

21,9

1,9

3,41

180,8

3

150,0

132,0

0,567

0,528

2,33

22,9

2,9

2,28

180,8

2

185,5

197,9

0,555

0,518

1,19

25,8

5,8

1,14

180,8

1

77,8

38,5

0,395

0,606

12,11

20,0

0,0

12,11

180,8

11

77,8

42,4

0,395

0,606

11,01

20,0

0,0

11,01

180,8

10

77,8

47,1

0,395

0,606

9,91

20,0

0,0

9,91

180,8

9

77,8

53,0

0,395

0,606

8,81

20,0

0,0

8,81

180,8

8

X

m

[m]

S

m

[

µ

g/m

3

]

B

A

ū

H

∆

h

u

h

Q

[kJ/s]

u

a

[m/s]

Dla v

≤

0,5u

h

∆

h = 0, (pr

ę

dko

ść

gazów odlotowych v = 4 m/s)

Warunek /2.3/ rozdziału 2.1 (strona 48) ustawy

Je

ż

eli z oblicze

ń

wynika,

ż

e spełniony jest warunek

S

mm

≤

0,1D

1

gdzie D

1

oznacza warto

ść

odniesienia substancji w powietrzu lub

dopuszczalny poziom substancji w powietrzu u

ś

redniony dla

1 godziny. Dla SO

2

D

1

=350 [

µ

g/m

3

].

to na tym ko

ń

czy si

ę

wymagania dla tego zakresu

obliczenia.

Je

ż

eli nie jest spełniony to na całym obszarze, na

którym dokonuje si

ę

oblicze

ń

nale

ż

y obliczy

ć

w sieci

obliczeniowej rozkład maksymalnych st

ęż

e

ń

substancji

w powietrzu u

ś

rednionych dla 1 godz., z uwzgl

ę

dnieniem

statystyki warunków meteorologicznych, aby sprawdzi

ć

czy w ka

ż

dym punkcie na powierzchni terenu został

spełniony warunek:

S

mm

≤

D

1

(12)

(13)

0,1

•D1 =

0,1

•

350 µ

g/m

3

=35 µ

g/m

3

W omawianym przykładzie

252,

7

µg/m

3

> 35 µg/m

3

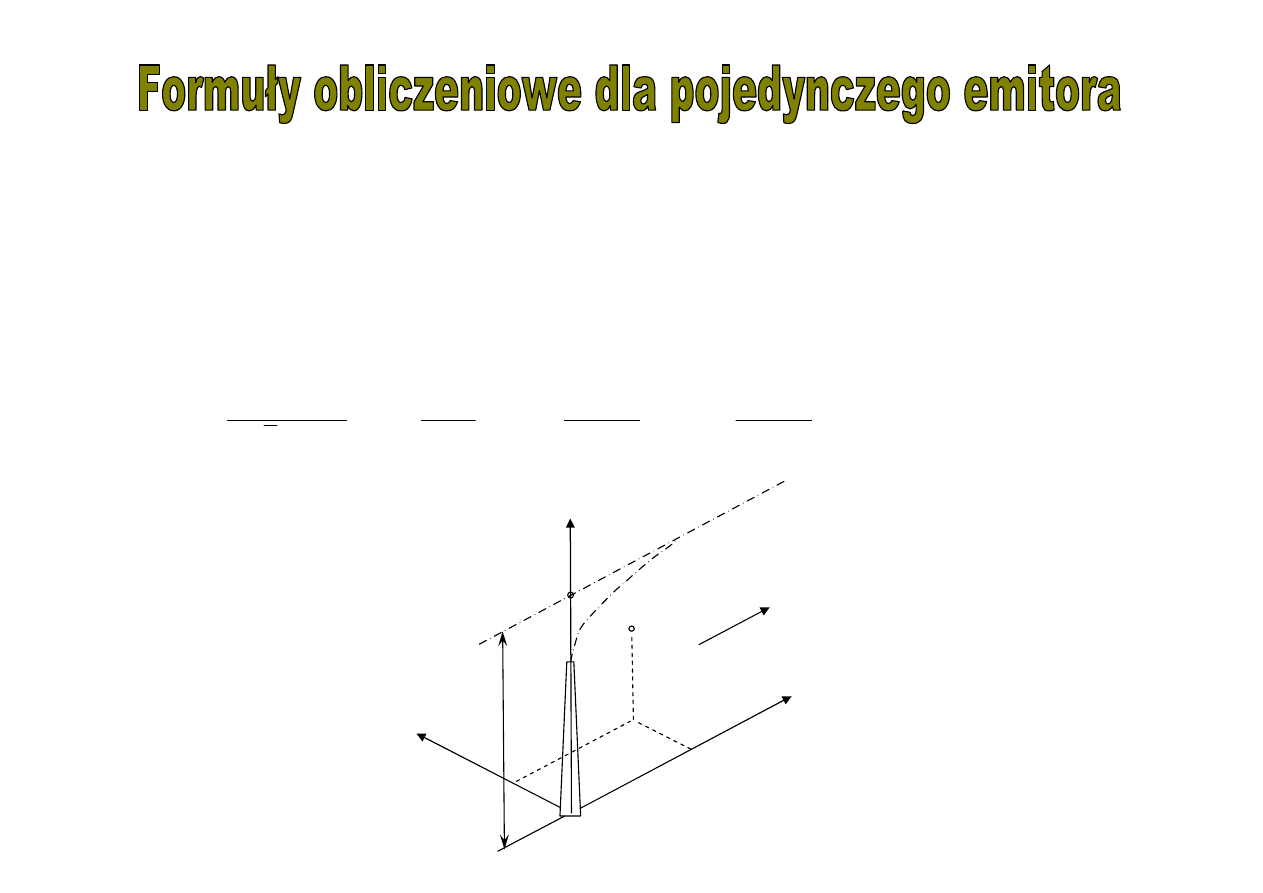
Poni

ż

sze formuły s

ą

słuszne dla:

-okre

ś

lonego stanu równowagi atmosfery i pr

ę

dko

ś

ci wiatru

-emitor znajduje si

ę

w pkt-cie o współrz

ę

dnych X

e

=Y

e

=0, Z

e

=H

-o

ś

X pokrywa si

ę

z kierunkiem wiatru, a o

ś

Y jest do niej prostopadła

( )

( )

[

]

3

µ

g/m

1000

2

z

2

σ

2

H

z

exp

2

z

2

σ

2

H

z

exp

2

y

2

σ

2

y

exp

z

σ

y

σ

u

2

π

g

E

xyz

S

⋅

+

−

+

−

−

−

=









































































































(14)

X

Y

Z

u

Xe=Ye=0, Ze=H

H

P

(xyz)

x

y

z

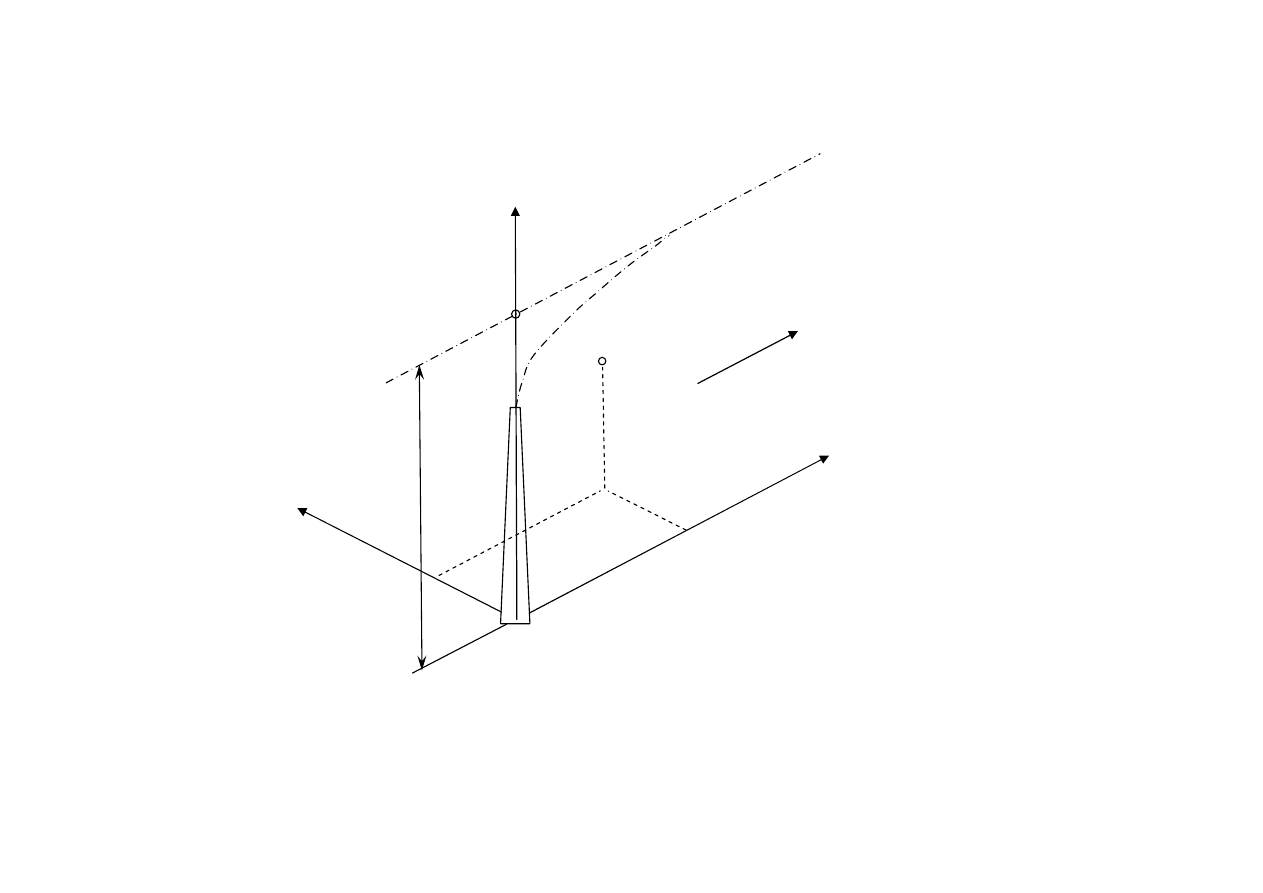
X

Y

Z

u

Xe=Ye=0, Ze=H

H

P

(xyz)

x

y

z

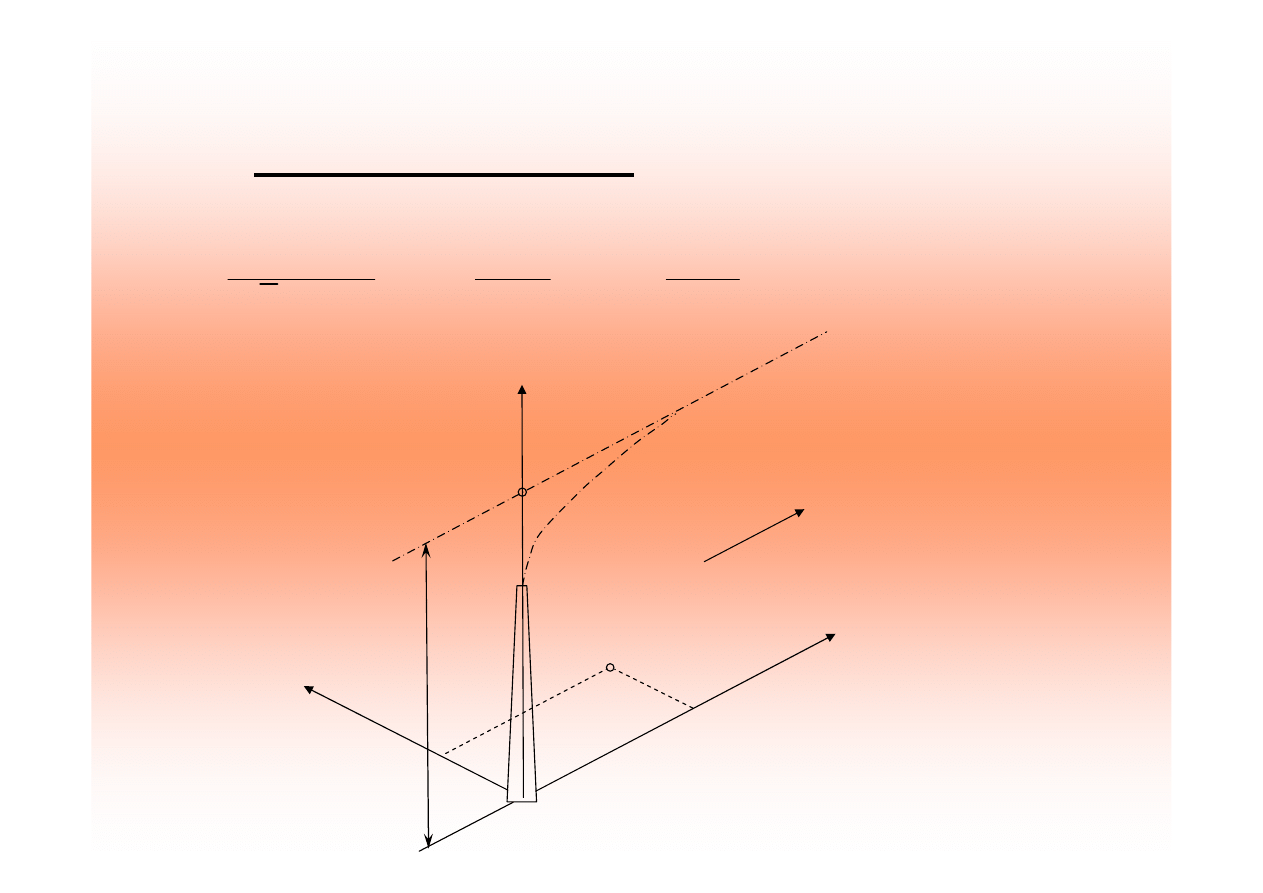
St

ęż

enie substancji gazowej w pkt. o współrz

ę

dnych

X

p

i Y

p

na powierzchni terenu oblicza si

ę

wg wzoru:









⋅





















−

−

=





























3

µ

g/m

1000

2

z

2

σ

2

H

exp

2

y

2

σ

2

y

exp

z

σ

y

σ

u

π

g

E

xy

S

(15)

X

Y

Z

u

Xe=Ye=0, Ze=H

H

P(x

p

,y

p

)

x

p

y

p

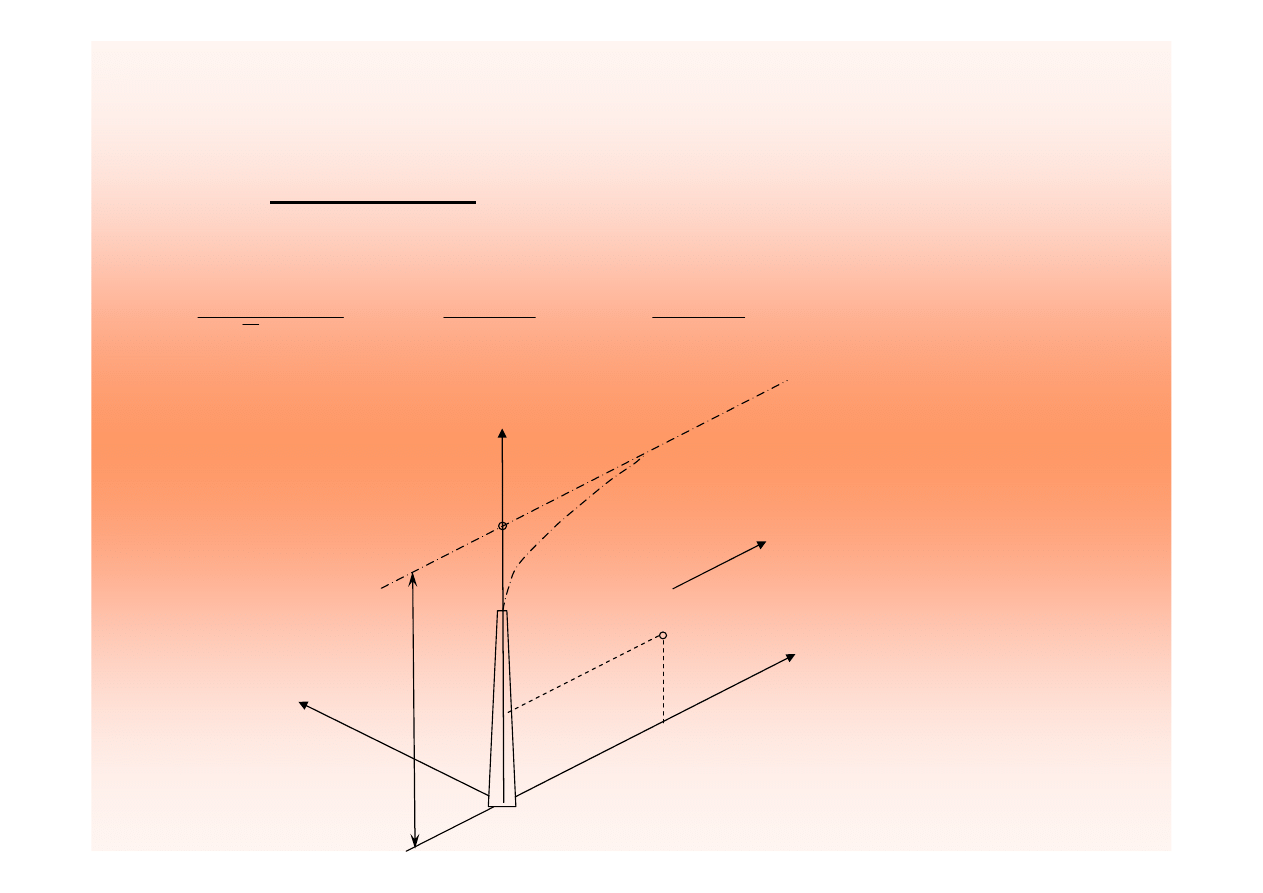
St

ęż

enie substancji gazowej w punkcie o współrz

ę

dnych

X

p

, Z

p

, w osi wiatru oblicza si

ę

wg wzoru:

( )

( )

[

]

3

µ

g/m

1000

2

z

2

σ

2

H

z

exp

2

z

2

σ

2

H

z

exp

z

σ

y

σ

u

2

π

g

E

xz

S

⋅

+

−

+

−

−

=













































































(16)

X

Y

Z

u

Xe=Ye=0, Ze=H

H

P(x

p

,z

p

)

x

p

z

p

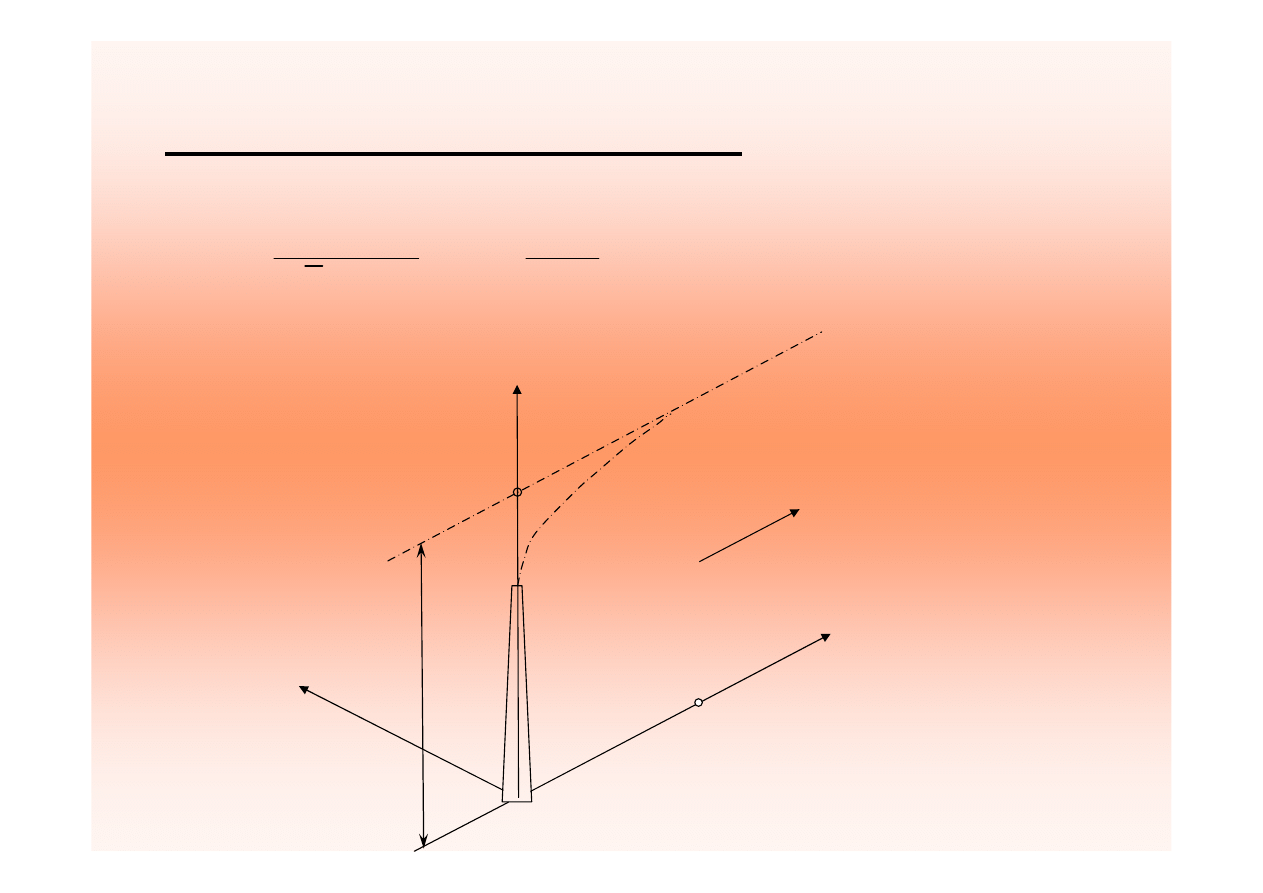
St

ęż

enie substancji gazowej w odległo

ś

ci x od emitora,

w osi wiatru i na powierzchni terenu oblicza si

ę

wg wzoru:









⋅

















−

=

3

µ

g/m

1000

2

z

2

σ

2

H

exp

z

σ

y

σ

u

π

g

E

x

S

(17)

X

Y

Z

u

Xe=Ye=0, Ze=H

H

P(x)

Imi

ę

i Nazwisko

Rok studiów, grupa

Rok akademicki

Wydział

Specjalizacja

Ć

wiczenie nr 1

z przedmiotu Monitoring Powietrza

Tytuł:
Obliczenie odległo

ś

ci X

m

wyst

ę

powania st

ęż

enia

maksymalnego zanieczyszczenia powietrza S

mm

dla SO

2

Kraków 2011

Opracowanie powinno zawiera

ć

:

1. Wskazanie aktu prawnego na podstawie, którego

dokonujemy oblicze

ń

2. Zestawienie danych

3. Przykładowe obliczenie dla wybranej pr

ę

dko

ś

ci

i stanu równowagi atmosfery

1. Tabel

ę

z wynikami

2. Sprawdzenie warunku na warto

ść

maksymaln

ą

st

ęż

enia

3. Wnioski