1

Zadanie
Dwa elementy R

a

i R

b

w połączeniu szeregowym reprezentowane są opornością zastępczą

R’ = 9

Ω , a w połączeniu równoległym R’’ = 2 Ω . Wyznaczyć wartości elementów R

a

i R

b

.

Odp. R

a

= 6

Ω , R

b

= 3

Ω .

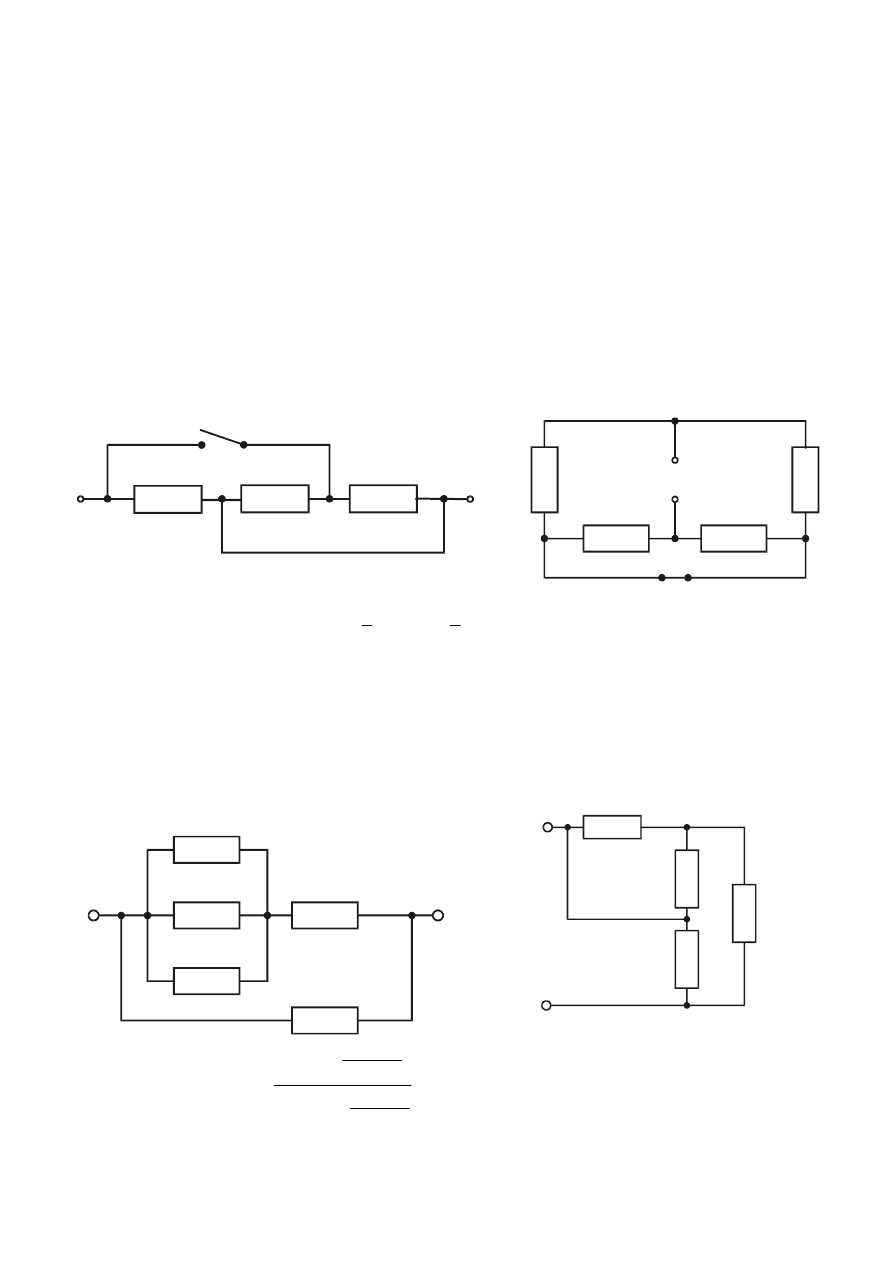
Zadanie

Wyznaczyć oporność zastępczą dwójników pasywnych o
elementach R

1

= 6

Ω

, R

2

= 2

Ω

,

R

3

= 3

Ω

, R

4

= 1

Ω

:

1. przy otwartym wyłączniku w
2. przy zamkniętym wyłączniku w.
a.

b.

Odp. R

a1

= 6

Ω , R

a2

= 1

Ω ; R

b1

=

3

8 Ω , R

b2

=

3

8 Ω .

Zadanie
Wyznaczyć oporności zastępcze dwójników pasywnych:


a.

b.

Odp. R

a

= 2

Ω , R

b

=

2

1

2

1

4

3

2

1

2

1

4

3

R

R

R

R

R

R

)

R

R

R

R

R

(

R

+

+

+

+

+

R

1

W

R

2

R

3

R

2

R

1

R

3

R

4

W

R =6

1

R =5

4

R =2

2

R =3

3

R =3

5

R

3

R

2

R

1

R

4

2

c. d.

Odp. R

c

= 4

Ω ,( Ponieważ zachodzi równość R

1

R

4

= R

2

R

3

, w gałęzi z elementem R

5

natężenie prądu wynosi zero; stanowi ona przerwę). R

d

= 2

Ω , ( po zastąpieniu

„sześcioomowego” trójkąta równoważną gwiazdą, powstaje dwójnik z połączeniami
szeregowo-równoległymi ).

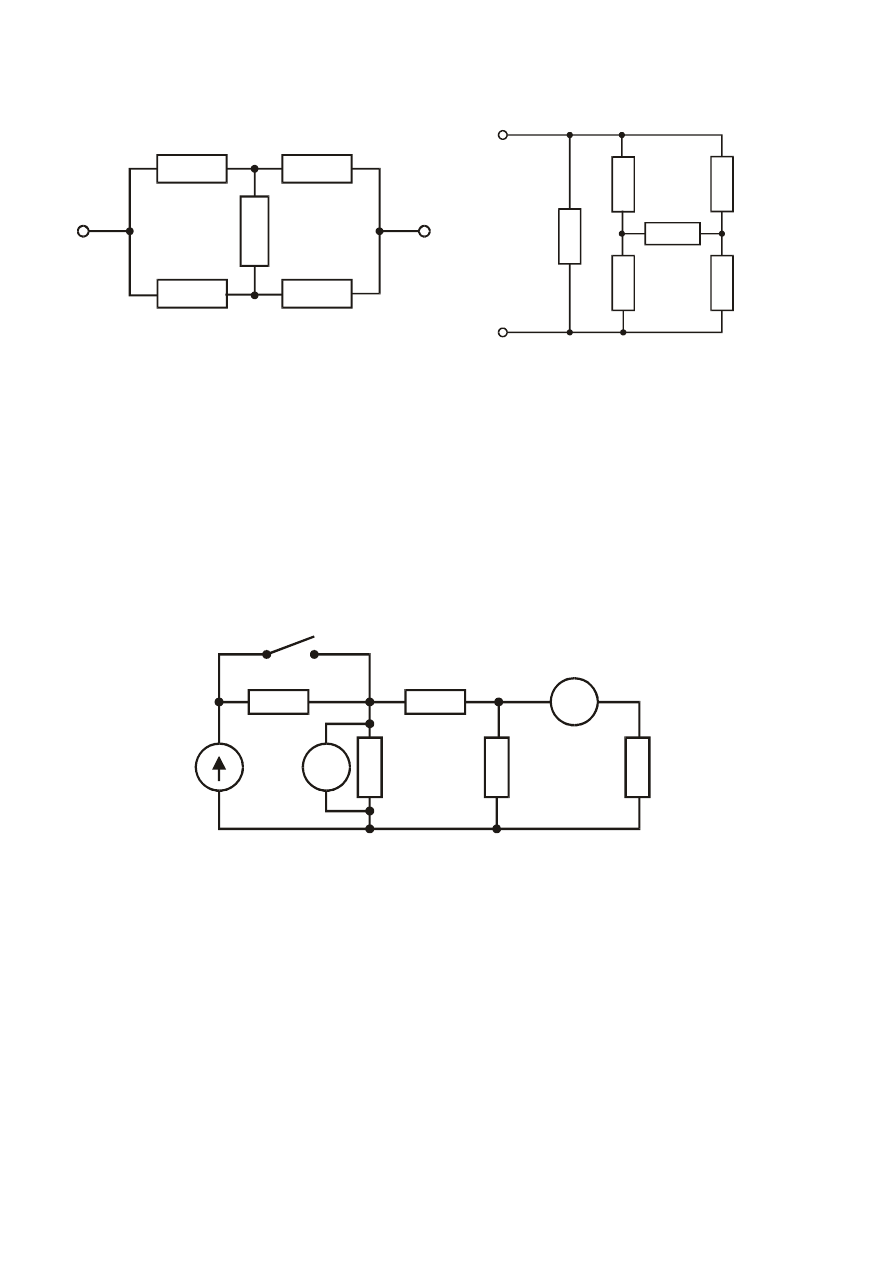
Zadanie
W liniowym obwodzie elektrycznym dane są: E = 20 V, U

V

= 12 V, I

A

= 3 A. Należy;

a. obliczyć wskazania przyrządów po zwiększeniu napięcia źródłowego do wartości
E’ = 50 V
b. obliczyć wskazania przyrządów po zamknięciu wyłącznika, przy zachowanej wartości

E =20 V.

Odp. a. U

V

= 30 V, I

A

= 7,5 A. b. U

V

= 20 V, I

A

= 5 A.

R =3

1

R =3

2

R =5

5

R =5

4

R =5

3

R =4

1

R =1

5

R =6

2

R =6

4

R =6

3

R =4

6

V

A

W

R

1

R

2

R

4

R

3

R

5

E

3

Zadanie
Obliczyć prądy I

A

, I

B

; napięcie U

1

w podanych obwodach jeśli; R

1

= 1

Ω , R

2

= 6

Ω ,

R

3

= 3

Ω , E

2

= 18 V, E

3

= 9 V, J

3

= 2 A. W obwodach b, c, d wyznaczyć moce źródeł.

a.

b.

c.

d.

Odp. a. I

A

= 2A, I

B

= 4 A, U

1

= 12 V.

b. I

A

= 0 , I

B

= 6 A, U

1

= 18 V, P

E2

= 0.

c. I

A

= 1 A, I

B

= 5 A, U

1

= 24 V, P

E2

= - 18 W, P

E3

= - 45 W.

d. I

A

= 8 A, I

B

= -2 A, U

1

= 66 V, P

E2

= - 144 W, P

J3

= 144 W.

Zadanie
W obwodzie o danych; E = 24 V, R

1

= 2

Ω , R

2

= 2

Ω , R

3

= 6

Ω , R

4

= 4

Ω , R

5

= 3

Ω ,

obliczyć prąd w gałęzi R

5

;

a. metodą transfiguracji
b. zastosować twierdzenie o źródle zastępczym

Odp. a. I

5

= 2 A, b. U

AB

=

7

72

V, R

w

=

7

15 Ω , I

5

= 2 A.

R

1

R

2

R

3

U

1

I =6A

1

I

B

I

A

R

1

R

2

R

3

U

1

I =6A

1

I

B

I

A

E

2

R

1

R

2

R

3

U

1

I =6A

1

I

B

I

A

E

2

E

3

R

1

R

2

R

3

U

1

I =6A

1

I

B

I

A

E

2

J

3

E

R

1

R

4

R

5

R

2

R

3

I

5

4

Zadanie
W obwodzie o elementach; E = 24 V, R

1

= 6

Ω , R

2

= 6

Ω amperomierz wskazuje natężenie

prądu I = 3 A. Wyznaczyć wskazania amperomierza po odłączeniu gałęzi z elementem R

2

.

Odp. I

A

=

3

8

A.

Zadanie
W elemencie R

0

, energia elektryczna rozprasza się z prędkością P

0

= 32 W. Obliczyć

oporność R

0

, jeśli źródło energii elektrycznej ma parametry; E = 24 V, R

W

= 4

Ω . Jaką

największą moc może pobierać odbiornik dołączony do tego źródła energii? Ile wynosiła by
wówczas oporność odbiornika? Narysować charakterystykę zewnętrzną źródła energii
U = f( I ), oraz zależność P

0

= g (R

0

).

Odp. R

01

= 2

Ω , R

02

= 8

Ω ; P

0max

= 36 W, R

0Pmax

= 4

Ω .

Zadanie
Załączenie do zacisków źródła energii elektrycznej elementu R

1

= 3

Ω , powoduje przepływ

prądu o natężeniu I

1

= 3 A, a elementu R

2

= 5

Ω prądu I

2

=2 A. Ile wynosi prąd I

Z

, w gałęzi

zwierającej zaciski źródła.
Odp. I

Z

= 12 A.

Zadanie
Wyznaczyć taką wartość elementu R

3

, aby odbiornik pobierał możliwie największą moc. Ile

wynosi wartość tej mocy jeśli ; E = 24 V, R

w

= 4

Ω , R

1

= 8

Ω , R

2

= 2

Ω .

E

R

1

R

3

R

2

W

E

R

w

R

o

U

I

E

R

w

R

3

R

2

R

1

Odbiornik

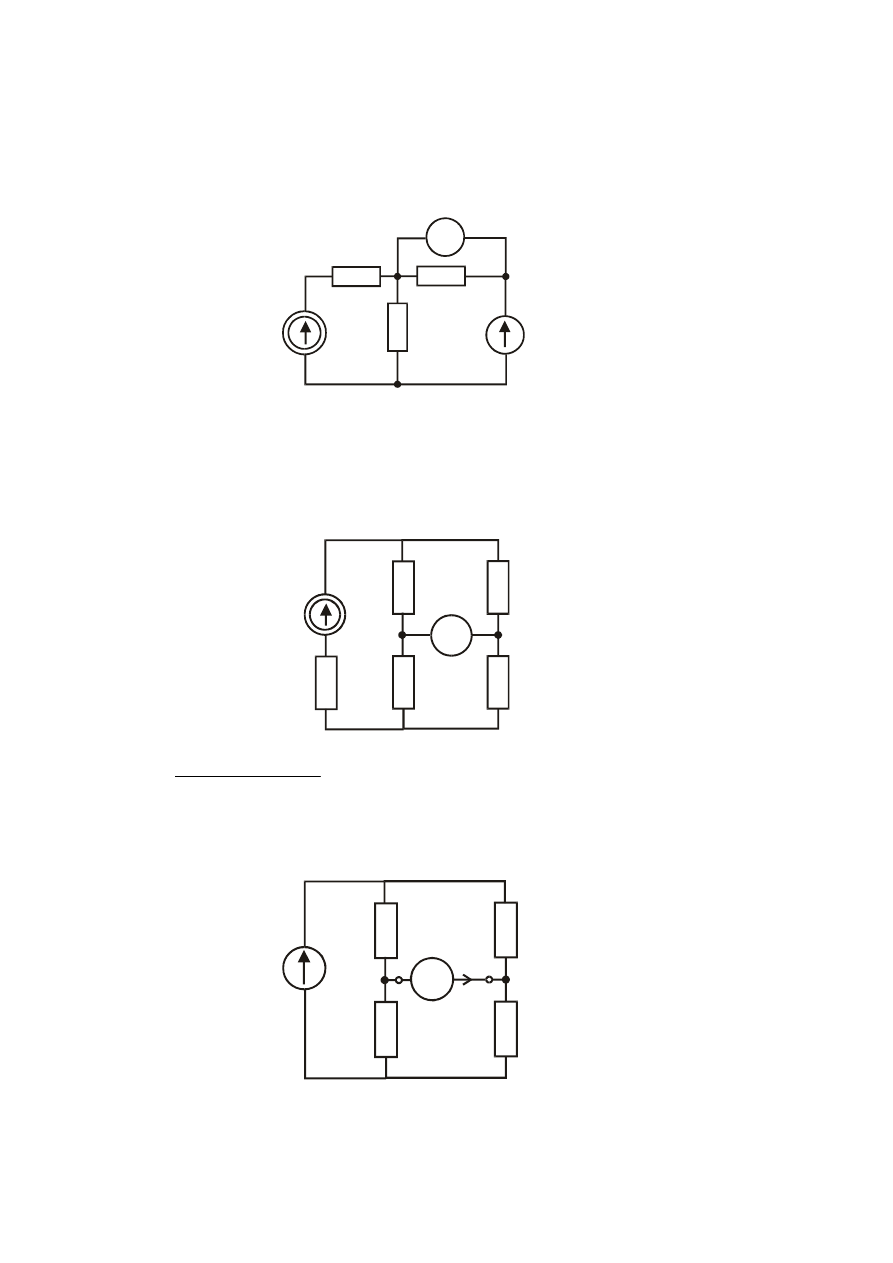
5

Odp. R

3

= 0, P

0max

= 32 W.

Zadanie
Ile wynosi napięcie źródłowe E, jeśli dane są; J, R

1

, R

2

, R

3

, a wskazanie woltomierza

wynosi zero?

Odp. E = -R

2

J

Zadanie
Wyznaczyć prąd źródłowy J, jeśli wskazanie amperomierza wynosi I

A

.

Odp. J =

5

2

4

3

5

4

3

2

R

R

R

R

)

R

R

)(

R

R

(

−

+

+

I

A

; gdy R

3

R

4

= R

2

R

5

, zadanie jest sprzeczne. W mostku

zrównoważonym prąd w gałęzi poprzecznej ( I

A

) musi być równe zero.

Zadanie
Wyznaczyć napięcie źródłowe E, jeśli wskazanie amperomierza wynosi I

A

.

V

E

J

R

1

R

3

R

2

R

1

J

R

4

R

2

R

3

R

5

A

E

A

B

R

4

R

2

R

3

R

5

A

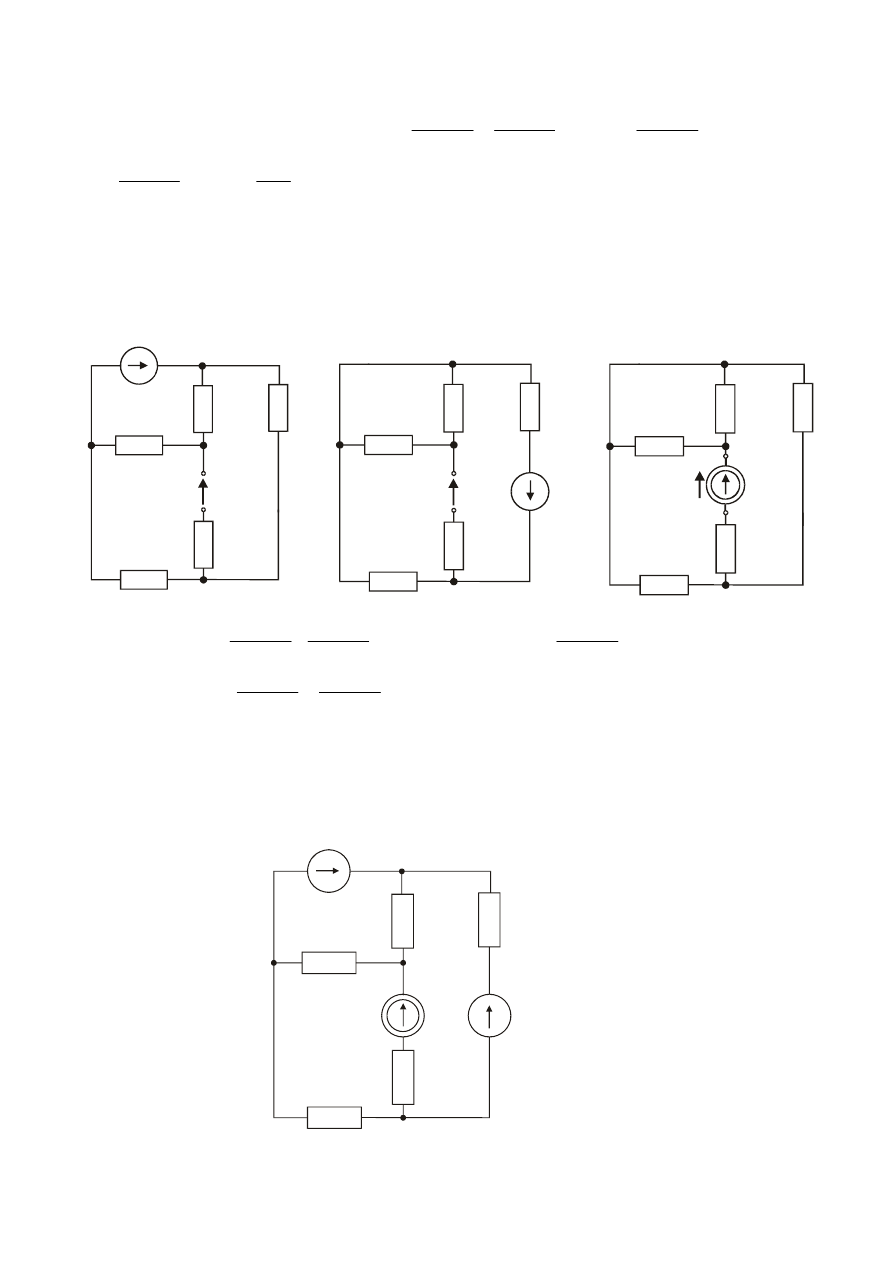
6

Odp. Z tw. o źródle zastępczym; U

AB

= (

4

2

2

R

R

R

+

-

5

3

3

R

R

R

+

) E, R

w

=

4

2

4

2

R

R

R

R

+

+

+

5

3

5

3

R

R

R

R

+

, I

A

=

w

AB

R

U

= k E

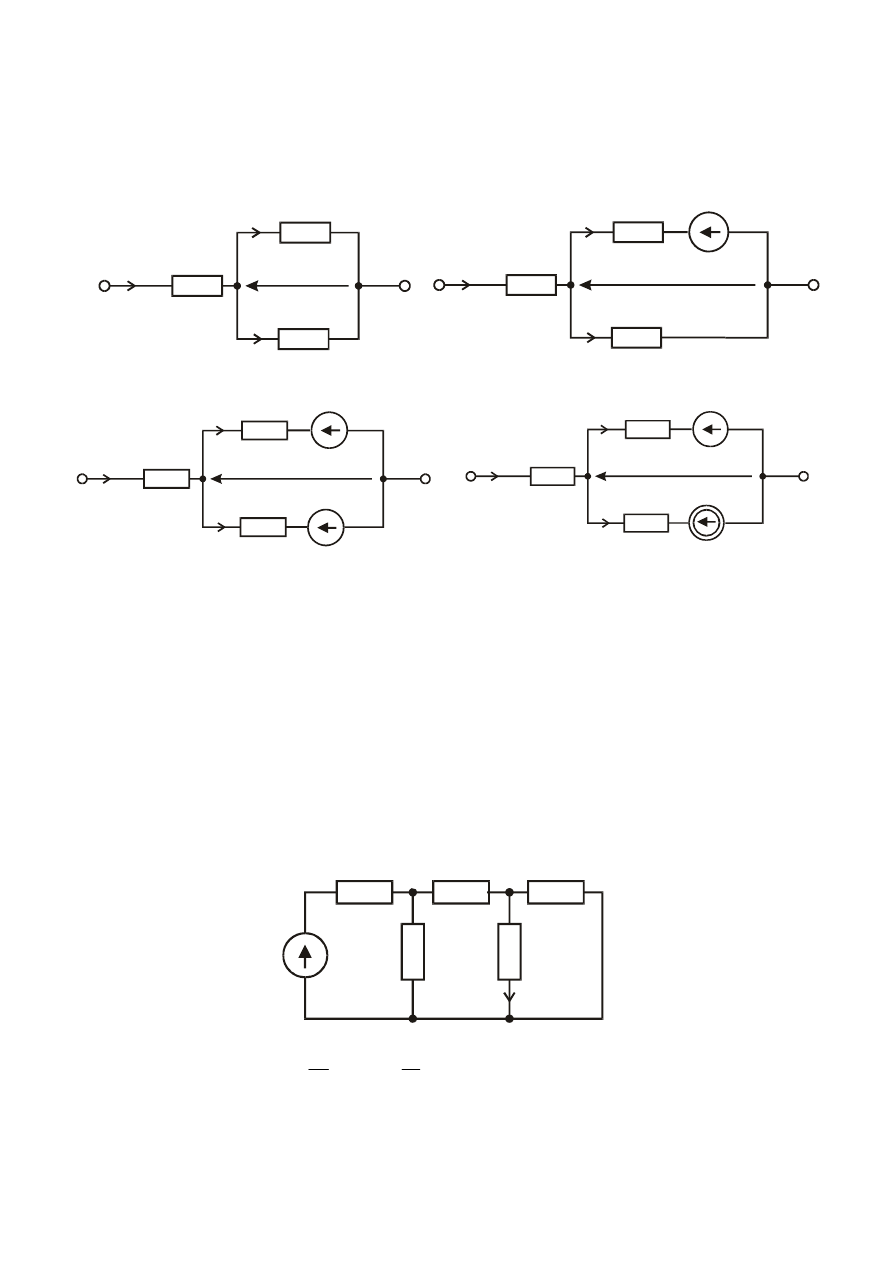
Zadanie
Traktując elementy aktywne i pasywne obwodów jako znane, wyznaczyć napięcie U

AB

w

obwodach;
a. b. c.

Odp. a. U

AB

= (

3

2

2

6

4

6

R

R

R

R

R

R

+

−

+

) E

1

, b. U

AB

= -

6

4

4

R

R

R

+

E

6

,

c. U

AB

= (R

5

+

3

2

3

2

R

R

R

R

+

+

6

4

6

4

R

R

R

R

+

) J

5

Zadanie
Wykorzystując wyniki poprzedniego zadania i stosując zasadę superpozycji, wyznaczyć
napięcie źródła prądu, a następnie moc źródła. Obliczenia przeprowadzić dla wartości
elementów: E

1

= 6 V, J

5

= 2 A, E

6

= 10 V, R

2

= R

3

= R

4

= R

5

= R

6

= 2

.

Ω

Odp. U

j

= 0 – 5+ 8 = 3 V, P

J

= 6 W.

R

3

R

2

R

4

R

5

R

6

E

6

J

5

E

1

R

3

R

2

R

4

R

5

R

6

U

AB

E

1

R

3

R

2

R

4

R

5

R

6

E

6

U

AB

R

3

R

2

R

4

R

5

R

6

J

5

U

AB

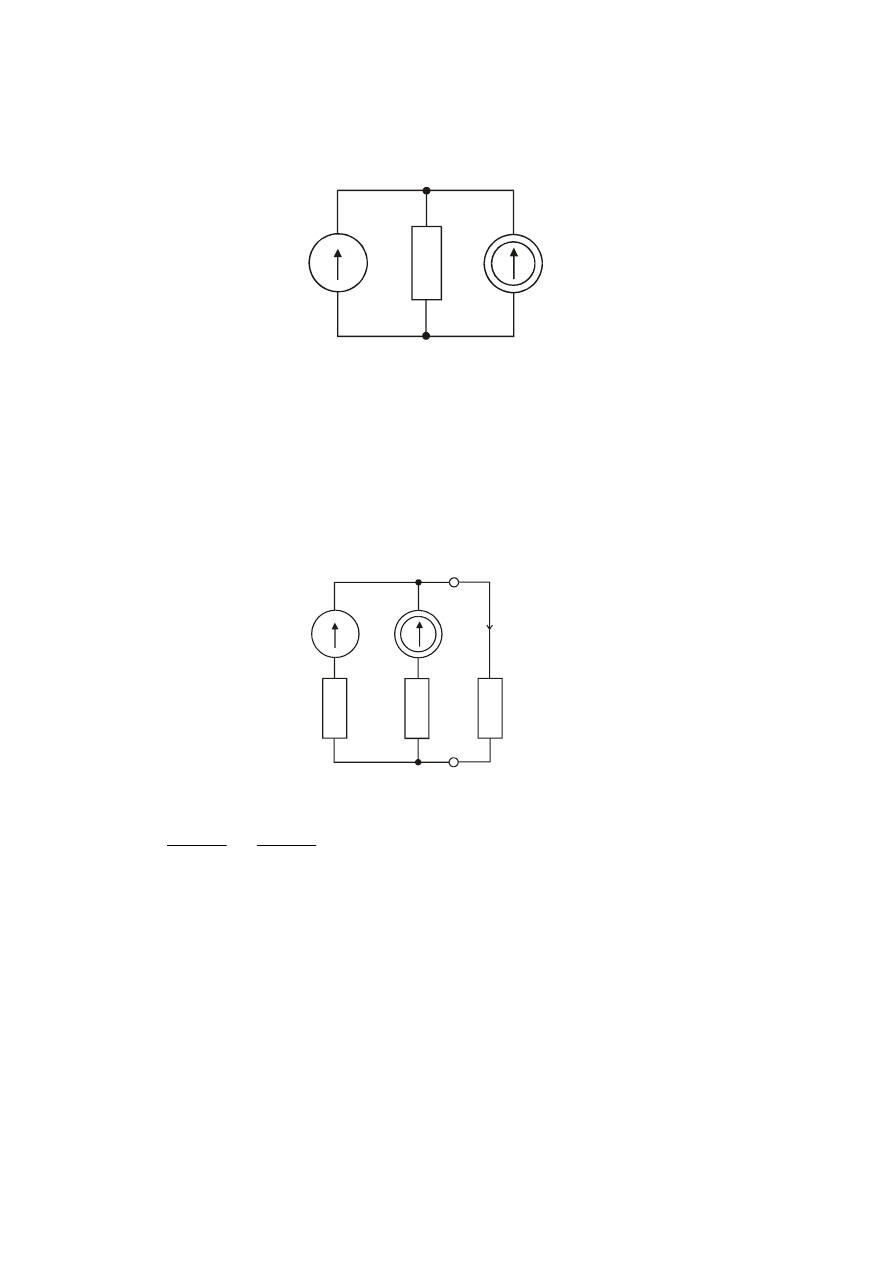
7

Zadanie
W obwodzie o danych; E = 10 V, J = 2 A, obliczyć moce źródeł i elementu R, dla jego
trzech wartości; R

1

= 2

Ω , R

2

= 5

Ω , R

3

= 10

Ω .

Odp. P

E1

= 30 W, P

J1

= 20 W, P

R

= 50 W; P

E2

= 0, P

J2

= 20 W, P

R

= 20 W;

P

E3

= - 10 W, P

J3

= 20 W, P

R

= 10 W.

Zadanie
Dany jest obwód o elementach; E =9 V, J = 3 A, R

1

= 1

Ω , R

2

= 2

Ω , R

3

= 3

Ω . Wyznaczyć

natężenie prądu I

3

stosując;

a. zasadę superpozycji
b. twierdzenie o źródle zastępczym

Odp.

a. I

3

=

3

1

R

R

E
+

+

3

1

1

R

R

R

+

J,

b. U

AB

= E + R

1

J ; R

w

= R

1

.

Zadanie
W obwodzie z poprzedniego zadania, o danych; ; E =9 V, R

1

= 1 Ω , R

2

= 2 Ω , R

3

= 3 Ω ,

dobrać taką wartość źródła prądu, aby prąd I

3

był równy zeru.

Odp. E + R

1

J = 0; J = - 9 A.

E

R

J

E

J

R

1

R

2

R

3

A

B

I

3

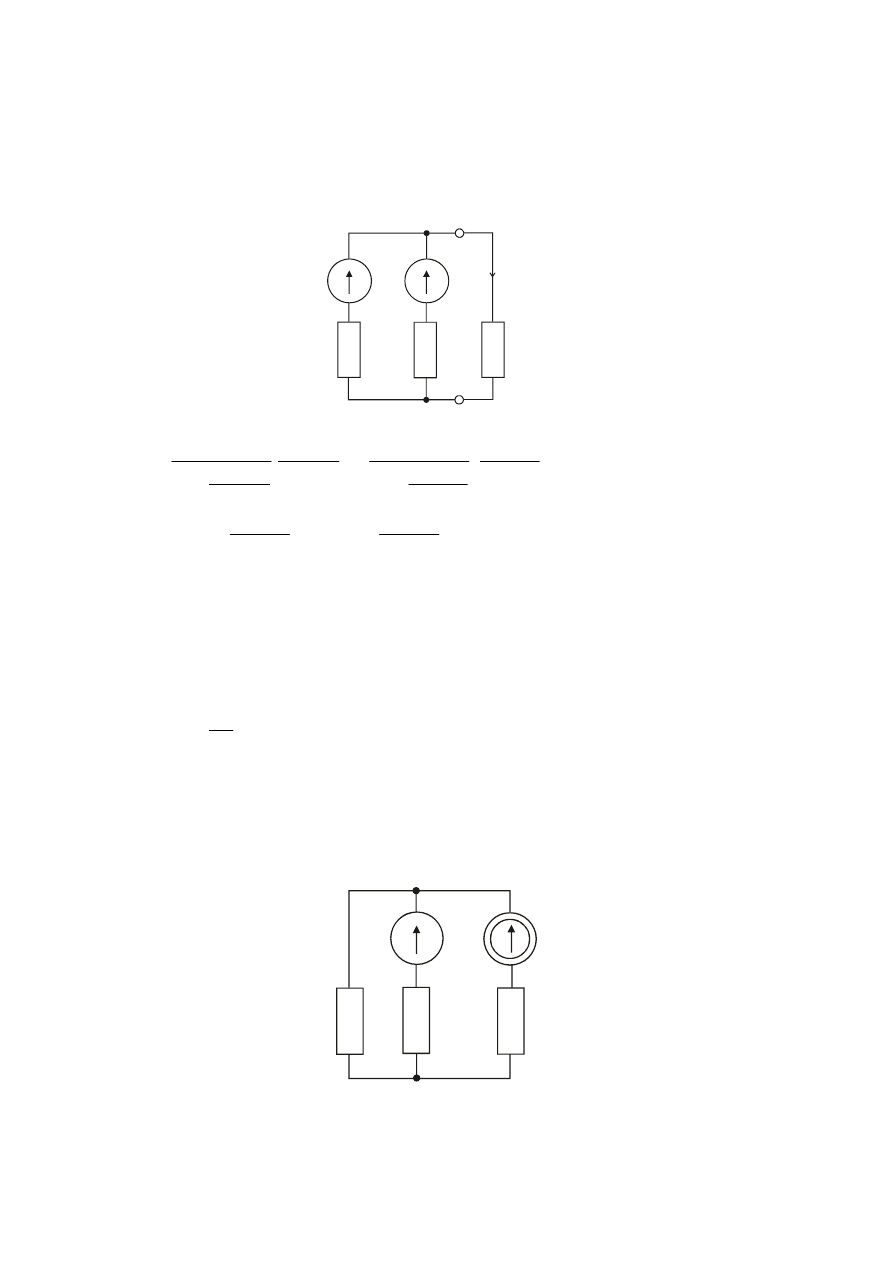
8

Zadanie
W obwodzie o elementach; E

1

= 12 V, E

2

= 24 V, R

1

= R

2

= 6

Ω , R

3

= 3

Ω ,

wyznaczyć prąd I

3

stosując;

a. zasadę superpozycji
b. twierdzenie o źródle zastępczym

Odp.

a. I

3

=

3

2

3

2

1

1

R

R

R

R

R

E

+

+

3

2

2

R

R

R

+

+

3

1

3

1

2

2

R

R

R

R

R

E

+

+

3

1

1

R

R

R

+

b. U

AB

= E

2

+

2

1

2

1

R

R

E

E

+

−

R

2

, R

w

=

2

1

2

1

R

R

R

R

+

Zadanie
W obwodzie z poprzedniego zadania o danych: E

1

= 12 V, R

1

= R

2

= 6 Ω , R

3

= 3 Ω ,

wyznaczyć taką wartość źródła napięcia E

2

, aby prąd I

3

był równy zeru.

Odp. E

2

= -

1

2

R

R

E

1

, i nie zależy od wartości elementu R

3

.

Zadanie
W podanym obwodzie wyznaczyć taką wartość napięcia E

2

, aby napięcie U

AB

, miało trzy razy

większą wartość niż

'
AB

U

, liczone po zmianie zwrotu źródła prądu.

Odp. E

2

= 2 R

2

J

3

E

1

E

2

R

1

R

2

R

3

A

B

I

3

E

2

J

3

R

1

R

2

R

3

B

A

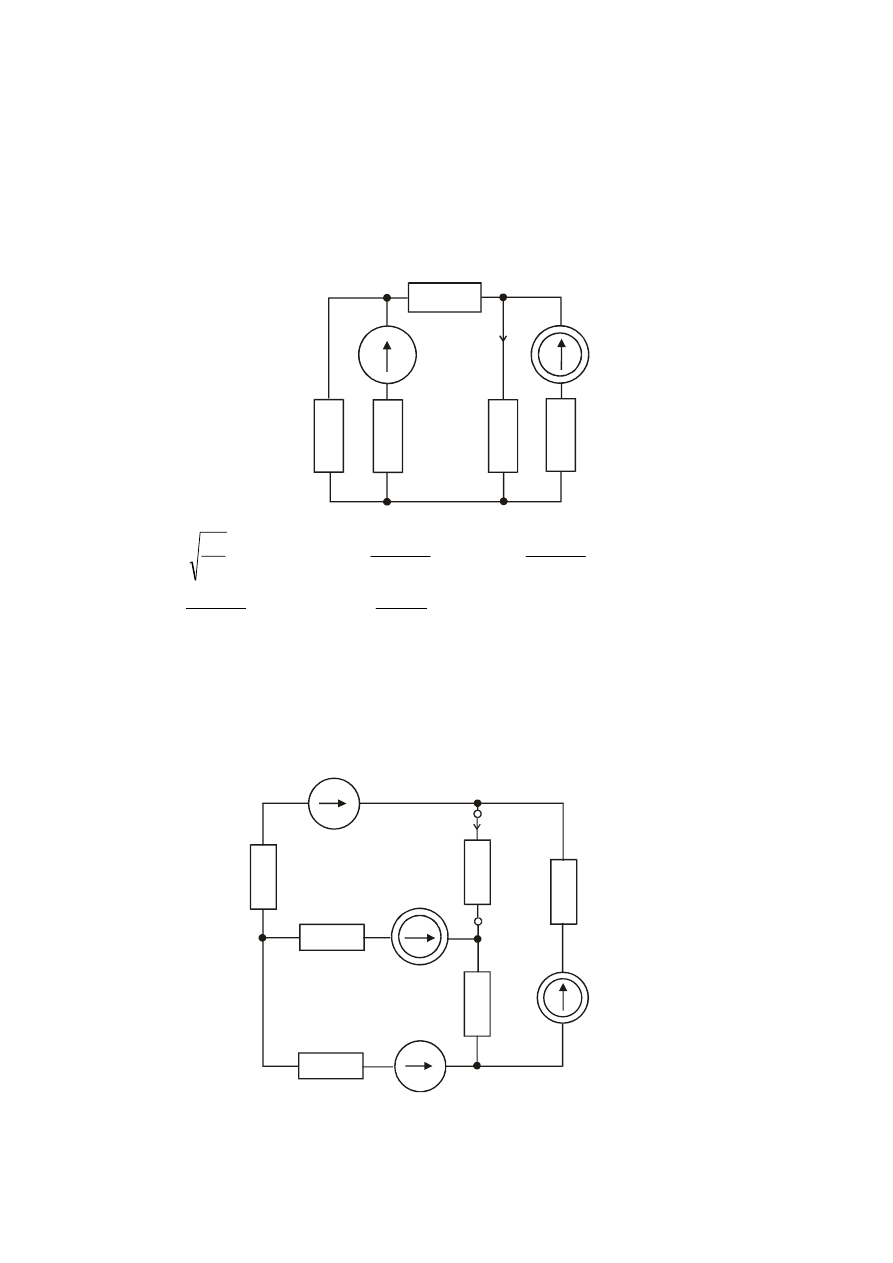
9

Zadanie
W obwodzie element R

4

, rozprasza energię z mocą P

4

= 16 W. Wyznaczyć prąd źródła prądu

jeśli pozostałe elementy mają wartości; E

2

= 24 V, R

1

= 3

Ω , R

2

= 6

Ω , R

3

= 2

Ω ,

R

4

= R

5

= 4

Ω .

Odp. I

4

=

4

4

R

P

=

± 2 A, U

AB

=

2

1

2

R

R

E

+

R

1

+ (R

3

+

2

1

2

1

R

R

R

R

+

) J

5

= 8 + 4 J

5

;

R

w

= R

3

+

2

1

2

1

R

R

R

R

+

= 4

Ω , ± 2 =

4

4

J

4

8

5

+

+

; J

5

= 2 A, J

5

= - 6 A.

Zadanie
W podanym obwodzie, traktując elementy aktywne i pasywne jako znane, wyznaczyć prąd I

2

stosując:
a. zasadę superpozycji
b. twierdzenie o źródle zastępczym.

Odp.

R

1

R

2

R

3

R

4

I

4

R

5

J

2

E

2

R

3

R

2

R

1

R

4

R

5

R

6

J

6

J

3

E

1

E

4

A

B

I

2

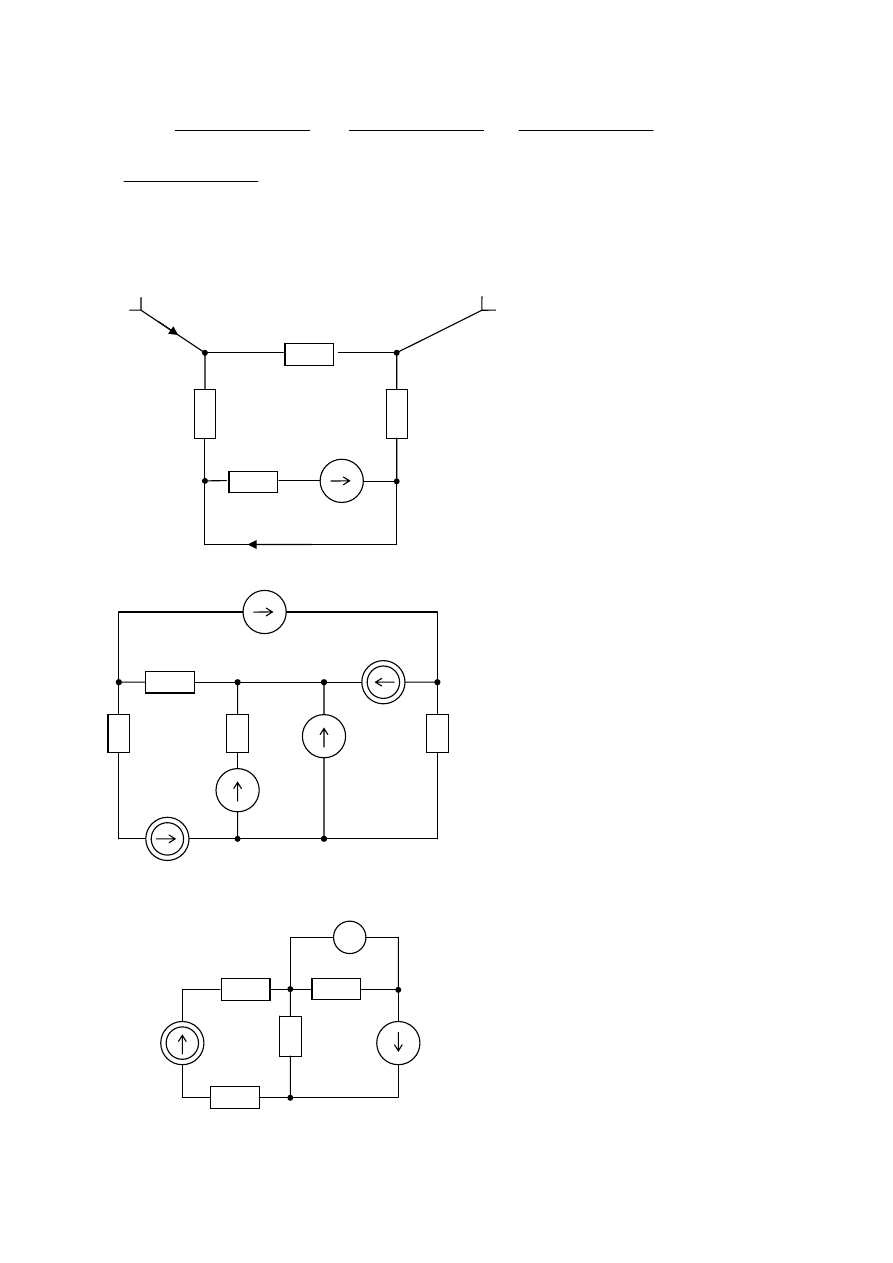
10

a. I

2

=

5

4

2

1

1

R

R

R

R

E

+

+

+

-

5

4

2

1

4

R

R

R

R

E

+

+

+

-

5

4

2

1

5

4

R

R

R

R

R

R

+

+

+

+

J

3

+

+

5

4

2

1

4

1

R

R

R

R

R

R

+

+

+

+

J

6

,

b. U

AB

= E

1

– E

4

- ( R

4

+ R

5

) J

3

+ ( R

1

+ R

4

) J

6

, R

w

= R

1

+ R

4

+ R

5

.

Zad

















Zad

















Zadanie

Zapisać macierzowe równania obwodu:
a. metodą prądów oczkowych,
b. metodą napięć węzłowych.
Korzystając z zapisanych równań wyznaczyć
moce źródeł prądu.

25V

5

Ω

2A

10V

5

Ω

10Ω

2A

20Ω

20V

E

R

R

R

R

I

1

I

2

Wyznaczyć wartość napięcia źródła E mając
dane:
R=1

Ω,

I

1

=I

2

=3A

E

R

2

J

V

R

4

R

3

Ile wynosi napięcie źródłowe E, jeśli dane są
J, R

1

, R

2

, R

3

, R

4

, a wskazanie woltomierza

wynosi zero ?

R

1

11

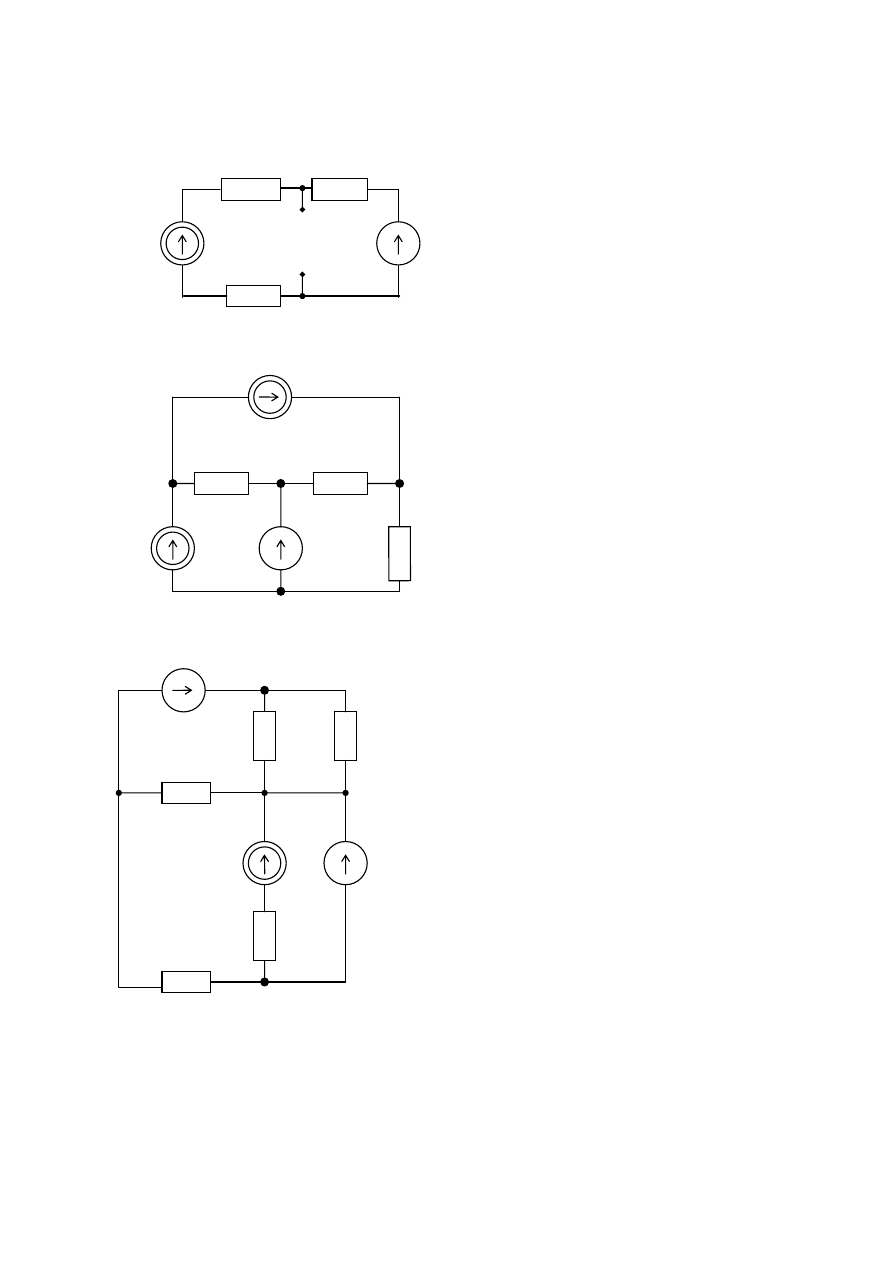
Zadanie












Zadanie

E

J

R

3

R

2

W podanym obwodzie mając dane J, R

1

, R

2

,

R

3

obliczyć taką wartość napięcia E, aby

napięcie U

AB

miało trzy razy większą wartość,

niż napięcie U

AB

‘ liczone po zmianie zwrotu

źródła prądu.

R

1

A

B

Dane:

R

1

= R

3

= 20

Ω

R

2

= 10

Ω

E = 30V
J

2

= 2 A

P

R2

= 10 W

Obliczyć moce źródeł.

J

1

J

2

E

R

1

R

2

R

3

Dane:

E

1

= 6V

J

5

= 2A

E

6

= 10V

R = 2

Ω

Korzystając z zasady superpozycji wyznaczyć
wartość napięcia na źródle prądu.

J

5

E

1

R

R

R

R

E

6

R

E

1

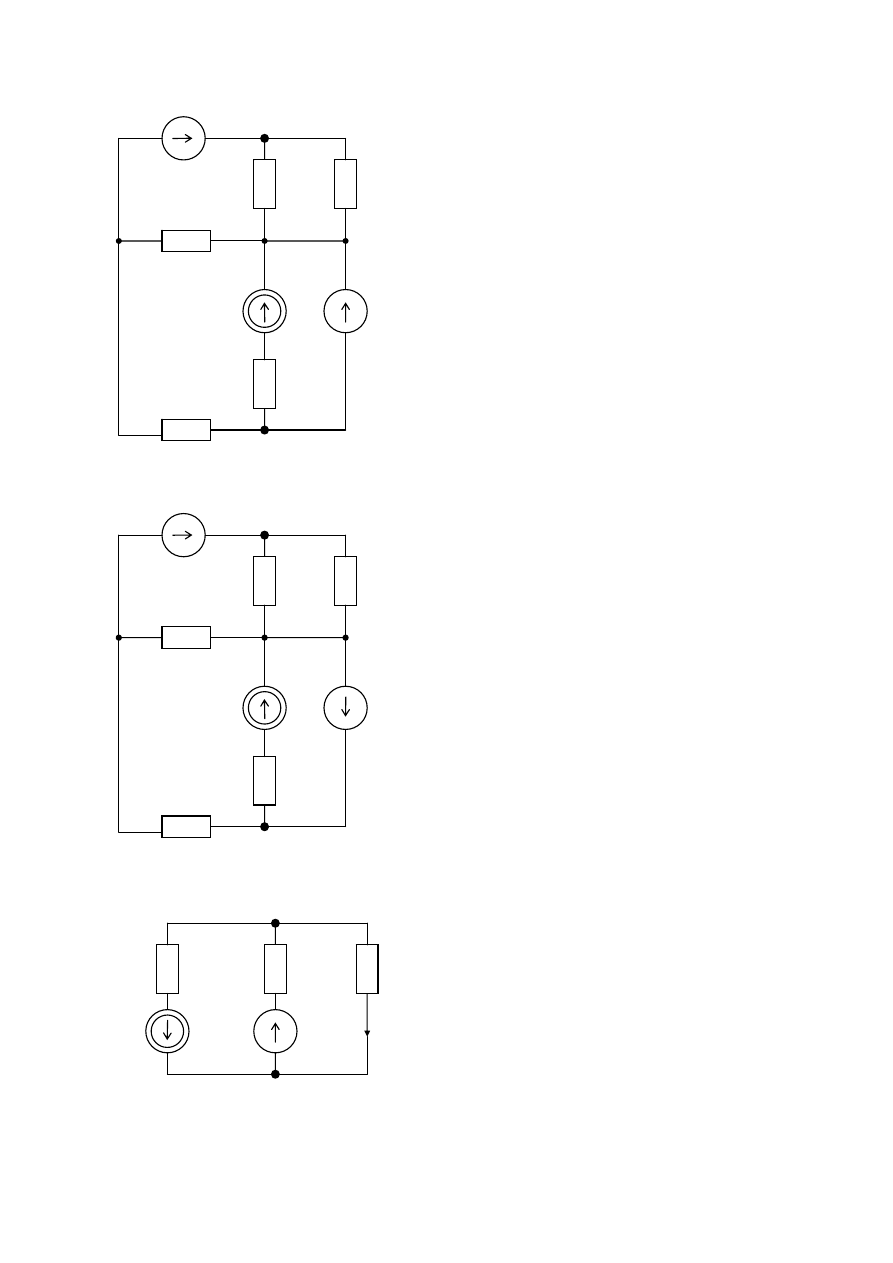
12

Dane:

E

1

= 6V

J

5

= 2A

E

6

= 10V

R = 2

Ω

Korzystając z zasady superpozycji wyznaczyć
moc źródła napięcia E

1

.

J

5

R

R

R

R

E

6

R

Dane:

E

1

= 6V

J

5

= 2A

E

6

= 10V

R

x

= R = 2

Ω

Korzystając z zasady superpozycji wyznaczyć
moc wydzieloną na rezystorze R

x

.

J

5

E

1

R

x

R

R

R

E

6

R

Dane:

E = 9V
R

1

= 2

Ω

R

2

= 3

Ω

R

3

= 3

Ω

Korzystając z twierdzenia Thevenina dobrać
taką wartość źródła prądu, aby prąd I

3

był

równy zero.

J

E

R

2

R

1

R

3

I

3

13

Korzystając z twierdzenia Thevenina dobrać
taką wartość rezystancji R

X

, aby wydzieliła się

na niej moc P

Rx

=25W.

J=4A

E

2

=4V

R

2

=2

Ω

R

3

=2

Ω

R

1

=2

Ω

R

X

E

1

=8V

Korzystając z twierdzenia Thevenina dobrać
taką wartość rezystancji R

X

, aby wydzieliła się

na niej moc P

Rx

=4W.

J

4

=3A

E

2

=4V

R

3

=2

Ω

R

2

=2

Ω

R

1

=2

Ω

R

X

E

1

=8V

R

5

=2

Ω

R

4

=4

Ω

14

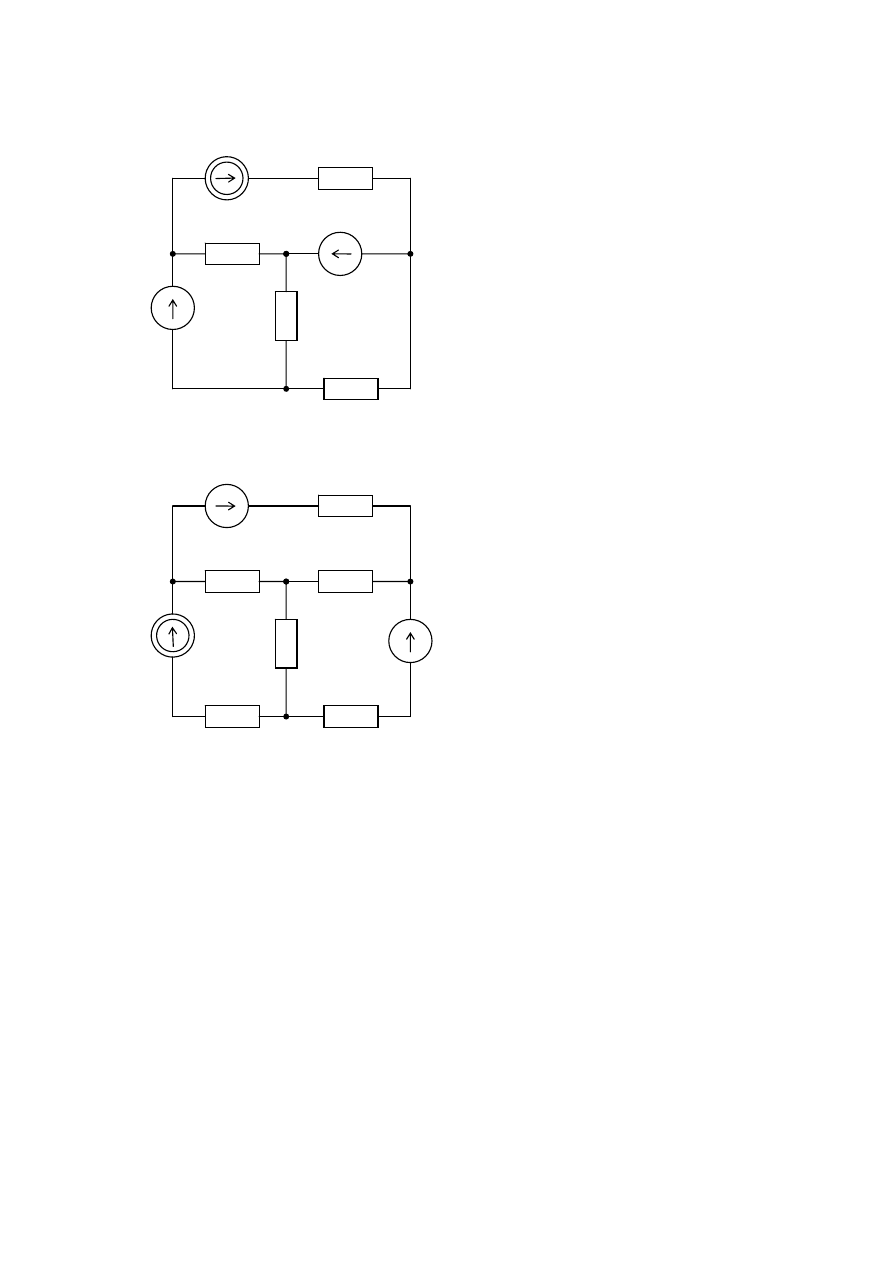
1. Obliczyć oporność zastępczą dwójników:
a. b.

5

Ω

6

Ω

3

Ω

2

Ω

3

Ω

2

Ω

A

B

6

Ω

9

Ω

3

Ω

A

B

9

Ω

9

Ω

6

Ω

c.

d. przy zamkniętym i otwartym „w”

5

Ω

2

Ω

3

Ω

3

Ω

3

Ω

A

B

3

Ω

4

Ω

2

Ω

3

Ω

W

A

B

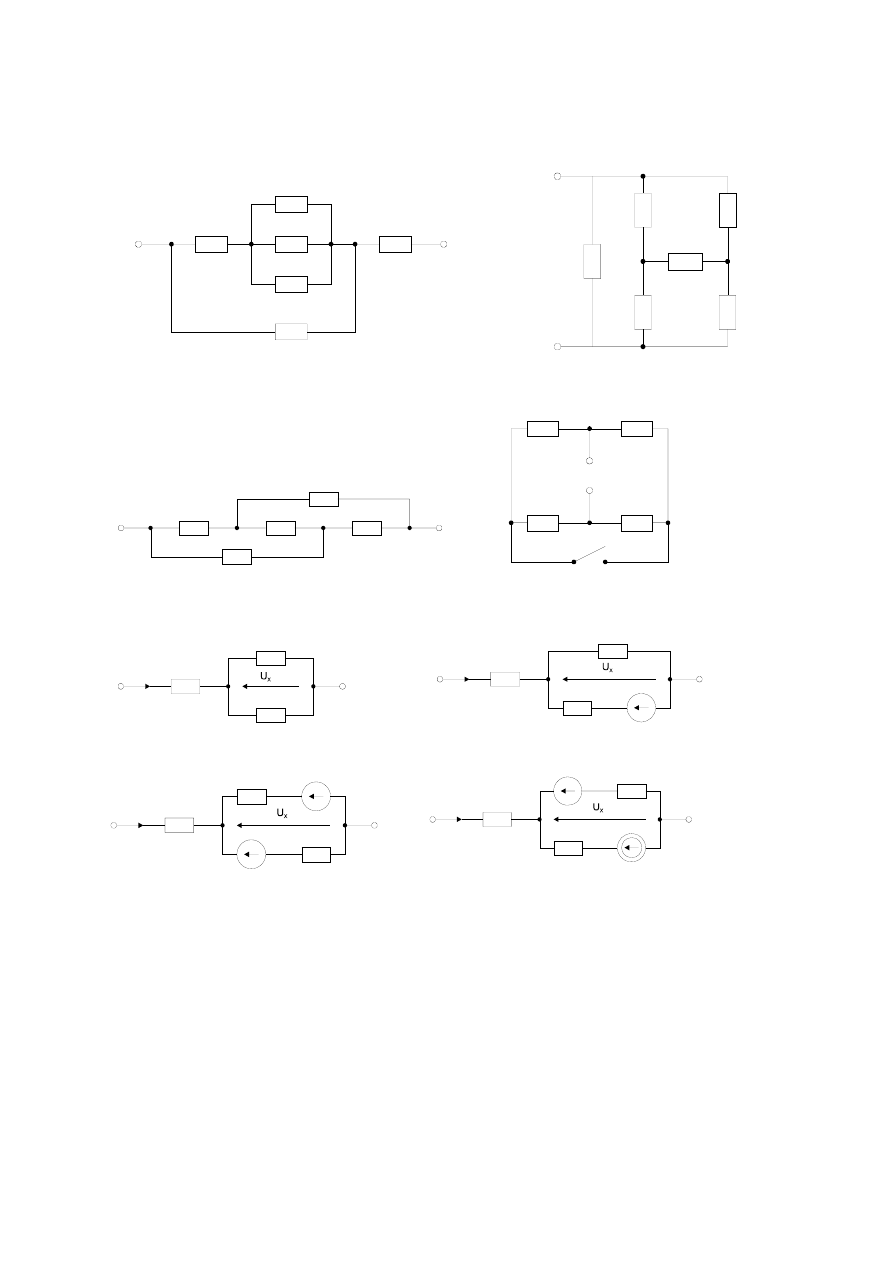
2. Obliczyć prądy I

a

, I

b

, napięcia U

x

oraz moce źródeł napięcia i prądu w podanych obwodach:

a. b.

1

Ω

6

Ω

3

Ω

I=6A

1

Ω

6

Ω

3

Ω

I=6A

18V

c. d.

1

Ω

6

Ω

3

Ω

I=6A

6V

18V

1

Ω

6

Ω

3

Ω

I=6A

9V

4A

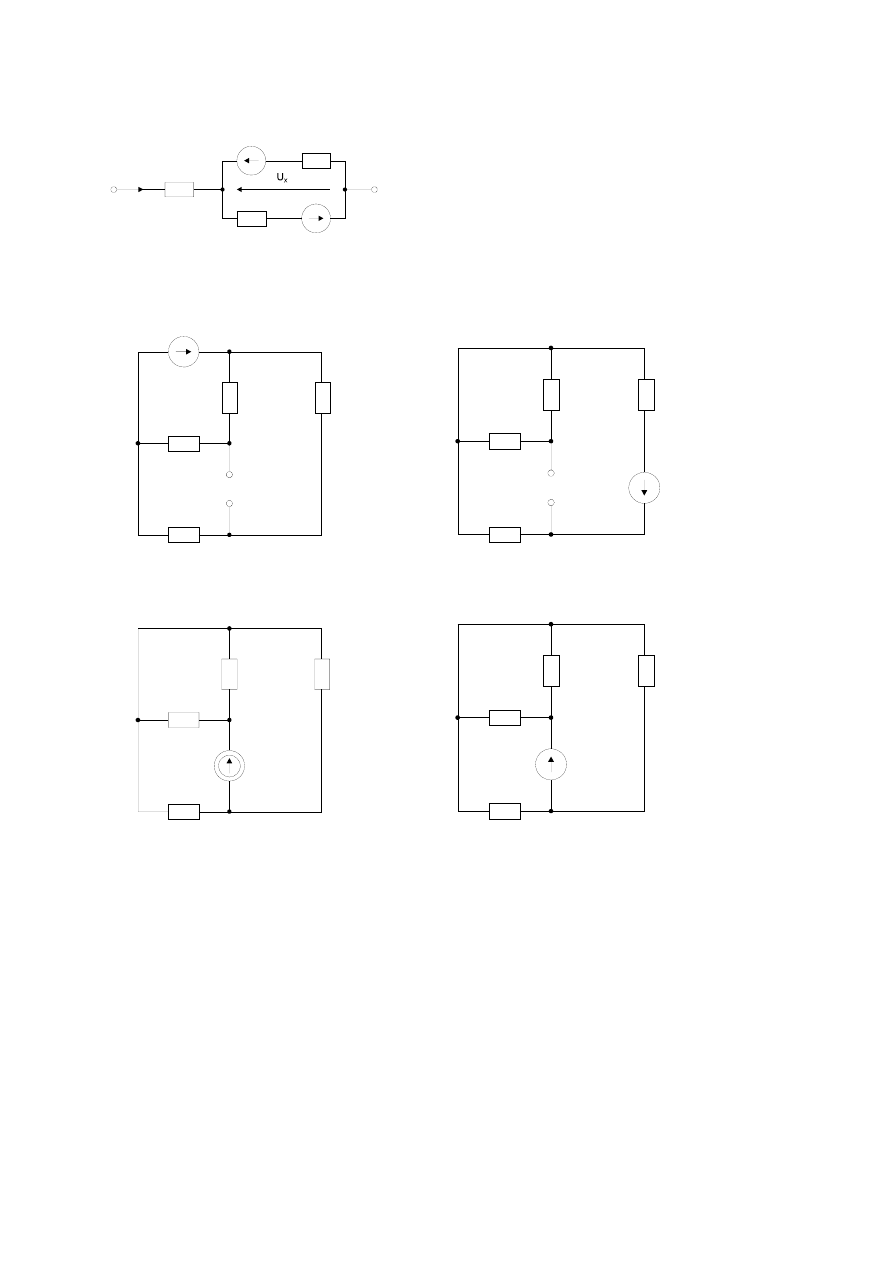
15

e.

1

Ω

6

Ω

3

Ω

I=6A

9V

18V

3. Obliczyć napięcie U

ab

w obwodach:

a. b.

2

Ω

A

B

2

Ω

2

Ω

2

Ω

2

Ω

6V

2

Ω

A

B

2

Ω

2

Ω

2

Ω

2

Ω

10V

c. d.

2

Ω

A

B

2

Ω

2

Ω

2

Ω

2A

2

Ω

A

B

2

Ω

2

Ω

2

Ω

8V

16

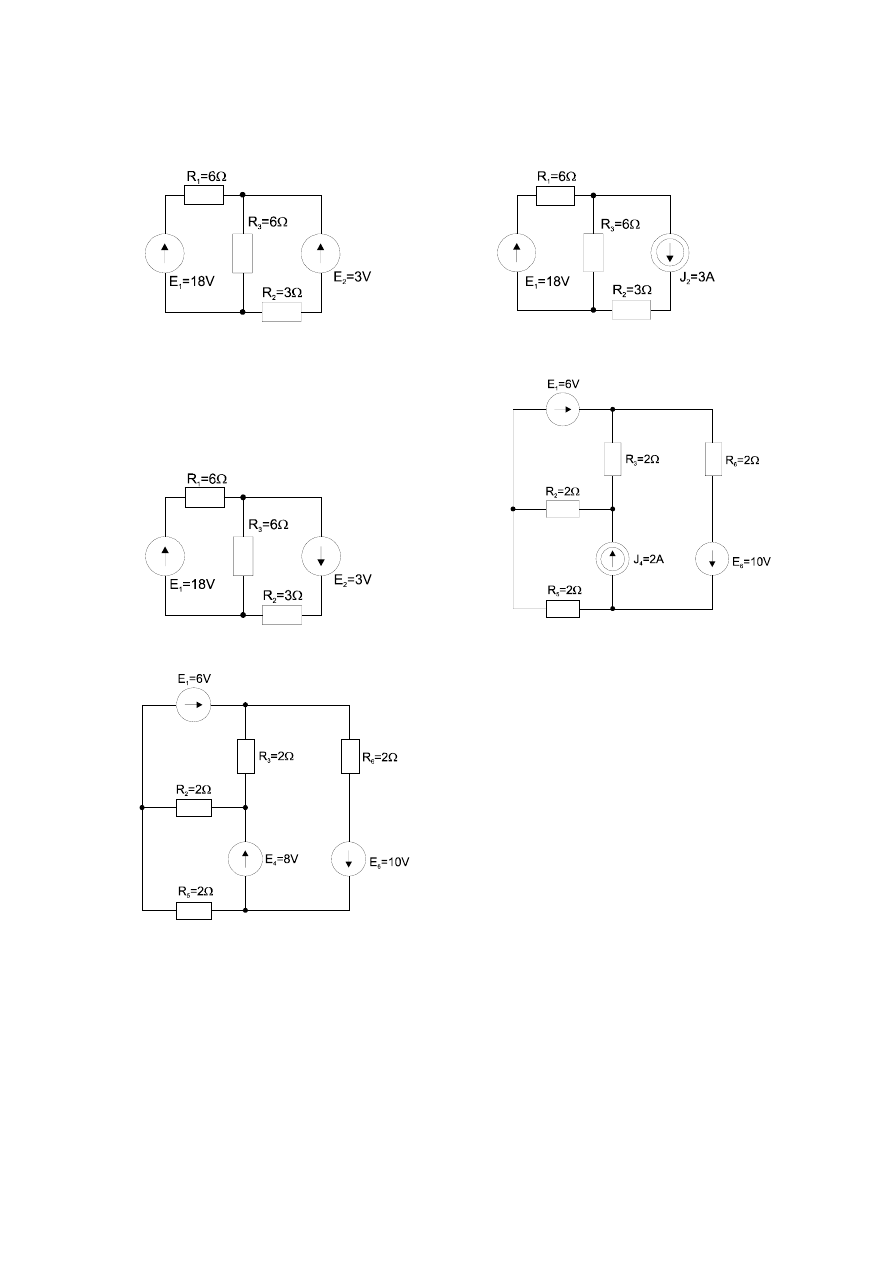
4. Obliczyć prądy gałęziowe stosując metodę równań Kirchoffa, obliczyć moce źródeł napięcia i źródeł prądu.
Sporządzić bilans mocy.
a. b.

c. d.

e.

5. W zadaniach 1.4 a, b, c, d zastosować twierdzenie o superpozycji do wyliczenia natężenia prądu w elementach
oznaczonych jako R

3

.

6. W zadaniach 1.4 a, b, c, d zastosować twierdzenie o źródle zastępczym do wyliczenia prądów w elementach
oznaczonych jako R

3

.

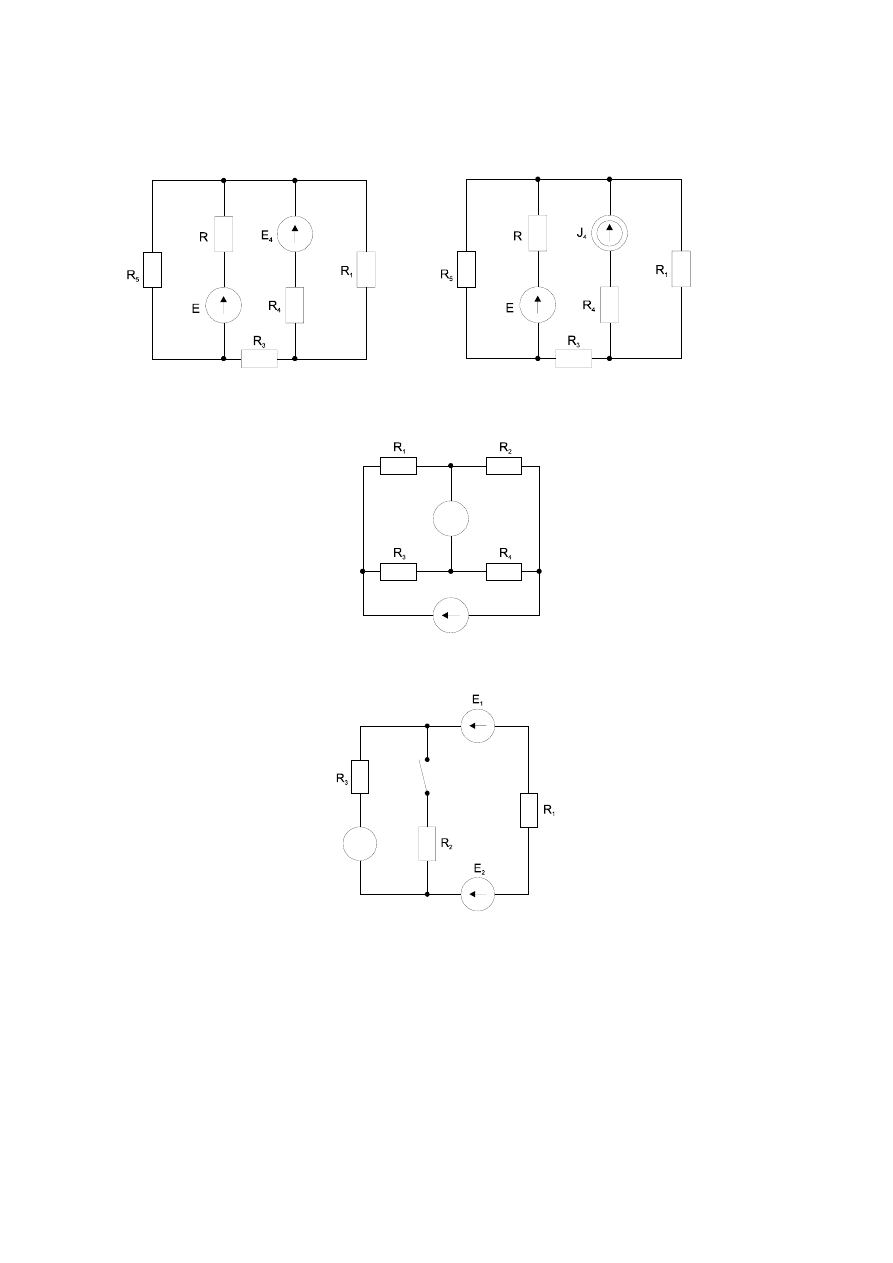
17

7. Moc źródła napięcia wynosi P

E

=100W. Wyznaczyć moc źródła w gałęzi 4 jeśli : E=20V, R=1

Ω, R

1

=1

Ω,

R

4

=1

Ω, R

5

=3

Ω.

a. b.

8. W obwodzie woltomierz wskazuje napięcie 15V. Obliczyć napięcie zasilające jeśli: R

1

=1

Ω, R

2

=2

Ω, R

3

=3

Ω,

R

4

=4

Ω.

V

E

9. Przy zamkniętym wyłączniku amperomierz wskazuje natężenie prądu 2A. Ile wskaże ten amperomierz przy
otwartym wyłączniku jeśli E

1

=4V, R

1

=2

Ω, R

2

=6

Ω, R

3

=3

Ω.

A

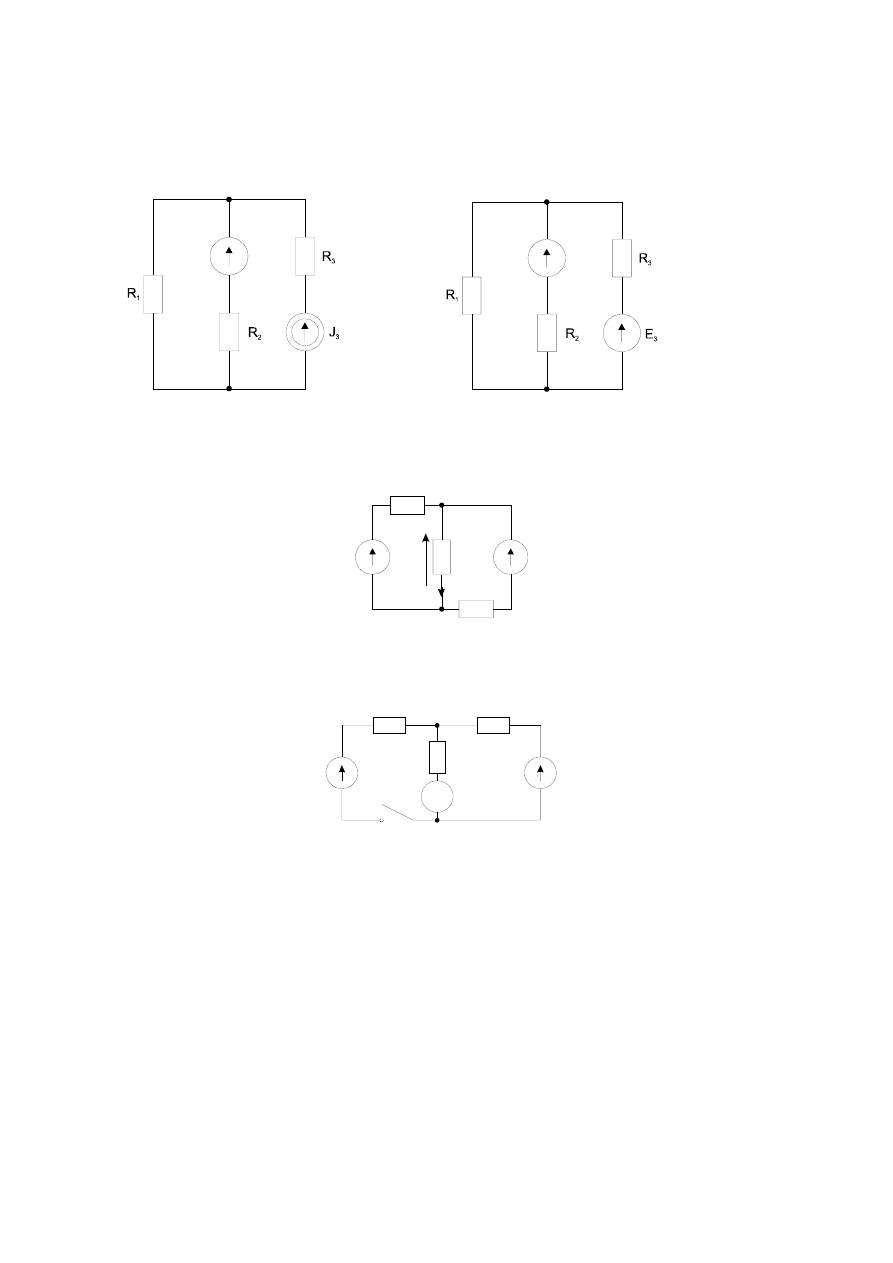
18

10. Wyznaczyć taką wartość E, aby napięcie U

ab

miało trzy razy większą wartość niż U

ab

’

w przypadku zmiany

zwrotu źródła w gałęzi 3.
a. b.

a

b

E

a

b

E

11. Wyznaczyć zależności: u=f(i), P=f(R) oraz naszkicować wykresy. Dla jakiej wartości R wydzieli się na
rezystorze maksymalna moc? Odpowiedź uzasadnić.

24Ω

6V

12

Ω

0V

R

U

I

12. Przy zamkniętym wyłączniku amperomierz wskazuje natężenie prądu I

3

=2A. Ile wskaże ten amperomierz

przy otwartym wyłączniku jeśli: E

1

=4V, R

1

=2

Ω, R

2

=6

Ω, R

3

=3

Ω ?

R

R

R

2

3

1

A

E

E

1

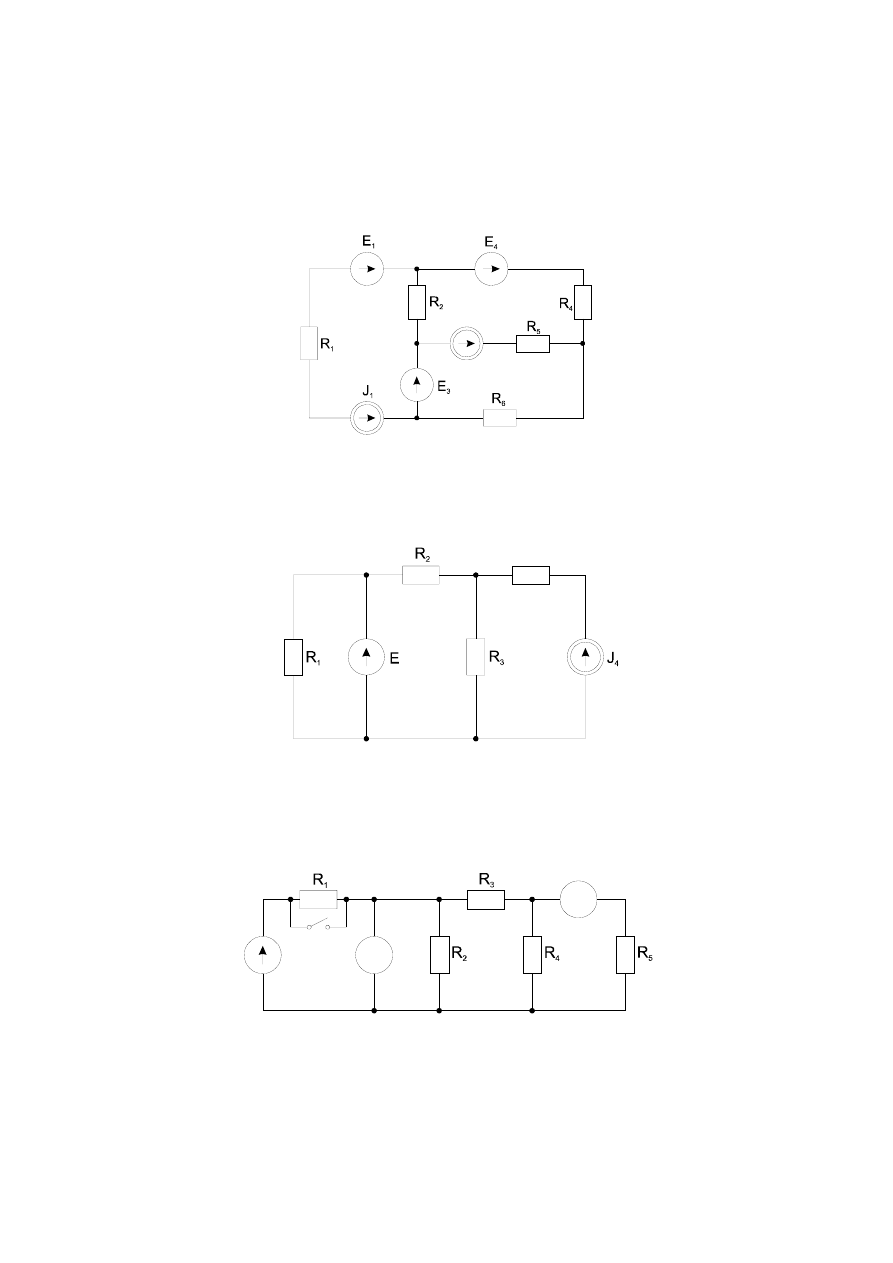
19

13. Zapisać równania obwodu stosując:

a. metodę prądów oczkowych,

b. metodę napięć węzłowych

Zastosować najkorzystniejszy wybór oczek oraz węzła odniesienia.

J

5

14. W elemencie R

3

rozpraszana jest energia elektryczna z mocą P

3

=108W. Wyznaczyć

natężenie prądu źródłowego J

4

jeśli dane są: E=12V, R

1

=1

Ω, R

2

=2

Ω, R

3

=3

Ω, R

4

=4

Ω. W

obliczeniach dla ułatwienia zastosować twierdzenia pomocnicze.

R

4

15. W liniowym obwodzie przy otwartym wyłączniku woltomierz wskazywał napięcie

U

VO

=80V, a amperomierz natężenie prądu I

5O

=1A. Obliczyć wskazanie amperomierza I

5Z

po

zamknięciu wyłącznika jeśli woltomierz wskazuje U

VZ

=100V.

V

A

W

E