Katedra Geodezji Szczegółowej 

UWM w Olsztynie 

Ćwiczenie nr 19-20 

Obliczanie powierzchni figur geometrycznych 

Nazwisko i imię Numer 

kolejny: 

 

Grupa: Data: 

 

1. Obliczanie powierzchni figur geometrycznych ze współrzędnych 

Cel ćwiczenia. Praktyczne zapoznanie się z obliczaniem powierzchni działek ze współrzędnych  
 

\

4

3

2

1

10

9

13

12

11

20

19

18

7

3

8

9

4

400 mm

MAPA SYTUACYJNA

Skala 1:1000

230

mm

80 mm

120 mm

90 mm

Grupa ???

Województwo:

gm Olsztyn

miasto Olsztyn

Niniejszą mapę
sporządził
Jan Kowalski

10 mm

X= 70.00 m.
y= 0.00 m

Wymiary punktu
granicznego i jego
numer zgodnie z
Instrukcją K1

 

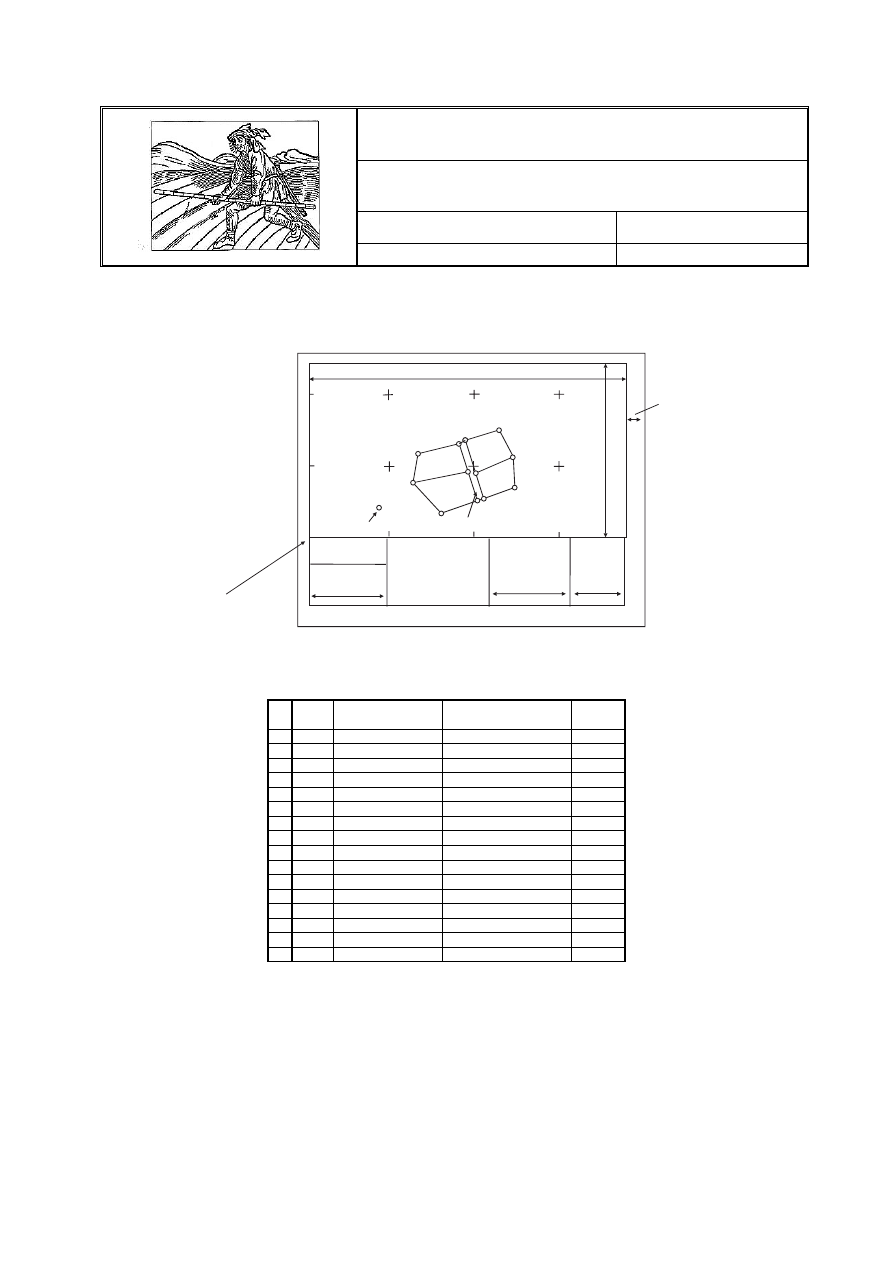
Rysunek 1 

Tabela 1 

Nr 

Bok 

Odległość 

 ze współrzędnych

Odległość 

z pomiaru graficznego

Różnica

1 1-2 

 

 

 

2 2-3 

 

 

 

3 3-4 

 

 

 

4 4-9 

 

 

 

5 9-13 

 

 

 

6 13-18 

 

 

 

7 18-19 

 

 

 

8 19-20 

 

 

 

9 20-21 

 

 

 

10 11-1 

 

 

 

11 1-10 

 

 

 

12 10-9 

 

 

 

13 11-12 

 

 

 

14 12-13 

 

 

 

15 19-12 

 

 

 

16 10-3 

 

 

 

 
Przebieg ćwiczenia.  

√  Na arkuszu brystolu formatu A3 nanieść siatkę kwadratów oraz ramkę mapy oraz krzyżyki (ołówek HB). 

Współrzędne dolnego lewego krzyżyka wynoszą x = 70.00 m, y = 0.00 m. Skala mapy jest 1:1000. 

√ Nanieść ze współrzędnych punkty podane w tabeli 1. Punkty połączyć zgodnie ze szkicem podanym na 

rysunku 1. Treść mapy: graniczniki, linie działek, numery ograniczników i numery działek wykreślić i 
opisać zgodnie z instrukcją K-1 !!!!! (ołówek HB). 

√ Sprawdzić poprawność naniesienia punktów. W tym celu porównać boki obliczone ze współrzędnych z 

bokami pomierzonymi graficznie. Wyniki porównania tj. boki obliczone ze współrzędnych i pomierzone 
graficznie wpisać do tabeli 1. Obliczyć różnicę między wartościami otrzymanymi ze współrzędnych i 
graficznie. W podręczniku znaleźć informację dotyczącą maksymalnych różnic między długościami 

 

1 

obliczonymi ze współrzędnych a długościami wyznaczonymi graficznie. Korzystając z tego warunku 
sprawdzić poprawność wyznaczenia długości 

√ Wykreślić mapę w tuszu, zgodnie z instrukcja K-1 !!!! 

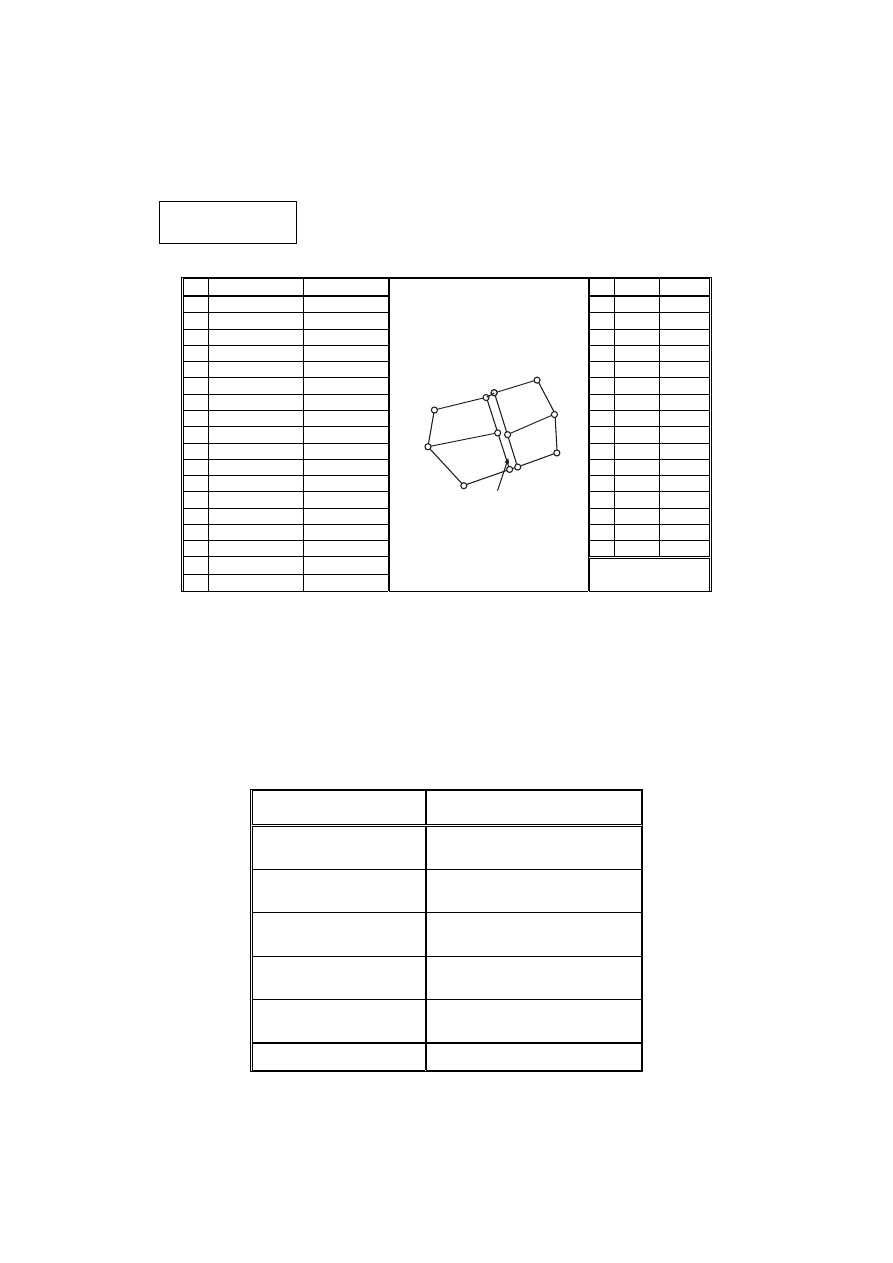
√ Obliczyć powierzchnię całej figury (1,2,3,4,9,13,18,19,20,11) ze współrzędnych (analitycznie) 

korzystając z kalkulatora. Obliczenia wykonać w tabeli 2 zgodnie ze wzorem: 

 

(

)

1

i

1

i

n

1

i

i

y

y

x

P

2

−

+

=

−

∑

=

 

Tabela 2 

nr x 

y 

Nr

x 

y 

  

 

 

…..… 

……… 

1 106.59+0.2xN  210.45 

1 

 

 

2 120.60  249.68 

2    

3 158.43  246.88 

3    

4 189.95  230.76 

4    

9 178.39  188.38 

9    

10 138.11 

200.99 

13

 

 

11 103.43 

203.44 

18

 

 

12 139.16 

191.53 

19

 

 

13 174.19 

181.03 

20

 

 

18 162.63 

130.24 

11

 

 

19 126.90 

123.23 

   

 

20 88.72 

158.96 

    

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

3

2

1

10

9

13

12

11

20

19

18

7

3

8

9

4

 

Powierzchnia = 

 
√ Obliczyć ponownie powierzchnię figury na komputerze korzystając z programu WinKalk. Porównać 

wyniki. 

2. Obliczenie powierzchni figur metodą graficzną 

Korzystając ze sporządzonej mapy (ćwicz. 18) oblicz metoda graficzną powierzchnię działek i dodatkowo 
powierzchnię drogi. Obliczenia wykonaj w odpowiednio zaprojektowanej tabeli 3. Porównaj sumę powierzchni 
działek obliczonych metodą graficzną z całkowitą powierzchnią obliczoną analitycznie. 
 
Powierzchnia  obliczona  graficznie =               , Powierzchnia obliczona analitycznie = 

Tabela 3 

Nr działki

 

Powierzchnia  

3  

4  

7  

8  

9  

Suma = 

 

 
 
 
 

 

2 

3. Obliczanie powierzchni figur geometrycznych metodą mechaniczną 

Cel ćwiczenia. Praktyczne zapoznanie się z obliczaniem konturów metodą mechaniczną.  
 

√  Na mapie wykonanej w ramach ćwiczenia 19, prowadzący zajęcia naniesie kontury klasyfikacyjne. 

 

√  W celu obliczenia powierzchni konturów klasyfikacyjnych w pierwszej kolejności wyznacz stałą mnożenia 

planimetru (tabela 4). W tym celu obwodzimy planimetrem kwadrat o boku 10 cm utworzony na mapie 
przez odpowiednie krzyżyki siatki. Wzór na pole powierzchni wyznaczone planimetrem (biegun 
planimetru na zewnątrz obwodzonej figury): jest następujący 

(

)

1

2

n

n

C

P

−

=

 gdzie n

1

 jest odczytem 

planimetru na punkcie początkowym, n

2

 odczytem po ukończeniu obwodzenia figury a C jest stałą 

mnożenia planimetru a P jest powierzchnią kwadratu w skali mapy. 

 

√ Oblicz 

powierzchnię konturu w granicach działek. Wyniki obliczeń zapisz w tabeli 5. 

Tabela 4. Wyznaczenie stałej planimetru C ( z dokładnością do m

2

) 

 odczyty 

różnica 

1

2

n

n

−

=

Δ

 

średnia 

różnica 

śr

n

Δ

 

śr

n

P

C

Δ

=

 

Powierzchnia 

konturu na 

mapie w cm

2

Dopuszczalna różnica 

dwukrotnego 

obliczenia pow. w 

działkach planimetru 

n

1

0 - 20 

2 

Pierwszy 

pomiar 

n

2

 

20 - 100 

3 

n

1

100 - 200 

4 

Drugi pomiar 

n

2

 

 

 

 

 

 

Tabela 5. Obliczenie powierzchni konturów klasyfikacyjnych metodą mechaniczną 

Obliczenie powierzchni metoda mechaniczną 

Nr 

działki 

Kontur 

klasyfikacyjny 

n

1

n

2

Δn 

Powierzchnia 

obliczona 

[m

2

] 

Suma 

powierzchni 

[m

2

] 

 

 

 

 

 

3 

 

 

 

 

 

 

 

 

 

 

 

4 

 

 

 

 

 

 

 

 

 

 

 

7 

 

 

 

 

 

 

 

 

 

 

 

8 

 

 

 

 

 

 

 

 

 

 

9  

 

 

 

 

Razem 

 

 

√  Porównaj powierzchnie działek obliczonych metodą graficzna z powierzchnią działek obliczoną metoda 

mechaniczną. 

Tabela 6 

Nr.  

działki

Powierzchnia obliczona 

metoda graficzną 

Powierzchnia obliczona

metoda mechaniczną 

Różnica 

3  

   

4  

   

7  

   

8  

   

9  

   

 
 

 

3