Inżynieria Biomedyczna I rok 

ćwiczenia z fizyki semestr 1  

 

Zestaw zadań na zajęcia nr 3 

1.   

Z  mostu  znajdującego  się  nad  wodą  na  wysokości  50 m  upuszczono  kamień.  Inny 

kamień  rzucono  pionowo  w  dół  w  sekundę  potem.  Oba  kamienie  uderzają  w 
powierzchnie wody w tej samej chwili. (a) Jaka była prędkość początkowa drugiego 

kamienia?  (b)  Sporządzić  wykres  zależności  prędkości  od  czasu  dla  każdego  z 
kamieni przyjmując, że pierwszy z nich upuszczono w chwili t = 0. 

2.   

Krople  deszczu  spadają  z  prędkością  u

d

 = 5m/s.  Na  przednią  szybę  stojącego 

samochodu  w  przeciągu  minuty  spada  V = 100 cm

3

  deszczu.  Ile  deszczu  zacznie 

spadać na szybę, jeśli samochód zacznie się poruszać z prędkością u

s

 = 72 km/h? 

3.   

Oblicz  średnią  szybkość  samochodu  poruszającego  się  ruchem  prostoliniowym, 

jeżeli  (a)  w  ciągu  pierwszej  połowy  czasu  swojego  ruchu  samochód  jechał  z 
szybkością  u

1

 = 80 km/h,  a  w  ciągu  drugiej  połowy  z  szybkością  u

2

 = 40km/h,  (b) 

pierwszą  połowę  drogi  przebył  z  szybkością  u

1

 = 80km/h  a  drugą  z  szybkością 

u

2

 = 40 km/h. 

4.   

Kolumna  wojska  o  długości  l = 1,5 km  przesuwa  się  wzdłuż  drogi  z  prędkością 
u

k

 = 6 km/godz.  Z  czoła  kolumny  dowódca  wysyła  motocyklistę  z  rozkazem  na  jej 

tył. Motocyklista jedzie z prędkością  u

m

 = 60 km/h, nie zatrzymując się przekazuje 

rozkaz i wraca. Jak długo był w drodze? 

5.   

Oblicz pochodne  

  
  

 następujących funkcji: 

(a)       

 

    

 

    

 

        ,  (b)            

 

 
 

,  (c)             ,  (d)     

 

   

 ,  

(e)                , (f)        , (g)        

 

. 

6.   

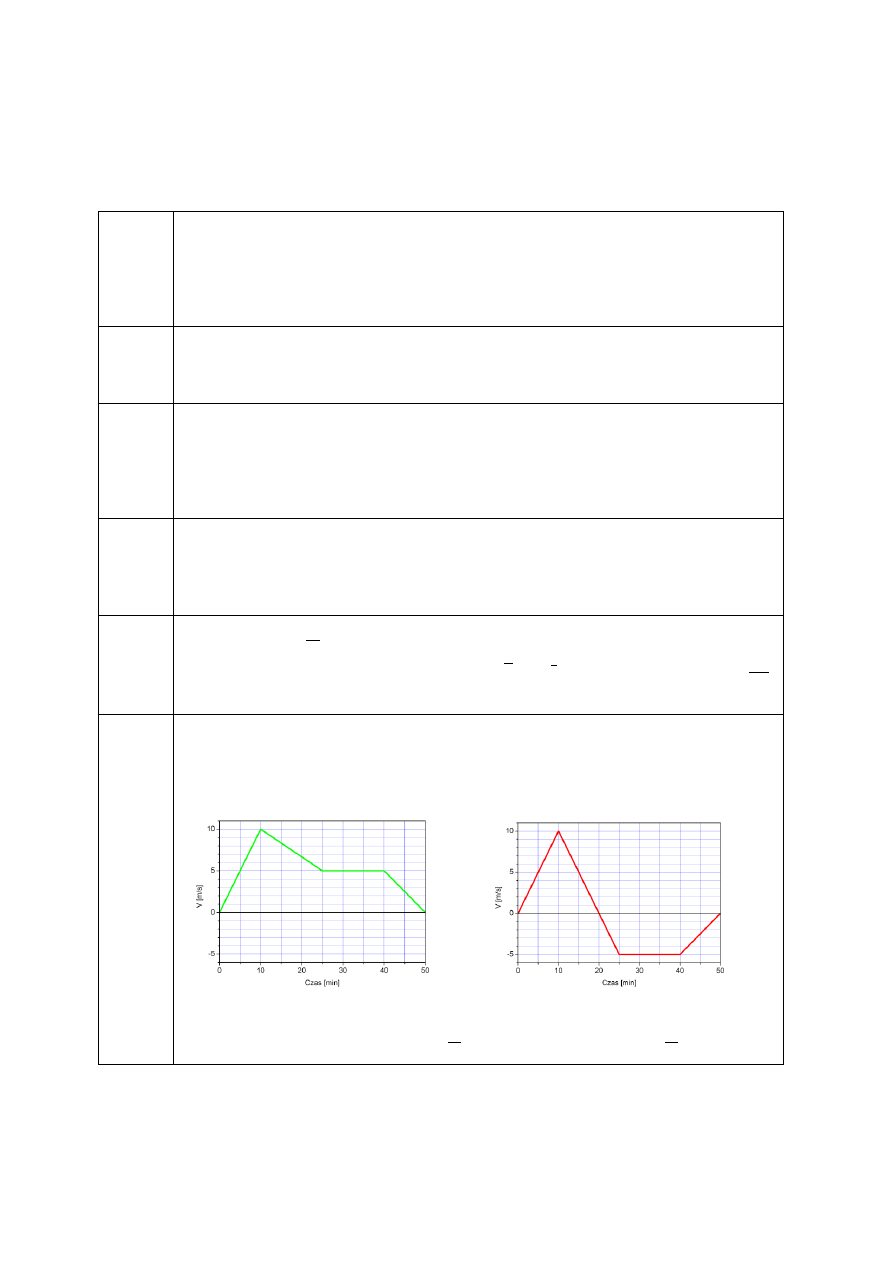
Hokeista  porusza  się  wzdłuż  linii  prostej.  Wykresy  przedstawiają  zależność  jego 
wektora prędkości od czasu. Oblicz jego średnią prędkość, całkowitą przebytą drogę 

oraz średnią szybkość w trakcie trwania ruchu. Narysuj wykres zależności drogi od 
czasu. 

 

 

 

 

 

(a) 

 

(b) 

 

średnia prędkość: 

  

        

   

  

 ,   średnia szybkość:  

  

 

  
  

  

7.   

Zależność  położenia  od  czasu  dwóch  punktów,  można  opisać  względem  środka 
prostokątnego układu współrzędnych, następującymi równaniami : 

r

1

(t)=(0,2,0)+(3,1,2)t+(1,1,0)t

2

 [m] , r

2

(t)=(1,0,1)+(0,2,1)t [m] 

Znaleźć: 

a)  prędkość punktu drugiego względem pierwszego 
b)  przyspieszenie punktu drugiego względem pierwszego 

8.   

Zależność  drogi  od  czasu  przebytej  przez  pewne  ciało  opisuje  równanie: 
           

 

    

 

,  gdzie  A=2m/s,  B=3m/s

2

,  C=4m/s

3.

.  Znaleźć  (a)  zależność 

prędkości  v  i  przyspieszenia  a  od  czasu  t,  (b)  drogę  przebytą  przez  to  ciało  oraz 
prędkość  i  przyspieszenie  ciała  po  upływie  2s  od  rozpoczęcia  ruchu.  Sporządzić 

wykres drogi, prędkości i przyspieszenia w przedziale 0 ≤ t ≤ 3s. 

 

Proszę sobie przyswoić pojęcia dotyczące rachunku różniczkowego. Polecana literatura: 
absolutne minimum: J.Massalski, M.Massalska „Fizyka dla inżynierów” cz.1 rozdział 2. 

dla przyjemności : G.M. Fichtenholz. Rachunek różniczkowy i całkowy tom 1, tom 2