1. Pojęcia podstawowe : sterowanie w układzie otwartym, zamkniętym, obiekt stacjonarny

i niestacjonarny, statyczny i dynamiczny, liniowy i nieliniowy, optymalny, nieoptymalny,
jedno- i wielowymiarowy

W sterowaniu w układzie zamkniętym występuje sprzężenie zwrotne. Pojęciem tym
określone jest działanie wsteczne wielkości regulowanej na wielkość regulującą. Czyli
inaczej mówiąc działanie na wielkości regulującej jest spowodowane zmianą wielkości
regulowanej.

Sterowanie w układzie otwartym różni się tym, że człowiek lub regulator nie posiada
informacji poprzez sprzężenie zwrotne o stanie wielkości regulowanej (wyjściowej)
Obiekt stacjonarny obiekt niezmieniający swoich własności w czasie tj. współczynniki nie
zależą od czasu

Obiekt niestacjonarny – własności obiektu zmieniają się w czasie a

i

= a

i

(t), b

i

= b

i

(t).

Obiekt dynamiczny- zmienne w równaniu obiektu zależą od czasu

Obiekt statyczny - zmienne w równaniu obiektu NIE zależą od czasu

Układ liniowy – funkcja, która spełnia dwie zasady



Superpozycji (składania) funkcji



Homogeniczności:

Powyższe własności można ująć w jeden warunek liniowości: Jeśli dane są dwa sygnały
wejściowe

i odpowiadające im sygnały wyjściowe

wówczas dla dowolnych wartości skalarnych

układ liniowy musi spełniać następującą zależność:

Funkcja nieliniowa – taka, która nie jest liniowa. Nie spełnia ona zasady superpozycji lub
homogeniczność
Optymalny model obiektu – minimalizuje lub maksymalizuje zadane kryterium jakości.

Metoda najmniejszych kwadratów minimalizuje kryterium

Q

– „odległość” pomiędzy znanymi n

punktami

f

(

x

i

) a przyjętą funkcją

.

..

.

1

2

3

1

2

(

,

,

,...,

,

,...)

0

F a y a y a y

b u b u



1

1

(

, 0, 0,...,

, 0,...)

0

F a y

b u



1

1

(

,

)

0

F a y b u



1

2

1

2

(

)

( )

( )

F u

u

F u

F u







(

)

( )

F ku

kF u



Jedno wejście u(t) i jedno wyjście y(t)

Dwa wejścia u

1

(t), u

2

(t) i jedno wyjście y(t)

T, k, k

1

, k

2

– stałe liczby

O układzie wielowymiarowym mówi się w przypadkach, gdy układ ma wiele zmiennych (często,

jest to też układ o wielu wejściach i/lub wielu wyjściach jednak niekoniecznie, gdyż część
zmiennych mogą stanowić zmienne stanu)

2. Układ automatycznej regulacji

Przypatrzmy się dokładniej jednoobwodowemu układowi stabilizacji automatycznej
(rys. 1.4). W schemacie tym można wyodrębnić podstawowe części składowe
występujące w każdym układzie regulacji automatycznej.
Urządzenie, albo zespół urządzeń, w których przebiega interesujący nas proces

technologiczny, nazywamy obiektem regulacji. Pojęcie obiektu regulacji jest
bardzo ogólne: może to być reaktor chemiczny, piec, silnik elektryczny, zbiornik

itd. Ponieważ w układzie regulacji interesuje nas przebieg procesu technologicznego,
często na schematach blokowych jako przedmiot oddziaływania układu

regulacji przedstawiany jest właśnie proces.
O tym, jak ma przebiegać proces technologiczny, mówią nam wielkości fizyczne
charakterystyczne dla danego procesu. Może to być ciśnienie, temperatura,
strumień (natężenie przepływu) itp. Ta wielkość fizyczna, która najlepiej odzwierciedla

przebieg procesu i której wartość
należy utrzymać na określonym
poziomie (stałym lub zmieniającym i

się), aby proces przebiegał prawidłowo,
nazywa się wielkością regulowaną.
W naszym przykładzie wielkością
regulowaną jest temperatura. Często

zdarza się, że w jednym obiekcie jest
kilka wielkości regulowanych. W
skomplikowanych przypadkach,
szczególnie przy regulacji procesów

chemicznych, buduje się układy regulacji
z wieloma wzajemnie zależnymi
wielkościami regulowanymi.
Wartość wielkości regulowanej mierzona jest przez urządzenie pomiarowe. Sygnał

wyjściowy z tego urządzenia stanowi dla układu regulacji informację, jaka
jest wartość rzeczywista, czyli wartość wielkości regulowanej w danej chwili.
Centralnym urządzeniem układu regulacji jest regulator. Jak wiemy, zadaniem f

układu regulacji jest utrzymywanie wartości wielkości regulowanej możliwie i
zbliżonej do wartości żądanej, gwarantującej najkorzystniejszy przebieg procesu
technologicznego. Wartość pożądana wielkości regulowanej, nazywana wartoś- |
cią zadaną, wytwarzana jest przez nadajnik wartości zadanej (zadajnik) stanowiący

często część regulatora. W regulatorze następuje porównanie wartości rzeczy- |
wistej z wartością zadaną i wytworzenie sygnału oddziałującego na obiekt w taki .
sposób, aby różnicę między wartością rzeczywistą a wartością zadaną sprowa- ł
dzić do zera. I

Oddziaływanie regulatora na przebieg procesu technologicznego odbywa się za |
pośrednictwem urządzenia wykonawczego, w którym można wyodrębnić element |

Obiekt

Obiekt

Obiekt o jednym wejściu i jednym wyjściu (SISO)

Obiekt o wielu wejściach i wielu wyjściach (MIMO)

.

( )

( )

( )

T y t

y t

ku t





.

1 1

2 2

( )

( )

( )

( )

T y t

y t

k u t

k u t







nastawczy i siłownik. Element nastawczy steruje wartością wielkości fizycznej |
nazywanej wielkością sterującą (nastawiającą). Wielkością sterującą może być [
czynnik mający decydujący wpływ na przebieg sterowanego procesu technologi- |

cznego. Najczęściej czynnikiem tym jest strumień materiału lub energii i dlatego I
najczęściej spotykanym elementem nastawczym jest zawór. Siłownik (element ?
napędowy) zapewnia uzyskanie siły niezbędnej do przestawiania elementu nasta- |
wczego. W układach, w których zmian wielkości sterującej dokonuje się inaczej |

niż przez zmiany położenia elementu mechanicznego, miejsce siłownika zajmuje wzmacniacz
mocy. Tak jest np. w serwomechanizmach.

3. Transformata Laplace’a, transmitancja
4. Linearyzacja równań nieliniowych

Linearyzacja -

polega na przybliżeniu modelu

układu nieliniowego

za pomocą modelu

układu

liniowego

.

Nie każdy

układ nieliniowy

można poddać linearyzacji. Może się także okazać, że nie istnieje stan

równowagi, wokół którego można by dokonać rozsądnej linearyzacji. Żądania: odpowiedniej
dokładności przybliżenia i odpowiednio szerokiego zakresu, dla którego ono ma obowiązywać, często
bywają przeciwstawne.

Szczególnie podatne dla idei linearyzacji są układy z nieliniowością

części statycznej

.

Do podstawowych metod linearyzacji należą:



metoda rozwinięcia w szereg - badając układ nieliniowy przy założeniu małych odchyleń od
pewnego

punktu pracy

układu (np. jego stanu równowagi) można rozwinąć funkcje nieliniowe

w

szereg Taylora

, pominąć człony nieliniowe (czyli wyrazy wyższych rzędów) i otrzymać w ten

sposób równania przybliżone liniowe;



metoda linearyzacji optymalnej -

polega na takim doborze elementów macierzy (czyli

współczynników nieliniowych

równań stanu

) który minimalizuje

błąd średniokwadratowy

pomiędzy

układem nieliniowym a dobranym w ten sposób modelem liniowym;



metoda nieliniowego sprzężenia zwrotnego - w metodzie tej odpowiednio zamienia się zmienne i
dobiera się nieliniowe

sprzężenie zwrotne

.

6) Charakterystyki częstotliwościowe

Co to jest? Odpowiedź obiektu w stanie ustalonym na sinusoidalny sygnał wejściowy. Po co?

Dokładnie identyfikują obiekt (określają jego własności dynamiczne)
Potrzebne do doboru nastaw regulatorów – układ regulacji musi posiadać odpowiednią jakość
np. w samochodzie nie mogą być odczuwalne drgania od drogi (aktywne zawieszenie w
samochodzie. Wpływ drgań typowej drogi z dziurami na komfort jazdy kierowcy)

W samojezdnych robotach – wpływ drgań drogi na zmianę kierunku jazdy

Pokazują jak zachowuje się obiekt, jeżeli wzrasta częstotliwość sygnałów wejściowych.
Przykład cieplny – budynek i zmiana temperatury powietrza zewnętrznego.

W ten sposób można określić zakres częstotliwości sygnałów, dla których regulacja ma pożądaną
jakość.
Pozwalają na określenie częstotliwości rezonansowej.
Można za ich pomocą badać stabilność układu regulacji.

Typy wykresów:
Wykres Bodego, 1927, przedstawia na dwóch różnych rysunkach zależność kąta przesunięcia
fazowego



od pulsacji



oraz modułu M od pulsacji



=



(



), M=M (



)

Wykres Nyquista – potraktujmy pulsację



jako parametr i narysujmy zależność (( M(



),



(



) )

we współrzędnych biegunowych

Wykres Nicholsa jest zależnością pomiędzy modułem M wyrażonym w dB i kątem przesunięcia
fazowego w stopniach. Karta Nicholsa pozwala na ocenę zapasu amplitudy i fazy, odległość
modułu układu zamkniętego od 1 oraz wartość modułu rezonansowego (patrz: wykres Bodego)

na podstawie charakterystyki częstotliwościowej układu otwartego.

Są trzy zmienne



, M ,



. W zależności od tego, która zmienna jest parametrem tego jest wykres.

Wykres Nyquista

( |G (



) |,



(



) ) = (( M(



),



(



) )

(wykres we współrzędnych biegunowych)
Wykres Bodego



=



(



) oraz M=M (



)

Wykres Nicholsa

M (



(



)), dB

Wykres Blacka M(



(



))

(wykres we współrzędnych kartezjańskich)

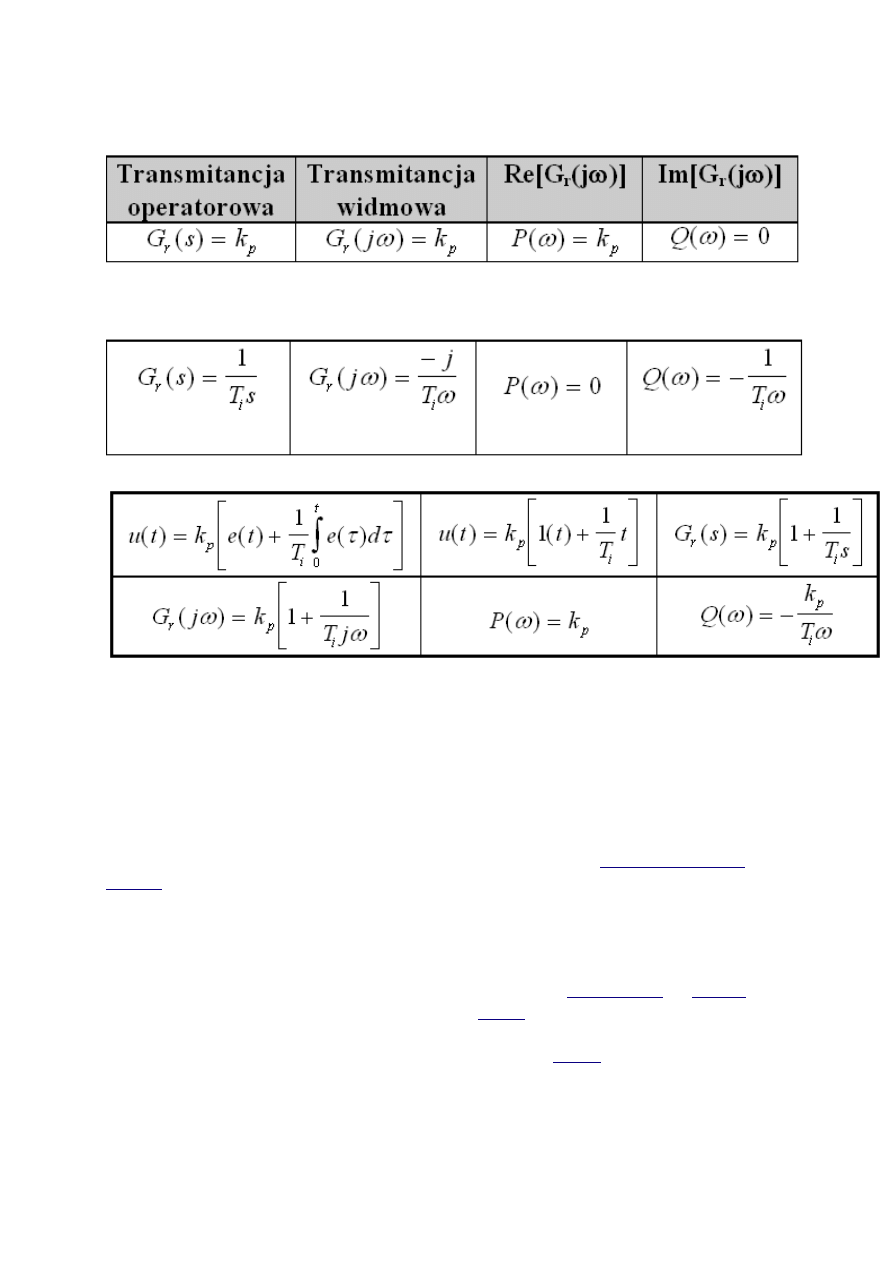
Charakterystyki członów podstawowych
Człon proporcjonalny

Człon całkujący

Człon proporcjonalno-całkujący

Obiekty nieminimalnofazowe

Def. Obiekt minimalnofazowy to taki, którego zera i bieguny znajdują się po lewej stronie

półpłaszczyzny Gaussa

Są to obiekty łatwe w regulacji.

Def. Obiekt nieminimalnofazowy to taki, który ma co najmniej jedno zero lub biegun znajdują się

po

prawej stronie półpłaszczyzny Gaussa

8. Stabilność układu regulacji

Stabilność układu automatycznej regulacji – niezbędny warunek pracy

układu automatycznej

regulacji

mówiący o tym, że układ po wyprowadzeniu go ze stanu równowagi sam powraca do tego

stanu. Ponieważ stan równowagi może być różnie interpretowany stosuje się także definicję
stabilności Laplace'a, która mówi, że układ liniowy jest stabilny, jeżeli jego odpowiedź na wymuszenie
(zakłócenie) o ograniczonej wartości jest ograniczona. Stabilność to jedna z najważniejszych
właściwości systemów dynamicznych. Istnieje wiele interpretacji pojęcia stabilności, które w zasadzie
są równoważne dobrze znanym pojęciom matematycznym, takim jak

ogranicz

oność

lub

ciągłość

.

Układ dynamiczny nazywamy stabilnym, gdy trajektorie

stanów

są ograniczone albo gdy zależą one w

sposób ciągły od stanów początkowych lub sterowań. Pojęcie stabilności układu można również
definiować poprzez stawianie odpowiednich wymagań trajektoriom

wyjścia

układu.

Większość definicji stabilności odwołuje się do pojęcia punktu/stanu równowagi. Najczęściej
spotykane definicje stabilności odnoszą się do układów opisywanych równaniem różniczkowym - mówi
się wówczas o stabilności poszczególnych rozwiązań równania różniczkowego otrzymanych przy

ustalonym sterowaniu

, przy czym przez stabilność rozwiązania rozumie się ciągłą zależność tego

rozwiązania od warunku początkowego

.

W

układzie liniowym

,

stacjonarnym

istnieje jednoznaczny związek między stabilnością a

wartościami

własnymi

tego układu. O stabilności

układu liniowego

najprościej można orzec, znając

jego

transmitancję

lub znając położenie pierwiastków

równania charakterystycznego

(czyli

biegunów

transmitancji

,

wartości własnych

układu).

Krótko mówiąc aby układ był stabilny wszystkie pierwiastki

równania charakterystycznego

układu

zamkniętego

powinny mieć ujemne części rzeczywiste, czyli znajdować się w lewej

półpłaszczyźnie

płaszczyzny zmiennej zespolonej s

.

Ponieważ w rozwiązaniu

równania stanu

pojawiają się składniki zawierające

wyrazy

(zob.

macierz przejścia

) dlatego:

Jeśli wszystkie

wartości własne

układu

mają ujemne części

rzeczywiste

dla

to układ jest stabilny. Ponadto

układ liniowy

jest stabilny

asymptotycznie

wtedy i tylko wtedy, gdy wszystkie bieguny transmitancji leżą w lewej półpłaszczyźnie

zmiennej zespolonej s (tzn. mają ujemną część rzeczywistą). W tym przypadku składowa przejściowa

odpowiedzi

zanika do zera przy

.

Jeśli występują wartości własne o zerowych częściach rzeczywistych (a więc rzeczywiste zerowe lub
czysto urojone) to układ pozostaje stabilny jeśli te wartości są pojedyncze. Wynika to z ograniczoności

wyrażeń

lub

. Nie zachodzi tu jednak warunek stabilności asymptotycznej.

Innymi słowy

układ liniowy

jest na granicy stabilności, jeżeli jeden jego biegun leży na osi urojonej, a

reszta biegunów - w lewej półpłaszczyźnie zmiennej zespolonej.

Jeśli choć jedna wartość własna układu ma dodatnią część rzeczywistą to układ jest
niestabilny.

Układ liniowy

jest niestabilny, jeżeli co najmniej jeden jego biegun leży w prawej

półpłaszczyźnie zmiennej zespolonej s lub więcej niż jeden biegun znajduje się na osi urojonej. Jeśli
wartość własna przy

jest wielokrotna, to w rozwiązaniu pojawiają się człony

typu

, itd., w zależności od krotności wartości własnej, co sprawia że rozwiązania

stają się nieograniczone. W tym przypadku składowa przejściowa odpowiedzi

rośnie do

nieskończoności przy

.

Kryterium stabilności Hurwitza jest metodą pozwalającą określić

stabilność układu regulacji

na

podstawie

równania charakterystycznego

układu

o współczynnikach

rzeczywistych.

Z punktu widzenia algebry kryterium Hurwitza pozwala sprawdzić, czy wszystkie pierwiastki
równania charakterystycznego leżą w lewej półpłaszczyźnie

zmiennej zespolonej

, co pociąga za

sobą stabilność układu

Kryterium logarytmiczne Nyquista

Układ zamknięty

jest stabilny, jeżeli

logarytmiczna charakterystyka amplitudowa

układu

otwartego

posiada wartość ujemną dla

pulsacji

odpowiadającej

przesunięciu fazowemu

.

2) kryteria graficzne -

stosowane w przypadku znajomości analitycznej postaci transmitancji układu

otwartego to

metoda linii pierwiastkowych

.

Transformata Z (transformata Laurenta) jest odpowiednikiem

transformaty Laplace'a

stosowanym do

opisu i analizy

układów dyskretnych

.

Powiązanie z transformatą Fouriera

Transformata Z stanowi uogólnienie

dyskretnej transformaty Fouriera

. Dyskretna transformata

Fouriera może być określona przez określenie wartości transformaty Z

dla

lub

innymi słowy określenie jej wartości na

okręgu jednostkowym

. Aby określić

charakterystykę

częstotliwościową

układu wartość transformaty Z musi być określona na okręgu jednostkowym, co

oznacza, że obszar zbieżności układu musi zawierać okrąg jednostkowy. W przeciwnym
przypadku dyskretna transformata Fouriera nie istnieje.

Transformatą Z dyskretnej (impulsowej) funkcji czasu

jest nazywana funkcja

określona wzorem

,

gdzie:

– transformata oryginału;

– oryginał dyskretny;

.

Transformaty Z istnieją dla funkcji dyskretnych, które nie rosną szybciej niż

funkcja

wykładnicza

, np. dla funkcji

lub

nie istnieją

transformaty Z, ponieważ nie spełniają one powyższego warunku.

Historia transformaty Z:

Zasadnicza idea transformaty znanej dziś jako transformata Z była znana jeszcze przez

Pierre Simon

de Laplace'a

. W

1947

roku transformatę wprowadził ponownie

Witold Hurewicz

jako dogodną metodę

rozwiązywania liniowych równań różniczkowych o stałych współczynnikach. W

1952

roku

John

Ragazzini

i

Lofti Zadeh

pracując z zagdanieniami

układów dyskretnych

w zespole na

Columbia

University

nadali jej nazwę transformaty Z.

Nazwa transformata Z

może pochodzić od litery "z" jako dyskretnej wersji litery "s" często używanej

jako zmienna ni

ezależna w

transformacie Laplace'a

co wydaje się zasadne jako, że transfomata Z jest

w istocie dyskretną wersją transformaty Laplace'a. Inne możliwe pochodzenie to litery "z" w
nazwiskach badaczy (Ragazzini, Zadeh) którzy opublikowali fundamentalny artykuł na jej temat. Tym
niemniej nazwa odbiega od powszechie przyjętej konwencji praktykowanej w świecie nauki by do
metod lub twierdzeń stosować nazwy związane z ich pierwszymi badaczami (na przykład transformata
Fouriera, transformata Laplace'a, transformata Hartley'a, itp).Nieco później E.I. Jury wprowadził i
spopularyzował

zmodyfikowaną transformatę Z

.Idea zawarta w transformacie Z w literaturze

matematycznej znana jest jako metoda

funkcji tworzących

, która to datuje się na rok

1730

kiedy to

została wprowadzona przez

Abrahama de Moivre

w powiązaniu z teorią prawdopodobieństwa.

Z matematycznego punktu widzenia transformatę Z można także traktować jako

szereg

Laurenta

gdzie występuje szereg liczb jako rozwinięcie (Laurenta) funkcji analitycznej.