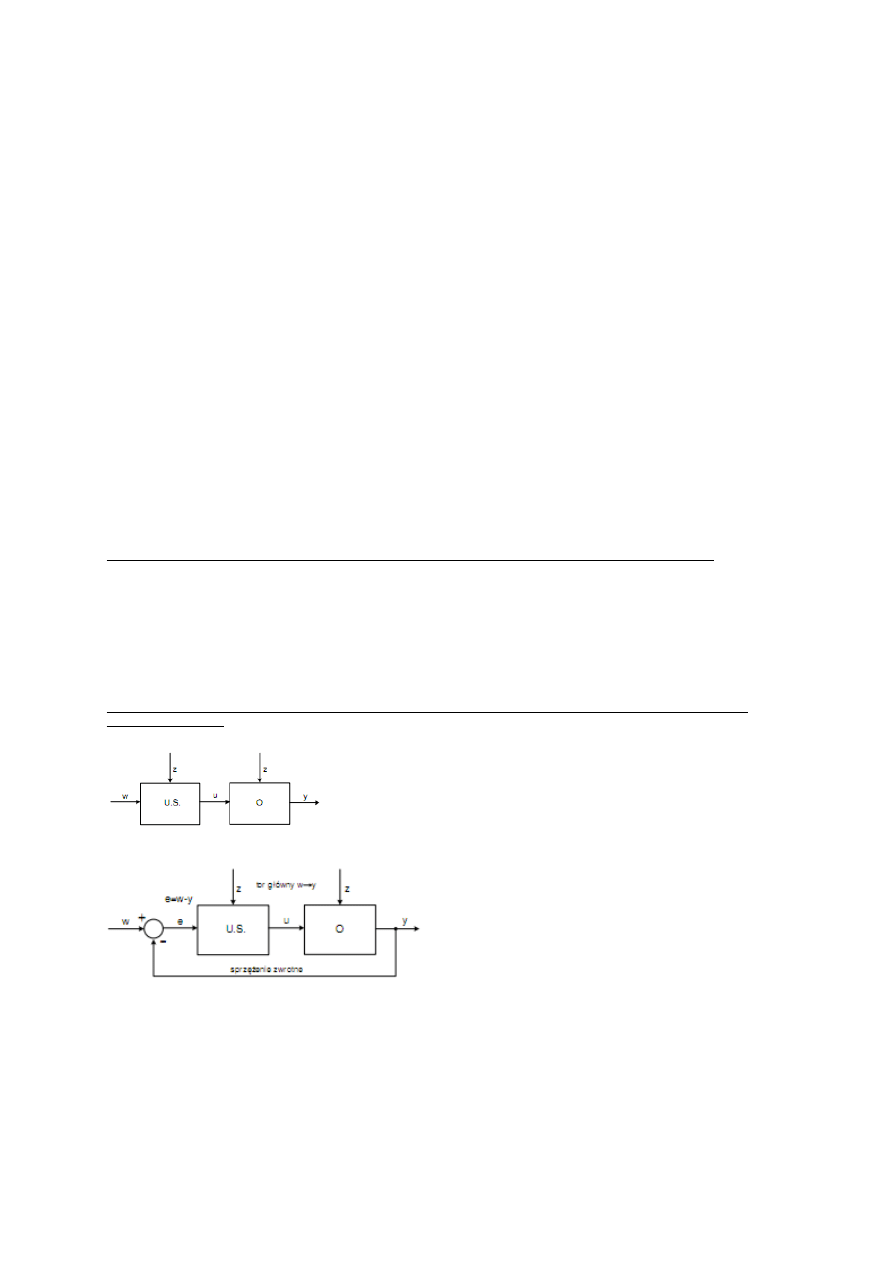
ZAGADNIENIA:
1. Klasyfikacja automatyki (mechanizacja, automatyzacja, robotyzacja, automat, uklad automatyki, sygnal, atrybuty sygnalu).
2. Schemat blokowy, rodzaje wezlow, uklad otwarty regulacji, uklad zamkniety, warunek konieczny poprawnego dzialania ukladu ze
sprzezeniem zwrotnym.
3. Podział automatyki ze wzgledu na postac sygnalu:
-uklady dyskretne (impulsowe i przelaczajace),
-uklady ciagle (liniowe i nieliniowe).
UKŁADY PRZEŁACZAJACE
4. Układy przełaczajace. Definicja automatu kombinacyjnego i sekwencyjnego, pamiec, uklady synchroniczne i asynchroniczne.
5. Kody liczbowe (binarny, szesnastkowy, dziesietny). Dzialania na liczbach binarnych. Algebra Bool'a, funkcja przelaczajaca, postac
kanoniczna, metody minimalizacji Karnaugh'a. System funkcjonalnie pelny (SFP), graficzna interpretacja funkcji logicznych. Synteza
ukladow przelaczajacych kombinacyjnych. Zjawisko hazardu (metody usuwania).
6. Elementy funkcjonalne ukladow przelaczajacych:
-stykowe (przekazniki),
-bezstykowe (elektroniczne i inne),
-hydrauliczne, pneumatyczne.
7. Uklady logiczne i bloki funkcjonalne ukladow przelaczajacych (przerzutniki, liczniki, konwentery kodow, rejestry, sumatory, kompatory i
inne).
UKLADY CIAGLE
8. Uklady liniowe. Modele matematyczne, transformacja Laplace'a, transmitancja operatorowa, odpowiedz na typowe wymuszenia.
9. Klasyfikacja ukladow liniowych ze wzgledu na wlasnosci dynamiczne.
10. Charakterystyki skokowe podstawowych czlonow liniowych.
11. Polaczenia czlonow liniowych, transmitancja zastepcza. Przeksztalcenia schematow blokowych, polaczenia rownowazne.
12. Charakterystyki czestotliwosciowe (podstwy teoretyczne, transformacja Fouriere, rodzaje charakterystyk. Charakterystyki
czestotliwosciowe podstawowych liniowych czlonow automatyki. Charakterystyki przyblizone - asymptotyczne.
13. Regulatory ciagle, regulatory PID (transmitancje, opis parametrow).
14. Wymagania stawiane uklada regulacji (URA).
15. Stabilnosc asymptotyczna (twierdzenia podstawowe, kryterium Hurwitza i Nyquista, logarytmiczne kryteria stabilnosci, zapis
stabilnosci).
16. Stany ustalone, uklady statyczne i astatyczne.
17. Wskazniki dotyczace cech odpowiedzi skokowej i charakterystyk czestotliwosciowych, calkowe wskazniki jakosciu URA.

1. Klasyfikacja automatyki (mechanizacja, automatyzacja, robotyzacja, automat, uklad automatyki, sygnal, atrybuty sygnalu).
Układ automatyki - zespół wzajemnie powiązanych elementów biorących udział w sterowaniu automatycznym danego procesu
(uporządkowany zgodnie z kierunkiem przekazywania sygnałów)
Automat - urządzenie, maszyna lub ich zestaw, wykonujące samoczynnie cykl czynności lub operacji określony konstrukcją lub programem,
nie wymagające bezpośredniego udziału człowieka.
Sygnał - wielkość fizyczna występująca w procesie sterowania będąca nośnikiem informacji.
mechanizacja zastąpienie pracy ręcznej pracą maszyn
automatyzacja praktyczne zastosowanie automatyki, dyscypliny naukowej, zajmującej się teorią i realizacją urządzeń sterujących procesami
(technologicznymi) bez udziału (a. z niewielkim udziałem) człowieka
robotyzacja, wprowadzanie do procesu produkcyjnego manipulatorów, robotów i urządzeń towarzyszących (podajniki, palety, magazyny
produktów) w celu wykonywania operacji procesu z ograniczonym udziałem lub bez udziału człowieka
2. Schemat blokowy, rodzaje wezlow, uklad otwarty regulacji, uklad zamkniety, warunek konieczny poprawnego dzialania ukladu ze
sprzezeniem zwrotnym.
Ogólny schemat otwartego układu sterowania przedstawiono niżej:

w - wartość zadana wielkości sterowanej
u - sygnał sterujący
y - wielkość sterowana

z - sygnały zakłócające (zakłócenia)
U.S. - urządzenie sterujące
O - obiekt (proces) podlegający sterowaniu

Zamknięty układ sterowania, nazywany często układem ze sprzężeniem zwrotnym, ma następujący schemat blokowy:

e - odchyłka (uchyb) sterowania

Tor główny wskazuje zawsze zasadniczą wielkość wejściową układu (w
tym przypadku w) i wielkość wyjściową y. Tor ten ilustruje zwykle
przepływ głównego strumienia materiału lub energii w układzie.
Tor sprzężenia zwrotnego służy do przekazywania informacji.
Zapotrzebowanie energetyczne tego toru jest zwykle pomijanie małe.
???Warunkiem koniecznym i dostatecznym stabilności liniowych
układów automatyki jest, aby pierwiastki układu zamkniętego leżały w

lewej półpłaszczyźnie zmiennej zespolonej s tzn. miały części rzeczywiste α

i

<0, (i = 1, 2 , ... , n).???

Schematy blokowe, nazywane również strukturalnymi, przedstawiają wzajemne powiązania pomiędzy poszczególnymi zespołami
analizowanego elementu lub układu, tzn. podają kierunki przepływu sygnałów oraz związki między sygnałami wejściowymi i
wyjściowymi wszystkich zespołów. Znajomość schematu blokowego ułatwia wyznaczenie opisu matematycznego (najczęściej
transmitancji) układu i analizę jego własności.
W celu minimalizacji elementów układu automatyki oraz uwidocznienia zależności poszczególnymi członami i kierunku przepływu
sygnałów posługujemy się tzw. schematem blokowym. Przedstawione są w formie prostokątów zwanych blokami, a sygnały w formie lini
łączących poszczególne bloki. Miejsca połączeń sygnałów noszą nazwę więzów: -sumacyjnych- gdzie sygnały ulegają algebraicznemu
sumowaniu; -informacyjnych- gdzie sygnały rozpływają się nie zmieniając swojej wartości

Rodzaje węzłów:

a) Węzły informacyjne (zaczepowe) reprezentują na schematach blokowych urządzenia, które pozwalają pobierać tę samą informację do
kilku gałęzi układu

a)

b)

b) Węzły sumacyjne reprezentują na schematach blokowych urządzenia, w których zachodzi algebraiczne (z uwzględnieniem znaków)
sumowanie sygnałów.
3. Podział automatyki ze wzgledu na postac sygnalu:
-uklady dyskretne (impulsowe i przelaczajace),
-uklady ciagle (liniowe i nieliniowe).
Układami dyskretnymi regulacji automatycznej nazywamy układy, w których informacja jest przekazywana za pomocą sygnałów
dyskretnych (nieciągłych) w poziomie lub w czasie.
Układy z kwantowaniem sygnału w czasie nazywa się układami impulsowymi. W układach tych informacja przekazywana jest
tylko w dyskretnych chwilach, tzw. chwilach impulsowania.
W układach impulsowych liniowych wartości sygnałów w dyskretnych chwilach czasu są związane zależnościami liniowymi.
Układy przełączające – regulacja odbywa się na zasadzie załączania lub wyłączania odpowiednich urządzeń procesu w odpowiedniej
kolejności (sekwencji), a rolę regulatora pełni najczęściej układ logiczny. Rozróżnia się dwie grupy układów: kombinacyjne i sekwencyjne.
Mówiąc krótko, układy kombinacyjne to takie, w których stan sygnałów wyjściowych w danej chwili zależy tylko od stanu sygnałów
wejściowych w danej chwili. Układy sekwencyjne to takie, w których stan sygnałów wyjściowych w danej chwili zależy od stanu sygnałów
wejściowych w danej chwili oraz od stanu sygnałów wyjściowych w chwili poprzedniej.
Układy ciągłe – wszystkie sygnały (wejściowe i wyjściowe) są funkcjami ciągłymi w czasie i mogą przybierać dowolną wartość z obszaru
swojej zmienności. Układy te opisuje się zwykle równaniami różniczkowymi.
Układy liniowe – można je opisać za pomocą równań liniowych algebraicznych, różniczkowych, różnicowych lub całkowych. Układy
liniowe spełniają zasadę superpozycji.
Układy nieliniowe – układ zawierający przynajmniej jeden element nieliniowy jest układem nieliniowym. W praktyce każdy układ jest
nieliniowy, lecz w przybliżeniu zakłada się jego liniowość lub linearyzuje się jego nieliniową charakterystykę. Robi się to zwłaszcza gdy
działanie procesu ogranicza się do niewielkiego obszaru wokół pewnego punktu pracy.
4. Układy przełaczajace. Definicja automatu kombinacyjnego i sekwencyjnego, pamiec, uklady synchroniczne i asynchroniczne.
Układ kombinacyjny jest układem przełączającym (automatem cyfrowym) służącym do przetwarzania sygnałów dwuwartościowych.
Sygnały wejściowe układu mogą pochodzić z czujników, wyłączników, przycisków itp. Sygnały wyjściowe mogą sterować np. lampkami
sygnalizacyjnymi. Stan wyjść układu kombinacyjnego zależy tylko od aktualnego stanu wejść. Charakteryzuje się brakiem pamięci, która
umożliwiłaby zapamiętywanie poprzednich stanów wejść.Zatem: wyjścia układu kombinacyjnego zależą (sa funkcją) tylko od wejść.
Układ sekwencyjny jest jednym z rodzajów układów cyfrowych. Charakteryzuje się tym, że stan wyjść y zależy od stanu wejść x oraz od
poprzedniego stanu, zwanego stanem wewnętrznym, pamiętanego w zespole rejestrów (pamięci). Jeżeli stan wewnętrzny nie ulega zmianie
pod wpływem podania różnych sygnałów X, to taki stan nazywa się stabilnym.
Rozróżnia się dwa rodzaje układów sekwencyjnych: asynchroniczne, synchroniczne
Pamięć jest to zdolność do rejestrowania i ponownego przywoływania zadań
W układach synchronicznych - zmiana sygnału wyjściowego następuję wyłącznie w określonych chwilach, które wyznacza sygnał
zegarowy (ang. clock). Każdy układ synchroniczny posiada wejście zegarowe oznaczane zwyczajowo symbolami C, CLK lub CLOCK.
Charakterystyczne dla układów synchronicznych, jest to, iż nawet gdy stan wejść się nie zmienia, to stan wewnętrzny - w kolejnych taktach
zegara - może ulec zmianie.
Jeśli układ synchroniczny nie ma wejść, a jedynie charakteryzuje go stan wewnętrzny, to taki układ nazywany jest autonomicznym (dobrym
przykładem takich układów są liczniki stosowane w popularnych zegarkach elektronicznych).
Jeśli układ reaguje na określony stan (logiczny) zegara, to mówi się że układ jest statyczny (wyzwalany poziomem), jeśli zaś układ reaguje
na zmianę sygnału zegarowego jest dynamiczny (wyzwalany zboczem). Układ dynamiczny może być wyzwalany zboczem (ang. edge)
opadającym lub narastającym, albo impulsem.
W układach asynchronicznych zmiana sygnałów wejściowych X natychmiast powoduje zmianę wyjść Y. W związku z tym układy te są
szybkie, ale jednocześnie podatne na zjawisko hazardu i wyścigu. Zjawisko wyścigu występuje, gdy co najmniej dwa sygnały wejściowe
zmieniają swój stan w jednej chwili czasu (np. ). Jednak, ze względu na niezerowe czasy przełączania bramek i przerzutników, zmiana
jednego z sygnałów może nastąpić [trochę] wcześniej niż innych, powodując trudne do wykrycia błędy. Dlatego też w analizie układów
asynchronicznych uznaje się, że jednoczesna zmiana kilku sygnałów jest niemożliwa.
5. Kody liczbowe (binarny, szesnastkowy, dziesietny). Dzialania na liczbach binarnych. Algebra Bool'a, funkcja przelaczajaca, postac
kanoniczna, metody minimalizacji Karnaugh'a. System funkcjonalnie pelny (SFP), graficzna interpretacja funkcji logicznych. Synteza
ukladow przelaczajacych kombinacyjnych. Zjawisko hazardu (metody usuwania).
binarny to pozycyjny system liczbowy, w którym podstawą jest liczba 2. Do zapisu liczb potrzebne są więc tylko dwie cyfry: 0 i 1.
Powszechnie używany w elektronice cyfrowej, gdzie minimalizacja (do dwóch) liczby stanów pozwala na zminimalizowanie przekłamań
danych. Co za tym idzie, przyjął się też w informatyce.
Jak w każdym pozycyjnym systemie liczbowym, liczby zapisuje się tu jako ciągi cyfr, z których każda jest mnożnikiem kolejnej potęgi
podstawy systemu. 1010=10

Szesnastkowy system liczbowy – pozycyjny system liczbowy, w którym podstawą pozycji są kolejne potęgi liczby 16. Często system
szesnastkowy jest określany nazwą Hex od słowa stworzonego przez firmę IBM hexadecimal. Do zapisu liczb potrzebne jest szesnaście
znaków. Poza cyframi dziesiętnymi od 0 do 9 używa się pierwszych sześciu liter alfabetu łacińskiego: A, B, C, D, E, F.
Jak w każdym pozycyjnym systemie liczbowym, liczby zapisuje się tu jako ciągi znaków, z których każdy jest mnożnikiem kolejnej potęgi
liczby stanowiącej podstawę systemu
Dziesiętny system liczbowy, zwany też systemem decymalnym lub arabskim to pozycyjny system liczbowy, w którym podstawą pozycji są
kolejne potęgi liczby 10. Do zapisu liczb potrzebne jest więc 10 cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Jak w każdym pozycyjnym systemie liczbowym, liczby zapisuje się tu jako ciąg cyfr, z których każda jest mnożnikiem kolejnej potęgi liczby
stanowiącej podstawę systemu. Część całkowitą i ułamkową oddziela separator dziesiętny.
Algebry Boole'a – struktury algebraiczne rozważane w matematyce, informatyce teoretycznej oraz elektronice cyfrowej. Typowymi
przykładami algebr Boole'a są: rodzina wszystkich podzbiorów ustalonego zbioru wraz działaniami na zbiorach jako operacjami algebry oraz
dwuelementowa algebra wartości logicznych {0, 1} z działaniami koniunkcji, alternatywy i negacji.
Teoria algebr Boole'a jest działem matematyki na styku teorii porządków częściowych, algebry, logiki matematycznej i topologii.
Metoda Karnaugh – sposób minimalizacji funkcji boolowskich.

Tablica Karnaugha, to uporządkowany w specyficzny sposób zapis wartości funkcji logicznej. Struktura mapy jest prostokątna, złożona z
elementarnych pól, gdzie każde pole reprezentuje iloczyn pełny w odniesieniu do zmiennych wejściowych, czyli argumentów danej funkcji.
Stąd też tablica ta zawiera wszystkie możliwe kombinacje wartości argumentów. Na marginesach tablicy wpisuje się w określonym porządku
(wg kodu Graya) wartości argumentów. Przy parzystej liczbie argumentów połowa z nich umieszczona jest na marginesie poziomym, a
druga połowa na marginesie pionowym.
Przy nieparzystej liczbie argumentów wpisuje się na jednym marginesie o jeden argument więcej niż na drugim.
Ułożenie tablicy polega na takim zgrupowaniu wszystkich wartości argumentów, aby przy przejściu z danego pola do pola sąsiedniego
zmieniała się wartość tylko jednego argumentu. Ta zasada sąsiedztwa obowiązuje również dla pól leżących przy krawędziach tablicy.
Funkcja przełączająca może być określona z wykresów czasowych, tablic wartości, opisu słownego itp. Najprostszym i najczęściej
stosowanym rodzajem opisu układu kombinacyjnego jest tablica wartości [1,3] (tablica zależności [2]), która ujmuje zależność wartości
zmiennych wyjściowych Y układu kombinacyjnego od wartości zmiennych wejściowych X. Funkcja przełączająca jest opisana przez
przyporządkowanie kolejnym kombinacjom wartości zmiennych wejściowych odpowiednich wartości zmiennych wyjściowych.
Zbiór funkcji boolowskich nazywa się systemem funkcjonalnie pełnym (bazą), jeśli dowolna funkcja boolowska może być przedstawiona
za pomocą stałych 0 i 1 oraz funkcji należących do tego zbioru i argumentów funkcji.
Funkcje sumy, iloczynu i negacji tworzą tzw. podstawowy system funkcjonalnie pełny. Nie jest to jednak system minimalny.
Hazard – niekorzystne zjawisko w układach cyfrowych, którego podłożem jest niezerowy czas propagacji (przenoszenia) sygnałów.
Hazardem nazywamy błędne stany na wyjściach układów cyfrowych, powstające w stanach przejściowych (przełączania) w wyniku
nieidealnych właściwości używanych elementów. Przyczyną są różnice w czasie dotarcia i wartości sygnału do określonego miejsca układu
w zależności od drogi.
Rozróżnia się dwa rodzaje hazardu: statyczny i dynamiczny.
6. Elementy funkcjonalne ukladow przelaczajacych:
-stykowe (przekazniki),
-bezstykowe (elektroniczne i inne),
-hydrauliczne, pneumatyczne.
7. Uklady logiczne i bloki funkcjonalne ukladow przelaczajacych (przerzutniki, liczniki, konwentery kodow, rejestry, sumatory, kompatory i
inne).
Układy cyfrowe to rodzaj układów elektronicznych, w których sygnały napięciowe przyjmują tylko określoną liczbę poziomów, którym
przypisywane są wartości liczbowe. Najczęściej (choć nie zawsze) liczba poziomów napięć jest równa dwa, a poziomom przypisywane są
cyfry 0 i 1, wówczas układy cyfrowe realizują operacje zgodnie z algebrą Boola i z tego powodu nazywane są też układami logicznymi.
Obecnie układy cyfrowe budowane są w oparciu o bramki logiczne realizujące elementarne operacje znane z algebry Boola: iloczyn logiczny
(AND, NAND), sumę logiczną (OR, NOR), negację NOT, różnicę symetryczną (XOR) itp. Ze względu na stopień skomplikowania
współczesnych układów wykonuje się je w postaci układów scalonych.
Zalety układów cyfrowych:
Możliwość bezstratnego kodowania i przesyłania informacji – jest to coś, czego w układach analogowych operujących na nieskończonej
liczbie poziomów napięć nie sposób zrealizować.
Zapis i przechowywanie informacji cyfrowej jest prostsze.
Mniejsza wrażliwość na zakłócenia elektryczne.
Możliwość tworzenia układów programowalnych, których działanie określa program komputerowy (patrz: mikroprocesor, koprocesor).
Wady układów cyfrowych:
Są skomplikowane zarówno na poziomie elektrycznym, jak i logicznym i obecnie ich projektowanie wspomagają komputery (patrz: język
opisu sprzętu).
Chociaż są bardziej odporne na zakłócenia, to wykrywanie przekłamań stanów logicznych, np. pojawienie się liczby 0 zamiast spodziewanej
1, wymaga dodatkowych zabezpieczeń (patrz: kod korekcyjny) i też nie zawsze jest możliwe wykrycie błędu. Jeszcze większy problem
stanowi ewentualne odtworzenie oryginalnej informacji.
Przerzutnik jest to podstawowy element pamiętający każdego układu cyfrowego, przeznaczonego do przechowywania i ewentualnego
przetwarzania informacji. Przerzutnik współtworzy najniższe piętro struktury układu i zdolny jest do zapamiętania jednego bitu informacji.
Grupa czterech lub ośmiu połączonych ze sobą przerzutników tworzy następne, wyższe piętro - tzw. rejestr, zdolny już do pamiętania
jednego bitu informacji., na ogół budowane są na 2 wyjściach i 1 lub 3 wejściach. Rozróżnia się:
a) Przerzutnik RS ma wejście S służące do ustawiania stanu Q — l i wejście R, służące do ustawiania stanu Q = 0. Równoczesne wy-
stępowanie stanu l na wejściach R i S jest zabronione,
b) Przerzutnik JK ma wejścia o roli takiej jak wejść S i R w poprzednim elemencie, z tym że równoczesne występowanie stanu l na
wejściach J i K jest dozwolone; przerzutnik zmienia wtedy swój stan (z 0 na l i z l na 0).
c) Przerzutnik D ma jedno wejście, wartość sygnału wejściowego
(wzbudzenia) jest przekazywana bez zmian na wyjście Q, wobec czego przerzutnik ten działa jak element opóźniający.
Licznik - układ cyfrowy, którego zadaniem jest zliczanie wystąpień sygnału zegarowego (impulsów). Licznik złożony najczęściej z kilku
przerzutników. Działanie licznika cyfrowego opiera się najczęściej na układzie dzielnika częstotliwości.
Konwerterami kodów układy służące do zamiany jednego kodu na drugi są nazywane
a) Koder układ zamieniający liczbę w kodzie „l z n" na binarną (Lp.0123;x3x2x1x0;y2y1)
b) Dekoder konwerter układ zamieniający liczbę binarna na liczbę zapisana w kodzie „1z n" (Lp.0123;x2x1;y3y2y1y0)
Rejestr zespół przerzutników służący do przechowywania informacji w postaci liczb binarnych (zespół 4 przerzutników pozwala na
zapisanie cyfry dziesiętnej)
Sumator układ realizujący sumę arytmetyczną liczb binarnych
Układy porównujące liczby, czyli komparatory, występują w trzech różnych odmianach, sygnalizując występowanie relacji: 1)A=B;A

≠

B 2)

A

≥

B; A <B 3)A>B; A = B; A<B

Komutatory układy służą do selektywnego przełączania sygnałów i dzielą się na dwie grupy.
a) Selektory (demultipleksery) przekazują sygnał wejściowy do jednego z kilku torów wyjściowych, przy czym numer (adres) toru
wyjściowego jest wybierany sygnałami pomocniczymi.
b) Kolektory (multipleksery) przekazują jeden z sygnałów wejściowych (wybrany adresem ) na wyjście układu.
8. Uklady liniowe. Modele matematyczne, transformacja Laplace'a, transmitancja operatorowa, odpowiedz na typowe wymuszenia.
Układy liniowe -Układy rzeczywiste zwykle są nieliniowe, ale dla uproszczenia opisu matematycznego przeprowadza się ich
linearyzację, co pozwala na sformułowanie przybliżonego opisu liniowego, ważnego w otoczeniu wybranego punktu pracy na
charakterystyce statycznejtransformacja Laplace'a jest przekształceniem zbioru funkcji, dla których całka Laplace'a jest zbieżna w zbiór
funkcji zespolonych zmiennej zespolonej. Ogólna postać równania różniczkowego:

Charakterystyka statyczna układu liniowego lub zlinearyzowanego w otoczeniu nominalnego punktu pracy (u,y są odchyłkami od tego
punktu) ma postać:

y=(b

0

/a

0

)u

Początek układu współrzędnych oznacza nominalny punkt pracy, a u i y są
odchyłkami sygnałów od tego punktu.

Typowe wymuszenia:

Transmitancja operatorowa:

+opis na schematach blokowych

Wyznaczenie charakterystyki statycznej z transmitancji operatorowej

Końcowe równanie charakterystyki statycznej dla układów o
jednym wejściu i jednym
wyjściu:

Jednostronną Transformatą Laplace'a funkcji

nazywamy następującą funkcję

:

często zapisywaną, zwłaszcza w środowisku inżynierskim, w następującej formie:

Niech X oznacza przestrzeń funkcji, dla których powyższa całka (zwana całką Laplace'a) jest zbieżna.

Funkcję

nazywamy transformacją Laplace'a

9. Klasyfikacja ukladow liniowych ze wzgledu na wlasnosci dynamiczne.
10. Charakterystyki skokowe podstawowych czlonow liniowych.
11. Polaczenia czlonow liniowych, transmitancja zastepcza. Przeksztalcenia schematow blokowych, polaczenia rownowazne.

Wielkością charakteryzującą człony jest transmitancja zastępcza, czyli
stosunek bezwymiarowych transformat wyjścia do wejścia wyrażająca się

w postaci wzoru:

G(s)=Y(s)/X(s)

G(S) – transmitancja zastępcza członu;
Y(S) – transformata wyjścia;
X(S) – transformata wejścia

12. Charakterystyki czestotliwosciowe (podstwy teoretyczne, transformacja Fouriere, rodzaje charakterystyk. Charakterystyki
czestotliwosciowe podstawowych liniowych czlonow automatyki. Charakterystyki przyblizone - asymptotyczne.
Transformacja Fouriera jest transformacją całkową w dziedzinie częstotliwości. Transformata jest wynikiem transformacji Fouriera
(transformata jest funkcją, a transformacja operacją na funkcji, dającą w wyniku transformatę). Transformata Fouriera opisana jest wzorem:

gdzie

oznacza transformatę dla danej funkcji

pulsacją (proporcjonalną do częstotliwości)

f(t) - funkcję w dziedzinie czasu
i - jednostkę urojoną (i2 = − 1).

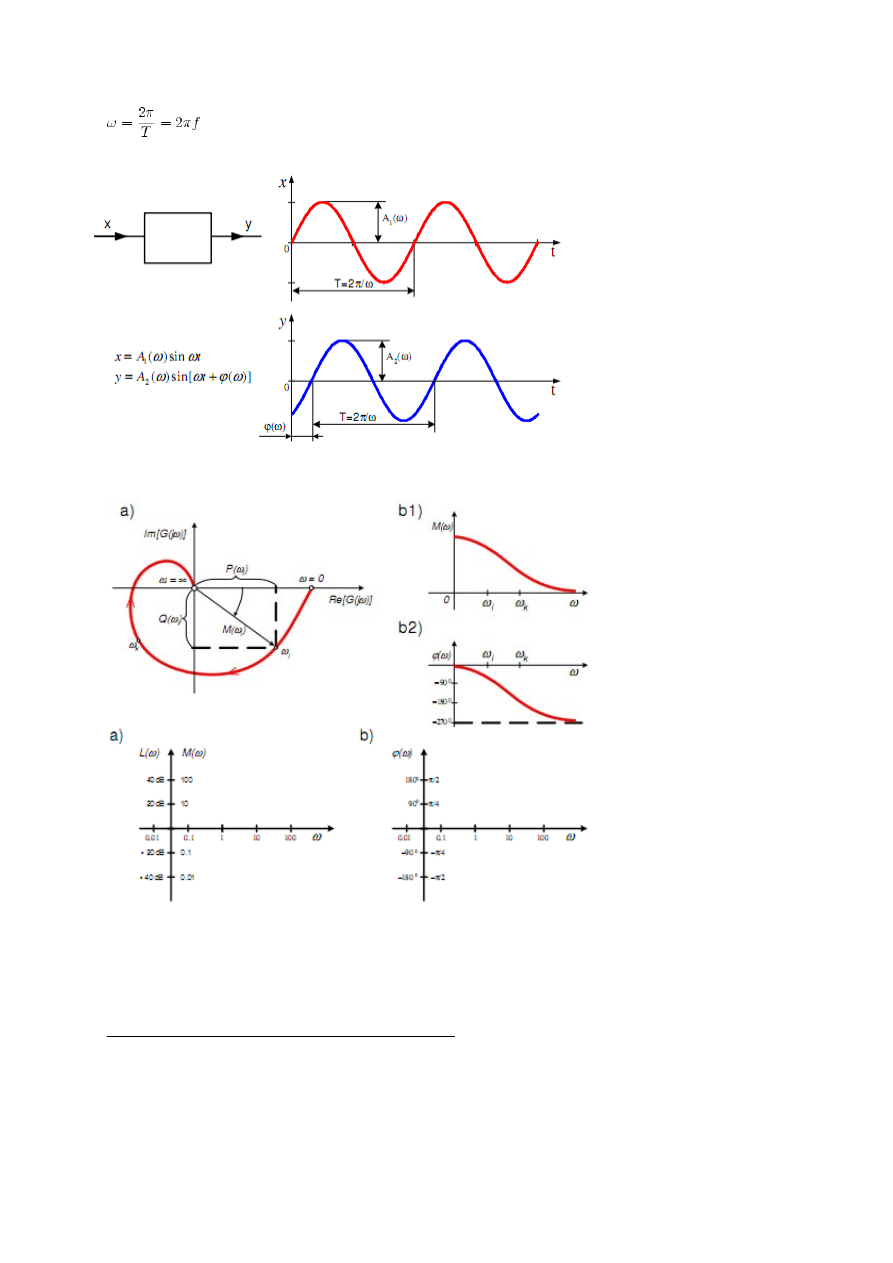
Charakterystyki częstotliwościowe
Jeżeli na wejście elementu lub układu
liniowego stabilnego wprowadzone
zostanie wymuszenie sinusoidalne o
stałej częstotliwości, to na wyjściu, po
zaniknięciu przebiegu przejściowego,
ustali się odpowiedź sinusoidalna o tej
samej częstotliwości, ale w ogólnym
przypadku, o innej amplitudzie i fazie niż
wymuszenie. Na rysunku przedstawiono
przypadek, gdy odpowiedź jest przesunięta
w kierunku ujemnym względem
wymuszenia, tzn. 0 ) ( < ω

ϕ .

Charakterystyki częstotliwościowe
określają zachowanie się elementu lub
układu przy wszystkich częstotliwościach

wymuszenia, podając stosunek amplitud odpowiedzi do wymuszenia oraz przesunięcie fazowe między odpowiedzią a wymuszeniem
jako funkcje
częstotliwości.

Charakterystyki częstotliwościowe:
a) charakterystyka amplitudowo-
fazowa (zespolona
charakterystyka częstotliwościowa),
bl) charakterystyka amplitudowa, b2)
charakterystyka fazowa

Współrzędne logarytmicznych
charakterystyk amplitudowej L(ω) i
fazowej

ϕ (ω)

Rodzaje:
Logarytmiczne charakterystyki amplitudowa i fazowa elementu inercyjnego pierwszego rzędu
Charakterystyka amplitudowo-fazowa elementu inercyjnego pierwszego rzędu
Charakterystyka amplitudowo-fazowa oraz logarytmiczne charakterystyki amplitudowa i fazowa elementu różniczkującego rzeczywistego
Charakterystyka amplitudowo-fazowa oraz logarytmiczne charakterystyki amplitudowa i fazowa elementu drugiego rzędu
Logarytmiczna charakterystyka amplitudowa elementu oscylacyjnego
Asymptotyczna charakterystyka amplitudowa elementu oscylacyjnego
Logarytmiczna charakterystyka fazowa elementu oscylacyjnego
13. Regulatory ciagle, regulatory PID (transmitancje, opis parametrow).
Regulator - [łac.] urządzenie sterujące, które stosownie do różnicy wartości między wielkościami zadanymi a mierzonymi tak
oddziałuje na obiekt sterowania (regulacji) za pomocą wielkości sterujących, aby wielkości regulowane miały pożądane wartości.
a) PROPORCJONALNY „P” – posiada właściwości członu proporcjonalnego.
b) CAŁKUJĄCY „I” – posiada właściwości członu całkującego.
c) RÓŻNICZKUJĄCY „D” – posiada właściwości członu różniczkującego.
d) PROPORCJONALNO – CAŁKUJĄCY „PI”
e) PROPORCJONALNO – RÓŻNICZKUJĄCY „PD”
f) PROPORCJONALNO – CAŁKUJĄCO – RÓŻNICZKUJĄCY „PID”

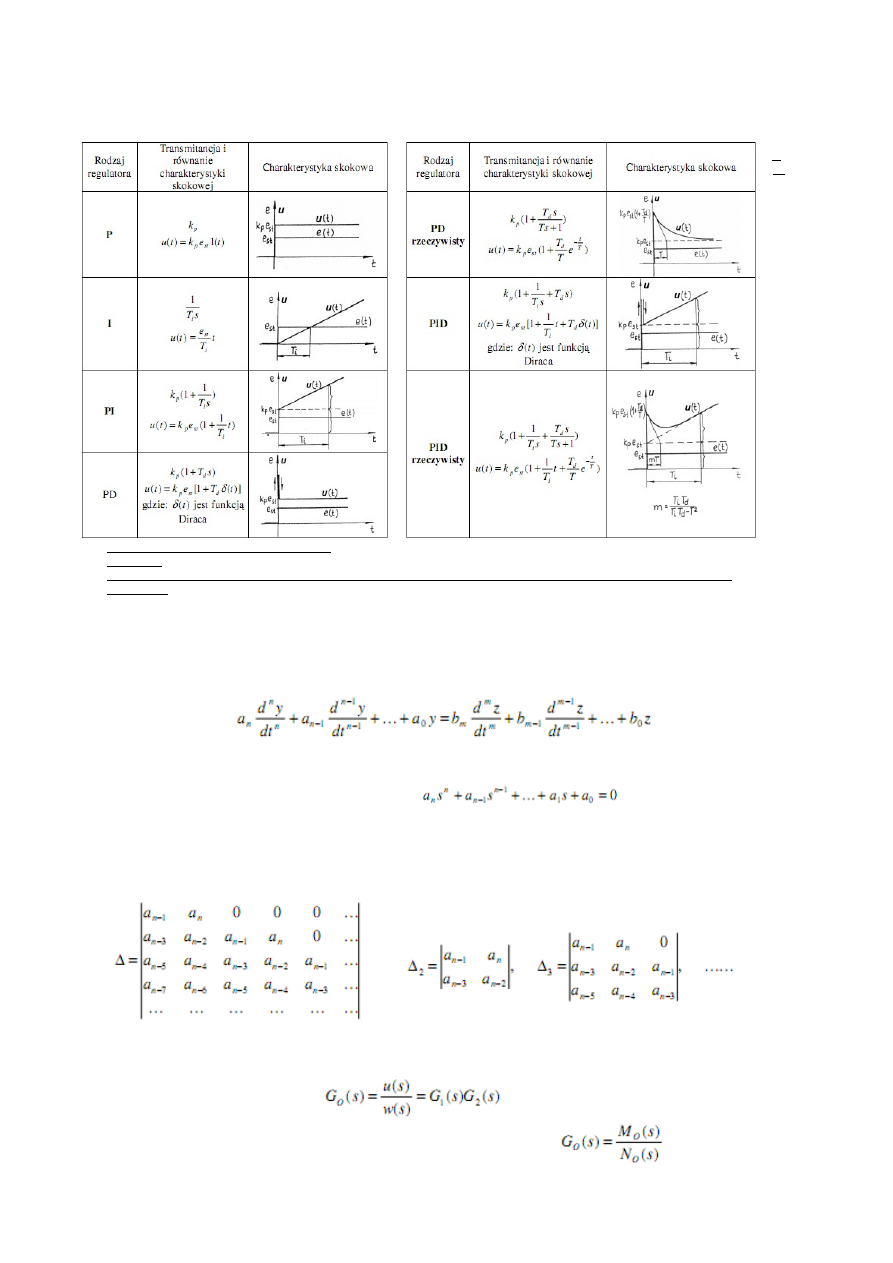
Podstawowe rodzaje regulatorów o działaniu ciągłym lub quasi-ciągłym realizują funkcje PID (działania: P – proporcjonalne, I – całkujące,
D – różniczkujące).

1
4.

Wymagania stawiane uklada regulacji (URA).
Żelazny 70
15. Stabilnosc asymptotyczna (twierdzenia podstawowe, kryterium Hurwitza i Nyquista, logarytmiczne kryteria stabilnosci, zapis
stabilnosci).
Stabilność jest cechą układu, polegającą na powracaniu do stanu równowagi stałej po ustaniu działania zakłócenia, które wytrąciło układ z
tego stanu.
Zamknięty układ liniowy będziemy więc uważać za stabilny, jeżeli przy każdej skończonej wartości zakłócenia z(t) i wartości
zadanej w(t) oraz dla dowolnych warunków początkowych sygnał wyjściowy y(t) dążyć będzie do skończonej wartości ustalonej dla
czasu t dążącego do nieskończoności. Niekiedy precyzuje się dodatkowo, że gdy po zaniknięcie zakłócenia układ powraca do tego
samego stanu równowagi co zajmowany poprzednio, wówczas jest stabilny asymptotycznie. Przykłady przebiegów y(t)
występujących w układach stabilnych i niestabilnych . Jeżeli układ zamknięty opisany jest za pomocą liniowego równania różniczkowego:

Koniecznym i dostatecznym warunkiem stabilności asymptotycznej układu jest, aby pierwiastki równania charakterystycznego
układu zamkniętego miały ujemne części rzeczywiste.

Re(s

k

)<0

Kryterium Hurwitza
Aby wszystkie pierwiastki równania charakterystycznego

miały części rzeczywiste ujemne, muszą być spełnione następujące warunki:
a) wszystkie współczynniki równania istnieją i są większe od zera (jest to warunek konieczny, ale nie dostateczny)

a

n

>0, a

n-1

>0, …a

0

>0

b) podwyznaczniki ∆i, od i=2 do i=n-1, wyznacznika głównego ∆n są większe od zera. Wyznacznik ∆n, utworzony ze współczynników
równania ma n wierszy i n kolumn:

Podwyznaczniki mają postać:

Kryterium Nyquista ma duże znaczenie praktyczne, ponieważ pozwala badać stabilność układu zamkniętego na podstawie
przebiegu charakterystyki częstotliwościowej układu otwartego, którą można wyznaczyć zarówno analitycznie, jak i doświadczalnie.
Rozpatrzmy układ liniowy o schemacie blokowym przedstawionym poniżej:

Transmitancja układu otwartego wynosi

Przedstawiając tę transmitancję w postaci ilorazu wielomianów zmiennej s otrzymamy:

(przy czym mianownik = 0)
jest równaniem charakterystycznym układu otwartego; zakładamy, że stopień tego równania równa się n.
Transmitancja układu zamkniętego wynosi

Równanie charakterystyczne układu zamkniętego ROWN jest również stopnia n, ponieważ stopień MO(s) nie jest nigdy większy od stopnia
N

0

(s).

Jeżeli otwarty układ regulacji automatycznej jest stabilny i jego charakterystyka amplitudowo-fazowa GO(jω) dla pulsacji ω od 0
do +∞ nie obejmuje punktu (-1,j0), to wtedy i tylko wtedy po zamknięciu będzie on również stabilny.
Jeżeli otwarty układ regulacji automatycznej jest niestabilny i ma m pierwiastków swego równania charakterystycznego w prawej
półpłaszczyźnie zmiennej s, to po zamknięciu będzie on stabilny wtedy i tylko wtedy, gdy charakterystyka amplitudowo-fazowa
układu otwartego dla pulsacji ω od 0 do +∞ okrąża m/2 razy punkt (-1,j 0) w kierunku dodatnim (przeciwny do wskazówek zegara)
Zamknięty układ regulacji automatyczne jest stabilny wtedy, gdy logarytmiczna charakterystyka amplitudowa stabilnego układu
otwartego ma wartość ujemną przy pulsacji odpowiadającej przesunięciu fazowemu -180stopni.
Stabilność Hurwitza
Równanie charakterystyczne o postaci

ma wszystkie pierwiastki na płaszczyźnie zmiennej zespolonej z wewnątrz okręgu o promieniu r = 1 ( w lewej półpłaszczyźnie w)
wtedy i tylko wtedy, gdy wszystkie wyrazy ciągu ∆1, ∆2,…, ∆k są dodatnie

16. Stany ustalone, uklady statyczne i astatyczne.
Układ statyczny - układ regulacji (np. z regulatorem P lub PD), w którym uchyb ustalony jest proporcjonalny do wartości wymuszenia w
postaci skokowej funkcji Heaviside'a.
Układ astatyczny - układ regulacji (np. z regulatorem PI lub PID), w którym uchyb ustalony jest równy 0, niezależnie od wartości
wymuszenia w postaci skokowej funkcji Heaviside'a.
W układach astatycznych występują uchyby ustalone przy pobudzeniach w postaci funkcji rosnących liniowo i parabolicznie.
17. Wskazniki dotyczace cech odpowiedzi skokowej i charakterystyk czestotliwosciowych, calkowe wskazniki jakosciu URA.
Wskaźniki dotyczące cech odpowiedzi skokowej
A. Czas regulacji t

r

- Jest to czas liczony od chwili wystąpienia zakłócenia do chwili, po której odchyłka regulacji e jest stale

mniejsza od |∆e|. Często przyjmuje się ∆e=5% e

m

. Podana definicja jest umowna, oparta na wynikach eksperymentów i obserwacji

zachowania układów rzeczywistych.
B. Odchyłka maksymalna e

m

- Jest to największa wartość odchyłki e(t), czyli różnicy między y(t) i w(t), występująca podczas przebiegu

przejściowego (dla 0 ≤ t ≤ ∞)
C. Przeregulowanie

Dość często e

1

= e

m

, ale zapis powyższy jest poprawny tylko dla przebiegów w układach z regulatorem

astatycznym (z akcją I), a dla pozostałych przypadków należałoby napisać:

Wskaźniki częstotliwościowe
a) Pasmo przenoszenia
• definicja: jest to zakres częstotliwości, w którym spełnione są wymagania dotyczące stosunku amplitud wyjścia do wejścia
(modułu) oraz przesunięcia fazowego pomiędzy wyjściem a wejściem
• interpretacja na wykresach charakterystyk częstotliwościowych

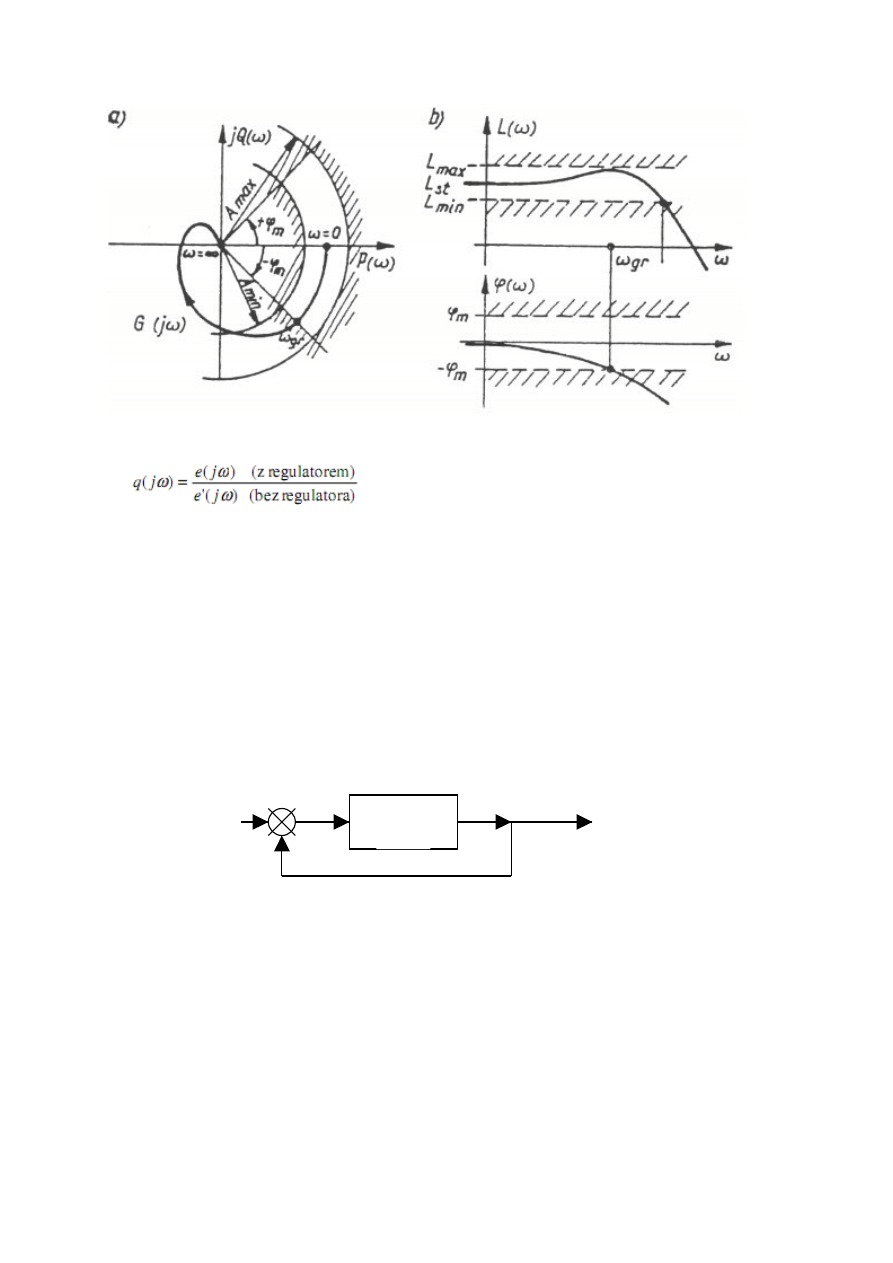
pasmo przenoszenia: 0 ≤ ω ≤ ω

gr

b) Wskaźnik regulacji (wskaźnik skuteczności regulacji)

Wymagania: q(jω)<1 dla zakresu częstotliwości pracy układu, im mniejsza jest wartość q(jω) tym skuteczniejsze oddziaływanie
regulatora

1. Przedstaw schemat montażowy realizacji funkcji NOR/NAND i podtrzymania sygnału na elementach stykowych
2. Pojęcie sygnału, co to jest element i układ liniowy automatyki, zdefiniuj charakterystyki: statyczną i skokową układu automatyki, podaj
definicję transmitancji operatorowej liniowego układu automatyki
3. Jakie są rodzaje charakterystyk częstotliwościowych, naszkicuj przykładowe układy współrzędnych i przykładowe charakterystyki
4. Wyznacz pulsację sprzęgającą Ws (podaj jednostki) dla członu o transmitancji operatorowej:

G(s)=10/(0,01s+1)

Oblicz jaja częstotliwość jej odpowiada (Hz), narysuj przybliżoną, częstotliwościową, logarytmiczną charakterystykę amplitudową tego
członu
5. Podaj definicję asymptotycznej stabilności układu liniowego automatyki oraz określ kryterium Hurwitza stabilności asymptotycznej tego
układu, zbadaj metodą Hurwitza stabilność tego układu na poniższym schemacie blokowym.

G

3

=(2(s+0,2))/((s

2

+1)(s+1))

-

Element automatyki - podstawowy element mechanizmu, dla którego można określić sygnał wejściowy i sygnał wyjściowy.
Charakterystyka statyczna – w automatyce, zależność między sygnałem wyjściowym y, a sygnałem wejściowym x w stanie ustalonym. W
odróżnieniu od wykresów charakterystyk dynamicznych (skokowej, impulsowej), wykres charakterystyki statycznej nie jest zależny od
czasu.
Charakterystyka skokowa (odpowiedź skokowa) – w automatyce, odpowiedź układu na wymuszenie w postaci skoku jednostkowego przy
zerowych warunkach początkowych. Przedstawia przebieg sygnału wyjściowego układu w stanie nieustalonym. Wraz z charakterystyką
impulsową oraz charakterystykami częstotliwościowymi stanowi podstawowy opis działania układu.

y(t)

y(t)

G

3