II pracownia fizyczna

Określenie struktury

krystalograficznej powierzchni

grafitu i sprawdzenie praw

rządzących prądem tunelowym za

pomocą skaningowego mikroskopu

tunelowego (STM)

Paweł Laskoś-Grabowski

prowadzący: prof. Jerzy Czyżewski

20-27 marca 2007

Rozdział 1

Wstęp teoretyczny

1.1

Zjawisko tunelowe

Przyjrzymy się rozwiązaniom stacjonarnego, jednowymiarowego równania Schr¨

odingera

−

~

2

2m

d

2

dx

2

+ V (x)

!

ψ = Eψ

(1.1)

dla bariery potencjału o skończonej szerokości

V (x) =

(

V

0

,

gdy 0 ¬ x ¬ a

0

w p. p.

(1.2)

gdzie V

0

> 0. Szczególnie interesujący jest przypadek, gdy rozpatrzymy przypadek 0 <

E < V

0

, czyli cząstkę o energii mniejszej niż wysokość bariery. Wtedy rozwiązanie ma

postać

ψ(x) =











e

ikx

+ Ae

−ikx

,

gdy x < 0

Be

iηx

+ Ce

−iηx

,

gdy 0 ¬ x ¬ a

De

ikx

,

gdy x > a

(1.3)

gdzie

k =

√

2mE

~

,

(1.4)

η =

p

2m(V

0

− E

~

.

(1.5)

Z warunków zszycia (równość lewostronnych i prawostronnych granic ψ,

dψ

dx

w punktach

x = 0, a) otrzymujemy (za [3]):

A =

(η

2

+ k

2

) sinh aη

(k

2

− η

2

) sinh aη + 2iηk cosh aη

(1.6)

B =

(iηk − k

2

)e

−aη

(k

2

− η

2

) sinh aη + 2iηk cosh aη

(1.7)

C =

(iηk + k

2

)e

aη

(k

2

− η

2

) sinh aη + 2iηk cosh aη

(1.8)

D =

2iηke

−iak

(k

2

− η

2

) sinh aη + 2iηk cosh aη

(1.9)

1

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–2–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

Rysunek 1.1: Uproszczony schemat zjawiska opisanego w części 1.1. Obraz zaczerpnięty
z [5]

Wobec przyjęcia amplitudy fali padającej za 1, współczynniki odbicia i przejścia równe są
po prostu R = |A|

2

, T = |D|

2

. Zauważmy, że w przypadku, w którym klasyczna cząstka nie

przeszłaby bariery potencjału, otrzymujemy niezerowe prawdopodobieństwo pojawienia się
cząstki za barierą. Zjawisko to nazywa się efektem tunelowym i jest jedną z kanonicznych
konsekwencji teorii kwantowej.

1.2

Zjawisko piezoelektryczne

Terminem piezoelektryczność określa się zjawisko występujące w niektórych krysz-

tałach, polegające na wytworzeniu na ich brzegach różnicy potencjałów pod wpływem
mechanicznego naprężenia. Występuje również efekt odwrotny, polegający na deforma-
cji kryształów pod wpływem przyłożonego do nich napięcia. Materiały, w których takie
zjawiska są obserwowane, nazywa się piezoelektrykami – są to zazwyczaj kryształy nie
posiadające środka symetrii. Typowe piezoelektryki to kwarc, turmalin, topaz.

Zjawisko piezoelektryczne wykorzystuje się szeroko w przemyśle i nauce. Efekt pie-

zoelektryczny prosty zastosowany jest m. in. w pewnego typu zapalniczkach – powstałe
na ściśniętym krysztale napięcie wywołuje iskrę zapalającą gaz. W bardziej wyrafinowany
sposób zjawisko to wykorzystano w gramofonach – ruchy igły w rowku płyty powodują
deformację kryształu, do którego igła jest zamocowana, te zaś pozwalają z powstałych
napięć odtworzyć dźwięk. Efekt piezoelektryczny odwrotny umożliwia bardzo precyzyjne
sterowanie sensorami i sondami na poziomie nano – przykładanie do specjalnie uformo-
wanego kryształu napięć w różnych kierunkach powoduje jego odpowiednie odkształcenia,
w związku z czym nieumocowany koniec kryształu przemieszcza się.

1.3

Własności grafitu

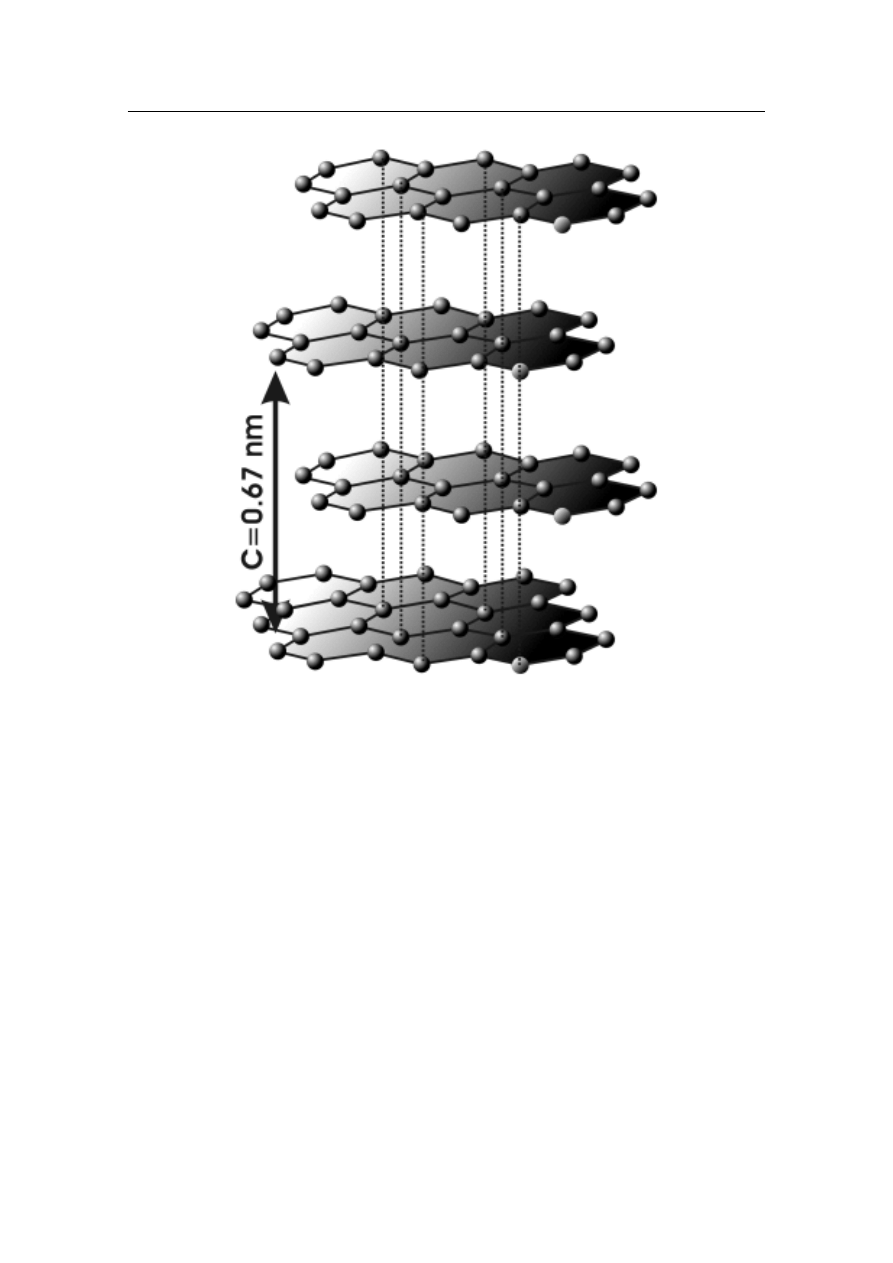
Grafit jest jedną z odmian alotropowych węgla (obok diamentu i fulerenów). Charak-

teryzuje się unikalną strukturą krystaliczną (rys. 1.2). Atomy węgla w strukturze grafitu
są ułożone w równoległych płaszczyznach, w obrębie których są powiązane wiązaniami
kowalencyjnymi i tworzą siatkę sześciokątną. Wiązania te są zdelokalizowane – podobnie
jak w cząsteczkach benzenu i innych arenów nie wyróżnia się wiązań podwójnych i poje-

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–3–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

Rysunek 1.2: Struktura krystaliczna grafitu. Obraz zaczerpnięty z [7]

dynczych, ale traktuje się wszystkie jako równorzędne, „półtorakrotne”, z uwspólnionym
sekstetem elektronowym w każdym pierścieniu. Płaszczyzny grafitu związane są ze sobą
dużo słabszymi siłami van der Waalsa. Wynika stąd duża anizotropia własności grafitu
– zarówno mechanicznych, jak i elektrycznych (grafit dobrze przewodzi prąd w kierunku
płaszczyzn, ale bardzo słabo w poprzek).

1.4

Analiza powierzchni na poziomie atomowym

Choć omówione w kolejnych działach metody analizy powierzchniowej określa się

mianem „mikroskopii”, należy podkreślić zupełną odrębność tych metod od klasycznej
mikroskopii. Z oczywistych powodów mikroskopy optyczne nie pozwalają na uzyskanie
rozdzielczości mniejszej, niż długość fal, w których prowadzone są obserwacje. Dlatego dla
obserwacji zjawisk na poziomie atomowym konieczne jest zastosowanie fal o dużo mniejszej
długości niż widzialne (np. elektronów), lub punktowy pomiar innych zjawisk (np. prądu
tunelowania), które – wykonane w wielu punktach próbki pozwalają na skonstruowanie
mapy obrazu.

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–4–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

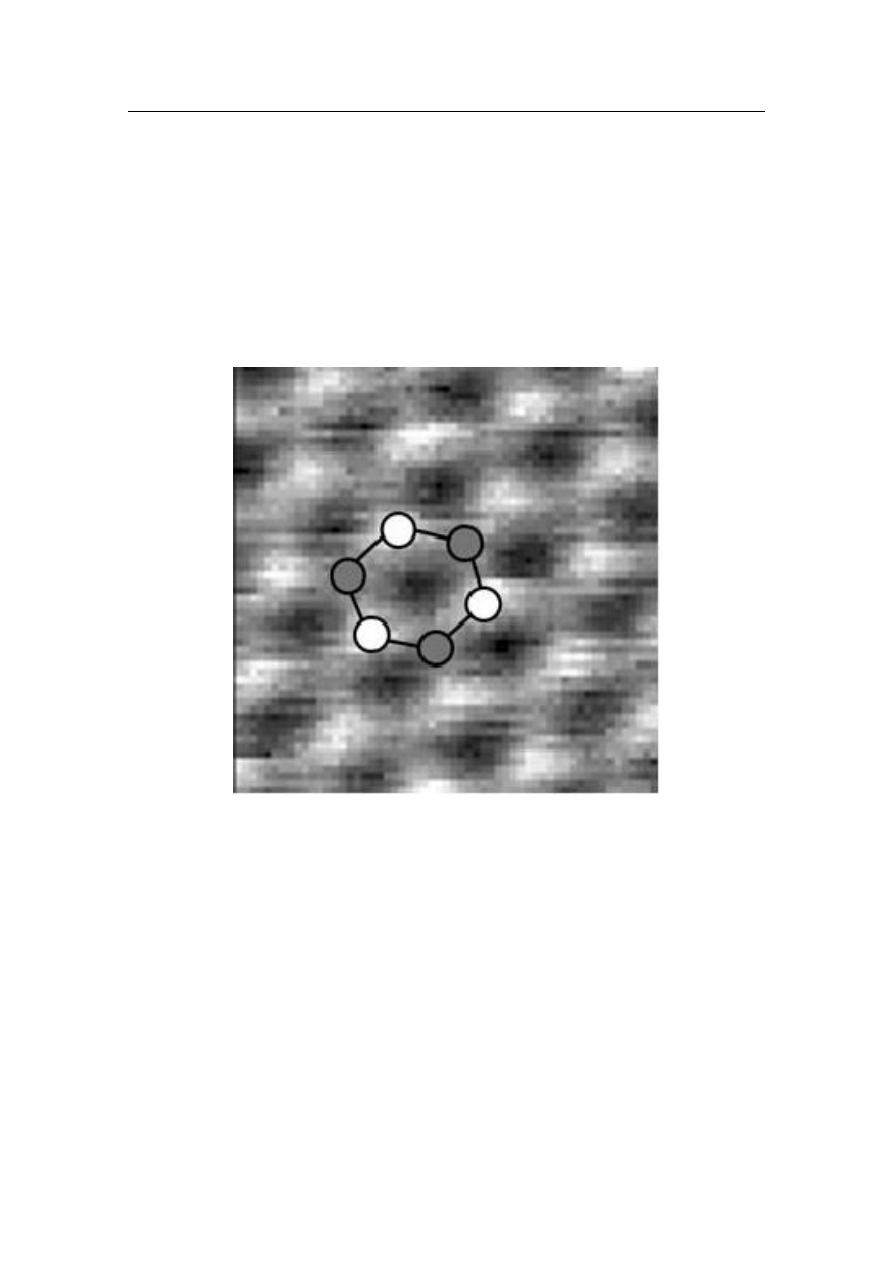
Rysunek 1.3: Wysokiej jakości obraz powierzchni grafitu uzyskany skaningowym mikrosko-
pem tunelowym. Zaznaczony sześciokąt to element struktury płaszczyzny atomów węgla.
Najjaśniejsze punkty to atomy z pierwszej płaszczyzny, pod którymi leżą atomy z drugiej,
dlatego gęstość elektronowa jest tam największa. Ciemniejsze punkty to te atomy, pod
którymi w drugiej płaszczyźnie znajduje się „luka” (por. rys. 1.2). Najciemniejsze obszary
to „luki” pierwszej płaszczyzny. Obraz zaczerpnięty z [6].

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–5–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

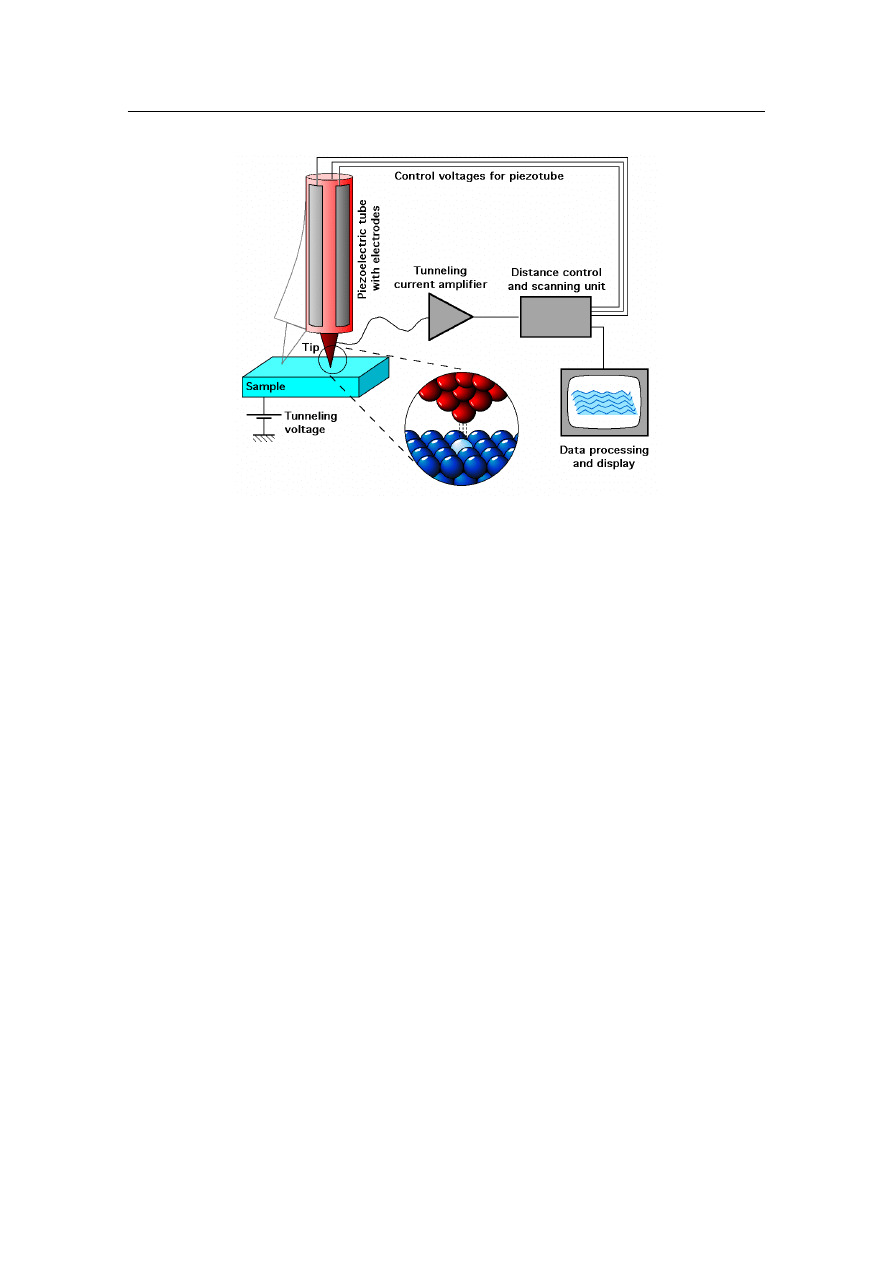
Rysunek 1.4: Uproszczony schemat STM. Obraz zaczerpnięty z [7].

1.4.1

Skaningowa mikroskopia tunelowa

Technika skaningowej mikroskopii tunelowej (scanning tunneling microscopy, STM

– skrót ten oznacza często również sam mikroskop realizujący tę technikę), jak sama nazwa
wskazuje, opiera się na zjawisku prądu tunelowego, czyli kwantowomechanicznego przepły-
wu elektronów zgodnie z rozumowaniem zaprezentowanym w części 1.1. Ważnym (przy-
bliżonym) wzorem opisującym prąd tunelowy jest zależność jego natężenia od bariery i jej
szerokości z:

I ≈ exp(−AV

1/2

0

z)

(1.10)

gdzie stała A ≈ 1 gdy V

0

wyrażona zostanie w elektronowoltach, a z w ˚

A [1]. Warto

pamiętać, że wbrew popularnemu skrótowi myślowemu STM nie modeluje powierzchni
próbki, a mapę gęstości elektronowej powierzchni, co nie zawsze jest jednoznaczne. Por.
podpis pod rys. 1.3.

Technika STM to pomysł Niemca Gerda Binniga i Szwajcara Heinricha Rohrera.

Skonstruowali oni w 1981 pierwszy mikroskop tego typu, co przyniosło im 5 lat później
nagrodę Nobla.

Budowa STM

Z podstawowej zasady działania STM wynika, że próbki mogą być wykonane wyłącz-

nie z materiałów przewodzących. Sondą, czy też ostrzem, manipuluje się poprzez skaner
piezoelektryczny – przykładając odpowiednie napięcia do kryształu, do którego przymo-
cowana jest sonda, powoduje się jej przesuwania. Niekiedy z powodów technicznych przyj-
muje się rozwiązanie odwrotne – sonda jest umocowana w sposób stały, zaś całą próbką
manipuluje się poprzez silnik piezo.

Schemat STM przedstawiony jest na rys. 1.4. Najważniejszym elementem bloku

kontrolnego jest układ ujemnego sprzężenia zwrotnego – gdy prąd tunelowy jest zbyt

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–6–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

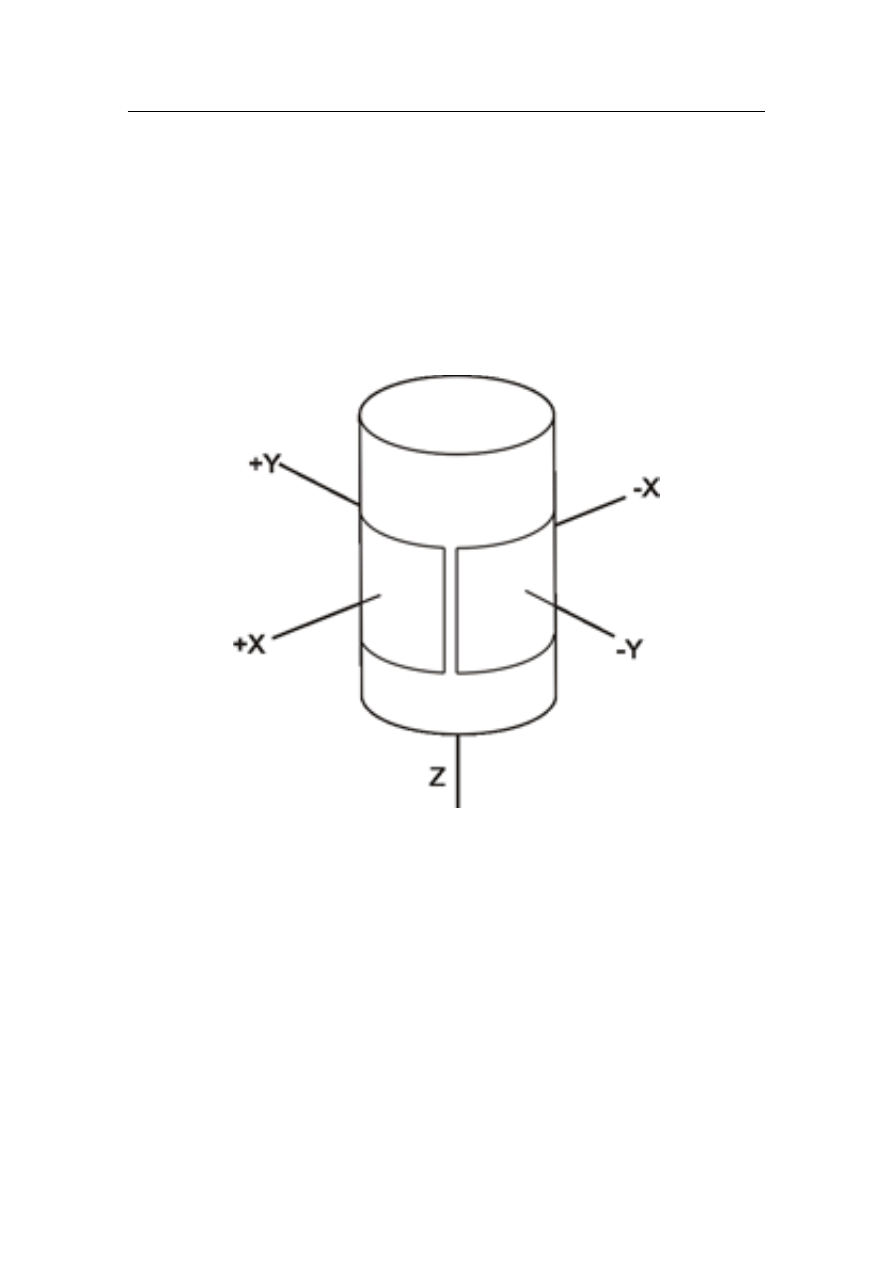
Rysunek 1.5: Zasadza działania skanera piezoelektrycznego w STM. Elektrody na po-
wierzchni bocznej kryształu pozwalają sterować jego wychyleniem, a więc położeniem po-
ziomym ostrza; poprowadzona wewnątrz wydrążonego tunelu elektroda wewnętrzna (po-
przez regulację różnicy potencjału względem pozostałych czterech) odpowiedzialna jest za
jego wydłużanie i skracanie, a więc za położenie pionowe ostrza. Obraz zaczerpnięty z [5]

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–7–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

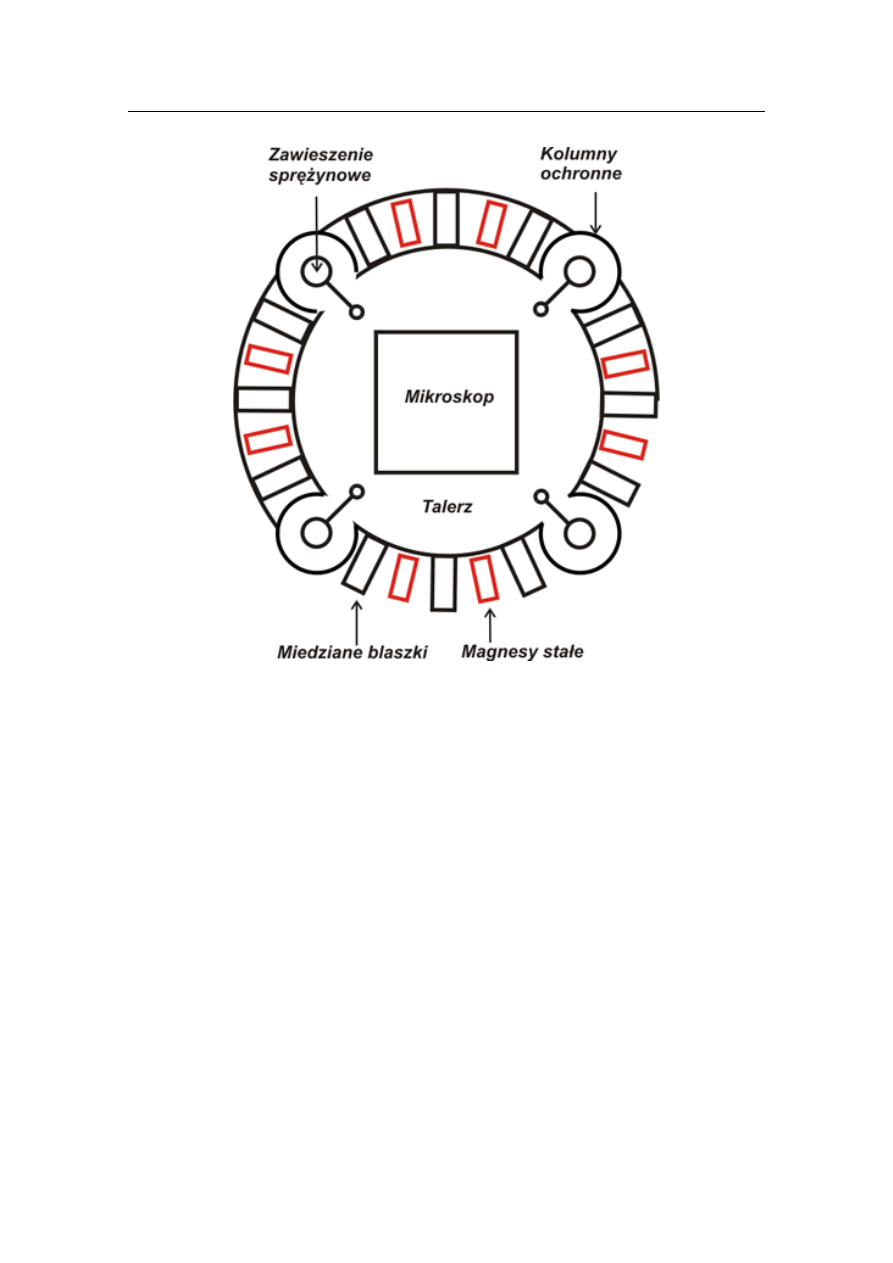
Rysunek 1.6: Jeden z typowych systemów amortyzacji STM. Talerz, stanowiący podstawę
mocowania skanera, zawieszony jest na czterech miękkich sprężynach ukrytych w me-
talowych kolumnach. Wibracje systemu zawieszenia są następnie przechwytywane przez
system tłumienia wykorzystujący prądy wirowe – pierścień miedzianych blaszek umiesz-
czonych pomiędzy magnesami stałymi. Obraz zaczerpnięty z [5]

duży, sonda zostaje odsunięta od próbki. Pozwala to m.in. uniknąć destrukcji ostrza, która
nastąpiłaby przy uderzeniu w próbkę.

Bardzo ważną sprawą w konstrukcji STM jest odizolowanie układu od zakłóceń

zewnętrznych. Wszelakie, nawet najmniejsze wstrząsy mają istotny wpływ na uzyskiwa-
ne z STM dane. Mikroskopy tunelowe powinny pracować w otoczeniu próżniowym, co
eliminuje wpływ cząstek gazu na pomiar, ale przede wszystkim minimalizuje zakłócenia
przenoszone przez fale dźwiękowe w powietrzu. Jeszcze ważniejszym czynnikiem są wibra-
cje pochodzące od podłoża – drgania budynków, wywoływane np. przez ruch uliczny, mają
niebagatelny wpływ na obrazy STM. Stąd w profesjonalnych badaniach stosuje się bardzo
wyrafinowane, niekiedy wielostopniowe systemy zawieszenia, tłumiące drgania układu.

Tryby pracy STM

Wyróżnia się trzy podstawowe tryby pracy STM.

W trybie stałej wysokości (constant height mode, CHM), odległość ostrza od prób-

ki nie zmienia się. Wartość prądu tunelowego zależy zatem od lokalnego ukształtowania

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–8–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

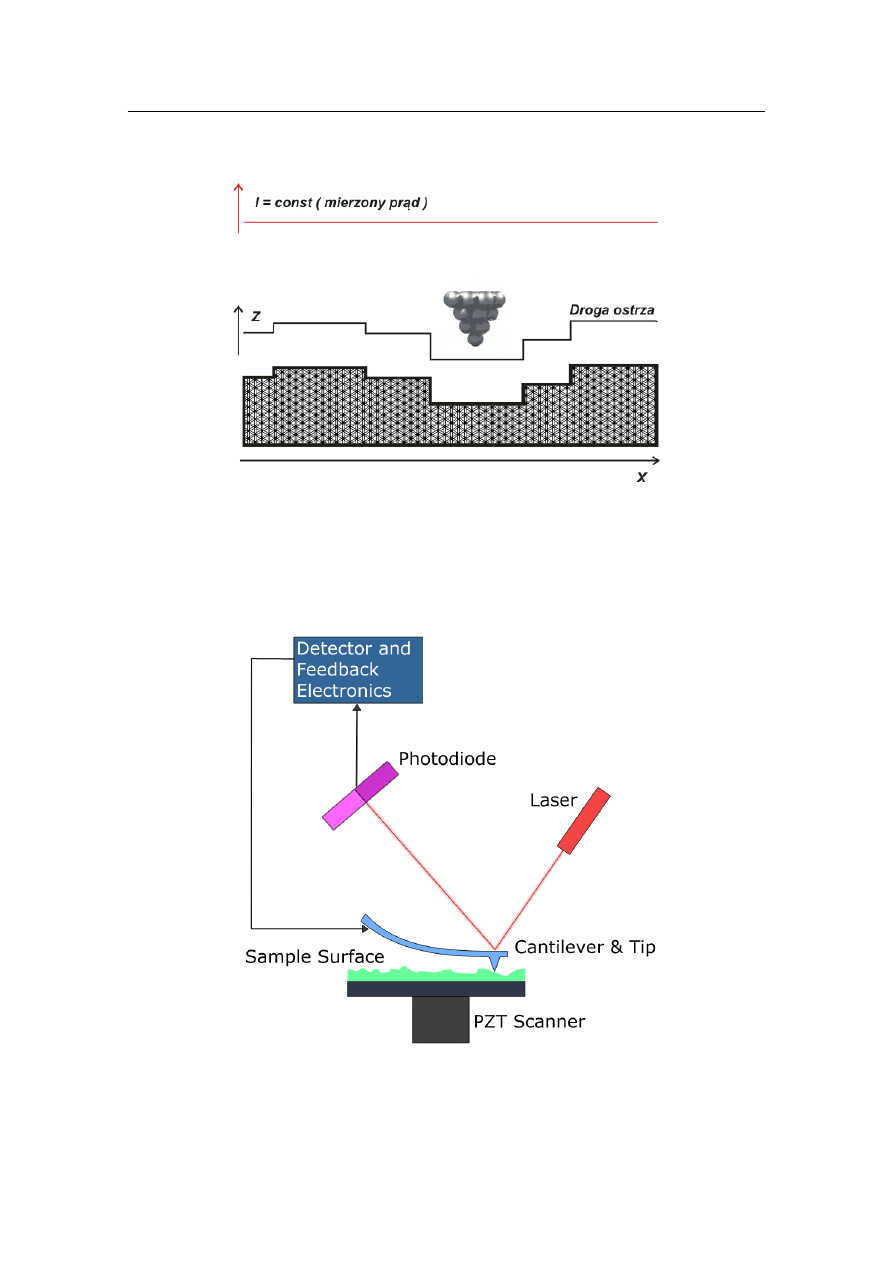
Rysunek 1.7: Schematyczny przebieg pracy STM w trybie stałej wysokości (CHM). Obraz
zaczerpnięty z [5]

próbki i gęstości elektronowej. Na podstawie odnotowanych w punktach całej płaszczyzny
wartości prądu można wymodelować „kształt” próbki.

W trybie stałego prądu (constant current mode, CCM) wykorzystuje się układ sprzę-

żenia zwrotnego do utrzymania ustalonej wartości prądu tunelowego. W przypadku odno-
towania zwiększenia prądu tunelowego układ wycofuje sondę, w przeciwnym przypadku
zaś przybliża. W trybie tym odnotowuje się położenie pionowe ostrza.

Tryb spektroskopowy opiera się na odrębnej zasadzie – nie skanuje się w nim całej

płaszczyzny, lecz mierzy w wybranych punktach charakterystykę prądu tunelowego, tj.
jego zależność od odległości ostrza od próbki czy też przyłożonego napięcia polaryzacji.
W tym trybie weryfikuje się prawo (1.10).

1.4.2

Inne gałęzie mikroskopii sond skanujących

Poza STM powstało wiele innych technik opartych o zasadę skanowania próbki

sondą (scanning probe microscopy, SPM). Poniższa lista zawiera najbardziej znaczące,
choć oczywiście nie wszystkie, spośród nich.

• W mikroskopie sił atomowych (atomic force microscope, AFM) ostrze zamocowane

jest na cienkim wsporniku. Gdy znajduje się w pobliżu próbki, oddziałują na nią
siły międzyatomowe (van der Waalsa, elektrostatyczne i in.) i powodują odchylenie
wspornika. Odchylenie to odnotowywane jest przez pomiar napięć powstałych w wy-
niku efektu piezoelektrycznego, a częściej – przez detekcję zmian miejsca padania
wiązki światła laserowego odbitego od wierzchu wspornika. Efekt piezoelektryczny
pozwala na sterowanie pionowe ostrzem, w celu uniknięcia kolizji z atomami próbki.
Niekiedy (tzw. tryb kontaktowy) bada się powierzchnię przez bezpośredni kontakt
ostrza z próbką, a system sprzężenia zwrotnego utrzymuje siłę nacisku ostrza na
próbkę na poziomie 10

−7

÷ 10

−11

N, co pozwala uniknąć zniszczenia ostrza i próbki.

• Mikroskop sił elektrostatycznych (electrostatic force microscope, EFM) posiada na-

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–9–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

Rysunek 1.8: Schematyczny przebieg pracy STM w trybie stałego prądu (CCM). Obraz
zaczerpnięty z [5]

Rysunek 1.9: Schemat działania mikroskopu sił atomowych (AFM). Obraz zaczerpnięty
z [7]

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–10–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

ładowane ostrze, które wibruje z częstością bliską rezonansowej. Oddziaływania elek-
trostatyczne z próbką zmieniają charakterystykę oscylacji, która jest mierzona i prze-
twarzana w opis badanej powierzchni. Tego typu analiza stosowana jest przy badaniu
pól elektrostatycznych w materiałach, np. obwodach scalonych podczas ich pracy.

• Mikroskop sił magnetycznych (magnetic force microscope, MFM) ma ostrze pokryte

warstwą ferromagnetyka. Podobnie jak w EFM wprowadzane jest w ruch wibracyjny,
którego zmiany – w wyniku oddziaływań magnetycznych z powierzchnią próbki – po-
zwalają na uzyskanie danych magnetycznych dotyczących tej powierzchni. Technika
ta stosowana jest w badaniu nośników magnetycznych, np. dysków twardych.

• W mikroskopii optycznej bliskiego zasięgu (near-field scanning optical microscope,

NSOM) „sondą” jest wiązka światła widzialnego. Jej odbicia od powierzchni rejestru-
je się, a z intensywności refleksów modeluje się kształt powierzchni. Technika ta daje
jednak słabą (na poziomie 15 nm) zdolność rozdzielczą – oczywiście w porównaniu
z innymi technikami STM.

Rozdział 2

Opis i przebieg doświadczenia

Doświadczenie zostało przeprowadzone za pomocą oprzyrządowania i oprogramowa-

nia Nanosurf easyScan (patrz rys. 2.1). Zgodnie z instrukcją doświadczenia najpierw zapo-
zano się z interfejsem oprogramowania w trybie symulacji mikroskopu. Pozostałe czynności
przeprowadzono dwukrotnie – 20 marca 2007 otrzymano obrazy bardzo niskiej jakości, więc
doświadczenie powtórzono 27 marca 2007. W obu przypadkach postępowano zgodnie z za-
lecaną procedurą. Po włączeniu przyrządów odczekano 30 minut w celu ustabilizowania
warunków przeprowadzania doświadczenia. Następnie przybliżono sondę do próbki, tak,
by zaczął płynąć prąd tunelowy. Następnie wielokrotnie skanowano powierzchnię próbki,
stopniowo zawężając pole skanowania, tak, by otrzymać regularne, powtarzalne obrazy w
skali nanometrowej, z widoczną strukturą powierzchni grafitu. Podczas przybliżania prób-
ki korygowano nachylenie jej powierzchni, tak, by była równoległa do płaszczyzny ruchu
ostrza. Ostatecznie, gdy udało się otrzymać zadowalające wyniki, zapamiętano obrazy dla
różnych kierunków skanowania (0

◦

, 45

◦

, 90

◦

). Drugą część doświadczenia stanowiły po-

miary w trybie spektrometrii. Dla kilku punktów wykonano pomiary zależności I(V ) oraz
I(z), wyniki zapamiętano.

Dokładne wyniki liczbowe nie są zawarte w tym sprawozdaniu z racji ich przytła-

czającej ilości, jednak autor z chęcią udostępni je zainteresowanym.

Rysunek 2.1: Głowica i kontroler zestawu przyrządów Nanosurf easyScan 2. Wygląd ze-
wnętrzny przedstawionego zestawu różni się od użytego w doświadczeniu Nanosurf easy-
Scan jedynie wyglądem kontrolera. Obraz zaczerpnięty z [6]

11

Rozdział 3

Obliczenia i wyniki

Na rysunkach 3.1–3.6 przedstawiono wyniki skanowania powierzchni dla różnych

kątów obrotu, zarówno w postaci mapy topograficznej w odcieniach szarości, jak i modelu
trójwymiarowego. Zauważyć można, że tylko jakość obrazów dla kąta skanowania 0

◦

jest

zadowalająca – chwilę później zakłócenia termiczne i akustyczne powiększyły się i obrazy
dla kątów skanowania 90

◦

i 45

◦

jest znacznie gorsza.

Do określenia odległości międzyatomowej posłużą dwa profile wykonane dla kąta

obrotu 0

◦

. Ich kierunki przedstawiono na rysunkach 3.7, 3.9, zaś wykresy – 3.8, 3.10. Kąt

między kierunkami profili – 57

◦

. Na pierwszym profilu mamy 5 maksimów (tj. 4 odległości

międzyatomowe między pierwszym a ostatnim maksimum), na drugim – 7 (czyli 6 odle-
głości). Ponieważ zgodnie z objaśnieniem do rys. 1.3, wyliczone w ten sposób odległości
(między „ jasnymi” atomami) są (zgodnie z prostą trygonometrią)

√

3 razy większe niż

szukane odległości międzyatomowe w graficie. Dla każdego z profili wyliczymy odległość
międzyatomową zgodnie z wzorem

a =

d

M

d

g

l

g

(n − 1)

√

3

(3.1)

gdzie d

M

– odległość w pikselach między skrajnymi maksimami, d

g

– szerokość wykresu

w pikselach, l

g

– długość profilu, n – ilość maksimów w profilu. Otrzymuje się wtedy

następujące wyniki (indeks oznacza numer profilu):

a

1

= 0,197 nm,

(3.2)

a

2

= 0,122 nm.

(3.3)

Należy ponadto określić możliwy błąd odczytu maksimów wykresu. Przekrój 1 jest dość
regularny, stąd można przyjąć, że dokładność wynosi 5 pikseli. W przypadku przekroju 2
jest ona znacznie gorsza i można ocenić ją na 10 pikseli. Jeśli oznaczymy tę dokładność δ,
to niepewność wyznaczenia powyższych wartości wynosić będzie

u(a) =

2δ

d

g

l

g

(n − 1)

√

3

(3.4)

zatem wynosi odpowiednio

u(a

1

) = 0,009 nm,

(3.5)

u(a

2

) = 0,012 nm

(3.6)

12

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–13–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

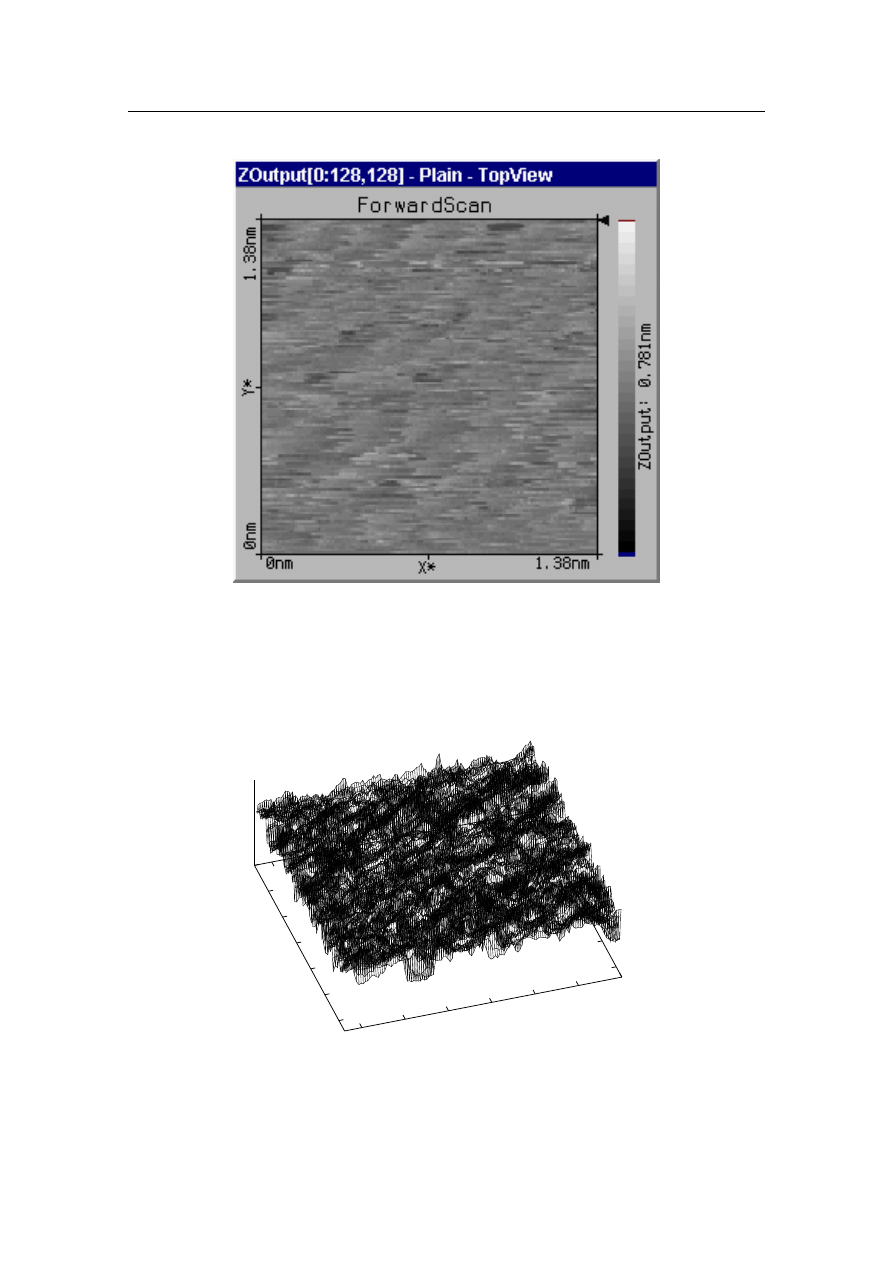
Rysunek 3.1: Dwuwymiarowa reprezentacja zapisu powierzchni dla kąta obrotu 0

◦

.

0

20

40

60

80

100

120

0

20

40

60

80

100

120

Rysunek 3.2: Trójwymiarowa reprezentacja zapisu powierzchni dla kąta obrotu 0

◦

.

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–14–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

Rysunek 3.3: Dwuwymiarowa reprezentacja zapisu powierzchni dla kąta obrotu 90

◦

.

0

20

40

60

80

100

120

0

20

40

60

80

100

120

Rysunek 3.4: Trójwymiarowa reprezentacja zapisu powierzchni dla kąta obrotu 90

◦

.

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–15–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

Rysunek 3.5: Dwuwymiarowa reprezentacja zapisu powierzchni dla kąta obrotu 45

◦

.

0

20

40

60

80

100

120

0

20

40

60

80

100

120

Rysunek 3.6: Trójwymiarowa reprezentacja zapisu powierzchni dla kąta obrotu 45

◦

.

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–16–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

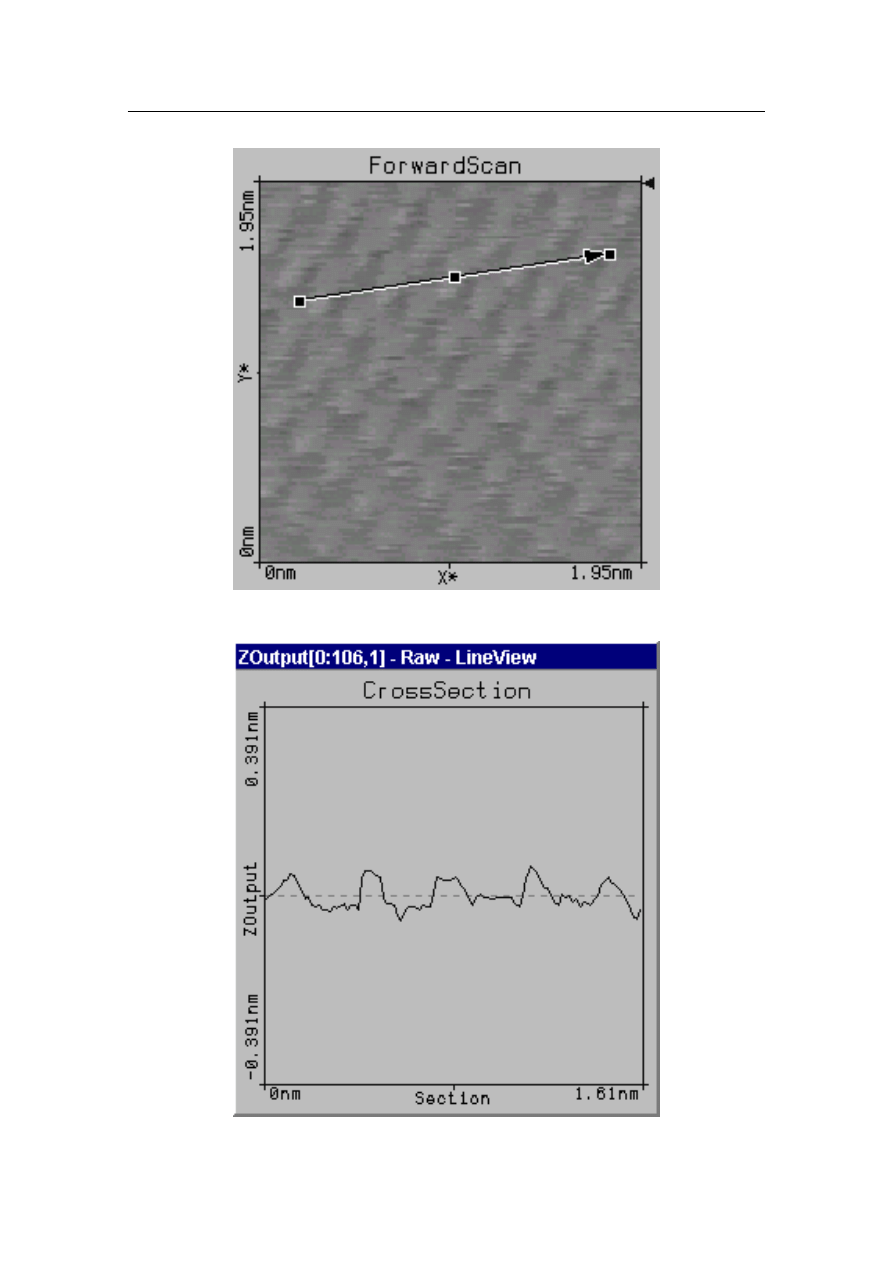
Rysunek 3.7: Kierunek przekroju 1.

Rysunek 3.8: Wykres dla przekroju 1.

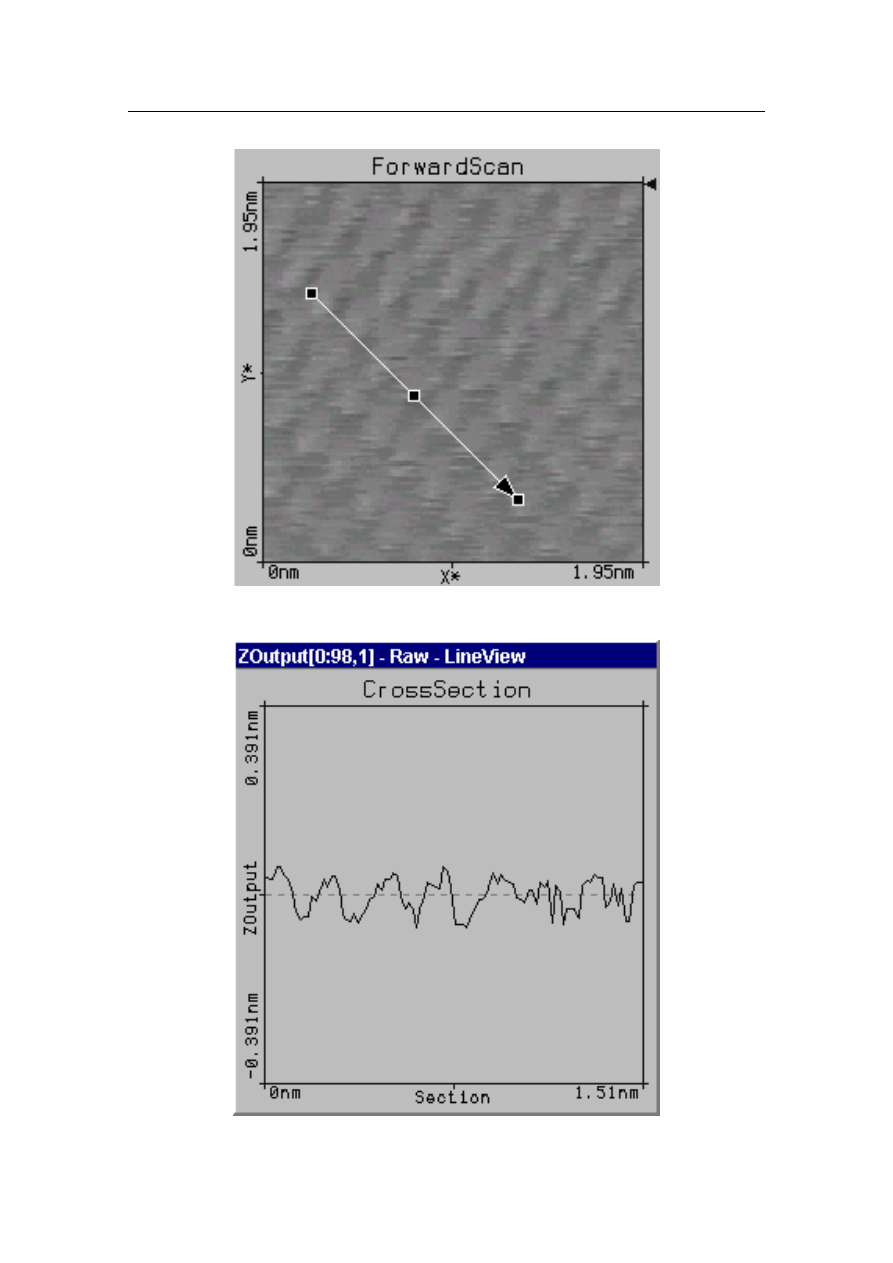
Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–17–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

Rysunek 3.9: Kierunek przekroju 2.

Rysunek 3.10: Wykres dla przekroju 2.

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–18–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

90

100

110

120

130

140

150

160

170

180

1

1.2

1.4

1.6

1.8

2

2.2

2.4

2.6

2.8

3

I[nA]

U[V]

Rysunek 3.11: Zależność prądu tunelowego od napięcia polaryzacji.

Na wykresach 3.11, 3.13 przedstawiono przykładowe zależności odpowiednio prądu

tunelowania od napięcia polaryzacji oraz prądu tunelowania od odległości ostrze-próbka;
na wykresach 3.12, 3.14 – odpowiednie zależności prądu zlogarytmowanego i proste regre-
sji. Widać, że otrzymane wyniki dość dobrze stosują się do zależności (1.10). Współczynniki
kierunkowe zlogarytmowanych zależności wraz z ich niepewnościami, wyliczone za pomocą
programu GNUplot są następujące:

a

U

= 0,3439(72) V

−1

(3.7)

a

z

= 0,2236(22) nm

−1

(3.8)

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–19–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

4.4

4.5

4.6

4.7

4.8

4.9

5

5.1

5.2

1

1.2

1.4

1.6

1.8

2

2.2

2.4

2.6

2.8

3

log I

U[V]

Rysunek 3.12: Zależność zlogarytmowanego prądu tunelowego od napięcia polaryzacji.

50

55

60

65

70

75

80

85

90

95

100

2

2.5

3

3.5

4

4.5

5

I[nA]

z[nm]

Rysunek 3.13: Zależność prądu tunelowego od odległości ostrze-próbka.

Paweł Laskoś-Grabowski, III rok fizyki teoretycznej
wtorek, 20-27 marca 2007, 14:15-20:00

–20–

Skaningowy mikroskop tunelowy

prowadzący: prof. Jerzy Czyżewski

3.9

4

4.1

4.2

4.3

4.4

4.5

4.6

4.7

2

2.5

3

3.5

4

4.5

5

log I

z[nm]

Rysunek 3.14: Zależność zlogarytmowanego prądu tunelowego od odległości ostrze-próbka.

Rozdział 4

Wnioski

W pierwszej części doświadczenia powstały obrazy (np. rys. 3.1) powierzchni gra-

fitu w skali atomowej. Gołym okiem widać, że taki obraz jest daleki od ideału – obrazy
„ jasnych” atomów nie są rozmieszczone w regularnej sieci trójkątów równobocznych, jak
powinny. Potwierdzają to wyliczenia – widać znaczną różnicę między odległościami mię-
dzyatomowymi wyliczonymi na podstawie profili w różnych kierunkach. Porównanie owych
wartości a

1

, a

2

z tablicową stałą sieci grafitu a

t

a

1

= 0,197(9) nm,

(4.1)

a

2

= 0,122(12) nm,

(4.2)

a

t

= 0,142 nm

(4.3)

ujawnia dysproporcję wyników i oczekiwanej wartości. Jednak wobec bardzo dalekich od
doskonałości warunków doświadczenia należy uznać dobrą zgodność rzędu wielkości otrzy-
manych wyników za sukces.

Wykresy 3.12, 3.14 uzyskane w drugiej części doświadczenia potwierdziły liniowość

zależności zlogarytmowanego prądu tunelowego od napięcia polaryzacji oraz odległości
ostrze-próbka, zgodnie z równością (1.10). Współczynniki kierunkowe prostych regresji
obarczone są w obu przypadkach niepewnością względną rzędu poniżej 3%, co świadczy o
dobrej zgodności wyników z teorią.

21

Bibliografia

[1] Antoni Ciszewski, Adam Kiejna, Skaningowa mikroskopia tunelowa, Postępy Fizyki,

tom 26, zeszyt 2, 1985.

[2] Leonard Schiff, Mechanika Kwantowa, PWN, Warszawa 1977.

[3] Ludwik Turko, Wykłady z mechaniki kwantowej I. Notatki wykładowcy, 2005.

[4] Ryszard Czajka, Zastosowania skaningowej mikroskopii tunelowej do badania własno-

ści fizycznych układów mezoskopowych, Wydawnictwo Politechniki Poznańskiej, Po-
znań 1997.

[5] Obrazowanie i analiza pomiarów skaningowym mikroskopem tunelowym STM, praca

zbiorowa Zakładu Fizyki Powierzchni i Nanostruktur UMCS, http://www.ostm.-
umcs.lublin.pl/.

[6] Witryna II pracowni fizycznej Instytutu Fizyki UMCS, http://tytan.umcs.lublin.-

pl/users/mlpar/.

[7] Wikipedia, Wolna Encyklopedia, praca zbiorowa, http://en.wikipedia.org/.

22