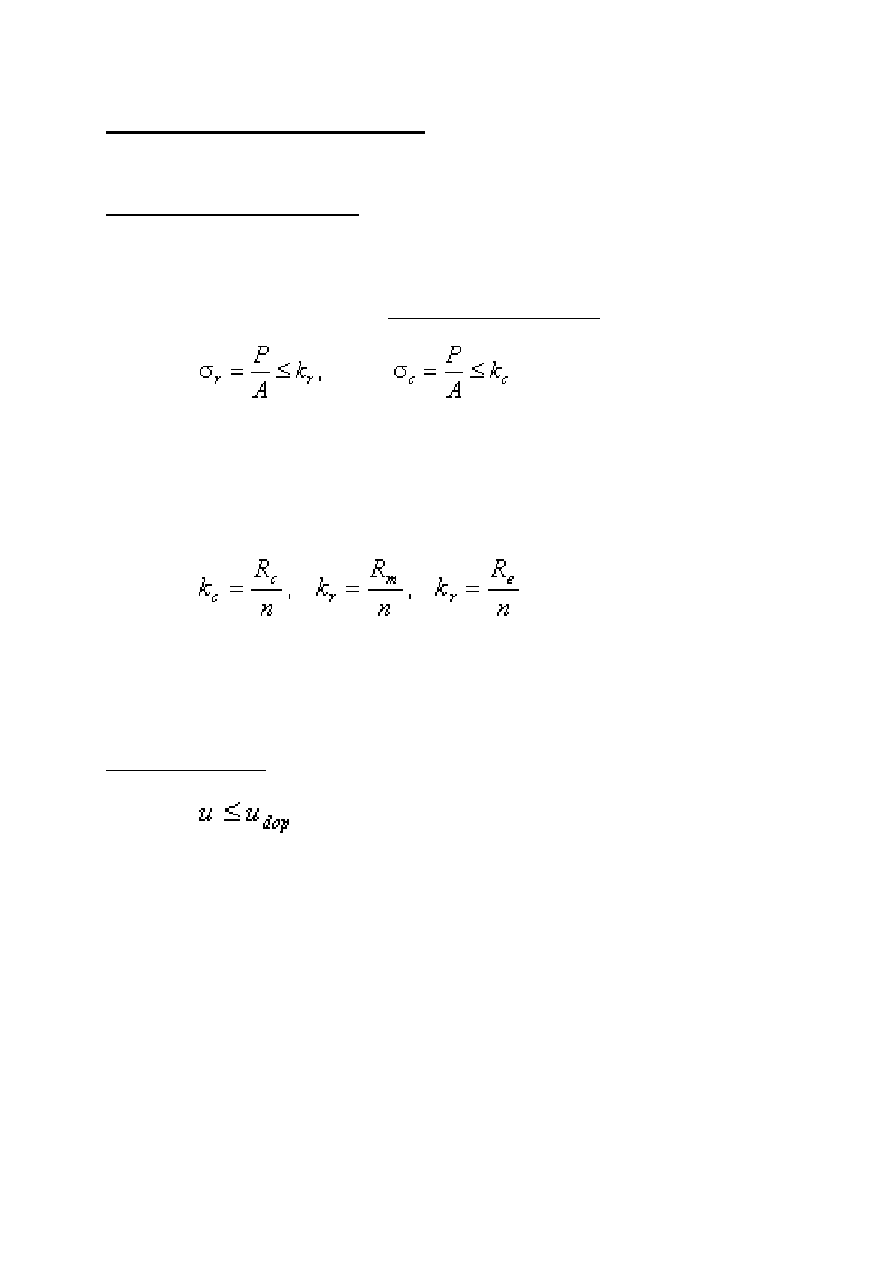
ROZCIĄGANIE I ŚCISKANIE

KONSTRUKCJE STATYCZNIE WYZNACZALNE

Układy statycznie wyznaczalne charakteryzują się tym, że siły wewnętrzne
występujące w poszczególnych elementach tych układów mogą być wyznaczone z
równań równowagi.

Obliczenia wytrzymałościowe elementu rozciąganego lub ściskanego wykonuje się w
celu sprawdzenia czy są spełnione warunki wytrzymałościowe

gdzie P - siła rozciągająca (ściskająca), A - pole przekroju poprzecznego elementu
rozciąganego (ściskanego), k

r

- naprężenie dopuszczalne przy rozciąganiu, k

c

-

naprężenie dopuszczalne przy ściskaniu.

Naprężenie dopuszczalne na rozciąganie i ściskanie k

r

i k

c

gdzie R

c

, R

m

, R

e

- wytrzymałość na ściskanie i rozciąganie, n - współczynnik

bezpieczeństwa.

Często spełnienie powyższych warunków wytrzymałościowych nie wystarcza do
właściwego zaprojektowania konstrukcji. Z tego względu musi być jeszcze spełniony
warunek sztywności

Według tego warunku odkształcenie lub przemieszczenie punktów projektowanego
elementu nie powinno przekroczyć wartości odkształcenia lub przemieszczenia,
przyjętego dla danej konstrukcji jako dopuszczalne.

KONSTRUKCJE STATYCZNIE NIEWYZNACZALNE

W przypadku, kiedy liczba równań równowagi jest mniejsza od liczby sił
wewnętrznych, to konstrukcje takie są nierozwiązywalne przy zastosowaniu równań
statyki ciał doskonale sztywnych i noszą nazwę układów statycznie
niewyznaczalnych.

Do obliczenia niewiadomych sił należy wtedy uwzględnić odkształcenia i
przemieszczenia prętów. Uzyskane w ten sposób dodatkowe równania
współzależności odkształceń stanowią zależności o charakterze geometrycznym.

W celu połączenia równań równowagi z równaniami geometrycznymi należy posłużyć
się związkami fizycznymi uzależniającymi wzajemnie siły wewnętrzne i
przemieszczenia.

W przypadku materiałów liniowosprężystych związki te wynikają bezpośrednio z
prawa Hooke'a.

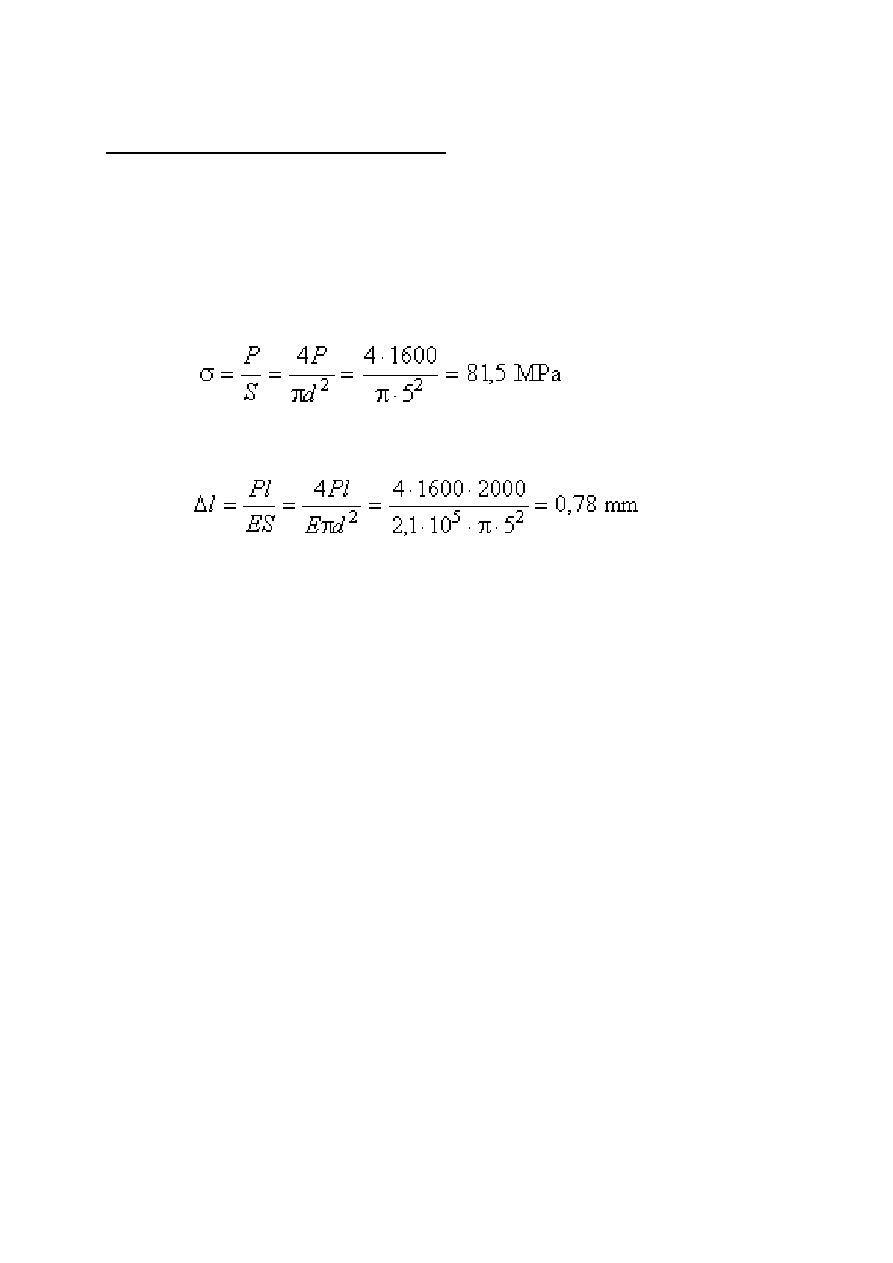
PRZYKŁADY OBLICZENIOWE

Przykład 1
Pręt stalowy o średnicy d = 5 mm i długości l = 2 m jest rozciągany siłą
P = 1600 N. Obliczyć naprężenia oraz wydłużenie całkowite i względne pręta. Moduł
Younga dla stali wynosi E = 2,1 · 10

5

MPa.

R o z w i ą z a n i e.
Naprężenia normalne w poprzecznym przekroju pręta wynoszą

a wydłużenie całkowite (z prawa Hooke'a)

Przykład 2
Obliczyć wydłużenie wywołane ciężarem własnym pręta pryzmatycznego o długości
l, wykonanego z materiału o ciężarze właściwym

γ i module Younga E.

R o z w i ą z a n i e .
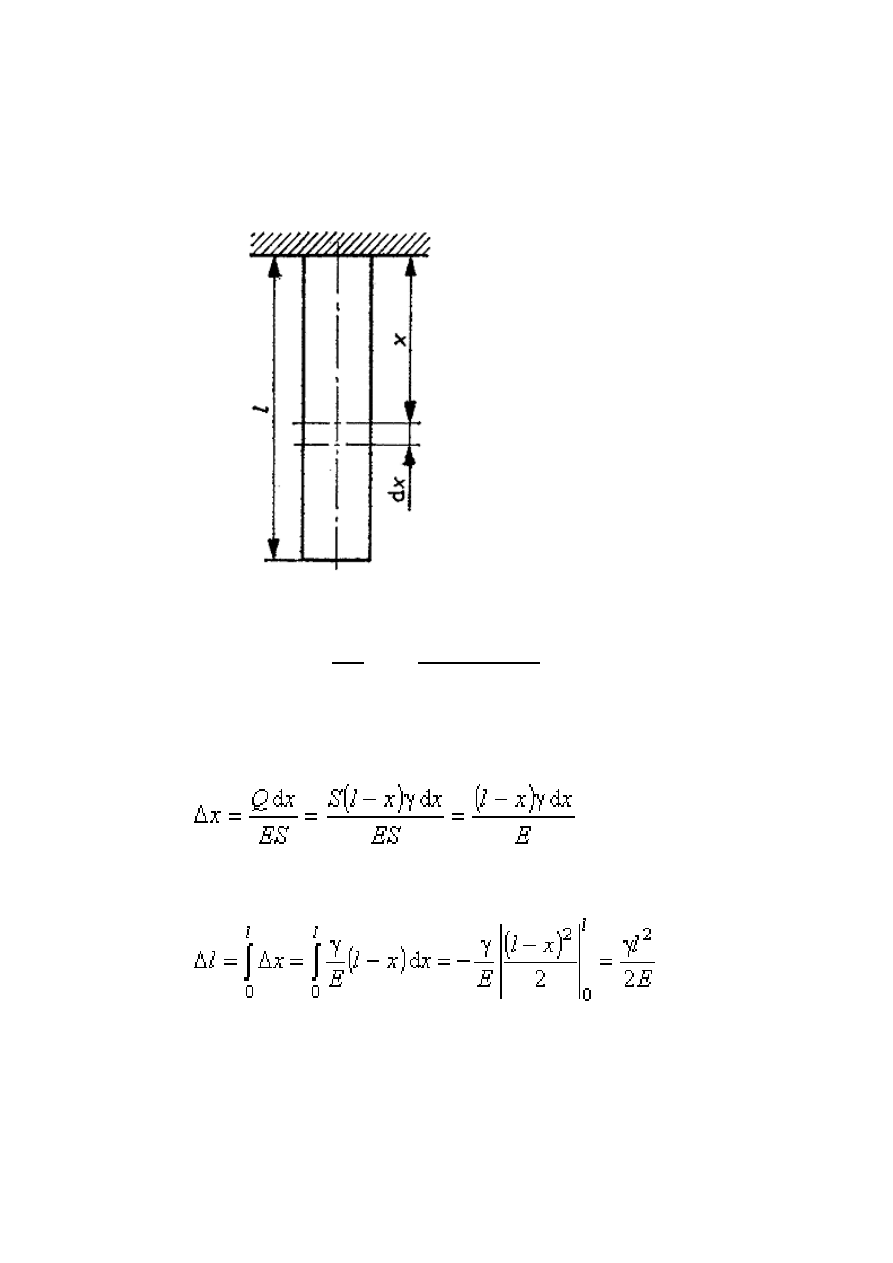
Wytnijmy z pręta odcinek o długości dx oddalony o x od górnego końca pręta.
Odcinek ten jest rozciągany siłą równą ciężarowi pręta o długości l - x, a więc

Q = S (l - x)

γ

Wydłużenie odcinka dx wynosi (z prawa Hooke'a)

Całkowite wydłużenie pręta jest równe

Wydłużenie to jest równe wydłużeniu wywołanemu siłą równą ciężarowi pręta,
przyłożoną w środku ciężkości pręta.

Przykład 3
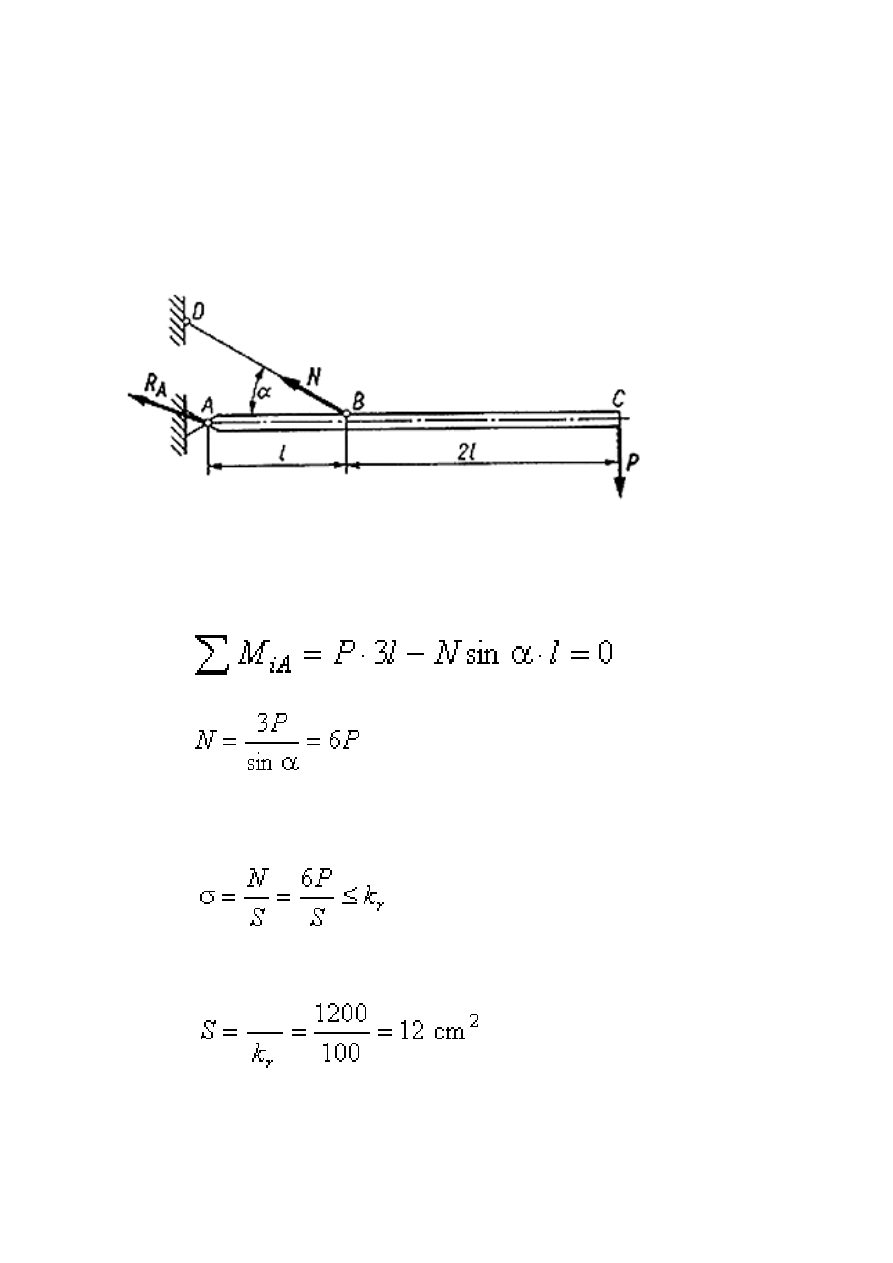
Doskonale sztywna belka AC = 3l = 5 m jest zamocowana jednym końcem A na stałej
podporze przegubowej i cięgnie BD. Cięgno tworzy z osią belki kąt

α = 30º.

Obciążenie belki stanowi pionowa siła P = 20 kN, przyłożona w punkcie C. Obliczyć
przekrój poprzeczny cięgna, jeżeli naprężenie dopuszczalne na rozciąganie wynosi
k

r

= 100 MPa.

R o z w i ą z a n i e.
Belka jest obciążona siłą P i reakcjami R

A

i N. Niewiadomą reakcję N w cięgnie

wyznacza się z równania momentów względem punktu A

Stąd

Naprężenia normalne w cięgnie nie mogą przekroczyć naprężeń dopuszczalnych na
rozciąganie

Zatem wartość przekroju poprzecznego cięgna wynosi

6P

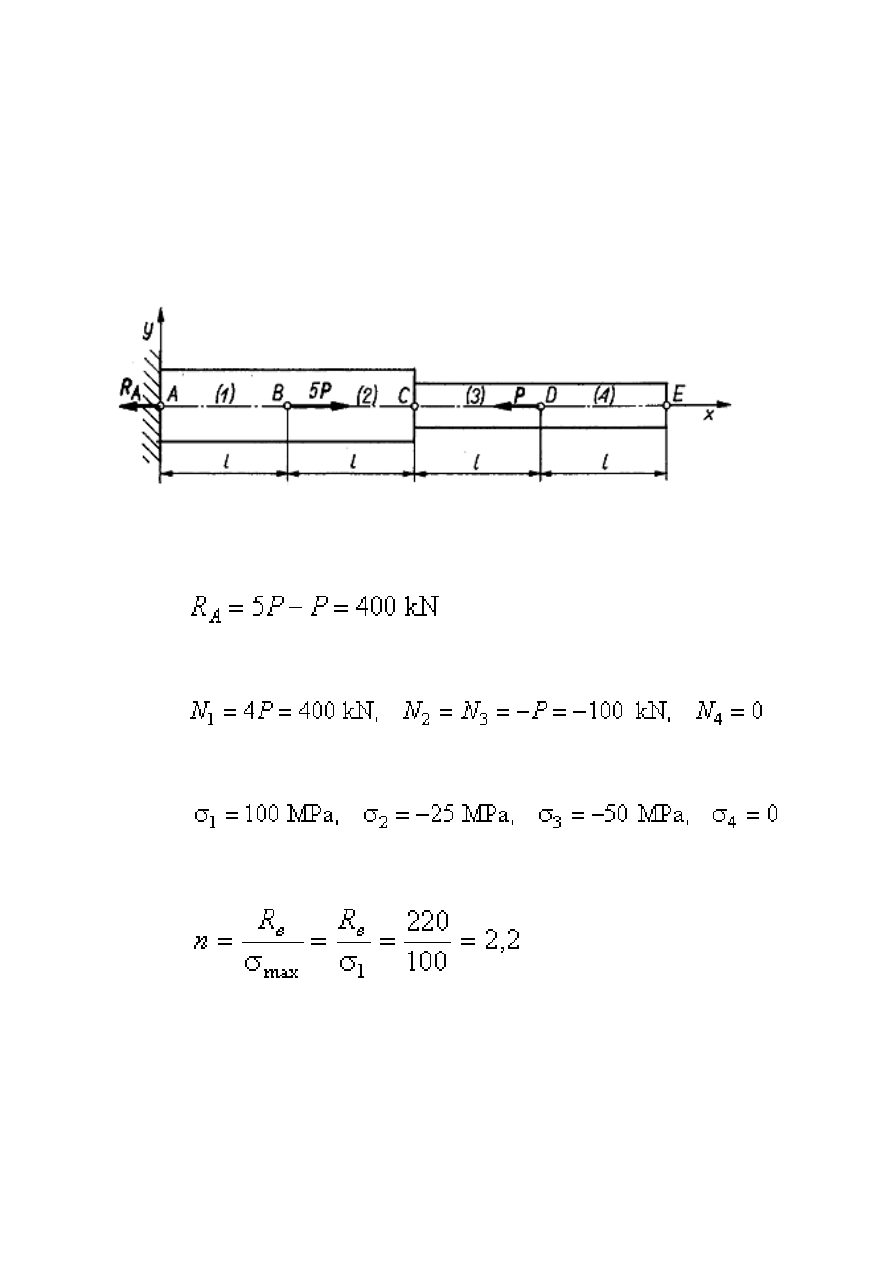
Przykład 4
Pręt ACE o dwóch różnych średnicach, utwierdzony w punkcie A, jest obciążony w
przekrojach B i D siłami 5P = 500 kN i P = 100 kN. Przekrój poprzeczny części pręta
AC = 2l = 1 m jest równy 2A = 4 · 10

-3

m

2

, a części CE = 2l = 1 m wynosi A = 2 · 10

-3

m

2

.

Pręt jest wykonany ze stali, dla której współczynnik sprężystości wzdłużnej wynosi E
= 2,1 · 10

5

MPa i granica plastyczności R

e

= 220 MPa. Obliczyć współczynnik

bezpieczeństwa n odniesiony do granicy plastyczności.

R o z w i ą z a n i e.
Reakcja w miejscu utwierdzenia pręta jest równa

Badając równowagę myślowo odciętych części pręta, otrzymuje się

Biorąc pod uwagę wartości tych sił obliczono naprężenia normalne

Współczynnik bezpieczeństwa, z jakim pracuje pręt, oblicza się ze wzoru