Mechanika Techniczna II
Ćwiczenie nr IV

JEDNOOSIOWE ROZCIĄGANIE

I ŚCISKANIE PRĘTÓW.

KOMPUTEROWE

PORÓWNANIE WYNIKÓW

Wykonali: Grzegorz Stachewicz, Sławomir Gutowski, Dominik Zasławski, Izabela Płatun,

Katarzyna Parkosz, Paulina Kurant, Anna Maciejowska

Grupa 3 ETI I MU niestacjonarne

1.Cel ćwiczenia

Celem

ćwiczenia

jest

statyczna

próba

rozciągania metali w temperaturze pokojowej.
Celem próby jest sprawdzenie wytrzymałości
materiału pręta i określenie przyrostu średnicy
przekroju poprzecznego pręta. W obliczeniach
pominąć ciężar pręta, przy założeniu, że Q=0
Następnie porównanie obliczeń badawczych z
komputerowymi przy założeniu, że Q=0 i
otrzymane wyniki porównać na wykresach gdy
Q≠0.

Własnościami

mechanicznymi

materiałów

używanych w technice do budowy maszyn i
urządzeń technicznych oraz wyrobu artykułów
użytkowych nazywamy zespół cech, które
związane są ze zdolnością do przenoszenia
obciążeń oraz zdolnością do sprężystego i
trwałego

odkształcania

się

elementów

wykonywanych z tych materiałów.

2. Podstawy teoretyczne

2.1. Własności mechaniczne materiałów

1) własności wytrzymałościowe, które wykazują
się odpornością materiałów na działanie różnego
rodzaju obciążeń, dzięki czemu elementy
techniczne wykonane z tych materiałów mogą
być poddawane działaniu sił rozciągających lub
ściskających,

momentów

zginających

lub

skręcających czy sił ścinających, nie ulegając
doraźnym uszkodzeniom w postaci odkształceń
trwałych lub pęknięć;

2) podatność sprężystą, które wykazują się.
zdolnością do odkształceń sprężystych;

3) podatność plastyczną, które wykazuje się.
zdolnością do odkształceń trwałych.

Do podstawowych własności mechanicznych

zaliczamy:

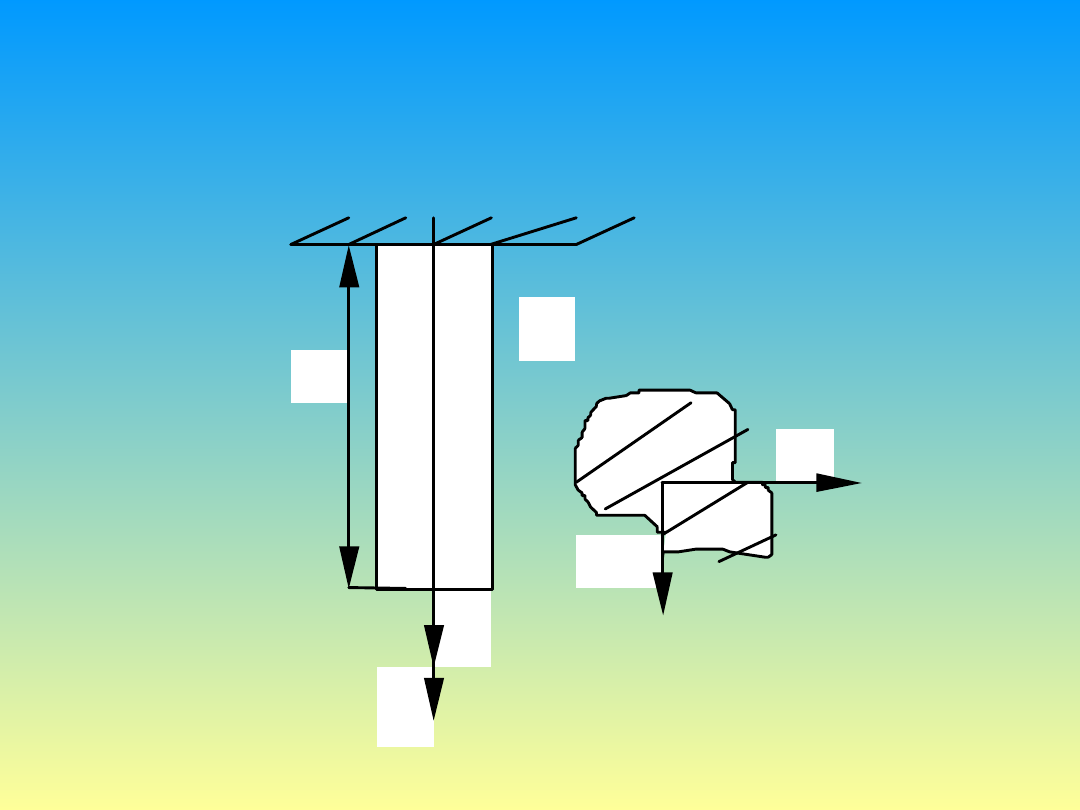
P

y

l

x

z

Q

Rys. 1. Jednoosiowe rozciąganie i ściskanie prętów.

2.2 Rodzaje obciążeń, naprężenia i
odkształcenia przy rozciąganiu i ściskaniu
prętów

Rozciąganie pręta o długości i wymiarach dowolnego pola przekroju

poprzecznego, którą obciążono wartością sił rozciągających

przedstawiono na rysunku 1.

Zakładamy, że maszyna lub inne urządzenie do
dokonania

próby

zapewnia

jedno-osiowe

obciążenie pręta, a tym samym równomierny
rozkład naprężeń normalnych w przekroju
poprzecznym. Wartość naprężenia obliczamy ze
stosunku siły rozciągającej lub ściskającej do
pola przekroju poprzecznego pręta

Q

P

N

F

N

c

r









,

,



gdzie:

P - jednoosiowa siła rozciągająca lub ściskająca
pręt,

Q - ciężar pręta.

W związku z tym, że w miarę rozciągania lub
ściskania pręta przekrój poprzeczny zmniejsza
się, mogą być tutaj stosowane dwie różne zasady.

Według jednej zasady obliczamy naprężenia

rzeczywiste dzieląc każdorazowo siłę P przez

pole F

rz

przekroju rzeczywistego, jaki ma pręt w

momencie działania tej siły, przy założeniu że

ciężar pręta pomijamy Q = 0

Według drugiej zasady pomijamy zmienność

przekroju pręta i naprężenia obliczamy w sposób

umowny, jako naprężenia nominalne dzieląc

każdorazowo siłę P przez początkowe pole F

o

przekroju poprzecznego

rz



o



Sprawdzenie wytrzymałości pręta dokonano na
podstawie warunku wytrzymałości:

c

r

c

r

k

,

,





gdzie:

K

r,c

naprężenia dopuszczalne na rozciąganie lub

ściskanie pręta.

Odkształcenie

liniowe

pręta

określono

następującym wzorem (prawo Hooke’a)

E







Całkowite wydłużenie pręta wynosi

l

l







Względne odkształcenie poprzeczne wynosi











p

Zmiana średnicy przekroju poprzecznego pręta jest równa

d

d

p







3. Opis stanowiska badawczego

Do przeprowadzenia próby rozciągania można
stosować maszyny różnych konstrukcji, pierwszej
klasy dokładności, spełniające wymagania
przepisów legalizacyjnych oraz PN-64/H-04313.

Maszyna wytrzymałościowa powinna ponadto
zapewnić:

- niezawodne zamocowanie i centrowanie pręta
(próbki) w uchwytach

- możliwość ustawienia i regulowania prędkości.

Jeżeli w normalnych warunkach przedmiotowych
lub warunkach zamówienia nie określono inaczej,
próbę przeprowadza się w temperaturze 20
stopni C.

Zakres pomiarowy siłomierza mechanicznego
maszyny wytrzymałościowej powinien być tak
dobrany, aby największa siła rozciągająca
stanowiła nie mniej niż 30 i nie więcej niż 90
procent

górnej

granicy

zakresu

wskazań

siłomierza maszyny wytrzymałościowej.

Pręt (próbkę) należy zamocować w uchwytach
maszyny wytrzymałościowej w taki sposób, aby
oś

próbki

pokrywała

się

z

kierunkiem

rozciągania.

Warunek

ten

powinien

być

zachowany

szczególnie

przy

wyznaczaniu

naprężeń przy wydłużeniach umownych.

Sposób zamocowania próbek powinien ponadto
zapobiec ich poślizgowi w uchwytach, zgnieceniu
powierzchni oporowych, odkształceniu główek i
rozerwaniu próbek w miejscu przejścia od
główek do roboczej części próbki oraz w
główkach. Siłę należy odczytać z dokładnością do
1 działki siłomierza. Na rysunku 2 przedstawiona
jest maszyna wytrzymałościowa, zwana inaczej
zrywarką, gdzie badaną próbkę zakłada się w
szczękach mocujących. Próbka pod wpływem
narastającej w wolnym tempie obciążeniem
zostaje

poddana

próbie

rozciągania.

Na

podstawie

tej

próby

jest

sprawdzenie

wytrzymałości

materiału

pręta

(próbki)

i

określenie

przyrostu

średnicy

przekroju

poprzecznego pręta (próbki), przy założeniu, ze
Q = 0

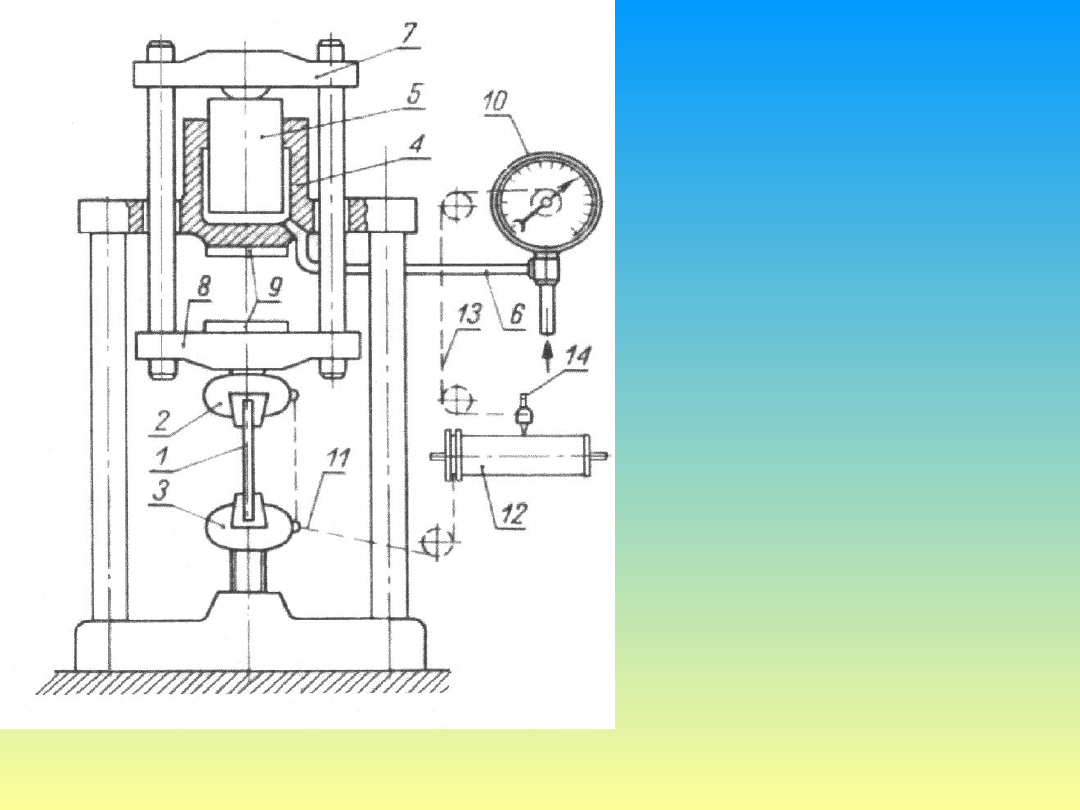
1 - próbka,

2 - szczęki,

3 - płyty,

4 -podpory,

5 -śruba,

6 - tłok,

7 - cięgna,

8 -
cylinderek,

9 - tłoczek

Rys. 2. Maszyna
wytrzymałościowa.

4. Przebieg ćwiczenia

Przykład liczbowy:

Stalowy pręt o długości l = 100 cm i przekroju
kołowym o średnicy d = 2 cm jest rozciągany
siłą osiową P = 30000 N . Dopuszczalne
naprężenia materiału pręta wynosi

Sprawdzić wytrzymałość materiału pręta i
określić

przyrost

średnicy

przekroju

poprzecznego.

Następnie

w

obliczeniach

uwzględnić ciężar pręta Q ≠ 0 i otrzymane
wyniki porównać na wykresach gdy Q = 0.
Dane materiałowe:

k

N

cm

r

10000

2

E

N

cm





21 10

03

7

2

. *

,

. .



4.1. Ścisła próba rozciągania
pręta (próbki)

Podczas ścisłej próby rozciągania pręta (próbki)
wyznaczamy takie wskaźniki materiału, które
wymagają pomiaru bardzo małych wydłużeń
próbki. Próbka jest rozciągana do osiągnięcia
wydłużenia trwałego wynoszącego najwyżej
0,5%, co stanowi tylko początkowe stadium
rozciągania.

Po

zamocowaniu

próbki

w

uchwytach zrywarki obciążamy ją powoli do
niewielkiej wstępnej siły rozciągającej Po, przy
której dokonujemy pierwszych odczytów. Siłę Po
należy obrać w ten sposób, aby była pewność, że
przy tym obciążeniu w próbce nie zajdą jeszcze
wyraźniejsze odkształcenia plastyczne, a jeśli
nawet takie odkształcenia nastąpią, to będą one
bardzo małe i mogą być pominięte w
obliczeniach. W dalszym ciągu siłę rozciągającą
zwiększamy wg postępu arytmetycznego, zwykle
jako kolejne wielokrotności siły Po.

Po każdym obciążeniu odczytujemy wskazania.

Wyniki pomiarów i wielkości obliczane należy
rejestrować na bieżąco i przedstawić w postaci
tabelek 1-4. Stalowy pręt o długości i przekroju
kołowym o średnicy jest rozciągany siłą osiową
P. Pole przekroju poprzecznego pręta (próbki)
określono wzorem :

]

[

4

2

2

cm

d

F





P [N]

500

0

100

00

1500

0

2000

0

2500

0

300

00

3500

0

Tab.1

Tab.2

]

[

2

cm

N

rc



P [N]

5000

10000 15000 20000 25000 30000 35000

∆l

[cm]



]

[

2

cm

N

F

P

rc





Tab.
3

P [N]

5000

10000 15000 20000 25000 30000 35000

∆d

[cm]

Tab.4

4.2.

Dydaktyczny

program

komputerowy

zagadnienia statycznego rozciągania pręta

EE=2.1 10^7;

ll=100;

dd=2;

PP=3 10^4;

gam=10^3;

Poisson=0.3;

FF=(Pi dd^2)/4//N;

QQ=gam FF xx//N;

NN=PP+QQ//N;

nap1a=NN/FF//N;

nap1b=PP/FF//N

ll1a=(NN xx)/(EE FF)//N;

ll1b=(PP xx)/(EE FF)//N;

Hooke=nap1b/EE//N

wydluzenie=Hooke ll//N

odkszpop=-(Hooke Poisson)//N

zmiasrednicy=odkszpop dd//N

nap1a=Plot[nap1a,{xx,0,ll},AxesLabel-
>{"x[cm]","naprezenia [N/cm^2]"}]

nap1b=Plot[nap1b,{xx,0,ll},AxesLabel-
>{"x[cm]","naprezenia [N/cm^2]"}]

odk1a=Plot[ll1a,{xx,0,ll},AxesLabel-
>{"x[cm]","przyrost dlugosci [cm]"}]

odk1b=Plot[ll1b,{xx,0,ll},AxesLabel-
>{"x[cm]","przyrost dlugosci [cm]"}]

naprezenia=Show[nap1a,nap1b]

odksz=Show[odk1a,odk1b]

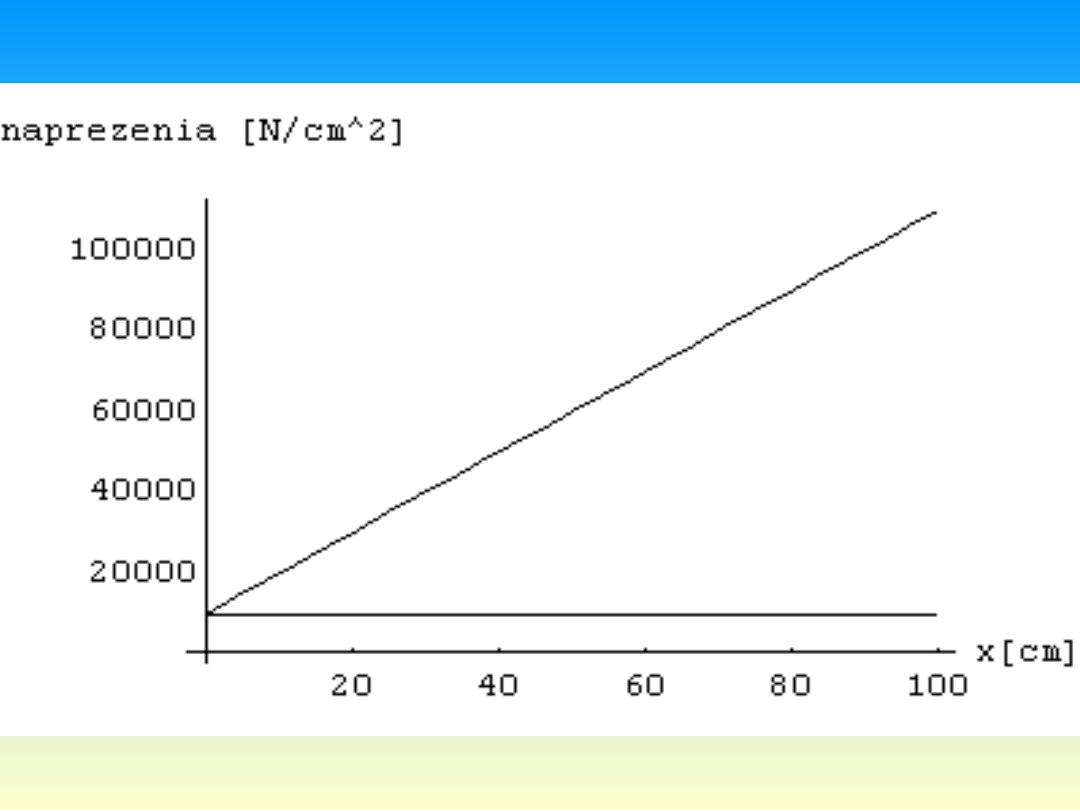
Wyniki obliczeń

Q  0

Q  0

Rys. 3. Zależność naprężeń od długości pręta.

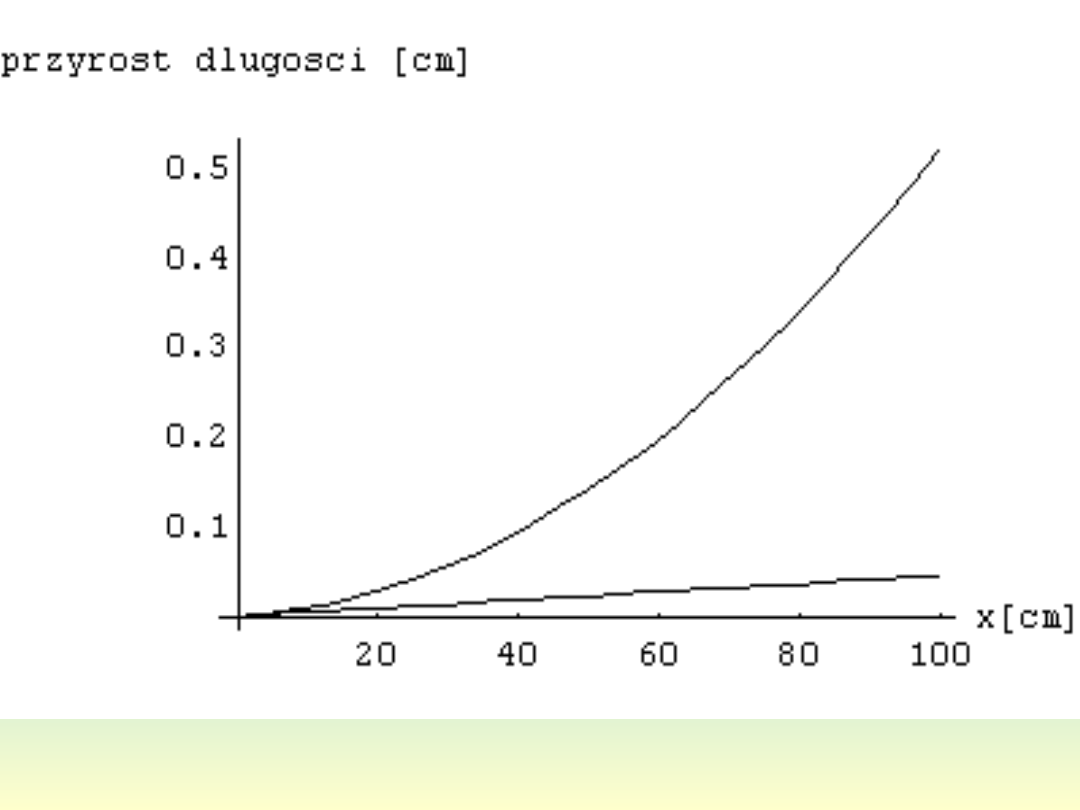
Q  0

Q  0

Rys. 4. Zależność przyrostu długości od
długości pręta.



= 9549.3

N

cm

2



=
0.00045472
8

l

= 0.0454728
cm



p = - 0.000136419

d

= -
0.000272837
cm

5. Treść sprawozdania

• opis stanowiska z rysunkiem
• wzory obliczone z wyjaśnieniem
• tabelki z wynikami pomiarów i obliczeń
• wykresy funkcji:

zależność naprężeń od długości pręta wg

wzorów:

l

,



E







l

l







zależność przyrostu długości od długości pręta
wg wzoru :

l

l,



l

l







•następnie porównanie obliczeń badawczych z
komputerowymi przy
założeniu, że Q = 0 i otrzymane wyniki porównać
na wykresach gdy Q≠0

•dyskusje wyników

LITERATURA

1. Botwin M.: Mechanika i wytrzymałość materiałów.

PWN, Warszawa.

2. Praca zbiorowa: Wernerowski K., Siołkowski B., Holka

H.: Laboratorium z kinematyki i dynamiki, WSI,
Bydgoszcz 1973.

3. Jakowluk A.: Mechanika techniczna i ośrodków

ciągłych, Ćwiczenia laboratoryjne, PWN, Warszawa
1977.

4. Jakubowicz A., Orłoś Z.: Wyrzymałość materiałów.

WNT, Warszawa.

5. Misiak J.: Mechanika techniczna, t. 1; Statyka i

wytrzymałość materiałów. WNT, Warszawa.

6. Siuta W.: Mechanika techniczna. WSiP, Warszawa.

7. Zielnica J.: Wytrzymałość materiałów. Wyd. Politechniki

Poznańskiej.

8. Kubik J. Mielniczuk J., Wilczyński A.: Wytrzymałość

techniczna. PWN, Warszawa 1980.