Suwałki 2005

Politechnika

Białostocka

Wydział (Instytut)

Mechaniczny

KATEDRA PODSTAW KONSTRUKCJI MASZYN

Instrukcja do zajęć laboratoryjnych

Temat ćwiczenia:

Badanie modułu sprężystości pasków klinowych

Numer ćwiczenia: 5

Laboratorium z przedmiotu:

Diagnostyka stanu technicznego maszyn

Kod:

MS 15005

Opracował:

dr. inż. Wiesława Załuska

- 2 -

1. Ogólna charakterystyka pasków klinowych

Materiałem podstawowym z którego wykonane są pasy klinowe jest guma, tworząca

osłonę oraz wewnętrzną warstwę pasa, wzmocnienie kompozytowe, czyli włókna o dużej
wytrzymałości na rozciąganie w postaci tkanin lub linek, stanowiące element nośny (siłowy).
Całość jest owinięta zwulkanizowaną tkaniną płócienną. Pas klinowy ma przekrój poprzeczny
w kształcie trapezu równoramiennego wykonane w postaci bezkońcowych okręgów,
wprowadzany w rowek koła pasowego działa jak klin. W efekcie otrzymuje się dobre
sprzężenie cierne. Dzięki temu mniejsze są obciążenia wałów i łożysk, co jest zaletą w
porównaniu z innymi rodzajami pasów.

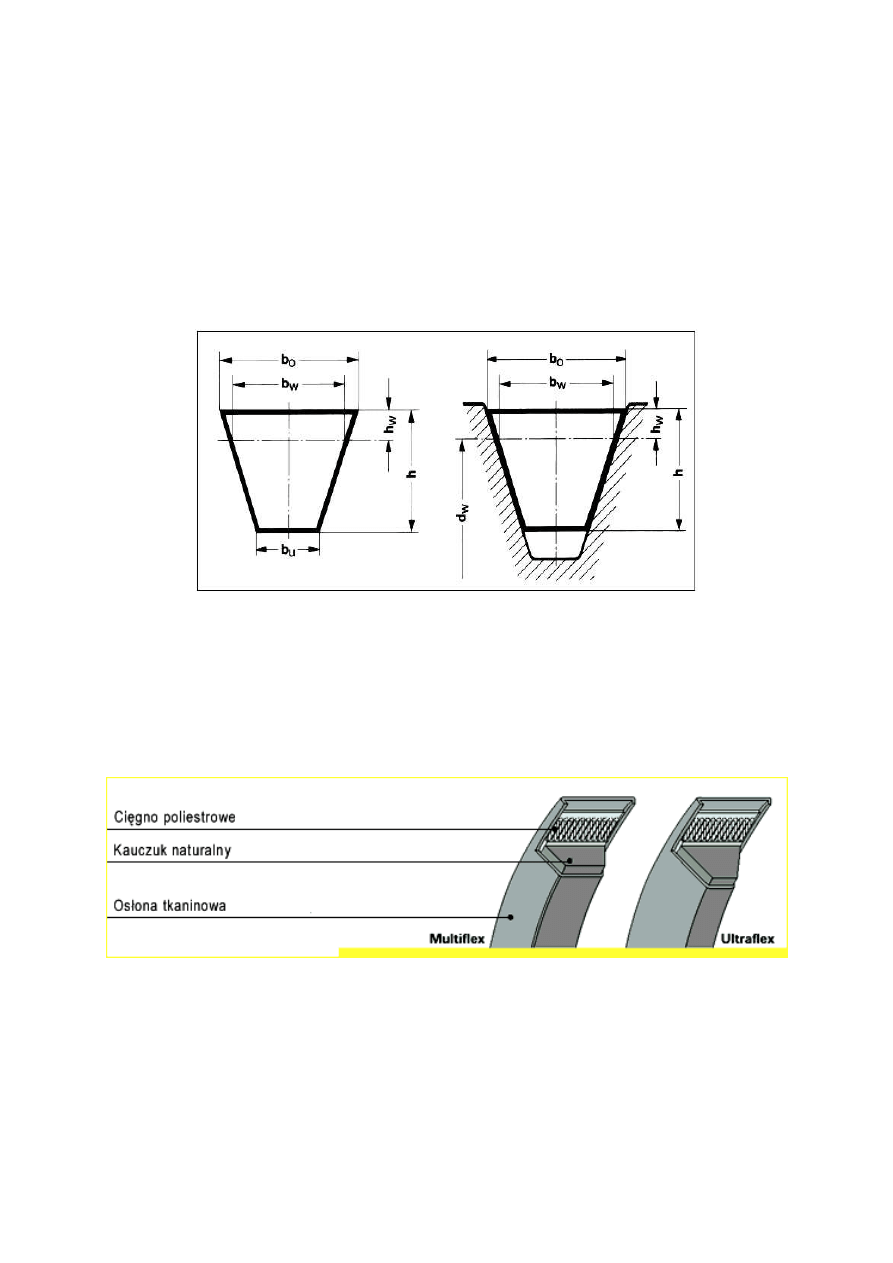
Budowa typowego pasa klinowego z podstawowymi wymiarami przedstawia

rysunek 1

Rys.1. Typowy pas klinowy z podstawowymi wymiarami

Podział i oznaczenia pasków klinowych

Pasy klinowe dzielimy ze względu na kształt oraz wymiary. Kształty oraz ich
strukturę w przekroju poprzecznym obrazuje rysunek 2

Pasy

klinowe zamknięte

P

Pasy klinowe z ciętymi brzegami

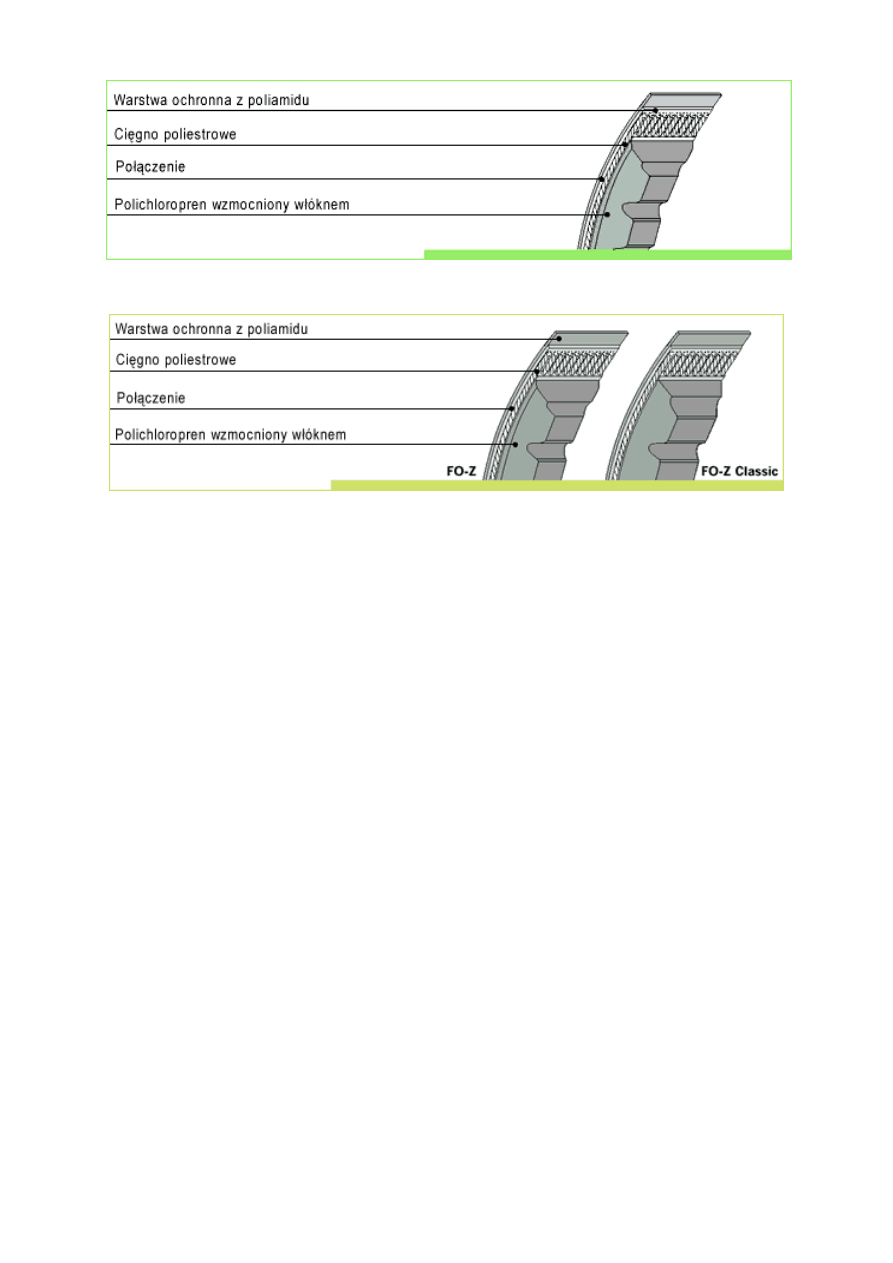
- 3 -

Pasy klinowe z ciętymi brzegami do napędów dużej mocy

Rys.2. Rodzaje pasów klinowych

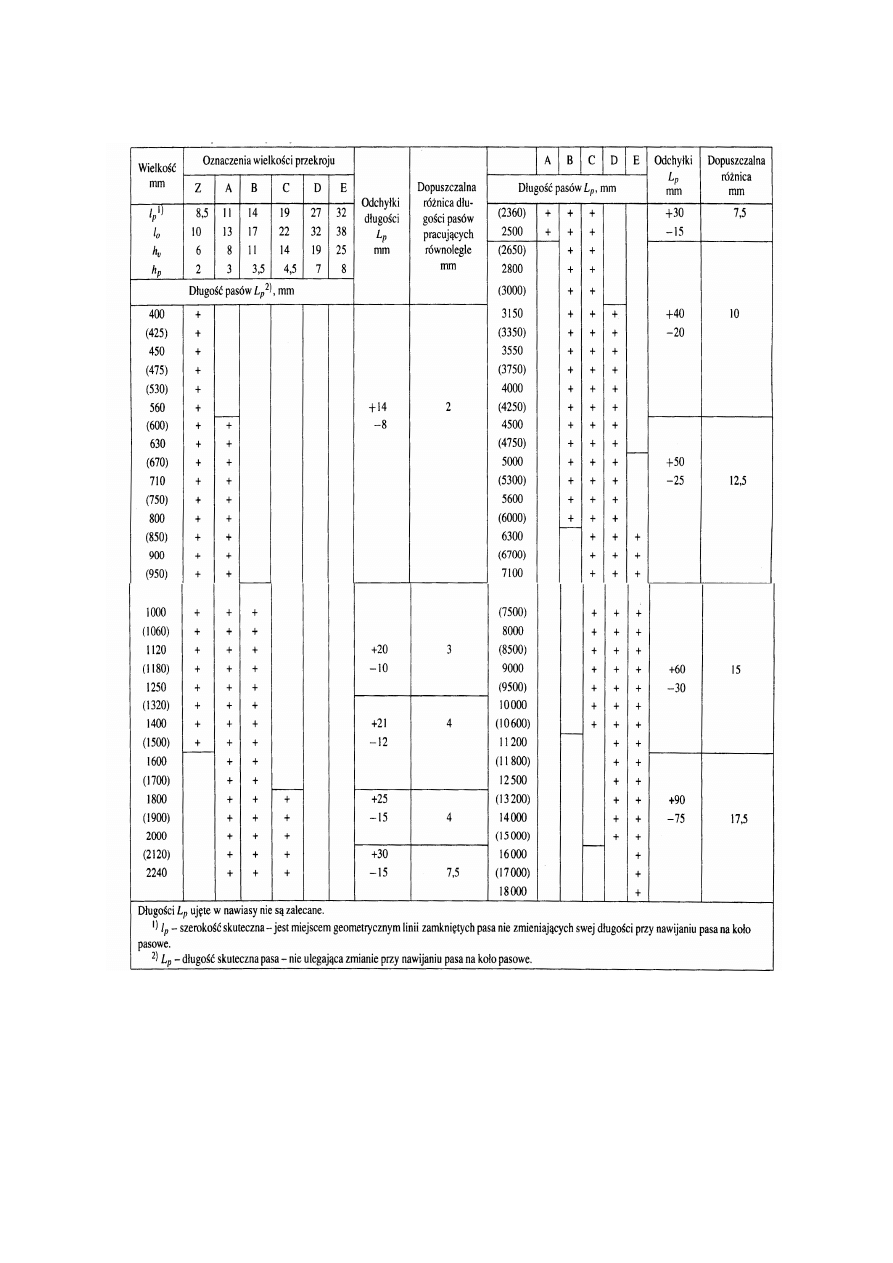
Wymiary poprzeczne zwykłych pasów klinowych oraz ich długości w obwodzie

zamkniętym są znormalizowane. Polska norma PN-86/M-85200 podaje 6 rozmiarów pasów
klinowych, oznaczonych symbolami Z oraz A, B, C, D, E. Wyciąg z tej normy podaję w
tabeli 1

2. Ogólne wymagania stawiane paskom klinowym

Eksploatacja przekładni pasowych wymaga częstej kontroli stanu powierzchni
bocznych pasa i przy pierwszych oznakach zużycia należy dokonywać natychmiast jego
wymiany. Ma to duże znaczenie szczególnie przy napędzie wieloma pasami. Rozrywanie
pojedynczych pasm wzmocnienia, prowadzi szybko do pęknięcia pasa i jest to zazwyczaj
poprzedzone zużyciem ściernym boków pasa. Jako materiał wzmacniający wierzchnią, nośną
stronę pasa stosuje się włókna szklane lub linki wiskozowe, poliestrowe, kordowe a także
stalowe. Spodnia, podatna strona pasa jest utworzona z gumy, niekiedy z dodatkiem ciętych
włókien bawełnianych, poliamidowych, szklanych lub celulozowych. Duża wytrzymałość
linek poliamidowych i stalowych pozwala zmniejszyć szerokość pasa, a tym samym
szerokość kół pasowych. Kąt zarysu przekroju pasa wynosi α = 40

0

. Przy zgięciu na kole kąt

rozwarcia α zmniejsza się. Jest tym mniejszy, im mniejsza jest średnica koła. Przy zginaniu
część pasa poniżej warstwy obojętnej pęcznieje, a powyżej tej warstwy zmniejsza swoją
szerokość.

Okresowo zmienne wydłużanie i zginanie cięgna oraz oddziaływanie na nie sił

odśrodkowych wywołuje typowe objawy zmęczenia, związane ze wzrostem temperatury oraz
rozwijającymi się w czasie drobnymi pęknięciami. Tak zachodzące niszczenie cięgna jest
potęgowane jego złym przewodnictwem cieplnym oraz niejednorodną budową.

- 4 -

Tabela 1. Wymiary pasów klinowych wg PN-86/M-85200

Od cięgien wymaga się przede wszystkim małej ich wydłużalności i małego udziału

odkształceń trwałych przy jednocześnie dużej giętkości, to znaczy dużego współczynnika E
przy rozciąganiu i małego przy zginaniu E

g

.

Materiały cięgnowe winny także wykazywać niezbyt duży współczynnik rozproszenia ς = 0.2
– 0.6 (określany stosunkiem pola histerezy sprężystej do pola wykonanej pracy), gdyż
podwyższa to sprawność przekładni cięgnowej oraz sprzyja małemu nagrzewaniu się cięgna.

Występujący wówczas wzrost wytrzymałości zmęczeniowej powoduje ponadto

zwiększenie żywotności cięgna. Pewna jednak histereza mechaniczna jest korzystna,

- 5 -

ponieważ powoduje tłumienie drgań. Od cięgien wymaga się również małego zużycia
ś

ciernego.

Zastosowanie w przemyśle

Przekładnie, w których zastosowano paski klinowe zastępują powszechnie z dużym

powodzeniem inne, na ogół droższe sposoby przenoszenia napędu. Pas klinowy należy
stosować wszędzie tam, gdzie z przyczyn ekonomicznych nie opłaca się stosować innych
rodzajów przekładni i nie zależy nam na dokładnym przekazaniu momentu obrotowego oraz
na sprawności przekładni.

Paski klinowe są stosowane do napędu: wentylatorów, dmuchaw, sprężarek

powietrznych, pras, pomp tłokowych, pomp wirnikowych, urządzeń oddalonych od centralnej
siłowni, urządzeń tworzących osprzęt silników spalinowych, maszyn i urządzeń służących do
zgrubnej obróbki materiałów (kruszarek, rozdrabniaczy), maszyn i urządzeń służących do
dozowania i transportu na niewielkie odległości (urządzeń podających, przenośników
taśmowych, pionowych), obrabiarek (np. napęd wrzeciennika tokarskiego bezpośrednio od
silnika, regulacja obrotów wiertarki stołowej)

Rys.3. Przekładnia pasowa, napęd przekazywany z silnika na maszynę roboczą poprzez kilka

pasów klinowych

3. Wielkości opisujące badania pasków klinowych

Badania pasków klinowych umożliwiają wyznaczenie modułu sprężystości pasków

klinowych, określenie wytrzymałości i trwałości pasków klinowych oraz ich odporności na
działanie temperatury.

Moduł sprężystości

Moduł sprężystości jest to stała charakteryzująca materiał poddany działaniom

różnych obciążeń zewnętrznych (sprężystych). W zależności od rodzaju obciążeń

- 6 -

zewnętrznych rozróżnia się dla obciążenia: rozciągania i ściskania współczynnik sprężystości
wzdłużnej oraz dla ścinania i skręcania współczynnik sprężystości poprzecznej.

Współczynnik sprężystości wzdłużnej E (moduł Younga) opisywany jest

stosunkiem naprężeń normalnych σ do wydłużenia względnego sprężystego ε i określa się go
zależnością

E=σ/ε

Symbol

σ

oznacza naprężenie normalne zdefiniowane jako stosunek siły do pola przekroju

próbki,

σ

= F/S , natomiast

ε

oznacza normalne odkształcenie względne, równe stosunkowi

przyrostu długości do długości początkowej

ε

=

∆

l/l

Moduły sprężystości wzdłużnej Younga

Badania polegające na wyznaczeniu modułu sprężystości pasków klinowych

określają statyczny moduł sprężystości podczas rozciągania i ściskania oraz dynamiczny
moduł sprężystości dla pasa rozciąganego i ściskanego.

Statyczne moduły sprężystości.

Charakterystyki przedstawiające zależność naprężenia występującego w pasku od

odkształcenia oraz statyczne moduły sprężystości Younga w zależności od liczby cykli
obciążenia N

i

oraz temperatury T, dla obu gałęzi pętli histerezy oraz dla przypadków

obciążenia: ściskania i rozciągania – są nieliniowe. Podczas ściskania, zarówno dla cyklu:
obciążenia i odciążenia w obszarze naprężeń około 1 MPa moduły sprężystości mają
minimum, a ich wartości są bliskie zeru.

Rys.4. Charakterystyki modułów sprężystości Younga podczas ściskania pasa klinowego

B17x11, w cykl obciążenia

)

,

,

(

T

N

f

E

i

σ

=

→

,gdzie N

i

-numer kolejny cyklu, i=1,2,3,4,5

Wraz ze wzrostem temperatury moduły maleją liniowo. Przyrost temperatury o

+60

o

K powoduje spadek wartości modułów sprężystości o kilkanaście procent [4].

Podczas rozciągania, w cyklu obciążenia, moduły sprężystości maleją nieliniowo

wraz ze wzrostem naprężenia. Natomiast w cyklu odciążania występuje podczas niskich
naprężeń minimum, ale dalszy wzrost naprężenia powoduje wzrost wartości modułów
sprężystości

Przyrost temperatury o +60 K zmniejsza wartość modułów o około 35% Z

porównania wartości statycznych modułów sprężystości podczas ściskania i rozciągania
wynika, że moduły rozciągania są od 4 do 20 razy większe od modułów sprężystości pasa
ś

ciskanego.

- 7 -

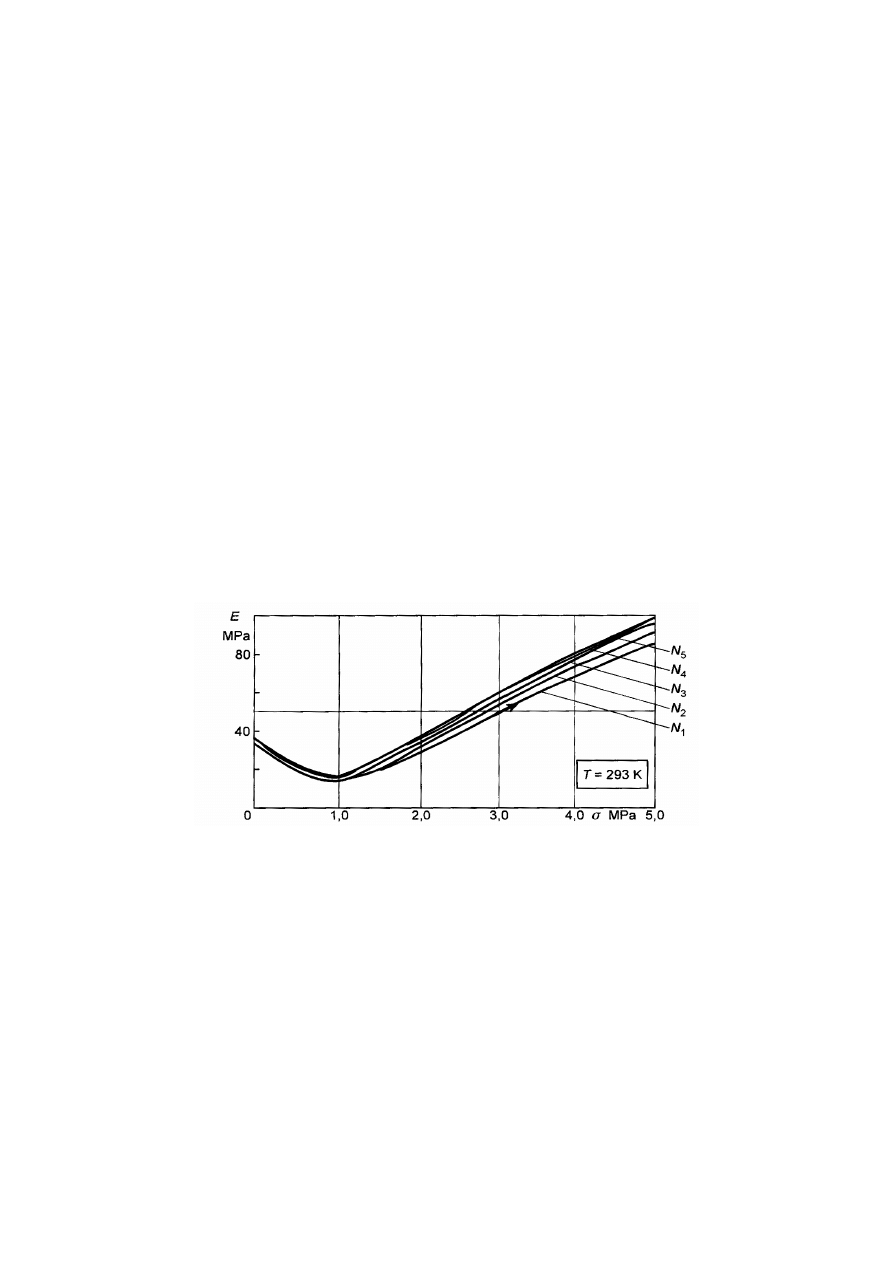
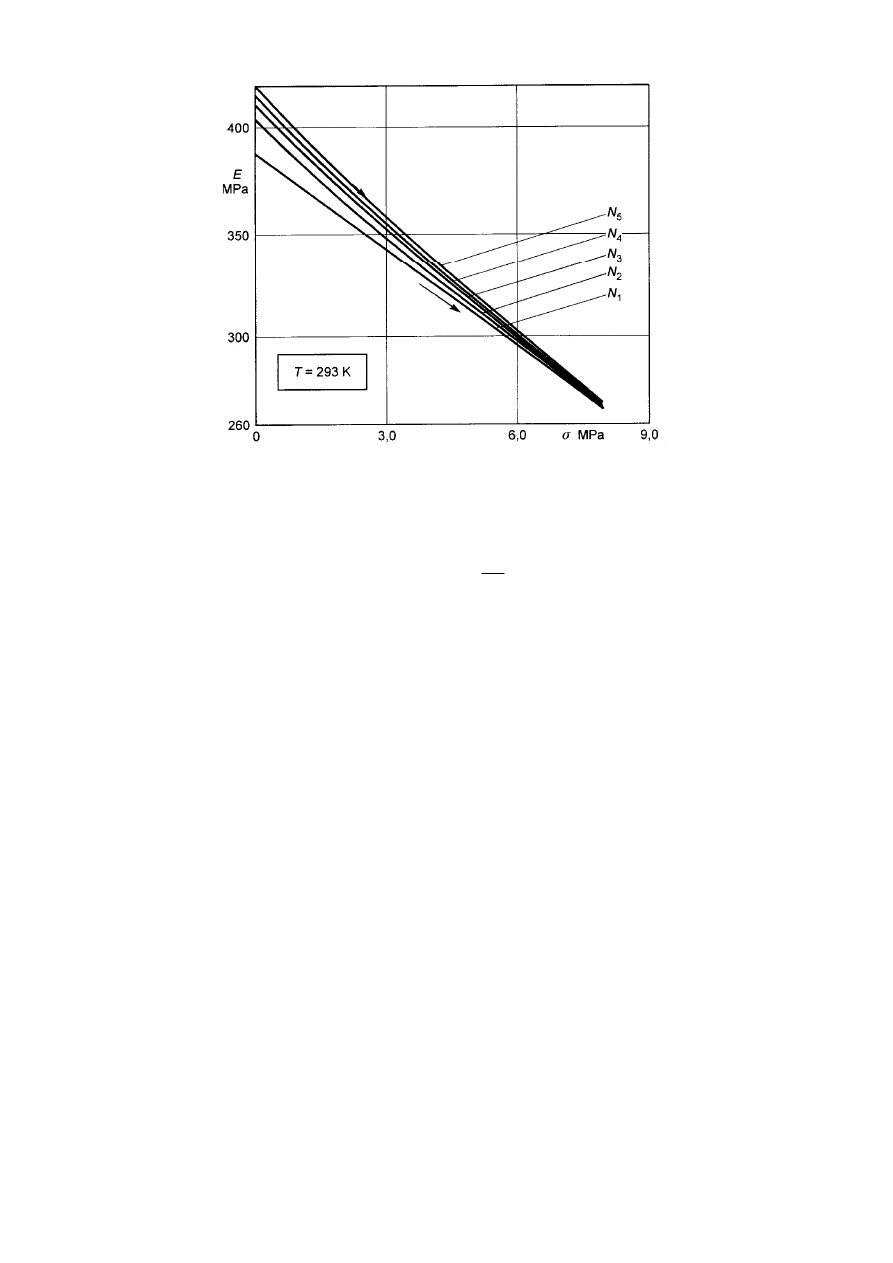
Rys.5. Charakterystyki modułów sprężystości Younga podczas rozciągania pasa klinowego

B17x11 w temperaturze 293 K w cyklu obciążenia, gdzie N

i

-numer kolejny cyklu, i=1,2,3,4,5

Wartość statycznego modułu sprężystości podłużnej E dla poszczególnych punktów

charakterystyki mechanicznej E=f(σ,N,θ) są wyznaczone ze stycznej do tych punktów

ε

σ

d

d

E

=

.

gdzie : σ – naprężenia, N – liczba cykli obciążeń, ε – odkształcenia, θ=T/T

w

– temperatura w

skali homologicznej, T

w

– temperatura wulkanizacji pasa (ok. 428 K), T – temperatura

otoczenia.

Materiał pasa klinowego po pierwszym cyklu obciążenia doznaje znacznej

stabilizacji rys.9. Krzywe pierwszego cyklu N

0

znacznie odbiegają od pozostałych cykli, które

szybko zagęszczają się w miarę wzrostu cykli i tworzą zwartą rodzinę krzywych opisanych
wzorem empirycznym

.

)

(

/

1

1

2

3

1

1

−

∧

=

∧

↔

+

=

∑

j

j

j

j

j

a

a

E

σ

θ

gdzie :

∧

ji

a

- stałe materiałowe.

Kształt pętli histerezy dla przypadku obciążeń ściskania i rozciągania, jak również

pasa rozciąganego bez kordu rys.10, jest odmienny. Pola powierzchni tych pętli (wielkość
strat energii od tarcia wewnętrznego) powiększają się wraz ze wzrostem temperatury.
Największymi stratami energii tarcia wewnętrznego charakteryzuje się materiał pasów – nie
stabilizowanych mechanicznie – dla zerowych cykli obciążeń.

Dynamiczne moduły sprężystości. Statyczne charakterystyki modułów sprężystości

istotnie różnią się od charakterystyk dynamicznych. Powodem występowania różnic jest
znaczny wpływ czasu trwania naprężenia. Odkształcenie materiału w czasie dynamicznego
obciążenia jest mniejsze od odkształcenia statycznego. Dlatego moduły dynamiczne muszą
być n- krotnie większe od statycznych. Badania kompleksowych modułów dynamicznych w
zależności od istotnych dynamicznych parametrów technicznych urządzenia dla prób
ś

ciskania i rozciągania przeprowadza się w temperaturze 293

o

K i 353

o

K.W materiałach o

właściwościach nieliniowo-lepkosprężystych, kompleksowy moduł dynamiczny E

k

składa się

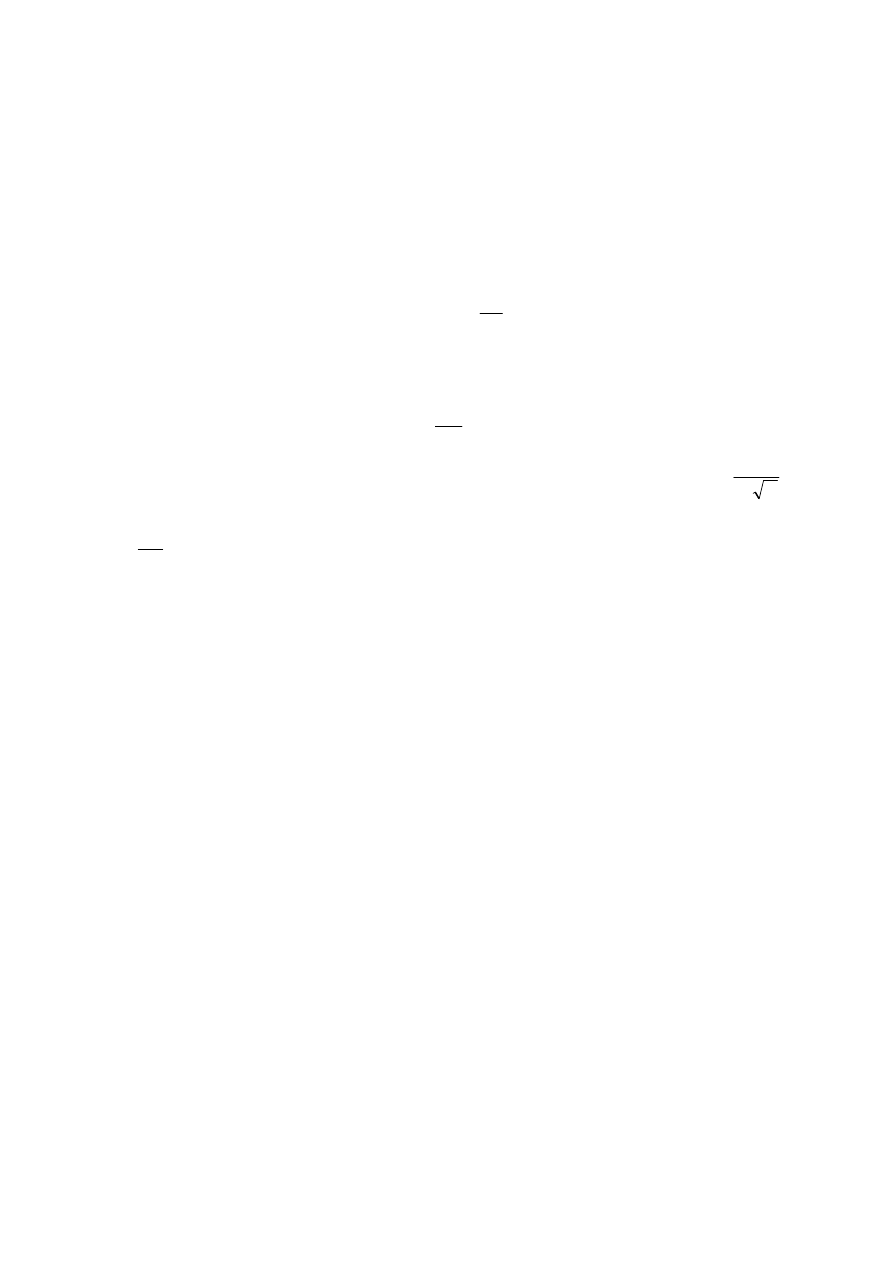
- 8 -

z części rzeczywistej E’ oraz urojonej E”. Część rzeczywista modułu kompleksowego
opisana jest wzorem

E’ = E

k

cosφ

a część urojona

E” = E

k

sinφ

gdzie φ – kąt przesunięcia fazowego.

Moduł kompleksowy E

k

wyznaczamy z zależności

E

k

=

,

a

a

ε

σ

gdzie σ

a

– amplituda naprężenia, ε

a

– amplituda odkształcenia.

E

k

=σ

m

F(λ, A

σ,

Φ),

gdzie: σ

m

– naprężenie średnie (σ

m

= σ

0

), γ =

,

m

Rm

σ

R

m

= 50 MPa – wytrzymałość na zerwanie

pasa klinowego, R’

m

=16 MPa – wytrzymałość na zerwanie pasa bez kordu, Φ

A

v

g

2

=

,

g

≅

9,80 m s

-2

, v – częstotliwość wymuszenia, A – powierzchnia przekroju poprzecznego pasa,

A

σ

=

m

a

σ

σ

- współczynnik amplitudy naprężenia.

Wzory empiryczne służące do wyznaczenia modułu kompleksowego mają postać:
dla ściskania w temperaturze 293K i 353K

],

)

)(

[(

1

4

3

3

2

2

1

1

γ

σ

σ

σ

σ

σ

Φ

+

+

Φ

+

Φ

+

+

Φ

+

=

A

q

A

p

q

p

A

q

A

p

q

p

E

m

k

dla rozciągania w temperaturze 293K i 353K

),

(

4

4

3

3

2

2

1

1

γ

γ

γ

γ

σ

σ

σ

σ

σ

Φ

+

+

Φ

+

+

Φ

+

+

Φ

+

=

A

q

A

p

q

p

A

q

A

p

q

p

E

m

k

(9)

dla rozciągania pasa bez kordu

{

}

.

]

)

)(

[(

4

4

3

3

2

2

1

1

σ

σ

σ

σ

A

m

k

q

p

q

p

A

q

A

p

q

p

E

Φ

+

Φ

+

+

Φ

+

+

Φ

+

=

Wzory empiryczne na sinus kąta przesunięcia fazowego mają postać:
dla ściskania w temperaturze 293K i 353K

sin

,

lg

lg

lg

2

2

1

σ

σ

ϕ

A

q

A

p

p

Φ

+

+

=

dla rozciągania w temperaturze 293K i 353K

sin

,

lg

lg

lg

2

2

1

1

σ

σ

ϕ

A

q

A

p

q

p

Φ

+

+

Φ

+

=

dla rozciągania pasa bez kordu

sin

.

lg

lg

lg

2

2

1

1

σ

σ

ϕ

A

q

A

p

q

p

Φ

+

+

Φ

+

=

Współczynniki p

i

i q

1

występujące we wzorach 8 - 9 oraz 11 - 12 obliczono metodą

najmniejszych kwadratów i podano w tabeli

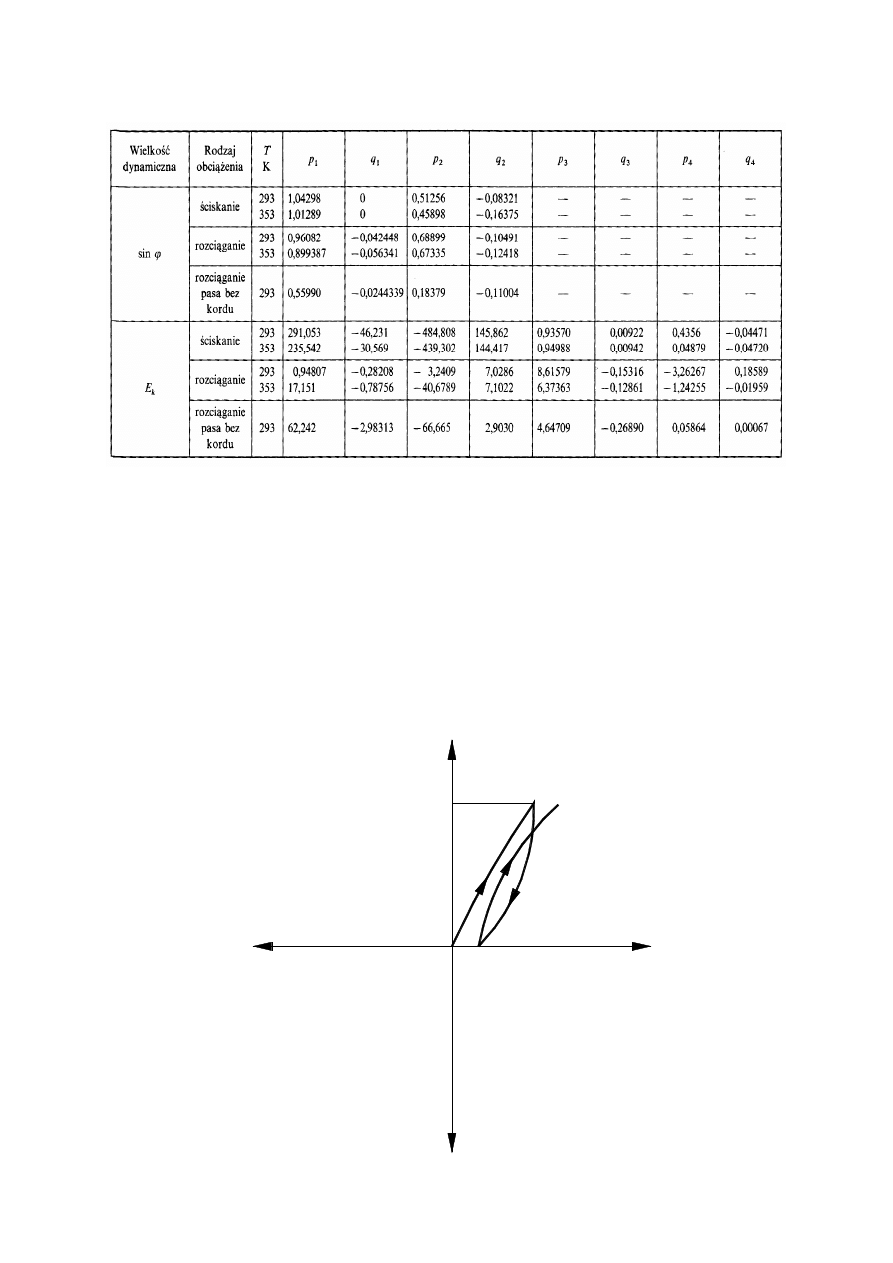
- 9 -

Tabela.2. Zestawienie współczynników do wzorów i dynamicznych modułów sprężystości

Kompleksowe moduły sprężystości Younga i jego składowe podczas ściskania i

rozciągania podlegają innym prawom empirycznym. Podczas ściskania moduły kompleksowe
E

k

i jego składowe E’, E” rosną wraz ze wzrostem naprężenia średniego σ

m

, a maleją ze

wzrostem współczynnika amplitudy naprężenia A

σ

rys.11. Wpływ częstotliwości v na moduł

E

k

i jego części rzeczywiste E’ jest nieznaczny, większy natomiast wpływ daje się zauważyć

na części urojone E” modułu kompleksowego.

Pętla histerezy sprężystej. Pętla histerezy sprężystej, przedstawia zależność naprężenia od
odkształcenia, jest to zjawisko zachodzące podczas obciążania i odciążania badanego pasa,
związkiem między odkształceniem sprężystym i plastycznym a naprężeniem je
wywołującym. Jeżeli jakikolwiek materiał poddamy po raz pierwszy rosnącemu obciążeniu,
wówczas wraz ze wzrostem naprężeń σ rosną odkształcenia ε wg krzywej 1 rys.6.

σ

r

σ

1

3

2

0

ε

−

ε

σ

−

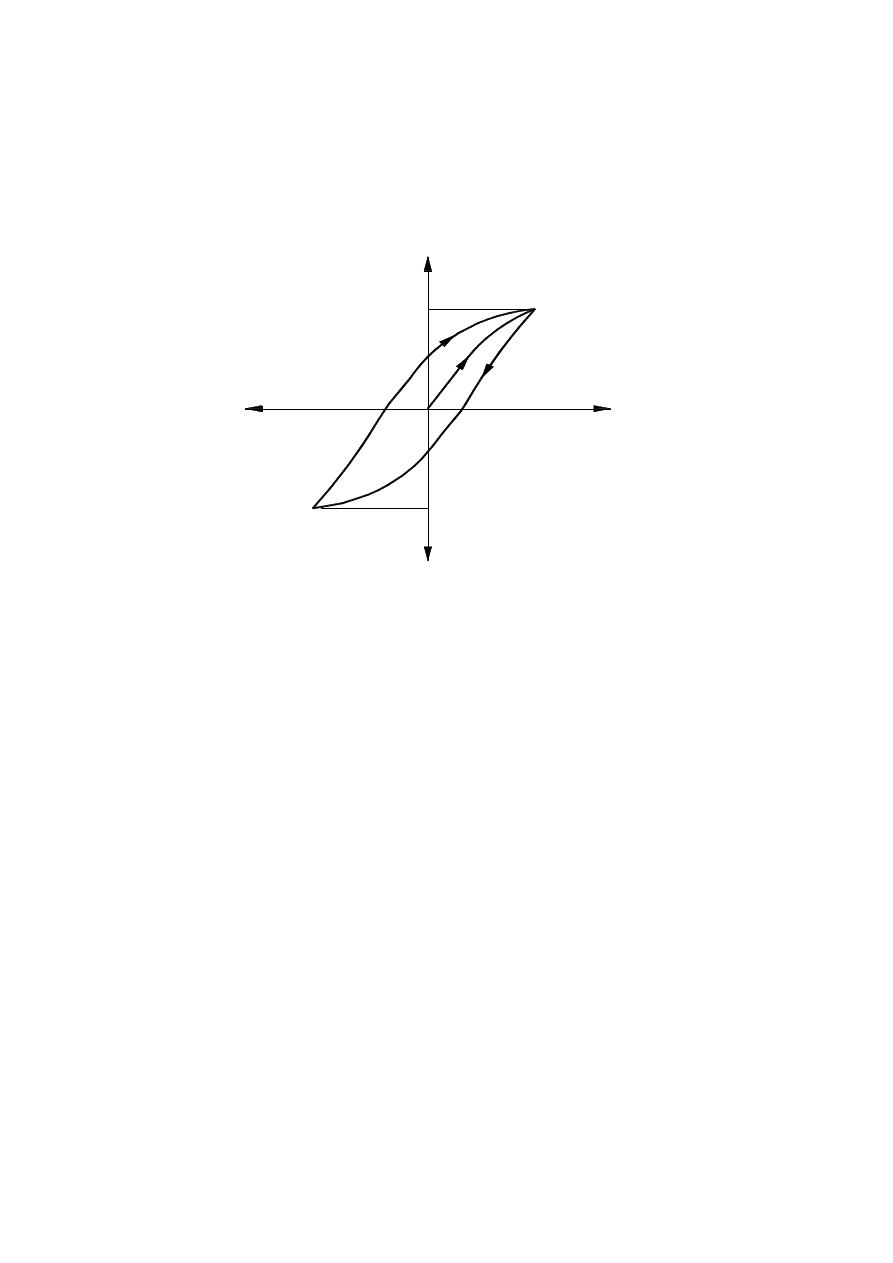
- 10 -

Rys.6. Rozciąganie od 0 do wartości naprężenia

r

σ

[9]

Po osiągnięciu wartości

r

σ

(naprężenie powstałe podczas rozciągania) następuje

odciążanie materiału, czyli spadek naprężeń, odkształcenia maleją wg krzywej 2, a podczas
ponownego wzrostu naprężeń

r

σ

rosną zgodnie z krzywą 3. Rys. 7, przedstawia rozciąganie

r

σ

oraz ściskanie

c

σ

, rysunek

13 przedstawia rozciąganie od 0 do wartości naprężenia

r

σ

.

A

A

B

C

D

E

F

3

1

2

r

σ

c

σ

σ

σ

−

ε

-ε

0

Rys.7. Rozciąganie σ

r

oraz ściskanie σ

c

Pole ABCDEFA powstałe w wyniku rozciągania i ściskania na wykresie zawarte

jest między krzywymi w pełnym cyklu obciążenia, jest miarą pracy (na jednostkę objętości
materiału w jednym cyklu podczas odciążania) wydzielanej energii cieplnej. Obie gałęzie
krzywej zamykającej to pole nazywa się pętlą histerezy odkształceń. Kształt pętli histerezy
odkształceń zależy od wielkości naprężeń, rodzaju materiału, szybkości odciążenia. Pętlę
histerezy odkształceń uzyskuje się również dla innych rodzajów obciążeń, np. skręcania
kolejno w przeciwnych kierunkach

4.Przedmiot badań, warunki pomiaru

W celu wykonania badania modułu sprężystości paska klinowego zastosuję dwa

rodzaje pasków:
- pas klinowy o wymiarach B 14 x 11. Pas ten posiada 6 włókien w postaci linek
poliamidowych jako element nośny, wzmocnienie, w celu przeniesienia większych obciążeń
wzdłużnych rozciągających oraz uzyskania większej sztywności, co ma wpływ na moc jaką
przenosi jeden pas klinowy.
- pas klinowy o wymiarach A 11 x 8. Pas ten nie posiada wzmocnienia w postaci linek
poliamidowych, czyli kordu jest to celowe by w przeprowadzonym badaniu obu różnych
pasów pokazać znaczące różnice w module sprężystości pasa z kordem, bez kordu oraz dla
różnych przekrojów.
Badanie przeprowadzić należy na stanowisku do badania modułu sprężystości pasków
klinowych Pasy klinowe poddać różnym obciążeniom rozciągającym statycznym i
dynamicznym. Wartość statycznego i dynamicznego modułu sprężystości wyznaczyć w
oparciu o kształt pętli histerezy powstałych w wyniku badań.

3

2

0

ε

−

ε

σ

−

- 11 -

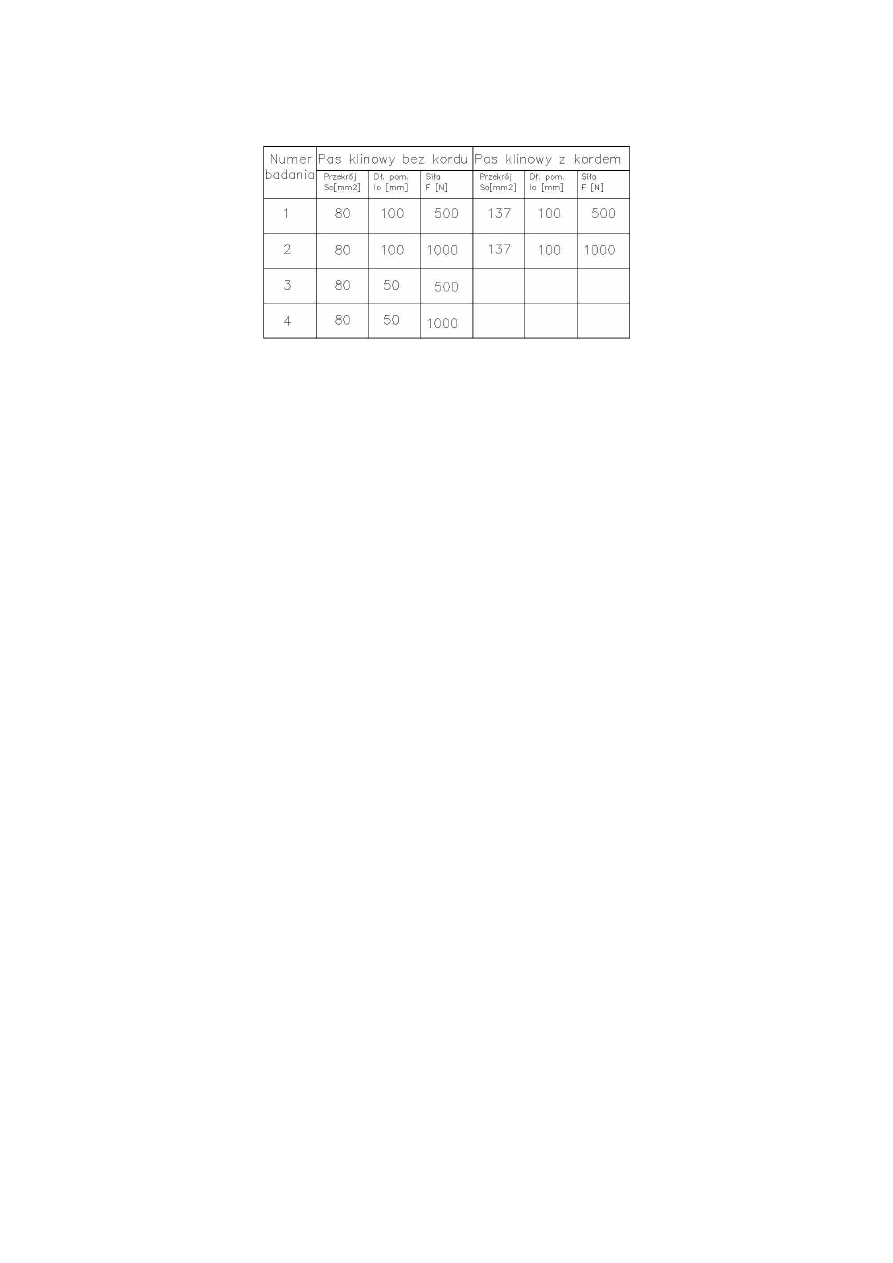
Tabela 3. Plan badań podczas wyznaczania

statycznego i dynamicznego modułu sprężystości

pasków klinowych

5. Opracowanie wyników pomiarów

Po otwarciu pliku z wynikami (pliki z rozszerzeniem *.dat) w programie Excel

uruchamia się automatycznie kreator importu tekstu, który ustala jakiego rodzaju są dane w
pliku. Ponieważ dane w plikach wynikowych są zapisane w postaci tabelarycznej, kreator
automatycznie dokonuje podziału na kolumny. Otwarty plik zapisujemy w formacie
skoroszytu Excel i przystępujemy do analizy.

Możemy usunąć kolumny które nie zarejestrowały żadnych wartości, w zależności

od rodzaju badania pozostawić należy kolumny z nagłówkiem:
badanie statyczne:

przes liniowe nowe [mm]-kanał 5,
karta bipolarna [V]-kanał 10,
badanie dynamiczne:
Piezo[m/s-2]-kanał 1,
przes liniowe nowe [mm]-kanał 5,
karta bipolarna [V]-kanał 10.

Kolejną czynnością do wykonania jest stworzenie dodatkowych kolumn, służących

do wyliczenia interesujących nas wielkości, w przypadku badań statycznych:

wartości naprężenia σ,
wartości odkształcenia ε,
modułu sprężystości E

W przypadku dynamicznych tworzymy kolumny:

naprężenie średnie σ

m

,

amplituda naprężenia σ

a

,

współczynnik amplitudy naprężenia A

σ

,

kąt przesunięcia fazowego φ,
współczynnik wytrzymałości pasa klinowego γ,
moduł kompleksowy dla pasa z kordem E

k

’,

moduł kompleksowy dla pasa bez kordu E

k

,

dynamiczny moduł Younga dla pasa z kordem E’,
dynamiczny moduł Younga dla pas bez kordu E.

W kolejnych kolumnach wpisujemy wartości stałe, dla badań statycznych:

długość bazy pomiarowej l

o

,

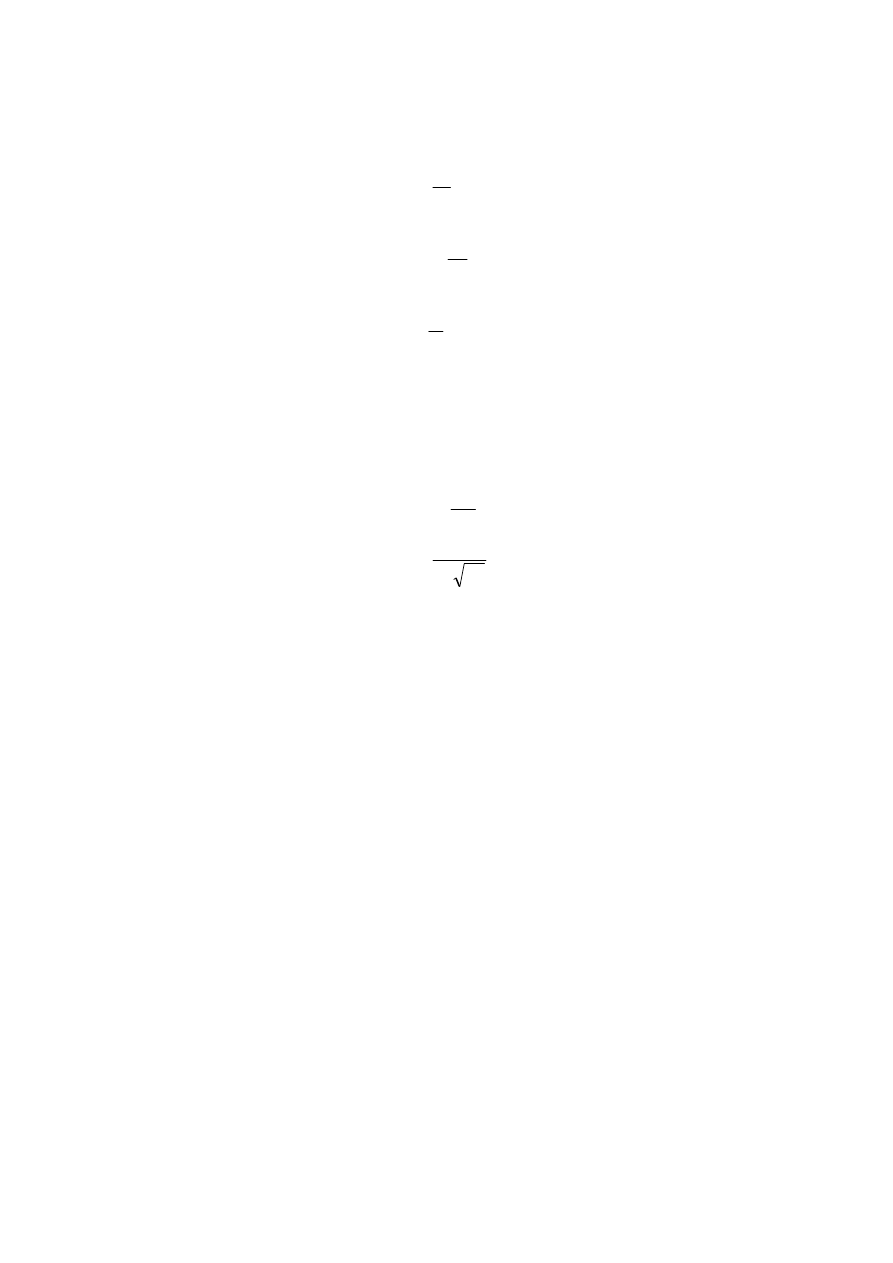
- 12 -

powierzchnię przekroju poprzecznego paska s

0

,

a w następnych tworzymy formuły do wyliczenia statycznego modułu sprężystości:
w kolumnie σ tworzymy formułę do wyliczenia naprężenia

],

[

0

MPa

s

F

=

σ

w kolumnie ε tworzymy formułę do wyliczenia odkształcenia

,

0

l

l

∆

=

ε

i w kolumnie E tworzymy formułę do wyliczenia statycznego modułu sprężystości

].

[MPa

E

ε

σ

=

Dla badań dynamicznych tworzymy formuły do wyliczenia:
sinusa kąta przesunięcia liniowego

,

lg

lg

lg

sin

2

2

1

1

σ

σ

ϕ

A

q

A

p

q

p

Φ

+

+

Φ

+

=

współczynniki amplitudy naprężenia

,

m

a

A

σ

σ

σ

=

,

2

o

S

g

ν

=

Φ

kompleksowego modułu dla pasa z kordem

),

(

'

4

4

3

3

2

2

1

1

γ

γ

γ

γ

σ

σ

σ

σ

σ

Φ

+

+

Φ

+

+

Φ

+

+

Φ

+

=

A

q

A

q

q

p

A

q

A

p

q

p

E

m

k

kompleksowego modułu dla pasa bez kordu

{

}

,

]

)

)(

[(

4

4

3

3

2

2

1

1

σ

σ

σ

σ

A

m

k

q

p

q

p

A

q

A

p

q

p

E

Φ

+

Φ

+

+

Φ

+

+

Φ

+

=

dynamicznego modułu dla pasa z kordem

E’ = E

k

‘sinφ,

dynamicznego modułu dla pasa bez kordu

E = E

k

sinφ.

Reszta współczynników niezbędnych do obliczeń opisana jest w punkcie 4.3.

Wartość obliczonych dla każdej pary współczynników i modułu sprężystości E nie

jest miarodajna, określa jedynie dyskretne wartości dla poszczególnych punktów
pomiarowych.

Na podstawie tak opracowanych wyników przystąpiono do narysowania wykresów

pętli histerezy statycznej lub dynamicznej i opracowania wyników wybranych punktów
pomiarowych w formie tabeli.

Na wykresach możemy zaobserwować trwałe odkształcenie badanego pasa. W celu

wyliczenia wartości ∆l należy w arkuszu kalkulacyjnym w kolumnie przes. liniowe nowe
[mm]-kanał 5 odjąć od siebie wartość przesunięcia w momencie rozpoczęcia obciążania od

- 13 -

wartości przesunięcia w momencie zakończenia odciążania. Wynik jest interesującym nas
odkształceniem trwałym ∆l.

9. Warunki BHP

Podczas wykonywania badania należy przestrzegać ogólnych przepisów BHP obowiązujących na

stanowisku badawczym. Przy obsłudze stanowiska do badań pasków klinowych należy:

- nie dotykać części będących w ruchu,

- nie dotykać przewodów zarówno elektrycznych jak i pneumatycznych będących pod zasilaniem,

- nie wolno zmieniać połączeń elektrycznych podczas pracy stanowiska,

- pamiętać o dokładnym zamocowaniu części rozłącznych,

- przed badaniem być pewnym o właściwym zamocowaniu i zabezpieczeniu wszystkich części
stanowiska.

Literatura:

1. Dudziak M.: Przekładnie cięgnowe, WNT, Warszawa 1997
2. Łączyński B..: Niemetalowe elementy maszyn, WNT, Warszawa 1988
3. Massalski J.M..: Fizyka dla inżynierów, WNT, Warszawa 1973
4. Praca zbiorowa.: Laboratorium Wytrzymałości Materiałów ,KWM IMB PK, Kraków 2002
5. Praca zbiorowa.: Podstawy techniki, WNT, Warszawa 1974
6. Woropay M..: Podstawy badań eksploatacyjnych wybranych El. maszyn, WU, Bydgoszcz
2001