Wykład IV.

Literatura: Miller i Starr rozdz.4(44), Tyszka i Zale

ś

kiewicz str.72-90

P u ł a p k i d e c y z y j n e

1. Bł

ę

dy w sformułowaniu problemu

2. Bł

ę

dy w oczekiwaniach

3. Dysonans post-decyzyjny i nieodwracalno

ść

podj

ę

tej decyzji (…)

4. Dysonans decyzyjny a presja na podj

ę

cie decyzji w grupie (…)

2

1 . B ł

ę

d y w s f o r m u ł o w a n i u p r o b l e m u

i. zakotwiczenie

ii. utrzymywanie status quo

iii. „utopione” koszty

iv. „framing”

v. selektywna percepcja

vi. dost

ę

pno

ść

psychologiczna

vii. nieuzwgl

ę

dnianie istotnego prawdopodobie

ń

stwa

vii.nieuzwgl

ę

dnianie istotnego prawdopodobie

ń

stwa

3

Podejmowanie decyzji w warunkach pewno

ś

ci, ryzyka i niepewno

ś

ci

typologia sytuacji

•

konsekwencje wyboru pewne = podejmowanie decyzji w warunkach pewno

ś

ci

•

konsekwencje wyboru niepewne ale przewidywalne (mo

ż

na okre

ś

li

ć

stopie

ń

prawdopodobie

ń

stwa ich wyst

ą

pienia) =

podejmowanie decyzji w warunkach ryzyka

•

konsekwencje wyboru niepewne i nieprzewidywalne (nie mo

ż

na okre

ś

li

ć

stopnia prawdopodobie

ń

stwa ich wyst

ą

pienia) =

podejmowanie decyzji w warunkach niepewno

ś

ci

4

J a k p o s t

ę

p o w a

ć

w sytuacji ryzyka ?

logika konsekwencji

1. okre

ś

l struktur

ę

problemu - czyli odrzu

ć

fabuł

ę

i skup si

ę

na tym, co najistotniejsze a wi

ę

c na:

•

alternatywach /strategiach działania

•

konsekwencjach przedstawiaj

ą

c je w postaci kwantyfikowanej

2.

przedstaw struktur

ę

problemu w formie:

•

macierzy decyzji

b

ą

d

ź

•

drzewa decyzji

3.

dokonaj wyboru stosuj

ą

c kryterium wyboru alternatywy wła

ś

ciwe w sytuacji ryzyka

5

Sytuacja decyzyjna I

(T.Tyszka, Sens i bezsens..,WSPiZ)

Firma produkuj

ą

ca podzespoły elektroniczne, na skutek niekorzystnej sytuacji rynkowej, zamkn

ę

ła ubiegłoroczny bilans znaczn

ą

strat

ą

finansow

ą

.

Bank jest skłonny udzieli

ć

jej nowego kredytu, aby rozwin

ąć

produkcj

ę

i zrekompensowa

ć

poniesione straty. Kierownictwo firmy zastanawia si

ę

, czy

wzi

ąć

nowy kredyt. Je

ż

eli firma nie we

ź

mie nowego kredytu, to przy korzystnej koniunkturze zamknie nast

ę

pny rok niewielkim zyskiem, który

pozwoli z ledwo

ś

ci

ą

pokry

ć

poprzednie straty, natomiast przy powtórzeniu si

ę

niekorzystnej sytuacji rynkowej, firma zwi

ę

kszy straty. Je

ż

eli firma

we

ź

mie nowy kredyt, to przy dobrej koniunkturze zamknie nast

ę

pny rok znacznym zyskiem, który nie tylko pozwoli

pokry

ć

poprzednie straty, ale doprowadzi firm

ę

do dobrej kondycji finansowej. Jednak w przypadku złej sytuacji rynkowej dodanie nowego kredytu

do ju

ż

wcze

ś

niej zaci

ą

gni

ę

tego mo

ż

e doprowadzi

ć

firm

ę

do utraty płynno

ś

ci, a tym samym - do upadku.

Wziąć kredyt czy nie brać kredytu?

Sytuacja decyzyjna II

(T.Tyszka, Sens i bezsens..,WSPiZ)

Firma sadownicza zajmuje si

ę

„produkcj

ą

” owoców, które nast

ę

pnie sprzedawane s

ą

kontrahentowi wytwarzaj

ą

cemu przetwory. Współpraca trwa

od kilku lat i jest jedynym

ź

ródłem dochodów firmy sadowniczej. W tym roku okazało si

ę

,

ż

e na skutek bł

ę

dów popełnionych w uprawie, zebrane

owoce nie spełniaj

ą

tak wysokich wymaga

ń

jako

ś

ci, jakie zapewnione były w kontrakcie. Kontrahent nie dokonuje ju

ż

u siebie kontroli jako

ś

ci, gdy

ż

w umowie okre

ś

lono,

ż

e nale

ż

y to do zada

ń

sadownika, który znany jest z solidnego dotrzymywania zobowi

ą

za

ń

. Je

ż

eli kierownictwo firmy

sadowniczej zdecyduje si

ę

nie dostarcza

ć

owoców swemu kontrahentowi, poniesie ogromne straty, które mog

ą

postawi

ć

pod znakiem zapytania

dalsze istnienie firmy. Kierownictwo firmy zastanawia si

ę

zatem, czy mimo wszystko, nie spróbowa

ć

sprzeda

ż

y nieco “wybrakowanej” partii

owoców, gdy

ż

jest pewna szansa nie wykrycia przez kontrahenta ni

ż

szej jako

ś

ci Je

ż

eli jednak partia owoców rozpoznana zostanie przez

kontrahenta jako wybrakowana, firma straci całkowicie dobr

ą

opini

ę

nie tylko u obecnego odbiorcy, ale tak

ż

e na rynku, na którym działa.

Sprzedać wybrakowaną partię owoców czy nie sprzedawać wybrakowanej partii ?

W jaki sposób podjąć właściwe decyzje w tych sytuacjach ?

Co jest dane ?

Co jest niewiadome ?

6

Formuła maksymalizacji warto

ś

ci oczekiwanej

Blaise Pascal do kawalera de la Meré:

"W swych działaniach (łącznie z grą w kości) obieraj takie postępowanie, które gwarantowałoby Ci przy danych szansach możliwie
największy zysk..."

W grze w ko

ś

ci 4 rzuty jedn

ą

kostk

ą

wystarcz

ą

do skutecznego (z szansami nieco wi

ę

kszymi od 50 %) obstawienia zakładu,

ż

e uda si

ę

wyrzuci

ć

szóstk

ę

. Takie prawdopodobie

ń

stwo wynosi:

,,pewno

ść

– 4-krotnie nie-szóstka” czyli 1 - (5/6)

4

= 1 - 625/1296 > 0.5

Ten wynik de Meré próbował uogólni

ć

na przypadek gry dwoma kostkami. „Przestrze

ń

zdarze

ń

” dla dwóch kostek wyznacza 6

x 6 czyli 36 mo

ż

liwo

ś

ci. De Meré próbował przenie

ść

mechanicznie proporcj

ę

z rzutów jedn

ą

kostk

ą

i zakładał 4/6 x 36 = 24, a

wi

ę

c zakładał si

ę

,

ż

e wyrzuci dwie szóstki w przynajmniej 24 rzutach i ... przegrywał. Szukał wi

ę

c pomocy u Pascala i j

ą

znalazł.

ś

eby gra

ć

bezpiecznie potrzeba a

ż

25 rzutów bowiem przy 24

rzutach prawdopodobie

ń

stwo podwójnej szóstki wynosi 1 –

(35/36)

24

=

0,4914

Warto

ść

0,4914 opisuj

ą

cej prawdopodobie

ń

stwo uzyskania

sonnez

czyli podwójnej 6 szóstki w serii 24 rzutów dwoma

kostkami przyj

ą

ł Blaise Pascal do okre

ś

lenia warto

ś

ci

oczekiwanej gry polegaj

ą

cej na obstawianiu 100 luidorów na

wyst

ą

pienie podwójnej szóstki w serii 24 rzutów par

ą

ko

ś

ci.

Warto

ść

oczekiwana takiej gry wynosi:

(-100 L) x 0,5086 + (100L) x

0,4914

= - 1,72 luidora

Zasada "nadziei matematycznej" (warto

ś

ci oczekiwanej)

czyli wielko

ś

ci uwzgl

ę

dniaj

ą

cej

wielko

ść

szansy

oraz

wielko

ść

wypłaty

. Od strony formalnej WO = sumie

warto

ś

ci oczekiwanych przy ka

ż

dej z rozpatrywanych

alternatyw

7

Sytuacja decyzyjna III

a) Warto

ść

oczekiwana zakładu zawartego - w formie umowy – z ubezpieczycielem

• Suma ubezpieczenia 2 000 000 zł
• Polisa 1 000 zł
• Prawdopodobie

ń

stwo włamania 0,002

Warto

ść

oczekiwana

0,002 x (2 000 000 – 1 000) + 0,998 x (- 1 000) = 3 000 zł

b) Warto

ść

oczekiwana zakładu zawartego - w formie umowy – z ubezpieczycielem

• Suma ubezpieczenia 1 000 000 zł
• Polisa 4 000 zł
• Prawdopodobie

ń

stwo włamania 0,0001

Warto

ść

oczekiwana

0,0001 x (1 000 000 – 4 000) + 0,9999 x (- 4 000) = - 3 900 zł

Który z tych zakładów warto zaakceptować / którą z umów warto zawrzeć ?

8

Sytuacja decyzyjna IV

Przedsi

ę

biorca musi podj

ąć

decyzj

ę

o podj

ę

ciu produkcji jednego z 2 mo

ż

liwych produktów kieruj

ą

c si

ę

motywem oczekiwanej zyskowno

ś

ci

produkcji ka

ż

dego z tych produktów. Uznaj

ą

c,

ż

e powodzenie na rynku zale

ż

y m.in. od mo

ż

liwo

ś

ci ulokowania jak najwi

ę

kszego wolumenu swych

produktów zastanawia si

ę

który z nich b

ę

dzie wprowadzonym do produkcji nowym produktem. Wyniki bada

ń

preferencji konsumentów oraz analiza

posiadanych mo

ż

liwo

ś

ci technologicznych nie pozwalaj

ą

podj

ąć

jednoznacznej decyzji. Skutki wyboru s

ą

niepewne ale przewidywalne. Otó

ż

je

ś

li w

gr

ę

wchodz

ą

2 mo

ż

liwe produkty: A i B, to realizacja celu przedsi

ę

biorcy poza wyborem jednego z 2 produktów, zale

ż

y tak

ż

e od przyszłej i

niepewnej koniunktury rynkowej, ta za

ś

mo

ż

e polega

ć

na o

ż

ywieniu gospodarczym wzgl

ę

dnie na stagnacji. Nie mo

ż

na te

ż

wykluczy

ć

depresji.

Odmienne charakterystyki ka

ż

dego z produktów sprawiaj

ą

,

ż

e A przyniesie najwi

ę

ksze przychody w sytuacji o

ż

ywienia gospodarczego, natomiast B

ze wzgl

ę

du na to,

ż

e mo

ż

e zaspakaja

ć

tzw. potrzeby podstawowe przyniesie wi

ę

ksze przychody ale – paradoksalnie – w sytuacji stagnacji.

Przedsi

ę

biorca zdaje sobie spraw

ę

,

ż

e jego powodzenie zale

ż

y nie tylko od jego wyboru jednego z produktów ale tak

ż

e od niekontrolowanych

przeze

ń

przyszłych warunków rynkowych.

Jakiego wyboru powinien dokonać ?

S t r u k t u r a p r o b l e m u przedstawiona jako

m a c i e r z d e c y z j i

Produkty

ożywienie gospodarcze

p=0,25

stagnacja

p=0,50

depresja gospodarcza

p=0,25

A

40 000

30 000

20 000

B

70 000

20 000

0

Rozwi

ą

zanie problemu

WO (A) = 40 000x0,25 + 30 000x0,50 + 20 000x0,25 = 30 000

WO (B) = 70 000x0,25 + 20 000x0,50 + 0x0,25 = 27 500

9

Produkty

ożywienie gospodarcze

p=

4/8

stagnacja

p=

3/8

depresja gospodarcza

p=

1/8

A

40 000

30 000

20 000

B

70 000

20 000

0

Rozwi

ą

zanie problemu

WO (A) = 40 000x4/8 + 30 000x3/8 + 20 000x1/8 = 33 750

WO (B) = 70 000x4/8 + 20 000x3/8 + 0x1/8 = 42 500

Czy w tej zmienionej sytuacji nie warto jednak zdecydować się na wybór produktu A ? Minimalny przychód w każdej z 3 niepewnych sytuacji wynosi co
najmniej 20 000 !!!

10

Zarz

ą

dzanie ryzykiem

1. dzielenie ryzyka

2. poszukiwanie informacji redukuj

ą

cej ryzyko

3. dywersyfikacja ryzyka

4. ubezpieczenie si

ę

od skutków ryzyka

5. manipulowanie ryzykiem (wykorzystanie teorii perspektywy)

11

Sytuacja decyzyjna V

Przedsi

ę

biorca – z racji niepowodze

ń

w dotychczasowej karierze postanowił zmieni

ć

bran

żę

. Postanowił specjalizowa

ć

si

ę

w ubezpieczeniach i

którego

ś

dnia stan

ą

ł przed zadaniem ograniczenia do minimum szkód z powodu utkwienia w odwiertach czterech cennych diamentowych wierteł

stosowanych podczas poszukiwania w Kazachstanie złó

ż

ropy naftowej. Ka

ż

de z wierteł jest warte 2 mln zł i wszystkie zostan

ą

bezpowrotnie

spisane na straty, je

ś

li w ci

ą

gu nadchodz

ą

cych 48 godzin nie nadejdzie pomoc. Przedstawiciel jednej z firm ratowniczych przedstawił mu do wyboru

2 plany działania (A i B) o takich samych kosztach realizacji.
Plan A – w ramach tego planu uda si

ę

uratowa

ć

jedno wiertło dzi

ę

ki czemu szkody zostan

ą

ograniczone o 2 mln.

Plan B – w ramach tego planu istnieje 1 szansa na 4,

ż

e uda si

ę

uratowa

ć

wszystkie wiertła ale i 3 na 4,

ż

e nie uda si

ę

uratowa

ć

ż

adnego.

Jakiego wyboru powinien dokonać ?

Przedstawiciel innej firmy ratowniczej opracował dwa inne plany (C i D).
W ramach planu C s

ą

3 szanse na 4 na utrat

ę

wszystkich wierteł ale i jedna szansa na cztery na uratowanie te

ż

wszystkich wierteł. Natomiast

realizacja planu D poci

ą

gnie za sob

ą

utrat

ę

trzech z czterech wierteł, co oznacza,

ż

e suma szkód z tego tytułu wyniesie 6 mln zł.

Jakiego wyboru powinien dokonać ?

12

13

Wykorzystanie teorii perspektywy

r o z d z i e l a j z y s k i




ł

ą

c z s t r a t y

ł

ą

c z m n i e j s z

ą

s t r a t

ę

z w i

ę

k s z y m z y s k i e m

o d d z i e l a j m n i e j s z y z y s k o d w i

ę

k s z e j s t r a t y

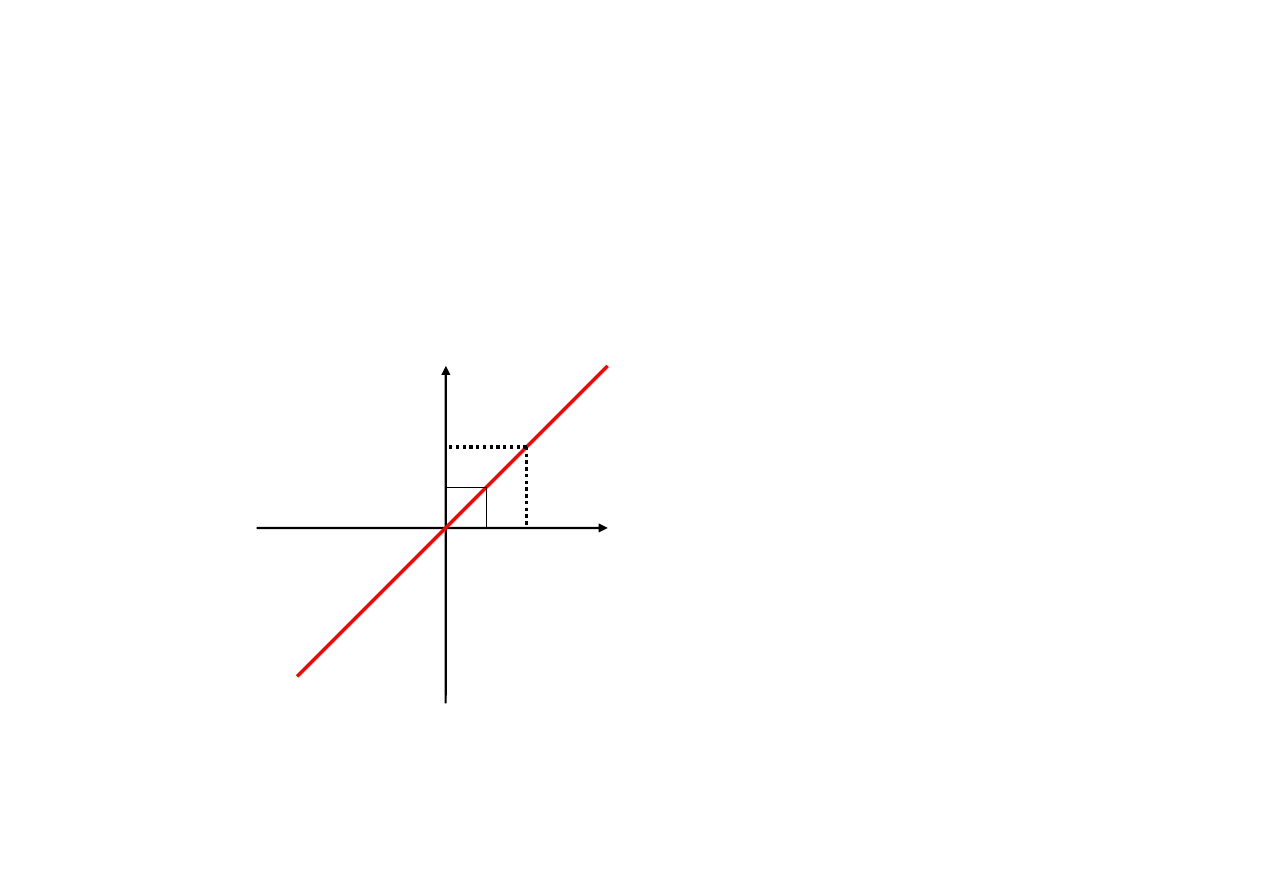
14

F

AKTYCZNY ZYSK A SATYSFAKCJA Z OSI

Ą

GNI

Ę

TEGO ZYSKU

F

AKTYCZNA STRATA A NIEZADOWOLENIE Z POWODU ODNIESIONEJ STRATY

ZALE

ś

NO

ŚĆ

POZORNA

F(zysk)

F(strata)

-200zł - 100zł

100zł 200zł

zyski

sa

ty

sf

a

k

cj

a

straty

n

ie

za

d

o

w

o

le

n

ie

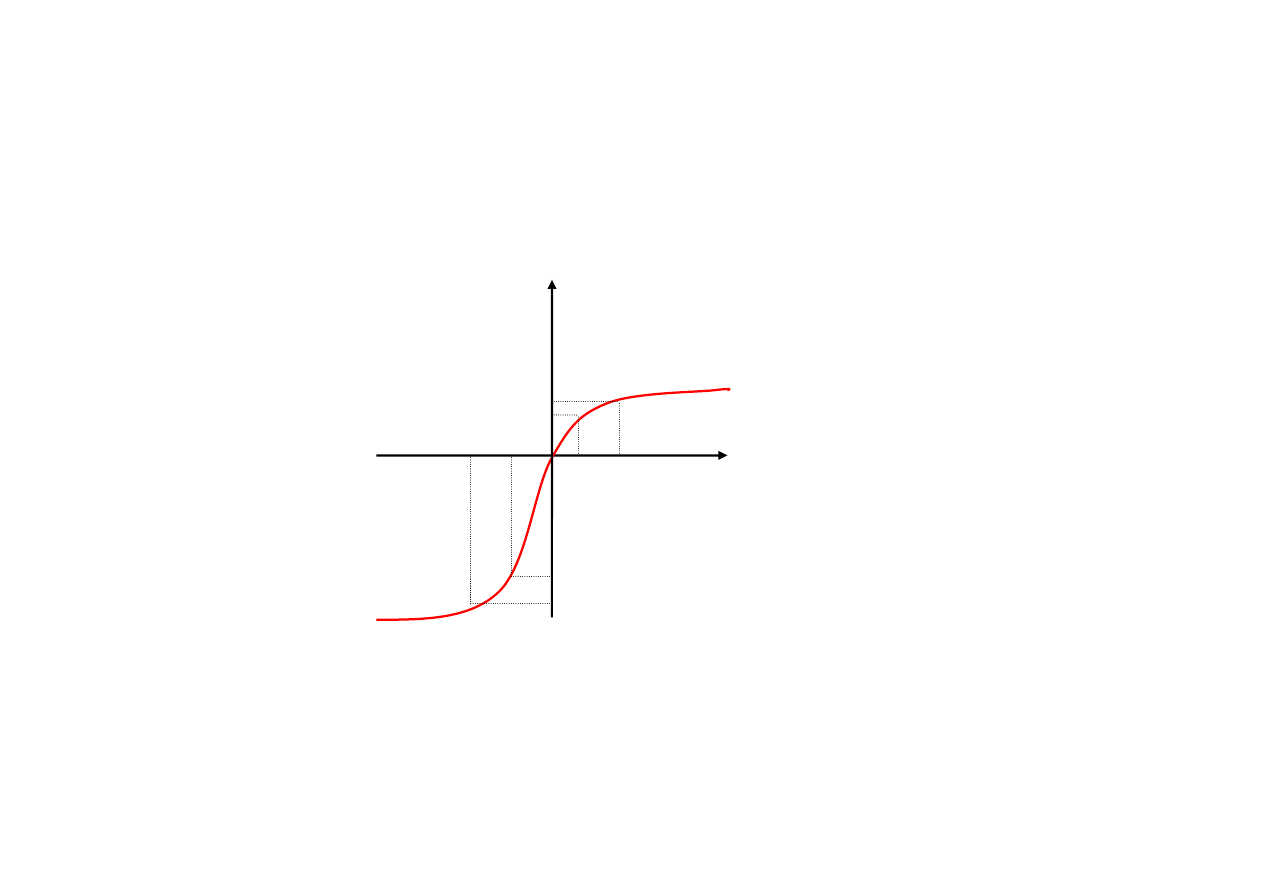
15

ZALE

ś

NO

ŚĆ

FAKTYCZNA

P o n i e w a

ż

o d c z u w a m y :

1. wi

ę

ksz

ą

satysfakcj

ę

z osi

ą

gni

ę

cia kilku mniejszych zysków ni

ż

z jednego wi

ę

kszego zysku b

ę

d

ą

cego ich sum

ą

, to …

F (100) + F (100) > F (200)

r o z d z i e l a j z y s k i

F(zysk)

F(strata)

F(-100zł)
F(-200zł)

-200zł -100zł

F(200zł)
F(100zł)

0

100zł 200zł

zyski

sa

ty

sf

a

k

cj

a

straty

n

ie

za

d

o

w

o

le

n

ie

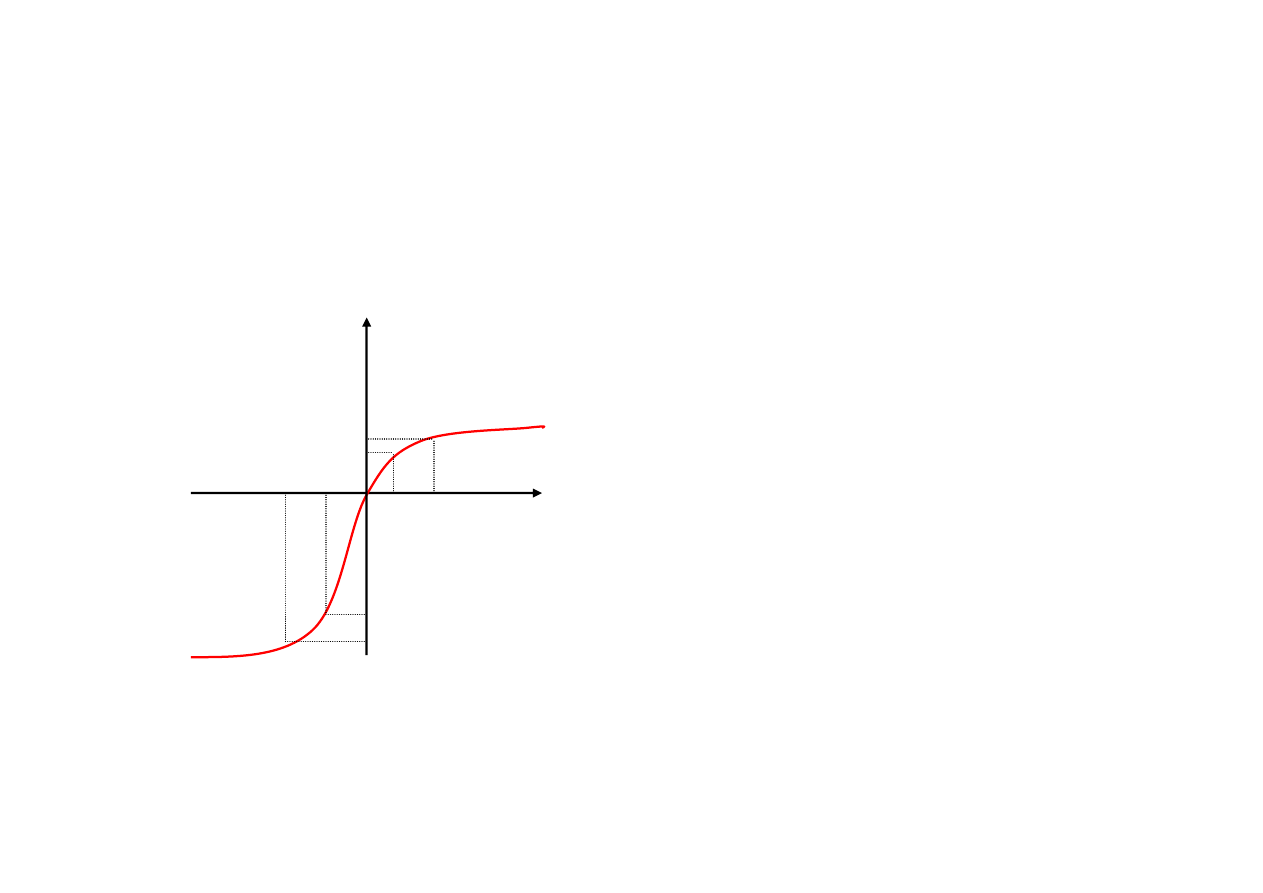
16

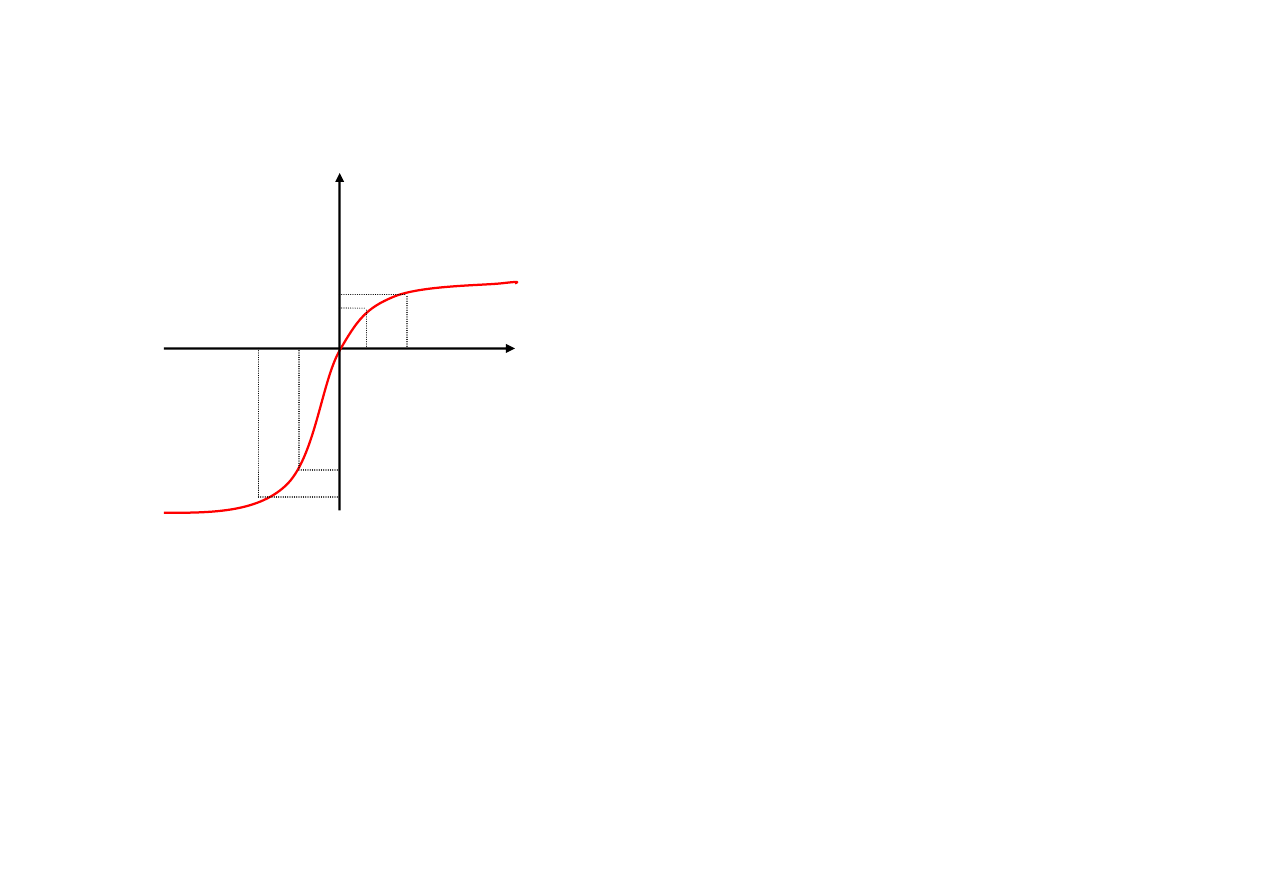
2. mniejsze niezadowolenie z poniesienia jednej, zsumowanej straty ni

ż

z kilku mniejszych strat, to …

skoro

F(-200) > F(-100) + F(-100)

ł

ą

c z s t r a t y

F(zysk)

F(strata)

F(-100zł)
F(-200zł)

-200zł - 100zł

F(200zł)
F(100zł)

0

100zł 200zł

zyski

sa

ty

sf

a

k

cj

a

straty

n

ie

za

d

o

w

o

le

n

ie

17

3. wi

ę

ksz

ą

satysfakcj

ę

z osi

ą

gni

ę

cia jednego zsumowanego zysku powstałego w wyniku poł

ą

czenia wi

ę

kszego zysku i mniejszej straty ni

ż

z

pojedynczego wi

ę

kszego zysku i pojedynczej mniejszej straty, to …

F ( 2 0 0 - 1 0 0 ) > F ( 2 0 0 ) + F ( - 1 0 0 )

ł

ą

c z m n i e j s z

ą

s t r a t

ę

z w i

ę

k s z y m z y s k i e m

F(zysk)

F(strata)

F(-100zł)
F(-200zł)

-200zł -100zł

F(200zł)
F(100zł)

0

100zł 200zł

zyski

sa

ty

sf

a

k

cj

a

straty

n

ie

za

d

o

w

o

le

n

ie

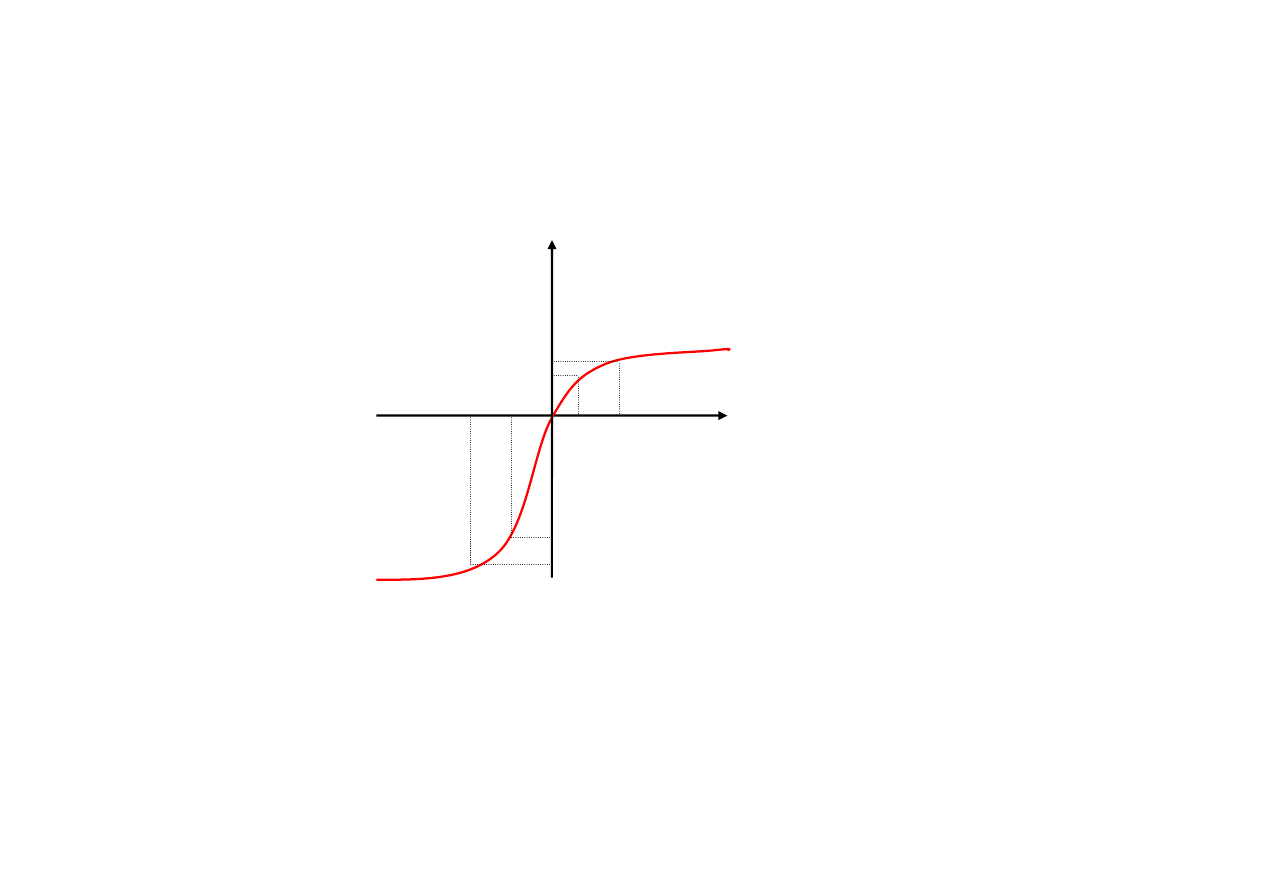
18

4.mniejsze niezadowolenie z poniesienia wi

ę

kszej straty i osi

ą

gni

ę

cia mniejszego zysku ni

ż

z jednej zsumowanej straty b

ę

d

ą

cej ró

ż

nic

ą

mi

ę

dzy wi

ę

ksz

ą

strat

ą

i mniejszym zyskiem, to …

F ( - 2 0 0 ) + F ( 1 0 0 ) > F ( - 1 0 0 )

o d d z i e l a j m n i e j s z y z y s k o d w i

ę

k s z e j s t r a t y

jak można wykorzystać te faktyczne zależności ?

jak inni wykorzystują te zależności ?

F(zysk)

F(strata)

F(-100zł)
F(-200zł)

-200zł -100zł

F(200zł)
F(100zł)

0

100zł 200zł

zyski

sa

ty

sf

a

k

cj

a

straty

n

ie

za

d

o

w

o

le

n

ie