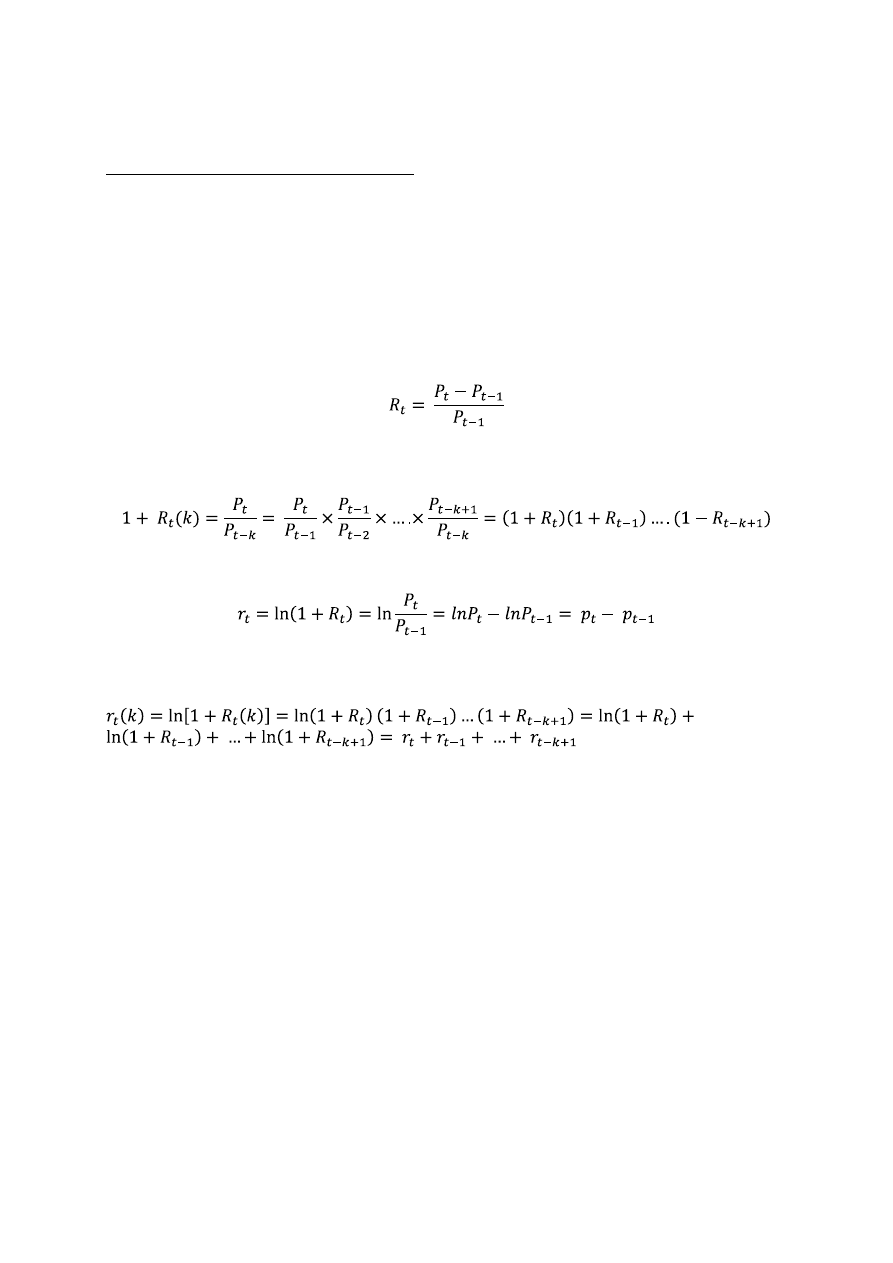
1

Modelowanie zmienności ryzyka rynkowego

Wykład I

Finansowe szeregi czasowe i ich charakterystyki
Finansowe szeregi czasowe charakteryzują się:
- wysoka częstotliwość obserwacji;
- bardzo duża zmienność stóp zwrotu;
- grupowanie wariancji – obserwując wykresy kwadratów stóp zwrotu z indeksu WIG, okresy skupiania się
wyższych wartości i okresy, gdy obok siebie znajdują się relatywnie niskie wartości ( wysoka zmienność 
podwyższone ryzyko, niska zmienność  obniżone ryzyko);
- empiryczne szeregi finansowe – niezbyt często przypominają rozkład normalny. Rozkłady te charakteryzują się
grubymi ogonami, co oznacza, że prawdopodobieństwo wystąpienia obserwacji nietypowej jest tu wyższe
aniżeli w rozkładzie normalnym.
Stopy zwrotu:

1. Zwykła stopa zwrotu – zwykła jednookresowa stopa zwrotu z inwestycji w papiery wartościowe jest

definiowana jako:

gdzie: R

t

- zwykła stopa zwrotu z akcji;

P

t

– cena instrumentu finansowego.

W praktyce wzór oznacza, że k-okresowa zwykła stopa zwrotu jest iloczynem jednookresowych stóp zwrotu,
czyli:

Zwykła stopa zwrotu jest multiplikatywna, czyli trzeba wyznaczyć średnią geometryczną.

2. Logarytmiczna stopa zwrotu – w analizach empirycznych często korzysta się z logarytmicznej stopy

zwrotu postaci:

gdzie: r

t

– logarytmiczna jednookresowa stopa zwrotu;

p

t

– logarytm ceny instrumentu finansowego.

Wzór definiuje jednookresową logarytmiczną stopę zwrotu K-okresowy odpowiednik jest następujący:

Z tego wynika, że k-okresowa

logarytmiczna stopa zwrotu jest sumą jednookresowych logarytmicznych stóp zwrotu, co daje jej przewagę nad
zwykła stopą zwrotu. Logarytmiczna stopa zwrotu jest addytywna.
Logarytmiczna stopa zwrotu jest lepszym narzędziem analizy niż zwykła stopa zwrotu, gdyż transformacja
logarytmiczna umożliwia liniowe przekształcenia i bezpośrednie stosowanie takich klasycznych narzędzi opisu
statystycznego, jak momenty zwykłe i centralne (np. średnia arytmetyczna i odchylenie standardowe).

Rodzaje efektywności:
Słaba efektywność ma miejsce wówczas, gdy nie jest możliwe uzyskanie ponadprzeciętnych zysków z tytułu
wykorzystania informacji tkwiących w cenach (bieżących i przeszłych ). Oznacza to, że historyczna analiza
szeregów czasowych cen giełdowych nie doprowadzi do uzyskania prognoz bardziej dokładnych niż te, które
można obliczyć, biorąc pod uwagę tylko bieżące ceny, które natychmiast i w pełni odzwierciedlają całą
informację zawartą w historii cen papierów wartościowych.

Jeżeli zachodzi słaba forma efektywności to:

E(P

t+1

)=P

t

z czego wynika, że
P

t+1

=P

t

+e

t+1

Jeśli słaba forma efektywności nie zachodzi, to w celu przewidywania cen można stosować narzędzia analizy
technicznej.
Średnia efektywność występuje wtedy, kiedy nie jest możliwe uzyskanie dodatkowych zysków z tytułu
wykorzystania wszystkich informacji powszechnie dostępnych dla uczestników rynku (publikowanych prognoz
cen, analizy i oceny ekspertów dotyczących sytuacji finansowej firmy, prognoz makroekonomicznych ).
Oznacza to, że wszystkie powszechnie dostępne inwestorom informacje zostały już odzwierciedlone w cenach

2

j

t

p

j

j

q

i

i

t

i

t

h

B

h

1

1

2

0

akcji przez działający mechanizm rynkowy. Jeśli średnia efektywność rynku nie zachodzi, to w celu
przewidywania cen można stosować narzędzia analizy fundamentalnej.
Silna efektywność występuje w przypadku, gdy nie jest możliwe uzyskanie dodatkowych zysków nawet
poprzez wykorzystanie informacji prywatnych, nieodstępnych dla innych uczestników rynku (np. wynikających
z funkcji wykonywanej przez inwestora).

Jeśli średnia i wariancja e

t+1

są przy danym P

t

nieprognozowalne, czyli:

E(e

t+1

|P

t

) =0,

var(e

t+1

|P

t

)=const,

to (1.27a) jest błądzeniem przypadkowym. Gdy tylko średnia jest nieprognozowalna, a
wariancja(lub jakikolwiek inny moment rozkładu) może być prognozowana, wówczas (1.27a) jest martyngałem.
Martyngał odzwierciedla proces opisujący uczciwą grę rynkową, tzn. taką, że jej wartość oczekiwana jest równa
zeru. Martyngał stanowi podstawę przyjmowanej obecnie wersji hipotezy słabej efektywności rynku.

Modele ARCH (GARCH)

Model ARCH(q) – Engle (1982)

(epsilon t pod warunkiem, że zbiór dostępnych
informacji znanych z okresu t-1 ma rozkład normalny)

gdzie: α

0

>0 oraz α

i

≥0 dla i=1,2,....q.

Model ten pozwala opisać zmieniającą się w czasie wariancję warunkową oraz efekt
skupiania się wariancji w niskich przedziałach czasu. (Ten model stosuje się dla rozkładów o
niskiej częstotliwości, małych obserwacji, w procesach makroekonomicznych, jeżeli efekt
ARCH jest silny to wtedy ten model nie jest odpowiedni).
W empirycznych zastosowaniach, przy większej liczbie obserwacji konieczne jest stosowania
bardzo dużych q. Aby uniknąć szacowania dużej liczby parametrów buduje się model
GARCH.
Model Garch (p,q) – Bollerslev (1986), Taylor (1986)

(2)

Nelson, Cao(1992) przedstawiają warunki, przy

których równanie (2) jest określone. Nie wszystkie

modelu (2) muszą być dodatnie, a by zapewnić dodatniość h

t

. Np. następujące warunki

zapewniają, że h

t

> 0:

- dla modelu GARCH (1,2):

Proces GARCH (p,q) jest stacjonarny w szerszym sensie, jeżeli spełniony jest warunek:

(w szerszym tzn. kowariancyjna).
Bezwarunkowa wariancja ε

t

jest równa:

Wariancja warunkowa – h

t

, )zmienia się z okresu na okres, jest codziennie inna, wystarczy,

że dzień wcześniej była większa, to na drugi dzień też będzie większa) odzwierciedla zmiany
bieżące na rynku, bierze pod uwagę zmiany bieżące na rynku.
Wariancja bezwarunkowa – (nie bierze pod uwagę tylko bieżących zmian, ona bierze pod
uwagę wszystkie informacje) informuje nas o zmianach w całym okresie na podstawie
średniej, na długi okres.

)

,

0

(

~

|

1

t

t

t

h

N

q

i

i

t

i

t

h

1

2

0

)

,

0

(

~

|

1

t

t

t

h

N

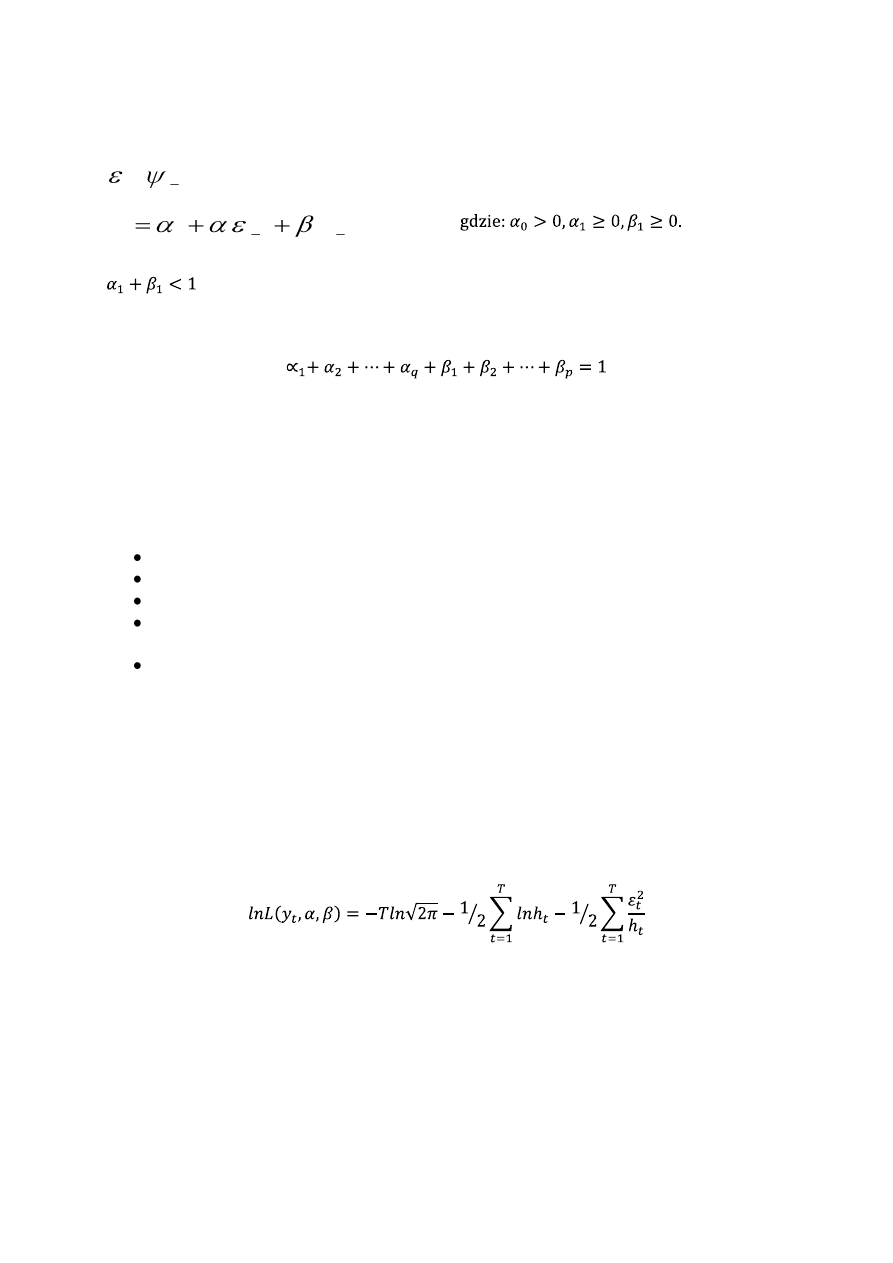
3

1

1

2

1

1

0

t

t

t

h

h

W praktyce najczęściej wykorzystywanym w modelowaniu finansowych szeregów
czasowych jest proces GARCH (1,1):

Proces ten jest stacjonarny w szerszym sensie, jeżeli:

Model IGARCH (p,q) – Engle, Bollerslev (1986)
Model GARCH(p,q) dla którego:

Informacja z dowolnie odległej przeszłości jest istotna w wyjaśnianiu bieżącej zmienności, a
brzegowa (bezwarunkowa) wariancja procesu jest nieskończona.
Analizy empiryczne wskazują, że modele GARCH z warunkowym rozkładem normalnym nie
są w stanie opisać zwiększonej kurtozy występującej w rozkładach brzegowych stóp zwrotu
większości instrumentów finansowych. Dlatego często stosuje się warunkowe rozkłady
posiadające grubsze ogony niż te, które występują w rozkładzie normalnym.

Grube ogony rozkładów warunkowych:

Rozkład t-studenta;

Skośny rozkład t-studenta dopuszczający asymetrię;

Rozkład GED (generalized error distribution);

Rozkład podwójnie wykładniczy (doubleexponential) szczególny przypadek rozkładu
GED;

Rozkłady stabilne.

Na ogół wystarczający jest model GARCH z warunkowym rozkładem t-studenta.
Metody estymacji:
- Metoda największej wiarygodności (MNW), najbardziej popularna, ma zastosowanie wtedy
gdy ma założenia takie same jak próba.
- Metoda quasi największej wiarygodności.
- Metody bayerowskie.
- Metoda momentów.
- Metody semiparametryczne i nieparametryczne.

Logarytm funkcji wiarygodności dla modelu GARCH (lub ARCH) dany jest wzorem:

Estymacja MNW sprowadza się do maksymalizacji powyższej funkcji.
Wartości pochodnych cząstkowych wykorzystywane w procesie estymacji są na ogół
przybliżone za pomocą metod numerycznych.

WYKŁAD 2

* To moje notatki

Zamiast zastosować model GARCH z warunkowym rozkładem o grubych ogonach można
zastosować QMNK.
Estymatory QMNW są zgodne i asymptotycznie normalne choć mogą być nieefektywne.
Należy zastosować odporne na odstępstwa od rozkładu normalnego średnie błędy szacunku.
Skuteczność takiego podejścia będzie zależała od konkretnego zastosowania.

)

,

0

(

~

|

1

t

t

t

h

N

4

*Rozwiązania:

1. Najczęściej rozkład t – Studenta i estymujemy metodą MNK
2. Zastosowanie QMNW – rozkład normalny warunkowy wiedząc, że jest on nieprawidłowy.

Nieprawidłowe jest gdy dalej na jego podstawie chcemy wnioskować

Wybór postaci modelu GARCH (rodzaju i rzędu opóźnień modelu)
Nie istnieje uniwersalne kryterium wyboru postaci modelu GARCH. Najczęściej stosuje się
kryteria informacyjne Akaike’a lub Schwarza:
Kryterium Akeike’a:

Kryterium Schwarza (BIC):

gdzie: L

T

– oznacza logarytm funkcji wiarygodności, q – liczba szacowanych parametrów

modelu, T – liczba obserwacji.

*kryterium Schwarza wybiera model, który ma mniej parametrów, dlatego lepiej jest go stosować.
*Należy pamiętać o teście na występowanie efektu ARCH i innych testach, które przeprowadza się
standardowo przy ocenie jakości modelu.

Kryteria informacyjne są powszechnie stosowane w analizach empirycznych, jednakże należy
pamiętać, że ich własności statystyczne nie są znane w kontekście modelu GARCH.
Wyboru postaci modelu można również dokonać na podstawie miar doskonałości prognoz
zmienności lub innych kryteriów, które można wykorzystać tylko w ściśle określonych
zastosowaniach.

*jeżeli w modelu występuje efekt ARCH trzeba wybrać model z większymi opóźnieniami. Wybrany
przez nas model powinien nie mieć efektu ARCH i istotne parametry przy największym opóźnieniu.

Testowanie występowania efektu ARCH
Jeden z najbardziej popularnych testów na występowanie efektu ARCH został
zaproponowany przez Engle’a (1982)
H

0

: α

1

= α

2

=…= α

q

=0  brak efektu ARCH

H

1

:

 występuje efekt ARCH

Hipoteza alternatywna oznacza, że składnik losowy ma zmienną wariancję warunkową.
Decyzję podejmuje się na podstawie statystyki LM=TR

2

, gdzie R

2

jest współczynnikiem

determinacji równania regresji oszacowanego metodą najmniejszych kwadratów.

e

t

są resztami otrzymanymi z równania dla średniej warunkowej.

Przy założeniu prawdziwości hipotezy zerowej statystyka TR

2

ma rozkład asymptotycznie

zbieżny do rozkładu

(chi kwadrat) o q stopniach swobody.

Alternatywnie:
Test Ljunga – Boxa dla kwadratów reszt.

ASYMETRYCZNA WARIANCJA

Asymetryczny wpływ dodatnich i ujemnych stóp zwrotu na wariancję. Złe wiadomości ε

t-i

<0

powodują zwiększenie zmienności, dobre wiadomości ε

t-i

>0 zmniejszają zmienność.

Występuje ujemna korelacja pomiędzy bieżącą stopą zwrotu a przyszłą zmiennością.

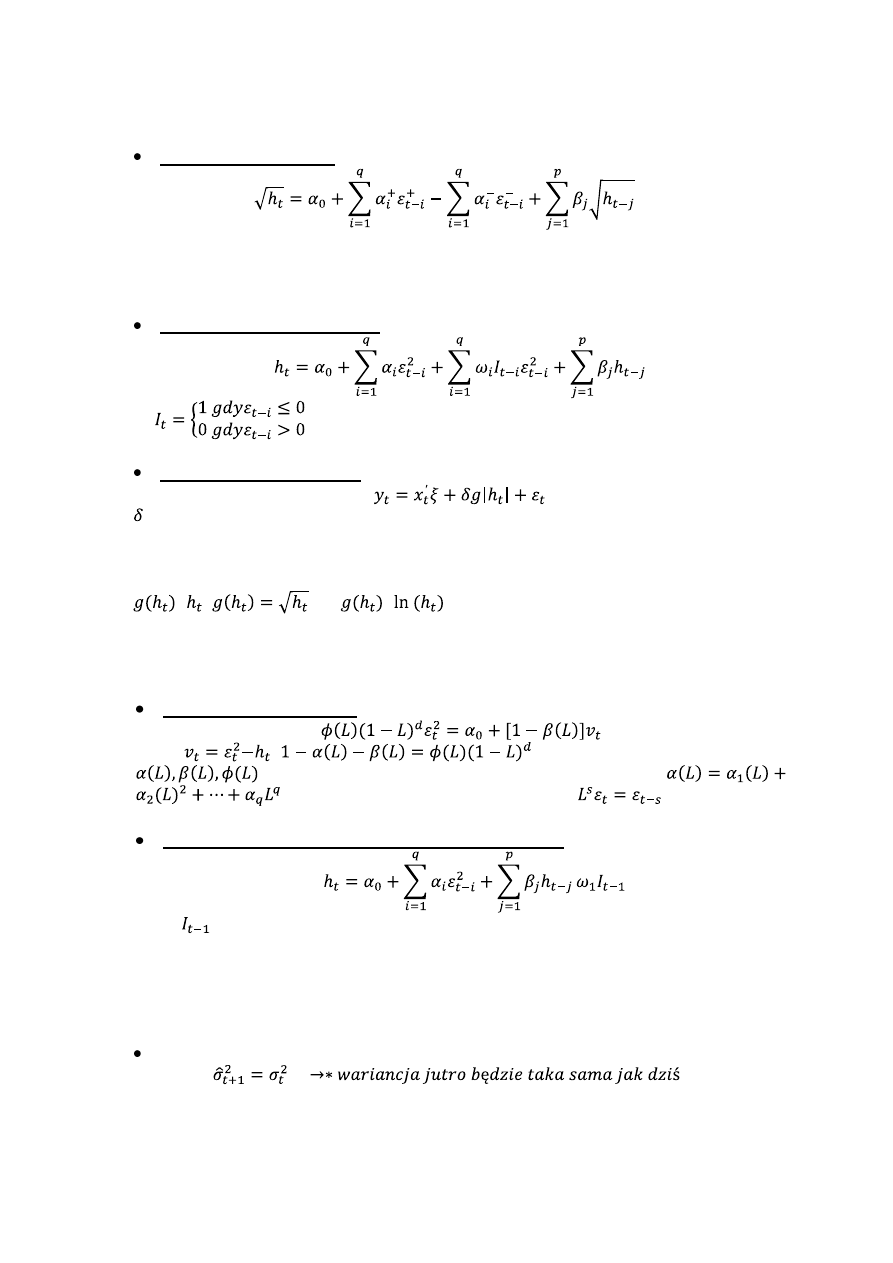
Model EGARCH (p,q) Nelson (1991)

gdzie: z

t

= ε

t/

jest procesem biało szumowym o wartości oczekiwanej równej 0 i wariancji

równej 1.
Model EGARCH (p,q) można przedstawić w nieco innej postaci:

5

*Efekt asymetrycznej wariancji zależy od parametru gamma. Kiedy gamma będzie ujemne powoduje
zwiększenie lnh

t

. ujemne stopy zwrotu zwiększają wariancję w porównaniu do dodatnich stóp zwrotu.

Model TGARCH (P,q)Rabemananjara, Zakoian (1993)

gdzie: ε

t

+

= max (ε

t

,0) ; ε

t

-

=max(ε

t

,0) – są to zmienne progowe dodatnie i ujemne.

*asymetryczna wariancja jest wtedy gdy ∑α

+

różni się od ∑α

-

. ∑α

-

będzie na ogół większe od

∑α

+

.

Model GJR – GARCH (p,q) – Glosten, Jsgannathan, Runkle (1993)

gdzie:

 zmienna zerojedynkowa

OCZEKIWANA STOPA ZWROTU A RYZYKO

Model GARCH – M (p,q) - Engle, Lilien, Robins (1987)

– można interpretować jako “parameter awersji do ryzyka”, g odnosi się do

modelowania interpretowania indeksów. Powinien być dodatni i im większa h

t

to stopy

zwrotu powinny być dodatnie. Badania wskazują, że na ogół tak nie jest. Odnosi się do
krótkookresowych stóp zwrotu.

=

,

lub

=

DŁUGOTERMINOWA ZALEŻNOŚĆ DANYCH

Funkcja autokorelacji szacowana dla wartości bezwarunkowych lub kwadratów stóp zwrotu
finansowych szeregów czasowych przyjmuje dodatnie wartości istotnie różniące się od 0 dla
bardzo długiego odstępu, sięgającego nawet kilkuset obserwacji.

Model FIGARCH(p,d,q) - Braillie, Bollerslev, Mikkelsen (1996)

gdzie:

,

- są symulacyjnymi operatorami liniowymi (np.

) a L oznacza przesunięcia wstecz:

oraz wszystkie

pierwiastki wielomianu φ(z)=0 leżą poza kołem jednostkowym.

Modele GARCH z dodatkową zmienną objaśniającą

gdzie za

przyjmuje się np. zmienność zrealizowaną aproksymowaną na podstawie

danych o częstotliwości wyższej niż dzienna, wielkość obrotów czy też zmienność innych
aktywów finansowych. (Na ogół są to wartości dodatnie, bo wariancja musi być > 0. Mogą to
być np. zmienność na walutach i sprawdzenie czy wpływa ona na zmienność akcji.) im mniej
stopni swobody tym grubsze ogony.

WYKŁAD 3

Random walk model

Two forecast for random walk model are constructed. Squared daily return and the sum of
squared intraday returns are used as a realized volatility.

6

Historical average (*średniahistoryczna)

Moving average model (*model średniej ruchomej dla zmienności)

Exponential smoothing model (*model wyrównywania wykładniczego dla wariancji)

where

The choice of the moving average estimation period (k) and value of smoothing parameter ( )
are arbitrary and should be determined empirically.

Stochastic volatility model

where

are series of independent, identically distributed random

disturbances and

The SV model is supposed to describe financial time series better than the ARCH-type
models, since it essentially involves two noise processes.
*Inny od GARCH, bo ma dwa składniki losowe i dlatego jest trudniejszy.
Literatura

1. Jajuga K. „Zarządzanie ryzykiem”, PWN, W-wa 2007,
2. Tarczyński W., Mojsiewicz…

*

Stopy zwrotu
Definicja ryzyka

Ryzyko a niepewność (mierzalne- niemierzalne)

Dwa podejścia do ryzyka
Dwa aspekty ryzyka (obiektywny, subiektywny)
Postawy wobec ryzyka

 Awersja do ryzyka,
 Obojętność (neutralność) względem ryzyka,
 Skłonność do ryzyka.

Podział ryzyka

Całkowite ryzyko dzieli się na ryzyko systematyczne (zewnętrzne) i specyficzne
(wewnętrzne).

 Ryzyko systematyczne jest determinowane przez siły zewnętrzne i nie podlega

kontroli danego podmiotu. Jest związane z siłami przyrody oraz wynika z warunków
ekonomicznych danego rynku. Nie może być przez inwestora wyeliminowane.
Do ryzyka systematycznego zalicza się: ryzyko stopy procentowej, ryzyko kursowe,
ryzyko rynku, ryzyko siły nabywczej, ryzyko polityczne, ryzyko pogodowe.

 Ryzyko specyficzne obejmuje obszar działania danego podmiotu i może być przez ten

podmiot kontrolowane.
W ramach ryzyka niesystematycznego wyróżnia się: ryzyko niedotrzymania
warunków umowy, ryzyko zarządzania, ryzyko finansowe, ryzyko bankructwa,
ryzyko rynkowej płynności, ryzyko zmiany ceny, ryzyko reinwestowania, ryzyko
wykupu na żądanie.

7

Poprzez dywersyfikację portfela można prawie w całości wykluczyć ryzyko specyficzne, a
systematycznego nie można.
Zarządzanie ryzykiem podmiotu jest to podejmowanie decyzji i realizacji działań
prowadzących do osiągnięcia przez ten podmiot akceptowanego poziomu ryzyka.
Czynniki wpływające na ryzyko:

 Rodzaj instrumentu finansowego,
 Emitent instrumentu finansowego,
 Okres do wykupu instrumentu finansowego.

Etapy procesu zarządzania ryzykiem

1. Identyfikacja,
2. Ocena (pomiar),
3. Sterowanie ryzykiem- wybór i wdrożenie odpowiedniej techniki zarządzania

ryzykiem,

4. Monitorowanie i kontrola ryzyka.

Identyfikacja polega na określeniu rodzajów ryzyka, na które narażony jest dany podmiot.
Zwykle etap odbywa się w sposób zdecentralizowany w poszczególnych obszarach
działalności oraz poszczególnych oddziałach firmy. Pomiar to wyrażenie poziomu ryzyka w
postaci liczbowej lub gdy nie jest to możliwe w postaci pewnych kategorii, np. niskie średnie,
wysokie ryzyko).
Sterowanie ryzykiem polega na podejmowaniu decyzji dotyczących działań dostosowujących
poziom ryzyka do akceptowalnego poziomu wynikającego jego strategii. Często są to
działania zmniejszające poziom ryzyka podmiotu.
Zarządzanie ryzykiem jest procesem, a nie działaniem jednorazowym, dlatego występuje
potrzeba monitorowania poziomu ryzyka i kontroli całego procesu.
Tradycyjne miary ryzyka wyznaczane są na podstawie sprawozdań finansowych, np.
wskaźnik zadłużenia, wskaźnik obsługi zadłużenia.
Ogół miar ryzyka rynkowego można podzielić na trzy grupy: miary zmienności, miary
wrażliwości i miary zagrożenia.
Zmienność nie jest bezpośrednio obserwowalna i jest pojęciem niejednoznacznym.
Najczęściej pod pojęciem zmienności instrumentu finansowego rozumie się miarę
niepewności, co do cen lub stóp zwrotu instrumentu finansowego.
Miary zmienności mierzą stopień rozproszenia danej zmienności wokół wartości średniej. Im
wyższa zmienność, tym większe ryzyko.
Do miar zmienności zaliczamy: wariancję, odchylenie standardowe, semiwariancję,
semiodchylenie standardowe, odchylenie przeciętne, odchylenie międzykwartylowe, rozstęp i
współczynniki zmienności, wariancję warunkową (wyliczoną na podstawie modelu
RiskMetrics lub modelu GARCH).
W przypadku takich miar jak wariancja, odchylenie standardowe, odchylenie przeciętne
ryzyko rozumiane jest zgodnie z koncepcją neutralną, czyli jako możliwość, że zrealizowany
dochód (stopa zwrotu) będzie różnił się od oczekiwanego.
Semiwariancja i semiodchyleniestandardowe odpowiadają wariancji i odchyleniu
standardowemu pry założeniu, że ryzyko rozumiane jest w kategoriach zagrożenia, co
oznacza, iż pod uwagę bierze się tylko ujemne odchylenia od oczekiwanej stopy zwrotu.
*Semiodchylenie jest lepsze, bo bierze pod uwagę ujemne wartości, jednak nie występuje ono
w pakietach (gotowych programach).
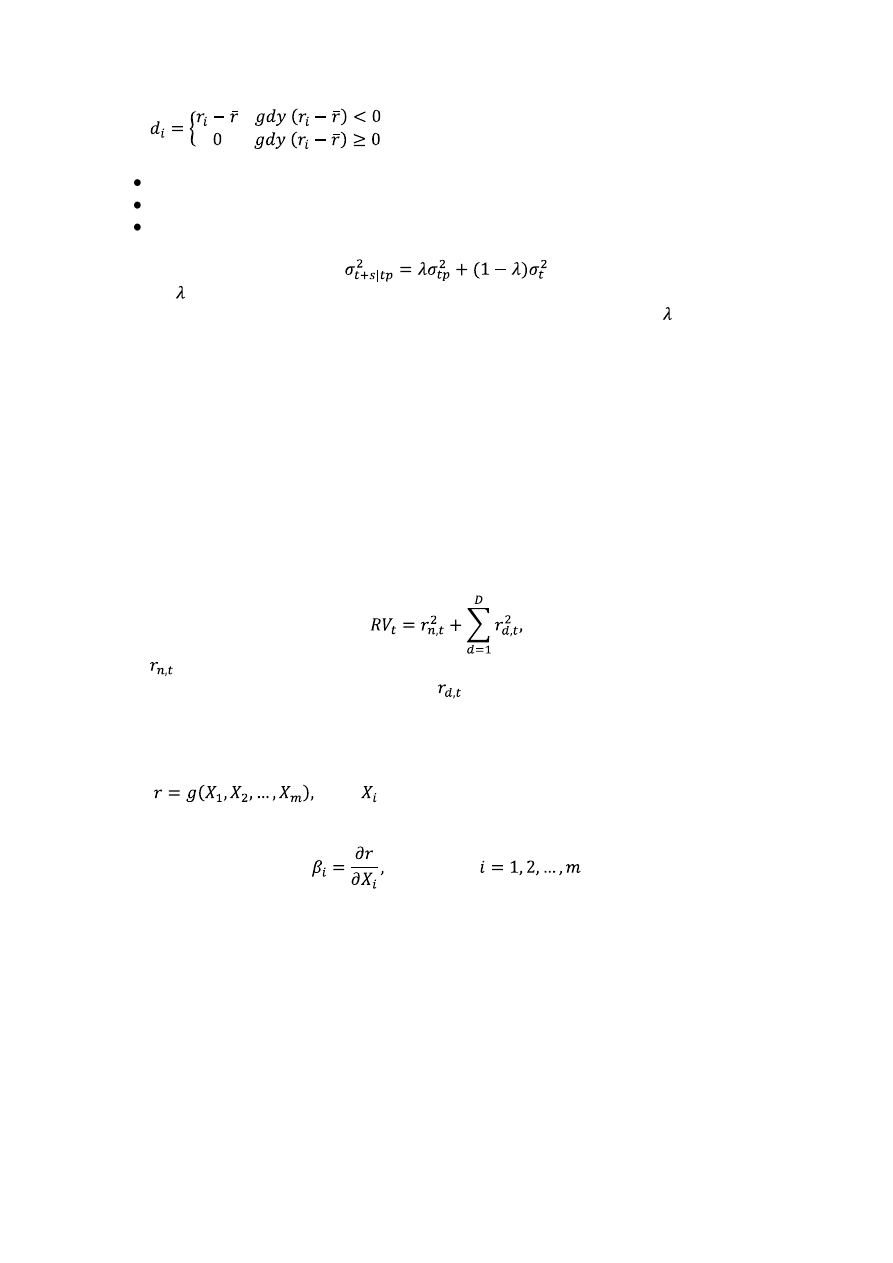
Semiodchylenie standardowe

8

gdzie

*Zmienność jest wykorzystywana w:

wycenie opcji,
analizie portfelowej,
zabezpieczaniu przed ryzykiem.

Metoda wyrównywania wykładniczego dla wariancji (EWMA)

Parametr jest nazywany parametrem wygasania i przyjmuje wartości z przedziału (0, 1).
Wadą tej metody jest niejednoznaczność przy określaniu wartości parametru . Jego wybór
zależy od charakteru prognozowanego procesu. Jeżeli nie ma częstych i znacznych zmian
„trendu w wariancji”, to większą wagę trzeba przywiązać do prognoz w poprzednim okresie
(parametr bliski jedności).
Metoda wyrównywania wykładniczego jest bardzo często określana w literaturze finansowej
jako model RiskMetrics.
Początkowo do szacowania wariancji i odchylenia standardowego wykorzystywano dane
dzienne lub ewentualnie dane o mniejszej częstotliwości.
Jako realizacje dziennej zmienności, do oceny prognoz, przyjmowano natomiast kwadraty
(rzadziej wartości bezwzględne) dziennych stóp zwrotu.
Pomimo tego, że kwadrat stopy zwrotu jest nieobciążonym estymatorem zmienności, to jest
zanieczyszczony szumem.
Z tego względu, jako zmienność zrealizowaną, lepiej jest przyjąć sumę kwadratów stóp
zwrotu o częstotliwości wyższej niż dzienna (dane intraday):

gdzie

jest to tzw. nocna stopa zwrotu, tzn. stopa zwrotu obliczana od ceny zamknięcia w

dniu t-1 do ceny otwarcia w dniu t; natomiast

to stopa zwrotu dla danych intraday (np.

dane 15-minutowe).
Miary wrażliwości odzwierciedlają wpływ zmiennej ryzyka (np. stopa zwrotu, cena) na
zmiany poszczególnych czynników ryzyka.
Im większa wrażliwość na zmiany czynnika, tym większe ryzyko.
Niech

gdzie

- i-ty czynnik ryzyka.

Miara wrażliwości zdefiniowana jest jako pochodna cząstkowa funkcji g względem czynnika
ryzyka:

Wskazuje ona ile zmieni się w przybliżeniu zmienna ryzyka, gdy i-ty czynnik ryzyka zmieni
się o jednostkę, a pozostałe czynniki ryzyka się nie zmieniają.
Do miar wrażliwości zaliczamy m. in. współczynnik beta, współczynnik zabezpieczenia,
duration oraz greckie współczynniki- delta, gamma, vega (keppa), theta i rho.
Miary wrażliwości mają szerokie zastosowanie w analizie ryzyka, np. tworzenie portfela akcji
o współczynniku beta równym zeru, zabezpieczenie portfela przed ryzykiem za pomocą opcji
lub kontraktów terminowych, uodpornienie.
Współczynnik beta
Obserwacje empiryczne potwierdzają, że na wielu rynkach kapitałowych stopy zwrotu
większości akcji są w dużym stopniu powiązane ze stopą zwrotu indeksu rynkowego,
odzwierciedlającego ogólną sytuację na rynku.

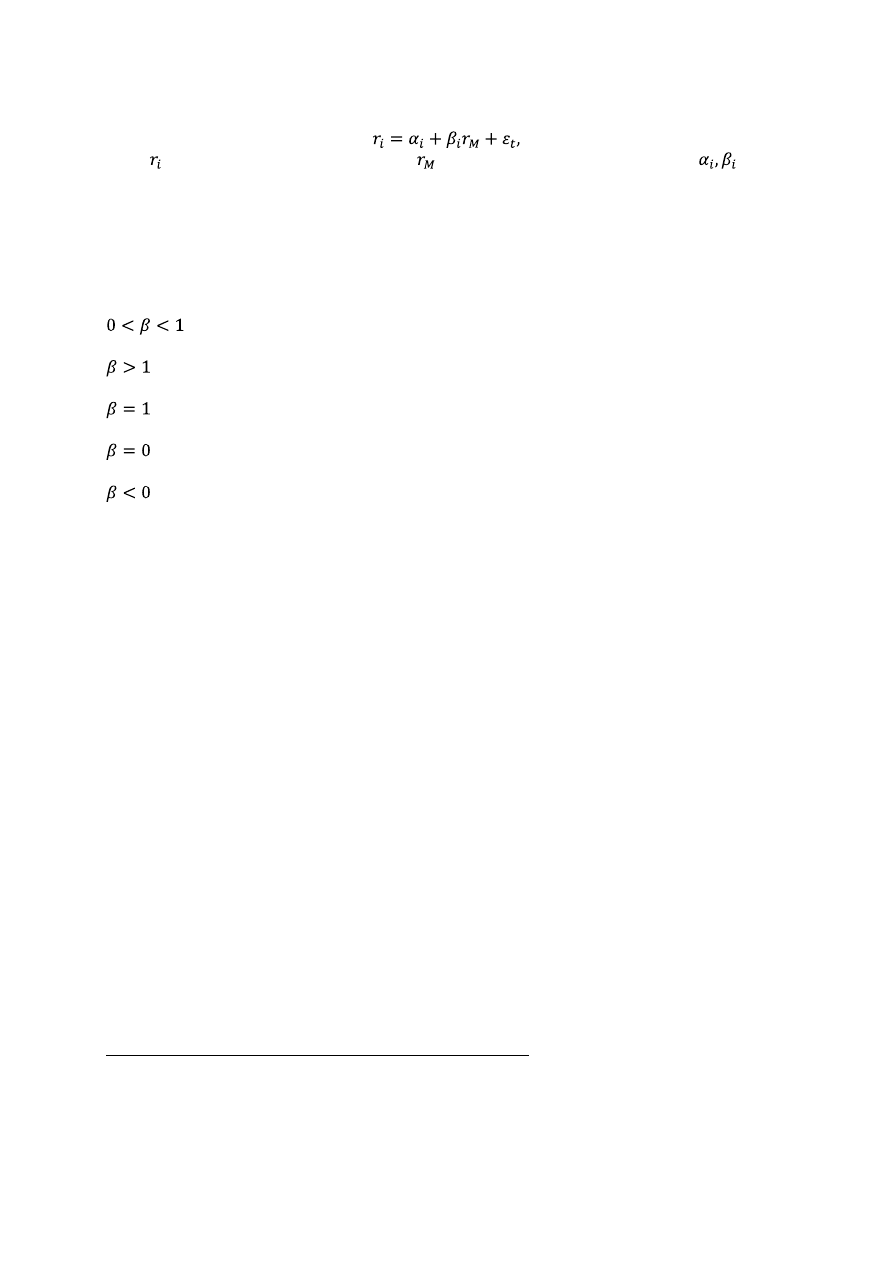
9

Jednowskaźnikowy model Sharpe’a.

gdzie jest to stopa zwrotu i-tego waloru,

- stopa zwrotu portfela rynkowego,

–

parametry strukturalne.
Współczynnik beta wskazuje, o ile procent w przybliżeniu wzrośnie stopa zwrotu akcji, gdy
stopa zwrotu indeksu rynku wzrośnie o 1%.
Współczynnik beta, uważany jest za miarę ryzyka systematycznego. Im współczynnik jest
wyższy tym wyższe ryzyko cen akcji. Współczynnik ten nie jest stabilny w czasie. Jego
wartość zależy od rodzaju spółki (czy młode – rozwijające o wysokim beta się czy dojrzałe o
niskim beta).

- stopa zwrotu akcji w małym stopniu reaguje na zmiany zachodzące na rynku. Jest

to akcja defensywna.

- stopa zwrotu akcji w dużym stopniu reaguje na zmiany zachodzące na rynku. Jest to

akcja agresywna.

- stopa zwrotu akcji zmienia się w takim samym stopniu jak stopa zwrotu rynku. Jest to

akcja neutralna.

- stopa zwrotu akcji nie reaguje na zmiany rynku. Akcja jest wolna od ryzyka rynku.

Instrumenty wolne od ryzyka, jak bony skarbowe.

- stopa zwrotu akcji reaguje na zmiany odwrotnie niż rynek.

WYKŁAD 4

Model wyceny arbitrażowej
Model wyceny arbitrażowej (APT) jest jednym z modeli równowagi rynku kapitałowego.
*

Opiera się na dwóch założeniach:

1) Obowiązuje prawo jednej ceny i arbitraż – oznacza, że jeden instrument finansowy na różnych rynkach

powinien mieć tę samą cenę, bowiem w przeciwnym razie pojawią się arbitrażyści z kapitałem
spekulacyjnym. Arbitraż polega na wykorzystaniu różnicy cen: kupowanie po niższej cenie na jednym
rynku i jednoczesnym sprzedawaniu po wyższej cenie na innym. Pojawienie się arbitrażystów powoduje
w praktyce wzrost ceny poprzez napędzenie popytu na rynek z niższą ceną. Z kolei zwiększona podaż na
rynku z wyższą ceną powoduje spadek ceny. Konsekwencje są zatem takie, że możliwość spekulacyjna
twa krótko i w rezultacie całej sytuacji ceny się wyrównują. Arbitraż zakłada, że w praktyce różnice
cenowe wyrównują się natychmiast.

2) Stopy zwrotu z akcji kształtują się zależnie od czynników rynkowych – umożliwia przedstawienie

wartości stóp zwrotu za pomocą modelu składającego się z dwóch równań wieloczynnikowych.
Wartości teoretyczne uzyskane z oszacowanych modeli, opartych na czynnikach rynkowych, pozwalają
ustalić stopy zwrotu w warunkach równowagi. Daje to w efekcie możliwość oceny niedoszacowania lub
przeszacowania poszczególnych akcji.

Model APT (wykorzystywany w teorii wyceny arbitrażowej) – Ross (1976):

r

i

= α

i

+ β

i1

F

1

+ β

i2

F

2

+ … + β

ij

F

j

+ ε

i

,

gdzie:
r

i

– stopa zwrotu i-tej akcji,

j – liczba czynników,
F

j

– j-ty czynnik ryzyka, i = {1, 2, …, k},

Β

ij

– współczynnik wrażliwości i-tej akcji względem j-tego czynnika,

α

i

– wyraz wolny

*Współczynnik wrażliwości wskazuje o ile procent w przybliżeniu wzrośnie stopa zwrotu i-tej
akcji, gdy j-ty czynnik zmieni się o jednostkę,
Czynniki ryzyka, które mogą występować w modelu APT:
- zmiany w różnicy stóp dochodu obligacji o wysokim i niskim ryzyku,
- zmiany indeksu produkcji przemysłowej,
- zmiany stopy inflacji,
- zmiany stopy bezrobocia,

10

- zmiany PKB itp.

* Parametry modelu estymuje się za pomocą KMNK. Dla stóp zwrotu poszczególnych akcji uzyskuje się zatem
oceny współczynników wrażliwości na te same czynniki rynkowe. Następnie uzyskane współczynniki wrażliwości
służą jako zmienne objaśniające do właściwego równania APM, które przestawia się następująco:
E(R

i

) = λ

0

+ λ

1

β

1

+ λ

2

β

2

+ … + λ

k

β

k

– jest rozszerzeniem modelu Sharpe’a

Powyższe równanie przedstawia zależność wartości stopy zwrotu (pojedynczej akcji lub portfela) od
współczynników wrażliwości na określone czynniki rynkowe (czynniki ryzyka). Znalezienie wartości
współczynników λ jest możliwe za pomocą kilku metod. Jedną z nich jest analiza czynnikowa. Na podstawie
modelu APM można wyciągnąć wnioski dotyczące bieżącej wyceny rynkowej akcji. Jeżeli spodziewana stopa
zwrotu jest równa stopie obliczonej za pomocą APM, to znaczy, że akcja jest dobrze wyceniona.
Jeśli okazałoby się, że spodziewana stopa zwrotu jest niższa niż obliczona z modelu, to będzie oznaczało, że
stopa z modelu jest niedowartościowana, gdy natomiast obliczenia dadzą wyższą wartość, wówczas stopa
teoretycznie jest przewartościowana.

Duration – czas trwania (średni termin wykupu) instrumentu dłużnego. Jest to miara ryzyka
stopy procentowej. Pozwala na określenie, jak zmieni się w przybliżeniu wartość instrumentu,
gdy zmianie ulegnie stopa procentowa.

ΔP

t

= - MD (r

t+1

– r

t

) = - MD Δr

t

ΔP

t

= (P

t+1

-P

t

)/P

t

– procentowana zmiana ceny obligacji

P

t+1,

P

t

– wartości instrumentu odpowiednio po i przed zmianą stopy dochodu

r

t+1

, r

t

– stopy dochodu przed i po zmianie

MD – zmodyfikowane duration

MD =

.

Np. MD = 1,798; r

t

= 8%, r

t+1

=8,25%,

ΔP

t

= -0,45%

Miary zagrożenia –przy konstrukcji miar zagrożenia bierze się przede wszystkim pod uwagę
niekorzystne wartości, np. niekorzystne odchylenia od oczekiwanych wartości cen lub stóp
zwrotu.
Do miar zagrożenie zaliczamy między innymi: VaR, expectedshortfall (ES, oczekiwana strata
lub oczekiwana niedobór), semiwariancja, semiodchylenia, poziom bezpieczeństwa,
prawdopodobieństwo niesiągnięcia aspiracji, dolny moment cząstkowy.

VaR – podstawowe informacje.

 VaR jest dana w postaci jednej liczby, która w sposób zagregowany przedstawia

możliwe straty inwestora, najczęściej instytucji finansowej.

 Łączy różne rodzaje ryzyka rynkowego w jedną całość.
 VaR to względnie prosta i łatwo interpretowalna miara określająca możliwą stratę w

warunkach zwykłego funkcjonowania rynku.

 VaR jest rekomendowana przez wiele instytucji nadzorujących sektor bankowy oraz –

ogólnie – rynek finansowy, np. Komitet Bazylejski do Spraw Nadzoru Bankowego.

Wartość zagrożona jest to taka strata wartości rynkowej (np. instrumentu, portfela
instrumentów), że prawdopodobieństwo jej osiągnięcia lub przekroczenia w zadanym
przedziale czasowym jest równe zadanemu poziomowi tolerancji – definicja dla inwestora
posiadającego długą pozycję. Strata występuje, gdy następuje spadek wartości IF. Dla
inwestora posiadającego krótką pozycję definicję należy zmodyfikować.

P(W

t+1

≤ W

t

– VaR) = α

α – zadany poziom tolerancji;
W

t

– wartość IF w czasie t.,

Im niższy poziom tolerancji, tym wyższa wartości zagrożona. Im wyższy poziom

tolerancji tym wyższe VaR.

Im dłuższy okres, tym na ogół wyższa wartość zagrożona.

11

VaR zależy od dwóch parametrów, które powinien określić decydent. Są to poziom
ufności (lub zamiennie poziom tolerancji – 5%, 10%) oraz horyzont czasowy, zwany
też okresem przetrzymania (holding period- 1 dzień, 5 dni, 10 dni, 1 miesiąc).
Oznacza on przedział czasu, dla którego oblicza się VaR, tzn. okres, w którym może
mieć miejsce obliczona potencjalna strata na portfelu. Inna definicja okresu
przetrzymania podkreśla, że jest to czas, w którym skład portfela pozostaje
praktycznie niezmieniony.

VaR może być wyznaczony na podstawie następującej formuły:
VaR = -R

α

W

t

R

α

–kwantyl rozkładu prostej stopy zwrotu.

Istnieje wiele metod szacowania VaR. Najbardziej popularnymi metodami wyznaczania VaR
są:

1. Metoda wariancji – kowariancji – zakłada, że rozkłady stóp zwrotu IF czy portfela IF

są rozkładami normalnymi. Wzór na prognozę zależy czy liczymy VaR dla prostych
czy logarytmicznych stóp zwrotu.

Dla prostych stop zwrotu:
VaR

t+1|tp

= -(µ

t

+Zασ)W

t

– absolutnyVaR

VaR

t+1|tp

= - Zα σ W

t

– względny VaR

Dla logarytmicznych stóp zwrotu:
VaR

t+1|tp

= (1- e

µt +Zασ

)W

t

– absolutnyVaR

VaR

t+1|tp

= W

t

e

µt

(1- e

Zασ

) – względny VaR

VaR dla jednego dnia ->µ

t

= 0, wówczas VaR względny równa się absolutnemu.

µ

t

– oczekiwana stopa zwrotu (średnia)

σ – odchylenia standardowe stóp zwrotu
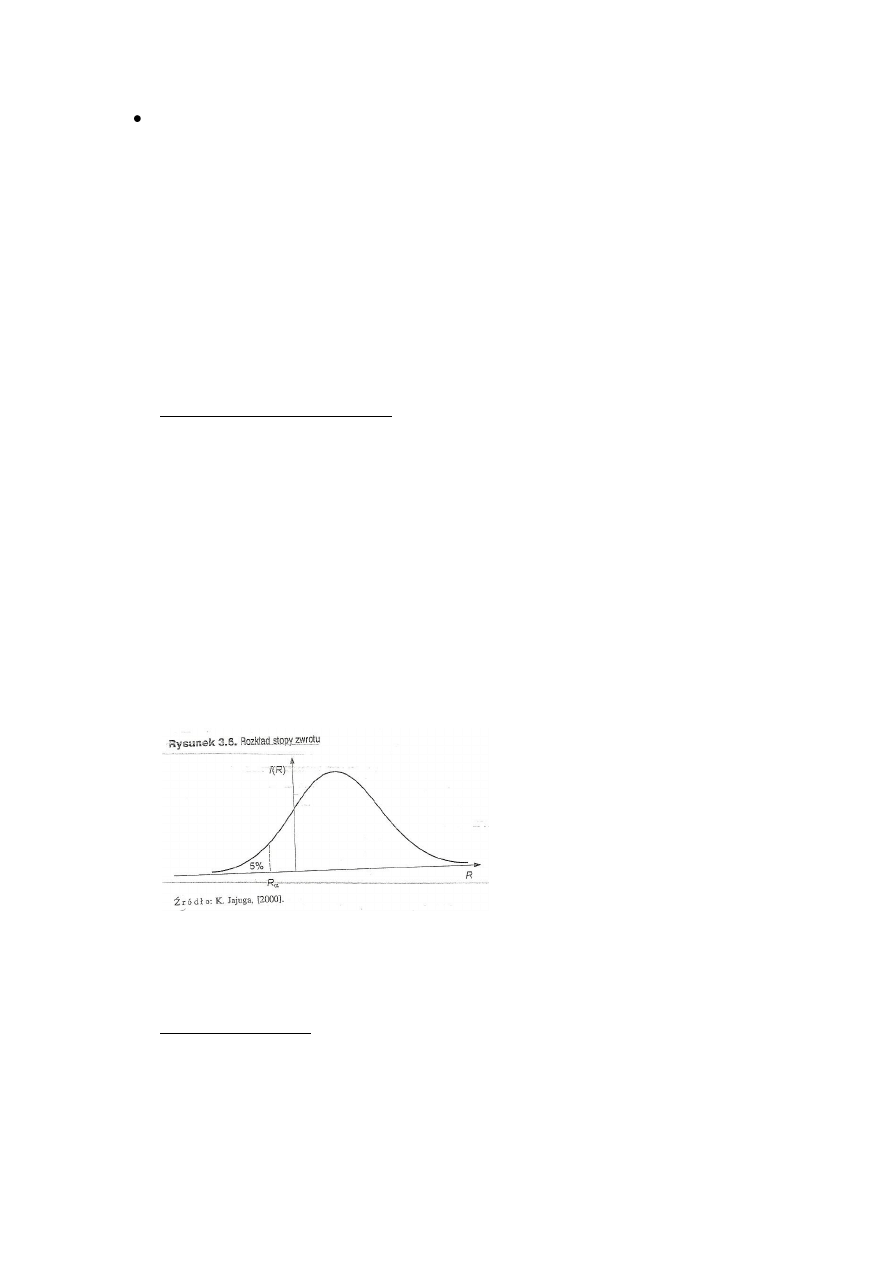
Zα – kwantyl odpowiadający prawdopodobieństwu dla standaryzowanego rozkłady
normalnego np. dla α=0,01, Zα = -2,326

Gdzie Rα = Zα, rysunek jest dla α=0,05 i przedstawia standaryzowany rozkład
normalny Z~N(0,1) – średnia 0 i odchylenie 1.
Z

α

= (x

i

- µ

t

)/(σ) – standaryzacja -> x

i

= µ

t

+ Zασ

Jeszcze dla miesięcznych stóp zwrotu można przyjąć rozkład normalny – ale tak wiadomo, że
nie bo są grube ogony w rozkładach stóp zwrotu o niskiej częstotliwości danych.

2. Metoda empiryczna – polega na wyznaczeniu kwantyla rozkładu stóp zwrotu

bezpośrednio na podstawie empirycznego rozkładu stóp zwrotu. Jest to metoda
nieparametryczna, która nie wymaga założenia o postaci modelu czy też postaci
rozkładu stóp zwrotu. Wymaga jednakże przyjęcia bardzo silnego założenia o stałości
rozkładu stóp zwrotu w przyjętym okresie. Aby zastosować tę metodę potrzebne jest
większa ilość obserwacji – żeby ująć jak najlepiej wszystkie zmiany w czasie.

12

3. Symulacja Monte Carlo – wymaga wiedzy i trudna do zastosowania. Stosuje się ją w

oparciu o istotny model (proces, np. GARCH, SV), który opisuje kształtowanie się
stóp zwrotu. Na podstawie przyjętego modelu generuje się bardzo duża liczbę (kilka
tysięcy lub więcej) realizacji stóp zwrotu. Na ich podstawie wyznacza się kwantyl
rozkładu stóp zwrotu.

GARCH – stosuje się na krótki okres do liczenia VaR

Wady VaR:
- różne metody dają różne szacunki VaR,
- nie daje odpowiedzi na pytanie jak duża może być strata, gdy nastąpi przekroczenie VaR.
Expectedshortfall (ES, oczekiwana strata lub oczekiwana niedobór) – jest odpowiedzią na
drugą wadę VaR. ES jest oczekiwaną wartością straty, pod warunkiem, że strata przekroczy
VaR.
ES = E (X|X>VaR), gdzie X to wielkość straty.
Po przeliczeniu ryzyka (odchylenia standardowego stóp zwrotu) pomiędzy danymi o różnej
częstotliwości obserwacji wykorzystuje się często regułę zwaną pierwiastka kwadratowego z
czasu:
σ (r

[t+1,t+k]

) =

σ (r

t+1

)

σ (r

[t+1,t+k]

) – odchylenia dla k- okresowej stopy

σ (r

t+1

) – odchylenia dla jedno okresowej stopy

Na przykład w celu określenia ryzyka dla danych rocznych na podstawie odchylenia stand.
stóp dla danych dziennych należy przyjąć na k=250 lub 252 (zależy od liczby sesji w roku).
Jednak szacunki na podstawie tej formuły mogą dawać duże błędy, bo zmienność nie jest
stała w czasie oraz ocena może być przeszacowana lub niedoszacowana (zależy wyliczeń
odchylenia dla jednookresowej stopy tzn. jaka była wtedy zmienność).
Sterowanie ryzykiem
- zapobieganie wystąpienia ryzyka (ryzyko o charakterze technicznym),
- dwa podstawowe sposoby zmniejszenia ryzyka: dywersyfikacja i transfer.
Dywersyfikacja – umiejętne tworzenie portfeli inwestycji prowadzących do zmniejszenia
ryzyka portfela.
Transfer ryzyka – ubezpieczenia i hedging.
Hedging – polega na wykorzystaniu instrumentów finansowych, przede wszystkim
instrumentów pochodnych do zmniejszania ryzyka poprzez transfer ryzyka na rynek
finansowy.

WYKŁAD V

Można wyróżnić dwa podstawowe cele strategii sterowania ryzykiem rynkowym:

1. Zabezpieczenie przepływu pieniężnego
2. Zabezpieczenie wartości portfela aktywów

Ad.1 Wyróżnia się dwa podstawowe grupy strategii:

Strategia dopasowania przepływów pieniężnych

Do każdego przepływu pieniężnego zostaje dopasowany przepływ odwrotny w tym samym
terminie i tej samej wielkości

Strategia zabezpieczenia z zastosowaniem instrumentów pochodnych

Ryzyko cen akcji

W celu zabezpieczenia się przed wzrostem wartości indeksu podstawowego należy zastosować jedną
za strategii:

zakup opcji call na ten indeks podstawowy

13

zakup ( długa pozycja ) kontraktu terminowego ( forward lub futures ) na ten indeks
podstawowy. Jest to strategia longhedge.

W celu zabezpieczenia się przed spadkiem wartości indeksu podstawowego należy zastosować jedną
za strategii:

zakup opcji put na ten indeks podstawowy

sprzedaż ( krótka pozycja ) kontraktu terminowego ( forward lub futures ) na ten indeks
podstawowy. Jest to strategia shorthedge.

[przypomnieć różnice między forward i futures ]!!!!!

Zastosowanie opcji oznacza eliminację zagrożenia a także wykorzystanie szansy w przypadku
wzrostu wartości indeksu podstawowego.
Zastosowanie kontraktuforward oznacza całkowite zabezpieczenie się. Eliminacja zagrożenia ale też
rezygnacja z szansy.
Doskonałe zabezpieczenie ( znamy wynik niezależnie od pzryszłej ceny indeksu podstawowego ) jest
możliwe, gdy jednocześnie:

indeks podstawowy, na który jest wystawiony instrument pochodny dokładnie odpowiada
zmiennej ryzyka,

termin realizacji instrumentu pochodnego jest zgodny z terminem na który podmiot chce się
zabezpieczyć.

Jeśli termin realizacji instrumentu nie jest zgodny z terminem na który podmiot chce się zabezpieczyć
to występuje ryzyko bazy.
Baza to różnica między wartością indeksu podstawowego a ceną kontraktu futures na ten indeks.

W dniu wygaśnięcia kontraktu futures baza wynosi zero.
Jeżeli podmiot jest zainteresowany zmniejszeniem ryzyka bazy, to sensownym kryterium
podejmowania decyzji może być minimalizacja wariancji stopy zwrotu portfela składającego się z
pozycji zajętej w kontraktach futures i pozycji zabezpieczanej.
Współczynnik zabezpieczenia jest ilorazem wielkości pozycji zajętej w kontraktach futures do
wielkości pozycji zabezpieczanej. Jest to miara wrażliwości. Jest to liczba kontraktów przypadających
na jednostkę instrumentu podstawowego.
Stopa zwrotu z portfela składającego się z pozycji zabezpieczanej i krótkiej pozycji zajętej w
kontraktach futures wynosi:

– stopa zwrotu z portfela instr. podstawowego

- stopa zwrotu z portfela kontraktu futures

– współczynnik zabezpieczenia

Optymalna wartość współczynnika zabezpieczenia minimalizująca wariancję stopy zwrotu

dana

jest formułą:

Współczynnik zabezpieczenia można wyznaczyć szacując metoda najmniejszych kwadratów
równanie regresji:

Optymalna wartość współczynnika zabezpieczenia jest wówczas równa szacunkowi parametru
W przypadku gdy skład portfela akcji różni się od składu indeksu giełdowego należy sprzedać
odpowiednią liczbę kontraktów futures na indeks giełdowy:
N =

P – wartość zabezpieczanego portfela
F – cena kontraktu futures

14

Ryzyko stopy procentowej

W celu zabezpieczenia przepływów pieniężnych przed wzrostem stopy procentowej należy zająć
długą pozycje w kontrakcie FRA.
W celu zabezpieczenia przepływów pieniężnych przed spadkiem stopy procentowej należy zająć
krótką pozycje w kontrakcie FRA.
Kontrakt FRA oferowany jest przez banki a indeksem podstawowym jest krótkoterminowa stopa
procentowa ( do 1 roku ). Jest to pewna referencyjna stopa procentowa np. Wibor. Wyróżnia się tu
dwa terminy. Np. FRA 6 9, termin rozliczenia kontraktu jest za 6 miesięcy, a stopa kontraktu ( stopa
FRA ) obowiązuje w okresie 3 miesięcy, między końcem szóstego a końcem dziewiątego miesiąca.

Ryzyko kursu walutowego

Gdy zabezpieczany jest wpływ pieniężny w obcej walucie możliwe są strategie:

1. zakup walutowy opcji put
2. sprzedaż walutowego kontraktu forward
3. sprzedaż walutowego kontraktu futures
4. zawarcie kontraktu swap, w którym podmiot dokonuje płatności w obcej walucie a otrzymuje

płatność w krajowej walucie.

Gdy zabezpieczany jest wypływ pieniężny w obcej walucie możliwe są strategie:

1. zakup walutowy opcji call
2. zakup walutowego kontraktu forward
3. zakup walutowego kontraktu futures
4. zawarcie kontraktu swap, w którym podmiot dokonuje płatności w krajowej walucie a

otrzymuje płatność w obcej walucie.

Zabezpieczanie wartości portfela aktywów

I.

strategie z zastosowaniem miar wrażliwości

Polega na takiej modyfikacji portfela aby odpowiednia miara wrażliwości przyjęła wartość
ustaloną przez podmiot

II.

strategie polegające na dywersyfikacji portfela

Ad. I Trzy strategie z zastosowaniem miar wrażliwości:

1. Utworzenie portfela o pożądanej wartości współczynnika beta poprzez wybór odpowiednich

udziałów poszczególnych składników
Współczynnik beta portfela =

– udział i-tego składnika portfela

– współczynnik beta i-tego składnika portfela

Strategia ta polega na rozwiązaniu równania lub układu równań ( jak jest więcej współczynników beta
w modelu APT ).

2. Utworzenie portfela o pożądanej wartości współczynnika beta z zastosowaniem kontraktu

futures

Jeśli podmiot chce zmniejszyć wsp. beta, należy sprzedać N kontraktów na indeks:

N= (

)P/

Jeśli podmiot chce zwiększyć wsp. beta, należy kupić N kontraktów na indeks:

15

N= (

)P/

– obecna wartość wsp. beta portfela

– docelowa wartość wsp. beta portfela

– wartość wsp. beta kontraktu futures

P – wartość zabaezpieczanego portfela
F – cena kontraktu futures

3. Wykorzystanie opcji i współczynników greckich

Strategia delta – gamma – vega hedging polega na utworzeniu portfela złożonego z akcji i opcji, tak
aby jednocześnie współczynniki delta, gamma i vega tego portfela były równe zeru.

Ad. II Strategie polegające na dywersyfikacji portfela( Markowitz )

maksymalizacja oczekiwanej stopy zwrotu
minimalizacja ryzyka

niesie współczynniki korelacji między składnikami portfela