Minimalizacja funkcji jednej lub wielu zmiennych
Wykład 13
Optymalizacja
= wyznaczenie minimum funkcji rzeczywistej wielu zmiennych
w danym obszarze (wraz z punktem w którym to minimum występuje).
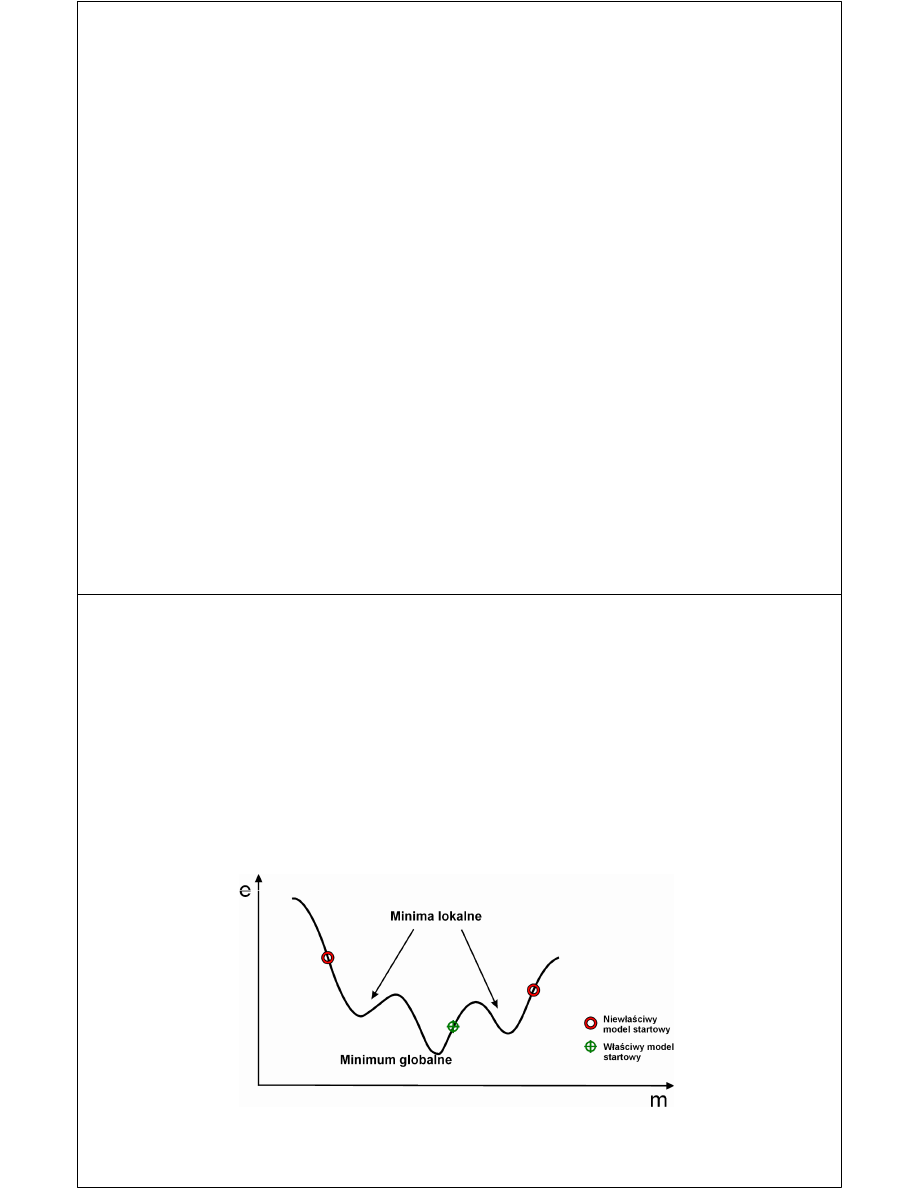
Jeśli funkcja jest nieliniowa i zawiera wiele minimów lokalnych zadanie jest
trudne do rozwiązania.
Wynik lokalnych procedur iteracyjnych (które opierają się na linearyzacji
minimalizowanej funkcji w otoczeniu wybranego punktu w przestrzeni n-
wymiarowej) jest silnie uzależniony od wyboru modelu startowego.
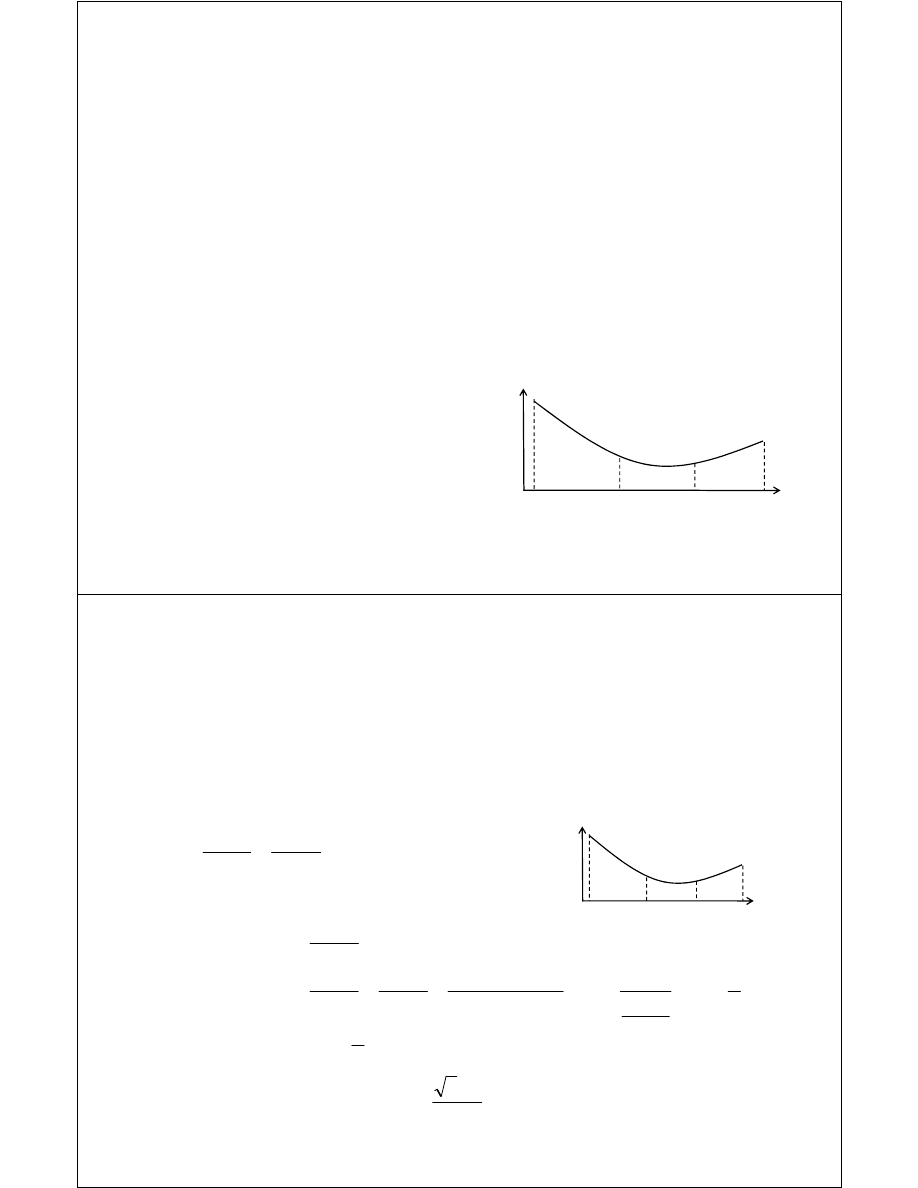
Rozpoczniemy od metod minimalizacji ciągłej funkcji unimodelnej tj takiej
która w przedziale [a,b] ma tylko jedno minimum lokalne.
Jeżeli zadana funkcja nie posiada tej własności, należy znaleźć jej przedziały
unimodalności i zastosować opisywaną metodę do każdego z nich.
Jeśli dla a < x* < b zachodzą warunki f(a) > f(x*) i f(x*) < f(b) to:
- funkcja ma w przedziale [a,b] minimum w punkcie x*
- potrzeba trzech punktów do zlokalizowania minimum
Metody eliminacji (złotego podziału,
Funkcja ciągła f w przedziale [a,b] posiada dokładnie
jedno minimum x*. Minimum to można znaleźć
poprzez kolejne podziały zadanego przedziału. W
tym celu należy obliczyć wartości funkcji w dwóch
punktach x
L
i x
R
takich, że a < x
L
< x
R
< b, a
następnie zbadać ich wielkości:
- Jeżeli f(x
L
) > f(x
R
), to szukane minimum
znajduje się w przedziale [x
L
,b].
- Jeżeli f(x
L
) < f(x
R
), to szukane minimum
znajduje się w przedziale [a,x
R
].
a
b
x
L
x
R
Przedziały [a,x
R
].i
[x
L
,b] zachodzą na
siebie. Przedział jest
zawężany w stosunku
k= [a,x
R
]./ [a,b]
Wielkość otrzymanego w wyniku powyższego postępowania przedziału po n
krokach wynosi: (b
(n)
− a
(n)
)k
n
gdzie k jest stałym współczynnikiem o który
zmniejszana jest wielkość przedziałów w kolejnych krokach algorytmu.
Wartość współczynnika k jest dobrana w taki sposób, aby przy kolejnych
iteracjach wykorzystywać obliczoną w poprzednim kroku wartość funkcji
jednej z dwóch próbek (f(x
L
) lub f(x
R
)). Obliczmy tę wartość:
a
b
a
x
a
b
x
b
k
R
L
−
−
=
−
−
=
a
x
x
b
L
R
−
=
−
czyli
ponieważ f(x ) > f(x ) zawężamy przedział do [x ,b].
Metoda złotego podziału
a
b
x
L
x
R
ponieważ f(x
L
) > f(x
R
) zawężamy przedział do [x
L
,b].
a → x
L
b → b
x
L
→
x
R
L
R
x
b
x
b
k
−
−
=
k
a
b
x
b
x
b
b
a
b
x
x
b
a
x
x
b
x
b
k
L
L
L
L
L
L
R
1
1
1
1
)
(
+
−
=
−
−
+
−
=
−
−
−
−
=
−
−
=
−
−
=
618
.
0
2
1
5
0
1
1
1
2
=
−
=
=
−
+
+
−
=
k
k
k
k
k
Strategię obliczania minimum funkcji można zapisać:
Jeśli:
Jeśli
to STOP, w przeciwnym wypadku powtórz
punkt 2.
Funkcja wystarczająco gładka:
•w pobliżu minimum funkcja
kwadratowa jest dobrym
przybliżeniem
•parabola dopasowana do dowolnych
Metoda interpolacji parabolicznej
( )
c
bx
Ax
x
p
+
−
=
2
2
1
( )
A
b
x
b
Ax
dx
x
dp
=
⇒
−
=
=
*
0
•parabola dopasowana do dowolnych
trzech punktów powinna wskazać
w jednym kroku minimum albo
przynajmniej w jego bliskie otoczenie.
( )
*
*
p
x
p
=
Jeśli
to
( )
(
)
2
*
*
2
1
x
x
A
p
x
p
−
=
−
Rozwijając dowolną funkcję f(x) w szereg Taylora otrzymujemy
( )
( )
( )(
)
( )(
)
K
+
−
′′
+
−
′
+
=
2
0
0
0
0
0
2
1
x
x
x
p
x
x
x
p
x
p
x
p
widać, że dla x
0
=x*
mamy p’(x
0
)=0 i parabola lokalnie przybliża f(x)
( )
0
1
2
2
a
x
a
x
a
y
x
p
+
+
=
=
Dla trzech punktów (x
a
,y
a
), (x
b
,y
b
) i (x
c
,y
c
) parabola
Przechodząca przez te punkty będzie miała postać:
(
)
(
)
0
1
2
2
c
x
x
c
x
x
c
y
b
b
+
−
+
−
=
gdzie
b
y
c =
0
Ponieważ dla pozostałych dwóch punktów mamy:
(
)
(
)
b
b
a
b
a
a
y
x
x
c
x
x
c
y
+
−
+
−
=
1
2
2
(
)
(
)
b
b
c
b
c
c
y
x
x
c
x
x
c
y
+
−
+
−
=
1
2
2
możemy wyznaczyć wartości parametrów c
1
i c
2
:
(
) (
) (
) (
)
[
]
b
c
b
a
b
a
b
c
y
y
x
x
y
y
x
x
C
c
−
−
−
−
−
=
2
2
1
(
)(
) (
)(
)
[
]
b
c
b
a
b
a
b
c
y
y
x
x
y
y
x
x
C
c
−
−
+
−
−
−
=
2
(
)(
)
(
)(
)
2
2
1
b
a
b
c
b
c
b
a
x
x
x
x
x
x
x
x
C
−
−
−
−
−
=
gdzie
2
1
*
2c
c
x
p
b
−
=
oraz wartość paraboli w maksimum
Metoda Brandta (wykorzystująca metodę złotego podziału i interpolacji
parabolicznej
1. Wyznaczamy przedział [x
a
,x
b
].
2. Wyznaczamy metodą złotego podziału punkt x
i
leżący w jego
wnętrzu będący pierwszym przybliżeniem minimum
3. Ponownie stosujemy „złoty podział” by znaleźć x
i+1
i zdefiniować
nowy, zawężony przedział
4. Wyznaczamy parabolę i wyznaczamy jej minimum x*
5. Jeśli x* leży w ostatnio zdefiniowanym przedziale
oraz gdy zmiana
położenia minimum jaka miała miejsce przy wykonaniu ostatniej
położenia minimum jaka miała miejsce przy wykonaniu ostatniej
iteracji była mniejsza od połowy zmiany położenia minimum w
przedostatniej iteracji kończymy procedurę, jeśli któryś z warunków
nie jest spełniony – powrót do punktu
3.
Metody minimalizacji funkcji n zmiennych (minimalizacja w
przestrzeni n-wymiarowej)
Numeryczne metody poszukiwania minimum funkcji wielu zmiennych można
podzielić na następujące klasy:
•metody poszukiwań prostych, takie jak metoda
Hooka-Jevesa
i metoda
Rosenbrocka
•metody poprawy kierunków, wśród których możemy wyróżnić następujące
grupy:
grupy:
•
metody bezgradientowe
, w przypadku których do znalezienia minimum
potrzebne jest wyznaczanie jedynie
wartości funkcji f(x), np. metoda
Gaussa-Seidela
i metoda Powella
•
metody gradientowe
, dla których w procesie poszukiwania minimum
korzystamy z wyznaczanych
wartości minimalizowanej funkcji f(x) oraz
jej
gradientu, np. metoda
najszybszego spadku
i metoda
gradientu
sprzężonego
;
•metody newtonowskie i quasi-newtonowskie, gdzie poszukiwanie
minimum przeprowadzamy z wyznaczaniem w kolejnych punktach
wartości funkcji, jej gradientu oraz hesjanu
Dla wszystkich typów metod należących do klasy metod poprawy
kierunków wykorzystujemy wspólny schemat prowadzenia obliczeń
iteracyjnych. Polega on na tym, że do punktu odpowiadającego minimum
funkcji f(x), dochodzimy w kolejnych krokach poszukiwania minimum wzdłuż
odpowiednio wyznaczonych kierunków d w przestrzeni n-wymiarowej,
zwanych kierunkami poszukiwań.
Jeżeli po k-1 krokach optymalizacji osiągnięto punkt poszukiwań x
k-1
to w
kolejnym k-tym kroku przeprowadza się minimalizację wzdłuż prostej
wyznaczonej przez punkt x
k-1
i wektor kierunku
d, tj. znajdujemy taką
optymalna wartość α
k
, że
optymalna wartość α
k
, że
(
)
d
min
:
1
k
k
k
x
f
k
α
α
α
+
−
a więc rozwiązujemy zagadnienie minimalizacji funkcji jednej zmiennej -
tą
zmienną jest α
k
Kierunki te mogą być stałe w trakcie całego iteracyjnego procesu
poszukiwań minimum bądź też mogą ulegać zmianie na kolejnych etapach
w zależności od wartości minimalizowanej funkcji, jej gradientu lub również
hesjanu.
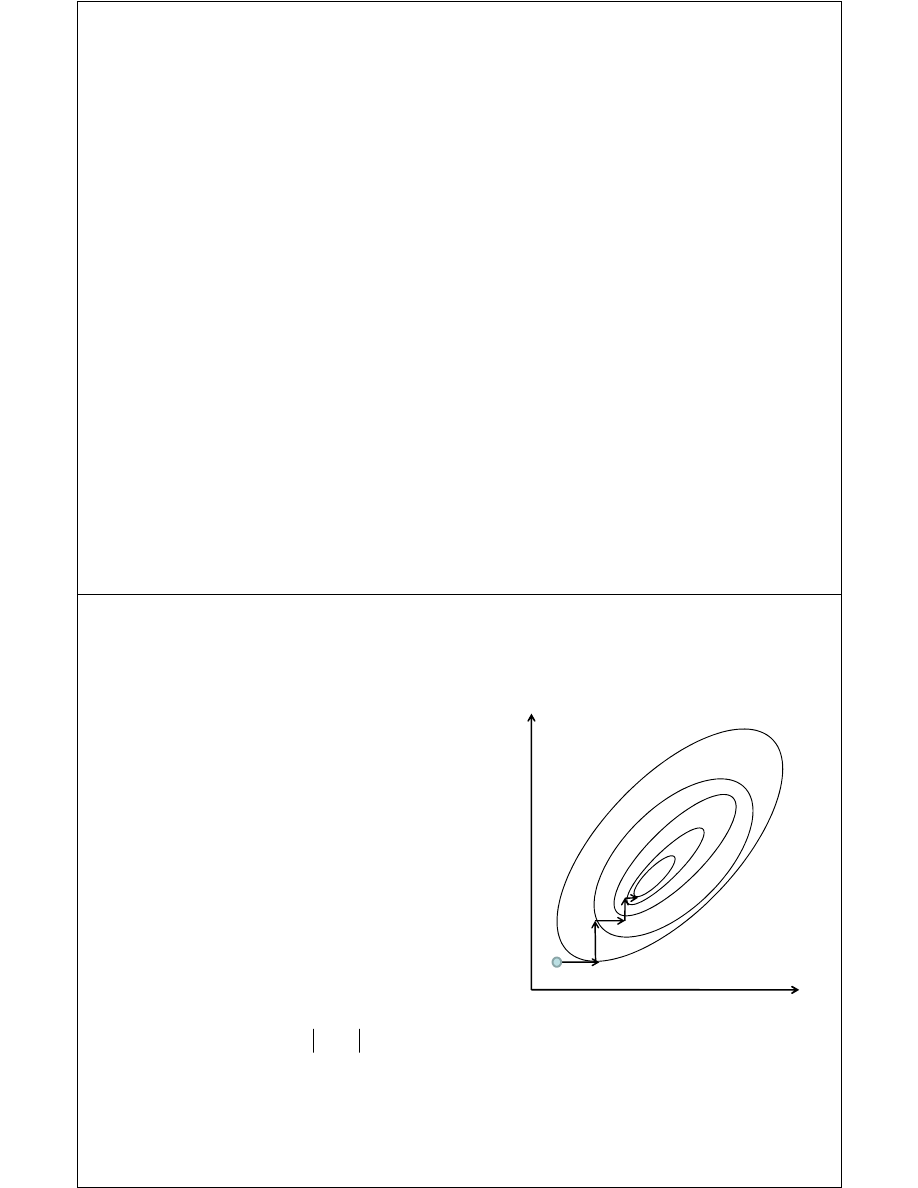
Iteracyjne algorytmy optymalizacji mają następujące fazy:
• wybór punktu początkowego poszukiwań x
0
•
wyznaczenie kolejnego punktu x
k
, stanowiącego przybliżenie minimum x*;
punkt ten wyznaczamy przez poszukiwania wzdłuż kierunku d
k
, którego
określenie, jak i również odległość przesunięcia w tym kierunku są zależne
od wybranej metody optymalizacji; kolejny punkt, będący nowym (lepszym)
przybliżeniem punktu minimalizującego funkcję f(x) , jest wyznaczany z
zależności:
• sprawdzenie warunków zbieżności (kryterium osiągnięcia punktu
k
1
d
k
k
k
x
x
α
+
=
−
• sprawdzenie warunków zbieżności (kryterium osiągnięcia punktu
minimalnego wskaźnika jakości) i – w zależności od wyniku – kontynuowanie
poszukiwań iteracyjnych albo ich zakończenie.
Ważna uwaga
: Punkt początkowy wybierany jest na podstawie posiadanych
informacji dotyczących położenia minimum (często po prostu losowany).
W przypadku minimalizacji funkcji wielu zmiennych dobór punktu
początkowego poszukiwań może w znaczący sposób przyspieszyć lub
opóźnić znalezienie minimum wskaźnika jakości albo wręcz zdecydować o
możliwości znalezienia minimum globalnego funkcji.
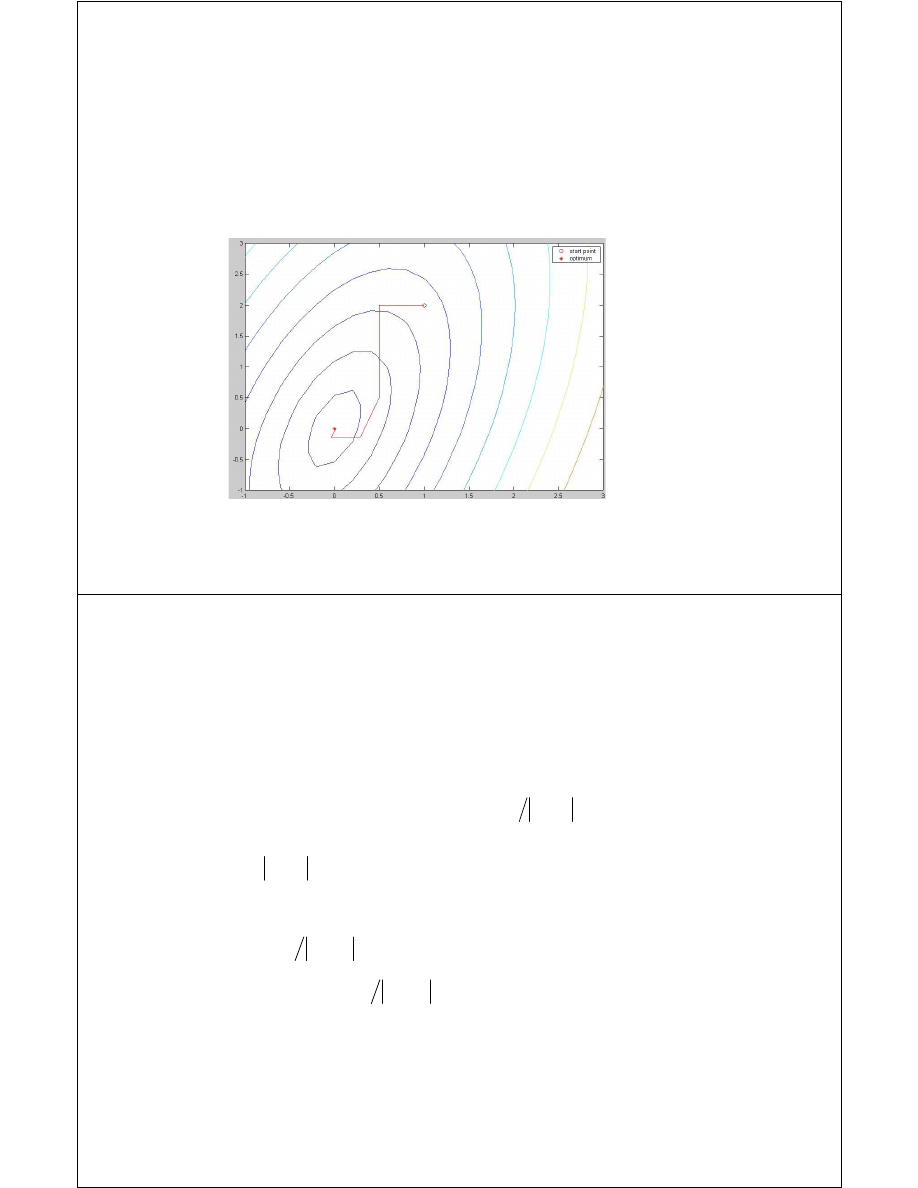
Minimalizacja wzdłuż kierunków współrzędnych
e
2
Wektorom bazy
e
i
, i=1,N przypisujemy kierunki w
których odbywać się będzie minimalizacja (tak jak
dla przypadku 1 zmiennej).
Algorytm:
1. Z punktu startowego x
0
minimalizujemy
funkcję wzdłuż prostej wyznaczonej przez
e
1
i
wyznaczamy minimum w punkcie x
1
2. Z punktu x
1
minimalizujemy funkcję w kierunku
e
2
i wyznaczamy kolejny punkt x
2
x
0
e
1
x
1
x
2
e
2
i wyznaczamy kolejny punkt x
2
3. Kontynuujemy wzdłuż kolejnych osi i
ostateczne znajdujemy punkt x
N
4. Powracamy do minimalizacji wzdłuż kierunku
e
1
i powtarzamy procedurę kolejny raz
5. Minimalizacja kończy się gdy spełniony jest
warunek:
gdzie ε jest dokładnością reprezentacji
maszynowej liczb użytą w obliczeniach a t
parametrem dobieranym indywidualnie.
(
)
( )
( )
t
x
f
x
f
x
f
n
n
n
+
<
−
−
ε
1
Metoda kierunków sprzężonych (Powell'a)
Metoda kierunków sprzężonych jest bezgradientową, iteracyjną metodą
optymalizacji bez ograniczeń. Dla form kwadratowych jest ona zbieżna w N
krokach. W metodzie Powell'a baza zmienia się w trakcie wykonywania algorytmu.
Modyfikacja bazy polega na stworzeniu i dodaniu do niej nowego sprzężonego
kierunku i równoczesnym usunięciu z niej takiego kierunku, wzdłuż którego
nastąpiło największe przesunięcie.
Metoda kierunków sprzężonych (Powell'a)
Algorytm:
1. x
p
:= x
2. Dla każdego z kierunków k=1, 2, ..., N wybieramy optymalny krok m
k
dokonując minimalizacji jednowymiarowej wzdłuż kierunku e
k
3. x := x + m
1
e
1
+ m
2
e
2
+ ... + m
N
e
N
4. Wyznacz kierunek sprzężony i podstawiamy
x := x + m
N+1
e
N+1
, gdzie m
N+1
jest optymalnym krokiem uzyskanym w
wyniku minimalizacji funkcji g(m
N+1
)=f(x+m
N+1
e
N+1
)
5. Jeżeli (zachodzi warunek stopu) to koniec obliczeń
6. x
p
:= x
p
p
N
x
x
x
x
e
−
−
=
+1
ε
<
−
p
x
x
6. x
p
:= x
7. wyznaczamy numer kierunku k (1≤k≤N), w którym nastąpiło największe
przesunięcie (kierunek dla którego m
k
było największe)
8. Jeżeli
(wyznacznik dla nowej bazy - stopień liniowej
niezależności - jest bezpiecznie duży), to zmień bazę:
e
k
:= e
N+1
i
9. przejdź do pkt. 2
ε
≥
−
p
k
x
x
d
m
p
k
x
x
d
m
d
−
=
: