1. Postulaty statyki

1. Zasada równoległoboku

2. Dwie siły przyłożone do ciała sztywnego równoważą się tylko wtedy, gdy działają

wzdłuż tej samej prostej, są przeciwnie skierowane i mają te same wartości liczbowe

3. Działanie układu sił przyłożonych do ciał sztywnego nie ulegnie zmianie, gdy do układu

dodamy lub odejmiemy dowolny układ równoważących się sił tzw. układ zerowy

4. Zasada zesztywnienia – równowaga sił działających na ciało odkształcalne nie zostanie

naruszona przez zesztywnienie tego ciała

5. Każdemu działaniu towarzyszy równe co do wartości i przeciwnie skierowane wzdłuż

tej samej prostej przeciwdziałanie

6. Każde ciało nieswobodne można myślowo oswobodzić od więzów, zastępując przy tym

ich działanie odpowiednimi reakcjami.

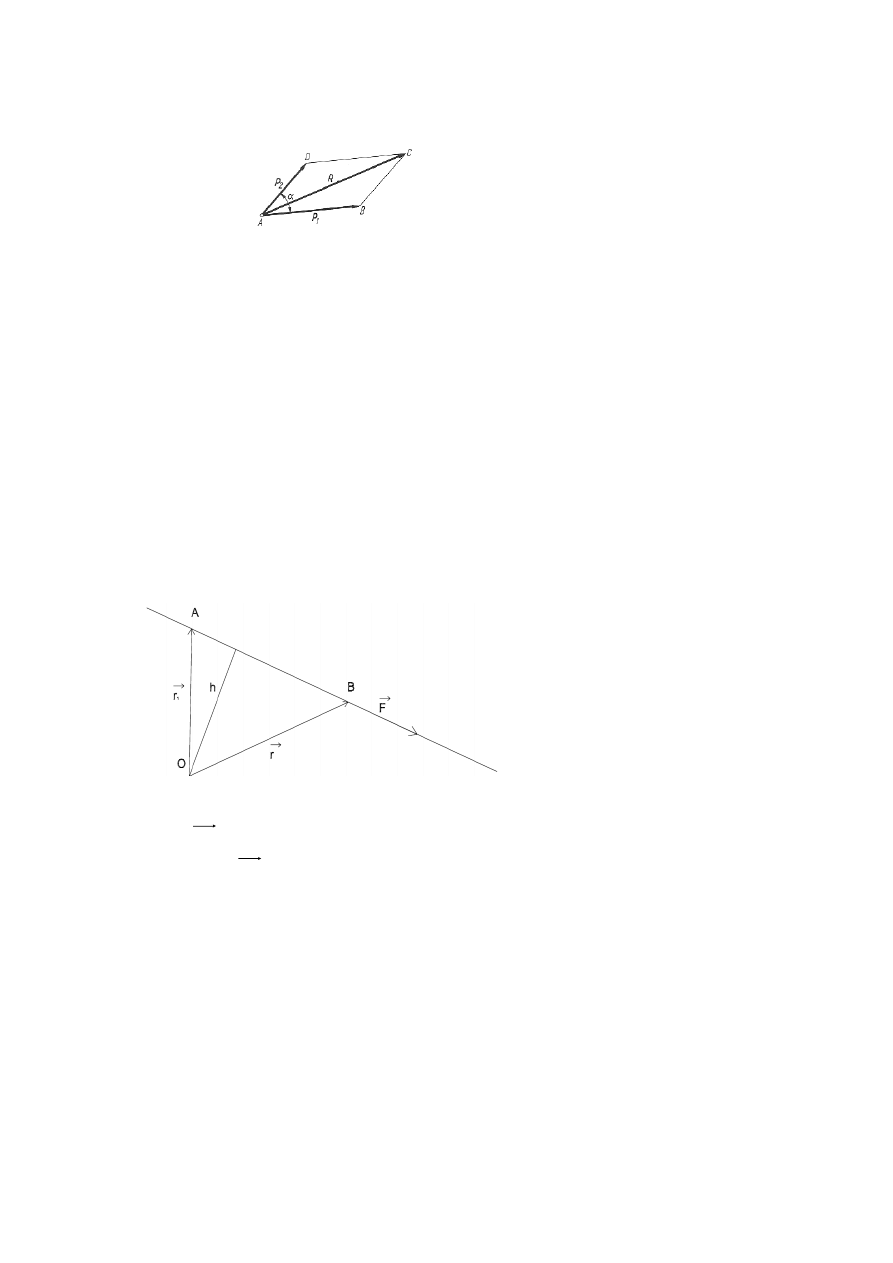
2. Twierdzenie o trzech siłach - Aby trzy nierównoległe do siebie siły działające na ciało

sztywne były w równowadze, linie działania tych sił musza˛ przecinać się w jednym
punkcie, a same siły musza˛ tworzyć trójkąt zamknięty.

3. Twierdzenie Varignon – Moment względem dowolnego punktu O wypadkowej dwóch sił

równy jest sumie momentów sił wypadkowych względem tegoż punktu

4. Para sił – układ dwóch sił równoległych nieleżących na jednej prostej. Odległość między

siłami nazywamy ramieniem pary sił

5. Moment siły

6. Kratownice – układ złożony z prętów, których końce są ze soba połączone przegubowo,

mający niezmienną postać geometryczną nazywamy kratownicą. Połączenia przegubowe
nazywamy węzłami.
1. Warunek sztywności: p=2w-3

7. ---------------------------------------------------------------------------
8. Redukcja przestrzennego downolnego układu sił

2

1

P

P

R







+

=

( )

hF

M

F

r

rF

M

F

r

F

AB

F

r

M

AB

r

r

F

r

M

O

O

O

O

=

=

×

=

×

+

×

=

+

=

×

=



























,

sin

1

1

1

9. Tarcie

1. W przypadku ciała pozostającego w spoczynku na chropowatej powierzchni zależność

między siłą tarcia T, a naciskiem normalnym N wyraża się następująco:
gdzie u-współczynnik tarcia statycznego

2. Jeżeli siła tarcia osiąga swą graniczną wartość, co oznacza, że tarcie jest całkowicie

rozwinięte, to w powyższym wzorze przyjmujemy znak równości.

3. Kierunek siły tarcia działającej na ciało znajdujące się w spoczynku jest przeciwny do

kierunku ruchu, który zaistniałby, gdyby tarcia nie było.

4. W przypadku ciała ślizgającego się po chropowatej powierzchni siła tarcia jest

skierowana przeciwnie do kierunku ruchu, a jej wartość określa wzór:

10. Kinematyczne równania ruchu punktu

11. Definicja prędkości – prędkość punktu jest wektorem określonym przez pierwszą pochodną

wektora położenia względem czasu

12. Definicja przyspieszenia – przyspieszeniem nazywamy wektor dany przez pierwszą

pochodną wektora prędkości lub drugą pochodną wektora położenia względem czasu

13. Przyspieszenie styczne, przyspieszenie normalne

1. Przyspieszenie styczne - Jest to składowa przyspieszenia styczna do toru ruchu,

powodująca zmianę wartości prędkości, ale nie powodująca zmiany kierunku ruchu.

N

T

µ

≤

N

T

'

'

µ

=

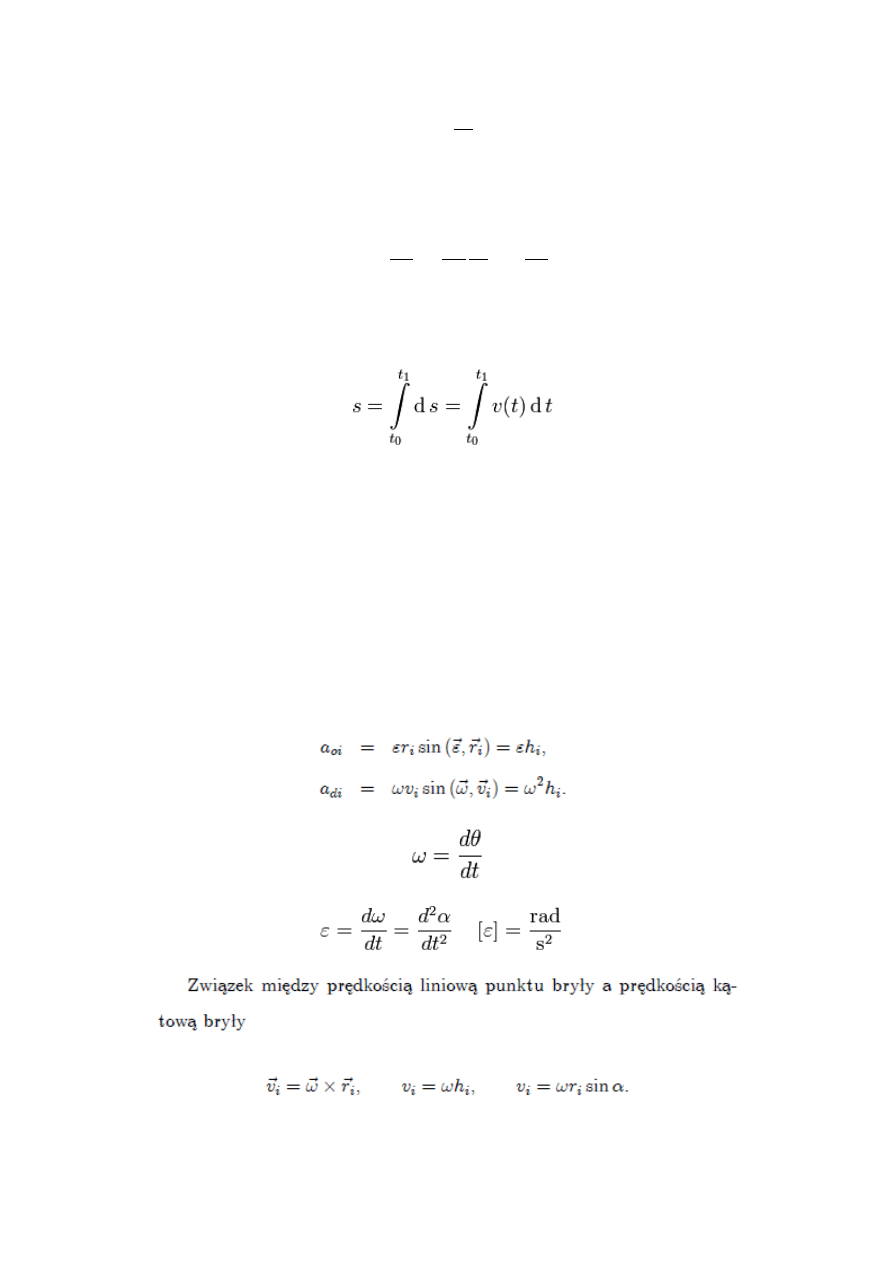
Przyspieszenie styczne a

t

określa wzór:

2. Przyspieszenie normalne - Jest to składowa przyspieszenia prostopadła do toru ruchu.

Reprezentuje tę część przyspieszenia, która wpływa na zmianę kierunku prędkości, a
zatem na kształt toru, ale nie wpływa na zmianę wartości prędkości. Wartość
przyspieszenie normalnego jest równa:

14. Droga - to długość odcinka toru (krzywej lub prostej), jaką pokonuje ciało lub punkt

materialny podczas swojego ruchu. Droga nie oznacza odległości pomiędzy dwoma
punktami wyznaczającymi początek i koniec ruchu. Liczy się ją po torze ruchu, czyli po
krzywej, po której porusza się ciało.

15. -----------------------------------------------------------------------------
16. -----------------------------------------------------------------------------
17. -----------------------------------------------------------------------------
18. Rodzaje ruchów bryły

1. podstawowe: ruch postępowy, ruch obrotowy
2. dodatkowo: ruch płaski, ruch kulisty

19. Prędkość i przyspieszenie punktu bryły w ruchu postępowym – prędkości(przyspieszenia)

wszystkich punktów bryły poruszajacej się ruchem postępowym są w danej chwili
wektorami równoległymi

20. Prędkość i przyspieszenie punktu bryły w ruchu obrotowym

1. Prędkość liniowa dowolnego punktu bryły w ruchu obrotowym jest równa iloczynowi

wektorowemu wektora prędkości kątowej przez wektor położenia puntu

2. Całkowite przyspieszenie dowolnego punktu bryły w ruchu obrotowym jest sumą

geometryczną przyspieszeń: obrotowego a

oi

i doosiowego a

di

21. Prędkość kątowa

22. Przyspieszenie kątowe

23. Prędkość liniowa punktu, a prętkość kątowa bryły

24. Prędkość i przyspieszenie bryły w ruchu płaskim

1. prędkość

dt

dv

a

=

τ

ds

d

v

dt

ds

ds

d

v

dt

d

v

a

n

ϕ

ϕ

ϕ

2

=

=

=

2. przyspieszenie w ruchu płaskim jest sumą geometryczną przyspieszenie ruchu

postępowego, przyspieszenia obrotowego i przyspieszenie doosiowego

25. Twierdzenie o rzutach prędkości dwóch punktów bryły poruszającej się ruchem płaskim –

rzuty prędkości dwóch punktów na kierunek łączocy te punkty są sobie równe

26. Chwilowy środek obrotu
27. ------------------------------------------------------------------------------
28. ------------------------------------------------------------------------------
29. Układ Eulera

φ – kąt obrotu własnego,
ψ – kąt precesji
υ – kąt nutacji

30. -------------------------------------------------------------------------------
31. -------------------------------------------------------------------------------
32. -------------------------------------------------------------------------------
33. Ruch złożony punktu
34. Prędkość bezwzględna – w ruchu względnym prędkość bezwzględna jest sumą

geometryczną prędkości względej i prędkości unoszenia

35. Przyspieszenie bezwzględne – w ruchu względnym przyspieszenie bezwzględne jest sumą

geometryczną przyspieszenia względnego, przyspieszenia unoszenia i przyspieszenia
Coriolisa

36. Przyspieszenie Coriolisa

37. Zasady Newtona

1. Zasada bezwładności – punt materialny, na który nie działają żadne siły lub wszystkie

działające nań siły znoszą się, pozostaje w spoczynku lub porusza się ruchem
jednostajnym prostoliniowym względem układu odniesienia. Układ odniesienia, w

di

oi

A

i

a

a

a

a









+

+

=

3

2

1

3

2

1

ω

ω

ω

ω

υ

ψ

ϕ

ω























+

+

=

+

+

=

k

k

k

którym słuszna jest ta zasada nazwyamy inercjalnym. Punkt w tym układzie nie może
udzielić sobie przyspieszenia.

2. W układzie inercjalnym zmiana ruchu punktu materialnego jest proporcjonalna do siły

działającej i odbywa się w kierunku działania tej siły

3. Zasada akcji i reakcji – Każdemu działaniu towarzyszy równe, lecz przeciwnie

skierowane przeciwdziałanie

4. Pod wpływem układu sił punkt materialny uzyskuje przyspieszenie rowne sumie

geometrycznej przyspieszeń, jakie uzyskałby w wyniku niezalneżnego działa każdej z
sił.

5. Zasada powszechnego ciążenia – Dwa punkty materialne o masach m

1

i m

2

działają na

siebie z siłą proporcjonalną do iloczynu tych mas, a odwrotnie proporcjonalnie do
kwadratu odległości tych mas

38. Zasada d'Alemberta – w ruchu punktu materialnego układ sił czynnych i reakcji więzów

równoważy się z pomyślaną siłą bezwładności

39. Zasada zachowania pędu – jeżeli na punkt materialny nie działają żadne siły, to pęd punktu

jest zachowany, jest stały

40. Zasada pędu i popędu - Przyrost pędu układu materialnego w skończonym przedziale czasu

jest równy popędowi wektora głównego sił zewnętrznych działających na ten układ.

41. Zasada zachowania krętu – Jeżeli moment główny sił działających na poruszający się punkt

jest względem jakiegoś bieguna równy zeru, to kręt poruszającego się punktu względem
tego bieguna jest zachowany, jest stał

42. Zasada krętu i pokrętu - Przyrost krętu układu materialnego względem dowolnego

nieruchomego punktu jest równy pokrętowi momentu głównego sił zewnętrznych względem
tego samego punktu.

43. Dynamiczne równania ruchu punktu materialnego

44. Definicja pracy – Jeśli na jakiś punkt działa siła P i punkt przesuwa się o s, to mówimy, że P

wykonała pracę

45. Moc mechaniczna - Pracę wykonaną przez siłę w jednostce czasu nazywamy mocą siły

46. Zasada równoważności pracy i energii kinetycznej – przyrost energii kinetycznej punktu

materialnego(ciała) równy jest pracy wykonanej przez siły działającej na ciało

47. Zasada równoważności pracy i energii potencjalnej
48. Potencjalne(zachowawcze) pole sił – Istnieją pola, w których praca zależy jedynie od

skrajnych położeń. Tego typu pole nazywamy zachowawczymi lub potencjalnymi.

49. Twierdzenie o ruchu środka masy układu punktów materialnych – Środek masy porusza się

a

m

F





=

2

2

1

r

m

m

k

F

=

∑

∑

=

−

+

+

0

)

(

a

m

R

F

i

i







α

cos

Ps

s

P

L

=

=







α

cos

Pv

v

P

M

v

P

dt

r

d

P

dt

dL

M

=

=

=

=

=



















jak punkt materialny, w którym skupiona jest całkowita masa układu i na który działają
wszystkie siły zewnętrzne.

50. Pęd układu punktów materialnych

51. Kręt układu punktów materialnych

52. Energia kinetyczna układu punktów materialnych – energia kinetyczna układu punktów jest

równa sumie energii poszczególnych punktów.

W ruchu postępowym prędkości wszystkich punktów są jednakowe więc:

53. Twierdzenie Koeniga – Energia kinetyczna układu punktów materialnych równa jest sumie

energii kinetyczne, jaką miałby punkt materialny o masie całego układu, poruszający się z
prędkością środka masy oraz energii kinetycznej tegoś układu zględem środka masu.

54. Zasada zachowania energii mechanicznej - W dowolnym ruchu przebiegającym bez tarcia (i

innych strat energii) energia mechaniczna układu izolowanego jest stała.

55. Wahadło matematyczne

∑

=

2

2

i

i

v

m

T

2

2

2

2

mv

m

v

T

i

=

=

∑

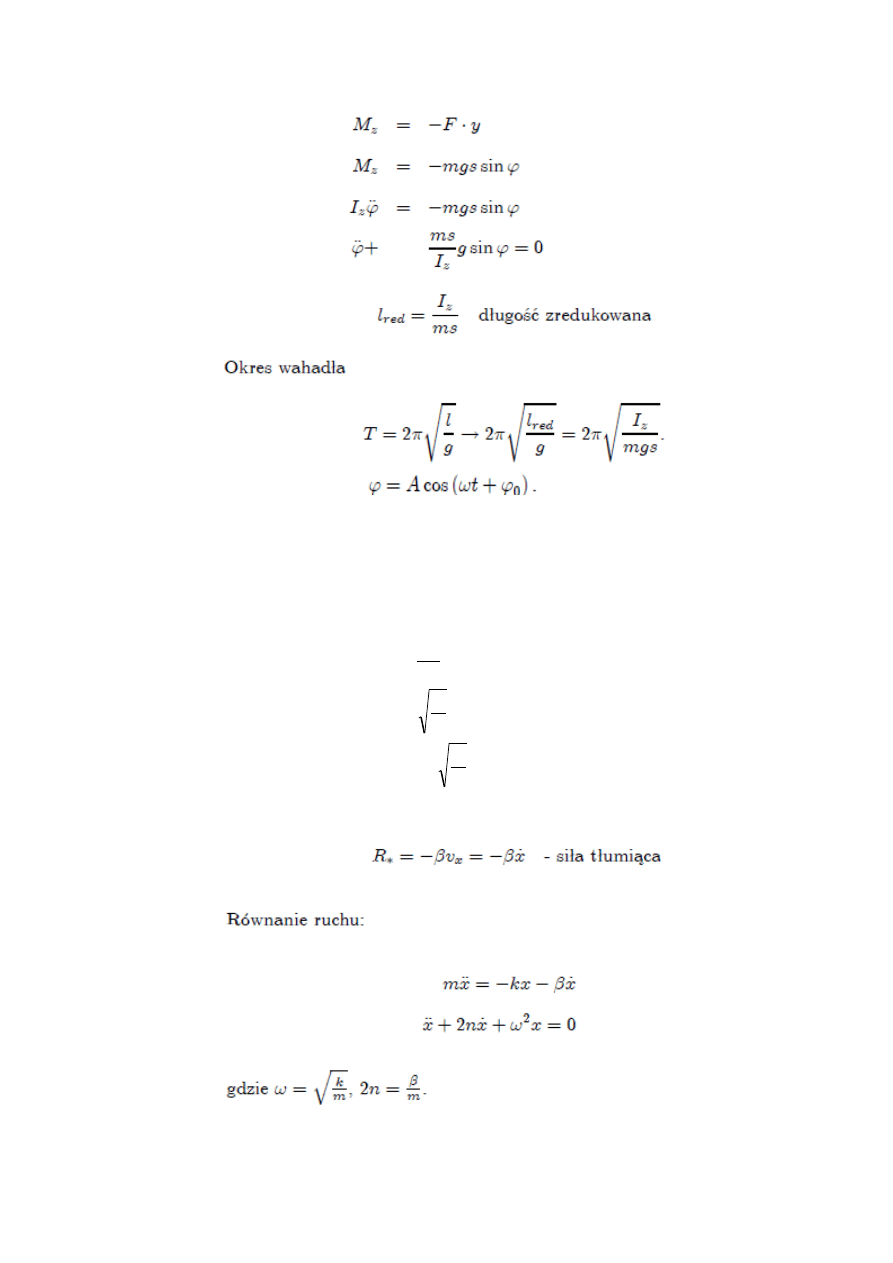
56. Wahadło fizyczne – swobodnie obracające się ciało materialne względem stałego punktu

57. Drgania swobodne – aby wystąpiły drgania, punkt musi poruszać się ruchem

prostoliniowym pod wpływem siły F przyciągajacej ten punkt do stałego punktu O zwanego
środkiem drgań

58. Drgania tłumione – występują w ośrodku stawiającym opór. Siły opory są proporcjonalne do

prędkości

59. Logarytmiczny dekrement tłumienia

k

m

T

m

k

T

t

a

x

kx

x

m

kx

F

π

ω

ω

π

ϕ

ω

2

2

)

sin(

=

=

=

+

=

−

=

−

=





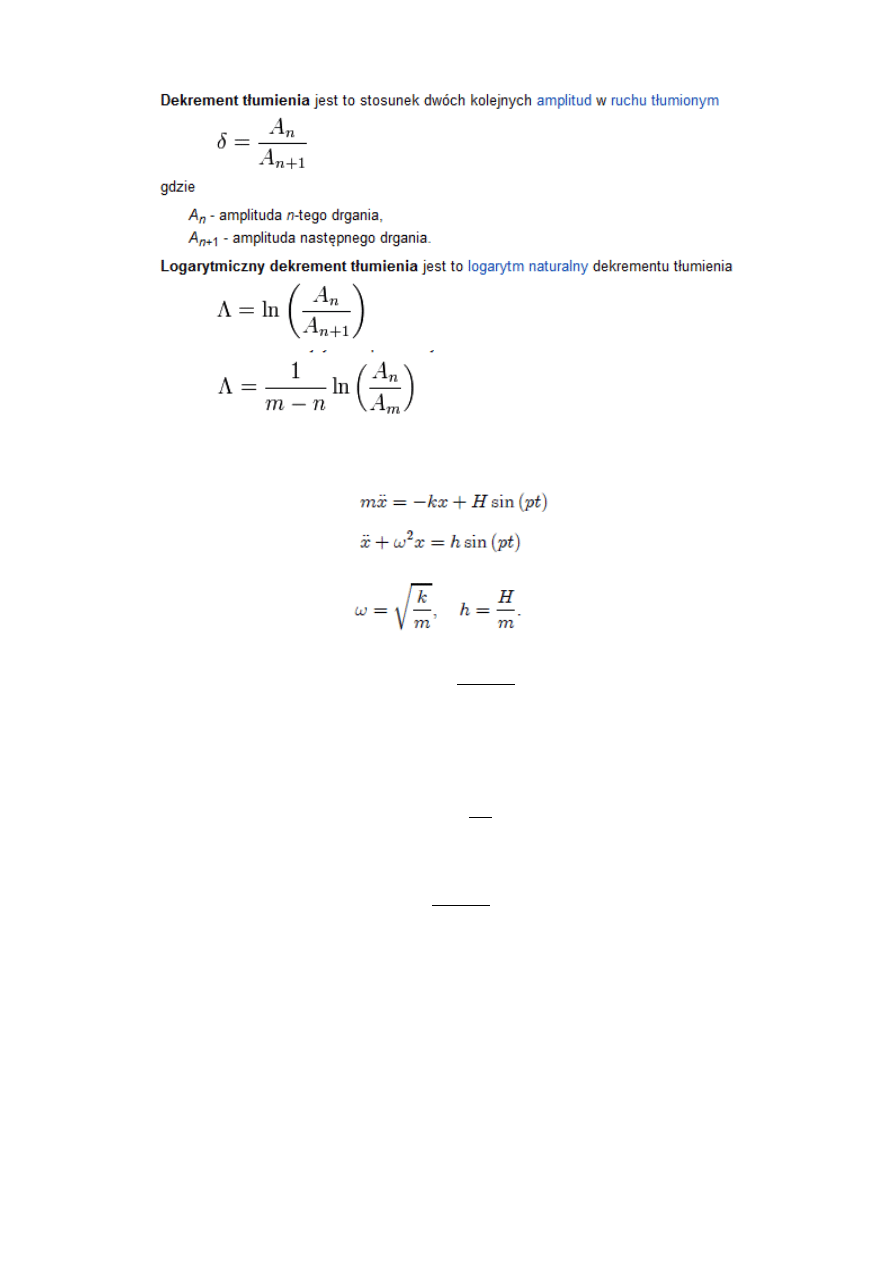
60. Drgania wymuszone – występują, jeżeli na punkt dodatkowo działa siła wymuszajaca

okresowa

Siła wymuszająca S=Hsin(pt), gdzie p-częstość

61. Rezonans - zjawisko fizyczne zachodzące dla drgań wymuszonych, objawiające się

pochłanianiem energii poprzez wykonywanie drgań o dużej amplitudzie przez układ
drgający dla określonych częstotliwości drgań.

62. Amplituda - nieujemna wartość określająca wielkość przebiegu funkcji okresowej. Dla

wymuszonych:

63. Okres drgań - czas wykonania jednego pełnego drgania w ruchu drgającym, czyli czas

pomiędzy wystąpieniami tej samej fazy ruchu drgającego. Okres fali równy jest okresowi
rozchodzących się drgań.

64. Częstotliwość drgań - określa liczbę cykli zjawiska okresowego występujących w jednostce

czasu

65. Częstość własna drgań - Ciała mogą mieć wiele częstotliwości drgań własnych. W

szczególności częstotliwości te mogą być wielokrotnością częstotliwości najmniejszej
(wyższe harmoniczne). Częstotliwość wzbudzania poszczególnych drgań własnych zależy
od sposobu wzbudzania i ilości dostarczonej energii.

66. Faza drgań

)

sin(

)

sin(

2

2

pt

p

h

t

a

x

−

+

+

=

ω

ϕ

ω

)

cos(

2

)

sin(

t

t

h

t

a

x

ω

ω

ϕ

ω

−

+

=

2

2

p

h

B

−

=

ω

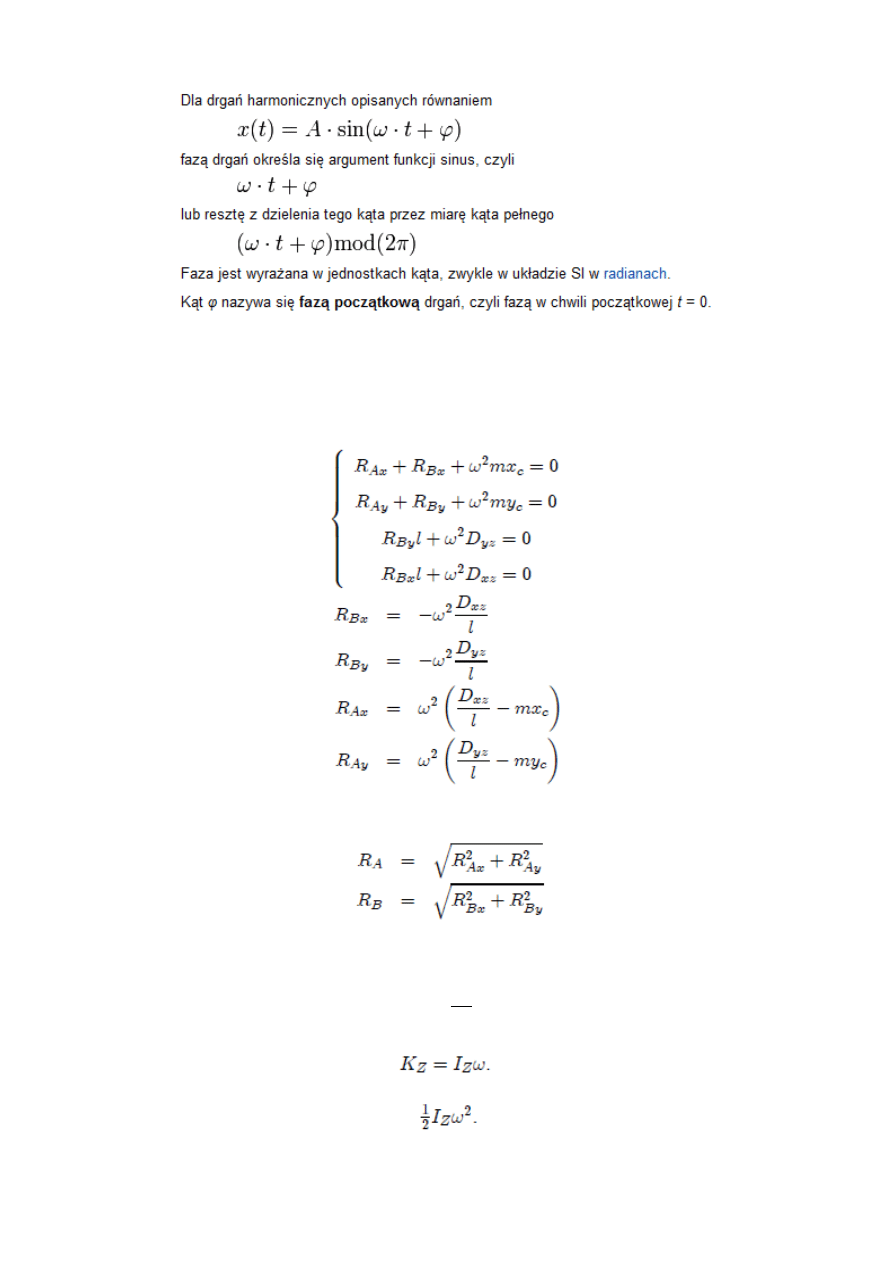
67. Faza początkowa drgań (patrz pkt. 66)
68. ---------------------------------------------------------------------
69. ---------------------------------------------------------------------
70. ---------------------------------------------------------------------
71. Reakcje dynamiczne - Aby reakcje dynamiczne były równe zeru oś obrotu musi być

centralną główną osią bezwładności.

72. Długość zredukowana wahadła fizycznego - jeden z parametrów wahadła fizycznego. Jest to

taka długość wahadła matematycznego, które wykonuje drgania o takim samym okresie jak
dane wahadło fizyczne. Wartość długości zredukowanej wyraża się równaniem

73. Kręt bryły w ruchu obrotowym

74. Energia kinetyczna w ruchu obrotowym

75. Energia kinetyczna w ruchu płaskim

ml

I

l

r

=

76. Środek masy bryły - jest punktem, w którym skupiona jest cała masa w opisie bryły jako

masy punktowej.

77. Środek masy układu punktów materialnych

78. Definicja momentu bezwładności – momentem bezwładności punktu materialnego

względem płaszczyzny, osi lub bieguna nazywamy iloczyn masy tego punktu przez kwadrat
odległości tego punktu od płaszczyzny, osi lub bieguna.

79. Główny moment bezwładności – W każdym punkcie układu materialnego istnieją co

najmniej trzy prostopadłe osie, takie że momenty dewiacyjne w utworzonym przez nie
kartezjańskim układzie współrzędnych są równe zeru. Osie te nazywamy głównymi osiami
bezwładności, a osiowe momenty względem nich głównymi momentami bezwładności.

80. Dewiacyjne momenty bezwładności

81. Twierdzenie Stainera – Moment bezwładności względem dowolnej osi jest równy

momentowi względem osi równoległej przechodzącej przez środek masy powiększonemu o
iloczyn masy całkowitej układu przez kwadrat odległości obu osi

82. --------------------------------------------------------------------------------
83. Główna oś bezwładności

84. Centralna oś bezwładności – oś przechodząca przez środek masy
85. Główna centralna oś bezwładności

2

md

I

I

s

l

+

=