
ELEKTRODYNAMO
Pozdro by HARRY
„Wytężony wysiłek umysłowy zasadniczo wykręca”
Treści na siwo są nie obowiązkowe, są to dodatkowe informacje pozwalające coś skminić
albo są to moje przemyślenia.
Część zadań jest po prostu przepisana.
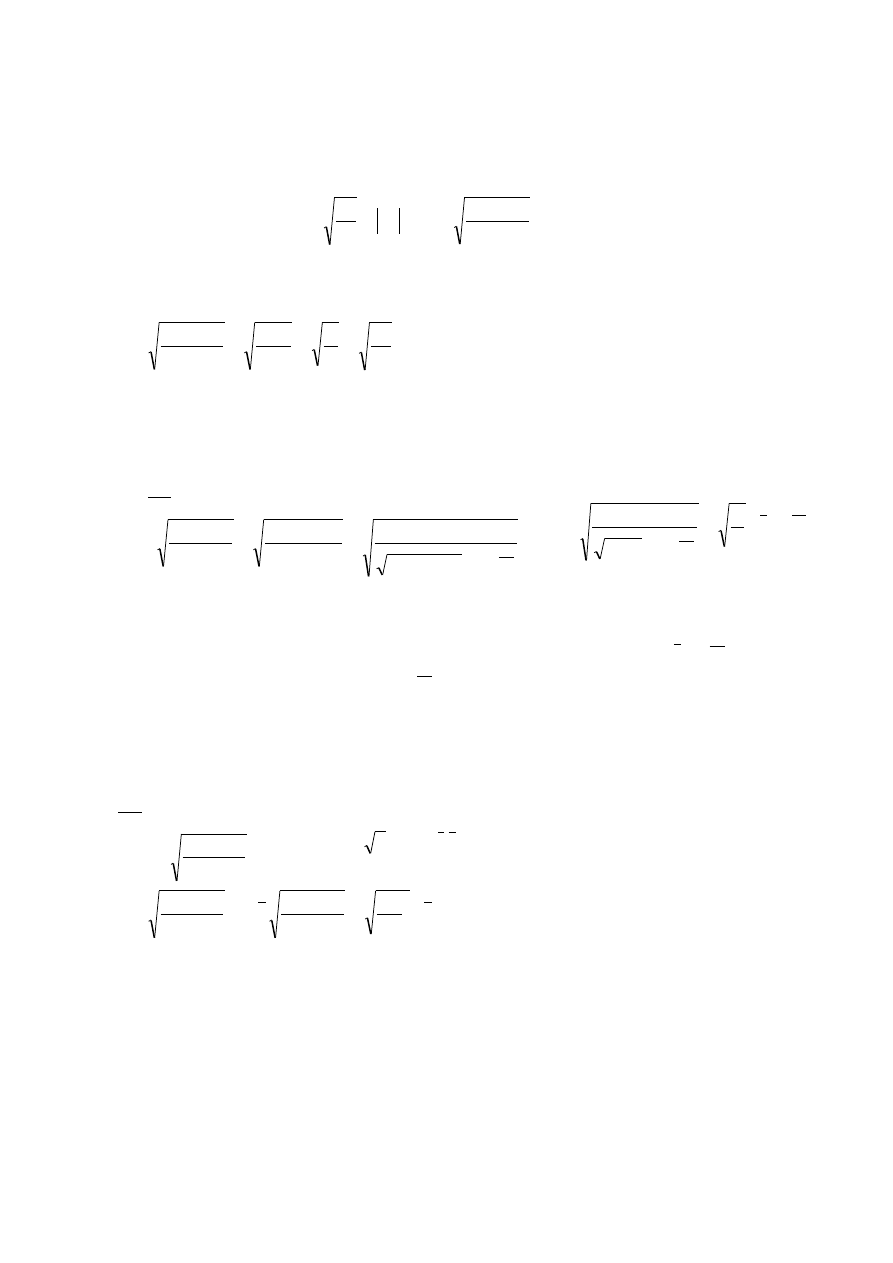
1(2). Fala płaska przedyskutować wartość impedancji falowej dla ośrodków typu:
idealny dielektryk, stratny dielektryk, dobry przewodnik. Ocenić relacje fazowe pól
E
i H
w każdym przypadku.
(przepisane poprawione i uzupełnione o przekształcenia)
W ogólnym przypadku:
ω ε
σ
ω µ
ε
µ
ϕ
j
j
e
Z
Z
f
Z
j
f
c
c
f
+
=
=
=
lub
•
W idealnym dielektryku
(
)
0
,
,
0
0
→
=
=
σ
ε
ε
µ
µ
:
[ ]
Ω
=
=
=
=
+
=
π
ε
µ
ε
µ
ω ε
ω µ
ω ε
σ
ω µ
120
0
0
0
0
j
f
e
j
j
j
j
Z
Impedancja falowa rzeczywista.
Składowe pól E
i H
nie są przesunięte względem siebie.
(
)
°
=
0
f
Z
ϕ
.
•
W stratnym dielektryku
(
)
0
,
,
→/
σ
ε
µ
:
ω ε
σ
ω ε
σ
ω ε
σ
ε
µ
ε
ω
ω µ
ε
ω
σ
ω µ
ω ε
σ
ω µ
ω ε
σ
ω µ
ω ε
σ
arctg
j
jarctg
f
jarctg
f
e
e
Z
e
j
j
j
Z
2
1
2
2
2
2
2
1
=
≈
⇒
+
=
+
−
=
+
=
< <
−
−
)
(
)
(
x
arctg
x
arctg
−
=
−
Impedancja falowa zespolona.
Składowe wektorowe pól E
i H
są przesunięte względem siebie o kąt
(
)
ω ε
σ
ϕ
arctg
Z
f
2
1
=
.
)
(
)
(
x
arctg
x
f
=
dla argumentów ponizej1(
1
< <
ω ε
σ
) przyjmuje wartości poniżej 45 stopni zatem
)
5
,
22
;
0
(
°
∈
f
Z
ϕ
w tym przypadku.
•
W dobrym przewodniku
(
)
∞
→
σ
ε
µ
,
,
:
+
=
> >
ω ε
σ
ω µ
ω ε
σ
j
j
Z
f
1
wiedząc, że
2
2
1
1
π⋅
⋅
⋅
=
j
e
j
4
4
π
π
σ
ω µ
ω ε
σ
ω µ
ω ε
σ
ω µ
j
j
f
e
j
e
j
j
Z
⋅
≈
+
=
+
=
Impedancja falowa zespolona.
Składowe wektorowe pól E
i H
są przesunięte względem siebie o kąt
(
)
°
=
45
f
Z
ϕ
.
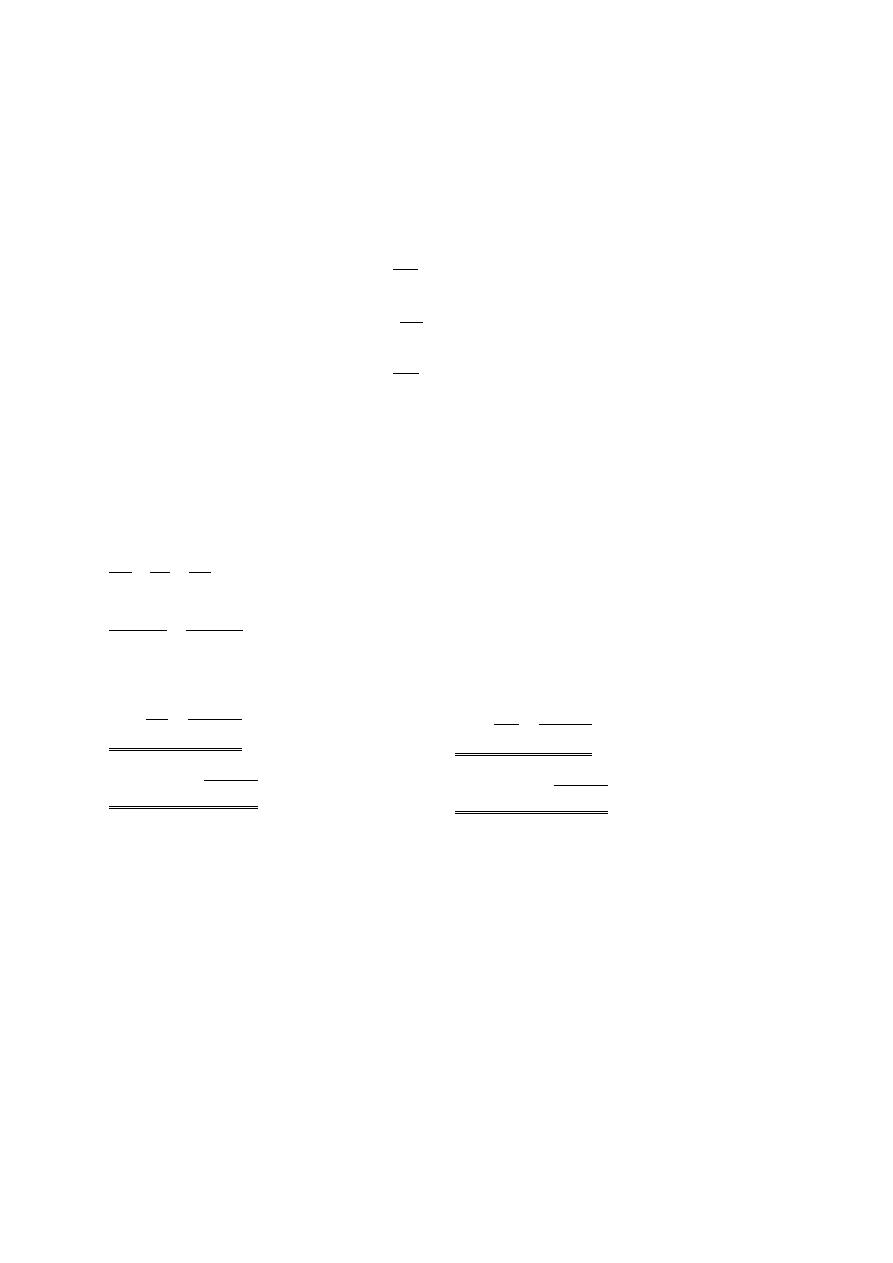
2(4). Korzystając z warunków brzegowych na granicy dwóch ośrodków materialnych o
znanych impedancjach falowych Z
1
i Z
2
znaleźć
E
Γ
ˆ oraz
E
Tˆ lub (
H
Γ
ˆ oraz
H
Tˆ ).
(przepisane małe uzupełnienie)
•
Oznaczenia
w
w
w
w
r
r
r
r
p
p
p
p
H
E
Z
H
E
H
E
Z
H
E
H
E
Z
H
E
ˆ
ˆ
wnikająwn
fala
ˆ
ˆ
ˆ
ˆ
odbita
fala
ˆ
ˆ
ˆ
ˆ
padająad
fala
ˆ
ˆ
2
1
1
=
−
−
=
−
=
−
•
Z warunków brzegowych (dla pola E
);
(
)
(
)
1
2
2
1
2
1
2
1
2
1
2
2
1
2
1
1
2
ˆ
1
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
Z
Z
Z
T
Z
Z
Z
Z
E
E
Z
Z
E
Z
Z
E
Z
E
E
Z
E
E
Z
E
Z
E
Z
E
H
H
H
E
E
E
E
E
p
r
E
r
p
r
p
r
p
w
r
p
w
r
p
w
r
p
+
=
Γ
+
=
+
−
=
=
Γ
+
=
−
+
=
−
=
−
=
+
=
+
↓
•
Z warunków brzegowych (dla pola H
);
(
) (
)
1
2
1
1
2
2
1
2
1
2
1
2
1
2
1
1
2
ˆ
1
ˆ
ˆ
ˆ
ˆ
)
(
ˆ
)
(
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
Z
Z
Z
T
Z
Z
Z
Z
H
H
Z
Z
H
Z
Z
H
H
H
Z
H
H
Z
Z
H
Z
H
Z
H
E
E
E
H
H
H
H
H
p
r
H
r
p
r
p
r
p
w
r
p
w
r
p
w
r
p
+
=
Γ
+
=
+
−
=
=
Γ
+
=
−
+
=
−
=
−
=
+
=
+
↓
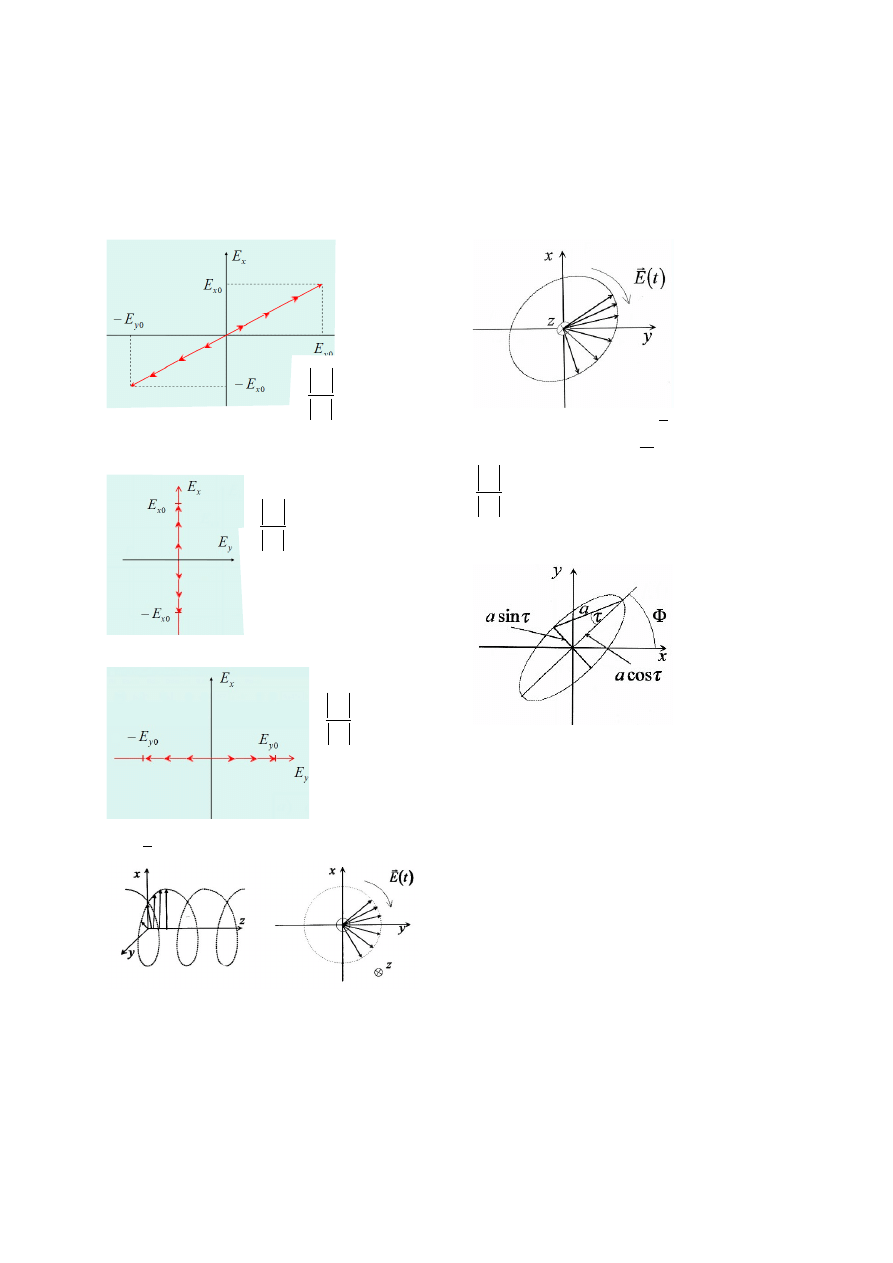
3(10). Omówić rodzaje polaryzacji fal elektromagnetycznych. Podać wartość
współczynnika polaryzacji dla poszczególnych przypadków.
(przepisane)
•
Polaryzacja liniowa ukośna
(
)
0
,
0
,
0
0
0
≠
≠
=
y
x
E
E
ϕ
)
,
0
(
∞
∈
x
y
E
E
•
Polaryzacja liniowa pionowa
(
)
0
,
0
,
0
0
0
=
≠
=
y
x
E
E
ϕ
0
=
x
y
E
E
•
Polaryzacja liniowa
pozioma
(
)
0
,
0
,
0
0
0
≠
=
=
y
x
E
E
ϕ
∞
=
x
y
E
E
•
Polaryzacj
a kołowa
(
)
0
0
,
2
y
x
E
E
=
=
π
ϕ
Wektor pola E
zatacza okrąg, a rzutowany
na płaszczyznę YZ daje sinusoidę.
Polaryzacja może być prawoskrętna(+
dodatnia) lub lewoskrętna (- ujemna)
•
Polaryzacja eliptyczna
(
)
0
0
0
0
,
0
,
0
,
0
y
x
y
x
E
E
E
E
≠
≠
≠
≠
ϕ
Prawoskrętna gdy
>
∈
2
,
0
(
π
ϕ
Lewoskrętna gdy
)
2
,
(
2
3
π
ϕ
π
∈
)
,
0
(
∞
∈
x
y
E
E
•
współczynnik eliptycznośc
τ
-współczynik eliptyczności
>
°
°
−
∈ <
45
,
45
τ
Dla polaryzacji liniowej
0
=
τ
Dla polaryzacji kołowej
→
°
=
→
°
−
=
a
lewoskręew
na
prawoskręr
45
45
τ
τ
Dla polaryzacji eliptycznej
→
°
−
∈
→
°
∈
a
lewoskręew
na
prawoskręr
)
0
,
45
(
)
45
,
0
(
τ
τ
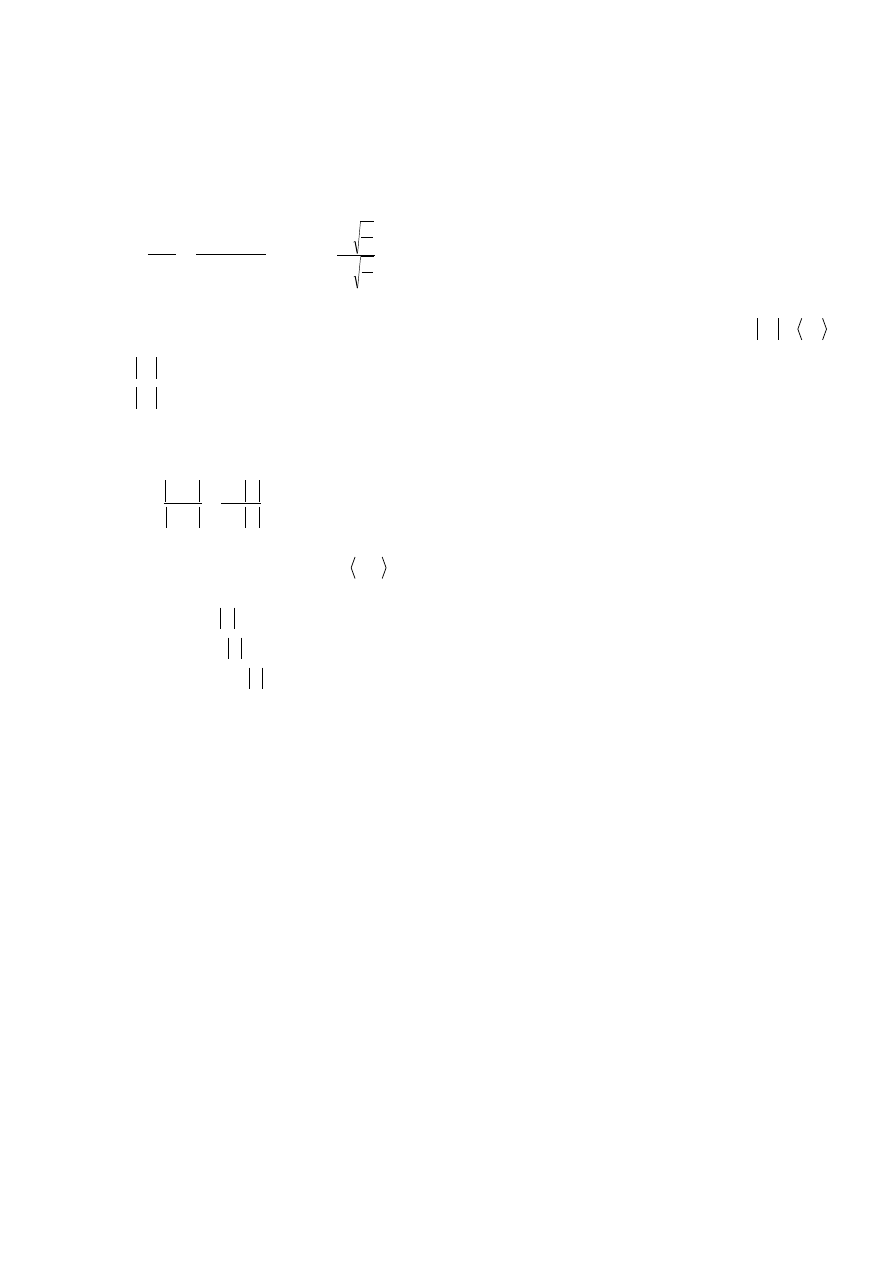
4(11). Padanie normalne: zdefiniować współczynnik odbicia
E
Γ
ˆ oraz współczynnik fali
stojącej
WFS
. Przedyskutować sens fizyczny, podać typowe wartości dla przypadków
ekstremalnych.
(przepisane)
•
Współczynnik odbicia
1
2
1
2
0
0
ˆ
ˆ
ˆ
f
f
f
f
p
r
def
E
Z
Z
Z
Z
E
E
+
−
=
=
Γ
lub
1
2
1
2
1
1
ε
ε
ε
ε
+
−
=
Γ
E
stosunek fali odbitej od granicy ośrodków do fali
padającej; określa ilościowo jaka część fali
została odbita od powierzchni; przyjmuje
wartości:
dla
0
=
Γ
E
brak odbicia
dla
1
=
Γ
E
odbicie całkowite
•
Współczynnik fali stojacej(VSWR - Voltage StandingWave Ratio)
Γ
−
Γ
+
=
=
1
1
min
max
E
E
WFS
def
- stosunek amplitud maksymalnej do minimalnej określa ilościowo,
czy fala jest bliższa fali stojącej, czy bieżącej; przyjmuje wartości:
∞
∈
;
1
WFS
Dla
(
)
0
1
=
Γ
=
WFS
brak fali stojącej
Dla
(
)
1
=
Γ
∞
=
WFS
pełna fala stojąca
Dla
( )
( )
(
)
1
;
0
;
1
∈
Γ
∞
∈
WFS
niepełna fala stojąca (amplitudy fal biegnący w obu kierunkach
nie są sobie równe).
1
;
0
∈
Γ
E

5(13). Pole elektryczne fali płaskiej
y
j
x
e
i
E
E
β
−
⋅
⋅
=
0
ˆ
ˆ
. Ocenić jego polaryzację. Wykazać,
że można ten sygnał traktować jako superpozycję dwóch sygnałów o polaryzacji kołowej
i przeciwnych kierunkach obrotu.
(przepisane)
Jest to polaryzacja liniowa (pionowa), ponieważ pole elektryczne zawiera tylko składową x
(propaguje się w kierunku + y):
x
y
j
x
i
y
t
E
t
y
E
e
i
E
E
)
cos(
)
,
(
ˆ
ˆ
0
0
β
ω
β
−
=
→
⋅
⋅
=
−
Rozważmy teraz 2 fale spolaryzowane kołowo o przeciwnych kierunkach obrotu ale tych samych
amplitudach:
)
)
sin(
)
(cos(
2
)
,
(
0
1
z
x
i
y
t
i
y
t
E
t
y
E
β
ω
β
ω
−
−
−
=
polaryzacja kołowa lewoskrętna
)
)
sin(
)
(cos(
2
)
,
(
0
2
z
x
i
y
t
i
y
t
E
t
y
E
β
ω
β
ω
−
+
−
=
polaryzacja kołowa prawoskrętna
wówczas superpozycja tych sygnałów ma postać:
x
x
i
y
t
E
i
y
t
E
t
y
E
t
y
E
t
y
E
)
cos(
)
cos(
2
2
)
,
(
)
,
(
)
,
(
0
0
2
1
β
ω
β
ω
−
=
−
=
+
=
c.n.d.

6(17). Przedstawić równanie opisujące ruch ładunków swobodnych w ośrodku
przewodzącym oraz znaleźć jego rozwiązanie. Wyjaśnić sens fizyczny występujących
wielkości.
(przepisane)
•
Równanie ruchu
V
m
E
q
dt
V
d
m
c
γ
−
=
•
Przy zerowych warunkach początkowych
)
(
)
(
s
V
m
E
q
s
V
ms
c
γ
−
=
Uwzględniając harmoniczna zmienność w czasie
ω
j
s
=
)
(
)
(
ω
γ
ω
ω
j
V
m
E
q
j
V
mj
c
−
=
•
Wyznaczając prędkość
m
mj
E
q
j
V
c
γ
ω
ω
+
=
)
(
•
Przypadku statycznym
0
=
ω
m
E
q
V
c
γ
=
)
0
(
•
Sens fizyczny wielkości:
V
- średnia prędkość nośników ładunku
c
γ
- średnia częstotliwość zderzeń
q - ładunek
m - masa nośnika ładunku
mV
c
γ
- siła tłumiąca spowodowana zderzeniami nośników ładunku z wezłami siatki
krystalicznej
E
q
- siła działająca na ładunek polu(elektryczna)
Jeżeli średnia częstotliwość zderzeń jest bardzo mała
0
→
c
γ
, to wtedy
∞
→
V
, co jest nie
realizowalne w rzeczywistości, a zatem należy uwzględnić wpływ masy
)
(V
m
tak aby
c
V
→
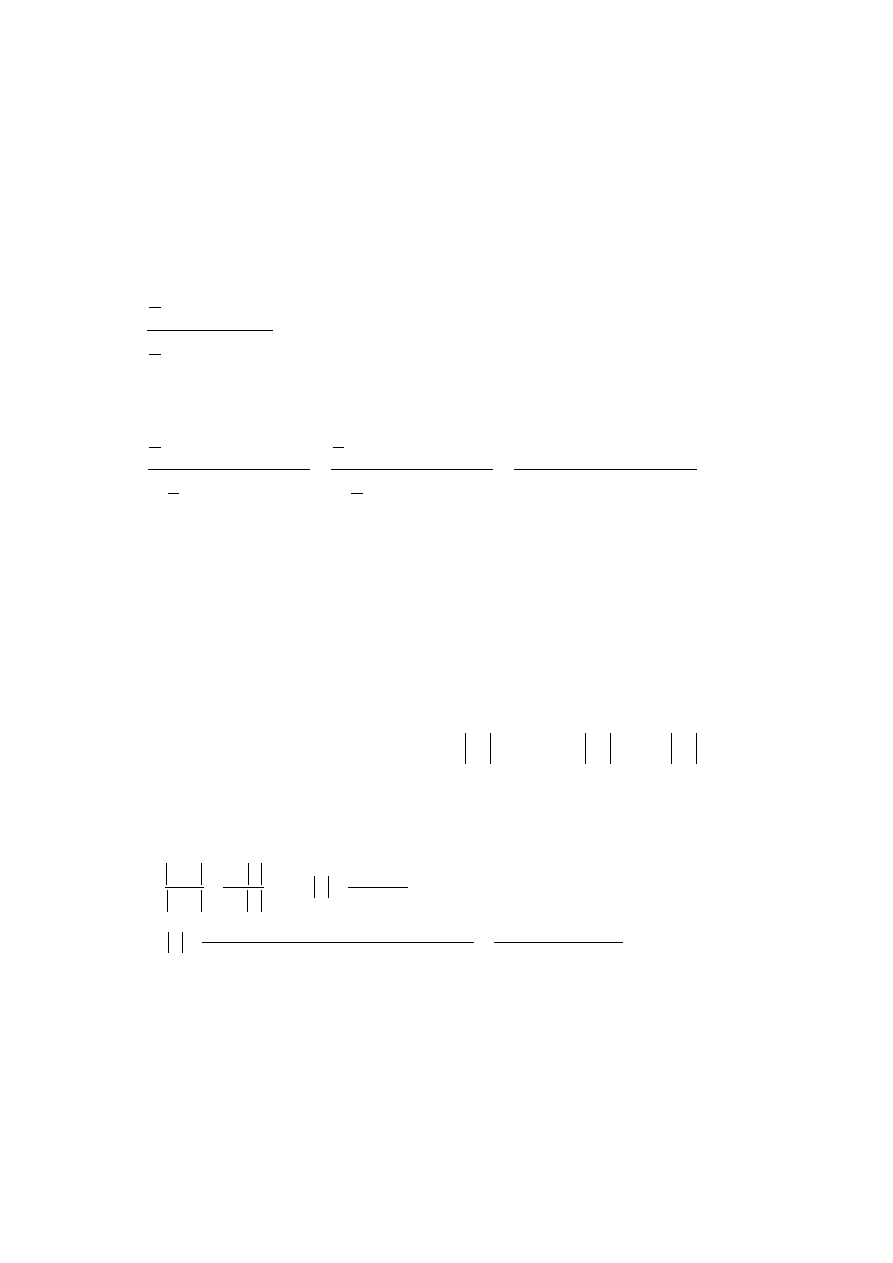
7(22). Wychodząc z definicji współczynnika transmisji mocy pokazać, w jaki sposób
zależy jego wartość od współczynnika odbicia
E
Γ
ˆ oraz od WFS (padanie normalne).
(przepisane)
•
Współczynnik transmisji mocy
{
}
{
}
=
=
×
ℜ
×
ℜ
=
0
0
0
0
*
0
0
*
0
0
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
2
1
ˆ
ˆ
2
1
p
H
w
p
E
w
p
p
w
w
p
H
T
H
E
T
E
gdzie
H
E
e
H
E
e
T
Stąd
{
}
{
}
{
}
{
}
{ }
{
}
{
}
{ }
*
*
0
0
*
0
0
*
*
0
0
*
0
0
*
*
0
0
*
0
*
0
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
2
1
ˆ
ˆ
ˆ
ˆ
2
1
ˆ
ˆ
2
1
ˆ
ˆ
ˆ
ˆ
2
1
H
E
p
p
p
p
H
E
p
p
p
p
H
E
p
p
p
H
p
E
p
T
T
e
H
E
e
H
E
e
T
T
e
H
E
e
H
E
T
T
e
H
E
e
H
T
E
T
e
T
ℜ
=
×
ℜ
×
ℜ
ℜ
=
×
ℜ
×
ℜ
=
×
ℜ
×
ℜ
=
Wiedząc że
*
*
ˆ
ˆ
ˆ
ˆ
ˆ
1
ˆ
ˆ
1
ˆ
H
E
H
E
H
H
E
E
oraz
T
T
Γ
−
=
Γ
⇒
Γ
−
=
Γ
Γ
+
=
Γ
+
=
{ }
{
} {
}
{
}
2
2
2
*
*
*
*
*
*
*
ˆ
1
}
ˆ
1
{
ˆ
ˆ
ˆ
1
ˆ
ˆ
ˆ
ˆ
1
ˆ
ˆ
ˆ
ˆ
1
)
ˆ
1
)(
ˆ
1
(
ˆ
ˆ
H
H
H
urojone
czysto
E
E
H
H
E
E
H
E
H
E
H
E
H
E
p
e
e
e
e
e
T
T
e
T
Γ
−
=
Γ
−
ℜ
=
Γ
−
Γ
−
Γ
+
ℜ
=
Γ
Γ
−
Γ
−
Γ
+
ℜ
=
=
Γ
Γ
+
Γ
+
Γ
+
ℜ
=
Γ
+
Γ
+
ℜ
=
ℜ
=
•
Współczynnik fali stojącej
1
1
1
1
1
min
max
+
−
=
Γ
⇒
≥
Γ
−
Γ
+
=
=
WFS
WFS
E
E
WFS
def
1
2
4
1
2
1
2
1
2
1
2
2
2
2
+
+
=
+
+
−
+
−
+
+
=
Γ
+
=
WFS
WFS
WFS
WFS
WFS
WFS
WFS
WFS
WFS
T
P
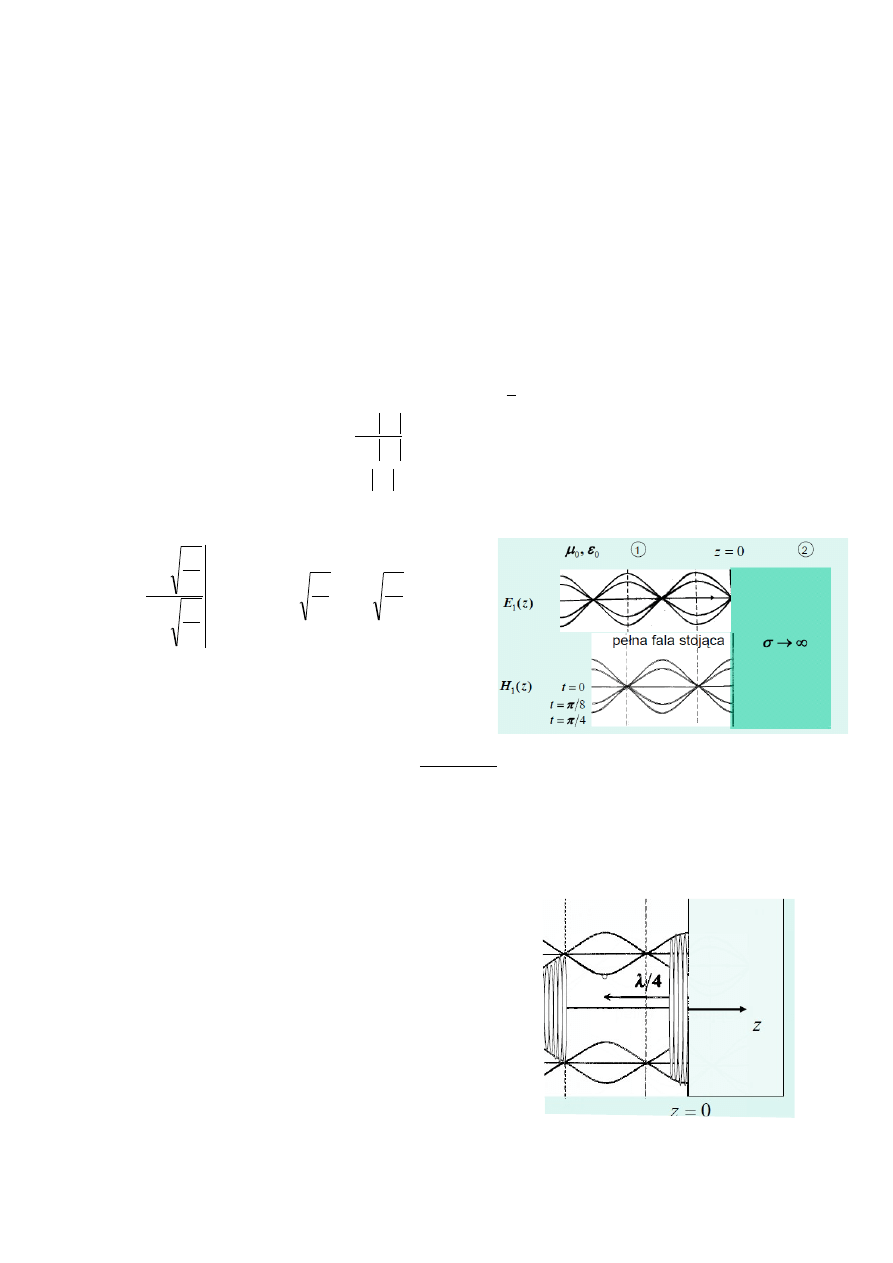
8(25). Zapisać amplitudę zespoloną pola elektrycznego pełnej fali stojącej oraz niepełnej
fali stojącej. Wynik zinterpretować graficznie. Podać warunki, w jakich możliwe jest
powstanie tego typu rozkładów.
•
Ogólnie fala
r
p
E
z
j
p
E
E
z
j
p
r
p
e
E
e
E
E
E
E
ˆ
0
ˆ
0
ˆ
ˆ
ˆ
ˆ
ˆ
β
β
Γ
+
=
+
=
−
•
Pełna fala stojąca
-występuje przy padaniu z idealnego dielektryka
0
→
σ
na idealny przewodnik
∞
→
σ
-sytuacja nie realizowalna w rzeczywistości
-analogiczna postać dla pola Hˆ
(przesunięte w fazie o
2
π
)
współczynnik fali stojącej
E
E
WFS
Γ
−
Γ
+
=
1
1
Dla pełnej fali stojącej
∞
=
WFS
1
1
1
=
Γ
∨
−
=
Γ
⇒
=
Γ
⇔
E
E
E
to drugie rozwiązanie
odrzucamy, gdyż fala odbita jest przeciwna do padającej zatem
1
−
=
Γ
E
,
lecz teraz
otrzymujemy sprzeczność ze wzorem.
0
2
1
1
1
1
1
2
1
2
1
1
2
1
2
=
⇒
−
=
−
−
⇒
+
−
=
Γ
−
=
Γ
ε
ε
ε
ε
ε
ε
ε
ε
E
E
,
No, ale trudno się mówi najwidoczniej wzór nie
jest słuszny dla idealnych przypadków
???
więc nasza fala przyjmie wzór
)
sin(
ˆ
2
2
ˆ
2
ˆ
ˆ
ˆ
ˆ
ˆ
0
0
0
0
z
E
j
j
e
e
E
j
e
E
e
E
E
E
E
p
z
j
z
j
p
z
j
p
z
j
p
r
p
β
β
β
β
β
−
=
−
−
=
−
=
+
=
−
−
•
Niepełna fala stojąca
-amplitudy fal biegnących w tym samym kierunku ale o przeciwnym zwrotach, nie są sobie
równe, stąd brak zerowych wartości w minimum
-sytuacja rzeczywista
-analogiczna dla pola Hˆ
pamiętając, że
H
E
Γ
−
=
Γ
Fala przyjmuje wzór
(
)
z
j
E
z
j
p
z
j
p
E
z
j
p
r
p
e
e
E
e
E
e
E
E
E
E
β
β
β
β
2
0
0
0
1
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
Γ
+
=
Γ
+
=
+
=
−
−
9(26). Zdefiniować głębokość wnikania. Znaleźć związek pomiędzy głębokością
wnikania, współczynnikiem tłumienia i długością fali w przewodniku.
(przepisane)
•
Głębokość wnikania
- To odległość
δ
, na której amplituda maleje e krotnie
- Określa prędkość zaniku amplitudy pola
Dla pola
(
)
α δ
δ
−
=
=
e
E
z
E
x
x
0
ˆ
ˆ
α
δ
α δ
δ
α δ
1
1
1
)
0
(
)
(
=
⇒
=
⇒
=
=
=
−
e
e
E
z
E
x
x
•
Długość fali:
π δ
ω µ σ
π
µ π σ
π
µ π σ
π
α
π
λ
π
ω
2
2
2
2
2
2
2
=
=
=
=
=
f
Stąd
ω µ σ
δ
2
=
10.(27) Zdefiniować kąt Brewstera. Wyznaczyć jego wielkość, gdy znane są jedynie
parametry materiałowe
( )
ε
µ
, obu przylegających ośrodków.
(przepisane lecz)
•
dla polaryzacji równoległej
,
1
1
||
||
||
K
K
+
−
=
Γ
gdzie
←
Γ
||
stosunek amplitudy fali odbitej do fali padającej
p
w
K
ϕ
ε
β
ϕ
ε
β
cos
cos
2
1
1
2
||
⋅
⋅
=
Dla kąta Brewstera mamy
1
0
||
||
=
⇒
=
Γ
K
stąd
w
p
ϕ
ε
β
ε
β
ϕ
cos
cos
2
1
1
2
=
dodatkowo wiemy
(ups powinnyśmy wiedzieć tylko nie wiem skąd)
p
w
ϕ
ε
µ
ε
µ
ϕ
2
2
2
1
1
sin
1
cos
−
=
wbrew pozorom nie jest to przekształcone prawo Seneliusa bo
2
2
2
1
1
1
ε
µ
β
ε
µ
β
≠
≠
i
i wyszedłby zły kąt w wyniku wiem bo 2 sprawdzałem
3
2
2
3
1
1
2
1
1
2
1
1
arcsin
ε
µ
ε
µ
ε
µ
ε
µ
−
−
z prawa Seneliusa
1
2
sin
sin
β
β
ϕ
ϕ
=
w
p
otrzymujemy zatem układ równań
=
−
=
=
1
2
2
2
2
1
1
2
1
1
2
sin
sin
sin
1
cos
cos
cos
β
β
ϕ
ϕ
ϕ
ε
µ
ε
µ
ϕ
ϕ
ε
β
ε
β
ϕ
w
p
p
w
w
p
Po rozwiązaniu tego układu otrzymamy
2
2
1
2
1
1
2
||
1
1
arcsin
−
−
=
=
ε
ε
ε
µ
ε
µ
ϕ
ϕ
p
B
to jest kąt Brewstera dla polaryzacji równoległej
•
dla polaryzacji prostopadłej
,
1
1
⊥
⊥
⊥
+
−
=
Γ
K
K
gdzie
←
Γ
⊥
stosunek amplitudy fali odbitej do fali padającej
p
w
K
ϕ
µ
β
ϕ
µ
β
cos
cos
2
1
1
2
⋅
⋅
=
⊥
Dla kąta Brewstera mamy

1
0
=
⇒
=
Γ
⊥
⊥
K
stąd
w
p
ϕ
µ
β
µ
β
ϕ
cos
cos
2
1
1
2
=
dodatkowo wiemy
p
w
ϕ
ε
µ
ε
µ
ϕ
2
2
2
1
1
sin
1
cos
−
=
z prawa Seneliusa
1
2
sin
sin
β
β
ϕ
ϕ
=
w
p
otrzymujemy zatem układ równań
=
−
=
=
1
2
2
2
2
1
1
2
1
1
2
sin
sin
sin
1
cos
cos
cos
β
β
ϕ
ϕ
ϕ
ε
µ
ε
µ
ϕ
ϕ
µ
β
µ
β
ϕ
w
p
p
w
w
p
Po rozwiązaniu tego układu otrzymamy
2
2
1
1
2
2
1
1
1
arcsin
−
−
=
=
⊥
µ
µ
ε
µ
ε
µ
ϕ
ϕ
p
B
•
Dla 2 ośrodków dielektrycznych
(
)
2
1
2
1
,
ε
ε
µ
µ
≠
=
⊥
B
ϕ
nie istnieje
1
2
2
2
1
||
1
1
arcsin
ε
ε
ε
ε
ϕ
arctg
B
=
+
=
•
Dla 2 ośrodków magnetycznych
(
)
2
1
2
1
,
ε
ε
µ
µ
=
≠
||
B
ϕ
nie istnieje
1
2
2
2
1
1
1
arcsin
µ
µ
µ
µ
ϕ
arctg
B
=
+
=
⊥
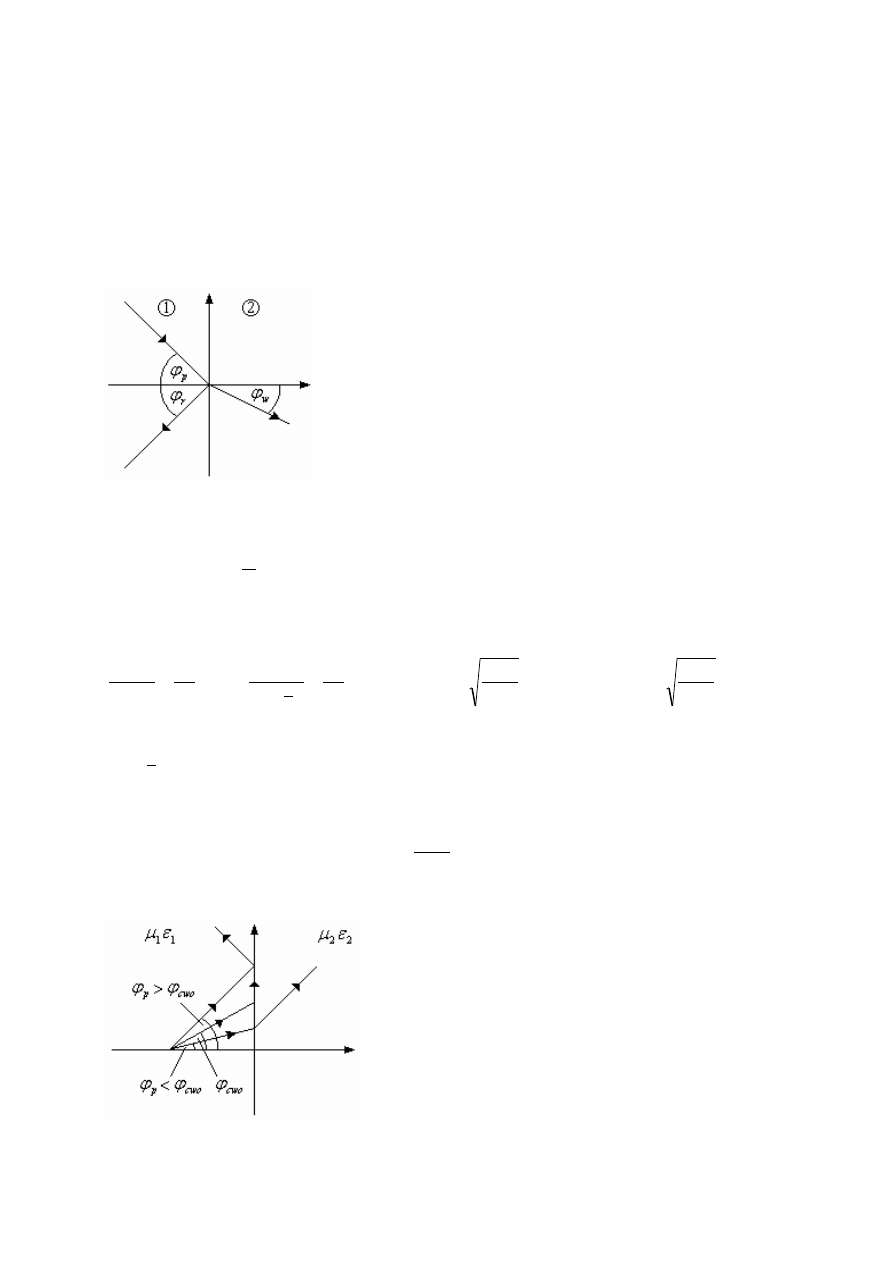
11(28). Zdefiniować kąt całkowitego wewnętrznego odbicia. Pokazać, w jaki sposób jego
wielkość zależy od parametrów ośrodków. Wyjaśnić, kiedy powyższe zjawisko nie może
wystąpić.
(przepisane mała zmiana)
Kąt całkowitego wewnętrznego odbicia to najmniejszy kąt padania, umożliwiający
przy danych parametrach ośrodków całkowite odbicie fali:
−
p
ϕ
kąt padania
−
r
ϕ
kąt odbicia
−
w
ϕ
kąt wnikania
•
przypadek graniczny:
2
π
ϕ
ϕ
ϕ
=
⇔
=
w
cwo
p
Z prawa Sneliusa:
1
1
2
2
1
1
2
2
1
2
2
1
2
arcsin
sin
sin
sin
sin
sin
ε
µ
ε
µ
ϕ
ε
µ
ε
µ
ϕ
β
β
ϕ
β
β
ϕ
ϕ
π
=
⇒
=
⇒
=
⇒
=
cwo
cwo
cwo
w
p
2
π
ϕ =
w
fala rozchodzi się po powierzchni granicznej
cwo
p
ϕ
ϕ >
nie następuje transmisja fali do drugiego ośrodka
Zjawisko może zachodzi tylko wtedy, gdy
1
1
1
2
2
<
ε
µ
ε
µ
, czyli przy padaniu fali z ośrodka
gęstszego do rzadszego. Nie zależy natomiast od propagacji fali.
1
1
2
2
ε
µ
ε
µ
<
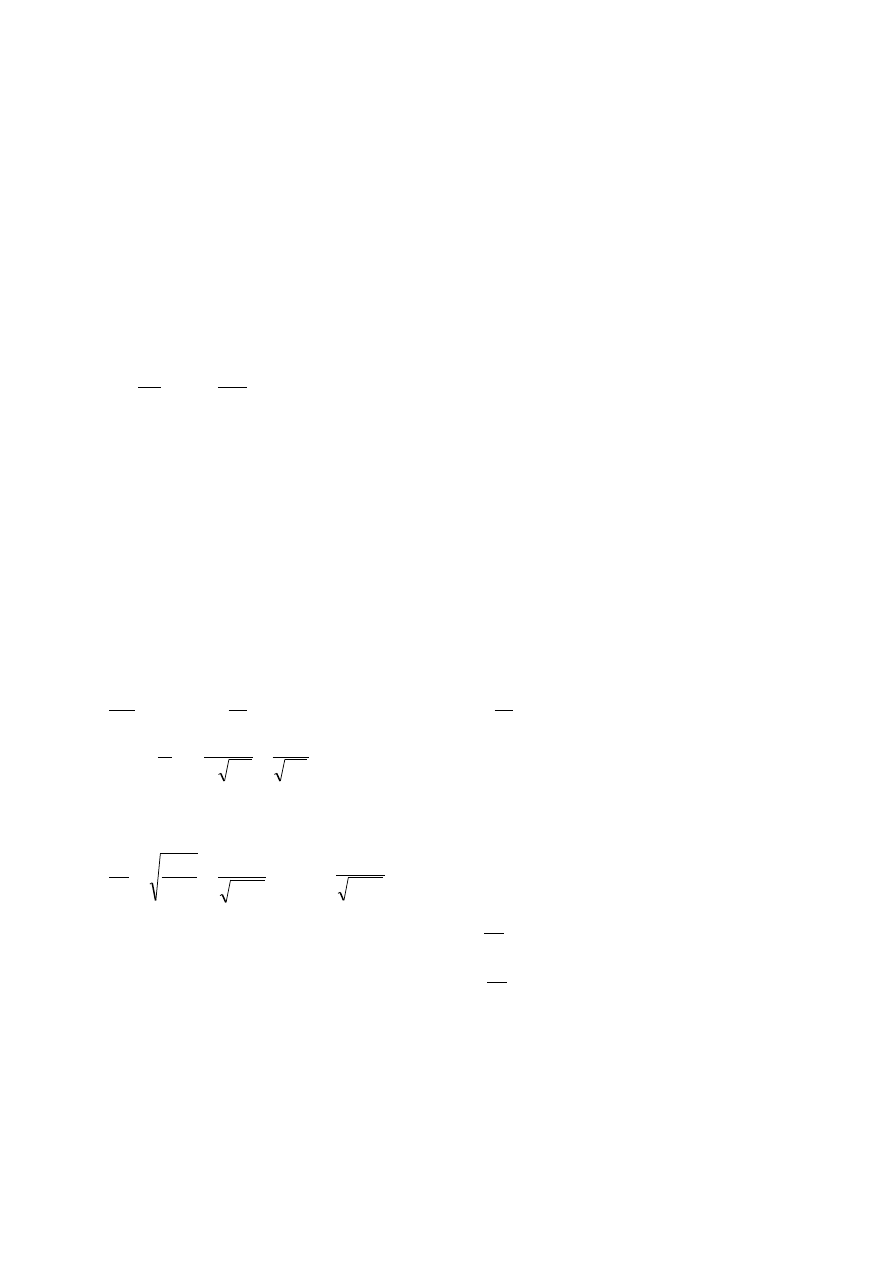
12. (29)Zdefiniować wektor propagacji, podać ogólne rozwiązanie równania falowego
dla fali płaskiej, wyznaczyć prędkość fazową.
(przepisane)
•
Definicja wektora propagacji
Wektor propagacji można zdefiniować w następujący sposób
→
→
→
→
+
+
=
z
y
x
i
k
i
k
i
k
k
3
2
1
,
Gdzie
3
2
1
,
,
k
k
k
współczynniki propagacji w kierunku
z
y
x ,
,
czasem nazywane
z
y
x
k
k
k
,
,
.
Wektor propagacji określa kierunek rozprzestrzeniania się (propagacji) fali tzn.
kierunek przenoszenia się energii i jest równy co do modułu liczbie falowej k danej fali, która
pośrednio określa długość fali propagacji w danym ośrodku.
=
m
rad
k
λ
π
2
•
Rozwiązanie równania falowego
(
)
r
k
t
j
e
−
=
ω
ψ
ψ
0
ˆ
ˆ
wiem, że
n
k
k
=
przechodzimy w
(
)
r
n
k
t
j
e
−
=
ω
ψ
ψ
0
ˆ
ˆ
←
postać ogólna
rozwiązania równania falowego.
•
Prędkość fazowa:
mamy równanie stałej fazy (równanie płaszczyzny (stąd określenie fali płaskiej))
const
kz
t
=
Φ
+
=
Φ
±
0
ω
obliczamy pochodną względem czasu: (pochodna z const =0)
0
0
=
→
=
Φ
dt
dz
k
dt
d
ω
naszą prędkością fazową jest
f
V
dt
dz
=
µ ε
µ ε
ω
ω
ω
1
=
±
=
±
=
k
V
f
chyba
±
znika dlatego, że interesuje nas wartość a nie znak
•
Znormalizowana prędkość fazowa
r
r
f
c
V
ε
µ
µ ε
ε
µ
1
0
0
=
=
,bo
0
0
1
ε
µ
=
c
dla ośrodka nieograniczonego i bezstratnego mamy
1
<
c
V
f
W ogólności jednak w metalowym FALOWODZIE
1
>
c
V
f
nie mylić z metalowym
światłowodem bo grozi to obniżeniem o połowę zdobnych punktów na kole (wykład
strona112), choć i tak jest to bez sensu.
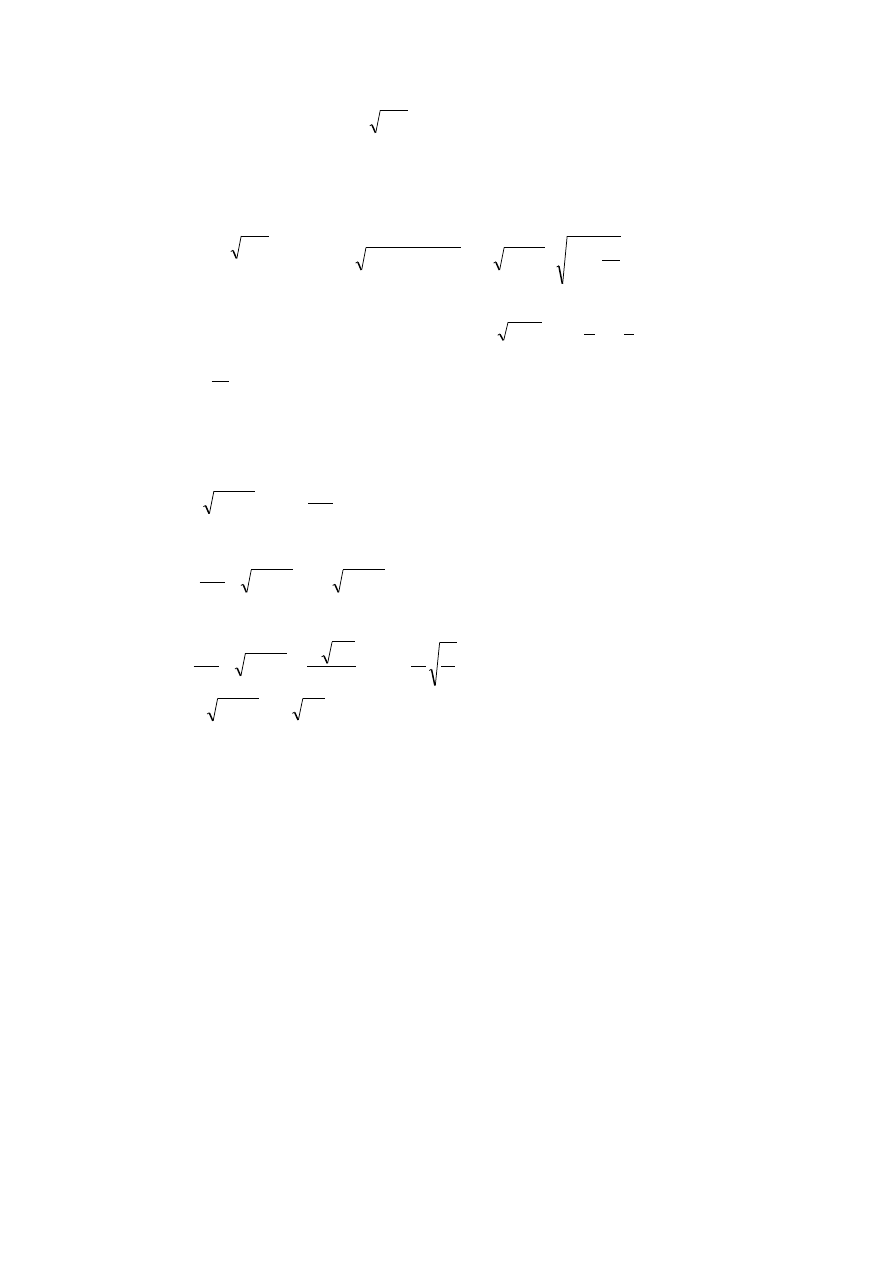
13(30). Znając liczbę falową
c
k
µ ε
ω
=
oraz wiedząc, że
)
(
2
1
0
ε
ε
ε
ε
j
c
−
=
wyznaczyć i
nazwać
γ
β
α
,
,
dla ośrodków dielektrycznych o niskim tłumieniu, tzn. spełniającego
warunek:
.
0
,
2
1
2
≠
< <
ε
ε
ε
(przepisane poprawiony błąd)
•
z treści zadania:
(
)
1
2
1
0
2
1
0
2
1
0
1
)
(
ε
ε
ε
µ ε
ω
ε
ε
µ ε
ω
ε
ε
ε
ε
µ ε
ω
j
j
k
j
k
c
c
−
⋅
=
−
=
⇒
−
=
=
stosując rozwinięcie w szereg Taylora funkcji
...
8
1
2
1
1
1
2
+
−
+
=
+
x
x
x
1
2
ε
ε
j
x
−
=
dla
1
2
ε
ε < <
czyli dla małego x
wystarczy, że weźmiemy dwa pierwsze wyrazy rozwinięcia, a zatem
−
⋅
=
1
2
1
0
2
1
ε
ε
ε
µ ε
ω
j
k
µ ε
ω
ε
µ ε
ω
β
ε
µ
σ
δ
µ ε
ω
ε
µ ε
ω
ε
ε
α
ε
µ ε
ω
ε
µ ε
ω
ε
ε
γ
β
α
=
=
=
=
=
+
=
=
+
=
1
0
1
0
1
2
1
0
1
0
1
2
2
2
2
2
E
tg
j
jk
j
jk
k
-liczba falowa
α
-współczynnik tłumienia(stała tłumienia)
β
-współczynnik fazowy(stała propagacji)
γ
-współczynnik propagacji

14. (--) Zapisać i nazwać prawa tworzące równania Maxwella w postaci zależności
czasowych.
∂
∂
+
=
×
∇
→
→
→
t
D
J
B
µ
Obwodowe prawo Ampera
lub
t
D
J
H
∂
∂
+
=
×
∇
→
→
→
prąd elektryczny lub zmienne
pole elektryczne wytwarzają wirowe pole magnetyczne.
Definicja2 Uogólnione prawo Ampère'a mówi, że cyrkulacja pola magnetycznego wzdłuż dowolnej krzywej zamkniętej związana jest z
szybkością zmian strumienia pola elektrycznego przez powierzchnię rozpięta na tej krzywej oraz wypadkowym prądem przebijającym tę
powierzchnię.
t
D
∂
∂
→
- gęstość prądu przesunięcia (prąd związany ze zmiana natężenia pola elektrycznego)
→
J
- gęstość realnego prądu
t
B
E
∂
∂
−
=
×
∇
→
→
Prawo Faraday’a
zmienne pole magnetyczne wytwarza wirowe pole elektryczne, które może
wywoływać prąd elektryczny.
Definicja2 (mówi, że zmienność pola magnetycznego powoduje (stwierdza) obecność pola elektrycznego. Co więcej brak pola elektrycznego
mówi o tym że pole magnetyczne jest stałe.)
ρ
=
∇
→
D
Prawo Gaussa
ładunek elektryczny wytwarza pole elektryczne
0
=
∇
→
B
Prawo źródeł magnetycznych
nie istnieje w przyrodzie ładunek magnetyczny, pole
magnetyczne jest bezźródłowe.
Definicja2 (mówi że Całkowity strumień pola magnetycznego przenikającego dowolną pow. Zamkniętą S jest równy 0 co oznacza, że tyle
samo pola wchodzi do tej objętości(ograniczonej tą pow) co z niej wychodzi ponadto mówi, że źródła pola magnetycznego nie mają
charakteru punktowego.)
Jeżeli ładunek i prądy w danym ośrodku rozmieszczone są w sposób ciągły, to obydwie formy
równań Maxwella (całkowa i różniczkowa(operatorowa)) są ekwiwalentne.
Jeżeli jednak istnieją powierzchnie, na których zachodzi skokowa zmiana tych wielkości, to
całkowa forma równań jest bardziej ogólna.
15(--). Zapisać i nazwać prawa tworzące równania Maxwella wykorzystując amplitudy
zespolone (pobudzenie harmoniczne).
+
=
×
∇
∧
∧
∧
→
→
→
D
j
J
B
ω
µ
Obwodowe prawo Ampera
∧
∧
→
→
−
=
×
∇
B
j
E
ω
Prawo Faraday’a
∧
→
=
∇
∧
ρ
D
Prawo Gaussa
0
=
∇
∧
→
B
Prawo źródeł magnetycznych
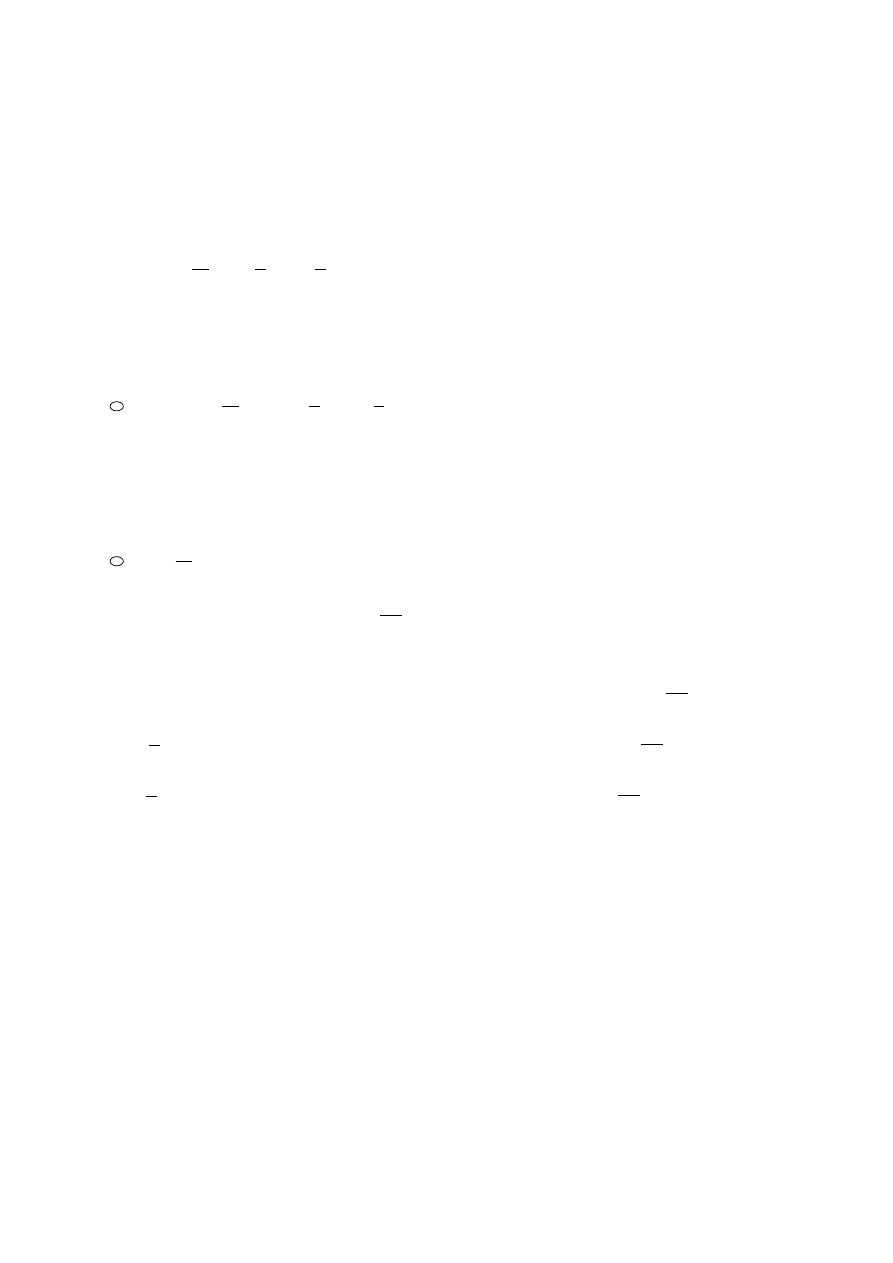
16(--). Podać zasadę zachowania energii i mocy (wektor Poyntinga). Wyjaśnić sens
fizyczny wszystkich wielkości.
•
Zasada zachowania energii:
- postać różniczkowa
0
2
1
2
1
)
(
=
+
+
∂
∂
+
×
∇
→
→
→
→
→
→
D
E
B
H
w
t
H
E
v
- postać całkowa (z tw. Gaussa-Ostrogradzkiego);
∫ ∫
∫ ∫ ∫
=
+
+
∂
∂
+
×
→
→
→
S
V
v
dV
E
H
w
t
S
d
H
E
0
2
1
2
1
2
2
ε
µ
v
w - gęstość objętościowa energii (przyspieszenie cząstek, grzanie przy zderzeniach)
•
Zasada zachowania mocy:
∫ ∫
∫ ∫ ∫
=
∂
∂
+
→
S
V
wdV
t
S
d
P
0
←
=
×
=
S
H
E
P
wektor Poyntinga
2
m
W
e
m
v
w
w
w
w
+
+
=
←
v
w
gęstość energii przekazanej przez pole cząstkom (nośnikom ładunku)
3
m
J
←
=
2
2
1
H
w
m
µ
gęstość energii zmagazynowanej w polu magnetycznym
3
m
J
←
=
2
2
1
E
w
e
ε
gęstość energii zmagazynowanej w polu elektrycznym
3
m
J
→
E - natężenie pola elektrycznego [V/m]
→
H - natężenie pola magnetycznego [A/m]
→
D - indukcja pola elektrycznego lub gęstość strumienia elektrycznego [C/m
2
]
→
B - indukcja pola magnetycznego lub gęstość strumienia magnetycznego [Wb/m
2
]
ε
- przenikalność elektryczna [F/m]
µ
- przenikalność magnetyczna [H/m]
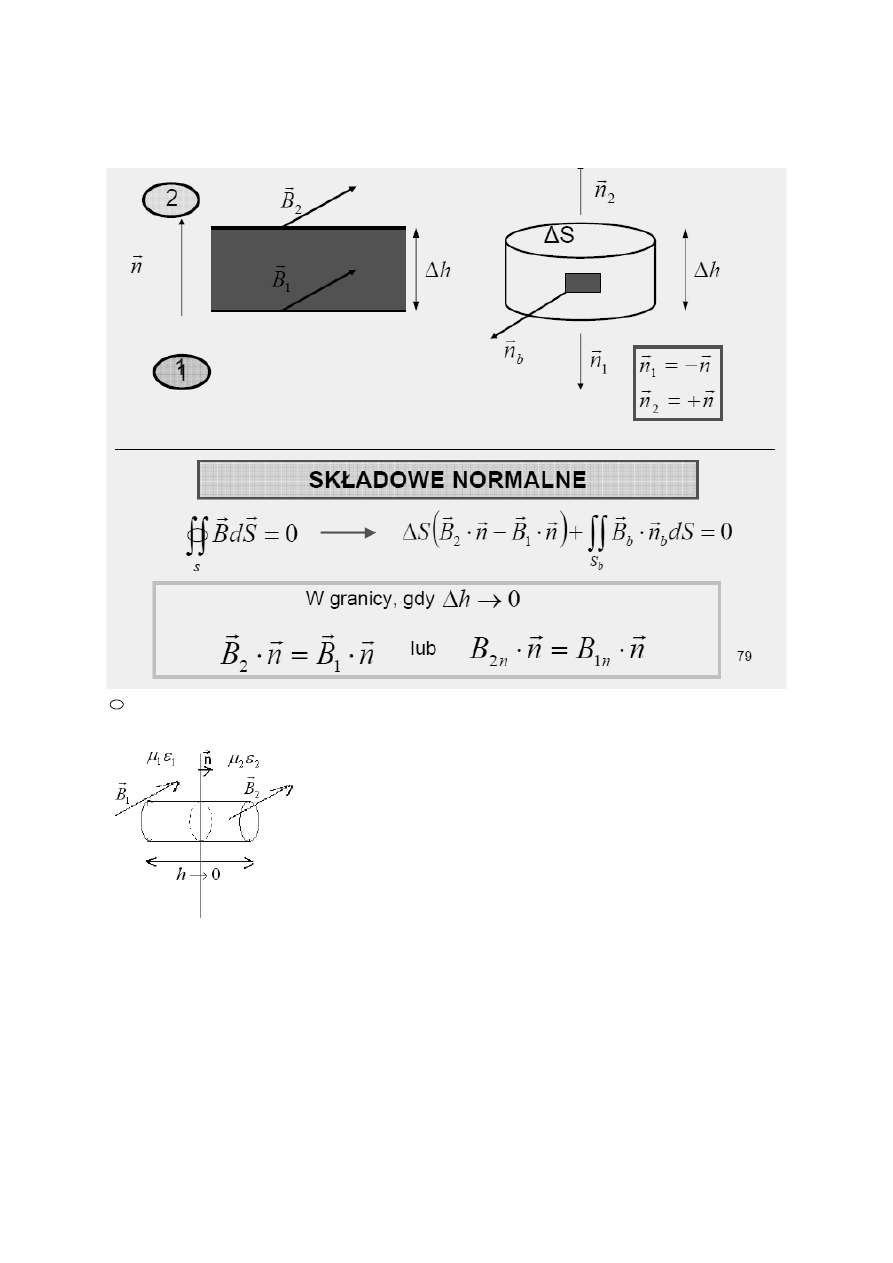
17(--). Korzystając z równań Maxwella wyznaczyć związek pomiędzy składowymi
normalnymi wektora B na granicy dwóch ośrodków materialnych.
←
=
∫ ∫
0
S
S
d
B
całkowe prawo źródeł magnetycznych (jedno z praw Maxwella)
Jako, że powierzchnia strumienia jest bardzo mała zastępujemy
całkę mnożeniem.
Ponieważ
0
→
h
możemy pominąć składową zależną od
powierzchni bocznej i wówczas:
dwie podstawy walca się pokrywają i pole
boczne przestaje istnieć.
∫ ∫
=
+
+
∆
b
S
b
b
dS
n
B
n
B
n
B
S
0
)
(
1
1
2
2
0
)
(
0
)
(
1
2
1
2
=
−
∆
→
=
+
−
∆
∫ ∫
n
B
n
B
S
dS
n
B
n
B
n
B
S
b
S
b
b
b
n
- jest to wektor prostopadły do przyczynka powierzchni bocznej walca
S
∆
- pole powierzchni podstawy walca
Jak widać na granicy dwóch ośrodków składowa normalna wektora indukcji magnetycznej się
nie zmienia
n
B
n
B
1
2
=
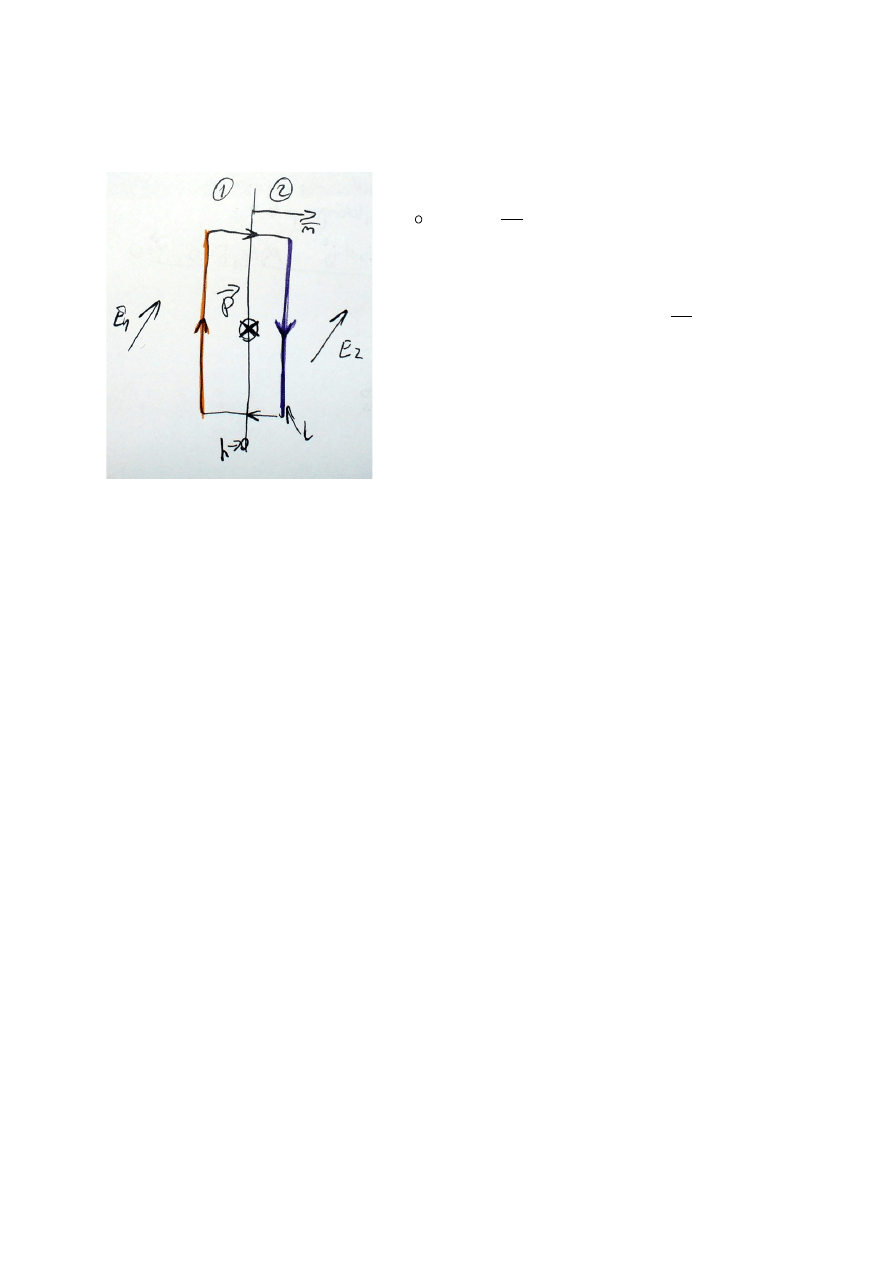
18(--). Korzystając z równań Maxwell wyznaczyć związek pomiędzy składowymi
stycznymi wektora E
na granicy dwóch ośrodków materialnych.
∫ ∫
∫
←
∂
∂
−
=
→
→
→
S
l
S
d
t
B
dl
E
całkowe prawo Faraday’a
lh
p
t
B
n
p
l
E
n
p
l
E
we
pomaranczo
fioletowe
∂
∂
−
=
×
−
+
×
→
→
)
(
)
(
1
2
Skracamy przez l bo to skalar
Gdy
0
→
h
to po prawej stronie równania mamy 0
0
)
(
)
(
0
)
(
)
(
0
)
(
)
(
0
)
(
)
(
1
2
1
2
1
2
1
2
=
×
×
−
×
×
=
×
−
×
=
×
−
×
=
×
−
×
→
→
→
→
→
→
→
→
n
E
n
n
E
n
n
E
n
E
n
E
p
n
E
p
n
p
E
n
p
E
Znając zależność, że
)
(
)
(
B
A
C
C
A
B
C
B
A
−
=
×
×
to można zapisać:
st
st
n
n
E
E
E
E
E
E
E
n
n
n
n
E
E
n
n
n
n
E
1
2
1
1
2
2
1
1
2
2
0
0
)
(
)
(
)
(
)
(
→
→
→
→
→
→
→
→
→
→
=
=
+
−
−
=
+
−
−
Jak widać na granicy dwóch ośrodków składowa styczna wektora natężenia pola
elektrycznego się nie zmienia
→
→
=
st
st
E
E
2
1
.
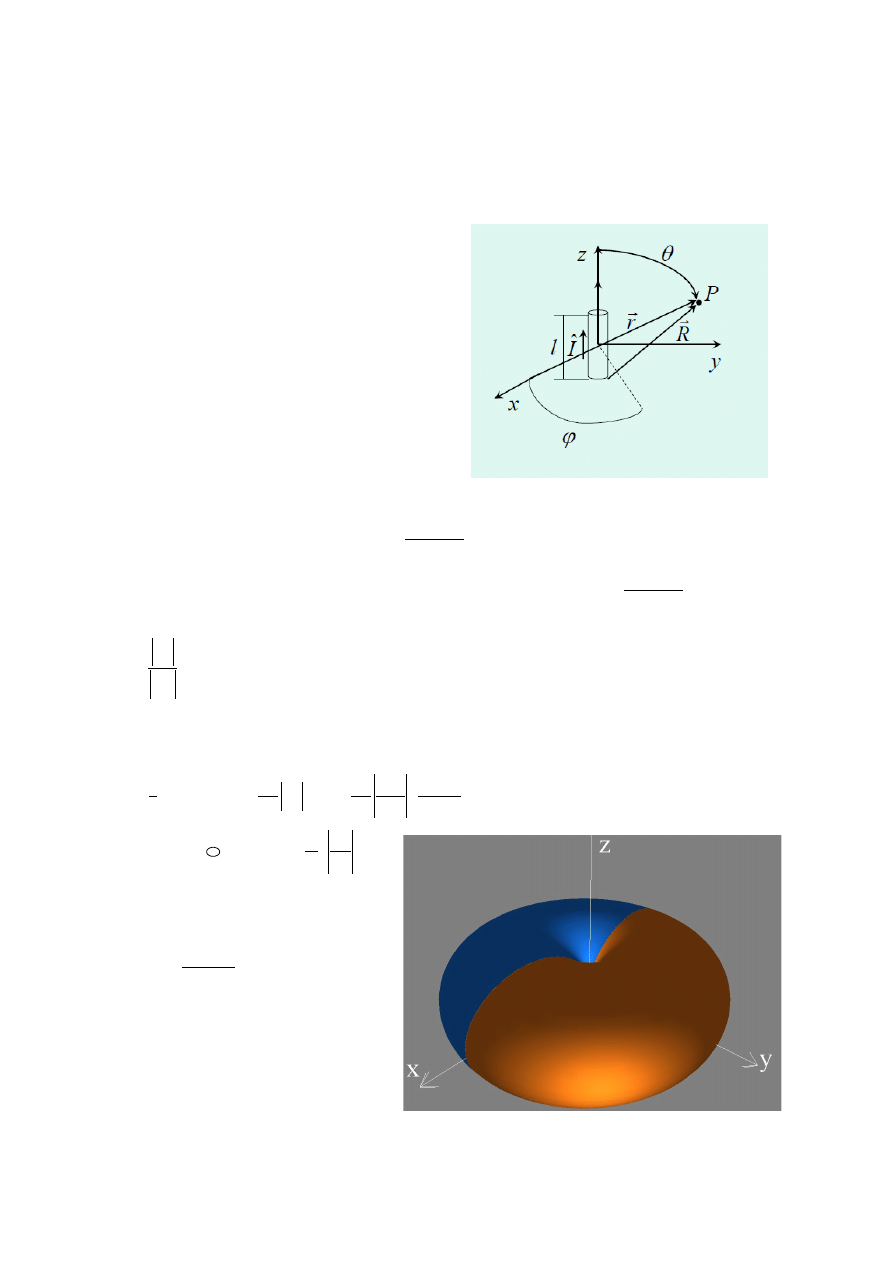
XX(--).Wyjaśnić pojęcie Dipol Hertza. Podać kształt charakterystyki promieniowania w
strefie dalekiej dla pola E i H oraz wektora powierzchniowej gęstości mocy.
•
Dipol Hertza to elementarna antena. Przewodnik w kształcie walca, w którym płynie prąd
zmienny.
•
Założenia
cienka
antena
krótka
antena
daleka
strefa
)
(
ˆ
2
ˆ
ˆ
0
z
f
I
a
l
r
l
e
I
I
t
j
≠
< <
< <
< <
⋅
=
λ
λ
ω
•
Strefa daleka (Fraunhofera)
0
ˆ
=
r
E
θ
π
θ
sin
4
ˆ
ˆ
0
0
r
le
I
k
jZ
E
jkr
−
=
0
ˆ
=
ϕ
E
0
ˆ
=
r
H
0
ˆ
=
θ
H
θ
π
ϕ
sin
4
ˆ
ˆ
0
r
le
I
k
j
H
jkr
−
=
]
[
377
]
[
120
ˆ
ˆ
0
Ω
=
Ω
=
=
=
π
ϕ
θ
Z
H
E
Z
f
•
Średnia gęstość mocy promieniowanej
{
}
2
2
2
0
0
2
0
2
1
*
2
1
sin
4
2
ˆ
Re
0
r
l
kI
Z
i
E
H
E
S
r
Z
śr
θ
π
=
⋅
=
×
=
2
0
0
3
λ
π
l
I
Z
s
d
S
P
S
śr
ana
promieniow
=
=
∫ ∫
•
Charakterystyka promieniowania
θ
θ
ϕ
θ
ϕ
2
max
sin
)
,
(
)
,
(
=
=
S
S
F
To nie Jest torus byłby nim gdyby
F(x)=sin x wiec jest to coś na styl
torusu.
SAM NARYSOWAŁEM
Wyszukiwarka
Podobne podstrony:
opracowanie pytan id 338374 Nieznany
Nhip opracowanie pytan id 31802 Nieznany
Opracowanie pytan 3 id 338376 Nieznany
Opracowanie pytan 5 id 338378 Nieznany
Opracowanie pytan 4 id 338377 Nieznany
MSI opracowanie pytan id 309782 Nieznany
opracowanie pytan id 338374 Nieznany
Nhip opracowanie pytan id 31802 Nieznany
Opracowanie pytan 3 id 338376 Nieznany
opracowane Notatek pl id 321371 Nieznany
GWIAZDA PYTAN id 198034 Nieznany
newsletter 19 06 id 317919 Nieznany
6 ZKM marzec 19 2012 id 44004 Nieznany (2)
90 pytan id 48496 Nieznany (2)
opracowanie et cw4 id 338175 Nieznany
opracowanie na kolosa id 338294 Nieznany
17 19 indd(1)id 17389 Nieznany
ARKUSZ PYTAN B id 272154 Nieznany (2)
Opracowane testy 2014 id 337688 Nieznany
więcej podobnych podstron