2013-POLSL-MT-MIBM-SEM6-PAIR

Opracował: Yanoo, grupa 2

1

Podstawy automatyki i robotyki

M

M

a

a

t

t

e

e

r

r

i

i

a

a

ł

ł

y

y

d

d

y

y

d

d

a

a

k

k

t

t

y

y

c

c

z

z

n

n

e

e

d

d

o

o

e

e

g

g

z

z

a

a

m

m

i

i

n

n

u

u

1. Pojęcia: sygnał, treść fizyczna sygnału, parametr informacji, zmienna sterowana, zmienna sterująca,
zakłócenie.
1.1. Sygnał – dowolna wielkość fizyczna, za pomocą której są przekazywane informacje.
1.2. Treść fizyczna sygnału – wielkość fizyczna, która jest nośnikiem informacji.
1.3. Parametr informacji – wartość wielkości fizycznej, będącej nośnikiem informacji.
1.4. Zmienna sterowana – wielkość lub warunek, który jest mierzony i sterowany.
1.5. Zmienna sterująca – wielkość lub warunek, który jest zmieniany przez sterownik tak, aby osiągnąć wartość
zmiennej sterowanej.
1.6. Zakłócenie – sygnał, który wywiera niekorzystny wpływ na wartość sygnału wyjściowego układu.

2. Podział układu automatycznej regulacji ze względu na charakter wielkości zadanej:
2.1. Układy regulacji stałowartościowej.
2.2. Układy regulacji programowej.
2.3. Układy regulacji nadążnej.
2.4. Układy regulacji ekstremalnej.
2.5. Układy regulacji adaptacyjnej.
2.6. Układy rozgrywające.

3. Węzeł zaczepowy i węzeł sumacyjny oraz ich możliwe realizacje techniczne.
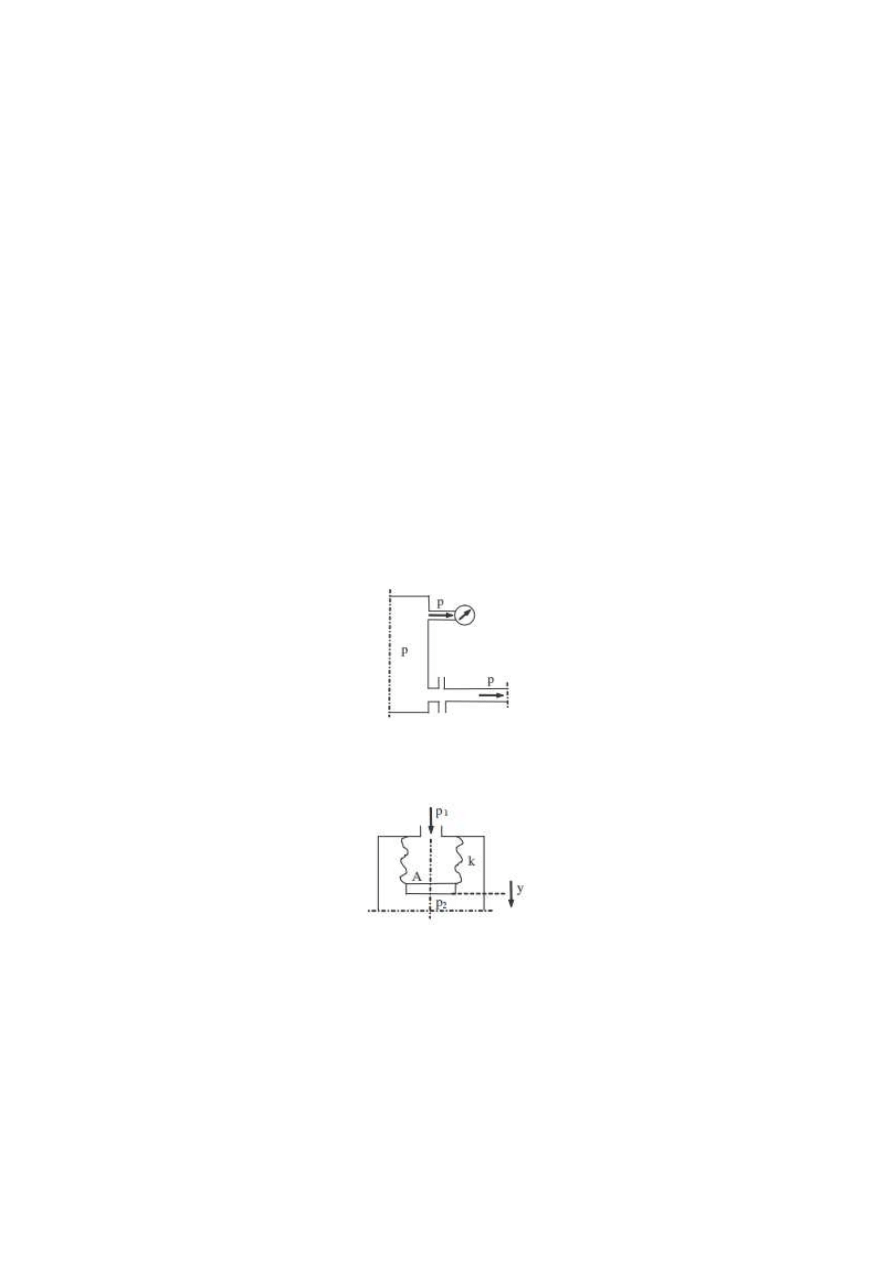
3.1. Węzeł zaczepowy – rozgałęzienie w torze przepływu sygnału, do którego nie stosuje się reguł dodawania
lub odejmowania. Przykład: zbiornik ciśnieniowy.

p – ciśnienie medium
3.2. Węzeł sumujący – węzeł układu automatyki, utworzony przez człon sumujący, posiadający dwa wejścia i
jedno wyjście, przy czym wielkości wyjściowe nie ulegają zmianie, jedynie dodają się do siebie algebraicznie.
Przykład: mieszek sprężysty.

A – powierzchnia mieszka,
k – współczynnik sprężystości,
p1 – ciśnienie wejściowe,
p2 – ciśnienie wyjściowe,
y - przesunięcie

4. Elementy dynamiczne układów automatyki:
4.1. Proporcjonalny.
4.2. Całkujący idealny.
4.3. Całkujący rzeczywisty.
4.4. Różniczkujący idealny.
4.5. Różniczkujący rzeczywisty.

2013-POLSL-MT-MIBM-SEM6-PAIR

Opracował: Yanoo, grupa 2

2

4.6. Inercyjny pierwszego rzędu.
4.7. Inercyjny drugiego rzędu.
4.8. Oscylacyjny drugiego rzędu.
4.9. Opóźniający.

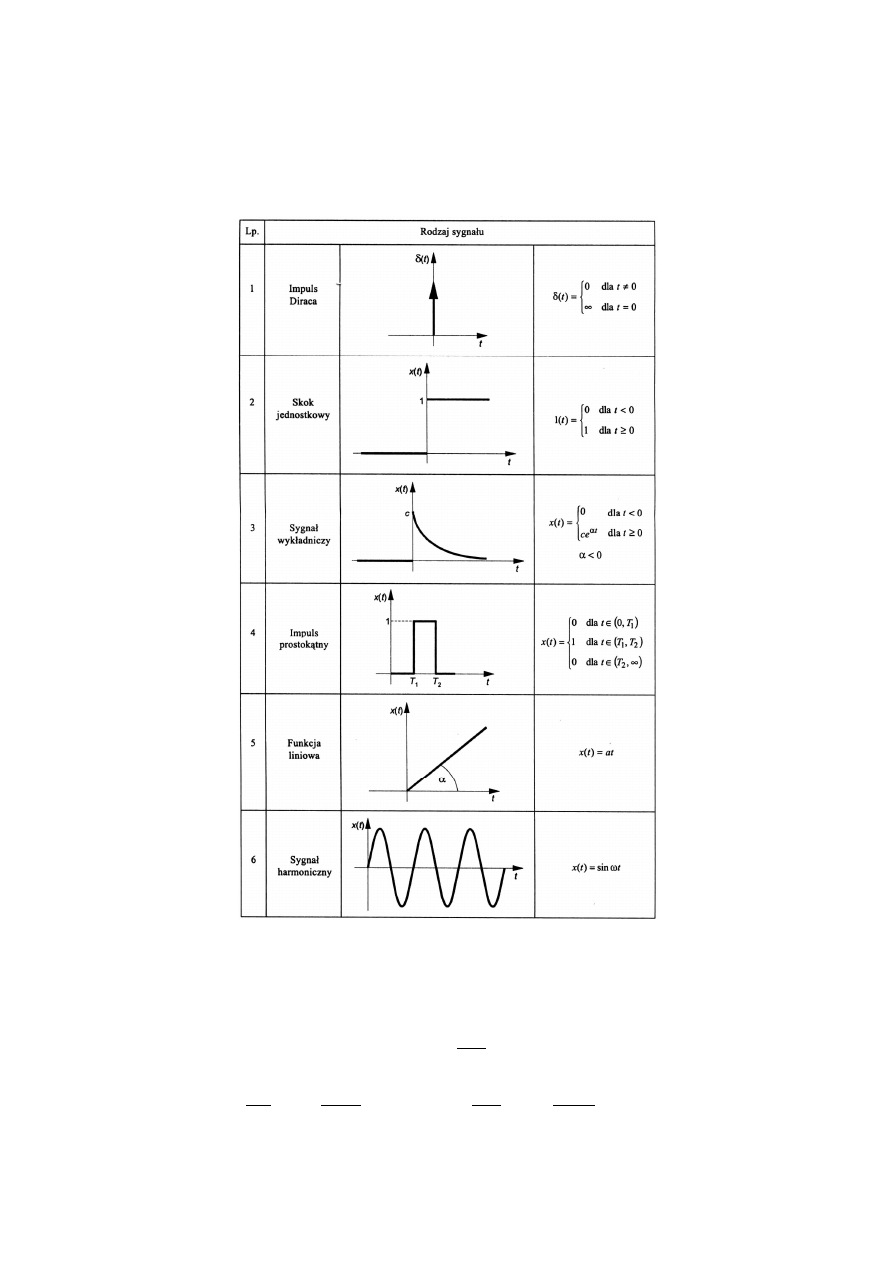
5. Standardowe wymuszenia stosowane w automatyce:

6. Pojęcie transmitancji operatorowej liniowego stacjonarnego układu dynamicznego i jej związek z
przepustowością widmową takiego układu. Postać transmitancji operatorowej liniowego stacjonarnego
układu dynamicznego o dwóch wejściach i dwóch wyjściach.
6.1. Transmitancja operatorowa – stosunek transformaty Laplace’a sygnału wyjściowego do transformaty
Laplace’a sygnału wejściowego, przy zerowych warunkach początkowych.

=

Rozważając liniowy, niezmienny w czasie układ zdefiniowany przez równanie różniczkowe

+

+ ⋯ +

=

+

+ ⋯ +

Dokonując przekształceń Laplace’a

+

+ ⋯ +

+

=

+

+ ⋯ +

+

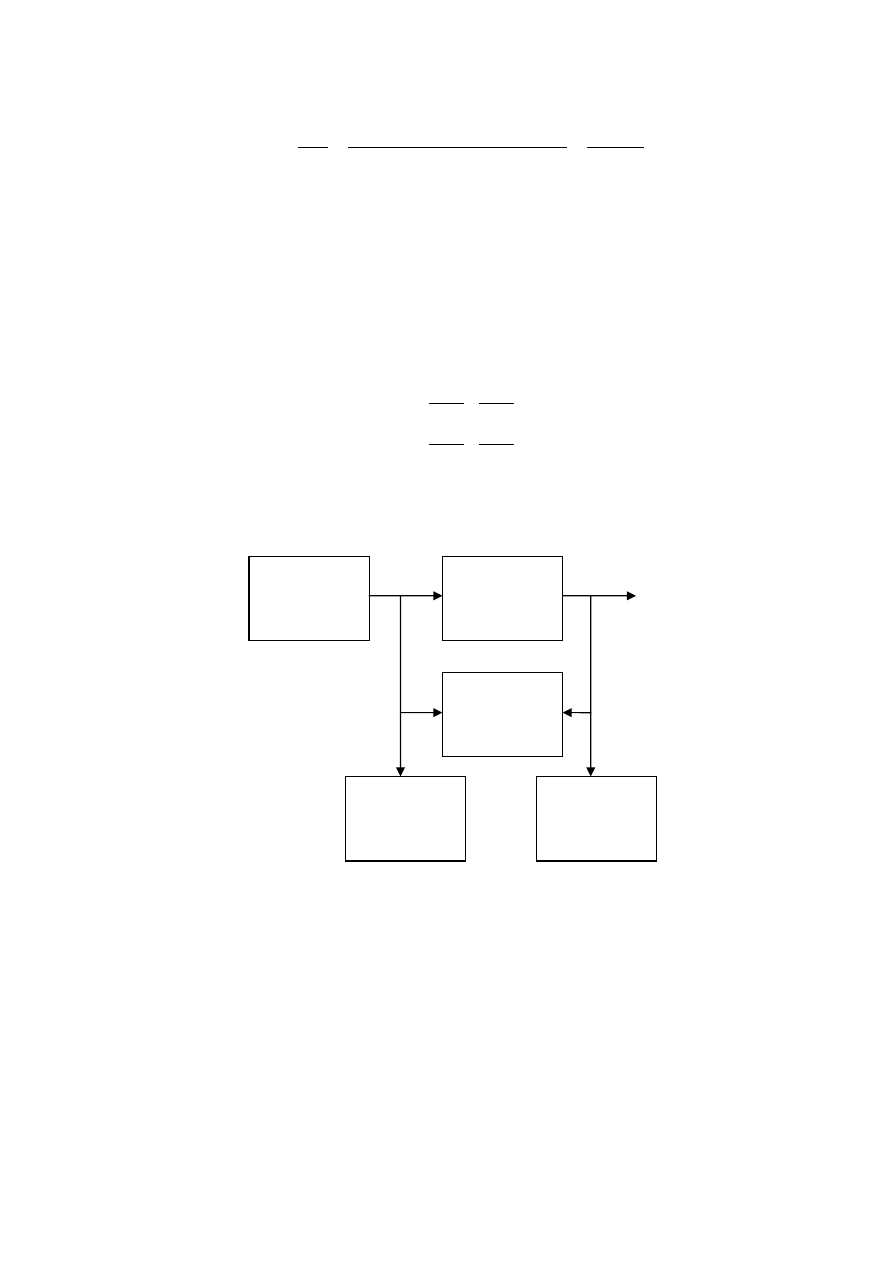
2013-POLSL-MT-MIBM-SEM6-PAIR

Opracował: Yanoo, grupa 2

3

Otrzymamy transmitancję operatorową danego układu

=

=

+

+ ⋯ +

+

+

+ ⋯ +

+

=

∑

∑

6.2. Transmitancję widmową wyznaczyć można na podstawie transmitancji operatorowej, stosując
podstawienie

=

|

.

6.3. Transmitancja operatorowa liniowego stacjonarnego układu dynamicznego o dwóch wejściach i dwóch
wyjściach:

=

+

!

!

!

=

!

=

!!

!

"

[

] = [

][

]

%

!

& = %

!

!

!!

& %

!

&

=

'

(

(

(

)

!

!

!

!

*

+

+

+

,

7. Analiza widmowa liniowych stacjonarnych układów dynamicznych. Schemat blokowy doświadczalnego
wymuszenia charakterystyki częstotliwości układu dynamicznego.
7.1. Analiza widmowa zajmuje się badaniem układów, na których wejście podano sygnał harmoniczny.
7.2. Schemat blokowy doświadczalnego wymuszenia charakterystyki częstotliwości układu dynamicznego:


















8. Różnica pomiędzy regulatorem ciągłego, a nieciągłego działania.
Regulator ciągłego działania wytwarza sygnał nastawczy bez przerwy podczas uchybu regulacji. Regulator
nieciągłego działania wytwarza sygnał nastawczy z przerwami podczas istnienia uchybu regulacji.

9. Pojęcia: charakterystyka statyczna, charakterystyka dynamiczna, charakterystyka dynamiczna
częstotliwościowa.
9.1. Charakterystyka statyczna – funkcja określająca zależność wielkości wyjściowej elementu lub układu od
wielkości wejściowej w stanie ustalonym.
9.2. Charakterystyka dynamiczna (czasowa) – przebieg w czasie odpowiedzi układu dynamicznego na zadane
wymuszenie, najczęściej funkcją Heaviside’a.
9.3. Charakterystyka dynamiczna częstotliwościowa – opisuje sygnał wyjściowy układu w zalezności od
amplitudy i częstotliwości sinusoidalnie zmiennego sygnału wejściowego.

Generator

funkcji

harmonicznej

Badany układ

Miernik

amplitudy y

0

Miernik

amplitudy x

0

Miernik fazy

ϕ(ω)

2013-POLSL-MT-MIBM-SEM6-PAIR

Opracował: Yanoo, grupa 2

4

10.

Bezinercyjny element automatyki: model matematyczny, transmitancja operatorowa, charakterystyka

statyczna, odpowiedź skokowa.
10.1. Model matematyczny:

= -

k – współczynnik wzmocnienia
10.2. Transmitancja operatorowa:

= -

=

= -

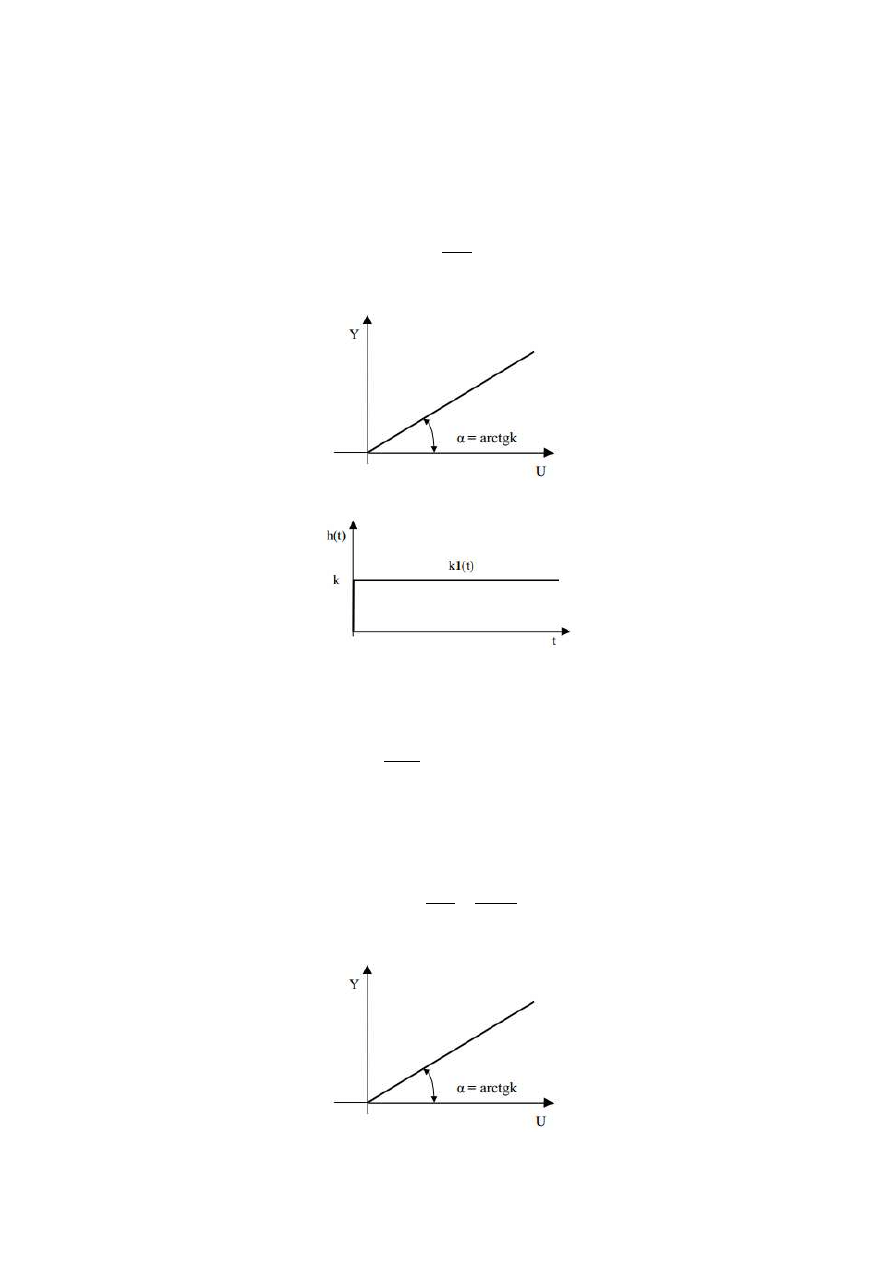
10.3. Charakterystyka statyczna:

= -

10.4. Odpowiedź skokowa dla wymuszenia u(t)=1(t):

ℎ

= -

11. Element inercyjny pierwszego rzędu: model matematyczny, transmitancja operatorowa, charakterystyka
statyczna, odpowiedź skokowa, odpowiedź czasowa (interpretacja stałej czasowej, praktyczna wartość
przedziału czasu, po którym uznaje się odpowiedź układu jako ustalonego).
11.1. Model matematyczny:

/

+

= -

k – współczynnik wzmocnienia w stanie ustalonym,
T – stała czasowa
11.2. Transmitancja operatorowa:

/

+

= -

/ + 1 = -

=

=

-

/ + 1

11.3. Charakterystyka statyczna:

= -

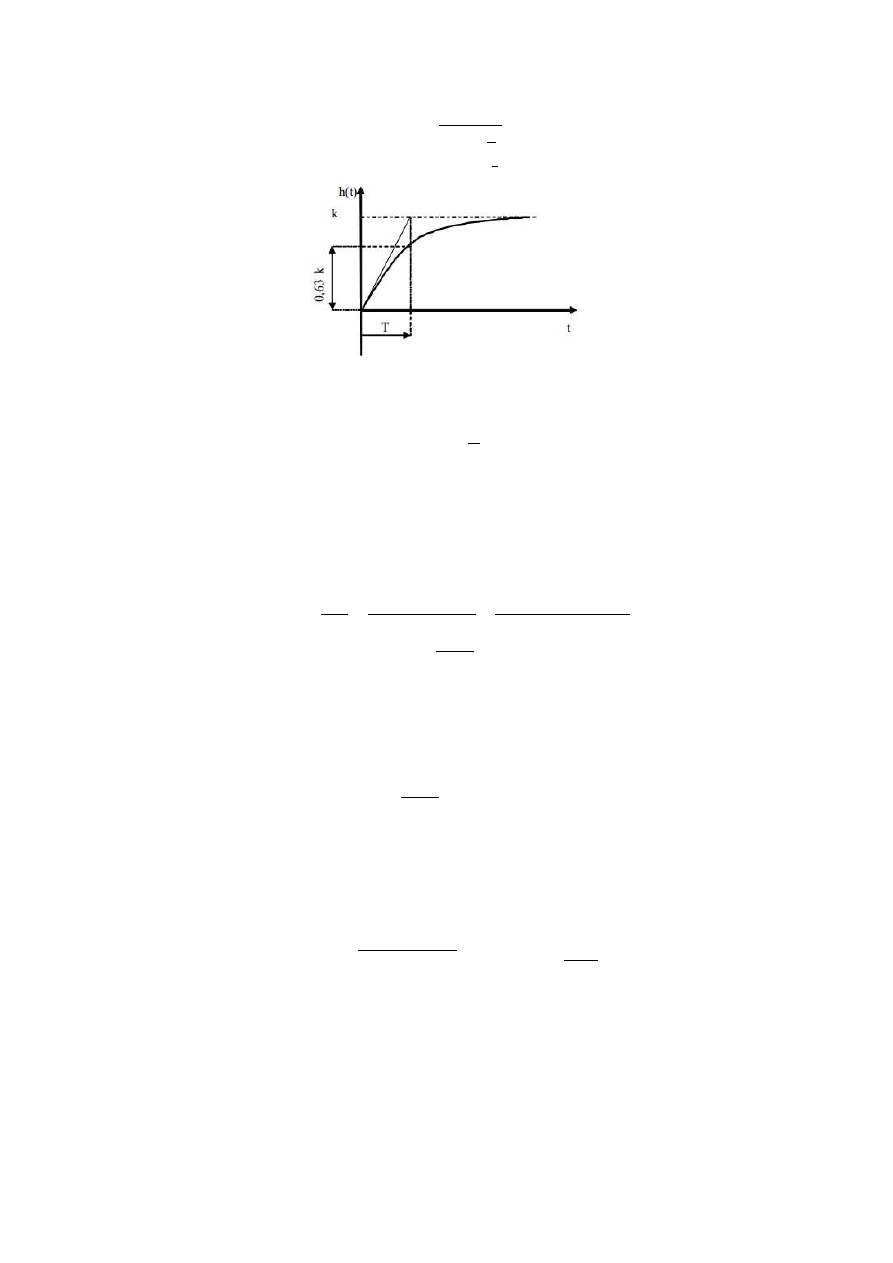
11.4. Odpowiedź skokowa:

2013-POLSL-MT-MIBM-SEM6-PAIR

Opracował: Yanoo, grupa 2

5

=

-

/

+ 1/

ℎ

= - 1 − 2

3

4

11.5. Odpowiedź czasowa:
Stan sygnału odpowiedzi w czasie równym T:

/ = - 1 − 2

= 0,632-

Nowy stan ustalony y

u

=0,999kx

0

następuje po czasie t

u

:

0,999- = - ;1 − 2

3

<

4

= →

?

= 4,63/

W praktyce przyjmuje się t

u

=5T.

12. Transmitancja widmowa liniowego, stacjonarnego układu dynamicznego: definicja, postać
matematyczna, moduł zespolonej funkcji transmitancji widmowej, argument zespolonej funkcji transmitancji
widmowej.
12.1. Transmitancja widmowa liniowego, stacjonarnego układu dynamicznego nazywa się zespolone
wyrażenie w postaci

=

A

̅

=

2

3CD

2

3

=

2

3

+ 2

D

2

3

=

2

D

Transmitancja widmowa związana jest z przekształceniem Fouriera, przyporządkowywującym funkcji czasu
zespoloną funkcję pulsacji zgodnie z całką Fouriera:

= E F

CG

G

2

3

12.2. Moduł zespolonej funkcji transmitancji widmowej (dynamiczne współrzędne wzmocnienia amplitudy):

= H

12.3. Argument zespolonej funkcji transmitancji widmowej:

I

= H

2

D

= J

+ K

J

= L2[

], K

= MN[

]

W przypadku ustalonej wartości częstości wymuszenia, transmitancja widmowa układu reprezentowana jest
przez jeden punkt na płaszczyźnie zespolonej o współrzędnych

J

= H

OP I

; K( ) = H( ) RSI( )

H( ) = TJ

!

( ) + K

!

( ) ; I( ) = UO V

K( )

J( )

13. Transmitancja widmowa elementu z opóźnieniem czasowym: postać matematyczna, wykres
charakterystyki amplitudowo-częstościowo-fazowej elementu na płaszczyźnie fazowej.
13.1. Postać matematyczna:

( ) = - ( − / )

13.2. Transmitancja operatorowa i widmowa:

( ) = -2

4

W

( ) = -2

4

W

= -OP /

X

− - RS/

X

J( ) = -OP /

X

; K( ) = −- RS/

X

2013-POLSL-MT-MIBM-SEM6-PAIR

Opracował: Yanoo, grupa 2

6

13.3. Moduł przepustowości:

H

= T-

!

RS

!

/

X

+ OP

!

/

X

= -

13.4. Argument przepustowości:

I

= UO V[− V/

X

] = −/

X

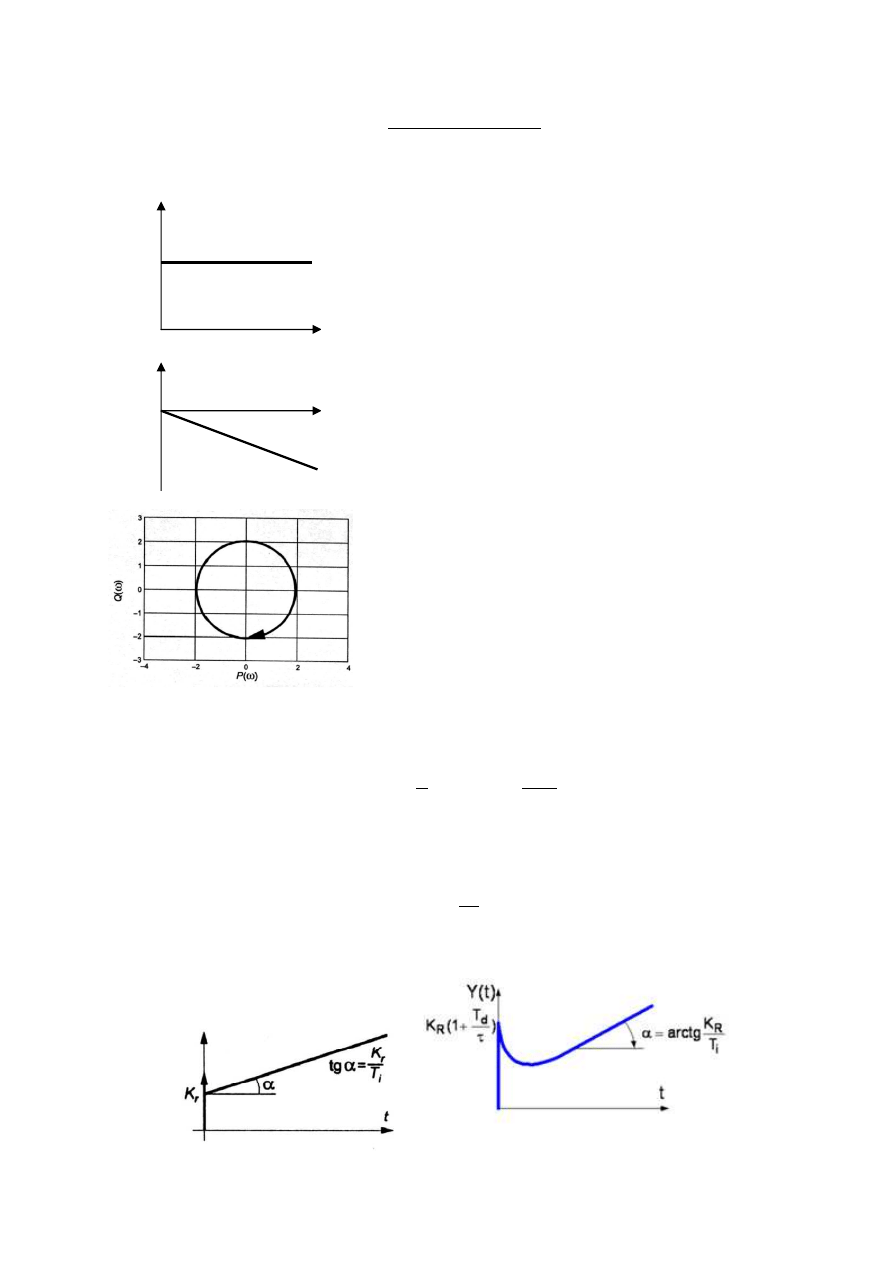
13.5. Charakterystyka amplitudowa:

13.6. Charakterystyka fazowa:

13.7. Charakterystyka amplitudowo-fazowa:

14. Regulator proporcjonalno-całkowo-różniczkujący (PID): model matematyczny, transmitancja
operatorowa, charakterystyka czasowa przy skokowej zmianie odchyłki regulacji .
14.1. Model matematyczny:

Y

= -Z2 [ +

1

/ E 2

+ /

\

2

3

+ Y

k - współczynnik wzmocnienia,
T

i

- czas zdwojenia,

T

d

- czas wyprzedzenia

14.2. Transmitancja operatorowa:

= - 1 +

1

/ + /

\

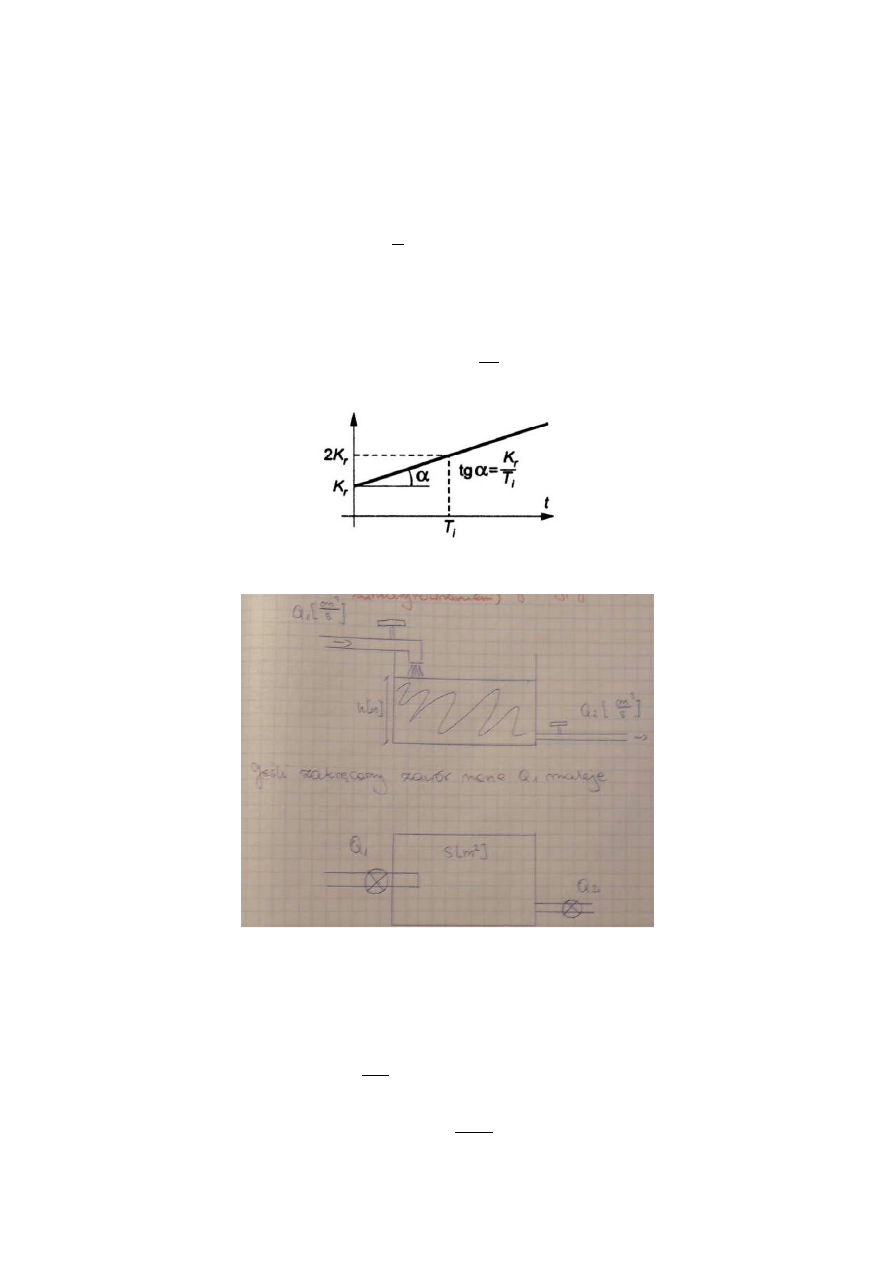
14.3. Charakterystyka czasowa:

A(ω)

ω

k

ϕ(ω)

ω

2013-POLSL-MT-MIBM-SEM6-PAIR

Opracował: Yanoo, grupa 2

7

15. Regulator proporcjonalno-całkowy (PI): model matematyczny, transmitancja operatorowa,
charakterystyka czasowa przy skokowej zmianie odchyłki regulacji.
14.1. Model matematyczny:

Y

=

-

/ E 2

+ -2

3

+ Y

k - współczynnik wzmocnienia,
T

i

- czas zdwojenia,

T

d

- czas wyprzedzenia

14.2. Transmitancja operatorowa:

= - 1 +

1

/

14.3. Charakterystyka czasowa:

16. Równanie różniczkowe opisujące zmianę poziomu cieczy w zbiorniku ze swobodnym wypływem w funkcji
zmian natężenia przepływu cieczy na jego wlocie.

Q

1

(t) – natężenie przepływu cieczy na wlocie,

Q

2

(t) – natężenie przepływu cieczy na wylocie,

h(t) – wysokość poziomu cieczy,
S(t) – powierzchnia tafli,
V(t) – objętość cieczy

∆^

= _∆ℎ

^

= _ ℎ

K

!

= Tℎ

− `U aP aP P S2VP a `ł ac

lub

K

!

( ) =

ℎ( )

L (ℎ)

2013-POLSL-MT-MIBM-SEM6-PAIR

Opracował: Yanoo, grupa 2

8

LS ℎ =

ℎ
√ℎ

=

√ℎℎ

ℎ =

√ℎ

eN

!

f − Y ę`OY P`PUSPść a `ł ac

Bilans zbiornika:

K ( ) = K

!

( ) +

^( )

^( )

− S ęż2SR2 `UY UP c P ę PśOR OR2OY

K ( ) =

ℎ( )

L (ℎ) +

_ ℎ( )

− UóaS SR2 UóżSROY-Pa2 `UY2`ł ac OR2OY

17. Model matematyczny czwórnika RLC.

Z drugiego prawa Kirchoffa:

c ( ) = l

R ( )

+ L R ( ) + c

!

( )

c

!

( ) = L

!

R

!

( ) ; R

m

( ) = n

c

!

( )

Z pierwszego prawa Kirchoffa:

R ( ) = R

!

( ) + R

m

( )

c

!

( ) = L

!

R

!

( ) ; R

m

( ) = n

c

!

( )

c ( ) =

c

!

( )

L

!

+ n

c

!

( )

c ( )

ln =

!

c

!

( )

!

+

lL L

!

n

L

!

ln

c

!

( )

+

L +L

!

L

!

ln c

!

( ) − UóaS SR2 UóżSROY-Pa2 OYaóUSR- Lln

18. Model matematyczny oscylatora z wymuszeniem dynamicznym.

18.1. Równanie dynamiki elementu oscylacyjnego drugiego rzędu:

/

!

!

( )

!

+ 2o/

( )

+ ( ) = - ( )

18.2. Model matematyczny oscylatora:

N p( ) + - q( ) + O ( ) = r( )

N

O p( ) +

-

O q( ) + ( ) =

1

O r( )

N

O = /

!

→ / = s

N

O

O = 2o/ → o = 2O

1

/ =

2OsNO

=

2√NO

1

O = -

m

c

b

F(t)

y(t)