1 kolokwium z Metod Probabilistycznych i Statystyki 2.04.2012

Część zadaniowa

Zadanie 1. (4p) Ile można utworzyć liczb parzystych pięciocyfrowych o nie powtarzających się cyfrach
i przy założeniu, że zero nie występuje na pierwszym miejscu.

Zadanie 2. (4p) Dwie osoby X i Y umówiły się na spotkanie w określonym miejscu między godziną 12 i
13 w ten sposób, że osoba która przyjdzie pierwsza czeka jedynie 30 minut, po czym odchodzi. Obli-
czyć prawdopodobieństwo, że osoby X i Y spotkają się, jeśli każda z nich przychodzi losowo w poda-
nym przedziale czasu i niezależnie od siebie.

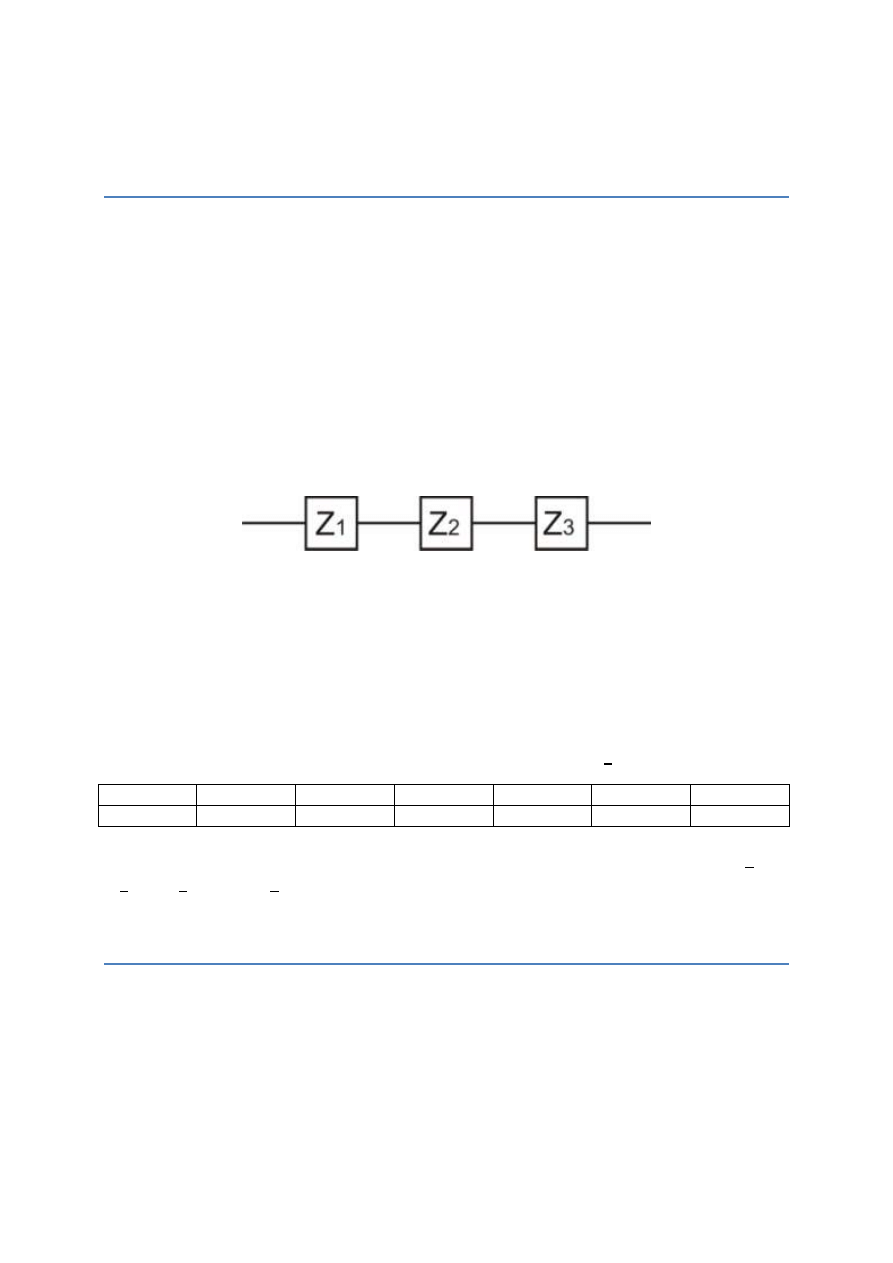
Zadanie 3. (4p) Na rys.1, gdzie z

1

, z

2

, z

3

, oznaczają żarówki, dany jest schemat fragmentu sieci elek-

trycznej. Prawdopodobieństwo nieprzepalenia się w czasie t godzin jest dla wszystkich żarówek jed-
nakowe i wynosi p. Zakładając, że żarówki przepalają się niezależnie od siebie, obliczyć prawdopodo-
bieństwo ciągłego przepływu prądu w czasie t.

Zadanie 4. (4p) Na linii łączności nadaje się dwa rodzaje sygnałów w postaci kodowych kombinacji 11
albo 00 z prawdopodobieństwami (a priori) odpowiednio równymi 0.8 i 0.2. Sygnały podlegają loso-
wym zakłóceniom, w rezultacie czego symbol 1 może być odebrany jako 0 z prawdopodobieństwem
0.1, i z takim samym prawdopodobieństwem symbol 0 może być odebrany jako 1. Zakładamy, że
symbole 1 i 0 ulegają zakłóceniom niezależnie jeden od drugiego. Obliczyć prawdopodobieństwa: a)
odebrania na wyjściu sygnału 11, b) na wyjściu odebrano sygnał 01, jakie jest prawdopodobieństwo,
że został on nadany jako sygnał 11.

Zadanie 5. (4p) Dana jest funkcja prawdopodobieństwa zmiennej losowej X:

x

i

–5

–2

0

1

3

8

pi

0.1

0.2

0.1

0.2

c

0.1

Obliczyć: a) stałą c, b) dystrybuantę i sporządzić jej wykres, c) prawdopodobieństwa: P(X = 1),
P(X = 2), P(X < 3), P(–2 ≤ X < 3)

Część teoretyczna

Pytanie 1. Podaj i opisz twierdzenie Bayesa dla zdarzeń losowych. (3p.)

Pytanie 2. Jak można obliczyć prawdopodobieństwo przyjęcia przez zmienną losową ciągłą wartości z
przedziału <a,b)? Podaj interpretację geometryczną. (3p.)

Pytanie 3. Czy dwa zdarzenia losowe, które są rozłączne są niezależne? Odpowiedź uzasadnij. (4p.)