Politechnika Poznańska

Instytut Konstrukcji Budowlanych
Zakład Konstrukcji Metalowych

Przykład 1.1

Zaprojektować swobodnie podpartą belkę stropu wykonaną z dwuteownika

walcowanego I PE ze stali St3S. Rozpiętość belki w świetle ścian L=600cm.

Obciążenia:

-

obciążenie stałe, stanowią warstwy stropu:

-

gładź cementowa grubości 2,0cm

-

płyta żelbetowa grubości 15,0cm

-

tynk grubości 1,5cm

-

belka stalowa – wstępnie przyjęto I 400PE

-

obciążenie zmienne – użytkowe 5,0kN/m

2

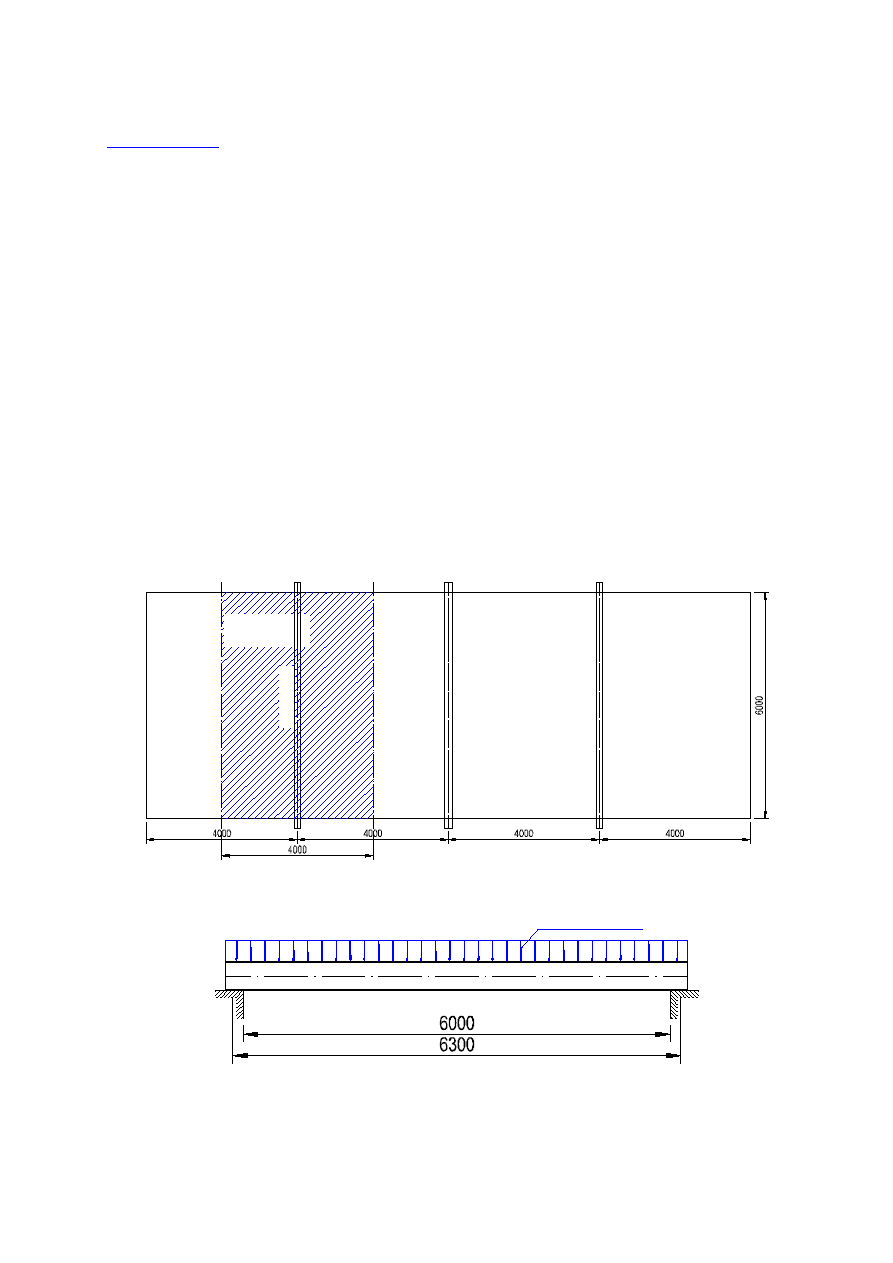
Przyjęto, że płyta stropu jest trwale połączona z stalowymi belkami

stalowymi i zabezpiecza je przed zwichrzeniem. Układ stropu przedstawiono na
poniższym rysunku.

q=g+p

I 4

00

P

E

I 4

00

P

E

I 4

00

P

E

q=g+p

I 400PE

© by Marcin Chybiński

1/4

http://www.ikb.poznan.pl/marcin.chybinski/

Politechnika Poznańska

Instytut Konstrukcji Budowlanych
Zakład Konstrukcji Metalowych

Zebranie obciążeń przydających na belkę stropową

Obciążenie

Wartość

charakterystyczna

[kN/m]

Współczynnik

obciążenia

γ

f

Wartość

obliczeniowa

[kN/m]

Obciążenia stałe
Gładź cementowa
0,02m·21,0kN/m

3

·4,0m

Płyta żelbetowa
0,15m·25, 0kN/m

3

·4,0m

Tynk
0,015m·22, 0kN/m

3

·4,0m

Belka stalowa – wstępnie przyjęto I 400PE
0,663kN/m

1,68

15,00

1,32

0,66

Σ g

k

= 18,66

1,3

1,1

1,3

1,1

2,18

16,50

1,72

0,73

Σ g

o

= 21,13

Obciążenia zmienne
Obciążenie użytkowe 5kN/m

2

5,0kN/m

2

·4,0m

20,00

Σ p

k

= 20,00

1,3

26,00

Σ p

o

= 26,00

Razem

Σ q

k

= 38,66

Σ q

o

= 47,13

Długość obliczeniowa belki stropowej

cm

l

l

630

600

05

,1

05

,1

0











Wartości sił wewnętrznych

kNcm

l

q

M

o

37

,

23382

8

630

4713

,

0

8

2

2

0

max











kN

l

q

V

o

46

,

148

2

630

4713

,

0

2

0

max











Przyjęcie potrzebnego przekroju belki stropowej ze względu na potrzebny

wskaźnik wytrzymałości

d

f

M

W

max

min



3

min

55

,

1087

5

,

21

37

,

23382

cm

W





Przyjęto I 400PE o

3

00

,

1160

cm

W

x



© by Marcin Chybiński

2/4

http://www.ikb.poznan.pl/marcin.chybinski/

Politechnika Poznańska

Instytut Konstrukcji Budowlanych
Zakład Konstrukcji Metalowych

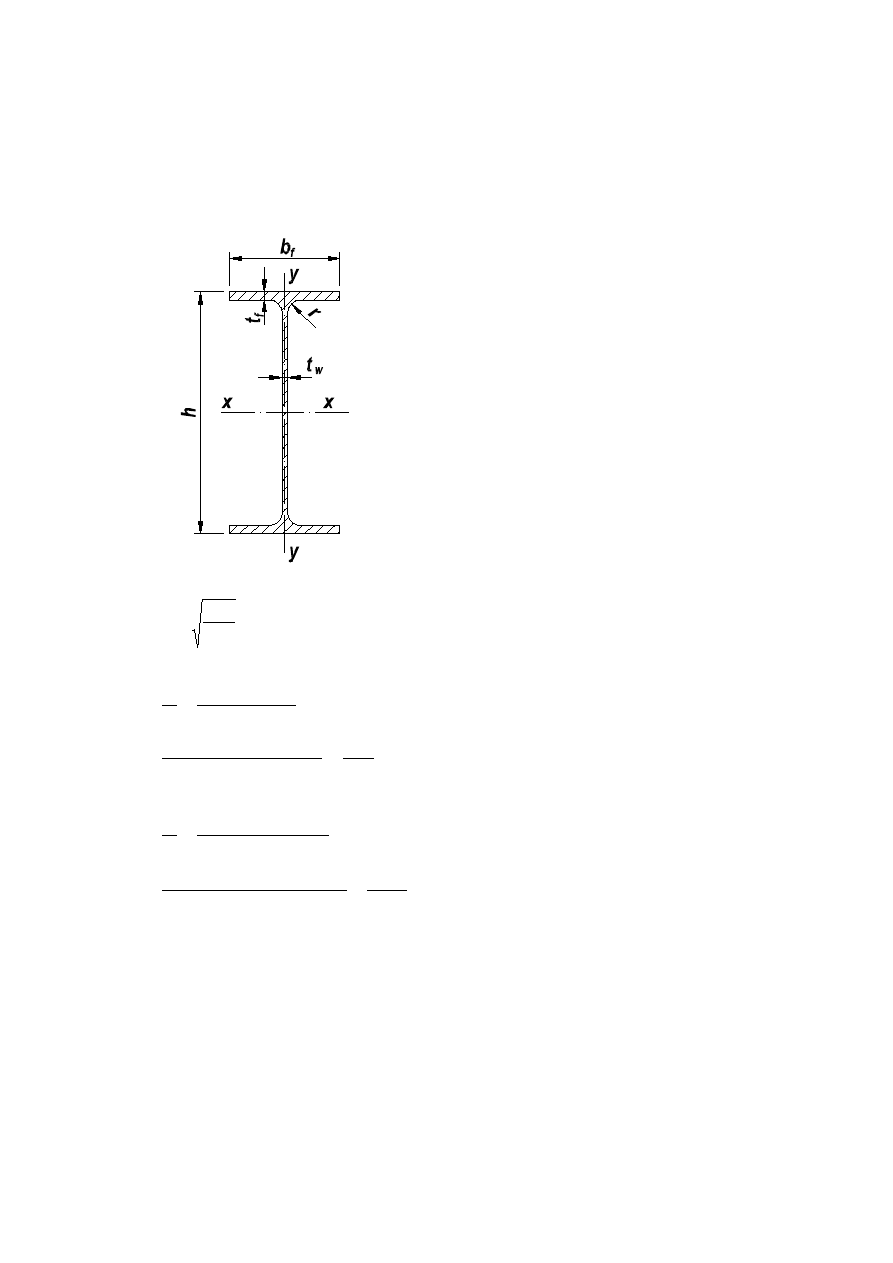
Charakterystyka geometryczna przekroju:

I 400PE

I 400PE

m

kg

m

mm

r

mm

b

mm

t

mm

t

mm

h

cm

i

cm

i

cm

W

cm

W

cm

I

cm

I

cm

A

f

f

W

Y

X

Y

X

Y

X

/

3

,

66

;

0

,

21

;

180

;

5

,

13

;

6

,

8

;

400

;

95

,

3

;

50

,

16

;

0

,

146

;

0

,

1160

;

1320

;

23130

;

50

,

84

3

3

4

4

2



























Określenie klasy przekroju

0

,1

215





d

f



-

Środnik



39

49

,

38

6

,

8

331

6

,

8

)

0

,

21

5

,

13

(

2

400

)

(

2

















w

f

t

r

t

h

t

b

(tabl. 6)

-

Stopka



9

79

,

4

5

,

13

7

,

64

5

,

13

)

0

,

21

2

6

,

8

180

(

5

,

0

)

2

(

5

,

0



















f

w

f

t

r

t

b

t

b

(tabl. 6)

Przekrój spełnia warunki przekroju klasy 2.

Stan graniczny nośności

Nośność obliczeniowa przekroju przy jednokierunkowym zginaniu
Przekrój I 400PE jest klasy 2 i jest zginany w płaszczyźnie środnika
przyjęto, więc obliczeniowy współczynnik rezerwy plastycznej

07

,1



p



kNcm

f

W

M

d

p

R

80

,

26685

5

,

21

00

,

1160

07

,1













 

(wzór 42)

© by Marcin Chybiński

3/4

http://www.ikb.poznan.pl/marcin.chybinski/

Politechnika Poznańska

Instytut Konstrukcji Budowlanych
Zakład Konstrukcji Metalowych

Nośność obliczeniowa przekroju przy ścinaniu

kN

f

A

V

d

V

R

97

,

428

5

,

21

4

,

34

58

,

0

58

,

0















(wzór 47)

2

4

,

34

86

,

0

0

,

40

00

,

70

70

51

,

46

6

,

8

0

,

400

cm

t

h

A

t

h

t

h

w

w

V

w

w

w

























(tabl. 7)

Nośność elementów jednokierunkowo zginanych

0

,1

88

,

0

80

,

26685

0

,1

37

,

23382

max











R

L

M

M



(wzór 52)

Warunek jest spełniony.

Nośność elementów ścinanych

0

,1

35

,

0

97

,

428

46

,

148

max







R

V

V

Warunek jest spełniony.

Stan graniczny użytkowania

Ugięcie graniczne

cm

l

f

52

,

2

250

630

250

0

max







(tabl. 4)

Ugięcie rzeczywiste

max

4

4

0

67

,1

00

,

23130

20500

00

,

630

3866

,

0

384

5

384

5

f

cm

I

E

l

q

f

x

k





















Uwaga!

W nawiasach podano numerację wzorów w PN-90/B-03200.

© by Marcin Chybiński

4/4

http://www.ikb.poznan.pl/marcin.chybinski/