Akcje i ich wycena

Akcja jest papierem wartościowym potwierdzającym udział jej posiadacza

(akcjonariusza) w kapitale spółki akcyjnej. Zapewnia ona prawo do decydowa-
nia o spółce oraz udział w jej zyskach, czyli dywidendę. Ściśle, dywidenda to
określona część zysku spółki akcyjnej za dany rok, przeznaczona walnemu
zgromadzeniu do podziału między akcjonariuszy, w stosunku do posiadanych
przez nich akcji. Wyznaczana jest w kwocie absolutnej, lub w przeliczeniu na
jedną akcję. My będziemy rozumieć dywidendę w znaczeniu dywidenda na
jedną akcję.

Ze względu na prawa posiadacza akcje dzieli się na:

•

akcje zwykłe, dające statutowe uprawnienia posiadaczom;

•

akcje uprzywilejowane, mające specjalny status.

Mówimy, że akcja uprzywilejowana jest hybrydą, gdyż z pewnych wzglę-

dów przypomina akcję, a z innych – obligację. Dzieje się tak dlatego, że akcja
uprzywilejowana zapewnia zazwyczaj właścicielowi regularną płatność stałych
dywidend (to przypomina płatności kuponowe obligacji), pierwszeństwo przed
wypłatami dywidendy ze zwykłych akcji, a także często dywidendy wyższej
niż z akcji zwykłych.

Oprócz dwóch wymienionych rodzajów akcji w obrocie występują rów-

nież:

•

akcje złote dające zwiększone uprawnienia do decydowania o spółce;

•

akcje milczące nie dające prawa głosu na walnym zgromadzeniu udzia-
łowców;

•

akcje groszowe o niskim nominale;

•

akcje pierwszorzędne najbardziej renomowanych firm.

Zajmiemy się teraz prostymi metodami wyceny akcji stosowanymi przez

praktyków.

Zysk z tytułu posiadania akcji pochodzi z dwóch źródeł: dywidendy oraz

przyrostu (spadku) wartości akcji. Dzisiejszą wartość akcji obliczymy jako
zdyskontowaną wartość strumienia dywidend przy założeniu bezterminowego
trzymania akcji przez jej posiadacza:

(1)

∑

∑

∑

∑

∞

∞

∞

∞

====

++++

====

1

)

1

(

i

i

i

i

A

r

D

P

,

gdzie

i

D

- wysokość dywidendy w i – tym roku,

i

r

- wymagana stopa zwrotu w i – tym roku,

A

P

- wartość dzisiejsza akcji.

Ponadto zakłada się, że

∞

∞

∞

∞

====

1

)

(

i

i

r

jest ciągiem rosnącym. Motywacja tego za-

łożenia jest dobrze znana: „lepszy wróbel w garści, niż gołąb na dachu”. Zna-
czy to, że wartość dywidendy w dalszych okresach będzie jeszcze mniejsza,
niż wynikałoby to z wartości pieniądza w czasie. Fakt ten odzwierciedla ryzy-
ko, które w przypadku akcji może być znaczne.

Najogólniejszy, zaprezentowany właśnie model wyceny akcji można zna-

cząco uprościć przyjmując pewne dodatkowe założenia i opuszczając fakt
zmienności stopy dyskontowej. Przyjmując, że stopa dyskontowa jest stała
wzór (1) przyjmuje postać

∑

∑

∑

∑

∞

∞

∞

∞

====

++++

====

1

)

1

(

i

i

i

A

r

D

P

.

Pierwszy model zakłada, stałą w czasie, dywidendę. Można go stosować w od-
niesieniu do akcji spółek, które nie są zbyt rozwojowe i nie oczekujemy wzro-
stu ich zysków. Wtedy mamy

∑

∑

∑

∑

∞

∞

∞

∞

====

++++

====

1

)

1

(

i

i

A

r

D

P

.

Zauważmy, że w tym przypadku akcję można traktować jako rentę wieczystą
(przynajmniej z matematycznego punktu widzenia) i otrzymujemy

r

D

P

A

====

.

Zadanie . Oblicz cenę rynkową akcji bezterminowej, która daje dywidendę

30 zł, a stopa korzyści jest równa 17%.

Z ostatniego wzoru mamy:

0

30

176,5

0,17

P

=

=

=

=

=

=

=

=

zł.

W drugim modelu, zwanym modelem Gordona – Shapiro zakłada się stałe

tempo g wzrostu dywidendy, przy czym

r

g

<<<<

. Wtedy

i

i

g

D

D

)

1

(

0

++++

====

,

,...,

2

,

1

====

i

gdzie

0

D

oznacza właśnie wypłaconą dywidendę. Po podstawieniu do (1)

otrzymujemy

∑

∑

∑

∑

∞

∞

∞

∞

====

++++

++++

====

1

0

)

1

(

)

1

(

i

i

i

A

r

g

D

P

.

Zauważmy, że wtedy

0

1

A

g

P

D

r

g

++++

====

−−−−

,

bowiem z uwagi na

r

g

<<<<

mamy

1

1

1

<<<<

++++

++++

r

g

.

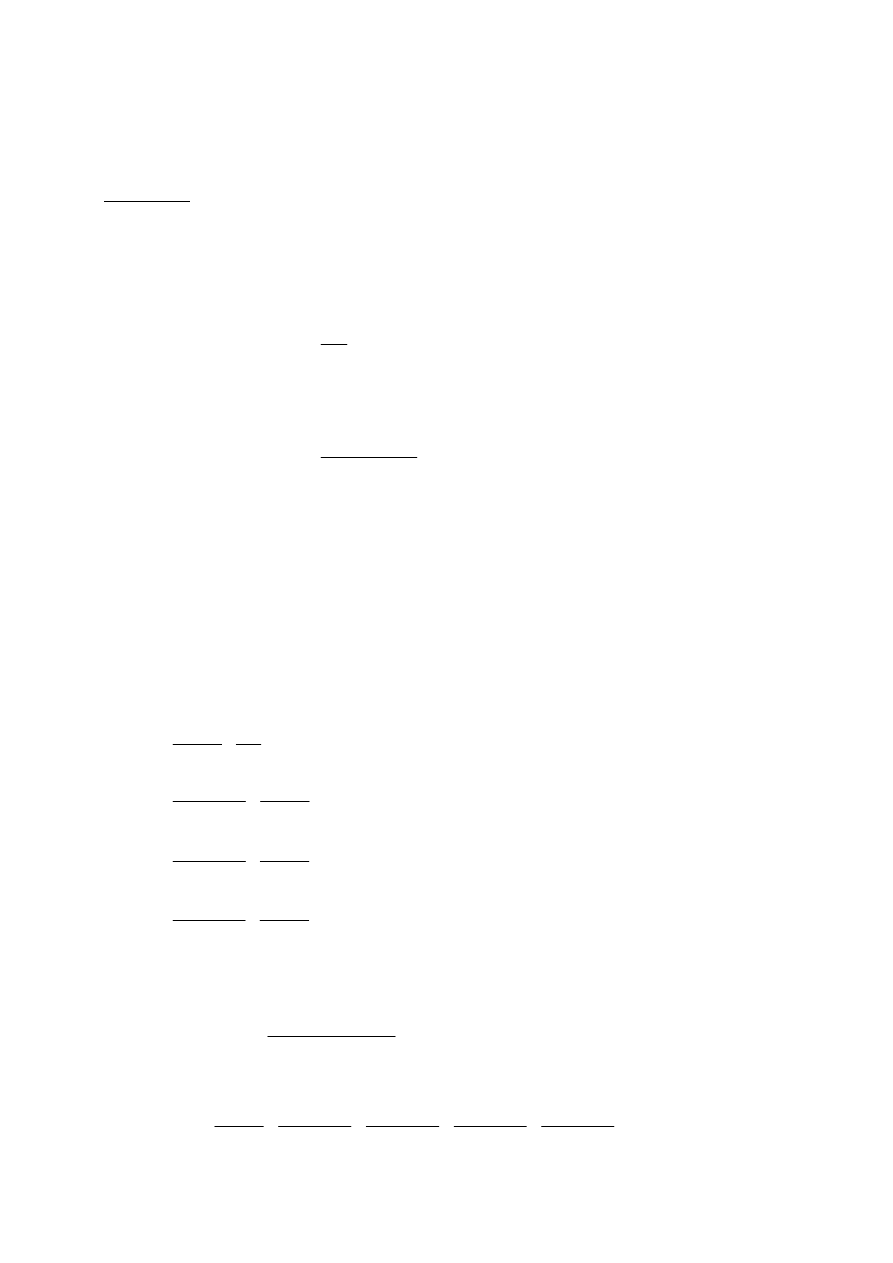
Oprócz dwóch, przedstawionych wyżej modeli stosuje się jeszcze inne, pocho-
dzące z „kombinowania” poznanych modeli. Można np. zakładać, że akcja
przez pewien czas daje stałą dywidendę, a następnie dywidendę rosnącą, itp.

Przykład. Rozważmy akcję zwykłą, którą inwestor zamierza trzymać bez-

terminowo. Wymagana stopa zwrotu wynosi 10%. W chwili obecnej firma
wypłaciła dywidendę w wysokości 50.
Przypuśćmy najpierw, ż dywidenda będzie wypłacana w stałej wysokości.
Wtedy

500

1

,

0

50

====

====

A

P

.

Jeśli natomiast założymy, że spółka będzie rozwijać się w stałym tempie, co
spowoduje wzrost dywidendy o 5% rocznie, to

1050

05

,

0

1

,

0

)

05

,

0

1

(

50

====

−−−−

++++

====

A

P

.

Załóżmy teraz, że dywidenda będzie rosłą w tempie 8% przez 4 lata, a następ-
nie cały czas w tempie 5%. Obliczamy wysokości czterech pierwszych dywi-
dend

54

)

08

,

0

1

(

50

1

====

++++

⋅⋅⋅⋅

====

D

32

,

58

)

08

,

0

1

(

54

2

====

++++

⋅⋅⋅⋅

====

D

99

,

62

)

08

,

0

1

(

32

,

58

3

≈≈≈≈

++++

⋅⋅⋅⋅

====

D

03

,

68

)

08

,

0

1

(

99

,

62

4

≈≈≈≈

++++

⋅⋅⋅⋅

====

D

i dyskontujemy je na chwilę obecną:

09

,

49

1

,

1

54

1

,

0

1

1

≈≈≈≈

====

++++

D

2

,

48

21

,

1

32

,

58

)

1

,

0

1

(

2

2

≈≈≈≈

====

++++

D

33

,

47

33

,

1

99

,

62

)

1

,

0

1

(

3

3

≈≈≈≈

====

++++

D

47

,

46

46

,

1

03

,

68

)

1

,

0

1

(

4

4

≈≈≈≈

====

++++

D

.

Ponieważ po czwartym roku dywidenda rośnie w stałym tempie możemy za-
stosować model Gordona – Shapiro

6

,

1428

05

,

0

1

,

0

)

05

,

0

1

(

03

,

68

1

≈≈≈≈

−−−−

++++

⋅⋅⋅⋅

====

A

P

.

Wartość dzisiejsza analizowanej akcji jest zatem równa

4

1

4

4

3

3

2

2

1

)

1

,

0

1

(

)

1

,

0

1

(

)

1

,

0

1

(

)

1

,

0

1

(

1

,

0

1

++++

++++

++++

++++

++++

++++

++++

++++

++++

====

A

A

P

D

D

D

D

P

.

Uwzględniając obliczone wcześniej wartości otrzymujemy

84

,

1166

≈≈≈≈

A

P

.

Z powyższych rozważań wynika, wartość dzisiejsza akcji zależy od preferencji
inwestora i przyjętego modelu.

Giełda

W tej części wykładu omówimy metody ustalania kursów akcji na giełdzie

oraz dokonamy przeglądu najważniejszych indeksów.

Obrót giełdowy akcjami na Giełdzie Papierów Wartościowych w War-

szawie odbywa się na różnych segmentach rynku giełdowego. Wyróżnia się
rynek podstawowy, równoległy oraz wolny. Rynek podstawowy to segment
rynku giełdowego, przeznaczony dla akcji o dużej płynności, których emitenci
charakteryzują się m. in. dużym kapitałem i długim okresem działalności. Ry-
nek równoległy jest przeznaczony dla akcji o niższej niż dla rynku podstawo-
wego płynności, których emitenci charakteryzują się m. in. mniejszym niż dla
rynku podstawowego kapitałem i krótszym okresem działalności. Natomiast
rynek wolny, to segment rynku giełdowego, na którym mogą być notowane
spółki dopuszczone do obrotu publicznego, które nie spełniają warunków do-
puszczenia do rynku podstawowego i równoległego. Wyróżnia się ponadto ry-
nek SiTech dla spółek tzw. nowej ekonomii, czyli spółek tworzących lub wy-
korzystujących innowacyjne technologie. Spółki już notowane na trzech gieł-
dowych rynkach, dodatkowo są prezentowane w segmencie SiTech.

Na Giełdzie Papierów Wartościowych w Warszawie, podobnie jak na in-

nych światowych giełdach, notowania odbywają się według dwóch systemów:
jednolitego i ciągłego. W systemie notowań kursu jednolitego cena papieru
wartościowego wyznaczana jest na podstawie zleceń zakupu i sprzedaży zło-
ż

onych przez maklerów przed rozpoczęciem notowań. Cena może być wyzna-

czana jednokrotnie lub dwukrotnie w ciągu dnia. Aby wziąć udział w sesji
giełdowej inwestorzy wystawiają zlecenia z określeniem limitu ceny (górnego
dla kupna lub dolnego dla sprzedaży), przy czym, limit ten nie może odbiegać
o więcej niż 10% od kursu dnia poprzedniego. W przypadku, gdy inwestor nie
określił takiego limitu mówi się o zleceniu po kursie dnia (PKD) i zlecenie ta-
kie oznacza zgodę na każdą ustaloną na sesji cenę. Kurs dnia ustala się w taki
sposób, aby mogło dojść do kupna – sprzedaży jak największej ilości danego
waloru. Ponadto muszą być spełnione następujące warunki:

•

zlecenia na zakup akcji z limitem wyższym niż wyznaczony kurs muszą
być zrealizowane w całości;

•

zlecenia na sprzedaż akcji z limitem niższym niż wyznaczony kurs muszą
być zrealizowane w całości;

•

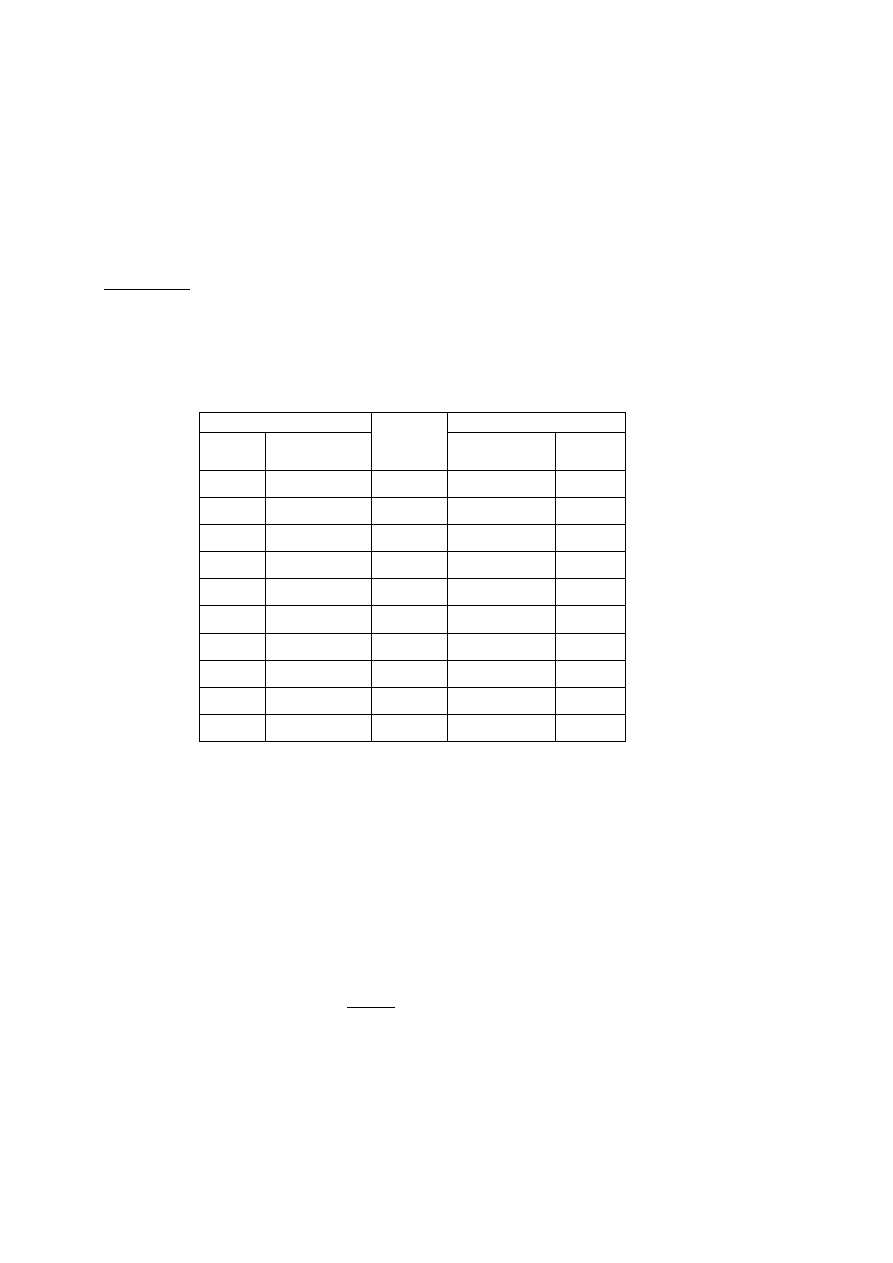
zlecenia zakupu i sprzedaży akcji bez określonego limitu ceny (PKD) mu-
szą być zrealizowane w całości;

•

zlecenia zakupu z limitem niższym oraz zlecenia sprzedaży z limitem wyż-
szym od ustalonego kursu pozostają bez realizacji.
Jeżeli nie jest możliwe takie ustalenie kursu, to mówimy o rynku niezrów-

noważonym.

Przykład. Na podstawie arkusza zleceń wyznaczymy kurs dnia pewnej ak-

cji. Z poniższej tabeli widzimy, że jeśli cena będzie ustalona na 10,4 to wła-
ś

ciciela zmienią jedynie 4 akcje. Podobnie, dla ceny 9,9 zostanie sprzedanych

jedynie 9 walorów. Analizując poszczególne pozycje tabeli zauważamy, że
dla kursu 10,1 obrót będzie maksymalny – 28 akcji.

Kupno

Limit
ceny

Sprzedaż

Liczba
akcji

Skumulowana
liczba akcji

Skumulowana
liczba akcji

Liczba
akcji

2

2

PKD

3

5

10,4

5

10

10,3

53

10

8

18

10,2

43

15

10

28

10,1

28

9

20

48

10

19

13

10

58

9,9

6

1

50

108

9,8

5

2

9,7

3

2

PKD

1

1

Zaprezentujemy teraz kilka najbardziej znanych światowych indeksów oraz

indeksy giełdy warszawskiej.

1.

Indeks Dow Jones Industrial Average (DJIA)
Jest to najpopularniejszy indeks giełdowy na świecie. Jest zmodyfikowaną
ś

rednią arytmetyczną 30 cen akcji wchodzących w jego skład. Oblicza się

go według wzoru:

t

i

t

i

t

d

P

DJIA

∑

∑

∑

∑

====

====

30

1

,

gdzie

t

DJIA

- wartość wskaźnika Dowa-Jonesa w chwili t,

t

i

P

- cena i – tej akcji w chwili t,

t

d

- dzielnik przyjęty chwili t.

Konieczność wprowadzenia dzielnika

t

d

wynika z tego, że czasem spółki,

których akcje występują w indeksie dokonują podziału akcji i fakt ten mógłby
spowodować nieuzasadnioną zmianę indeksu.

2.

Indeks Standard & Poor’s 500 (S&P 500).
Jest to jeden z najbardziej znanych indeksów giełdowych na świecie. skła-
dają się na niego akcje 500 spółek. Jest przykładem indeksu kapitałowo –
ważonego, tj. uwzględnia wartości rynkowe spółek, a nie jedynie ceny ak-
cji. Indeks SP oblicza się według wzoru:

∑

∑

∑

∑

∑

∑

∑

∑

====

====

⋅⋅⋅⋅

====

500

1

500

1

10

i

B

i

B

i

i

t

i

t

i

t

t

P

w

P

w

k

SP

, gdzie

t

SP

- wartość indeksu w chwili t,

t

k

- współczynnik korygujący (koryguje zmiany średniej nie związane
ze zmianą wartości rynkowej spółek, przykładowo, wynikające z
wprowadzenia nowej spółki na giełdę),

t

i

w

- liczba akcji i – tej spółki w momencie t,

B

i

w

- liczba akcji i – tej spółki w okresie bazowym,

t

i

P

- cena akcji i – tej spółki w momencie t,

B

i

P

- cena akcji i – tej spółki w okresie bazowym.

Okresem bazowym dla tego indeksu są lata 1941 – 43.

3.

Indeks Deutsche Aktienindex (DAX).

Najważniejszy indeks niemiecki. Jego wartość zależy od kursów 30 naj-

większych spółek giełdowych. Do obliczania jego wartości stosuje się for-
mułę kapitałowo – ważoną, analogiczną, jak w przypadku indeksu SP.
Momentem bazowym jest 30 grudnia 1987 r.

4.

Warszawski Indeks Giełdowy (WIG).
Główny indeks Giełdy Papierów wartościowych w Warszawie. Charakte-
ryzuje rynek podstawowy. Od 1993 roku liczony według formuły kapita-
łowo-ważonej:

∑

∑

∑

∑

∑

∑

∑

∑

====

====

⋅⋅⋅⋅

====

5

1

1

100

i

B

i

B

i

N

i

t

i

t

i

t

t

P

w

P

w

k

WIG

,

gdzie N jest liczbą wszystkich spółek notowanych na rynku podstawowym, a
pozostałe oznaczenia są takie jak poprzednio. Datą bazową jest pierwsza sesja
giełdowa z 16 kwietnia 1994 roku (notowano wtedy 5 spółek: Exbud, Kable,

Krosno, Próchnik, Tonsil). Wartość indeksu w okresie bazowym była ustalona
na 1000 punktów.

5.

Warszawski Indeks Giełdowy (WIG 20).
Indeks ten jest obliczany na podstawie akcji 20 spółek o największej war-
tości rynkowej największym obrocie. Oblicza się go według formuły kapi-
tałowo – ważonej , podobnie jak WIG. Momentem bazowym jest 16
kwietnia 1994, a wartością bazową – 100 punktów. Również charaktery-
zuje rynek podstawowy.

6.

Warszawski Indeks Rynku Równoległego (WIRR).
Charakteryzuje rynek równoległy, przy czym pod uwagę bierze się
wszystkie notowane tam spółki. Wyznaczany podobnie jak WIG. Datą ba-
zową jest 31 grudnia 1994, a wartością bazową – 1000 punktów.