LABORATORIUM 

PRZEPŁYWÓW PŁYNÓW 

I 

MIESZANIN WIELOFAZOWYCH 

  

 

 
 
 

 

 
 
 

 

Temat:

 Pomiar własności reologicznych płynów nienewtonowskich 

 

   
 
 
 

 

dr inż. Jerzy Wiejacha 

 

 

  
 
 
 
 
 
 
 
 
 
 
 

 

ZAKŁAD APARATURY PRZEMYSŁOWEJ 

POLITECHNIKA WASZAWSKA 

WYDZIAŁ BMiP 

 

PŁOCK 2002 

 

 

2 

1. Cel ćwiczenia 

 
- zapoznanie sposobu pomiaru własności teologicznych płynów nienewtonowskich, 
- wyznaczenie krzywej płynięcia cieczy Binghama

 

 
2. Podstawy teoretyczne 

 

  

 

Ponieważ  przepływ  jest  jedną  z  postaci  odkształcenia  ciał,  Reiner  i  Scott  Blair 

zaproponowali  następującą  definicji:  reologia  jest  nauką  o  odkształceniu  materii,  między 
innymi ojej przepływie.  

Reologia  jako  gałąź  fizyki  gałąź  fizyki  zajmuje  się  mechaniką  ciał  rzeczywistych, 

ulegających odkształceniu pod działaniem sił zewnętrznych. Celem reologii jest umiejętność 
przewidywania  układu  sił,  który  spowoduje  określone  odkształcenie  lub  odwrotnie  - 
przewidywanie odkształcenia wynikającego z przyłożenia określonego układu sił.  

Reologię dzielimy na mikro- i makroreologię. Mikroreologia, stanowiąca przedmiot 

zainteresowań fizykochemików, zajmuje się związkami, jakie występują między rzeczywistą 
strukturą  
   

2.1. Odkształcenie 

 

Pod działaniem sił zewnętrznych wszystkie ciała rzeczywiste ulegają odkształceniu 

(deformacji). Odkształceniem nazywamy zmianę wzajemnego położenia elementów ciała.  
   

2.1.1  Odkształcenie sprężyste, plastyczne i przepływ 

   

Odkształcenia  mogą  być  podzielone  na  trzy  rodzaje:  odkształcenia  sprężyste, 

odkształcenia plastyczne, przepływ.  
   

Odkształcenie  nazywamy  sprężystym,  gdy  jest  ono  samorzutnie  odwracalne,  tzn. 

gdy zanika natychmiast i całkowicie po ustaniu działania siły.  
   

W  przeciwieństwie  do  odkształcenia  sprężystego,  odkształcenie  plastyczne  jest 

nieodwracalne.  Nie  zanika  ono  po  ustaniu  działania  siły.  Energia  zużyta  na  odkształcenie 
plastyczne ulega rozproszeniu (dyspersji), czyli zmianie na energię cieplną. 
 

Przepływem  nazywamy  nieodwracalne  odkształcenie,  którego  stopień  -  pod 

działaniem sił o ograniczonej wartości - wzrasta ciągle z upływem czasu. Energia zużyta na 
wymuszenie przepływu ulega rozproszeniu.  
   

2.1.2 Odkształcenie objętościowe i postaciowe 

   

Odkształcenie,  które  zmienia  jedynie  objętość  ciała  -  bez  zmiany  jego  kształtu  - 

nazywamy odkształceniem objętościowym. W wyniku np. wzrostu ciśnienia ciało o kształcie 
kuli  zmniejszy  swoją  objętość,  lecz  zachowa  kształt  kulisty.  Odkształcenie  objętościowe 
powodujące  zmniejszenie  objętości  nazywamy  kompresją,  zaś  powodujące  zwiększenie 
objętości - dylatacją.  

Drugim  prostym  rodzajem  odkształcenia  jest  odkształcenie  postaciowe.  Powoduje 

ono  zmianę  kształtu  ciała  bez  zmiany  jego  objętości  (oczywiście  gęstość  ciała  nie  ulega 
wówczas  zmianie).  Najprostszym  z  kolei  przypadkiem  odkształcenia  postaciowego  jest  tzw. 
ścianie proste.  
 

 

 

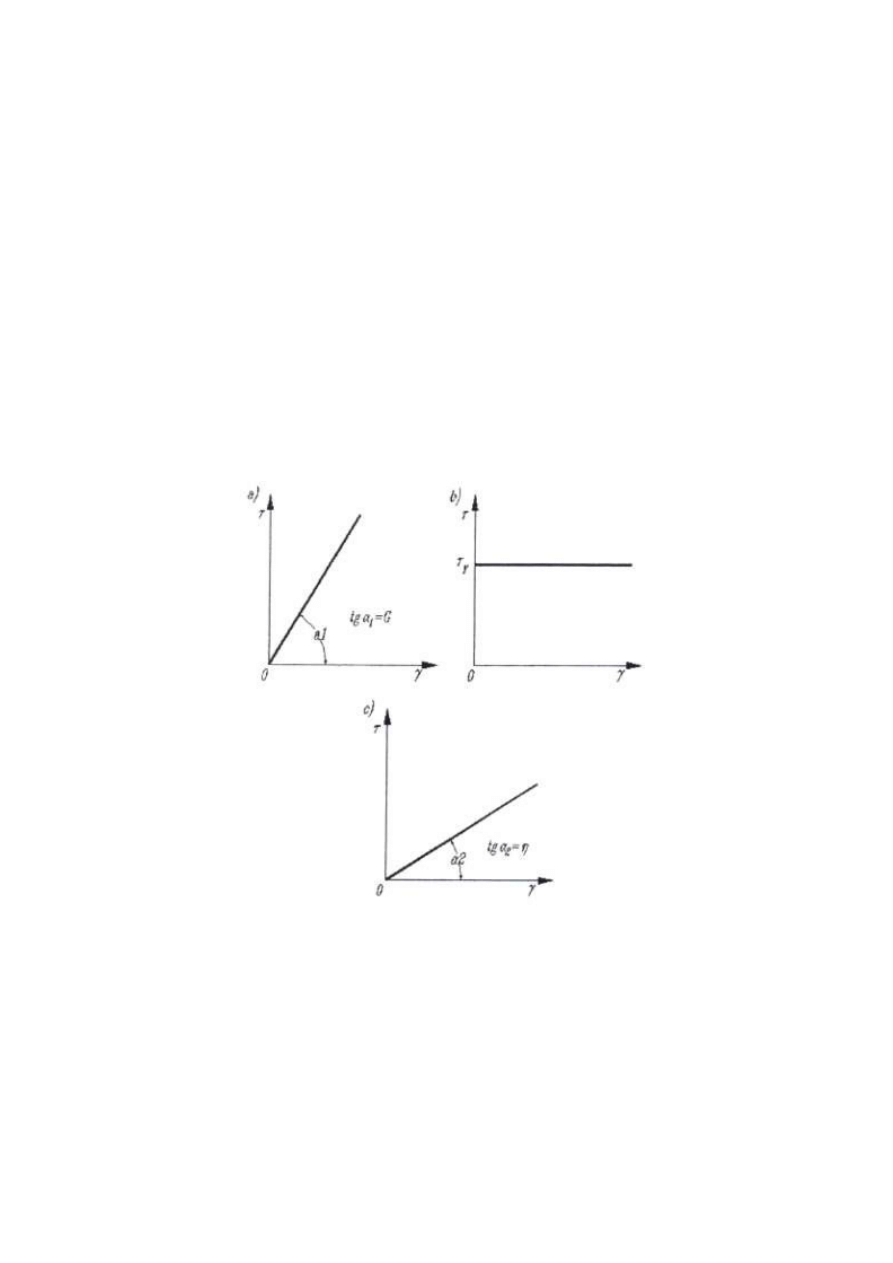
3 

2.2. Reologiczne ciała doskonałe

 

 

Zgodnie  z  drugim  aksjomatem  reologii  każde  ciało  rzeczywiste  ma  wszystkie 

możliwe własności reologiczne  ujawnia je tylko w różnym stopniu, zależnie od konkretnych 
warunków. Stąd nie możemy nigdy o ciele rzeczywistym mówić w sposób zupełnie ścisły, że 
ma określone własności reologiczne. Oczywiste jest, że ciała doskonałe w rzeczywistości nie 
istnieją. 

Ciała  doskonałe  definiowane  są  za  pomocą  odpowiednich  reologicznych  równań 

stanu 

(zwanych 

także 

po 

prostu 

równaniami 

reologicznymi 

lub 

równaniami 

konstytutywnymi).  Reologiczne  równanie  stanu  podaje  zależność  między  naprężeniem, 
odkształceniem  i  czasem,  zaś  parametry  występujące  w  tym  równaniu  definiują  własności 
reologiczne danego ciała.  
 

W określonych warunkach własności reologiczne ciał rzeczywistych przybliżane są 

przez matematyczne modele reologiczne:  
a) ciało doskonale sprężyste Hooke'a,  
b) ciało doskonale plastyczne St. Venanta,  
c) płyn doskonale lepki Newtona.  
 

 

Rys. l Wykresy reologiczne:  

a) ciała sprężystego Hooke'a, b) ciała plastycznego St. Venanta, c) płynu lepkiego Newtona. 

   
 

2.3. Płyny newtonowskie i nienewtonowskie

 

 

Za  pomocą  przedstawionej  w  poprzednim  rozdziale  koncepcji  płynu  doskonale 

lepkiego  Newtona,  czyli  płynu  newtonowskiego,  opisać  można  własności  reologiczne  wielu 
układów  rzeczywistych.  Są  to  płyny,  w  których  lepkie  rozpraszanie  energii  następuje  w 
wyniku zdarzeń stosunkowo małych cząsteczek. 

Wykres reologiczny płynu newtonowskiego sporządzony w układzie współrzędnych 

naprężenie styczne 

ττττ jako funkcja szybkości ścinania γγγγ. Wykres zależności ττττ=ƒƒƒƒ(γγγγ) nazywamy 

 

 

4 

krzywą  płynięcia.  Jak  wiadomo,  krzywa  płynięcia  płynu  newtonowskiego  jest  linią  prostą 
przechodzącą przez początek układu współrzędnych (rys. lc). 

Wszystkie  płyny,  dla  których  krzywa  płynięcia  -  w  ustalonych  warunkach 

temperatury  i  ciśnienia  -  nie  jest  linią  prostą  przechodzącą  przez  początek  układu 
współrzędnych, nazywamy płynami nienewtonowskimi.  
 

2.3.1 Ogólna klasyfikacja płynów nienewtonowskich  

 

Płynami nazwać będziemy wszystkie substancje, które płyną: a więc zarówno gazy i 

ciecze,  jak  również  te  ciała  stałe,  które  w  pewnych  -  łatwych  do  zrealizowania  warunkach 
wykazują przepływ. 
 
Płyny nienewtonowskie zwykle dzieli się na trzy następujące podstawowe grupy:  
a) Płyny reostabilne, których własności reologiczne nie zależą od czasu ścinania.  
b) Płyny reologicznie niestabilne, których własności reologiczne zależą od czasu ścinania.  
c)  Płyny  sprężystolepkie,  łączące  własności  reologiczne  płynów  lepkich  i  ciał  stałych 

sprężystych. Wykazują one częściowy powrót sprężysty po usunięciu naprężenia stycznego 
powodującego odkształcenie.  

   

2.3.2 Model cieczy Binghama 

   

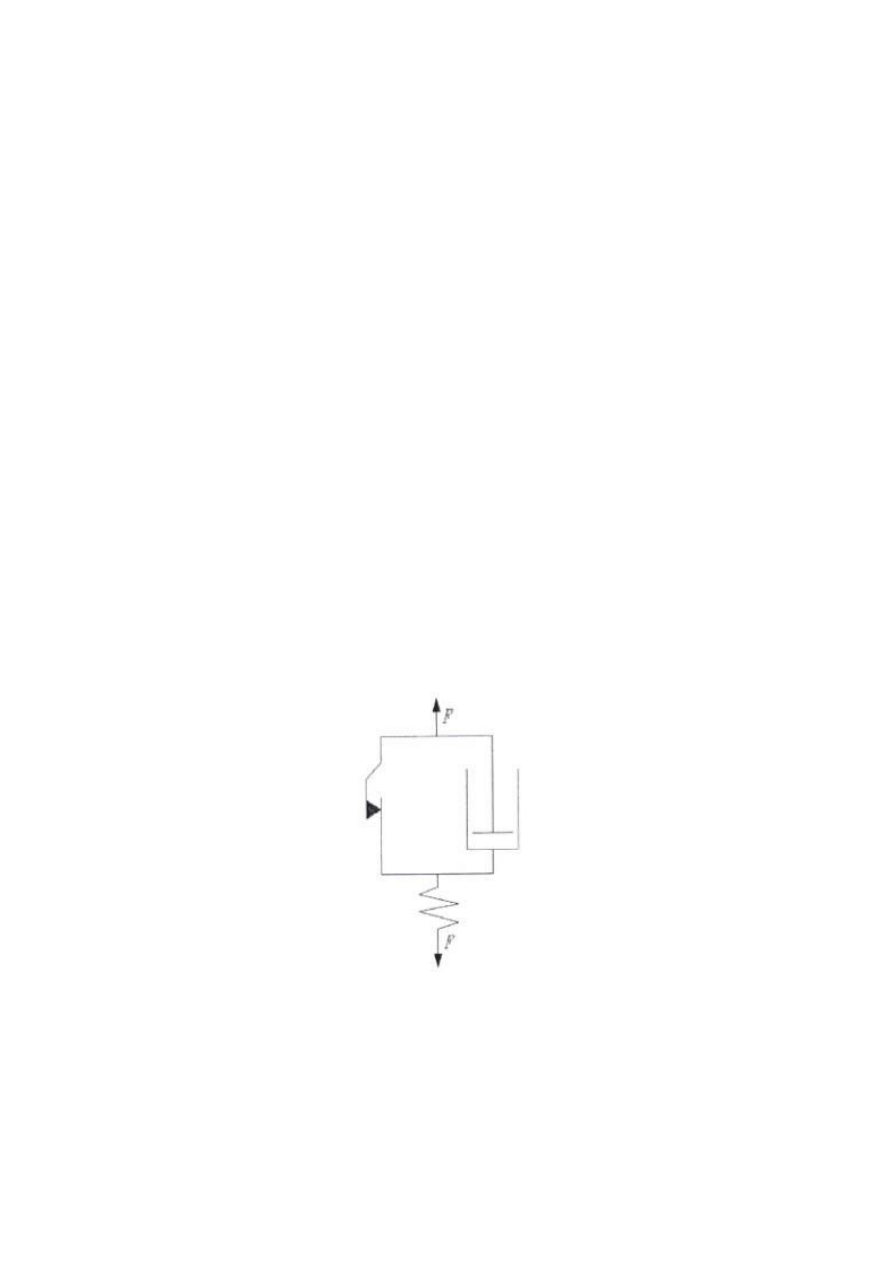
Model  ten  skład  się  z  trzech  elementów.  Do  układu,  zbudowanego  z  równolegle 

połączonych elementów  St. Venanta i Newtona dołączony jest szeregowo element Hooke'a. 
Jest to model ciała, które przy niskich naprężeniach stycznych zachowuje się jak ciało stałe, 
przy wysokich zaś - jak ciecz. Poniżej bowiem pewnej wartości przyłożonej siły odkształcać 
się będzie sprężyna, czyli cały model będzie analogią ciała sprężystego Hooke'a. Dopiero po 
przekroczeniu granicznej wartości, równej sile tarcia stycznego elementu St. Venanta, model 
znacznie  się  wydłużać  (płynąć),  przy  czym  szybkość  odkształcenia  będzie  wprost 
proporcjonalna do różnicy między przyłożoną siłą a siłą tarcia elementu St. Venanta.  

 

Rys. 2 Model mechaniczny ciała Binghama. 

   

Z powyższej analizy modelu mechanicznego wynika, że reologiczne równanie stanu 

ciała  Binghama  -  dla  naprężeń  stycznych  większych  od  naprężenia  granicznego 

ττττ

y

  - 

przybierze postać  

 

 

 

(1)  

 

 

lub 

(2) 

γ

η

τ

τ

p

y

+

=

g

h

t

t

p

y

=

−

 

 

5 

gdzie: 

ηηηη

p 

oznacza  współczynnik  proporcjonalności  w  równaniu  wyżej  zwany  lepkością 

plastyczną, N s/m

2

. 

 
2.4. Płyny reostabilne

 

 

Płyny reostabilne można podzielić z kolei na: rzeczywiste płyny nie mające granicy 

płynięcia (tzn. granicznego naprężenia stycznego 

ττττ

y 

) oraz ciała stałe zachowujące się jak płyn 

dopiero po przekroczeniu tej granicy. 
 

2.4.1 Płyny nie mające granicy płynięcia 

 

Płyny lepkie nie mające granicy płynięcia noszą nazwę płynów Stokesa. 

Z  fenomenologicznego  punktu  widzenia  płyn  Stokesa  może  zachować  się,  w  warunkach 
laminarnego ścinania, w różny sposób: 
a)  może  występować  prosta  proporcjonalność  między  naprężeniem  stycznym  a  szybkością 

ścinania - mamy wówczas do czynienia z płynem newtonowskim; 

b) dwukrotny wzrost naprężenia stycznego może spowodować więcej niż dwukrotny wzrost 

ścinania - mamy wówczas do czynienia ze zjawiskiem rozrzedzenia ścinaniem (ang. shear 
thinning); 

c)  dwukrotny  wzrost  naprężenia  stycznego  może  spowodować  mniej  niż  dwukrotny  wzrost 

szybkości ścinania - będzie to zjawisko zagęszczania ścinaniem (ang. shear thickening). 

 

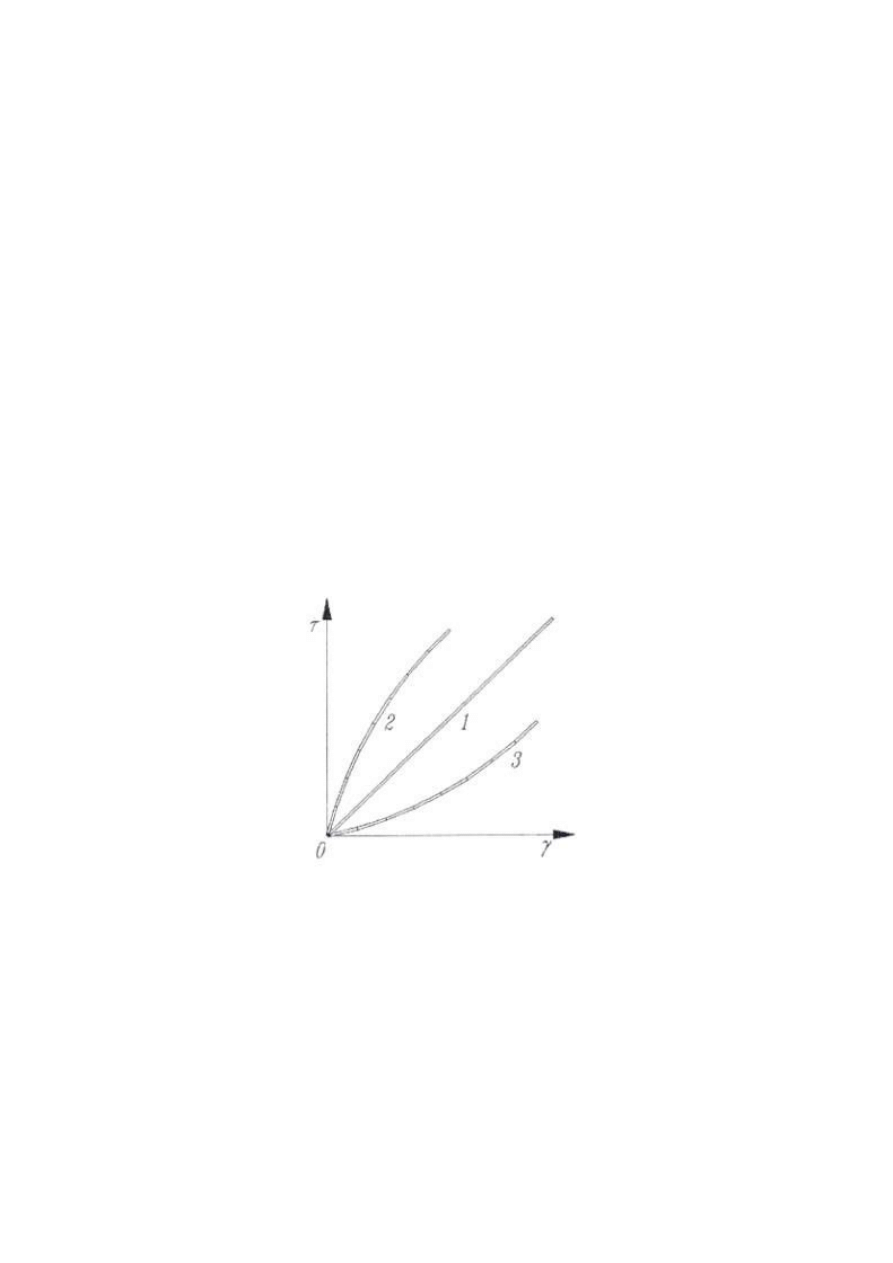
Krzywe  płynięcia  dla  powyższych  trzech  przypadków,  w  układzie  współrzędnych    

ττττ = ƒƒƒƒ ( γγγγ  ) przedstawiono na wykresie rys. 3. 

 

Rys.3 Krzywe płynięcia płynów reostabilnych nie wykazujących granicy płynięcia: 

l- płyn newtonowski, 2 - płyn rozrzedzany ścinaniem, 3 - płyn zagęszczany ścinaniem. 

 

2.4.2 Płyny rozrzedzane ścinaniem 

 

Płyny 

rozrzedzane 

ścinaniem 

stanowią 

najliczniejszą 

grupę 

płynów 

nienewtonowskich.  Z  punktu  widzenia  częstości  występowania  zajmują  one  drugie  miejsce 
bezpośrednio  po  płynach  newtonowskich.  Ponieważ  obie  kategorie  płynów  wykazywały 
pewne  wspólne  cechy  (ich  lepkość  pozorna  malała  ze  wzrostem  szybkości  ścinania) 
omawiane  płyny  nazywano  pseudoplastycznymi.  W  niemieckiej  literaturze  przedmiotu 
stosowane jest określenie ciecze o lepkości strukturalnej wprowadzone przez Wo. Ostwalda. 
Rainer  zaproponował  dla  tych  układów  nazwę  uogólnione  płyny  newtonowskie  i  termin  ten 
przyjął się w literaturze. 
 

 

 

6 

 

Rys.4 Krzywa płynięcia uogólnionego płynu newtonowskiego według Ostwalda. 

 

Krzywą  płynięcia  uogólnionych  płynów  newtonowskich  według  Ostwalda 

przedstawiono na wykresie rys.4; ma ona cztery charakterystyczne zakresy: 
a)  W  zakresie  małych  szybkości  ścinania  występuje  stały  stosunek  naprężenia  stycznego  do 

szybkości  ścinania,  czyli  układ  zachowuje  się  jak  płyn  newtonowski  o  stałej  lepkości 

ηηηη

o

. 

Wielkość 

ηηηη

o 

jest więc graniczną lepkością układu przy szybkości ścinania dążącej do zera. 

b) 

W 

zakresie 

pośrednich 

szybkości 

ścinania 

występuje 

obszar 

przepływu 

nienewtonowskiego. Stosunek naprężenia stycznego do szybkości ścinania w tym obszarze 
nie  jest  stały.  Ten  zmienny  stosunek  -  przez  analogię  do  definicji  lepkości  dynamicznej 
układów newtonowskich gdzie 

ηηηη = ττττ ⁄⁄⁄⁄ γγγγ =CONST - nazywać będziemy lepkością pozorną i 

oznaczać symbolem 

ηηηη

’ 

 

(3) 

 

W  omawianym  zakresie  lepkość  pozorna  uogólnionego  płynu  newtonowskiego 

maleje ze wzrostem szybkości ścinania. 
c)  Przy  bardzo  dużych  szybkościach  ścinania  (np.  rzędu  l0

5

-10

6

s

-1

)  występuje  drugi  obszar 

przepływu newtonowskiego. Nachylenie krzywej płynięcia jest tu ponownie stałe. 

d)  Powyżej  pewnej  granicznej  szybkości  ścinania  występuje  charakterystyczny  wzrost 

nachylenia krzywej płynięcia zawiązany z pojawieniem się turbulencji. 

 

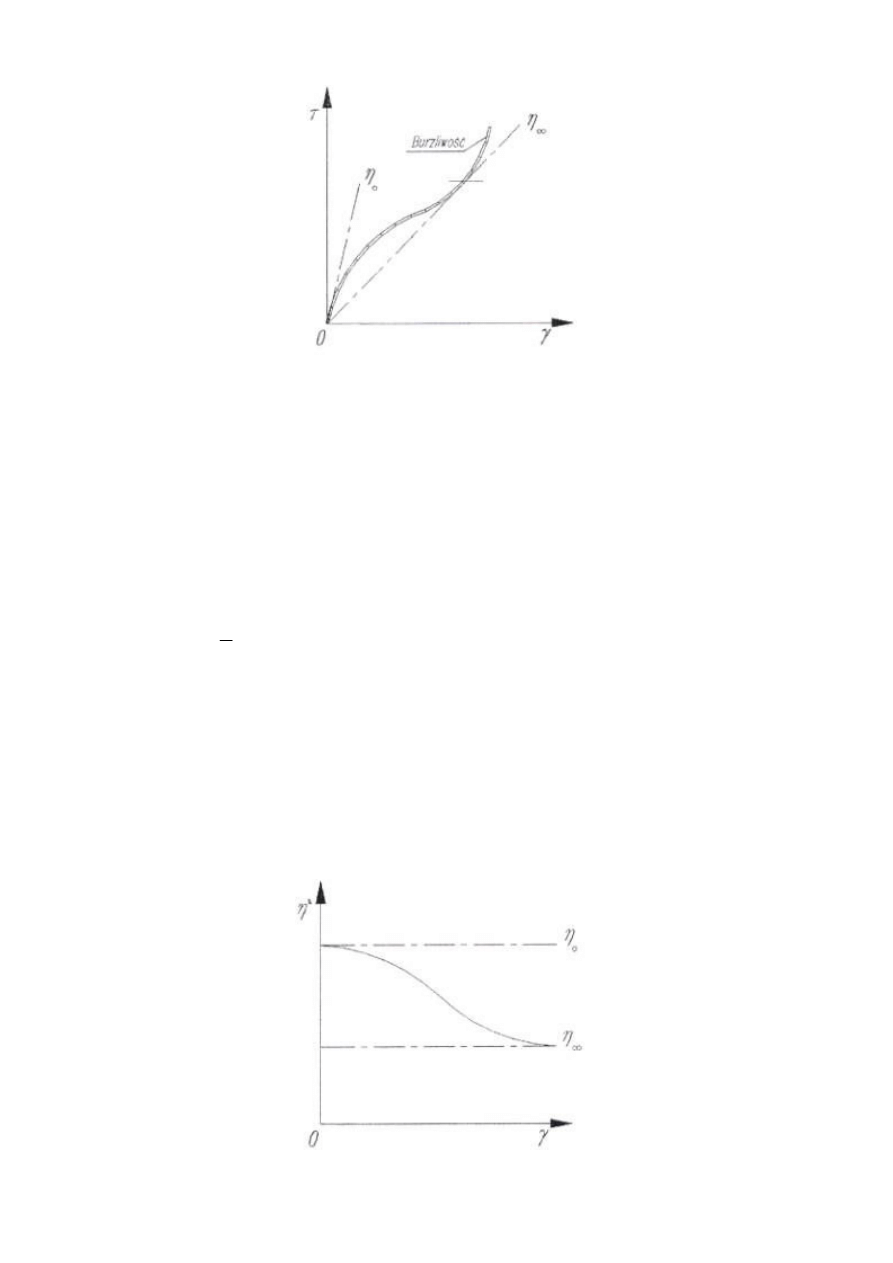
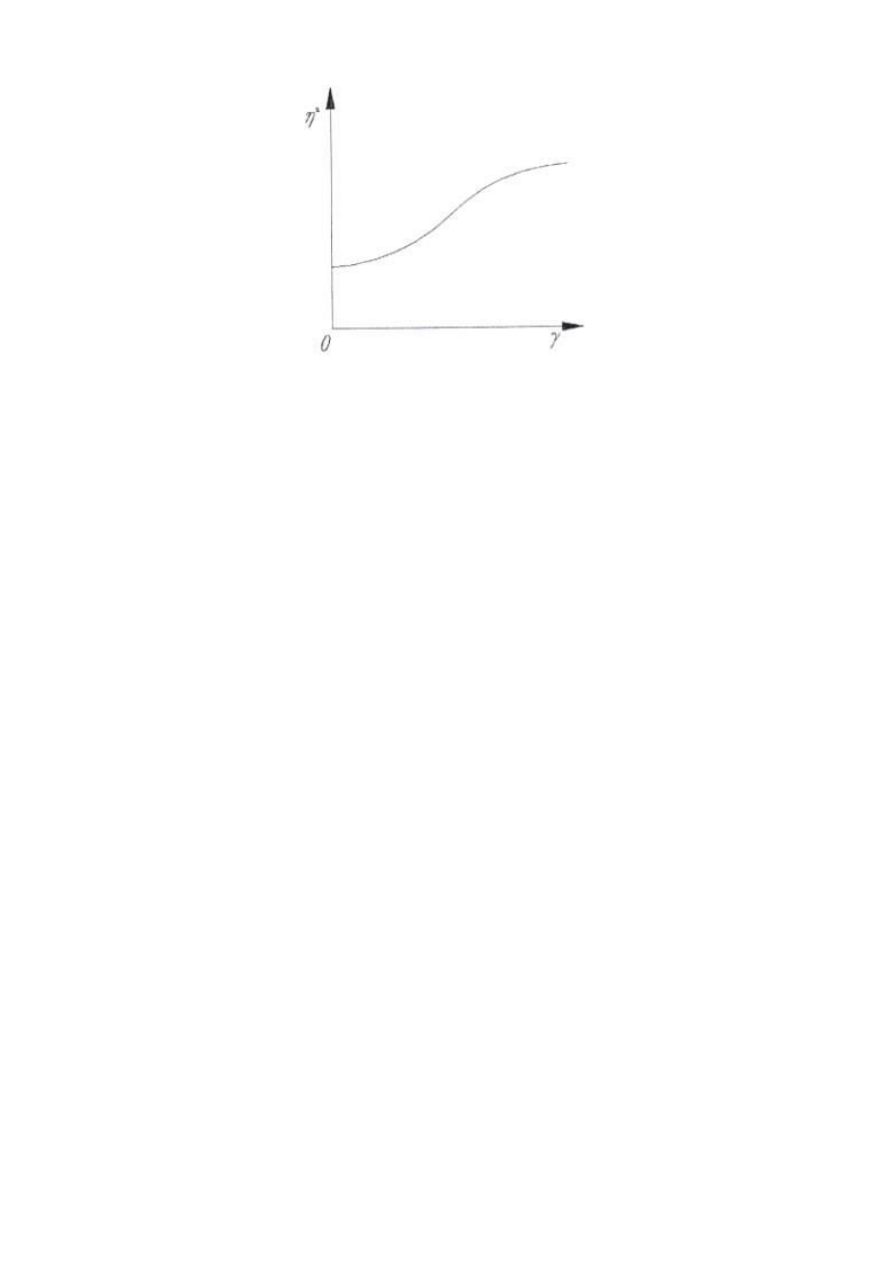
Drugi sposób przedstawienia powyższych zależności polega na wykreśleniu krzywej 

lepkości  pozornej 

ττττ  w  funkcji  ścinania  γγγγ.  Wykres  taki  dla  uogólnionego  płynu 

newtonowskiego pokazano na rys. 5. 

 

const

≠

=

γ

τ

η

'

 

 

7 

Rys.5 Zależność lepkości pozornej od szybkości ścinania dla uogólnionych płynów 

newtonowskich. 

 

W  literaturze  przedmiotu  podejmowane  były  bardzo  liczne  próby  opisu  krzywej 

płynięcia  uogólnionego  płynu  newtonowskiego  odpowiednim  matematycznym  modelem 
reologicznym . 

Najprostszym  matematycznym  modelem  reologicznym,  opisującym  krzywą 

płynięcia  uogólnionych  płynów  newtonowskich  w  zakresie  pośrednich  szybkości  ścinania, 
jest  tzw.  model  potęgowy,  zaproponowany  przez  Ostwalda  i  de  Wale.  Wyniknął  on  z 
doświadczalnie  stwierdzonego  faktu,  że  dla  omawianych  płynów  zależność  naprężenia 
stycznego  od  szybkości  ścinania,  przedstawiona  na  wykresach  sporządzonych  w  podwójnie 
logarytmicznym układzie współrzędnych 

(4) 

 
daje się często przybliżyć linią prostą w 100 do 1000-krotnym zakresie szybkości ścinania.  

Wskazuje to na potęgową zależność typu: 

(5) 

 

gdzie stała  k (N s

n 

/ m

2

)i wykładnik potęgi n są parametrami reologicznymi wyznaczonymi 

doświadczalnie dla danego układu. 

Dla  omawianych  płynów  wykładnik  potęgi  ma  wartość  n  <  l.  Zauważmy,  że 

podstawiając do wyrażenia (3) zależność na naprężenie styczne (5) otrzymamy 

 

(6) 

 

Wynika stąd, że dla parametru n < 1 lepkość pozorna maleje ze wzrostem szybkości 

ścinania. 

Model  potęgowy  Ostwalda  -  de  Waele  (5)  jest  najprostszym  matematycznym 

modelem reologicznym uogólnionego płynu newtonowskiego, zawierającym tylko dwie łatwe 
do wyznaczenia stałe. Przeciwko modelowi temu wysuwane są jednak następujące zarzuty; 
a)  Miano  współczynnika  k  zależy  od  wykładnika  potęgi  n  gdyż  k  ma  wymiar 

(siła)·(czas)

n

/(długość)

2

. Dla różnych substancji współczynnik k zmienia się więc nie tylko 

ilościowo,  lecz  także  jakościowo,  a  parametry  reologiczne  n  i  k  mają  sens  fizyczny  tylko 
wówczas, gdy są rozpatrywane łącznie. 

b)  Jeżeli  wyznaczamy  lepkość  pozorną  korzystając  z  zależności  (6),  to  zauważymy,  że  w 

przypadku n < 1 

ηηηη’ →

→

→

→ ∞

∞∞

∞ 

 

dla 

γγγγ →

→

→

→ 0 

zaś 

(7) 

ηηηη’ →

→

→

→ 0000  

 

dla 

γγγγ →

→

→

→ ∞

∞∞

∞ 

Jak  wynika  to  z  krzywej  płynięcia  Ostwalda  oba  wnioski  są  sprzeczne  z 

doświadczeniem. 

Na podstawie powyższych zarzutów Reiner stwierdził, że model potęgowy nie jest 

reologicznym  równaniem  stanu,  lecz  jedynie  empiryczna  formuła  interpolacyjną,  którą 
przestaje być słuszna poza zakresem interpolacji. 
 

2.4.3 Płyny zagęszczone ścinaniem 

 

Płynami zagęszczonymi ścinaniem nazywamy układy, których lepkość pozorna 

ηηηη’- 

w stałej temperaturze - nie maleje, lecz rośnie odwracalnie ze wzrostem szybkości ścinania 

γγγγ 

(nie wykazując przy tym dającej się zmierzyć zależności od czasu ścinania). Krzywą 

ηηηη’= f (γγγγ) 

przedstawiono dla tej kategorii płynów na wykresie rys. 6.  

(

)

γ

τ

log

log

f

=

( )

n

k

γ

τ =

( )

( )

n

n

k

k

−

=

=

1

'

γ

γ

γ

η

 

 

8 

 

Rys.6 Zależności lepkości pozornej od szybkości ścinania dla płynów reostabilnych bez 

granicy płynięcia wykazujących zjawisko zagęszczenia ścinaniem. 

 

Krzywą  płynięcia  układu  zagęszczonego  ścinaniem  (rys.  3)  można  na  ogół,  w 

dużym  zakresie  pośrednich  szybkości  ścinania  opisać  podobną  uprzednio  zależnością 
potęgową  (5).  Parametr  reologiczny  n  przybiera  wówczas  wartości  liczbowe  większe  od 
jedności n > 1. Oznacza to, że lepkość pozorna 

(8) 

 

rośnie ze wzrostem szybkości ścinania. 

 
2.4.4 Płyny mające granicę płynięcia 

 

Płyny  reostabilne  mające  granicę  płynięcia  nazywać  będziemy  płynami  plastyczne 

lepkimi.  Występowanie  w  tych  układach  granicznego  naprężenia  stycznego,  poniżej  którego 
substancja zachowuje się jak ciało stałe, wyjaśnimy w sposób następujący: 

W układzie dyspersyjnym, w którym jedna lub więcej faz jest rozproszona w postaci 

cząstek  lub  pęcherzyków  w  ośrodku  ciągłym,  tworzy  się  struktura  odporna  na  naprężenia 
styczne nie przekraczające wartości granicznej 

ττττ

y 

. Im bardziej cząstki dyspersyjne przylegają 

do  siebie,  tzn.  im  bardziej  sztywna  jest  struktura,  tym  większa  jest  wartość  naprężenia 
granicznego 

ττττ

y 

. Po przekroczeniu granicy płynięcia struktura ulega całkowitemu zniszczeniu i 

układ  zachowuje  się  jak  ciecz,  na  którą  działa  naprężenie  styczne  równe  różnicy  miedzy 
rzeczywistym naprężeniem i naprężeniem granicznym 

ττττ

y 

. Z kolei przy obniżeniu naprężenia 

stycznego  poniżej  wartości 

ττττ

y 

zakładamy,  że  struktura  ulega  natychmiastowej  odbudowie 

(układ jest bowiem reostabilny). 

( )

1

'

−

=

n

k

γ

η

 

 

9 

 

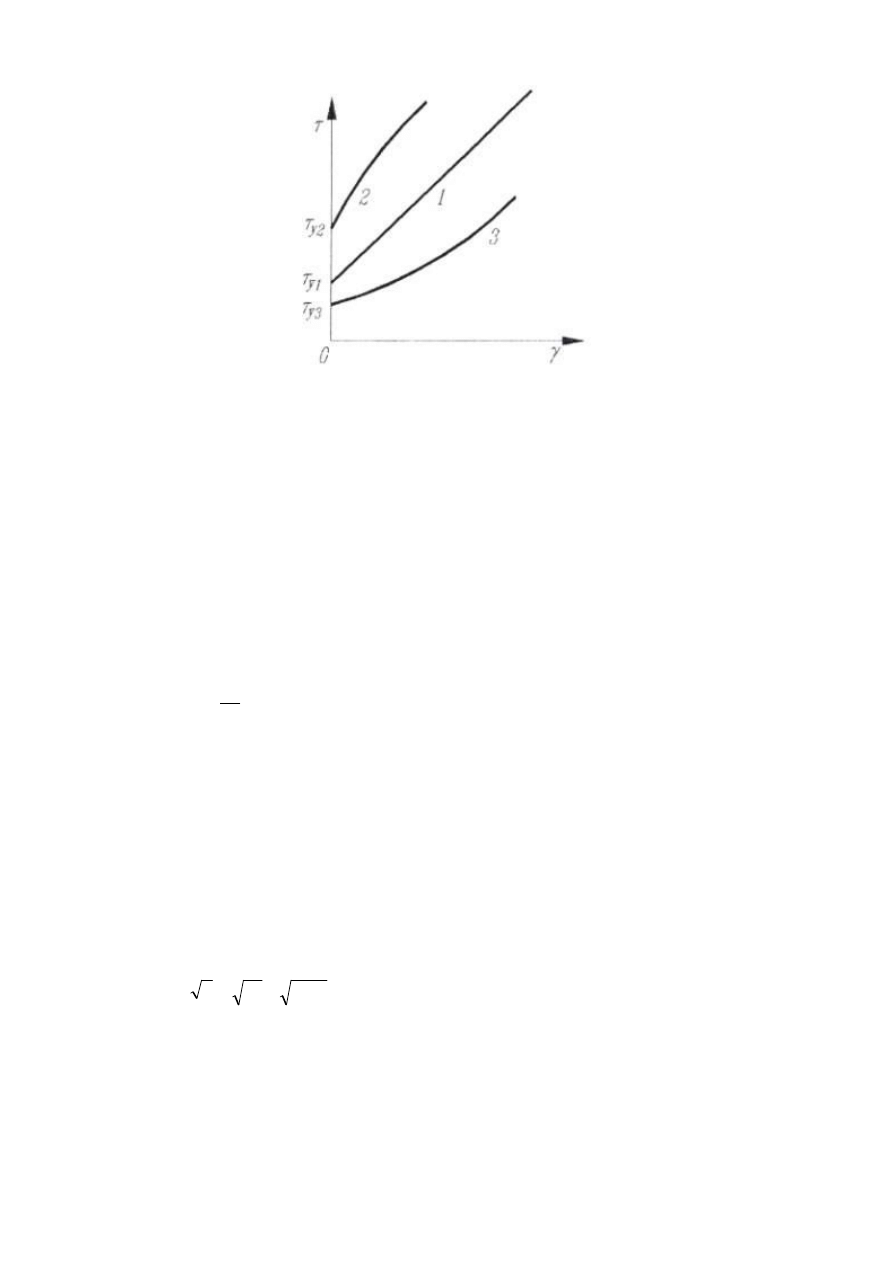
Rys.7 Krzywe płynięcia płynów reostabilnych wykazujących granicę płynięcia 

l-płyn plastycznolepki Binghama, 2,3 - nieliniowe płyny plastycznolepkie. 

 

Krzywe  płynięcia  omawianych  układów  przy  naprężeniach  stycznych 

ττττ  >  ττττ

Y  

przedstawiono  na  wykresie  (rys.  7).  Prosta  l  na  tym  wykresie  reprezentuje  własności 
reologiczne ciała doskonałego Binghama. Zależność 

ττττ = f ( γγγγ ) da się w tym przypadku opisać 

podanym uprzednio równaniem reologicznym (2) 

(9) 

 
gdzie granica płynięcia 

ττττ

y

, N/m

2 

oraz wielkość 

ηηηη

p

, N s/m

2

, nazywana lepkością plastyczną, są 

parametrami reologicznymi określonymi doświadczalnie. 

W 

przeciwieństwie 

do 

lepkości 

plastycznej, 

lepkość 

pozorna 

płynu 

plastycznolepkiego  Binghama  (jak  każdego  płynu  nienewtonowskiego)  nie  jest  wielkością 
stałą. Zgodnie z definicją lepkości pozornej - wzór (3) - można ją wyrazić jako: 
 

(10) 

 

Wynika  stąd,  że  w  omawianym  przypadku  lepkość  pozorna  maleje  ze  wzrostem 

szybkości ścinania. 

Krzywe płynięcia tzw. nieliniowych płynów plastycznolepkich przedstawiono na rys. 

7  (krzywa  2  i  3).  Według  Van  Wazera  i  innych  o  charakterze  przepływu  po  przekroczeniu 
granicy płynięcia decydują często własności reologiczne ośrodka rozpraszającego. 
Najprostszym 

modelem 

opisującym 

własności 

reologiczne 

nieliniowych 

płynów 

plastycznolepkich jest model Herschela i Bulkleya 

(11) 

 

gdzie granica płynięcia 

ττττ

y

, N/m

2 

oraz wielkości 

ηηηη

pm

, N

m

s/m

2m   

i bezwymiarowa wielkość m, 

występująca w wykładniku potęgi, są to parametry reologiczne określone doświadczalnie. 
Casson zaproponował dla omawianych układów wzór w postaci 

(12) 

 
gdzie 

ττττ

y

, N/m

2 

i 

ηηηη

p2

, N s/m

2 

są to parametry reologiczne. 

W  przypadku  niektórych  układów  okazuje  się,  że  model  Cassona  (12)  z 

wykładnikiem  potęgi  1/2  nie  opisuje  zadowalająco  doświadczalnych  krzywych  płynięcia. 
Lepsze rezultaty uzyskuje się, jeżeli wykładnik potęgi ma inną wartość liczbową. Prowadzi to 
do następującego uogólnienia modelu Cassona 

(13) 

 

γ

η

τ

τ

P

Y

+

=

P

Y

η

γ

τ

η

+

=

'

( )

m

pm

y

/

1

γ

η

τ

τ

+

=

γ

η

τ

τ

2

p

y

+

=

( )

n

pn

n

y

n

/

1

/

1

/

1

γ

η

τ

τ

+

=

 

 

10 

przy  czym  miano  parametrów  reologicznych 

ττττ

y 

i 

ηηηη

pn 

nie  ulega  zmianie,  zaś  trzecim 

parametrem reologicznym jest bezwymiarowa wielkość n. 

 
3.  Ogólne  zasady  pomiaru  własności  reologicznych  płynów  nienewto-

nowskich 

 

Własności  reologiczne  płynów  charakteryzują  ich  zachowanie  się  w  czasie 

przepływu  i  tylko  w  warunkach  przepływu  mogą  być  mierzone.  Ogólne  zasady  reometrii 
płynów  nienewtonowskich  wynikają  z  ich  specyficznych  cech,  dyskusję  nad  tymi  zasadami 
podzielmy je na dwa etapy. 
 
a) płyny nie wykazujące efektów naprężeń normalnych 
 

Do kategorii płynów nie wykazujących efektów naprężeń normalnych należą płyny 

nienewtonowskie  reostabilne  oraz  reologicznie  niestabilne.  Do  pomiaru  własności 
reologicznych tych układów stosujemy metody wiskozymetryczne.  

Większość  jednak  wiskozymetrów,  stosowanych  w  laboratoriach  do  pomiaru 

lepkości  cieczy  newtonowskich,  jest  nie  przydatna  do  określenia  własności  reologicznych 
płynów  nienewtonowskich.  Ze  względu  na  cechy  konstrukcyjne  nie  jest  możliwe 
równoczesne  określenie  naprężenia  stycznego  i  szybkości  ścinania  w  jakimkolwiek  punkcie 
tego przyrządu (wiskozymetry takie nazywamy porównawczymi). 

Aby określić rzeczywistą wartość naprężenia stycznego i szybkości ścinania musimy 

dysponować  tzw.  przyrządem  absolutnym.  W  przyrządzie  absolutnym  dokonujemy 
oznaczenia na podstawie znajomości praw fizycznych opisujących występujący w przyrządzie 
przepływ  oraz  na  znajomość  geometrii  przyrządu.  Najczęściej  stosowane  w  wiskozymertii 
cieczy  newtonowskich  wiskozymetry  absolutne  dają  jednak  tzw.  pomiar  jednopunktowy. 
Określamy  za  ich  pomocą  tylko  jedną  wartość  naprężenia  stycznego  i  szybkości  ścinania, 
czyli uzyskujemy tylko jeden punkt na krzywej płynięcia. 

Jeden punkt na krzywej płynięcia charakteryzuje oczywiście w sposób jednoznaczny 

płyn  newtonowski,  natomiast  zupełnie  nie  określa  własności  reologicznych  płynu 
nienewtonowskiego.  Tę  samą  lepkość  pozorną  przydanej  szybkości  ścinania  mogą  mieć 
układy o diametralnie różnych własnościach reologicznych, jeżeli tylko ich krzywe płynięcia 
przecinają  się  przypadkowo  w  badanym  punkcie.  Wynika  stąd,  że  wnioskowanie  o 
własnościach 

reologicznych 

płynu 

nienewtonowskiego 

na 

podstawie 

pomiaru 

jednopunktowego  może  prowadzić  do  bardzo  poważnych  błędów.  Pomiary  takie  mogą  być 
wykorzystywane ewentualnie do bieżącej kontroli produkcji w tym sensie, że odstępstwo od 
wartości  standardowej  sygnalizuje  zmianę  własności  produktu,  natomiast  nie  prowadzą  do 
gromadzenia informacji o znaczeniu naukowym lub technicznym. 

Określenie 

własności 

reologicznych 

płynu 

nienewtonowskiego 

wymaga 

wyznaczenia  krzywej  płynięcia  tego  płynu.  Pomiary  muszą  bezwzględnie  objąć  zakres 
szybkości  ścinania  występujący  w  zagadnieniu  praktycznym,  które  jest  celem 
przeprowadzonych badań.  

Z  powyższych  rozważań  wynika,  że  pomiary  własności  reologicznych  płynów 

nienewtonowskich 

muszą 

być 

wykonane 

za 

pomocą 

przyrządów 

absolutnych 

wielopunktowych.  Przyrządy  te  w  odróżnieniu  od  zwykłych  wiskozymetrów  absolutnych 
jednopunktowych  nazywać  będziemy  reometrami.  Ściśle  mówiąc  reometrami  nazywamy 
przyrządy do pomiaru własności reologicznych nie tylko płynów, lecz także ciał stałych 
W  przypadkach  każdego  reometru  powinniśmy  dysponować  ścisłym  rozwiązaniem  równań 
ruchu  opisujących  realizowany  w  przyrządzie  rodzaj  przepływu.  Jeżeli  rozwiązanie  równań 
ruchu  jest  przybliżone,  to  błąd  popełniony  przez  to  przybliżenie  musi  być  mniejszy  od 
dopuszczalnego  błędu  pomiaru.  Konieczność  zachowania  tego  warunku  powoduje,  że 
pomiary  reologiczne  wykonujemy  dla  szczególnie  prostych  przypadków  przepływu,  w 

 

 

11 

których  występuje  tylko  jedna  składowa  prędkości  różną  od  zera.  Są  to  tzw.  przepływy 
wiskozymetryczne.  Dla  przepływów  wiskozymetrycznych  jesteśmy  w  stanie  w  sposób 
jednoznaczny  określić  zależność  między  naprężeniem  stycznym  a  szybkością  ścinania. 
Jedynym  założeniem  przy  tym  dotyczącym  płynu  jest  to,  że  jest  on  nieściśliwy  i  może  być 
traktowany jako continuum (ośrodek ciągły). 
 
b) płyny wykazujące efekty naprężeń normalnych. 
 

Płyny  o  złożonych  własnościach  reologicznych,  wykazujące  efekty  naprężeń 

normalnych, uważamy za płyny sprężystolepkie.  

W  przypadku  omawianych  układów  różnica  naprężeń  normalnych  może  przy 

pewnej  szybkości  ścinania  być  większa  od  naprężenia  stycznego.  Oczywiste  jest,  że  sam 
pomiar  zależności  naprężenie  styczne  -  szybkość  ścinania  nie  wystarcza  do  określenia 
własności  reologicznych  takiego  układu.  Niezbędny  jest  wówczas  pomiar  nie  tylko 
naprężenia stycznego, ale i różnic naprężeń normalnych jako funkcji szybkości ścinania. 

Składową  styczną  naprężenia  mierzy  się  za  pomocą  metod  wiskozymetrycznych. 

Natomiast  do  pomiaru  różnicy  naprężeń  normalnych  stosujemy  metody  reogoniometryczne. 
Reogoniometria jest działem reometrii zajmującym się zagadnieniami ilościowego określenia 
wszystkich  naprężeń  w  przypływającej  substancji,  za  pomocą  przyrządów  zwanych 
reogoniometrami.  W  metodach  reogoniometrycznych  wykorzystujemy  te  same,  co  w 
metodach wiskozymetrycznych szczególnie proste przypadki przepływu.  

Aby  uzyskać  możliwie  pełną  charakterystykę  układu  o  złożonych  własnościach 

reologicznych  oprócz  metod  wiskozymetrycznych  i  reogoniometrycznych  w  pewnych 
przypadkach 

stosujemy 

metody 

wykorzystujemy 

przepływy 

niewiskozymetryczne. 

Przykładem  takiej  metody,  która  może  dostarczyć  dodatkowych  informacji  o  własnościach 
reologicznych układu, są badania wykonywane przy użyciu drgań o małej amplitudzie (tzw. 
metoda oscylacyjna). 

 
4. Zasada działania reometru kapilarnego 

 

Zasada  działania  reometru  kapilarnego  polega  na  przetłaczaniu  badanego  płynu 

przez  długie,  cylindryczne  rurki  o  gładkiej  powierzchni  wewnętrznej.  Warunki  pracy 
przyrządu muszą być tak dobrane, aby przepływ był ustalony, izotermiczny i laminarny. Przy 
zwianych  rozmiarach  kapilar  dążymy  wówczas  do  określenia  zależności  między 
objętościowym  natężeniem  przepływu  a  spadkiem  ciśnienia  wywołanym  tarciem 
wewnętrznym  płynu.  Jeżeli  pomiary  wykonane  są  w  sposób  umożliwiający  wyznaczenie 
powyższej  zależności  dla  różnych  wartości  natężenia  przepływu,  to  stosując  odpowiednie 
obliczenia możemy określić w sposób jednoznaczny krzywą płynięcia badanego czynnika. 

Reometry  kapilarne  mają  kilka  cennych  zalet.  Przede  wszystkim  stosując  zmienne 

średnice kapilar oraz zmienne ciśnienia można uzyskać niezwykle szeroki zakres przyrządu, 
nie dostępny w pojedynczym urządzeniu o innej zasadzie działania ( reometry rotacyjne mają 
ograniczony  zakres  szybkości  ścinania  i  zakres  ten  trudno  jest  zmienić).  Następnie  w 
przypadku  przyrządu  kapilarnego  nie  występują  -  oprócz  przypadków  skrajnych  -  trudności 
związane  z  koniecznością  zachowania  izotermicznych  warunków  pomiaru.  Płyn  przebywa 
bowiem  w  kapilarze  przez  bardzo  krótki  okres  czasu.  Nie  zachodzi  więc  niebezpieczeństwo 
akumulowania się ciepła powstającego z lepkiego rozproszenia energii, co może zachodzić w 
reometrach  rotacyjnych,  wreszcie  bardzo  ważne  jest  to,  że  reometry  kapilarne  cechują  się 
prostą  konstrukcją.  Mogą  być  one  wykonywane  w  zwykłych  warunkach  warsztatowych,  w 
przeciwieństwie do bardziej skomplikowanych przyrządów rotacyjnych. 

Należy  jednak  podkreślić,  że  reometry  kapilarne  służą  tylko  do  pomiaru  tych 

własności  reologicznych,  które  charakteryzują  ustalony  przepływ  płynów  reostabilnych  i 

 

 

12 

sprężystolepkich.  Są  one  natomiast  mało  przydatne  do  badania  układów  reologicznie  nie 
stabilnych. 

Zakres  pracy  przyrządu  kapilarnego  jest  ograniczony  w  przypadku  małych 

szybkości  ścinania,  zaś  czas  potrzebny  do  wykonania  jednego  pomiaru  w  reometrze 
kapilarnym jest wielokrotnie dłuższy niż w przyrządach rotacyjnych. 

 
5.  Przepływ  laminarny  płynu  newtonowskiego  przez  kapilarę  (  równanie 

Hagena - Poiseuille'a) 

 

Rozważmy laminarny przepływ płynu newtonowskiego przez cylindryczną kapilarę 

o  promieniu  R  i  długości  L.  Załóżmy,  że  mamy  do  czynienia  z  ustalonym,  izometrycznym 
przepływem płynu nieściśliwego, zaś stosunek długości kapilary do jej średnicy jest tak duży, 
iż  można  zaniedbać  wpływ  efektów  końcowych  (występujących  na  wlocie  i  wylocie  z 
kapilary). 

W pełni uformowany przepływ laminarny płynu przez przewód o przekroju kołowy  

możemy  sobie  wyobrazić  jako  ruch  nie  mieszających  się  ze  sobą  warstewek  o  kształcie 
współosiowych cylindrów. Prędkość lokalna u w kierunku osiowym, będąca jedyną składową 
prędkości, jest stała na obwodzie każdej cylindrycznej warstewki o różniczkowej grubości dr. 
Przepływ jest więc osiowo - symetryczny, a prędkość u jest wyłącznie funkcją odległości od 
osi r. 

Zakładamy,  że  wskutek  działania  sił  adhezji,  prędkość  przepływu  warstewki  płynu 

stykającej  się  bezpośrednio  ze  ścianką  kapilary,  tzn.  gdy  r  =  R,  jest  równa  zeru.  Jest  to 
założenie dotyczące braku tzw. efektywnego poślizgu przy ścianie. Założenie to jest zawsze 
spełnione dla płynów czystych, nie będących układami dyspersyjnymi. 

W osi przewodu (r = 0) prędkość lokalna osiąga wartość maksymalną. Przy istnieniu 

gradientu  prędkości  w  kierunku  promieniowym  występuje  między  poszczególnymi 
warstewkami płynu naprężenie styczne. 

Ruch  płyny  w  kapilarze  następuje  pod  wpływem  różnicy  ciśnienia  w  kierunku 

osiowym.  W  warunkach  przepływu  ustalonego,  gdy  nie  występują  siły  bezwładności,  siły 
pochodzące od ciśnień równoważną się z siłami tarcia. 

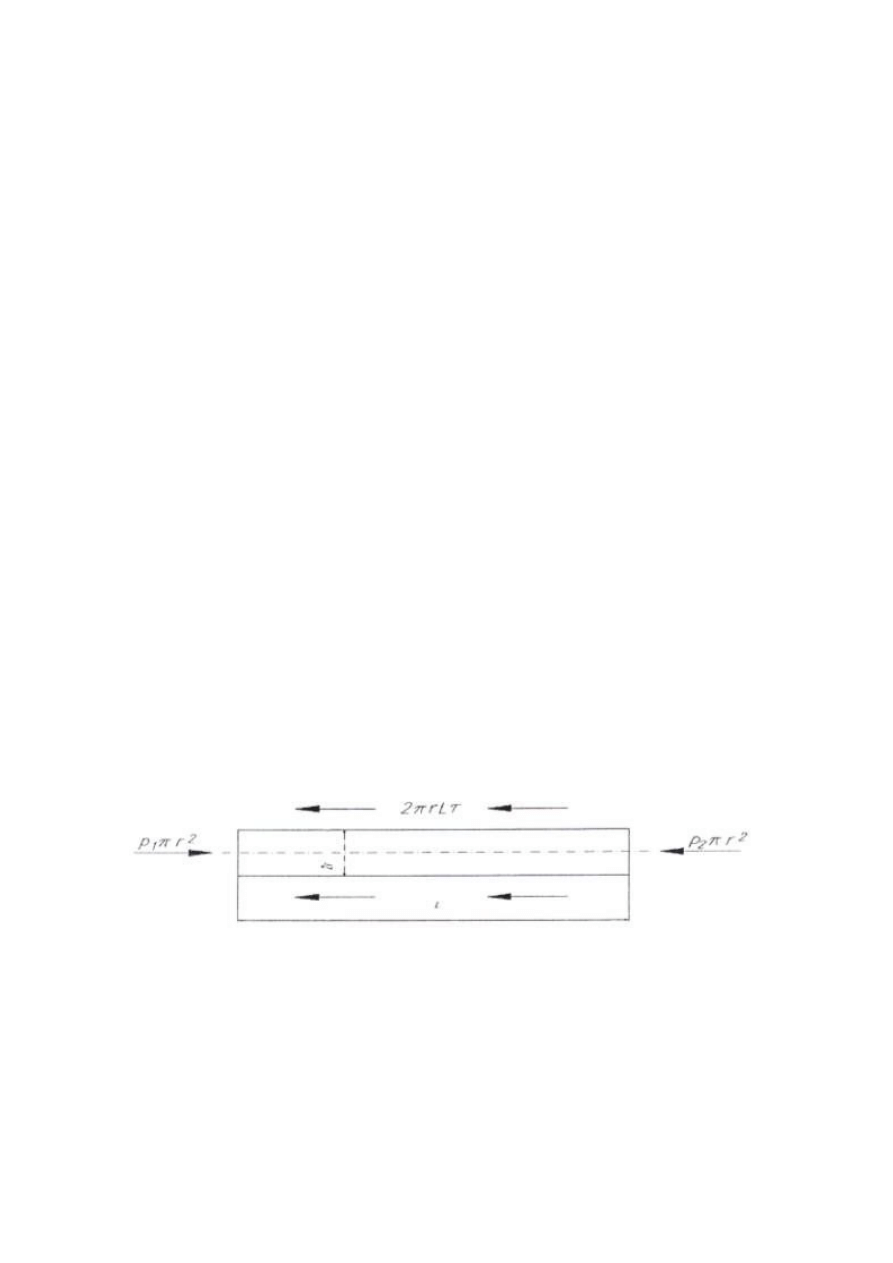
Wyodrębnimy myślowo część przepływającego płynu w postaci walca o promieniu 

r  i  długości  L  współosiowego  z  kapilarą  (rys.  8).  Siły  parcia  i  przeciwparcia  na  podstawę 
rozważanego  walca  równe  są,  uwzględniając  kierunek  działania  siły,  odpowiednio  p

1

ππππr

2 

i 

p

2

ππππr

2

 , gdzie p

1 

jest wartością 

 

Rys. 8 Siły powierzchniowe działające na walec cieczy o promieniu r i długości L. 

 

Ciśnienia  na  wlocie,  a  p

2 

-  na  wylocie  z  kapilary.  Siła  tarcia  działająca  na 

powierzchnię boczną walca jest równa iloczynowi tej powierzchni i naprężenia stycznego 

ττττ w 

odległości  r  od  osi.  Uwzględniając,  że  kierunek  działania  siły  tarcia  jest  przeciwny  do 
kierunku przepływu otrzymamy - 2

ππππrLττττ. Warunek równowagi sił wymaga, aby suma rzutów 

sił zewnętrznych na kierunek osi rury była równa zeru. Stąd 

(14) 

 

 

0

2

2

2

2

1

=

−

−

τ

π

π

π

rL

r

p

r

p

 

 

13 

Oznaczając  różnicę  ciśnień  p

1 

-  p

2 

= 

∆∆∆∆p  uzyskamy  po  prostym  przekształceniu 

równania (14) następującą zależność na naprężenie styczne 
 

(15) 

 

Zrównania  (15)  wynika,  że  naprężenie  styczne  w  płynie  przepływającym  w 

kapilarze  jest  wprost  proporcjonalne  od  osi  r  i  do  spadku  ciśnienia  na  jednostkę  długości 
kapilary 

∆∆∆∆p / L. Zwrócimy przy tym uwagę, że naprężenia styczne w osi jest równe zeru, 

osiąga  zaś  wartość  maksymalna  przy  ścianie  kapilary.  Podstawiając  do  wzoru  (15)  r  =  R, 
uzyskamy zależność na naprężenie styczne przy ścianie kapilary 

 

(16) 

 
 

Podkreślmy, że powyższa liniowa zależność naprężenia stycznego od odległości od 

osi r wynika z ogólnego bilansu sił przy przepływie laminarnym przez kapilarę i jest słuszna 
dla wszystkich płynów zarówno newtonowskich, jak i nienewtonowskich. 

Dalsze  nasze  rozważania  dotyczyć  będą  tylko  płynów  newtonowskich,  dla  których 

w warunkach izotermicznego przepływu laminarnego istnieje prosta proporcjonalność między 
naprężeniem  stycznym  a  szybkością  ścinania.  Dla  przypadku  przepływu  przez  cylindryczną 
kapilarę równanie Newtona przybierze postać: 

 

(17) 

 

Gradient  prędkości  du  /  dr  jest  ujemny,  ponieważ  prędkość  maleje  ze  wzrostem 

odległości od osi r. 
Korzystając z zależności (15) przedstawimy wzór (17) w postaci 

  

(18) 

 

lub po rozdzieleniu zmiennych 

 

(19) 

 

Całkując równanie (19) otrzymamy 

 

(20) 

 

 

Stałą  całkowania  C  określimy  z  warunku  brzegowego,  wynikającego  z  założenia 

braku poślizgu przy ścianie 
dla r  = R  

u = 0  

Stąd 
 
 
 

 

 

 

 

i ostatecznie 

 

(21) 

 

 

Z  otrzymanego  wzoru  na  prędkość  lokalną  widać,  że  przy  osiowo  -  symetrycznym 

przepływie  rozkład  prędkości  w  zależności  od  promienia  jest  paraboloidalny.  Na  rys.  9 

L

p

r

2

∆

=

τ

L

p

R

w

2

∆

=

τ











 −

=

dr

du

η

τ

dr

du

L

p

r

η

−

=

∆

2

rdr

L

p

du

η

2

∆

−

=

C

r

L

p

u

+

∆

−

=

2

4

η

L

pR

C

η

4

2

∆

=

(

)

2

2

4

r

R

L

p

u

−

∆

=

η

 

 

14 

przedstawiono  rozkład  naprężeń  stycznych  i  paraboliczny  profil  prędkości,  w  płaszczyźnie 
przechodzącej przez oś kapilary, podczas laminarnego przepływu płynu newtonowskiego. 
Dysponując  wzorem  na  rozkład  prędkości  (21)  obliczymy  łatwo  objętościowe  natężenie 
przepływu  Q,m

3

/s.  W  tym  celu  wyodrębnimy  myślowo  w  przekroju  poprzecznym  kapilary 

dwa  koncentryczne  koła  o  promieniach  odpowiednio  r  oraz  r  +  dr.  Przez  pierścieniowy 
przekrój  poprzeczny  o  różniczkowej  grubości  dr  płyn  przepływać  będzie  z  jednakową 
prędkością  u  =  f  (  r  ).  Objętościowe  natężenie  przepływu  przez  rozważaną  powierzchnię 
pierścienia wyniesie 
 

(22) 

 
 

 

Rys.9 Rozkład naprężeń stycznych i profil prędkości płynu newtonowskiego podczas 

przepływu laminarnego przez przewód o przekroju kołowym. 

 

Stąd natężenie przepływu dla całego przekroju poprzecznego 

 

(23) 

 

 

Korzystając z równania (21) 

 

(24) 

 

 

 

 

po scałkowaniu otrzymamy 

 

(25) 

 

Jeśli zamiast promienia wprowadzimy średnicę rury, to 
 

(26) 

 

 

Stwierdziliśmy  więc,  że  objętościowe  natężenie  przepływu  przy  laminarnym  ruchu 

płynu  newtonowskiego  przez  kapilarę  jest  wprost  proporcjonalne  do  różnicy  ciśnień 
powodującej  przepływ,  proporcjonalne  do  czwartej  potęgi  promienia  kapilary  i  odwrotnie 
proporcjonalne do jej długości. Jest to znane prawo Hagena – Poiseuille’a. 

 
6.Podstawy teoretyczne reometrii kapilarnej dla płynów nienewtonowskich.

 

6.1 Równanie Rabinowitscha-Mooneya. 

 

Przy wyprowadzeniu równania jedynym założeniem dotyczącym płynu jest to, że w 

warunkach przepływu przez kapilarę jego własności reologiczne nie zależą od czasu ścinania 
oraz że nie wykazuje on poślizgu przy ścianie. 

rdr

u

dQ

π

2

=

∫

∫

=

=

Q

R

urdr

dQ

Q

0

0

2π

(

)

∫

−

∆

=

R

rdr

r

R

L

p

Q

0

2

2

2

η

π

L

pR

Q

η

π

8

4

∆

=

L

pD

Q

η

π

128

4

∆

=

 

 

15 

Rozpoczniemy od identycznego, jak w przypadku wprowadzenia równania Hagena - 

Poiseuille'a, stwierdzenia że objętościowe natężenie przepływu przez przekrój pierścieniowy 
różniczkowy  między  r  oraz  r+dr  wynosi  dQ=u2π

π

π

πr  dr,  gdzie  u  jest  prędkością  lokalną  w 

odległości r od osi. Stąd natężenie przepływu przez cały przekrój poprzeczny kapilary

 

 

(27) 

 

Korzystając z tego, że 

d(r

2

)=2rdr

 napiszemy 

(28) 

 

 

i całkując następnie otrzymamy 

(29) 

 
 

Z założenia braku poślizgu przy ścianie wynika, że u = 0 dla r = R i wyrażenie ur

2 

odpada.  Z  kolei  z  założenia,  że  przepływ  jest  laminarny  a  płyn  w  rozważanych  warunkach 
reostabilny wynika, iż gradient prędkości jest wyłącznie funkcją naprężenia stycznego 
 

(30) 

 

czyli 

(31) 

 

Następnie  łącząc  równania  (15)  i  (16)  możemy  napisać  wyrażenia  na  naprężenie 

styczne w odległości r od osi w postaci 
 

(32) 

 

Zrównania (32) wynika, że 
 

(33) 

 

zaś 

 

(34) 

 

Wprowadzając  zależności  (33),  (31)  i  (34)  do  równania  (29)  uzyskany  po  prostym 

przekształceniu tzn. ogólne równanie, przepływu w rurze 

 

(35) 

 

lub używając średnicy zamiast promienia kapilary 

 

(36) 

 
 

Równanie (35) jest ogólną zależnością wiążącą objętościowe natężenie przepływu Q 

z  naprężeniem  stycznym  przy  ścianie  τ

τττ

w

.  Przypomnimy,  że  jest  ono  słuszne  w  przypadku 

laminarnego przepływu przez przewód o przekroju kołowym dowolnego płynu reostabilnego, 
spełniające go zależność (30). Dzięki temu równanie (35) odgrywa znaczną rolę w inżynierii 
płynów  nienewtonowskich,  gdyż  może  być  wykorzystane  dookreślenia  zależności  Q  od 

∫

∫

=

=

Q

R

rdr

u

dQ

Q

0

0

2

π

( )

∫

=

2

0

2

R

r

ud

Q

π

[

]

2

0

2

2

R

du

r

ur

Q

∫

−

= π

( )

τ

f

dr

du

=

−

( )

dr

f

du

τ

−

=

R

r

w

τ

τ =

2

2

2

2

w

R

r

τ

τ

=

τ

τ

d

R

dr

w

=

( )

∫

=

w

d

f

R

Q

w

τ

τ

τ

τ

τ

π

0

2

3

3

1

( )

∫

=

w

d

f

D

Q

w

τ

τ

τ

τ

τ

π

0

2

3

3

1

8

 

 

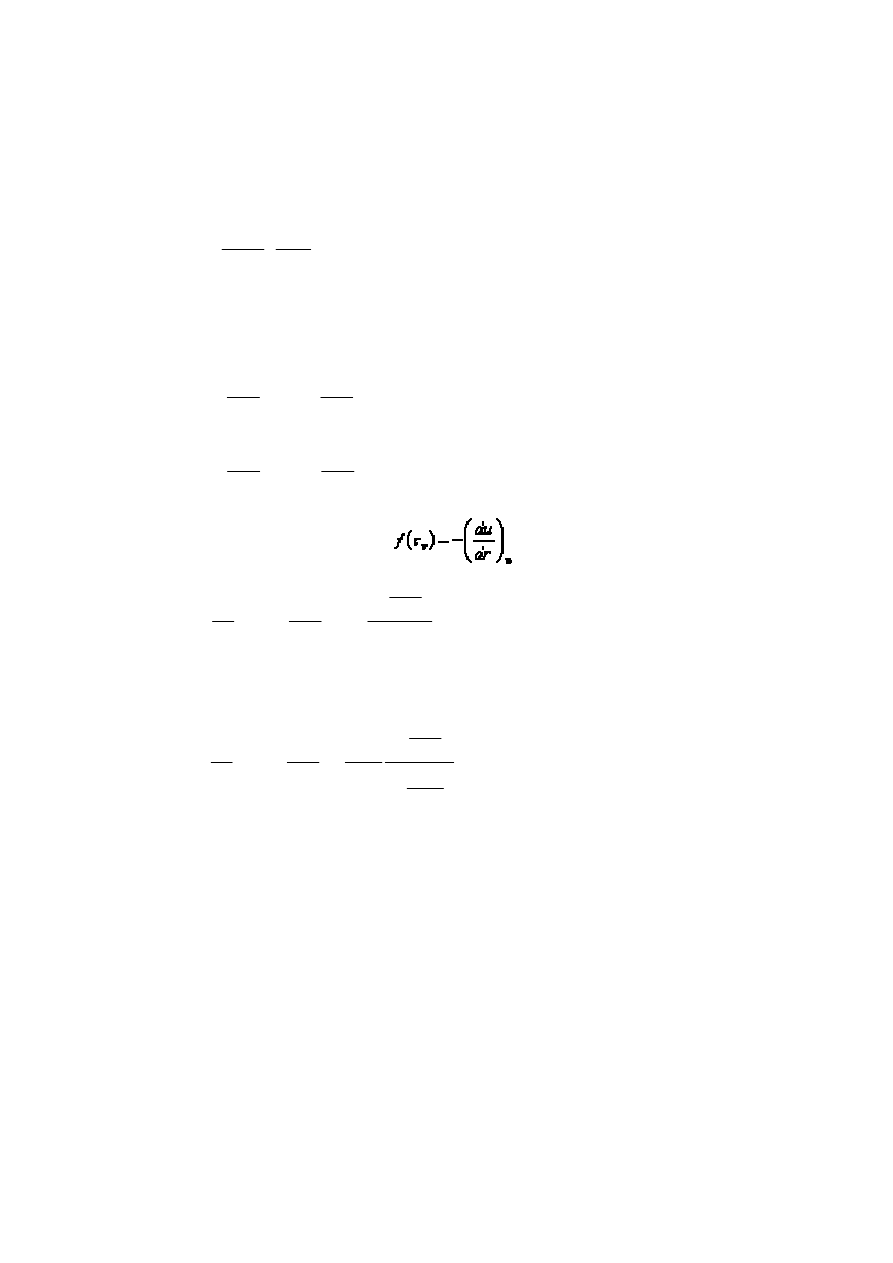
16 

spadku  ciśnienia 

∆∆∆∆p  wywołanego  tarciem  wewnętrznym  dla  płynów  spełniających  różne 

modele  reologiczne.  W  tym  celu  należy  wprowadzić  do  wzoru  (35)  właściwą  zależność 
funkcjonalną (30) i dokonać całkowania. Dla płynu newtonowskiego, podstawiając  f( 

ττττ ) = ττττ 

/ 

ηηηη  otrzymamy  po  scałkowaniu  równanie  Hagena  -Poiseuille'a  (26).  Podobnie  dla  płynu 

spełniającego  zależność  potęgową  Ostwalda  -  de  Waele  (5),  podstawiając

 

ƒƒƒƒ(ττττ)=(ττττ/k)

1/n

 

uzyskamy tzw. uogólnione równanie Hagena - Poiseuille'a 

 

(37) 

 

Analogicznie  uzyskać  można  uzyskać  odpowiedniki  równania  Hagena-Poiseuille’a 

dla innych modeli reologicznych płynów nienewtonowskich. Wracając do zasadniczego nurtu 
naszych  rozważań,  pomnóżmy  obie  strony  równania  (36)  przez 

ττττ

w

3

,  a  następnie 

zróżniczkujmy je względem 

ττττ

w

. Otrzymamy wówczas 

 

(38) 

 

Korzystając z twierdzenia Leibniza - Newtona możemy napisać 

 

(39) 

 
 

Z zależności (30) wynika, że 

 

           . Stąd 

 

 

 

 
 

(40) 

 

 

i zastępując, zgodnie z zależnością (16), 

ττττ

w 

przez D

∆∆∆∆p/4L ostatecznie otrzymamy 

 

 

(41) 

 
 
 

Równanie Rabinowitscha-Mooneya (41) jest szukaną przez nas zależnością z której 

można wyznaczyć szybkość ścinania przy ścianie kapilary. 

 
 
 
 
 
 
 
 
 
 
 
 

n

kL

p

R

n

R

n

Q

/

1

3

2

1

3











 ∆

+

=

π

( )

∫

=













+













w

d

f

d

d

D

Q

D

Q

d

w

w

w

τ

τ

τ

τ

τ

π

τ

π

τ

0

2

3

2

3

2

8

3

8

( )

w

w

w

w

w

w

d

f

d

D

Q

D

Q

d

τ

τ

τ

τ

π

τ

π

τ

2

3

2

3

3

8

3

8

=













+













w

w

w

d

D

Q

d

D

Q

dr

du

τ

π

τ

π













+













=











 −

3

3

8

8

3











 ∆













∆

+













=











−

L

p

D

d

D

Q

d

L

p

D

D

Q

dr

du

w

4

8

4

8

3

3

3

π

π

 

 

17 

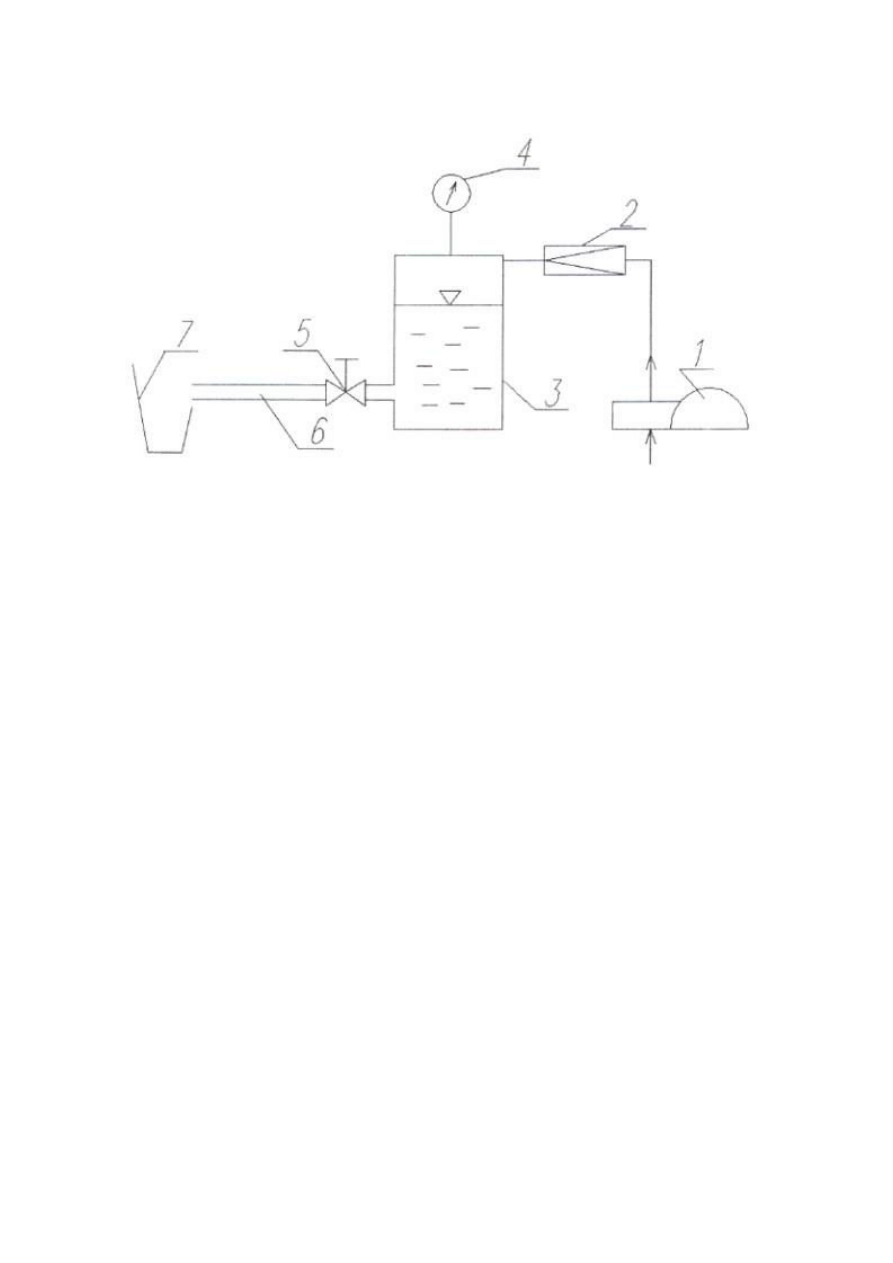
9.  Schemat  stanowiska  do  pomiaru  własności  reologicznych  płynów 

nienewtonowskich. 

 

1- sprężarka tłokowa 
2- zawór redukcyjny 
3- zbiornik reometru 
4- manometr kontrolny 
5- zawór przelotowy 
6- kapilara 
7- naczynie pomiarowe 

 
10. Wykonanie ćwiczenia 

 

Zmierzyć  średnicę  i  długość  kapilary.  Otworzyć  zawór  (5)  i  uruchomić  sprężarkę. 

Po  uruchomieniu  sprężarki  (l)  należy  ustawić  na  zaworze  redukcyjnym  (2)  jak  najniższą 
wartość  ciśnienia,  a  następnie  odczytać  jego  wartość  na  manometrze  kontrolnym  (4). 
Zwiększać  powoli  zaworem  redukcyjnym  (2)  ciśnienie  w  zbiorniku  (3)  tak  długo,  dopóki 
ciecz  nie  zacznie  wypływać  z  kapilary  (6).W  momencie  rozpoczęcia  mchu  cieczy  odczytać 
ciśnienie na manometrze (4) i wpisać jego wartość do tabeli. Dla różnych wartości ciśnienia 
zmierzyć  natężenie  przepływu  cieczy  wypływającej  przez  kapilarę  (6)  do  naczynia  (7).  Po 
wykonaniu pomiarów wyłączyć sprężarkę. 

 
11. Pomiary i obliczenia 

 

Podczas ćwiczenia wykonuje się następujące pomiary i obliczenia: 

- średnica kapilary D[m]; 
- długość kapilary L[m]; 
- ciśnienie w zbiorniku P[N/m

2

]; 

- natężenie wypływu cieczy Q[m

3

/s]; 

- granica płynięcia [N/m

2

]; 

- naprężenia styczne [N/m

2

]; 

- lepkość plastyczna [N s/m

2

]; 

- szybkość ścinania [l/s], 

 
 

 

 

18 

12.Przykładowe pytania 
 

1.  jak możemy podzielić odkształcenia, krótko zdefiniować? 
2.  ogólna klasyfikacja płynów nienewtonowskich. 
3.  jak zachowuje się płyn Stokesa w warunkach laminarnego ścinania? 
4.  wymień  oraz  opisz  jak  wykonuje  się  pomiary  własności  reologicznych  płynów 

nienewtonowskich. 

5.  wymień zalety reometru kapilarnego. 
6.  narysuj  rozkład  naprężeń  stycznych  i  profil  prędkości  płynu  newtonowskiego  podczas 

przepływu laminarnego przez przewód o przekroju okrągłym. 

7.  naszkicuj stanowisko do pomiaru własności reologicznych płynów nienewtonowskich. 

 
13. Literatura 
 

Z.Kembłowski - „Reometria płynów nienewtonowskich"