Marek Jarosz

dr Andrzej Baranowski

Fizyka techniczna I rok

Wtorek 16:00 – 18:15

nr. 24 WYZNACZANIE MECHANICZNEGO

RÓWNOWAŻNIKA CIEPŁA

1.Tabela pomiarowa, aparatura użyta do przeprowadzenia doświadczenia

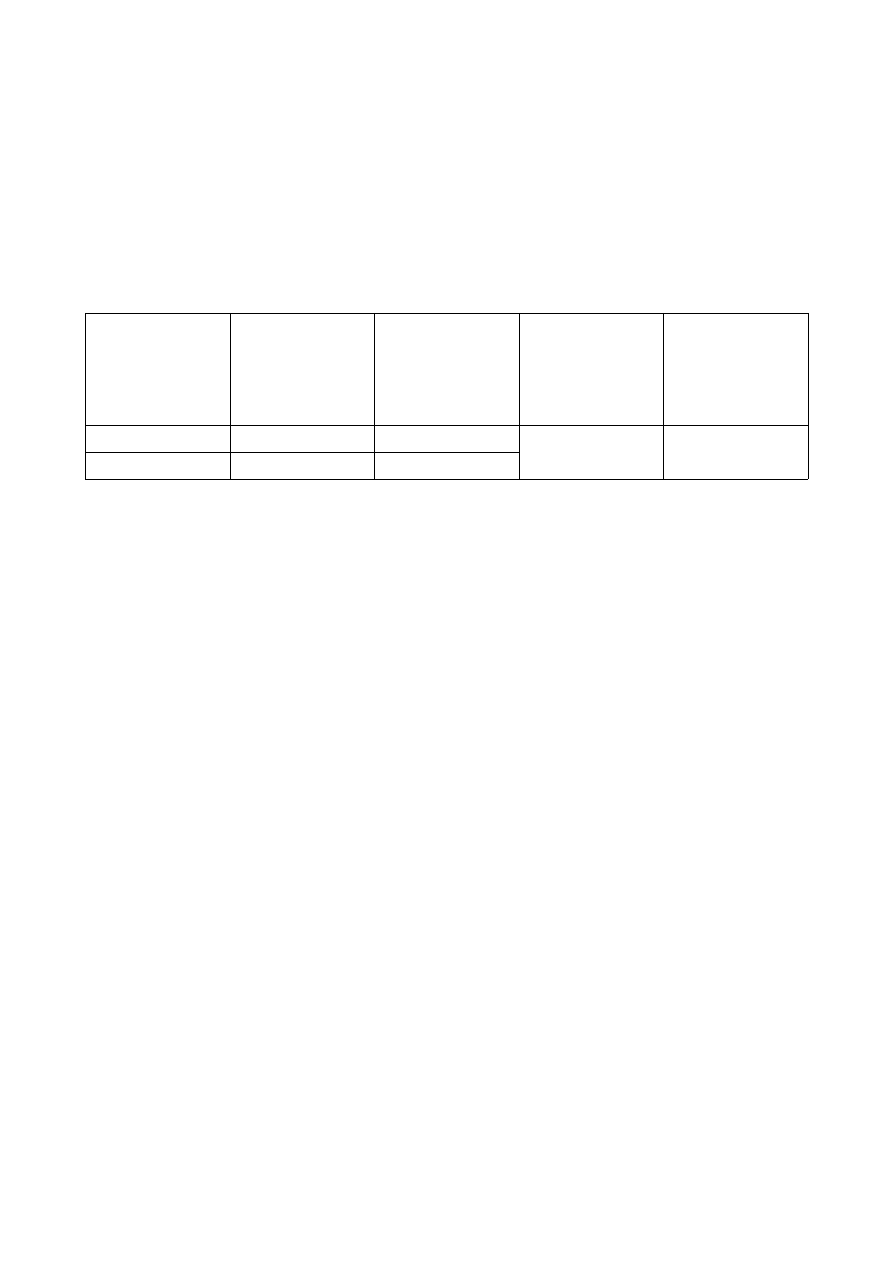
Tabela pomiarowa

Nr pomiaru

Obliczona wartość

mech.

równoważnika

ciepła ∆J

J/cal

Niepewność

pomiarowa

Uc (J)

Średnia wartość

mech.

równoważnika

ciepła

ΔJ

Średnia

niepewność

pomiarowa

Uc(J)

1

5,17 J / cal

1,36

5,07

1,16 ~ 23%

2

4,98

0,96

Aparatura użyta do przeprowadzenia doświadczenia:

Zasilacz

napięcie maksymalne – 24V

Amperomierz analogowy

zakres maksymalny – 3A

Woltomierz analogowy

zakres maksymalny – 75V

Termometr cyfrowy
Opornica suwakowa
Kalorymetr
Stoper cyfrowy

Waga naczyńka kalorymetrycznego - 92,8g
Waga naczyńka kalorymetrycznego z wodą - 228,2g
Masa wody - 135,4g
Początkowa temperatura wody dla pierwszego pomiaru - 26,9°
Początkowa temperatura wody dla drugiego pomiaru - 30,7°

Błąd przy pomiarze temperatury: +/-0,1°
Błąd przy pomiarze czasu: +/-0,1s
Błąd przy pomiarze masy: +/-0,1g
Błąd pomiaru woltomierza=1V+75V x 2/100=2,5V
Błąd pomiaru amperomierza= 0,02A+3A x 2/100=0,08A

2. Zagadnienia teoretyczne

Praktycznie wszystkie zjawiska fizyczne da się wytłumaczyć na podstawie kinetyczno-molekularnej

teorii budowy ciała. Materią nazywamy wszystkie ciała, z których zbudowany jest otaczający nas świat.
Współczesna fizyka rozszerza pojęcie materii na fale radiowe, świetlne, promienie kosmiczne i inne rodzaje
energii. Aby odróżnić materię w rozumieniu fizyki współczesnej od materii rozumianej jako ciała stałe ciecze i
gazy, tą ostatnią nazwano materią korpuskularną. Zalążki teorii atomistycznej budowy świata powstały już w
starożytnej Grecji stworzone przez Demokryta. Uważał on, że ciała zbudowane są z maleńkich drobin
zbudowanych z elementów materii zwanych atomami. Teoria atomistyczna rozwijana była następnie przez wielu
badaczy: Daltona, Avogadro, Maxwella, Boltzmanna, Łomonosowa, Smoluchowskiego i innych.

Kinetyczno - molekularna teoria budowy ciał umożliwia wytłumaczenie większości zjawisk cieplnych.

Podstawowym założeniem tej teorii jest ruch cząstek materii z tym większą prędkością im wyższa jest
temperatura ciała. W przypadku ciał stałych gdzie cząsteczki nie mogą zmienić swojego położenia ruch ten jest
ruchem drgającym wokół położenia równowagi. W przypadku płynów, gdzie położenie cząstek nie jest ściśle
związane z konkretnym miejscem ruch ten może przybierać inne formy.

Energia kinetyczna cząstek dla wszystkich trzech stanów skupienia jest wprost proporcjonalna do

temperatury bezwzględnej ciała:

Ek = 3/2 * k * T

Dlatego uważa się, że ciepło jest ściśle związane z energią kinetyczną cząsteczek ciała.

Kinetyczno – molekularna budowa ciała mówi, że przekazywanie ciepła polega na zwiększeniu energii

kinetycznej cząsteczek. Cząsteczki ciała o wyższej temperaturze poruszają się z większą prędkością. W momencie
zderzenia z cząsteczkami ciała o niższej temperaturze przekazują im część swojej energii kinetycznej pobudzając
je do szybszego ruszania się. W ten sposób zwiększana jest energia kinetyczna cząsteczek ciała o niższej
temperaturze co w rezultacie prowadzi do zwiększenia jego temperatury. Podobnie tłumaczy się zjawisko
przewodzenia ciepła przez ciała. Przyjęcie zasady, że ciepło jest energią kinetyczną cząsteczek pozwala wyjaśnić
istotę zamiany energii mechanicznej w ciepło.

Pierwsza zasada termodynamiki mówi, że zmiana energii wewnętrznej układu jest równa sumie

dostarczonej energii Q i pracy wykonanej nad układem W:

ΔU = Q + W

W życiu codziennym często spotykamy przemianę energii mechanicznej w ciepło np. w tokarce podczas

obróbki skrawaniem. Zjawisko to doświadczalnie zbadał Joule. Doświadczenie Joule'a polegało na umieszczeniu
w kalorymetrze mieszadełka. Mieszadełko to podłączone było za pomocą przekładni krążkowej do ciężarków.
Praca wykonana przez opadające ciężarki przekładana była na ruch obrotowy mieszadełka. Ponieważ ciecz
stawiała opór mieszadełku, praca wykonana przez to mieszadełko została zamieniona w ciepło. Joule wykonał
jeszcze kilka doświadczeń ( mieszanie rtęci, przepychanie wody przez wąskie rury, wzajemne pocieranie
pierścieni zanurzonych w rtęci ). Na podstawie swoich doświadczeń stwierdził, że zamiana energii mechanicznej
na ciepło zachodzi zawsze w jednakowym stosunku ilościowym:

L = J * Q

Q – ciepło
L – doprowadzona praca
J – współczynnik proporcjonalności nazywany mechanicznym równoważnikiem ciepła (4,19 J/cal).

Procesy zachodzące w przyrodzie mają charakter nieodwracalny. Cechę tą wyraża II zasada

termodynamiki. Możliwa jest zamiana całej energii mechanicznej w ciepło, natomiast zamiana całego ciepła na
energię mechaniczną jest już dość trudna i nigdy nie zachodzi całkowicie. Ciepło może być zamienione na prace
tylko wtedy gdy istnieje różnica temperatur ciał wymieniających ciepło ( istnieje ciało o wyższej temperaturze –
grzejnica i ciało o niższej temperaturze – chłodnica ). II zasada termodynamiki mówi, że całkowita zamiana
energii cieplnej w mechaniczną jest niemożliwa a także niemożliwe jest przekazywanie ciepła od ciała
chłodniejszego do cieplejszego.

Energia prądu elektrycznego. Jeżeli opór przewodnika pomiędzy dwoma punktami A i B wynosi R i przez

ten przewodnik płynie prąd o natężeniu I, to w czasie t przeniesiony jest z punktu A do punktu B ładunek q = It W
punkcie A ma on potencjał Va a w punkcie B Vb. Przeniesienie tego ładunku jest pewną pracą, która pojawia się w
przewodniku w postaci ciepła.

W = (Va - Vb)It = JQ

J – mechaniczny równoważnik ciepła
Po przekształceniach z wykorzystaniem prawa Ohma otrzymujemy

W = R I² t

Ciepło, które zostało wydzielone w przewodniku nosi nazwę ciepła Joule’a. Prawo Joule’a: ciepło wydzielone
podczas przepływu prądu stałego przez przewodnik jest proporcjonalne do oporu przewodnika, kwadratu
natężenia prądu i do czasu jego przepływu.

3. Opis przeprowadzenia doświadczenia

Najpierw dokonałem pomiaru masy pustego kalorymetru, kalorymetru napełnionego wodą do 2/3 wysokości oraz
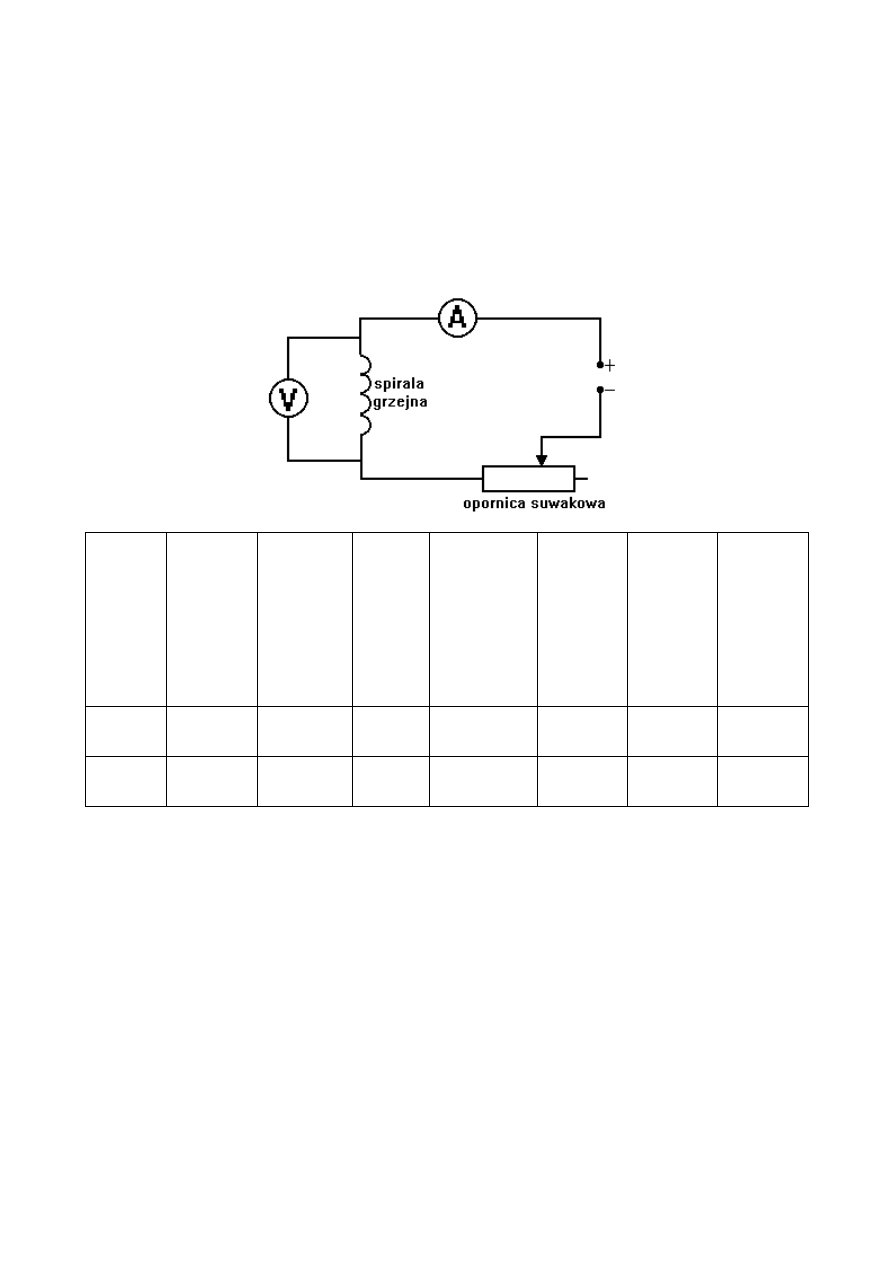
temperatury wody. Następnie złożyłem układ tak jak jest pokazane na schemacie.

Aby ustalić mechaniczny równoważnik ciepła, zmierzyłem czas, jaki jest

potrzebny na podgrzanie wody w naczynku kalorymetrycznym o 5°C, przy natężeniu prądu stałego I=1A.
Następnie powtórzyłem pomiar przy natężeniu prądu stałego I=1,4A. W trakcie przeprowadzania
doświadczenia zapisałem odpowiednie napięcia na elemencie grzejnym, wyniki wszystkich
pomiarów są przedstawione w tabeli która mieści się na pierwszej stronie.

Schemat układu pomiarowego:

Napięcie

zasilające

[V]

Napięcie na

spirali

grzewczej

[V]

Prąd

[A]

Temperatura

wody przed

ogrzaniem

[°C]

Temperatu

ra wody po
podgrzaniu

[°C]

Czas

jakiego

potrzeba

na

podgrzanie

wody o

5°C

[s]

Czas

jakiego

potrzeba

na

podgrzanie

wody o

0.1°C

[s]

Pomiar

nr. 1

10,4

7,4

1,0

26,9

31,9

503

( 8'23” )

9

Pomiar

nr. 2

15

10,4

1,40

30,8

35,8

246

( 4'6” )

7

4.Opracowanie otrzymanych wyników

Opracowanie wyników.
Najpierw obliczam ilość ciepła potrzebną do ogrzania kalorymetru z wodą o 5°C korzystając ze
wzoru:

Q=( m

w

c

w

+ m

k

c

k

)* ∆T

c

w

=0.998 cal/ g*K , c

k

=0.094 cal/ g*K ,m

w

=135.4g ,m

k

=92.8g

Q=135.4 g

∗0.998 cal/ gK92.8 g∗0.094 cal / gK ∗



5=135.1292 cal/K8.7232 cal /K

∗



5=

=719.262 cal

Następnie obliczyłem wartość pracy W

1

dla natężenia I

1

= 1 A ,U

1

= 7.4 V i t

1

= 503 s i wartość pracy W

2

dla

natężenia I

2

= 1.4 A, U

2

= 10.4 V t2= 246s

W tym celu skorzystałem ze wzoru

W=U*I*t

,

W

1

= 7,4 V*1 A*503 s = 3722,2 J

W

2

= 10,4 V*1,4 A* 246 s = 3581,76 J.

Teraz obliczam mechaniczny równoważnik ciepła dla uzyskanych danych:
J

1

= W

1

/ Q = 3722,2 J / 719,262 cal = 5,175 J / cal

J

2

= W

2

/ Q = 3581,76 J / 719,262 cal = 4,98 J / cal.

Ostateczną wartość mechanicznego równoważnika ciepła ustalam dzięki średniej
arytmetycznej pomiarów, co daje ostatecznie w wyniku 5,0775 J / cal.

5. Ocena błędu pomiarowego

Obliczam złożoną niepewność standardową i w tym celu korzystam z prawa przenoszenia
niepewności maksymalnej.

1. Dla natężenia prądu równego I=1A
ΔJ

1

= 1/719,262 ( 7,4*503*0,08 + 1*503*2,5 + 1*7,4*0,1 + (7,4*1*503*0,1)/5 +

1/719,262 (7,4*1*503*135,4*5*0,01 + 7,4*1*503*0,998*5*0,1 +
7,4*1*503*92,8*5*0,01 + 7,4*1*503*0,94*5*0,1) = 2,36 J/cal
2. Dla natężenia prądu równego I=1.4A
ΔJ

2

= 1/719,262 ( 10,4*246*0,08 + 1,4*246*2,5 + 1,4*10,4*0,1 + (10,4*1,4*246*0,1)/5 +

1/719,262 (10,4*1,4*246*135,4*5*0,01 + 10,4*1,4*246*0,998*5*0,1 +
10,4*1,4*246*92,8*5*0,01 + 10,4*1,4*246*0,94*5*0,1) = 1,67 J/cal

Niepewność pomiarowa wynosi U

c

( J ) = ΔJ/√3

czyli dla pierwszego pomiaru wynosi 1,36

dla drugiego pomiaru wynosi natomiast 0,96 co jest przedstawione w tabeli na 1 stronie

6. Wnioski

Wyznaczony przez mnie błąd średni wartości mechanicznego równoważnika ciepła (5,0775

J/cal) różni się od tablicowej wartości (4.187 J/cal) o 23%.
Jest to niedokładna wartość ponieważ nie jest mi znana dokładna proporcja metali w stopie
mosiądzu z jakiego wykonane jest naczynko kalorymetryczne, jak również nie znany mi jest stopień
izolacji kalorymetru od środowiska zewnętrznego. Wypaczenie wyników pomiaru wprowadza
również brak informacji czym została przymocowana spirala grzewcza do naczynka
kalorymetrycznego ( prawdopodobnie jest to jakiś klej lub żywica ). Błąd przy pomiarze napięcia i
natężenia prądu wynika z faktu iż opornica suwakowa nie trzyma cały czas zadanego oporu.

Najlepsze odwzorowanie dało by umieszczenie elementu grzewczego bezpośrednio w

małym naczynku a dopiero po tym zmierzenie czasu potrzebnego do ogrzania wody o zadaną
temperaturę.

+

∆

⋅

+

+

∆

⋅

+

+

∆

⋅

+

=

∆

t

T

m

c

m

c

IV

V

T

m

c

m

c

It

I

T

m

c

m

c

Vt

k

k

w

w

k

k

w

w

k

k

w

w

δ

δ

δ

)

(

)

(

)

(

( )

( )

=

∆

⋅

+

+

∆

⋅

+

+

∆

⋅

+

+

T

T

m

c

m

c

IVt

m

T

m

c

m

c

T

c

IVt

m

T

m

c

m

c

T

c

IVt

k

k

w

w

k

k

k

w

w

k

w

k

k

w

w

w

2

2

2

2

2

)

(

)

(

)

(

)

(

)

(

δ

δ

δ

δ

δ









∆

⋅

+

∆

⋅

+

∆

⋅

+

∆

⋅

+

∆

⋅

+

∆

⋅

⋅

=

T

T

IVt

m

Q

T

c

IVt

m

Q

T

c

IVt

t

IV

V

It

I

Vt

Q

k

k

w

w

δ

δ

δ

)

(

)

(

1