1. Układ biegunowy 
 
2. Ruch ze stałą prędkością i stałym przyspieszeniem z warunkami początkowymi 
 
3.Zasady dynamiki Newtona 
 
4.Zasada zachowania pędu w układzie N czastek 
 
5. Zasada zachowania energii mechanicznej układu N cząstek 
 
6. Zaleznośd L od M 
 
7. Tłumiony oscylator harmoniczny 
Siła harmoniczna, Warunki początkowe, rozwiązanie równania 
 
8. Rezonans, częstośd rezonansowa, wymuszony oscylator harmoniczny. 
 
9.przyspieszenie, prędkośd styczna normalna. 
 
10. Definicja bryły sztywnej 
 
11.Wektor prędkości kątowej 
 
12. Środek masy bryły sztywnej. 
 
13.Energia kinetyczna bryły sztywnej, zależnośd wektora prędkości kątowej od tensora momentu 
bezwładności. 
 
14. Twierdzenie Steinera 
 
15. Równania Eulera bąka symetrycznego. 
Precesja, stożek polodii i herpolhodii 
 
16. Wartośd stałej grawitacji, zasada superpozycji sił grawitacyjnych, prawo powszechnego ciążenia 
 
17. Prawo 1 keplera uogólnione i rozszerzone 
 
18. Udowodnienie 3 prawa Keplera 
 
19. Udowodnienie 2 prawa Keplera 
 
20.Prawo hooka, moduł Younga 
 
21. Zmiana wymiarów poprzecznych dla rozciągania sciskania, wspolcznynik poisonna 
 
22. co to jest energia potencjalna, zasada zach en (suma Ep i Ek) 
 
23. Okres drgao wahadła,oscylatra 

 

13. 

 

W przypadku układu odniesienia pokrywającego się z osiami głównymi: 

 

Składowe tensora momentu bezwładności to 9 liczb opisujących rozkład masy w bryle sztywnej 

14. 

 

Il’-moment bezwładności bryły sztywnej względem osi równoległej 

d-odległośd między osiami 

m-masa 

Il-moment bezwładności bryły sztywnej względem osi przechodzącej przez środek masy 

15. 3 równania Eulera 

 

 

 

Dla bąka symetrycznego 

 

 

 

 

Rozwiązania 

wx=Acos(Ωt) 

wy=Asin (Ωt) 

Stożek polodii – stożek który jest zakreślany przez wektor prędkości kątowej 

Stożęk Herpolhodii-stożek który jest zakreślany przez wektor momentu pędu 

Precesja- Zjawisko zmiany kierunku osi obrotu obracającego się ciała. Oś obraca się wtedy zakreślając 
powierzchnię stożkową. 

11. Wektor prędkości kątowej 

W ruchu obrotowym bryły sztywnej istnieje jednoznacznie zdefiniowany wektor   w ruchu o takiej 
własnoci że dla każdego punktu bryły sztywnej wyznaczonego przez wektor wodzący jego prędkośd 
(tego wektora w) dana jest wzorem 

 

4. Zasada zachowania pędu w układzie N cząstek 

P=p1+p2+…+pn 

 

 

Całkowity pęd układu N cząstek zmienia się tylko pod wpływem sił zewnętrzych. 

Dla sił zewnętrznych równych 0: 

 

6. Zależnośd L od M 

L=r x p 

M=r x F 

=(v x mv) + r x F = M  

(v x mv w tym przypadku sie rowan zero co 

trzeba napisad pod spodem w równaniu, a dlaczego tak jest to nei jestem pewien :P) 

 

 

 

 

 

 

9. Przyspieszenie styczne i przyspieszenie normalne związek z krzywizną toru 

 -przyspieszenie styczne (zmienia szybkośd) 

 

 - przyspieszenie normalne ( zmienia kierunek) 

a=an+as                     ρ-promieo krzywizny toru 

10. definicja bryły sztywnej 

Jest to układ N cząstek spełniający dwie własności 

 

 

 

 

3.I zasada dynamiki Newtona 

W inercialnym układie odniesienia cząstka na którą nie działa żadna siła lub siły się równoważą 
porusza sięruchem jednostajnym prostoliniowym 

IzdN 

W inercialnym układie odniesienia przyspieszenie cząstki jest wprost proporcjonalne do działającej na 
nią siły i odwrotnie proporcjonalne do jej masy 

F=ma 

IIIzdn 

Jeśli cząsta A działa na cząstkę B siłą Fba to siła Fab którą działa cząsta B na cząstkęA jest jej równa co 
do wartości i kierunku ale różna co do zwrotu. 

Fab=-Fba 

 

 

22. Zasada zachowania energii mechanicznej 

Ep(B)-Ep(A) = 

=

 

Ep(B)+Ep(A) = Ek(A)+Ek(B) 

Energia potencjalna to funkcja skalarna której gradient (ze znakiem minus) jest równy sile 
opisującej określone pole 

F=-gradEp (r) 

9. Zwykły oscylator harmoniczny 

 

Rozwiazanie: 

 

Okres drgao 

 

 

7. Tłumiony oscylator harmoniczny 

Rownanie Newtona: 

 

 

Gdzie 

  

 

 

Rozwiązanie: 

 

Gdzie:  

                         

 

 

Siła harmoniczna- siła proporcjonalna do wychylenia ciała z punktu równowagi skierowana do 
poczatku układu 

 

Warunki poczatkowe 

8. Wymuszony OH 

Rownanie Newtona: 

 

 

Rozwiązanie 

 

 

Rezonans 

 

 ,x0 osiąga maximum dla częstości rezonansowej wrez 

 

Rezonans polega na tym że amplituda drgao wymuszonych osiąga wartośd maksymalną 

Czestośd rezonansowa-czestośd wymuszeo dla którego następuje wzrost amplitudy. 

Przy słabym tłumieniu wrez jest prawie jak czestośd drgao swobodnych 

w-czestośd siły wymuszającej,F0-diła wymuszająca, wrez-czestośd rezonansowa, x0-amplituda 

17. Poszezone I prawo keplera 

Masa zredukowana porusza się po krzywych stozkowych a srodek masy znajduje się w ognisku 
krzywych stozkowych 

Uogulnione- planety poruszaja się po torach eliptycznych a w ognisku tych elips jest slonce. 

5. zasada zachowania energi mechanicznej Nczastek (bez dowodu) 

Ek+Ep = const 

16. 

Każda czasta przyciaga kazda inna czastke siła grawitacyjna o wartosci 

 

Zasada superpozycji. 

Całkowita siła działająca na czastke jest suma wektorowa sił pochodzacych od innych czastek 

Wartosc stałej grawitacyjnej z jednotka 

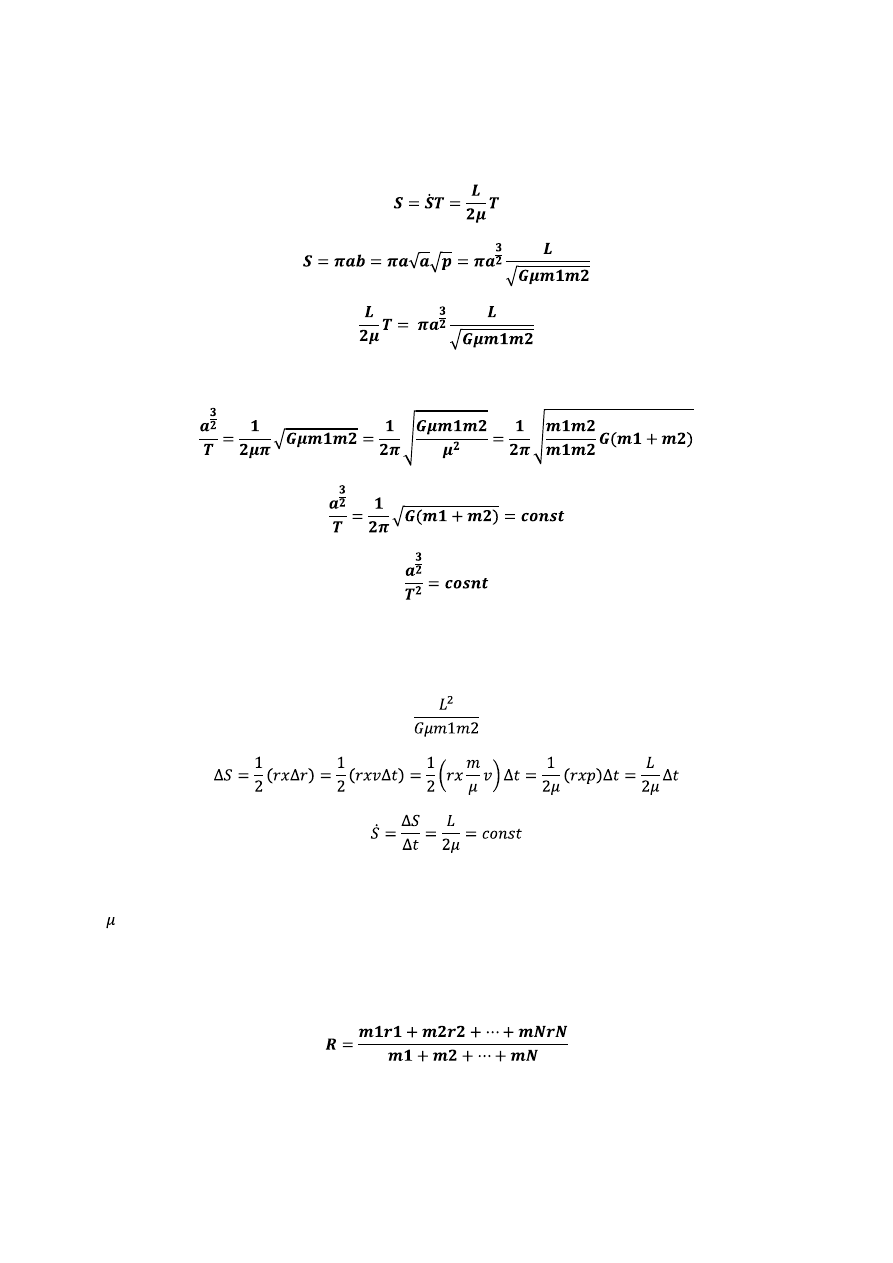
18. Udowodnienie III prawa keplera 

 

 

 

 

 

 

 

 

19. Udowodnienei II prawa keplera 

 

 

 

S-powierzchnia zakreślana przez promieo wodzący planety 

- masa zredukowana, T –okres, p-parametr krzywej stożkowej 

12. Środek masy układu N czastek 

Można wyznaczyd wektor wodzący środka masy dany rowaniem 

 

1,b  opis predkosci przyspieszenia sredniego i chwilowego ( limesy, delty i te sprawy) 

20. Prawo hooka 

 

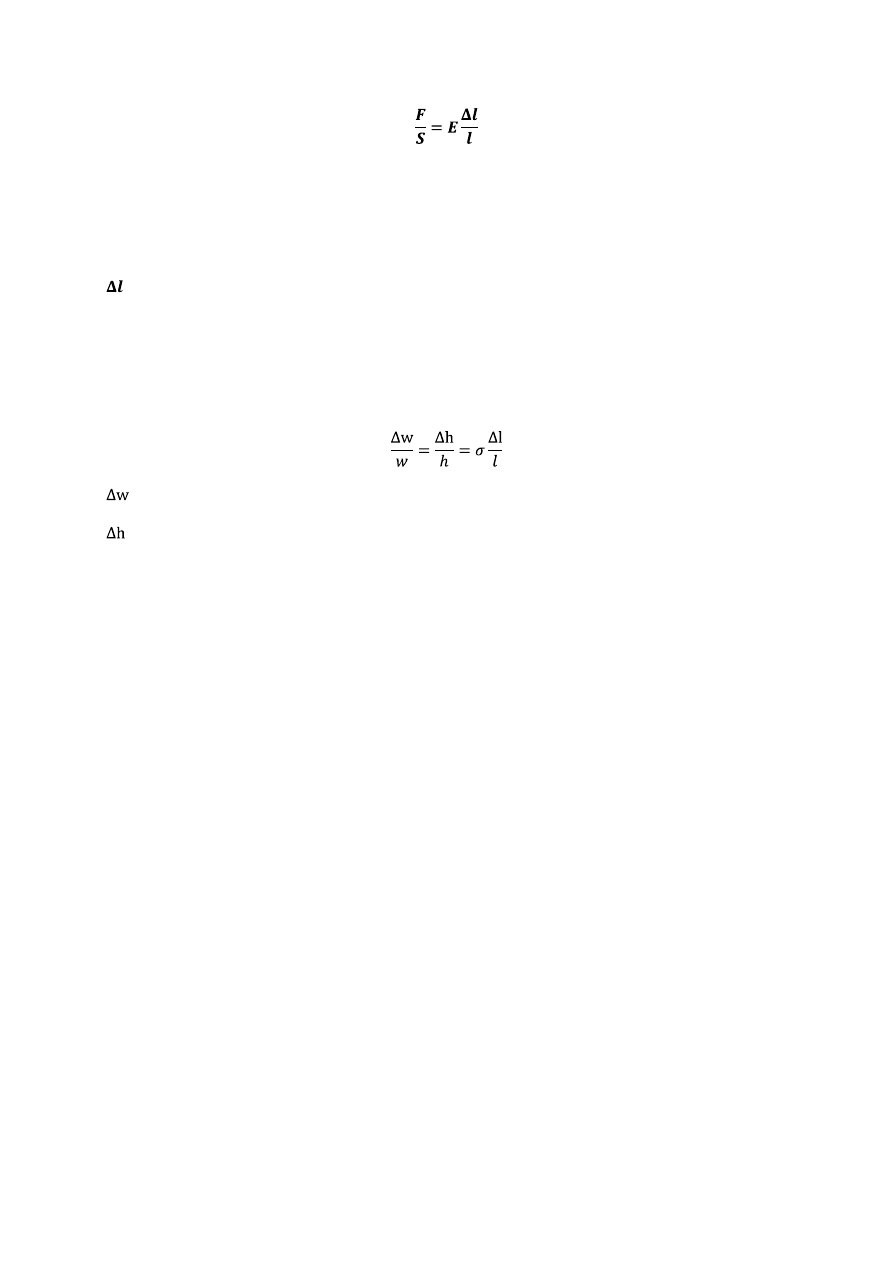
F-siła 

S-pole 

l-długosc poczatkowa 

 –wydluzenie 

E-moduł younga (wielkośd uzależniajaca odksztalcenie liniowe od naprezenia, stała materiałowa) 

Odksztalcenie ciała pod wpływem siły jest wprost proporcjonalne do tej siły 

21. wspolczynnik poissona- okresla w jaki sposób odksztalca się ciało 

 

- odksztalcenie na szerokosc (width) 

- odksztalcenie na wysokosc (height)