4-1

4. Warunki brzegowe i zależności energetyczne w polu EM

4.1. Warunki brzegowe na powierzchniach rozgraniczających dwa różne

ośrodki

Najwygodniejszą podstawę do otrzymania związków między składowymi
stycznymi i normalnymi (do powierzchni granicznej) pól EM po obu stro-
nach powierzchni rozgraniczającej dwa różne ośrodki stanowi całkowa po-
stać równań Maxwella. Rozważmy dwa równania

d

d

C

S

t

∂

⎛

⎞

⋅ =

+

⋅

⎜

⎟

∂

⎝

⎠

∫

∫

D

H l

J

s

v

(prawo Ampére’a z poprawką Maxwella) (4.1)

d

d

C

S

t

∂

⋅ = −

⋅

∂

∫

∫

B

E l

s

v

(prawo

Faradaya)

(4.2)

Dopuszczamy możliwość istnienia ładunku powierzchniowego ρ

S

[C/m

2

]

i powierzchniowej gęstości prądu J

S

[A/m] na rozgraniczającej po-

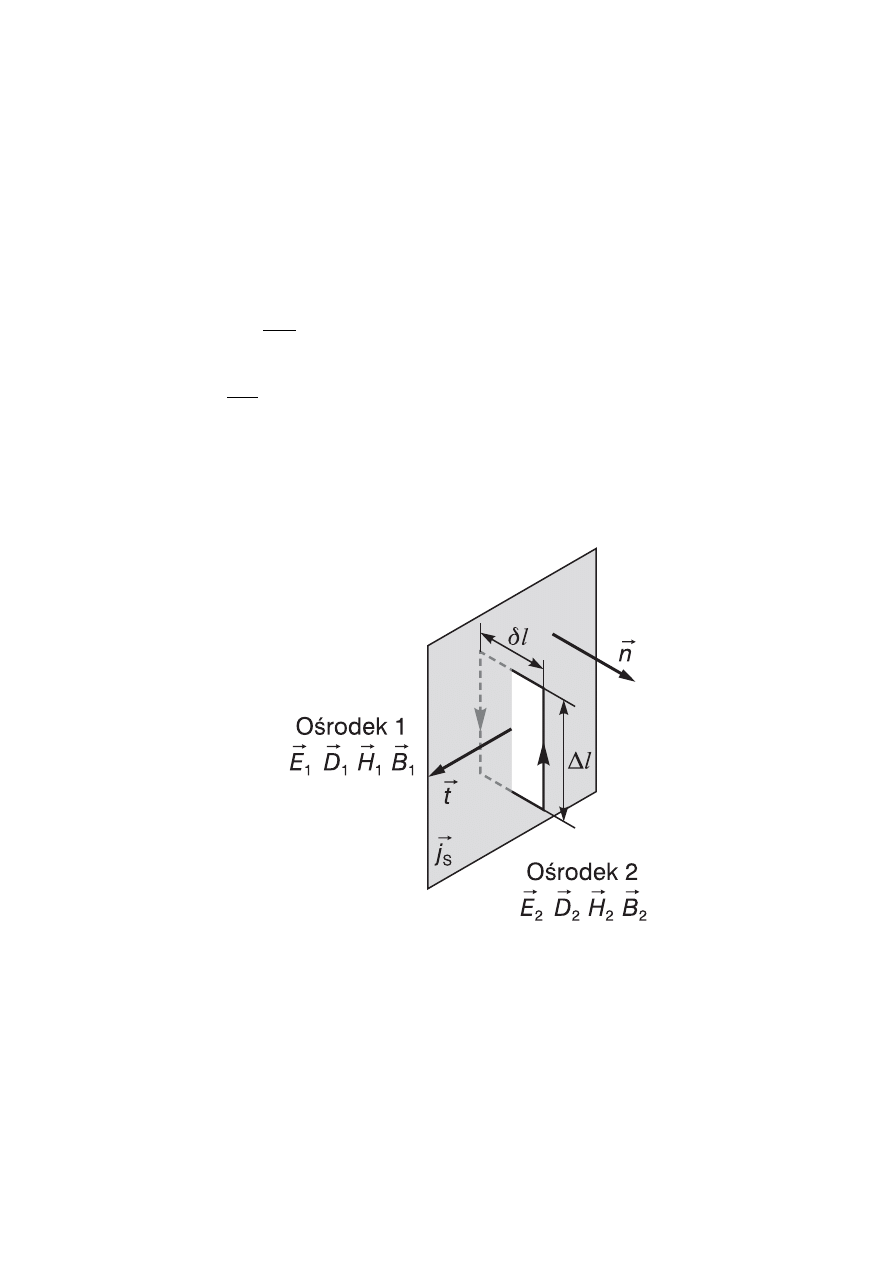
wierzchni. Odpowiednia konstrukcja geometryczna pokazana jest na ry-
sunku 4.1.

Rys. 4.1. Infinitezymalnie cienki kontur C

będący brzegiem powierzchni S.

Wektor ˆn jest jednostkowym wektorem normalnym do powierzchni roz-
graniczającej dwa ośrodki (skierowanym od ośrodka 1 do 2), wektor

ˆt

jest

jednostkowym wektorem normalnym do powierzchni S ograniczonej
krzywą C. Zakładamy, że rozmiary liniowe krzywej C są na tyle małe, że
całki można zastąpić odpowiednimi iloczynami, ponadto

l

l

δ

<< Δ

(4.3)

4-2

W całkach po dłuższych bokach prostokąta we wzorach (4.1) i (4.2) infini-
tezymalny przyrost dl zapisujemy w postaci

ˆ ˆ

d

dl

= ×

l t n

w ośrodku 2

(4.4a)

ˆ ˆ

d

dl

= − ×

l

t n

w ośrodku 1

(4.4b)

Rozpatrzmy najpierw wzór (4.2). W całce konturowej po lewej stronie
wzoru możemy pominąć wkład od krótszych boków ze względu na waru-
nek (4.3) co daje

2

1

2

1

ˆ

ˆ

ˆ

ˆ

(

) (

)

[

(

)]

l

l

−

⋅ × Δ = ⋅ ×

−

Δ

E

E

t n

t n

E

E

. (4.5)

Skorzystaliśmy z tożsamości wektorowej

(

)

(

)

(

)

⋅ × = ⋅ × = ⋅ ×

a b c

b c a

c a b

.

Prawa strona wzoru (4.2) przyjmie postać

ˆ l l

t

δ

∂

−

⋅

Δ

∂

B

t

(4.6)

W granicy

0

l

δ

→ wyrażenie to zeruje się i otrzymujemy

2

1

ˆ ˆ

[

(

)] 0

⋅ ×

−

=

t n

E

E

(4.7)

Wyrażenie (4.7) jest słuszne dla dowolnego położenia prostokątnego kon-
turu, aby tylko związany z konturem wektor

ˆ

t

pozostawał nadal prostopa-

dły do ˆn, co jest możliwe wtedy i tylko wtedy gdy

2

1

ˆ (

) 0

×

−

=

n

E

E

(4.8)

Identyczne rozważania możemy przeprowadzić dla pól magnetycznych
opisanych równaniem (4.1). W tym przypadku wygodnie jest przyjąć, że
przez powierzchnię konturu S może płynąć prąd nawet gdy

0

l

δ

→ . Prąd

ten określa wektor powierzchniowej gęstości prądu J

S

. Tak więc

2

1

S

ˆ

ˆ

ˆ

[

(

)] l

l

⋅ ×

−

Δ =

⋅ Δ

t n

H

H

J t

(4.9)

Wyrażenie to jest słuszne dla dowolnego wektora ˆt prostopadłego do ˆn,
stąd otrzymujemy warunek brzegowy dla pól magnetycznych

2

1

S

ˆ (

)

×

−

=

n

H

H

J

(4.10)

4-3

Rozważamy teraz pozostałe dwa równania Maxwella

d

d

S

V

Q

V

ρ

⋅

= =

∫

∫

D s

v

(prawo

Gaussa)

(4.11)

d

0

S

⋅

=

∫

B s

v

(bez

nazwy)

(4.12)

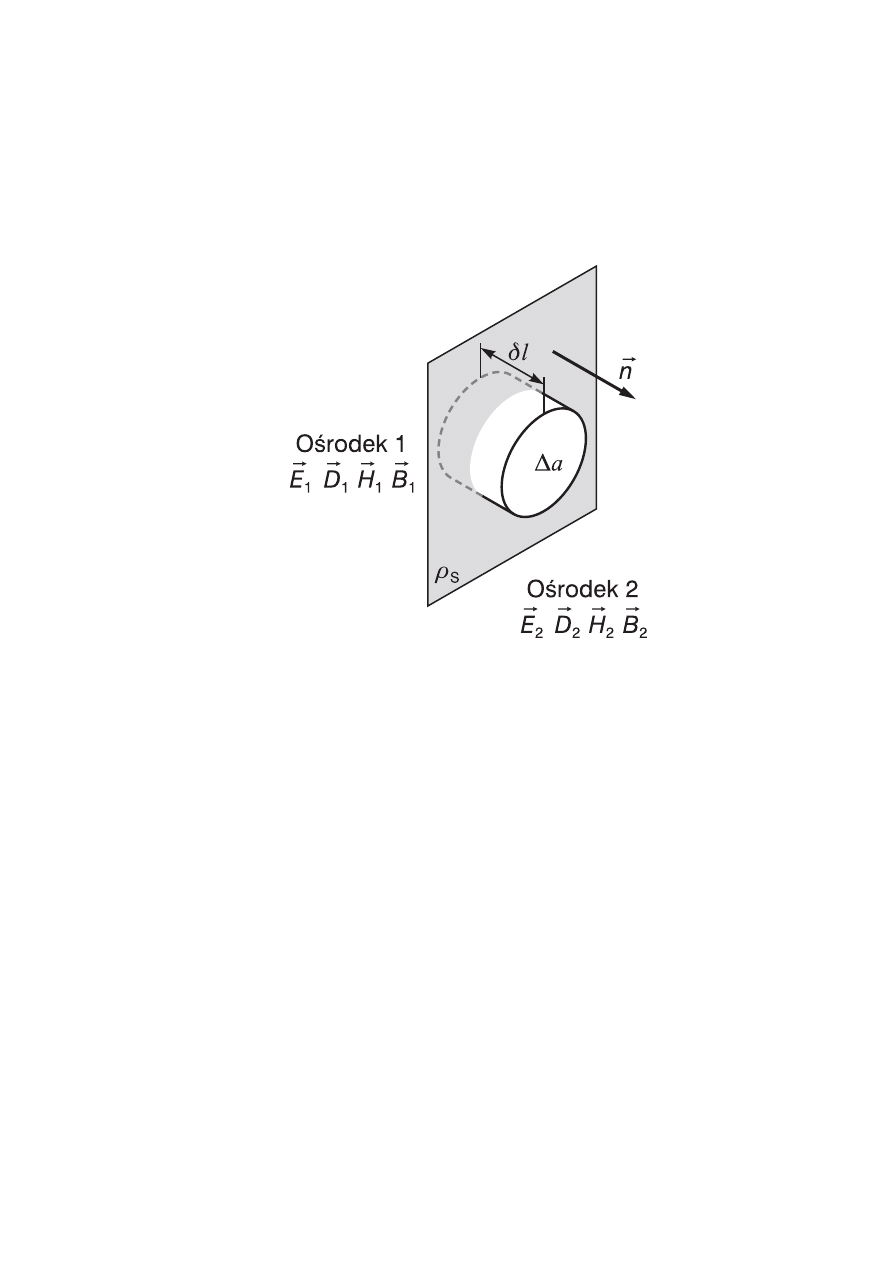
Przeanalizujmy pola w walcowej objętości V (o powierzchni S) przedsta-
wionej na rys. 4.2.

Rys. 4.2. Obszar całkowania V ograniczony powierzchnią cylindryczną S.

Δa jest powierzchnią podstawy walca.

Z równania (4.11) przyjmując

0

l

δ

→ otrzymamy

2

1

S

ˆ

(

)

a

a

ρ

−

⋅ Δ = Δ

D

D

n

(4.13)

gdzie ρ

S

jest gęstością ładunku powierzchniowego rozumianego podobnie

jak powierzchniowa gęstość prądu.
Ostatecznie otrzymujemy kolejny warunek brzegowy dla pola elektrycz-
nego

2

1

S

ˆ

(

)

ρ

−

⋅ =

D

D

n

(4.14)

Natomiast dla pola magnetycznego z równania (4.12) mamy

2

1

ˆ

(

)

0

−

⋅ =

B

B

n

(4.15)

4-4

Podsumowanie

Warunków granicznych używa się do powiązania ze sobą równań

Maxwella opisujących różne obszary. Otrzymujemy w ten sposób przebieg
pól w całej przestrzeni.

Wzory do zapamiętania (uwaga: normalna ˆn skierowana jest od

ośrodka 1 do 2)

2

1

ˆ (

) 0

×

−

=

n

E

E

(4.16)

2

1

S

ˆ (

)

×

−

=

n

H

H

J

(4.17)

2

1

S

ˆ

(

)

ρ

−

⋅ =

D

D

n

(4.18)

2

1

ˆ

(

)

0

−

⋅ =

B

B

n

(4.19)

Rozkładając wektory na składowe styczne do powierzchni granicznej

(z indeksem „t” – ang. tangential) oraz prostopadłe do tej powierzchni
(z indeksem „n” – ang. normal) można podać warunki równoważne wzo-
rom (4.16):

• dla składowych stycznych pól

2t

1t

0

−

=

E

E

(4.20a)

2t

1t

S

−

=

H

H

J

(4.20b)

• oraz dla składowych normalnych pól

2n

1n

S

D

D

ρ

−

=

(4.20c)

2n

1n

0

B

B

−

= (4.20d)

Przykład. Napisać warunki brzegowe dla pól zmiennych w czasie na
granicy dielektryka (ośrodek 1) i idealnego przewodnika (ośrodek 2).

W ośrodku 2 pole elektryczne musi być równe zeru, gdyż w przeciw-

nym przypadku wywoływałoby przepływ prądu o nieskończonym natęże-
niu ( J

E

σ

=

). Podobnie nie może istnieć zmienne pole magnetyczne, gdyż

zgodnie z prawem Faradaya wywoływałoby pole elektryczne co jest
sprzeczne z poprzednią tezą. Stąd warunki brzegowe przyjmą postać

t1

0

=

E

t1

S

= −

H

J

n1

S

D

ρ

= −

n1

0

B

=

Stąd wynika, że pole elektryczne jest prostopadłe, a pole magnetyczne
równoległe do granicy.

4-5

4.2. Zależności energetyczne w polu elektromagnetycznym

Żadna teoria propagacji fal nie może być uważana za kompletną jeśli nie
sformułuje się zasady zachowania energii. Powinna ona przedstawiać za-
leżności między mocą dostarczaną przez źródło fal, mocą traconą na sku-
tek dyssypacji, szybkością zmian energii magazynowanej w polu falowym
i strumieniem mocy fal. W teorii pola elektromagnetycznego relacja tego
rodzaju jest nazywana twierdzeniem Poyntinga.

Twierdzenie Poyntinga w postaci rzeczywistej

Zapiszmy równania Maxwella dla pól rzeczywistych

t

∂

∇ × = +

∂

D

H J

(4.21)

t

∂

∇ × = −

∂

B

E

(4.22)

Po pomnożeniu pierwszego z nich przez wektor E a drugiego przez wektor
H i odjęciu pierwszego od drugiego otrzymamy

t

t

∂

∂

⋅ ∇ × − ⋅∇ × = − ⋅

− ⋅

− ⋅

∂

∂

B

D

H

E E

H

H

E

E J

(4.23)

Korzystając z tożsamości wektorowej (por. tabela 1.2)

(

)

∇ ⋅

×

= ⋅ ∇ × − ⋅∇ ×

E H

H

E E

H

(4.24)

otrzymujemy postać różniczkową twierdzenia Poyntinga

(

)

0

t

t

∂

∂

∇ ⋅

×

+ ⋅

+ ⋅

+ ⋅ =

∂

∂

B

D

E H

H

E

E J

(4.25)

Całkując (4.25) po objętości V i stosując twierdzenia Gaussa

(

)d

d

V

S

V

∇ ⋅

=

⋅

∫

∫

v

v s

v

uzyskujemy całkową postać twierdzenia Poyntinga

(

) d

d

d

0

S

V

V

V

V

t

t

∂

∂

⎛

⎞

×

⋅ +

⋅

+ ⋅

+

⋅

=

⎜

⎟

∂

∂

⎝

⎠

∫

∫

∫

B

D

E H

s

H

E

E J

v

(4.26)

gdzie S jest zamkniętą powierzchnią obejmującą objętość V.
Interpretacja fizyczna: Pierwsza całka przedstawia moc dostarczaną do
układu z zewnątrz. Druga całka wyraża szybkość zmian energii magazy-
nowanej w układzie. Trzecia całka wyraża moc traconą w układzie na sku-
tek przepływu prądu przewodzenia.

Problem: Dlaczego podejrzewamy, że równanie (4.26) opisuje bilans
energii w polu elektromagnetycznym? Wskazówka: Sprawdzić jed-
nostki dla poszczególnych składników równania (E [V/m], H [A/m],
D [C/m

2

], B [Wb/m

2

= V·s/m

2

], J

0

[A/m

2

]).

4-6

Straty w polu elektromagnetycznym (dyssypacja energii)

Zinterpretowanie poszczególnych członów wzoru (4.26) zaczniemy od
trzeciej całki.

Dla pojedynczego ładunku q dostarczana mu moc P

q

(pochodna pracy

W po czasie t) przez pola elektromagnetyczne E i B wynosi

d

d

d

d

q

W

P

t

t

⋅

=

=

F l

(4.27)

gdzie: dl – infinitezymalne przesunięciem ładunku w czasie dt związane

z prędkością jego ruchu zależnością d

dt

=

l v

,

F – siła Lorentza określona wzorem

(

)

q

=

+ ×

F

E v B

.

Podstawiając powyższe zależności do wzoru (4.27) otrzymujemy

(

) d

d

q

q

t

P

q

t

+ ×

⋅

=

=

⋅

E v B v

E v

(4.28)

Pole magnetyczne nie wykonuje pracy gdyż siła magnetyczna jest prosto-
padła do prędkości.

Jeżeli mamy do czynienia z ciągłym rozkładem ładunku swobodnego

określonego gęstością ρ to we wzorze (4.28) zamiast q podstawimy

d

d

q

V

ρ

=

i całkujemy po skończonej objętości V, wtedy całkowita moc

dostarczona od pola ładunkom zawartym w tej objętości wynosi

d

d

q

V

V

P

V

V

ρ

=

⋅

=

⋅

∫

∫

E v

E J

(4.29)

W powyższym wzorze wykorzystano związek

ρ

=

v J

który wynika

z założenia, że ruch ładunków swobodnych powoduje powstanie odpo-
wiedniej swobodnej gęstości prądu J.

Ta moc odpowiada wielkości energii EM zamienianej w jednostce

czasu na energię mechaniczną lub cieplną. Musi być ona skompensowana
przez równe jej w jednostce czasu straty energii pola EM w objętości V.
Wprowadza się pojęcie objętościowej gęstości mocy strat wynikających
ze zjawiska przewodzenia

2

3

V A

W

m m

m

q

p

⎡

⎤

= ⋅

⋅

=

⎢

⎥

⎣

⎦

E J

(4.30)

która dla ośrodka izotropowego jest równa

2

q

p

E

σ

= ⋅ =

E J

(4.31)

4-7

Energia magazynowana w polach elektrycznym i magnetycznym

Zarówno w polu elektrycznym jak i magnetycznym magazynowana jest
pewna energia. Jest ona gromadzona w czasie wytwarzania pola i może
być potem wydatkowana, np. na pracę związaną z przesuwaniem ładun-
ków w polu elektrycznym. Podamy bez wyprowadzenia wzory służące do
obliczania tej energii. Założymy, że nasz ośrodek makroskopowy jest li-
niowy zarówno w odniesieniu do zjawisk elektrycznych, jak i magnetycz-
nych.

Energia pola elektrycznego gromadzona w elemencie objętości dV

jest równa

e

e

2

3

3

1

d

d

d

2

1

V C

VAs

J

2

m m

m

m

e

W

V

w V

w

=

⋅

=

⎡

⎤

=

⋅

⋅

=

=

⎢

⎥

⎣

⎦

E D

E D

(4.32)

przy czym w

e

jest nazywana objętościową gęstością energii pola elek-

trycznego.

Dla ośrodka izotropowego

2

e

1
2

w

E

ε

=

(4.33)

Podobnie energia pola magnetycznego gromadzona w elemencie ob-

jętości dV jest równa

m

m

m

2

3

3

1

d

d

d

2

1

A Wb

AVs

J

2

m m

m

m

W

V

w V

w

=

⋅

=

⎡

⎤

=

⋅

⋅

=

=

⎢

⎥

⎣

⎦

H B

H B

(4.34)

przy czym w

m

jest nazywana objętościową gęstością energii pola magne-

tycznego.

Dla ośrodka izotropowego

2

m

1
2

w

H

μ

=

(4.35)

Wykorzystując wyrażenia (4.32) i (4.34) możemy zdefiniować obję-

tościową gęstość energii całkowitej wzorem

e

m

1

(

)

2

u w

w

=

+

=

⋅ + ⋅

E D H B

(4.36)

4-8

Zauważając, że dla ośrodka liniowego zachodzą następujące tożsamości

1

(

)

2

t

t

∂

∂

=

⋅

∂

∂

D

E

E D

oraz

1

(

)

2

t

t

∂

∂

=

⋅

∂

∂

B

H

H B

(4.37)

stwierdzamy, że druga całka we wzorze (4.26) jest pochodną czasową cał-
kowitej energii pola elektromagnetycznego

d 1

d

(

)d

d

2

V

V

V

V

t

t

t

∂

∂

⎛

⎞

⋅

+ ⋅

=

⋅ + ⋅

⎜

⎟

∂

∂

⎝

⎠

∫

∫

B

D

H

E

E D H B

(4.38)

Wektor Poyntinga

Aby energia była zachowana pierwsza całka we wzorze (4.26) musi okre-
ślać moc dostarczoną do układu z zewnątrz. Wynika stąd, że wektorowa
wielkość nazywana wektorem Poyntinga

2

V A

W

m m

m

⎡

⎤

≡ ×

⋅

=

⎢

⎥

⎣

⎦

S E H

(7.19)

stanowi powierzchniową gęstość strumienia mocy przenoszoną przez pola
(falę elektromagnetyczną). Inaczej wektorem Poyntinga nazywamy ener-
gię przenoszoną przez pola w jednostce czasu na jednostkę powierzchni.

Twierdzenie Poyntinga dla pól harmonicznych (w postaci zespolonej)

Będziemy dalej opisywać harmoniczną zależność czasową wszystkich pól
i źródeł za pomocą czynnika

exp( j )

t

ω

, pisząc na przykład

j

j

*

j

1

2

( , ) Re

( )e

( )e

( )e

t

t

t

t

ω

ω

ω

−

⎡

⎤

⎡

⎤

=

≡

+

⎣

⎦

⎣

⎦

E r

E r

E r

E r

(7.20)

Przy tej konwencji pole ( )

E x

jest w ogólności polem zespolonym, a jego

amplituda i faza zmieniają się z położeniem. Dla iloczynów skalarnych ta-
kich jak

( , ) ( , )

q

p

t

t

=

⋅

E r

J r

, mamy wtedy

j

*

j

j

*

j

1

4

*

*

2j

*

2 j

1

4

( , ) ( , )

( )e

( )e

( )e

( )e

[ ( )

( )

( ) ( )

( ) ( )e

* ( ) ( )e

]

t

t

t

t

q

t

t

p

t

t

ω

ω

ω

ω

ω

ω

−

−

−

⎡

⎤ ⎡

⎤

=

⋅

=

+

⋅

+

=

⎣

⎦ ⎣

⎦

=

⋅

+

+

+

E r

J r

E r

E r

J r

J r

E r J r

E r J r

E r J r

E

r J r

(7.21)

W większości zagadnień interesują nas wartości średnie w czasie

0

1

( )d

T

q

q

T

p

p t t

T

=

∫

(7.22)

Wzór (7.21) zawiera dwa składniki zmienne w czasie, których wartość
średnia za okres wynosi zero, a więc

*

*

*

1

1

4

2

[ ( )

( )

( ) ( )

Re[ ( )

( )]

q T

p

=

⋅

+

=

⋅

E x J x

E x J x

E x J x

(7.23)

4-9

Widzimy stąd, że średnie czasowe dla iloczynów skalarnych równe są
połowie części rzeczywistej iloczynu skalarnego jednej z wielkości ze-
spolonych i sprzężenia zespolonego drugiej.

Dla pól harmonicznych równania Maxwella przyjmą postać

j

ω

∇ × = +

H J

D

(7.24)

j

ω

∇ × = −

E

B

(7.25)

ρ

∇ ⋅ =

D

(7.26)

0

∇ ⋅ =

B

(7.27)

gdzie zgodnie z prawą stroną zapisu (7.20) wszystkie występujące tu wiel-
kości są zespolonymi funkcjami położenia r.
Pierwsze z tych równań zapisujemy w postaci zespolonej sprzężonej,
mnożymy przez E i odejmujemy od drugiego pomnożonego przez H*.
Wykorzystując przytoczoną wyżej tożsamość wektorową uzyskujemy róż-
niczkowe twierdzenie Poyntinga w postaci zespolonej

(

*) j ( *

*)

* 0

ω

∇ ⋅

×

+

− ⋅

+ ⋅

=

E H

H B E D

E J

(7.28)

Całkując wyrażenie (7.28) po objętości V i stosując twierdzenia o dywer-
gencji (Gaussa) uzyskujemy całkową postać twierdzenia Poyntinga

(

)

(

*) d

j

*

* d

*d

0

S

V

V

V

V

ω

×

⋅ +

⋅ − ⋅

+

⋅

=

∫

∫

∫

E H

s

H B E D

E J

v

(7.29)

Zdefiniujemy teraz zespolony wektor Poyntinga

*

≡ ×

S E H

(7.30)

Podobnie jak dla iloczynów skalarnych średnie czasowe dla iloczynów
wektorowych równe są połowie części rzeczywistej iloczynu wektoro-
wego jednej z wielkości zespolonych i sprzężenia zespolonego drugiej.

Uśrednienie wektora Poyntinga za okres daje

1

2

( )

Re(

*)

T

t

=

×

S

E H

(7.31)

4-10

Wykazać, że średnia czasowa (po okresie) rzeczywistego wektor Poyn-
tinga jest równa połowie części rzeczywistej zespolonego wektora
Poyntinga

1

2

0

1

( , )

( , )d

Re[ ( , )]

T

T

t

t t

T

≡

=

∫

S r

S r

S r ω

(1)

Rozwiązanie
Rzeczywisty wektor Poyntinga definiuje się jako

( , )

( , )

( , )

t

t

t

=

×

S r

E r

H r

(2)

Zespolony wektor Poyntinga ma sens tylko dla fal monochromatycznych
(o jednej częstotliwości). Opisując zależność czasową wszystkich pól
i źródeł za pomocą czynnika

exp( j )

t

ω

, pisząc na przykład

j

j

j

1

2

( , ) Re

( , )e

( , )e

( , )e

t

t

t

t

∗

−

⎡

⎤

⎡

⎤

=

≡

+

⎣

⎦

⎣

⎦

E r

E r

E r

E r

ω

ω

ω

ω

ω

ω

(3)

j

j

j

1

2

( , ) Re

( , )e

( , )e

( , )e

t

t

t

t

∗

−

⎡

⎤

⎡

⎤

=

≡

+

⎣

⎦

⎣

⎦

H r

H r

H r

H r

ω

ω

ω

ω

ω

ω

(4)

można zdefiniować zespolony wektor Poyntinga

( , )

( , )

( , )

∗

=

×

S r

E r

H r

ω

ω

ω

(5)

W tej konwencji pola

( , )

E r ω

,

( , )

H r ω

są w ogólności polami zespolo-

nym, zależnymi od częstości

ω

a ich amplituda i faza zmieniają się

z położeniem. Rzeczywisty wektor Poyntinga (2) można zapisać jako

j

j

j

j

1

4

1

4

2j

2 j

1

4

( , )

( , )

( , )

( , )e

( , )e

( , )e

( , )e

[ ( , )

( , )

( , )

( , )]

[ ( , )

( , )e

( , )

( , )e

]

t

t

t

t

t

t

t

t

t

∗

−

∗

−

∗

∗

∗

∗

−

=

×

=

⎡

⎤ ⎡

⎤

=

+

×

+

=

⎣

⎦ ⎣

⎦

=

×

+

×

+

+

×

+

×

S r

E r

H r

E r

E r

H r

H r

E r

H r

E r

H r

E r

H r

E r

H r

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

(6)

Wzór (6) zawiera dwa składniki zmienne w czasie, których wartość

średnia za okres wynosi zero, a więc

1

4

1

1

2

2

( , )

[ ( , )

( , )

( , )

( , )]

Re[ ( , )

( , )]

Re[ ( , )]

T

t

∗

∗

∗

=

×

+

×

=

=

×

=

S r

E r

H r

E r

H r

E r

H r

S r

ω

ω

ω

ω

ω

ω

ω

(7)

To kończy dowód.