Wykład 07

Witold Obłoza

2 grudnia 2010

CIĄGŁOŚĆ FUNKCJI

TWIERDZENIE 81

Niech funkcja f b

,

edzie określona w O(x

0

) otoczeniu punktu x

0

. Funkcja

jest ci

,

agła w punkcie x

0

wtw, gdy jest jednocześnie ci

,

agła lewostronnie i

prawostronnie.

TWIERDZENIE 82

Niech funkcja f b

,

edzie określona w O(x

0

) otoczeniu punktu x

0

, ci

,

agła w

punkcie x

0

i niech f (x

0

) > 0 wtedy ∃O

1

(x

0

) ⊂ O(x

0

) otoczenie punktu

x

0

takie,że ∀x ∈ O

1

(x

0

)

f (x) > 0.

CIĄGŁOŚĆ FUNKCJI

TWIERDZENIE 83

Złożenie funkcji ci

,

agłych jest ci

,

agłe.

DOWOD:

Z ciągłości f i g

dla x

n

−→ x

0

mamy f (x

n

) −→ f (x

0

)

więc g(f (x

n

)) −→ g(f (x

0

)).

Jeżeli x

n

−→ x

0

to (g ◦ f )(x

n

) −→ (g ◦ f )(x

0

).

TWIERDZENIA O CIĄGŁOŚCI

TWIERDZENIE 84

Niech funkcje f, g b

,

ed

,

a określone w O(x

0

) otoczeniu punktu x

0

i ci

,

agłe

w punkcie x

0

wtedy,f ± g, f · g s

,

a ci

,

agłe w punkcie x

0

. Jeżeli ponadto

g(x

0

) 6= 0 to

f

g

jest ci

,

agła w punkcie x

0

.

DOWÓD:

Wynika natychmiast z twierdzenia o granicach sumy, różnicy, iloczynu
i ilorazu dla ciągów.

CIĄGŁOŚĆ FUNKCJI

TWIERDZENIE 85

Funkcja ci

,

agła na przedziale domkni

,

etym osi

,

aga swoje kresy.

DOWÓD:

Niech f : [a, b] −→ R będzie ciągła i niech {x

n

}

∞

n=1

⊂ [a, b] taki, że

f (x

n

) −→ M = sup{f (x) : x ∈ [a, b]}.

Ciąg {x

n

}

∞

n=1

ma podciąg zbieżny {x

n

k

} do x

0

∈ [a, b].

Wówczas f (x

0

) = lim

n→∞

f (x

n

k

) = M

TWIERDZENIE 86

Funkcja ci

,

agła na przedziale ma własność przyjmowania wartości

pośrednich.

CIĄGŁOŚĆ FUNKCJI

DOWÓD:

Niech a < b,

f [a, b] −→ R jest ciągła i f (a) < 0 < f (b).

Niech γ = sup{x ∈ [a, b] : f ([a, x]) ⊂ (−∞, 0]} ≤ b.

Wówczas f (γ) = 0.

Gdyby f (γ) 6= 0 to w pewnym otoczeniu γ funkcja f nie przyjmowałaby
wartośxi 0 i otrzymalibyśmy sprzeczność z określeniem γ.

Niech a < b,

f [a, b] −→ R jest ciągła i f (a) < c < f (b).

Wówczas dla g(x) = f (x) − c

g(a) < 0 < g(b) więc istnieje γ ∈ (a, b)

takie, że g(γ) = 0, czyli f (γ) = c.

CIĄGŁOŚĆ FUNKCJI

TWIERDZENIE 87

Jeżeli f : [a, b] −→ [c, d] jest ciągłą bijekcją to f jest funkcją slnie
monotoniczną.

DOWÓD:

Przypuśćmy, że istnieją x

1

, x

2

, x

3

∈ [a, b] takie, że x

1

< x

2

< x

3

i

f (x

1

) < f (x

2

) > f (x

3

).

Wówczas dla c ∈ (max{f (x

1

), f (x

3

)}, f (x

2

) istnieją u

1

∈ (x

1

, x

2

)

oraz

u

2

∈ (x

2

, x

3

) takie, że f (u

1

) = c = f (u

2

).

Sprzeczność z injektywnością dowodzi silnej monotoniczności.

TWIERDZENIE 88

Jeżeli f : [a, b] −→ [c, d] jest ciągłą bijekcją to f

−1

jest funkcją silnie

monotoniczną i ciągłą.

CIĄGŁOŚĆ FUNKCJI

DOWÓD:

Niech f będzie rosnąca i niech f (x

n

) = y

n

−→ y

−

0

= f (x

0

).

Przypuśćmy, że c = sup{x

n

: n ∈ N} < x

0

.

Wówczas ∀n y

n

≤ f (c) < y

0

sprzeczne z y

n

−→ y

−

0

= f (x

0

).

Zatem ∀ε > 0

∃n

0

takie, że ∀n > n

0

f (x

0

− ε) < y

n

< y

0

.

Dla n > n

0

mamy x

−

ε < x

n

< x

0

.

Czyli f

−1

jest ciągła lewostronnie, a prawostronną ciągłość pokazujemy

analogicznie.

Dowód dla funkcji f malejacej jest podobny.

CIĄGŁOŚĆ FUNKCJI ELEMENTARNYCH

TWIERDZENIE 89

Funkcje x −→ sin x

x −→ cos x

x −→ a

x

x −→ x

α

x −→ log

a

x

x −→ tg x

x −→ ctg x

x −→ arctg x

x −→ arcctg x

x −→ arcsin x

x −→ arccos x

są ciągłe w swojej dziedzinie.

DOWÓD:

Z uwagi na

sin x − sin x

0

= 2 · sin

x−x

0

2

cos

x+x

0

2

i

ograniczoność funkcji kosinus wystarczy wykazać ciągłość funkcji

sinus w zerze.

Z uwagi na nieparzystość funkcji sinus wystarczy wykazać jej ciągłość
prawostronną w zerze.

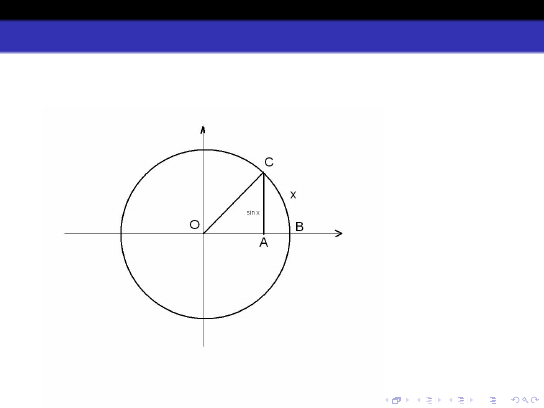
CIĄGŁOŚĆ FUNKCJI ELEMENTARNYCH

Dla x > 0 mamy 0 < sin x < x i z twierdzenia o granicy trzech funkcji
mamy lim

x→0

+

sin x = 0.

CIĄGŁOŚĆ FUNKCJI ELEMENTARNYCH

Wzór

cos x − cos x

0

= −2 · sin

x+x

0

2

· sin

x−x

0

2

implikuje ciągłość funkcji kosinus.

Z ciągłości sinusa i kosinusa wynika ciąglość tangensa i kotangensa.

Ciągłość funkcji trygonometrycznych daje nam na mocy Twierdzenia 87
ciągłość funkcji cyklometrycznych.

Ciągłość funkcji potęgowej i wykładniczej wynika z Twierdzenia 24 i
definicji Heine’go ciągłości funkcji w punkcie.

Funkcja logarytmiczna jest funkcja odwrotną do funkcji wykładniczej i na
mocy Twierdzenia 87 mamy z ciągłości funkcji wykładniczej ciągłośc
funkcji logarytmicznej.

GRANICE SPECJALNE DLA FUNKCJI

TWIERDZENIE 90

Mamy nast

,

epuj

,

ace granice specjalne:

lim

x→∞

(1 +

1

x

)

x

= e,

Jeżeli lim

x→x

0

f (x) = ∞ to lim

x→x

0

(1 +

1

f (x)

)

f (x)

= e,

lim

x→0

ln(1 + x)

x

= 1,

Jeżeli lim

x→x

0

f (x) = 0 to lim

x→x

0

ln(1+f (x))

f (x)

= 1,

lim

x→0

e

x

− 1

x

= 1,

Jeżeli lim

x→x

0

f (x) = 0 to lim

x→x

0

e

f (x)

−1

f (x)

= 1,

GRANICE SPECJALNE DLA FUNKCJI

lim

x→0

(1+x)

α

−1

x

= α,

Jeżeli lim

x→x

0

f (x) = 0 to lim

x→x

0

(1+f (x))

α

−1

f (x)

= α,

lim

x→0

sinx

x

= 1.

Jeżeli lim

x→x

0

f (x) = 0 to lim

x→x

0

sin f (x)

f (x)

= 1.