Podstawy automatycznego rozpoznawania mowy

Podstawy segmentacji sygnału mowy:

1. alfabet bazowy - dla mowy polskiej 37 fonemów
2. segmenty fonetyczne

- odcinki o jednorodnej strukturze fonetycznej decydującej o

przynależności do określonego fonemu
3. segmentacja stała

- odcinki o stałej długości - kwazistacjonarne

- "implicit segmentation" - mikrofonemy

4. segmentacja zmienna

- segmenty zdefiniowane przez transkrypcję fonetyczną

- "explicit segmentation" - dłuższe niż poprzednio

5. rodzaje segmentów dla sygnału mowy:
stacjonarne, transjentowe, krótkie, pauza.
6. granice segmentów:

dźwięcznych - płynne przejścia formantów

dźwięczny i bezdźwięczny - połączenie struktur formantowych i

szumowych

fonem i cisza - niepełna realizacja struktury widmowej

Wymagania:

- algorytm segmentacji powinien generować funkcję czasu, na podstawie której
można oznaczyć granice segmentów
- wybór metod parametryzacji
- kryteria podziału i wybór desygnatów znaczeniowych

Fonetyczna funkcja mowy :

Fonetyczna funkcja mowy jest funkcją czasu, na podstawie której można
wyznaczyć granice segmentów:

gdzie: R(t,p) – wektor parametrów w oknie czasowym (t, t+

∆

t),

∆

t – długość okna czasowego,

a

p

– waga p-tego parametru,

P – liczba parametrów,

τ

– przesunięcie czasowe, krok analizy .

( )

(

)

( )

∑

=













+

⋅

=

P

p

p

p

t

R

p

t

R

P

t

P

1

2

,

,

ln

1

τ

α

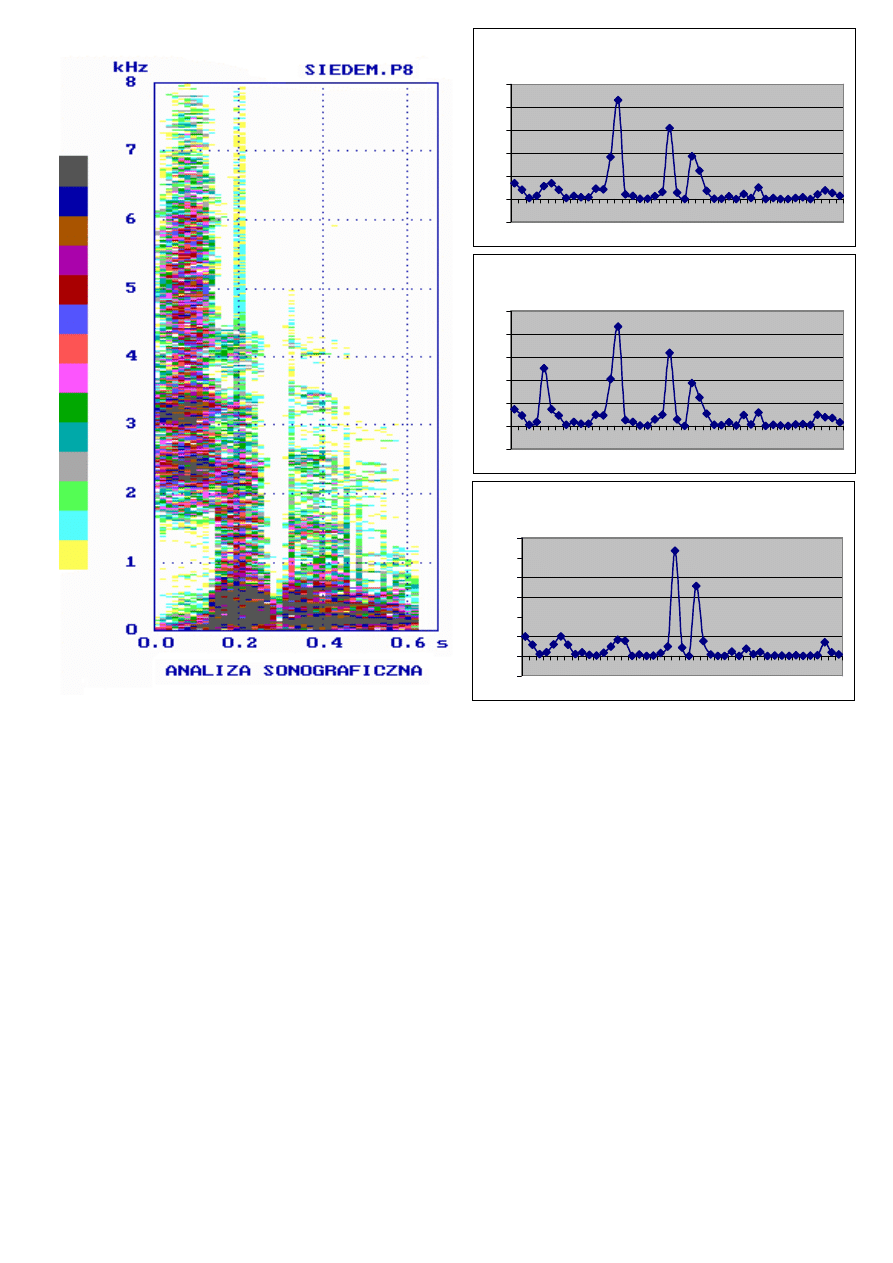
Porównanie wyników analizy sonograficznej z wynikami segmentacji

dla różnych długości P wektora parametrów

Analiza jest wykonywana na odcinku czasowym o długości około 40ms, czyli obejmuje
pojedyncze mikrofonemy. Odbywa się porównanie pomiędzy kolejnymi mikrofonemami w
oparciu o obrany system parametrów, małe różnice wskazują na to, że oba mikrofonemy
wchodzą w skład tego samego fonemu, duźe różnice wskazują na zmianę sygnału, czyli na
granicę między fonemami.

Funkcje bloku segmentacji fonematycznej:

- parametryzacja (dla mikrofonemów)
- obliczenie fonetycznej funkcji mowy
- detekcja granic segmentów (na podstawie maksimów ffm)

Problemy:

- nie każde lokalne maksimum jest granicą segmentu (stosuje się filtry

wygładzające, algorytmy eksperckie, itp.),

- dobór wag dla poszczególnych parametrów,

- dobór systemu parametryzacyjnego

Fonetyczna funkcja mowy dla P=1

-0,5

0

0,5

1

1,5

2

2,5

3

1

5

9

1

3

1

7

2

1

2

5

2

9

3

3

3

7

4

1

4

5

Fonetyczna funkcja mowy dla P=2

-1

0

1

2

3

4

5

1

5

9

1

3

1

7

2

1

2

5

2

9

3

3

3

7

4

1

4

5

Fonetyczna funkcja mowy dla P=3

-1

0

1

2

3

4

5

1

5

9

1

3

1

7

2

1

2

5

2

9

3

3

3

7

4

1

4

5

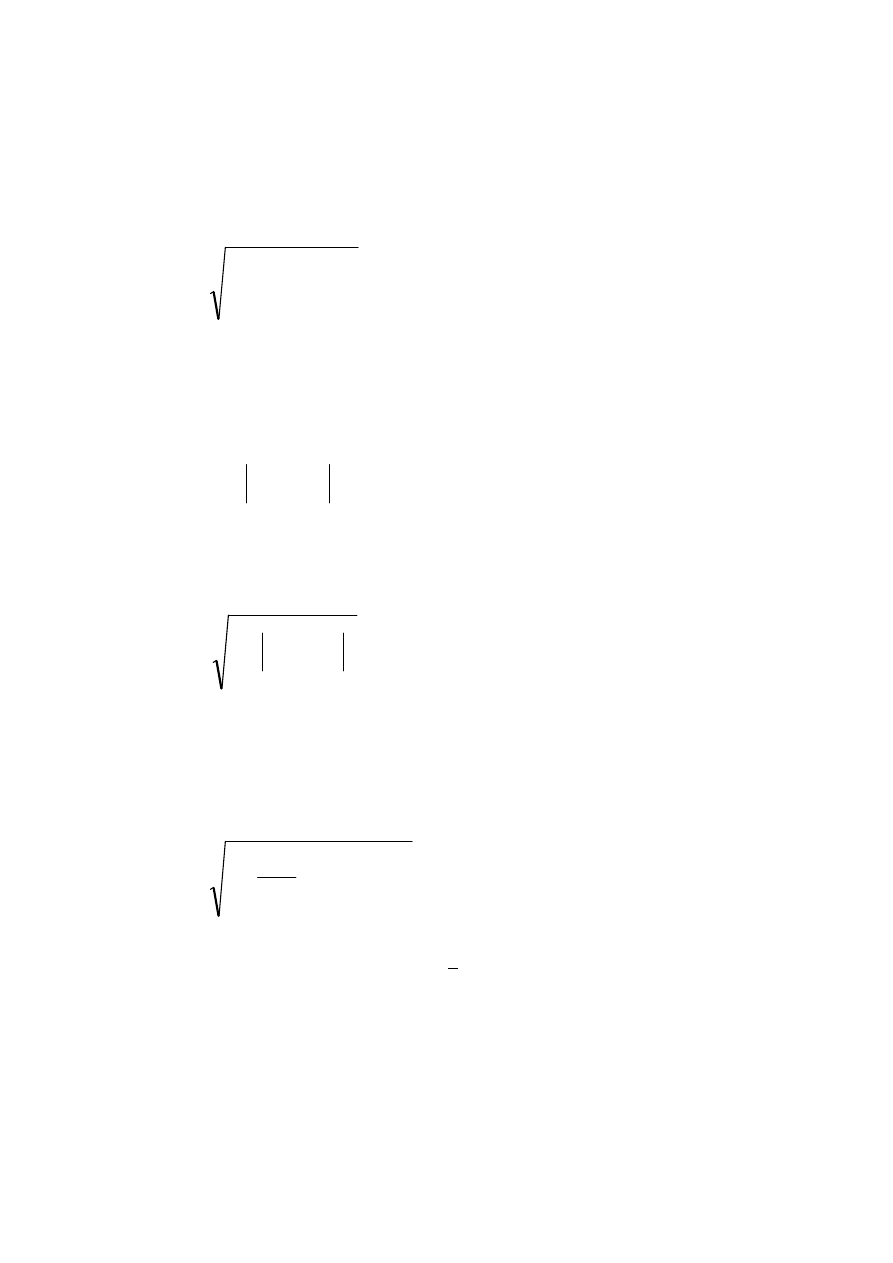
METRYKI STOSOWANE W PRZESTRZENI PARAMETRÓW:

Przestrzeń metryczna to zbiór z wprowadzonym uogólnieniem pojęcia odległości
dla jego elementów.

Euklidesa:

gdzie:
x

p

, y

p

– wartość p-tego parametru dla porównywanych obiektów,

P – liczba parametrów,

Hamminga (uliczna):

Charakteryzuje się prostotą obliczeń.

Minkowskiego:

Uwaga:
szczególne przypadki metryki Minkowskiego to: metryka Euklidesa dla r=2
i metryka Hamminga dla r=1

Euklidesa znormalizowana:

gdzie: S

P

– odchylenie standardowe parametru p populacji referencyjnej (X lub Y)

Potrzeba normalizacji metryk wynika z silnego wpływu różnic rzędów wartości poszczególnych
składowych wektora cech – różne typy mogą przyjmować wartości z różnych zakresów. Za
współczynnik normalizujący przyjmuje się zazwyczaj odwrotność wariancji (kwadrat
odchylenia standardowego). Ponadto różne parametry mogą reprezentować różne cechy
fizyczne opisywanych obiektów, obok siebie mogą występować parametry o różnych
wymiarach fizycznych, których dodawanie nie ma sensu. Normalizacja powoduje, że składniki
są bezwymiarowe.

( )

(

)

∑

=

−

=

P

p

p

p

y

x

y

x

D

1

2

,

( )

r

P

p

r

p

p

y

x

y

x

D

∑

=

−

=

1

,

( )

∑

=

−

=

P

p

p

p

y

x

y

x

D

1

,

( )

(

)

∑

=

−

⋅

=

P

p

p

p

p

y

x

S

y

x

D

1

2

2

1

,

Camberra:

Jest to metryka samonormalizująca


Czebyszewa:

Mahalanobisa:

gdzie:

C

– macierz kowariancji

Metryka Mahalanobisa jest związana tzw. regułą optymalną. Metryka Mahalanobisa
uwzględnia stopień skorelowania pomiędzy parametrami, jeśli zaś parametry są
nieskorelowane zamienia się w zwykłą ważoną metrykę Euklidesa (macierz

C

staje się

diagonalna). Przy obliczaniu odległości pomiędzy populacjami wymaga się, aby zachodziła
równość ich macierzy kowariancji (test statystyczny Boxa). Przypadek jednowymiarowy dla
tej metryki to w istocie rzeczy zmodyfikowana statystyka Behrensa-Fishera, z tym
wyjątkiem, że nie jest wymagana równość odchyleń standardowych.

FUNKCJE BLISKOŚCI:

Kosinus kierunkowy:

Tanimoto:

( )

∑

=

+

−

=

P

p

p

p

p

p

y

x

y

x

y

x

D

1

,

( )

p

p

p

y

x

y

x

D

−

=

max

,

( )

( )

( )

y

x

C

y

x

y

x

D

T

−

⋅

⋅

−

=

−

1

,

( )

y

x

y

x

y

x

B

T

⋅

=

,

( )

y

x

y

y

x

x

y

x

y

x

B

T

T

T

T

−

+

=

,

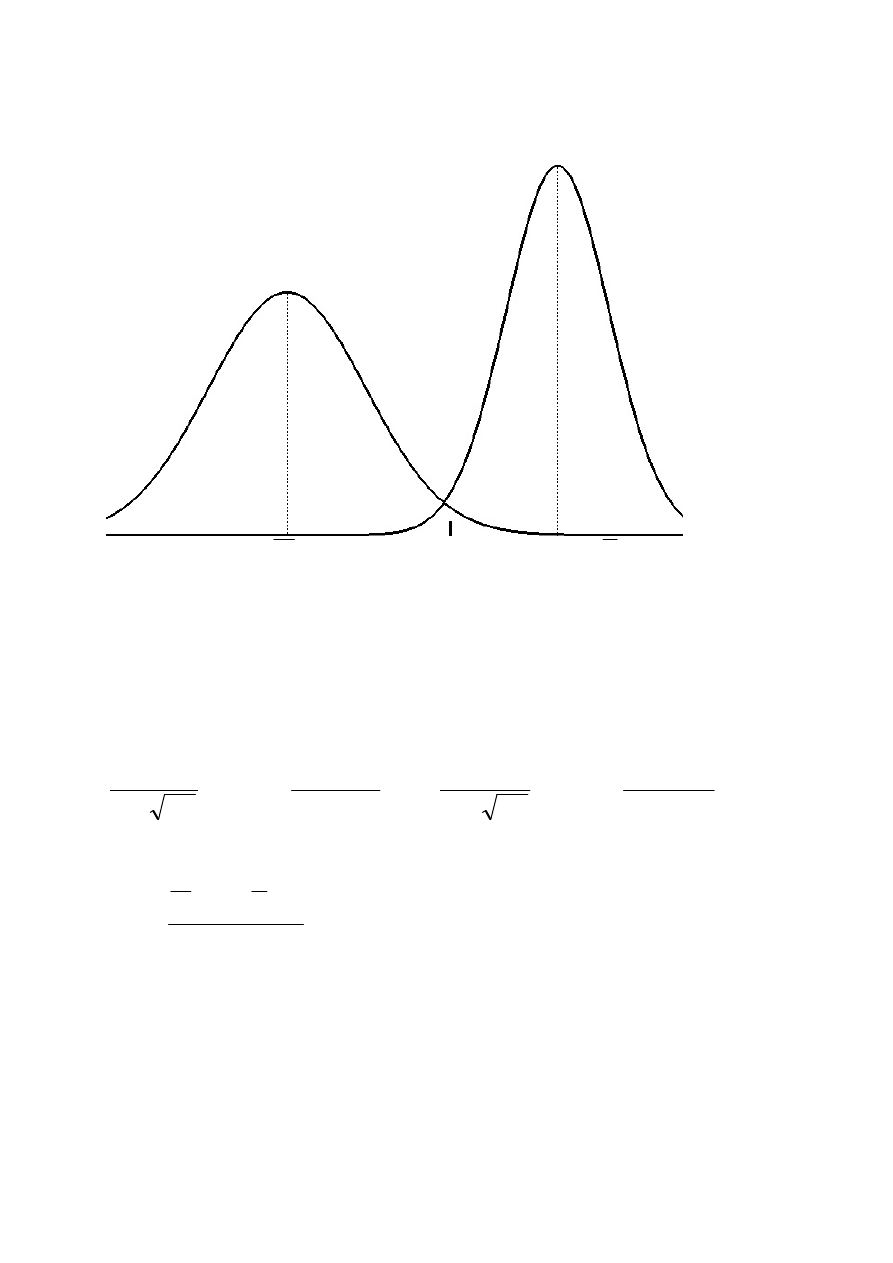
Przykład jednowymiarowego optymalnego systemu dyskryminacji

X

d

xy

Y

Przy

wyrównanym

prawdopodobieństwie

apriorycznym

wartość

dyskryminacyjna d

xy

powinna spełniać zależność:

(

) (

)

xy

xy

d

y

P

d

x

P

<

=

>

czyli:

(

)

(

)

∫

∫

∞

−

∞

+















−

−

⋅

=















−

−

⋅

xy

xy

d

d

dx

x

dx

x

2

2

2

2

2

2

1

2

1

1

2

exp

2

1

2

exp

2

1

σ

µ

π

σ

σ

µ

π

σ

zatem wartość dyskryminacyjna:

2

1

1

2

S

S

S

Y

S

X

d

xy

+

⋅

+

⋅

=

,

zapewniająca regułę o najmniejszym prawdopodobieństwie popełnienia błędu,
pod warunkiem, że założenie o kształtach funkcji gęstości prawdopodobieństwa
(gaussowskie) są spełnione

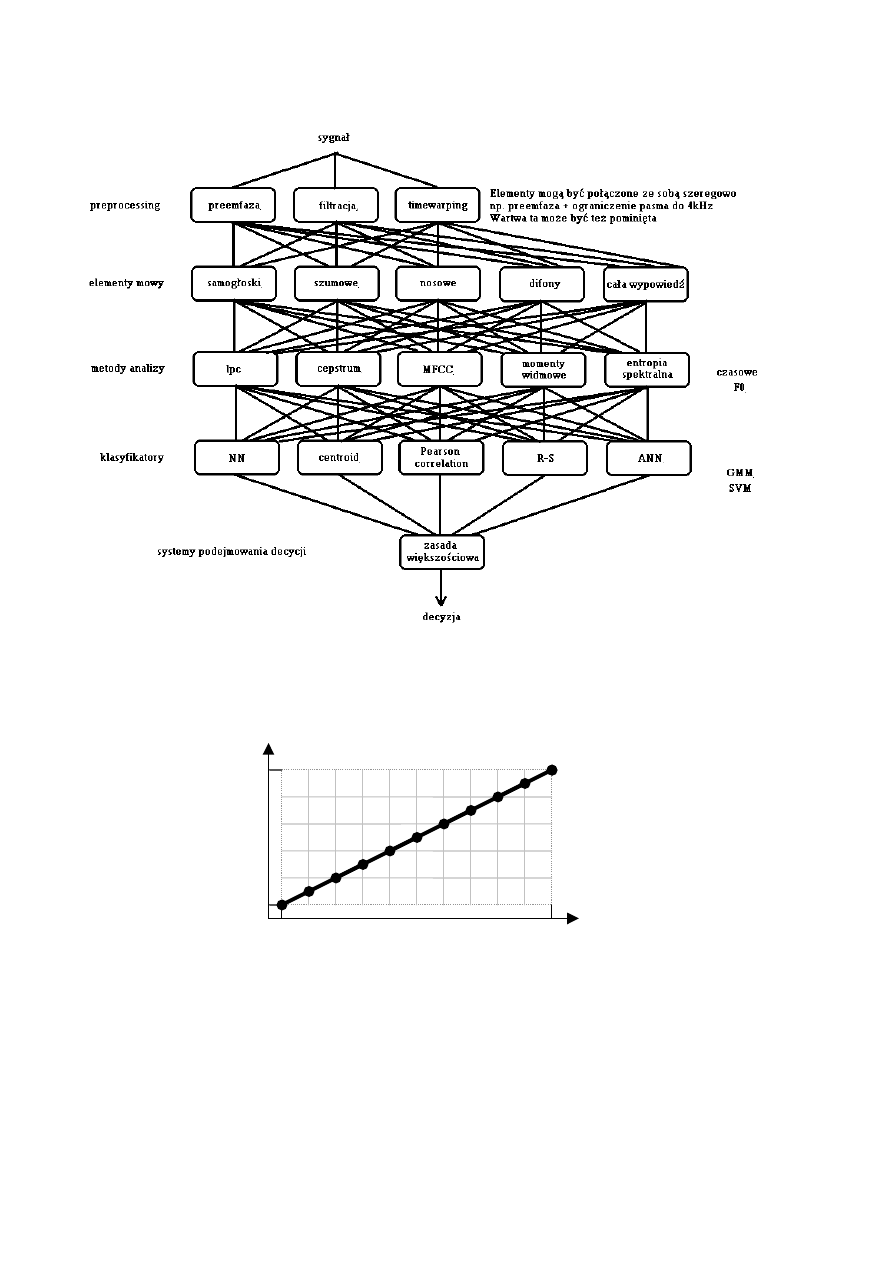
Schemat ogólny przetwarzania sygnału mowy w procesie rozpoznawania

Ilustracja liniowej normalizacji czasowej

1

1

N

M

T(t

1

, t

2

,… t

N

)

R

(r

1

, r

2

,…
r

M

)

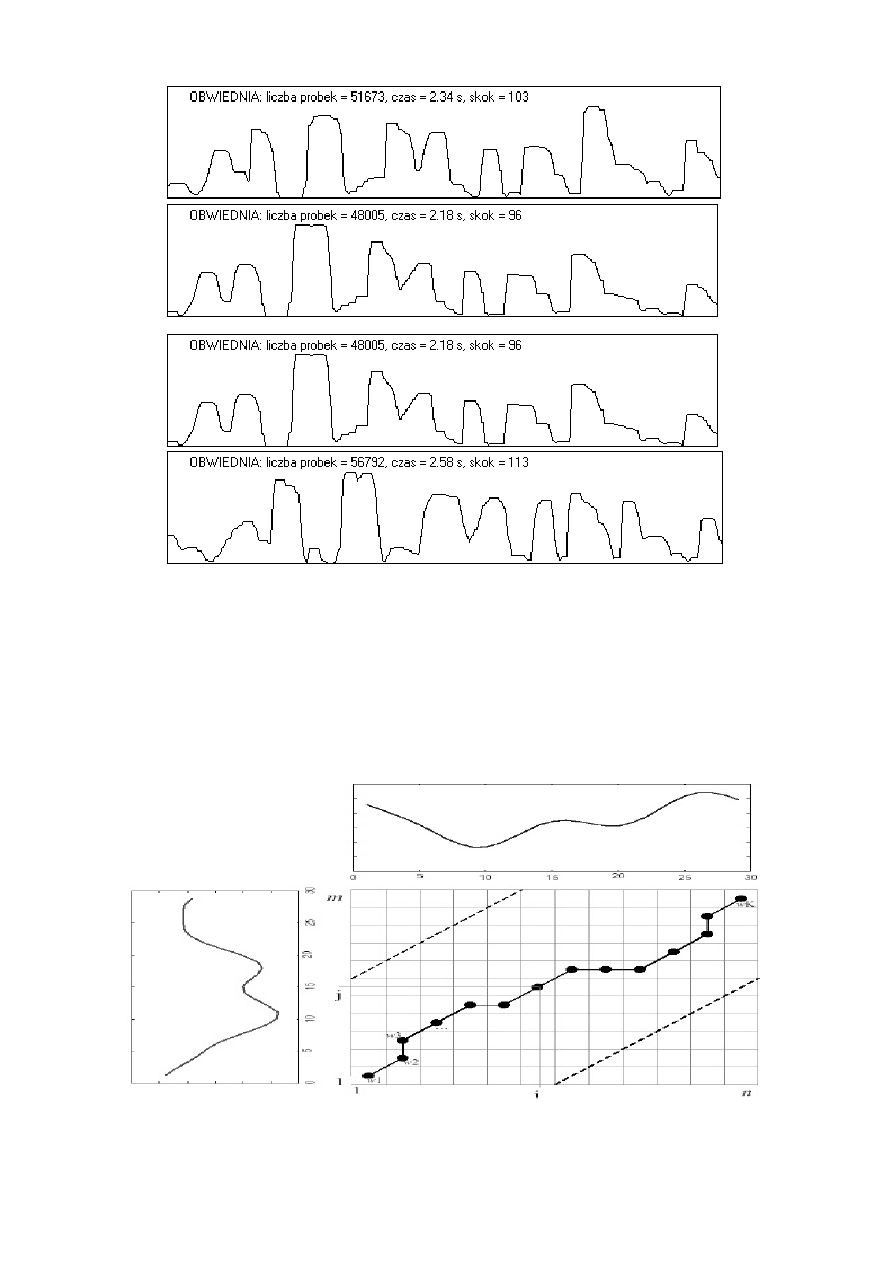
Porównanie obwiedni sygnału mowy dla czterech różnych wypowiedzi tego

samego zdania ("zdzisiek patrzy na świecące liście") przez dwóch mówców.

Pomimo zastosowania liniowej normalizacji czasowej widoczne są różnice

zależne od zmiennego tempa wypowiedzi.

Ilustracja nieliniowej normalizacji czasowej (dynamic time warping)

Procedura dynamicznego dopasowania czasowego polega na segmentacji stałej i
parametryzacji mikrofonematycznej. Umożliwia dopasowanie dwóch różnych
wypowiedzi różniących się czasem trwania i tempem poszczególnych
elementów. Parametry sygnału referencyjnego znajdują się w bazie danych (m
wektorów), zaś sygnału przeznaczonego do identyfikacji są obliczane na bieżąco
(n wektorów). Następnie obliczane są odległości pomiędzy wszystkimi
wektorami parametrów tworząc tablicę o wymiarach m

.

n. Kolejnym krokiem

jest znalezienie drogi łączącej przeciwległe narożniki tej tablicy zgodnie z
zasadą mającą na celu minimalizację sumy odległości z napotykanych komórek
tablicy. Tak obliczona suma nosi nazwę odległości skumulowanej. Warunkiem
uzyskania poprawnego wyniku jest właściwe zaznaczenie początku i końca
wypowiedzi. Po zastosowaniu procedury „time-warping” wobec wszystkich
danych z bazy można podjąć decyzję o klasyfikacji badanego sygnału.

Tablica odległości pomiędzy wektorami parametrów dwóch wyrazów (oś y

– referencyjny, oś x - rozpoznawany) w procedurze nieliniowej normalizacji

czasowej (dynamic time warping). Liczby segmentów obu wyrazów nie są

sobie równe (m=9, n=11). Lewy dolny narożnik odpowiada początkom

wypowiedzi. Zaznaczona jest ścieżka ustalająca sposób obliczania odległości

skumulowanej.

Klasyfikatory parametryczne i nieparametryczne:

Wynikiem klasyfikacji jest prawdopodobieństwo przynależności do danej klasy (w
pierwszym przypadku) albo wskazanie klasy (w drugim przypadku).
W pierwszym przypadku potrzebna jest znajomość funkcji (parametrów statystycznych)
gęstości prawdopodobieństwa dla wartości parametrów obiektów wchodzących w skład
wszystkich klas, w drugim przypadku istnieje potrzeba stworzenia modelu (lub modeli) dla
każdej klasy na podstawie pewnej liczby przykładów (obiektów) tzw. ciągu uczącego
(treningowego).
Do klasyfikatory nieparametrycznych należą klasyfikatory minimalnoodległościowe, np.:
NN, k-NN, NM, VQ.

Algorytm „najbliższy sąsiad” (NN - ang. Nearest Neighbour)
Podczas procesu uczenia zapamiętywany jest cały ciąg uczący (zbiór odniesienia).
Procedura algorytmu NN oblicza funkcję podobieństwa (w sensie ustalonej miary
odległości) pomiędzy wszystkimi obiektami ciągu uczącego, a nieznanym obiektem. Po
obliczeniu wszystkich wartości odległości, wyszukiwana jest najmniejsza z nich.
Klasyfikator podejmuje decyzję o przydziale nazwy, kodu lub numeru klasy, do której
należał obiekt ciągu uczącego, który okazał się najbliższy do obiektu rozpoznawanego.
Zalety algorytmu NN to: skrajna prostota, brak fazy uczenia (o ile pominie się selekcję
cech), możliwość redukcji zbioru odniesienia w celu przyspieszenia klasyfikacji,
zazwyczaj dość wysoka jakość klasyfikacji.
Wady algorytmu NN: wolna klasyfikacja, konieczność przechowywania całego zbioru
odniesienia w pamięci, duża wrażliwość na zbędne cechy i na szum.

Algorytm „k - najbliższych sąsiadów” (k–NN)
Algorytm ten jest modyfikacją algorytmu NN. Pozwala on zmniejszyć wrażliwość systemu
rozpoznawania w stosunku do ciągu uczącego. Procedura algorytmu k-NN dokonuje
obliczeń odległości pomiędzy obrazem rozpoznawanym, a wszystkimi obrazami ciągu
uczącego i porządkuje te odległości w kolejności rosnącej. Następnie rozpatrywanych jest
k pierwszych wartości odległości, dla których określa się, ile z nich odpowiada
poszczególnym klasom. Klasyfikator wybiera tą klasę, która najczęściej pojawiała się
wśród k pierwszych odległości. Podkreślić należy, że kolejność k najbliższych sąsiadów (w
sensie ich odległości od próbki testowej) nie ma wpływu na wynik klasyfikacji.
Zalety algorytmu k-NN: prostota koncepcji/implementacji i łatwość wprowadzania
modyfikacji, możliwość estymacji błędu na etapie uczenia przy pomocy metody minus
jednego elementu (leave-one-out), w praktyce na ogół wysoka jakość klasyfikacji;
stosunkowo szybkie uczenie (wybór k) i selekcja cech;
Wady algorytmu k-NN: wolna klasyfikacja (nieco wolniejsza niż 1-NN), konieczność
przechowywania całego zbioru odniesienia w pamięci, duża, w porównaniu z wieloma
innych klasyfikatorami, wrażliwość na zbędne cechy.
Modyfikacje algorytmu k-NN:

- odmiana ważona (ang. weighted k-NN), w której waga sąsiada zadanej próbki q

uzależniona jest od jego odległości od q.

- wprowadzenie progu k’ oznaczającego minimalną liczbę sąsiadów z danej klasy

potrzebną do przypisania danej próbki do tej klasy.

- rozmyta reguła k-NN (ang. fuzzy k-NN) poszerza przestrzeń poszukiwań poprzez

zastąpienie „twardych” etykiet (ang. hard labels, crisp labels) próbek zbioru uczącego
etykietami rozmytymi o stopniach przynależności do poszczególnych klas, które w
pewnym sensie oddają charakter sąsiedztwa danej próbki.

- „k dyplomatycznych najbliższych sąsiadów” (k Diplomatic Nearest Neighbors, k-

DNN), reguła ta szuka k sąsiadów z każdej klasy osobno, a następnie wybiera tę klasę,
dla której średnia odległość opisanych sąsiadów do testowej próbki jest najmniejsza.

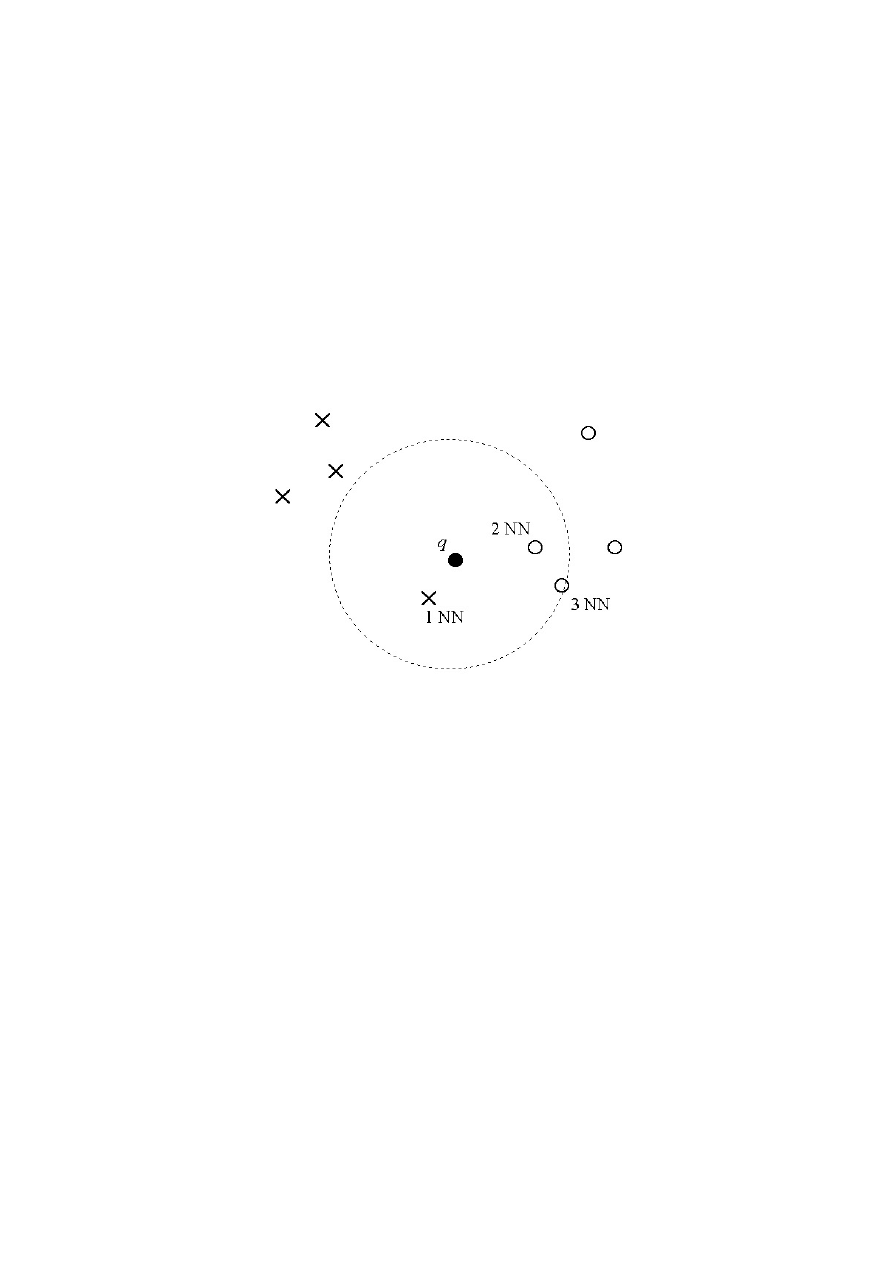
Przykład obrazujący działanie algorytmu k-NN dla k=3. Nieznany obiekt q

zostaje sklasyfikowany jako element klasy oznaczonej kółkami, gdyż

spośród trzech najbliższych obiektów danych treningowych dwa pochodzą z

tej klasy. Należy zauważyć, że dla k=1 decyzja będzie odmienna.

Algorytm „najbliższa średnia” (NM - ang. Nearest Mean)
W algorytmie NM wzorcem klasy rozpoznawanych obiektów jest wartość średnia lub
modalna (centroid). Podobnie też, jak w algorytmie NN, obliczane są odległości obiektu
rozpoznawanego od wszystkich obiektów wzorcowych (średnich) i wybierana jest
najmniejsza z nich.
Podstawowe zalety algorytmu NM w stosunku do k-NN to mniejsza ilość obliczeń oraz
brak konieczności pamiętania wszystkich obiektów ciągu uczącego. Do wad należy
zaliczyć niepoprawne działanie algorytmu w przypadku rozkładów wielomodalnych lub
opisanych funkcjami o kształtach odmiennych od gaussowskich. Wówczas obliczona
ś

rednia może leżeć z dala od obszaru zajmowanego przez obiekty treningowe.

Algorytm kwantyzacji wektorowej (VQ - ang. Vector Quantization)
W tej technice klasa jest reprezentowana przez zbiór kilku (lub więcej, zwykle < 100)
wektorów, zwanych kodowymi, które możliwie najdokładniej odzwierciedlają cechy całej
klasy (wielomodalność i rozmieszczenie w przestrzeni parametrów). Zbiór ten tworzy tzw.
książkę kodową. Podobnie jak dla metody NN, w trakcie rozpoznawania dla każdego
wektora testowego jest znajdowany jego najbliższy sąsiad z książki kodowej i jest
obliczana odległość pomiędzy nimi, która jest podstawą do podjęcia decyzji o rozpoznaniu.
Złożoność obliczeniowa rozpoznawania na podstawie kwantyzacji wektorowej jest
znacznie mniejsza w porównaniu z algorytmami NN i k-NN.
Problemem jest jednak algorytm tworzenia książki kodowej na podstawie sekwencji
treningowej. Jedną z dróg rozwiązania tego problemu jest zastosowanie standardowych
algorytmów k-średnich lub LBG. Idea polega na znalezieniu takich wektorów kodowych,
które minimalizują błąd kwantyzacji, czyli sumaryczną odległość pomiędzy sekwencją
treningową a danym modelem.
Inną metodą prowadzącą do stworzenia książki kodowej jest analiza skupień obiektów
danej klasy. Przy zastosowaniu metod klasteryzacji dla zbioru obiektów klasy wydzielane
są skupienia. Z każdego znalezionego skupienia wyznaczany jest wzorzec (centroid)
wpisywany następnie do książki kodowej. Algorytm ten nosi także nazwę: „najbliższe
skupienie” (NTuple - ang. Nearest Tuple).


Klasyfikator Support Vector Machine:
Jest możliwy do zastosowania w przypadku 2 klas (weryfikacja typu: „klasa- klasa” lub
„klasa-reszta”).
Składa się z 2 etapów:
1. nieliniowe przekształcenie hiperprzestrzeni
2. wyznaczenie hiperplaszczyzny dyskryminacyjnej (klasyfikacja metoda klasa-reszta lub
klasa-klasa)
Etap 1 ma na celu zapewnienie takiej konfiguracji parametrów, aby po etapie 2
wyznaczona hiperplaszczyzna była podstawa do optymalnego systemu decyzyjnego
(minimalne prawdopodobienstwo popełnienia bledu).
W etapie 1 stosuje sie różne funkcje nieliniowe (wielomianowa, gaussowska i inne)
dobierając odpowiednio ich współczynniki (zagadnienie Lagrange'a) - to jest etap treningu
systemu, bo opiera sie na zgromadzonych danych.
Zastosowana funkcja nazywa się kernel.
Do etapu 2 parametry dochodzą już przekształcone, dając możliwość wyznaczenia
hiperpłaszczyzny na podstawie wektora wspierającego (prostopadłego do tej
hiperpłaszczyzny, opartego na obiektach znajdujących się w sąsiedztwie regionu
granicznego).
Samo rozpoznawanie nieznanych obiektów to przekształcenie wg kernela i nastepnie
określenie po której stronie hiperplaszczyzny ten nieznany obiekt się znajduje.

Podział systemów rozpoznawania mówców

1. podział ze względu na cel rozpoznawania

- weryfikacja mówcy – potwierdzenie deklarowanej przez mówcę tożsamości

- identyfikacja mówcy – określenie, który z mówców się wypowiada, na podstawie

zbioru modeli odniesienia, przy założeniu, że mówca ma swój model głosu w bazie danych

- autentyzacja mówcy – określenie, czy głos mówcy należy do posiadanego zbioru

modeli

2. podział ze względu na zależność od tekstu

- niezależne od treści – skuteczne dla dowolnej wypowiedzi, wykorzystywane gdy nie

można liczyć na współpracę mówcy

- zależne od treści – skuteczne tylko dla niektórych wypowiedzi, wykorzystywane gdy

można się spodziewać, że mówca wymówi hasło, numer identyfikacyjny lub
podpowiedziany przez system tekst

3. podział identyfikacji mówcy ze względu na charakter zbioru modeli mówców

- z zamkniętym zbiorem – każdemu mówcy musi odpowiadać jakiś model

odniesienia, wybierany jest najbliższy spośród wszystkich modeli mówców

- z otwartym zbiorem – możliwe jest uznanie, że żaden z modeli odniesienia nie jest

wystarczająco podobny do danej wypowiedzi, wybierany jest najbliższy spośród
wszystkich modeli, pod warunkiem, że jego podobieństwo przekracza określony próg