METODY ADAPTACYJNE

Modele ze

stałym poziomem

zmiennej prognozowanej:

Metoda naiwna;
Metoda średniej ruchomej prostej i ważonej;
Prosty model wygładzania wykładniczego;
Modele autoregresji i średniej ruchomej.

Modele z

tendencją rozwojową

zmiennej prognozowanej:

Analityczne modele trendu,
Model liniowy Holta, Browna II i III rzędu;
Model trendu pełzającego z wagami harmonicznymi.

Modele z

wahaniami sezonowymi

zmiennej prognozowanej:

Metoda wskaźników;
Model Wintersa;
Metoda trendów jednoimiennych okresów;.
Analiza harmoniczna;
Metoda L.R Kleina ze zmiennymi zero-jedynkowymi.

Modele z

wahaniami cyklicznymi

zmiennej

prognozowanej

Modele autoregresji i średniej ruchomej

ARMA i ARIMA

METODY PROGNOZOWANIA NA PODSTAWIE

SZEREGÓW CZASOWYCH

Podstawowe wyróżniki:

•

brak postulatu stałości postaci analitycznej funkcji trendu;

•

uwzględniają zmiany kierunku trendu;

•

prognozy średnio i krótkookresowe;

•

zmienność szeregu determinowana przez I, TI, lub TSI;

•

błędy prognoz wygasłych -korekta modelu;

•

prognoza ilościowa o charakterze ekastrapolacyjnym;

•

wg zasady status quo, postawa pasywna;

•

prognozowanie oraz wygładzanie szeregów czasowych;

•

brak możliwości obliczenia mierników błędów ex ante.

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Prognozowanie

wyrównanie szeregu czasowego

za pomocą trendu pełzającego

szacowanie przyszłego

kształtowania się zjawisk, prognoz

za pomocą wag harmonicznych

Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Ś

rednią przyrostu W obliczamy według wzoru:

1

1

1

1

+

−

+

+

⋅

=

∑

t

n

t

n

t

W

C

W

n

t

C

1

=

- wartości współczynnika wagi harmonicznej

Prognoza -

Do ostatniego wyrazu trendu łamanego

dodajemy prostą o nachyleniu , ekstrapolując trend

W

t

t

t

Y

Y

W

ˆ

ˆ

1

1

−

=

+

+

Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

wyrównanie szeregu czasowego za pomocą trendu pełzającego

1 -

stały segment wygładzania

-

szacowanie parametrów funkcji

liniowych na podstawie kolejnych fragmentów szeregu tej samej długości

2 -

zmienny segment wygładzania

-

szacowanie parametrów

funkcji liniowych na podstawie kolejnych fragmentów szeregu różnej
długości

Wygładzeniem jest ciąg średnich :

( )

∑

=

=

1

1

1

ˆ

m

j

ij

i

t

t

Y

m

Y

)

(t

Y

ij

- wartości teoretyczne funkcji w okresie t

Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Krok I. Ustalenie wartości stałej wygładzania 1<k<n

(najczęściej k=3).

duże różnice w poziomach zjawiska >> mała wartość
stałej wygładzania.
powolne zmiany >> stała wygładzania o wyższej wartości.

Wyższa wartość stałej wygładzania >> większe
wygładzenie szeregu, >> słabsze reagowanie na zmiany
w szeregu czasowym.

Krok II. Oszacowanie parametrów funkcji trendu na

podstawie kolejnych fragmentów szeregu o
długości k.

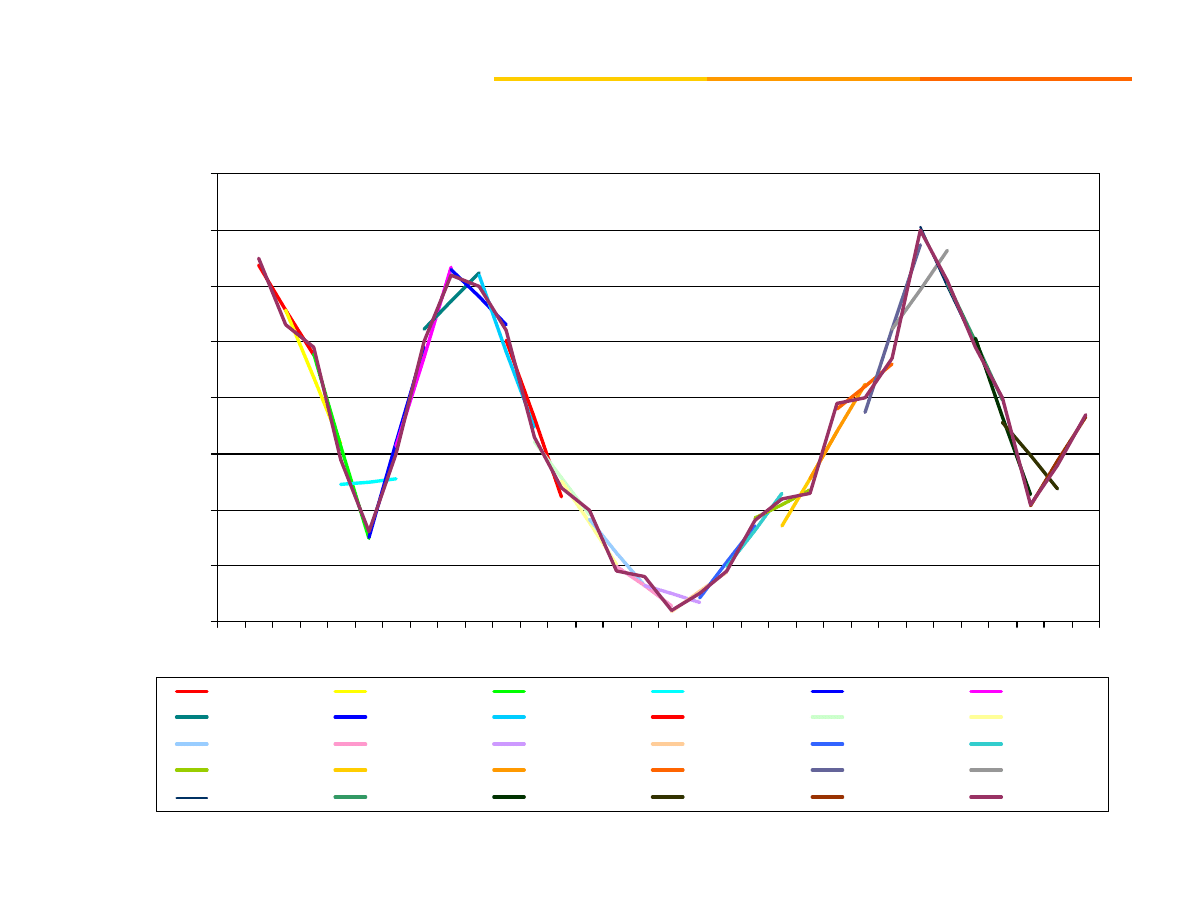
100

101

102

103

104

105

106

107

108

t

2

4

6

8

10

12

14

16

18

20

22

24

26

28

30

Liniowy 1

Liniowy 2

Liniowy 3

Liniowy 4

Liniowy 5

Liniowy 6

Liniowy 7

Liniowy 8

Liniowy 9

Liniowy 10

Liniowy 11

Liniowy 12

Liniowy 13

Liniowy 14

Liniowy 15

Liniowy 16

Liniowy 17

Liniowy 18

Liniowy 19

Liniowy 20

Liniowy 21

Liniowy 22

Liniowy 23

Liniowy 24

Liniowy 25

Liniowy 26

Liniowy 27

Liniowy 28

Liniowy 29

PKB

Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Krok III Obliczenie wygładzonych wartości

zmiennej wynikających z danej funkcji
trendu. Wartości oszacowanej odpowiada zbiór
aproksymant

, otrzymany na podstawie

funkcji trendu.

Krok IV. Obliczenie średniej wartości wygładzonej

dla każdego okresu t jako średniej
arytmetycznej wartości wygładzonych ,
wyznaczonych dla tego okresu w kroku III.

t

yˆ

t

yˆ

t

y

~

t

yˆ

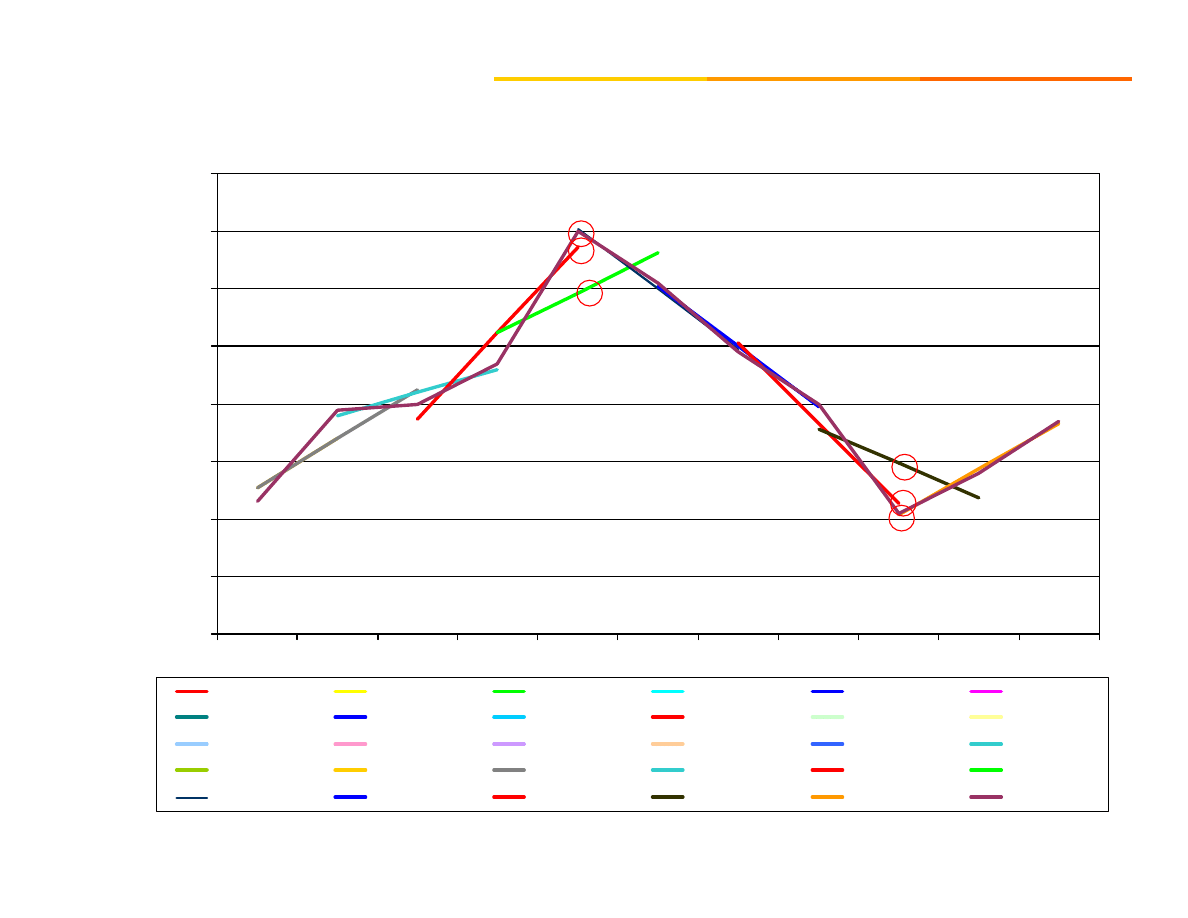
100

101

102

103

104

105

106

107

108

21

22

23

24

25

26

27

28

29

30

31

Liniowy 1

Liniowy 2

Liniowy 3

Liniowy 4

Liniowy 5

Liniowy 6

Liniowy 7

Liniowy 8

Liniowy 9

Liniowy 10

Liniowy 11

Liniowy 12

Liniowy 13

Liniowy 14

Liniowy 15

Liniowy 16

Liniowy 17

Liniowy 18

Liniowy 19

Liniowy 20

Liniowy 21

Liniowy 22

Liniowy 23

Liniowy 24

Liniowy 25

Liniowy 26

Liniowy 27

Liniowy 28

Liniowy 29

PKB

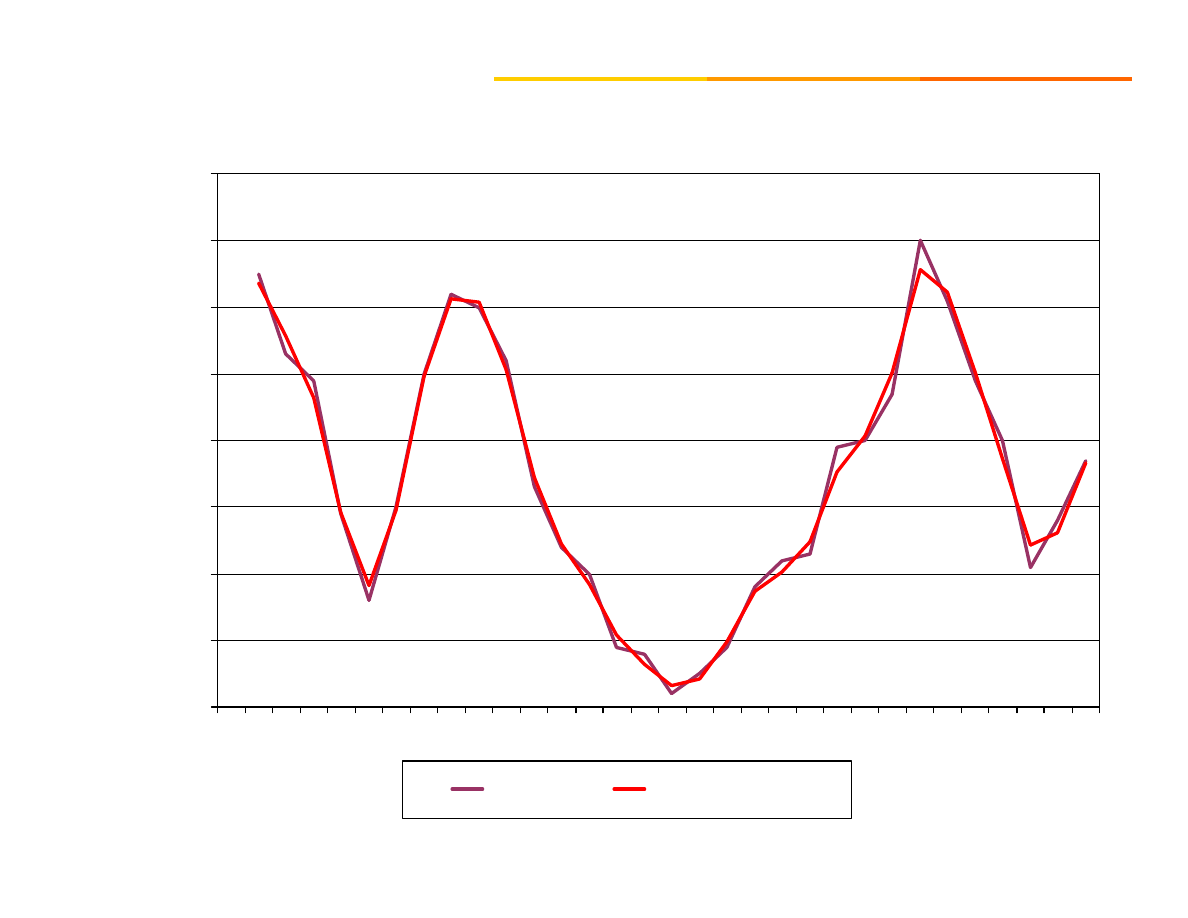
100

101

102

103

104

105

106

107

108

t

2

4

6

8

10

12

14

16

18

20

22

24

26

28

30

PKB

szereg wygładzony

Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Krok V Obliczenie przyrostów dla wartości
wygładzonych

Krok VI Nadanie wag poszczególnym przyrostom, tak

aby najnowsze przyrosty miały największe
znaczenie. Suma wag wynosi 1.

1

,...,

2

,

1

~

~

1

1

−

=

−

=

+

+

n

t

dla

y

y

w

t

t

t

1

,...,

2

,

1

1

1

1

1

1

−

=

−

−

=

∑

=

+

n

t

dla

i

n

n

C

t

i

n

t

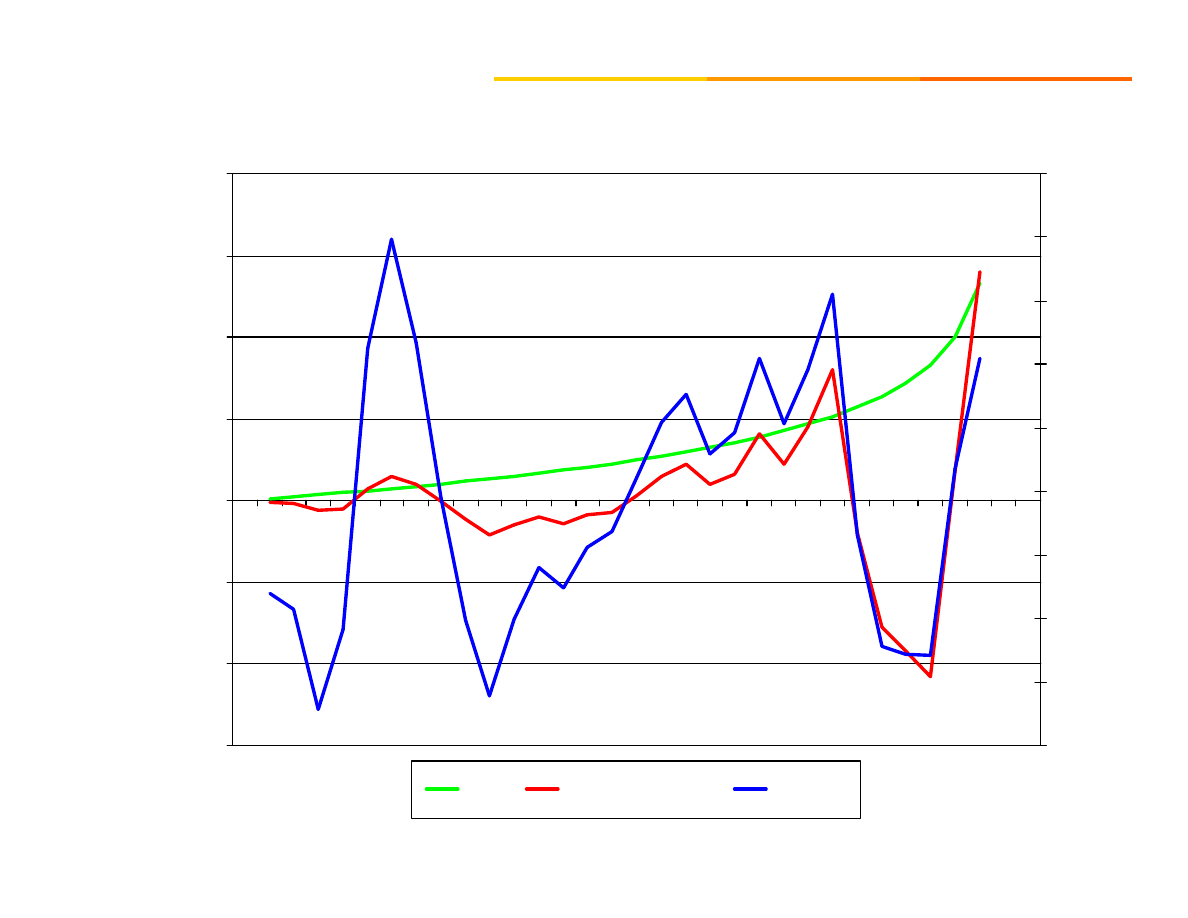
-0,15

-0,1

-0,05

0

0,05

0,1

0,15

0,2

t

2

4

6

8

1

0

1

2

1

4

1

6

1

8

2

0

2

2

2

4

2

6

2

8

3

0

3

3

-2

-1,5

-1

-0,5

0

0,5

1

1,5

2

2,5

wagi

ważone przyrosty

przyrosty

Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Krok VII Określenie średniego przyrostu trendu jako

średniej ważonej (wagami harmonicznymi)
wszystkich przyrostów obliczonych w kroku V.

Krok VIII Wyznaczenie prognozy punktowej na

moment/okres T

∑

−

=

+

+

⋅

=

1

1

1

1

n

t

t

n

t

w

C

w

w

n

T

y

y

n

T

⋅

−

+

=

)

(

~

Modele ze

stałym poziomem

zmiennej prognozowanej:

Metoda naiwna;
Metoda średniej ruchomej prostej i ważonej;
Prosty model wygładzania wykładniczego;
Modele autoregresji i średniej ruchomej.

Modele z

tendencją rozwojową

zmiennej prognozowanej:

Analityczne modele trendu,
Model liniowy Holta, Browna II i III rzędu;
Model trendu pełzającego z wagami harmonicznymi.

Modele z

wahaniami sezonowymi

zmiennej prognozowanej:

Metoda wskaźników;
Model Wintersa;
Metoda trendów jednoimiennych okresów;.
Analiza harmoniczna;
Metoda L.R Kleina ze zmiennymi zero-jedynkowymi.

Modele z

wahaniami cyklicznymi

zmiennej

prognozowanej

Modele autoregresji i średniej ruchomej

ARMA i ARIMA

METODY PROGNOZOWANIA NA PODSTAWIE

SZEREGÓW CZASOWYCH

Budowa prognozy według wzoru:

gdzie:

- prognoza dla t

-

poziom zmienne prognozowanej w okresie t-1

-

prognoza dla okresu t sporządzona w t-1

α

α

α

α

-

stała wyrównywania 0

≤

≤

≤

≤ α

α

α

α ≤

≤

≤

≤

1

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

(

)

1

1

ˆ

1

ˆ

−

−

⋅

−

+

⋅

=

t

t

t

Y

Y

Y

α

α

t

Yˆ

1

−

t

Y

1

ˆ

−

t

Y

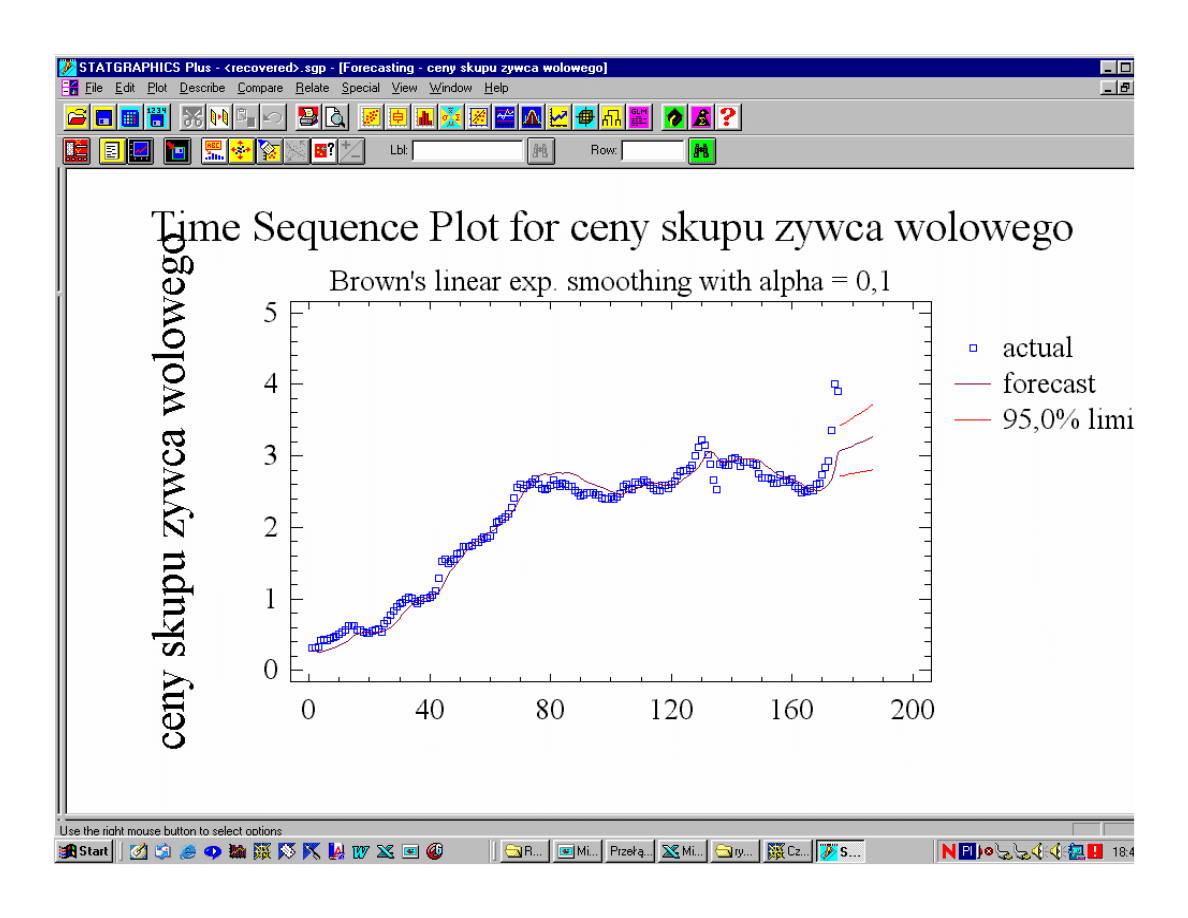
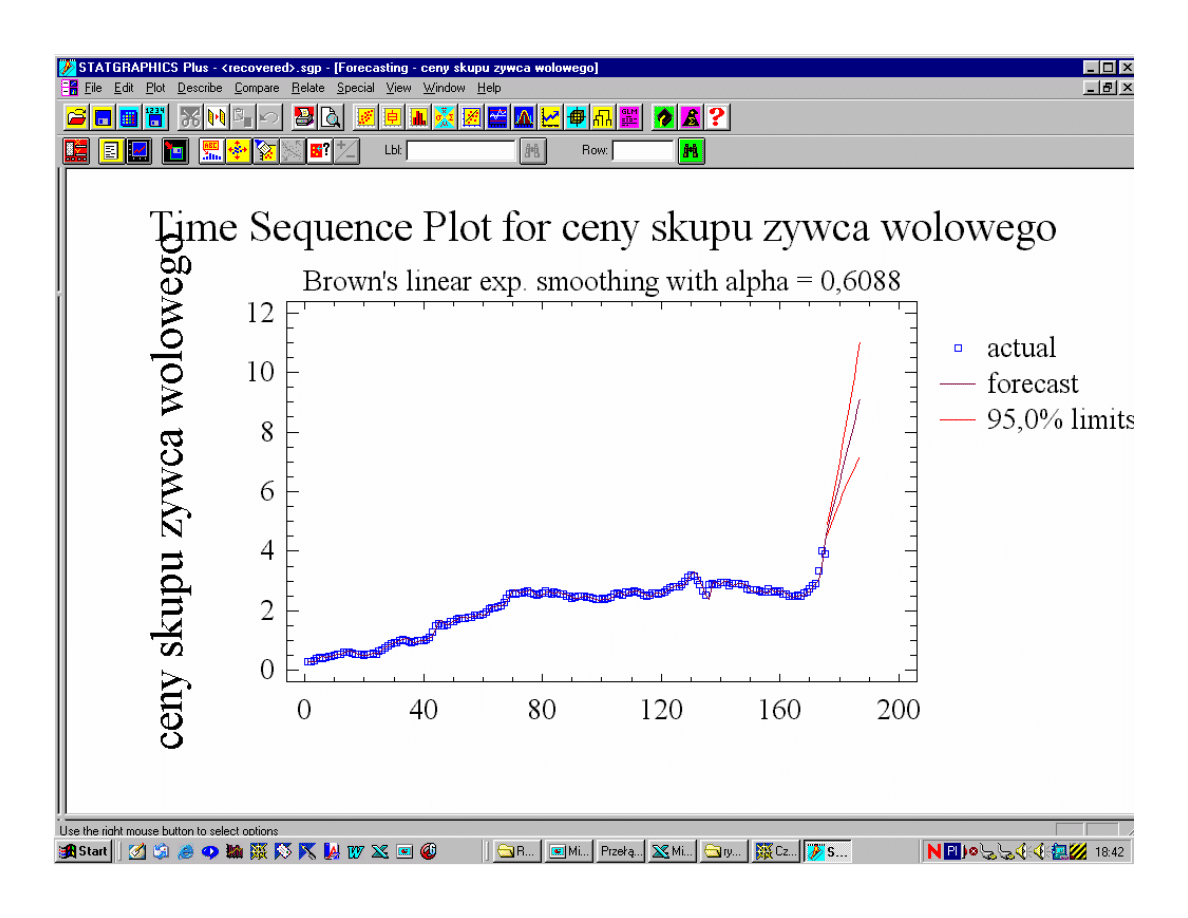
Wyrównywanie wykładnicze Browna rzędu I:

Prognoza - wartość wygładzona z okresu poprzedniego
(prognoza) skorygowana o wartość α jej błędu ex post.

1

ˆ

ˆ

−

+

=

t

t

Y

e

Y

α

Wyrównywanie wykładnicze Browna rzędu I

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

(

)

1

1

ˆ

1

ˆ

−

−

⋅

−

+

⋅

=

t

t

t

Y

Y

Y

α

α

1

1

1

ˆ

ˆ

ˆ

−

−

−

−

+

⋅

=

t

t

t

t

Y

Y

Y

Y

α

α

(

)

1

1

1

ˆ

ˆ

ˆ

−

−

−

+

−

=

t

t

t

t

Y

Y

Y

Y

α

nowe oceny poziomu zjawiska otrzymujemy, dodając do poprzednich
szacunków część błędu, w kierunku którym poprawia on nowe szacunki

Problem do rozwiązania

:

•

wybór stałej wygładzania α

α

α

α;

•

wybór wartości początkowych

•

kryterium wyboru stałej wygładzania α

α

α

α;

»

minimalizacja błędu prognoz ex post;

»

ekspercka ocena.

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Problem do rozwiązania

:

•

wybór wartości początkowych

»

za wartość początkową bierzemy średnią z

kilku pierwszych okresów

»

metodą prognozowania "wstecz”

»

estymacja metodą najmniejszych

kwadratów

»

przyjęcie, że =Y

1

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Stała wygładzania α

α

α

α, determinuje

:

•

siłę wpływu wcześniejszych informacji na budowane

prognozy (nadaje wagi);

•

wygładzenie szeregu;

•

korektę o błędy prognoz wygasłych;

•

wysoka wartość stałej wygładzania α

α

α

α :

»

słaby efekt wygładzania;

»

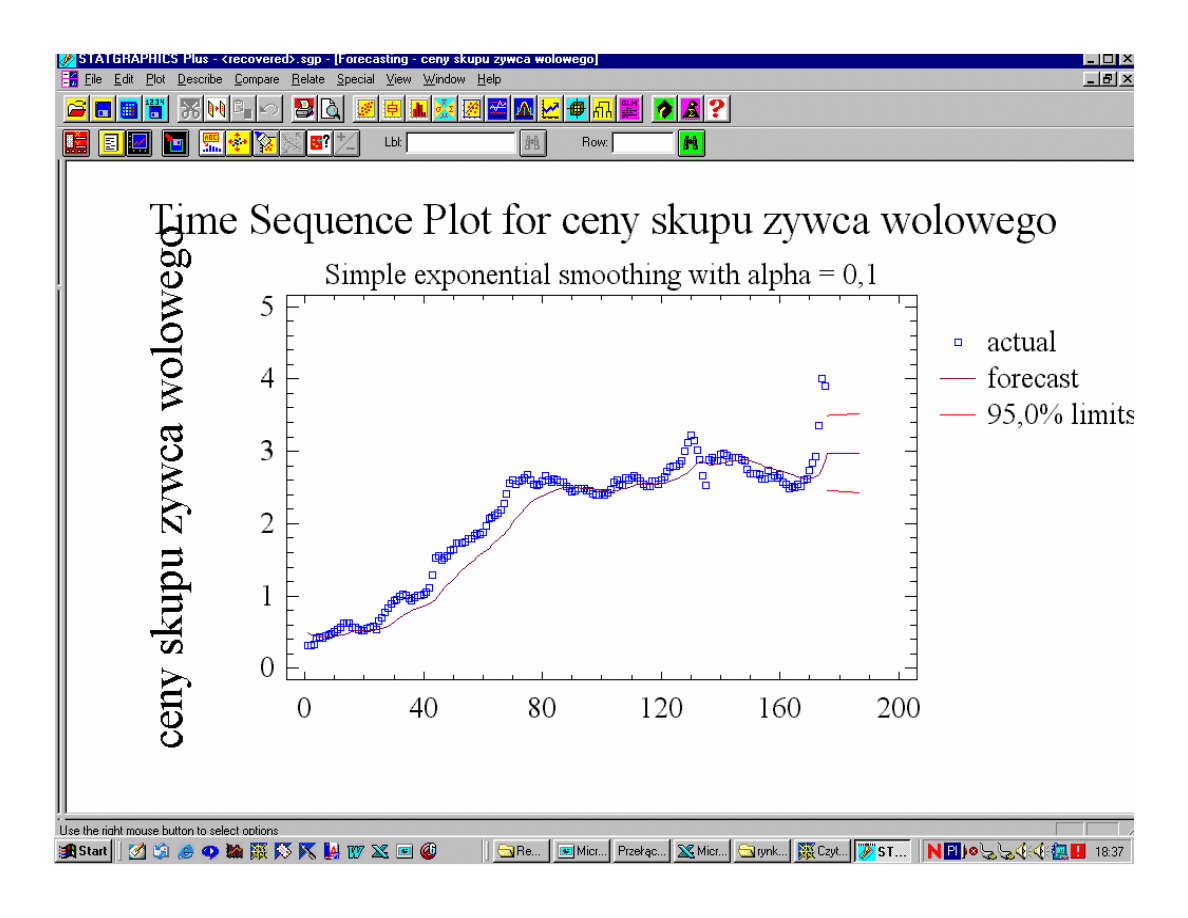
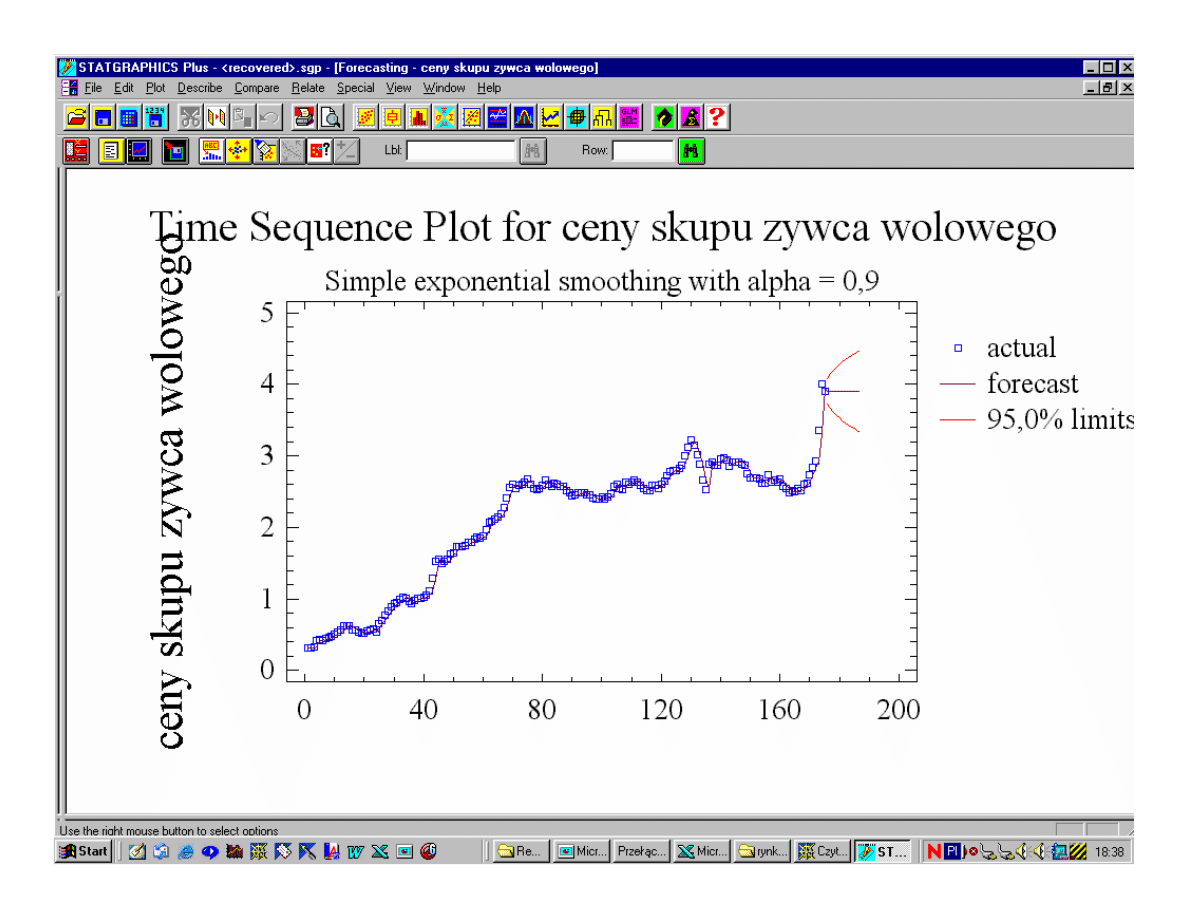
prognoza determinowana najnowszą informacją;

»

uwypuklenie krótkookresowych zmian poziomu

zjawiska;

»

silna reakcja na zmiany poziomu zmiennej

prognozowanej;

»

słaba eliminacja wpływu wahań przypadkowych;

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Wyrównywanie wykładnicze Browna rzędu II

:

gdzie:

-

wygładzona wartość zmiennej prognozowanej metodą wyrównywania

wykładniczego rzędu drugiego w okresie t

- wygładzona wartość zmiennej prognozowanej metodą wyrównywania

wykładniczego rzędu drugiego w okresie t-1

- wygładzona wartość zmiennej prognozowanej metodą wyrównywania

wykładniczego rzędu pierwszego w okresie t

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

(

)

(

)

1

1

1

1

ˆ

1

ˆ

ˆ

ˆ

1

ˆ

−

∗

−

∗

−

−

⋅

−

+

⋅

=

⋅

−

+

⋅

=

t

t

t

t

t

t

Y

Y

Y

Y

Y

Y

α

α

α

α

t

Y

∗

ˆ

1

ˆ

−

∗

t

Y

t

Yˆ

Wyrównywanie wykładnicze Browna rzędu II

:

Budowa prognozy w okresie t dla p okresów

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

(

)

(

)

1

1

1

1

ˆ

1

ˆ

ˆ

ˆ

1

ˆ

−

∗

−

∗

−

−

⋅

−

+

⋅

=

⋅

−

+

⋅

=

t

t

t

t

t

t

Y

Y

Y

Y

Y

Y

α

α

α

α

( )

t

t

t

Y

Y

t

T

∗

−

⋅

=

ˆ

ˆ

2

ˆ

( )

(

)

t

t

Y

Y

t

∗

−

⋅

−

=

ˆ

ˆ

1

ˆ

1

α

α

β

( )

( )

t

p

t

T

Y

t

p

t

1

ˆ

ˆ

ˆ

β

⋅

+

=

+

- ocena poziomu trendu w okresie

t

- ocena zmian trendu w okresie

t

nowe oceny poziomu trendu i jego zmian otrzymujemy,
dodając do poprzednich szacunków część błędu, w kierunku
w którym poprawia on nowe szacunki

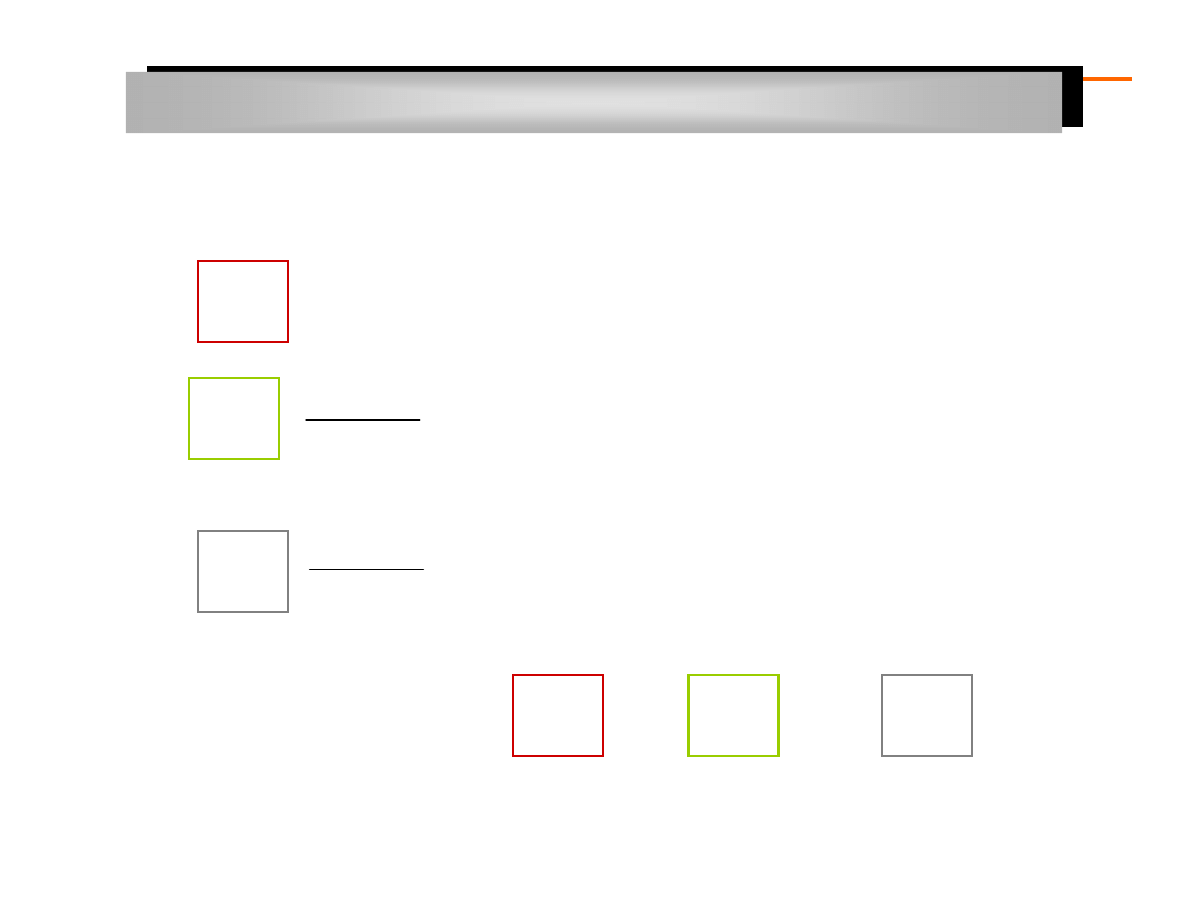
Wyrównywanie wykładnicze Browna rzędu III

:

gdzie:

-

wygładzona wartość zmiennej prognozowanej metodą wyrównywania

wykładniczego rzędu trzeciego w okresie t

- wygładzona wartość zmiennej prognozowanej metodą wyrównywania

wykładniczego rzędu trzeciego w okresie t-1

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

(

)

(

)

(

)

1

1

1

1

1

1

ˆ

1

ˆ

ˆ

ˆ

1

ˆ

ˆ

ˆ

1

ˆ

−

∗

∗

−

∗

∗

∗

−

∗

−

∗

−

−

⋅

−

+

⋅

=

⋅

−

+

⋅

=

⋅

−

+

⋅

=

t

t

t

t

t

t

t

t

t

Y

Y

Y

Y

Y

Y

Y

Y

Y

α

α

α

α

α

α

t

Y

∗

∗

ˆ

1

ˆ

−

∗

∗

t

Y

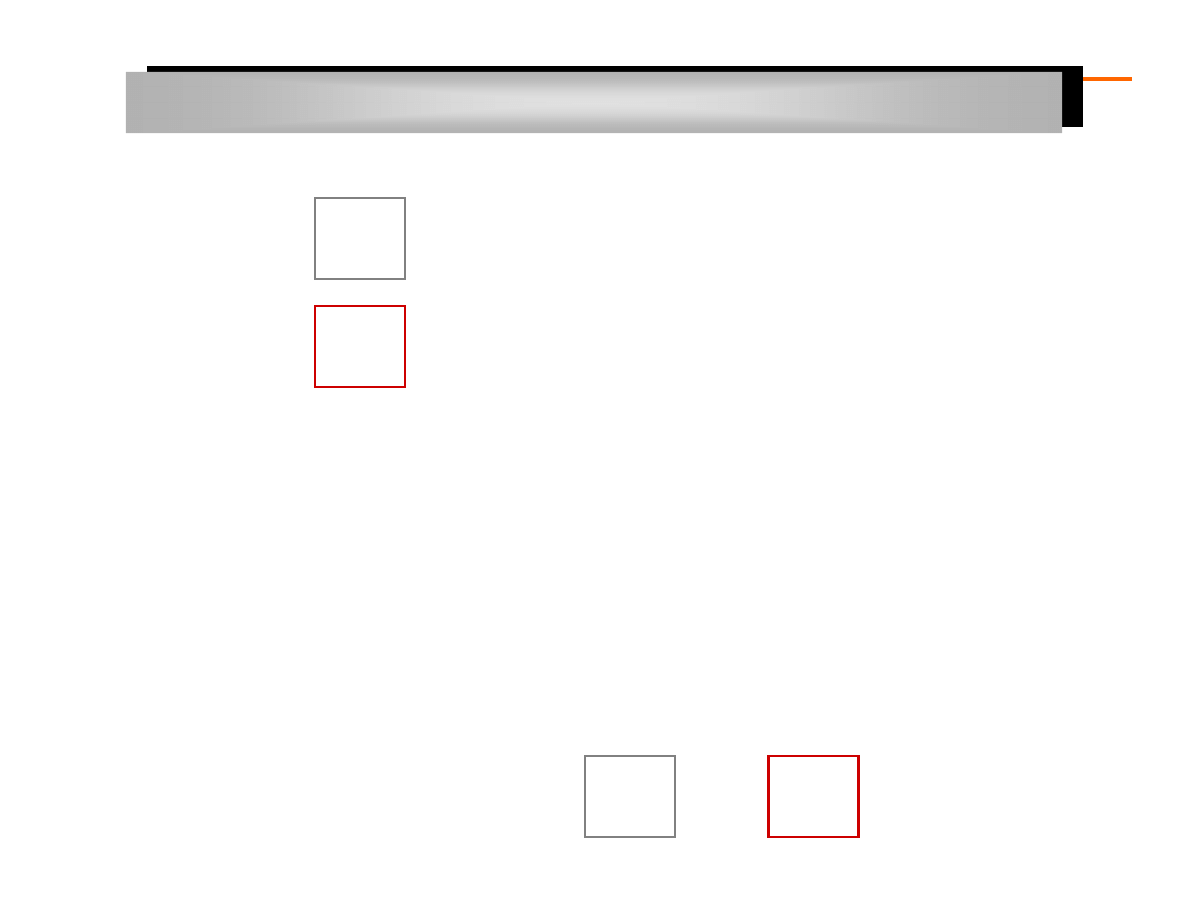
Wyrównywanie wykładnicze Browna rzędu III

:

Budowa prognozy:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

( )

( )

(

)

(

)

(

)

(

)

[

]

( )

(

)

[

]

t

t

t

t

t

t

t

t

t

Y

Y

Y

t

Y

Y

Y

t

Y

Y

Y

t

∗

∗

∗

∗

∗

∗

∗

∗

∗

+

⋅

−

−

=

−

+

−

−

−

−

=

+

⋅

−

⋅

=

ˆ

ˆ

2

ˆ

2

1

ˆ

ˆ

3

4

ˆ

4

5

2

ˆ

5

6

1

2

ˆ

ˆ

ˆ

3

ˆ

3

ˆ

2

2

2

2

1

0

α

α

β

α

α

α

α

α

β

β

( )

( )

( )

t

p

t

p

t

Y

p

t

2

2

1

0

ˆ

ˆ

ˆ

ˆ

β

β

β

⋅

+

⋅

+

=

+

Wyrównywanie wykładnicze Holta

:

gdzie:

- ocena zmian trendu w okresie t,

- ocena zmian trendu w okresie t-1,

- ocena poziomu trendu w okresie t-1

γγγγ

- stała wygładzania dla zmian trendu (0,1)

α

α

α

α

- stała wygładzania dla poziomu trendu (0,1)

Budowa prognozy:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

( ) (

) (

)

( ) (

)

(

)

( )

(

)

[

]

1

ˆ

ˆ

1

ˆ

1

ˆ

1

ˆ

1

ˆ

1

1

−

−

⋅

+

−

⋅

−

=

⋅

+

−

⋅

−

=

t

T

t

T

t

t

Y

t

Y

t

T

t

t

t

t

t

γ

β

γ

β

α

α

( )

t

1

ˆ

β

(

)

1

ˆ

1

−

t

β

(

)

1

ˆ

1

−

−

t

T

t

( )

( )

t

p

t

T

Y

t

p

t

1

ˆ

ˆ

ˆ

β

⋅

+

=

+

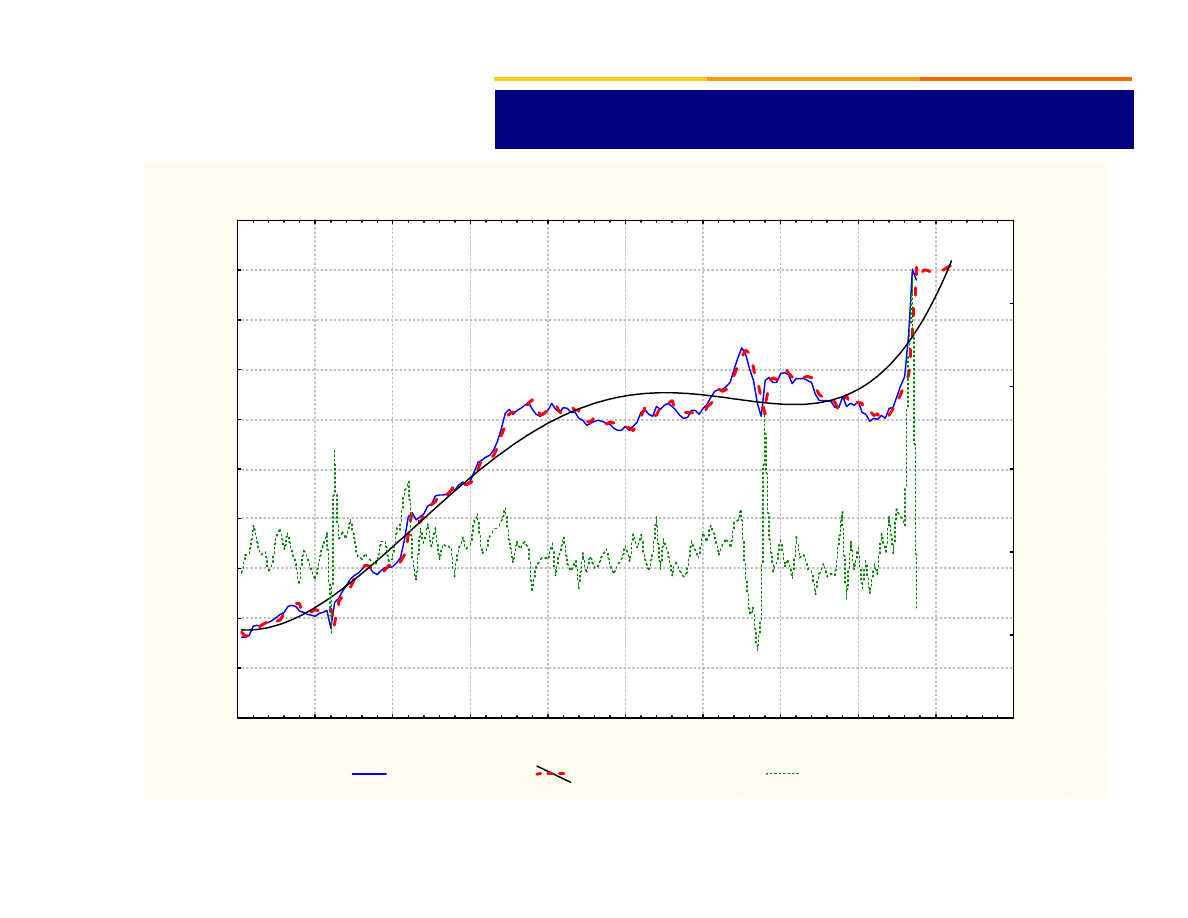
Model Holta. add.sezon.; Alfa=1,00 Delta=,116

Cena skupu(L)

Wyrówn. Szereg (L)

Reszty (R)

C

ena

s

k

upu

R

es

z

ty

-0,4

-0,2

0,0

0,2

0,4

0,6

0,8

-0,5

0,0

0,5

1,0

1,5

2,0

2,5

3,0

3,5

4,0

4,5

0

20

40

60

80

100

120

140

160

180

200

CENY SKUPU ŻYWCA WOŁOWEGO

Wyrównywanie wykładnicze Wintersa

:

gdzie:

- ocena zmian trendu w okresie t, bez sezonowości

- ocena zmian trendu w okresie t-1, bez sezonowości

- ocena poziomu trendu w okresie t-1, bez sezonowości

- wygładzone wielkości dla wahań sezonowych.

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

( )

t

1

ˆ

β

(

)

1

ˆ

1

−

t

β

(

)

1

ˆ

1

−

−

t

T

t

( )

(

)

[

]

(

) (

)

1

ˆ

1

1

ˆ

ˆ

−

⋅

−

+

−

−

⋅

=

t

T

t

S

Y

t

T

t

t

α

α

( )

( )

(

)

[

]

(

)

(

)

1

ˆ

1

1

ˆ

ˆ

ˆ

1

−

⋅

−

+

−

−

⋅

=

t

t

T

t

T

t

t

t

β

γ

γ

β

( )

( )

[

]

(

) (

)

1

ˆ

1

ˆ

ˆ

−

⋅

−

+

−

⋅

=

t

S

t

T

Y

t

S

i

t

t

δ

δ

t

Sˆ

Wyrównywanie wykładnicze Wintersa

:

Model addytywny

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

( )

( )

( )

( )

( )

( )

t

S

t

p

t

T

t

S

t

T

t

Y

p

t

t

p

t

p

t

p

t

+

+

+

+

+

⋅

+

=

+

=

ˆ

ˆ

ˆ

ˆ

ˆ

1

β

(

)

t

t

t

S

t

t

Y

ε

β

β

+

+

+

=

1

0

)

(

(

)

t

1

0

β

β

+

gdzie:

- model opisujący tendencję,

S

t

-

wahania sezonowe,

εεεε -

składnik losowy.

Budowa prognozy

Ocena poziomu trendu

Ocena zmian trendu

Sezonowość

Wyrównywanie wykładnicze Wintersa

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Model multiplikatywny

(

)

t

1

0

β

β

+

gdzie:

- model opisujący tendencję,

S

t

-

wahania sezonowe,

εεεε -

składnik losowy.

Budowa prognozy

(

)

t

t

t

S

t

Y

ε

β

β

+

⋅

⋅

+

=

1

0

( )

( )

( )

( )

( )

( )

t

S

t

p

t

T

t

S

t

T

t

Y

p

t

t

p

t

p

t

p

t

+

+

+

+

⋅

⋅

+

=

⋅

=

ˆ

]

ˆ

[

ˆ

ˆ

ˆ

1

β

Ocena poziomu trendu

Ocena zmian trendu

Sezonowość