Abstract The postfusion oscillation cycle method of
electrofused cells was applied to red blood cell mem-
branes to induce repetitive membrane ruptures and test
the mechanical membrane resistance against sequential
events of membrane strain and rupture. After producing
doublets from pairs of electrofused cells, they entered
the oscillation cycle, providing a sequence of at least
four consecutive colloidosmotic-driven rupture events.
Different gradations of colloidosmotic pressure loads be-
tween 3230 Pa and 8640 Pa were established with vari-
ous buffer types. The independence of buffer type and
geometrical and mechanical observations has been veri-
fied independently for both parts of the oscillation
sequence. With decreasing colloidosmotic inducement,
caused by repetitive oscillation cycles, an increasing sus-
ceptibility of the cell membrane against membrane rup-
ture was measurable. Since side-effects had been elimi-
nated, it could be concluded that the cell membrane re-
sistance against repetitive mechanical ruptures decreases.

Keywords Colloidosmotic pressure · Electrofusion ·
Membrane area dilatation · Membrane rupture ·
Postfusion oscillation cycle · Red blood cell

Introduction

The mechanical stability of cell membranes is a funda-
mental precondition for cell survival. Since demands for
the stability vary with the function of the tissue regarded,
stability definitions and measurement procedures also
vary widely. For example, epithelial cells need strong
cell-to-cell adhesion resources, connective tissue mem-
branes must withstand one- or two-dimensional stress and
strain, and red blood cells require a great membrane
bending elasticity [38, 39]. The mechanical properties are

time dependent and may also alter on changing physical
parameters such as temperature [44], osmolarity [40],
electromechanical strain [8] or any combination thereof.
Many methods have been developed for the deformation
measurement of red blood cells in particular, some of
which are: filterability tests with metal filters [15, 28, 41],
paper filters [17], or even single pores [28]; flow chamber
techniques such as the Ectacytometer [7, 28] and Rheo-
scope [27, 28]; viscosity measurements in capillary and
rotation viscosimeters [28], or micropipette aspiration
[10, 25, 31, 32, 33]. These techniques either require a
suspension medium of extremely high viscosity, or they
make use of physical contacts between the cell membrane
and artificial materials. Since it can be shown that physi-
cal contact with manipulating devices changes the local
composition of the cell membrane [16], contact-free
working methods can deliver more physiological results.
In order to apply the forces needed for the measurements,
electric fields can be used [4, 13, 19, 21, 30, 37]. Depend-
ing on the field characteristics, different forces act on the
cell membrane. High-frequency electric fields are used to
elongate erythrocytes [18, 19, 37], and pulse-shaped elec-
tric fields initiate red blood cell shape change [2, 23, 24],
cell and ghost fusion [6, 34, 37, 45, 46], membrane perm-
eabilization [11, 12, 34, 36, 46] or any combination there-
of. With the electrically initiated cell fusion procedure de-
scribed previously [1, 4], it is possible to create isotropic
tension in the cell membrane up to a grade that causes
measurable area dilatation followed by membrane rup-
ture, without mechanical contact of a manipulation de-
vice. This mechanical load oscillates between two states:
an almost relaxed membrane and a membrane with maxi-
mum possible tension; the latter is always terminated by a
membrane rupture. Therefore, this procedure is used to
measure the changes of membrane stability against lateral
tension and rupture.

The work presented here shows that the tolerance

against rupture of red blood cell membranes is reduced
by the occurrence of repetitive rupture events, even if
they are too short (about 4.7 ms) to induce a consider-
able lysis of haemoglobin.

M. Baumann (

✉

)

Institut für Physiologie der RWTH Aachen, Pauwelsstr. 30,
52057 Aachen, Germany
e-mail: [e-mail]
Tel.: [phone], Fax: [phone]

Pflügers Arch - Eur J Physiol (2002) 444:153–158
DOI 10.1007/s00424-001-0776-7

O R I G I N A L A R T I C L E

Martin Baumann

Cell membrane destabilizes progressively during repetitive
mechanical rupture events

Received: 14 September 2001 / Revised: 6 December 2001 / Accepted: 6 December 2001 / Published online: 15 January 2002
© Springer-Verlag 2002

Materials and methods

Blood treatment and cell fusion

Human blood was drawn from healthy volunteers by finger prick
and diluted instantly in PBS buffer (Life Technologies, Maryland,
USA), pH 7.4, with added Dextran 4 (Serva, Germany) in six dif-
ferent concentrations made from isotonic PBS and PBSD4 buffers
as given in Table 1. The PBSD4 buffer was made from 8.84 g
Dextran 4 in 100 ml PBS [24]. The Dextran 4 that was used had
an average molecular weight of 5000 Da (4000–6000 Da). Only a
negligible number of fusion events were observed in PBSD4–17.5,
and no fusions at all in PBSD4–20 (data not shown). Therefore,
data are only given for buffers PBSD4–0 to PBSD4–15. Control
cells were stored in PBS buffer without additions. A haematocrit
of 2.6% was adjusted. Samples were stored at 0–4°C until usage
and experiments were carried out not later than 2.25 h after bleed-
ing. All experiments were performed in a temperature-controlled
observation chamber at 20±0.5°C.

The fusion setup used for these experiments was identical to

that described elsewhere [1] and bears four separate fusion cham-
bers on a single glass slide. For each experiment, one of the four
chambers was filled with dispensing solution from a pipette tip.
Two platinum electrodes (1 mm in width and 100 µm in height
with rounded tips) were introduced into the two openings of the
chamber and adjusted to a distance of 1 mm.

Erythrocytes in their discocyte shape were allowed to sediment

on the bottom glass slide, giving an almost continuous cell mono-
layer. Fusion was initiated by a set of three rectangular voltage
pulses (amplitude of 800±20 V, duration of 100±2 µs), applied to
the monolayer. The electrical field strength thus reached was
8 kV/cm, calculated from an 800-V pulse amplitude divided by
the 1 mm electrode spacing. All fusion products were of the
“open-lumen” fusion type [14]. The beginning of membrane and
cell fusion could not be predicted precisely: it was observed to
occur at any time from almost instantly after the third pulse to up
to 30 s later [43]. The upcoming doublet oscillation showed clear-
ly observable (Fig. 1A1–A4) and measurable (Fig. 2A) geometri-
cal changes and consisted of two phases. The swell phase is due to
colloid-osmotically driven water uptake and induces a spherical
shape change [26, 29] to each of the two fused blood cells, thus
preventing the membrane from creating overlapping areas. The
pump event is caused by membrane rupture, after the maximum
possible membrane area enlargement of 3% [1, 20] has been
reached in the swell phase. During the pump event, intracellular
solution was ejected into extracellular space, and was observable
as a “jet”. This method has been shown to be a reliable test for

154

Table 1 Composition of the buffers for the fusion experiments

Buffer type

Fraction

Fraction

Colloidosmotic

PBSD4 (vol%)

PBS (vol%)

pressure (Pa)

PBS

0.0

100.0

0

PBSD4–7.5

7.5

92.5

3230

PBSD4–10.0

10.0

90.0

4307

PBSD4–12.5

12.5

87.5

5384

PBSD4–15.0

15.0

85.0

6460

PBSD4–17.5

17.5

82.5

7537

PBSD4–20.0

20.0

80.0

8614

Colloid buffers prevent red blood cells from swelling even if the
membrane is being electroporated [23, 24] provided that their col-
loidosmotic pressure is comparable to that resulting from intracel-
lular haemoglobin. Since the driving force for cell swelling after
electroporation is only the colloidosmotic pressure gradient, the
osmotic pressure was not taken into account in the following cal-
culation. The colloidosmotic pressure p in the last column was cal-
culated using the van’t Hoff equation: p=cRT [where c=solute
concentration, R=8.314J/(K·mol), T=temperature]

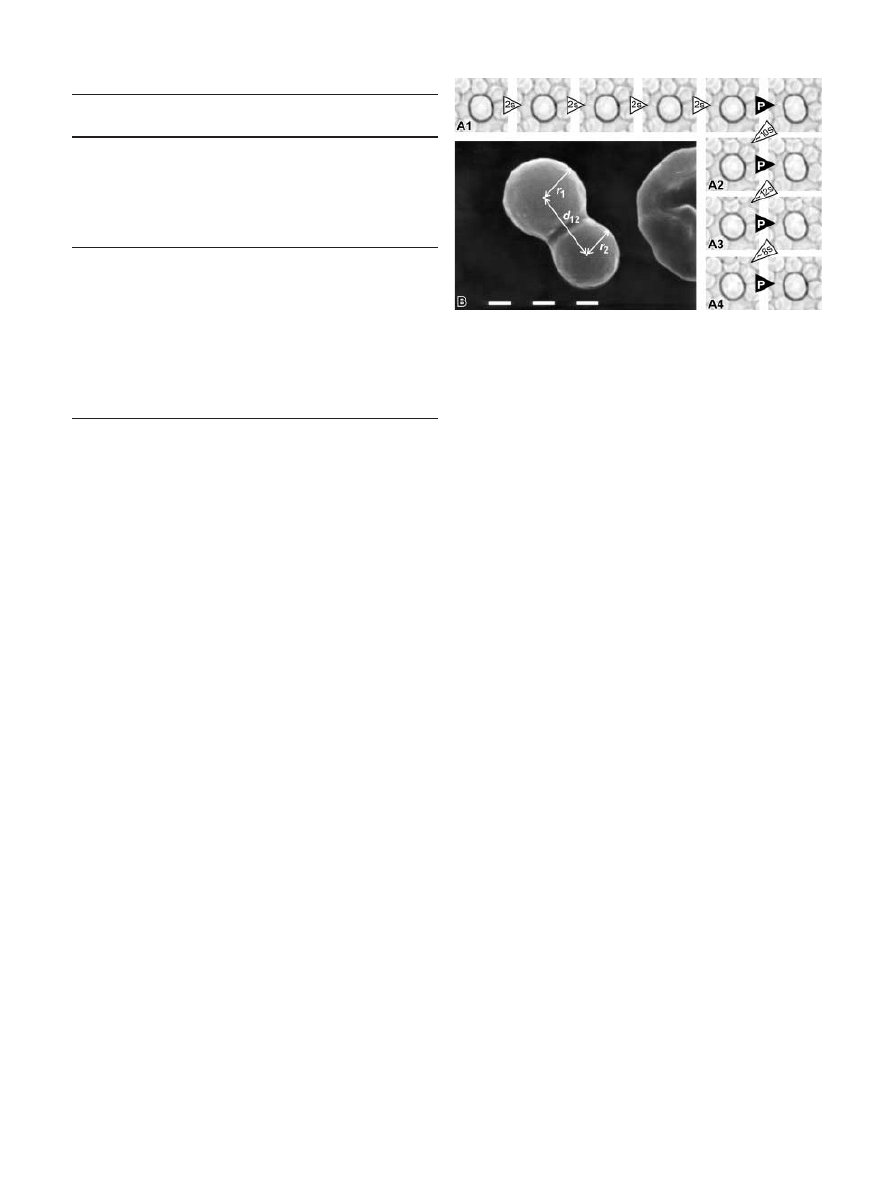
Fig. 1A, B Row A1 The first five images show a doublet during
the swell phase (white triangles) before entering the first pump
event (black triangle). Time between the images of the swell
phase is 2 s and for the pump event 0.25 s. Rows A2, A3, and A4
Images of the following three pump events just before (left side)
and after (right side) the event took place. Pump events A2, A3,
and A4 occurred about 10 s, 12 s and 8 s after the preceding pump
event, respectively. Comparison between the four pump events
reveals a decrease in the geometrical change, as shown in Fig. 2.
B Scanning electron photomicrograph of a pair of fused swollen
red blood cells with the definitions of the extracted parameters r

1

,

r

2

and d

12

. The doublet’s smooth transition in the fusion zone be-

tween the two spheres is due to the shrinking process during cell
preparation. Each white bar represents a length of 1 µm

membrane area dilatation load [1, 4, 6] and generates reproducible
results without mechanically contacting the cell surfaces.

The measurement period lasted from the first pump event up to

the fourth pump event, thus covering a total of three swell phases
in-between. Cells were observed and measured in the chamber
centre between both electrodes, because there the change of pH
due to electrolytic reasons [35] was expected to be minimal, and
the homogeneity of the electrical field distribution was maximal
[1]. Due to the low haematocrit, the concentration of extracellular
colloidosmotic active solutes was unaffected from the jets and re-
mained practically constant.

Image acquisition and parameter extraction

The geometrical shape changes were recorded by a digitally oper-
ating high-speed CCD-camera MD4256 (Reticon, USA) operating
at 1000 FPS (frames per second) for measurements of the pump
event time constant and at 4 FPS for measurements of the doublet
geometry during the swell phases. The images were recorded into
a 2048-images memory buffer installed on standard PC, each hav-
ing 256

×

256 pixels and 256 levels of grey, thus providing an opti-

cal resolution of 0.42 µm per pixel. All images were analysed off-
line by an image-analysis computer program [5]. Three geometri-
cal values r

1

, r

2

and d

12

(radius of the bigger sphere, radius of the

smaller sphere and distance between the centres of both spheres,
respectively, see Fig. 1B for definition) were extracted from each
single image (see Figs. 1A, 2A for examples). These values allow
the complete calculation of the fusion zone diameter (FZD), mem-
brane area A and doublet volume V [1, 5], Fig. 2B. The extraction
of the parameters r

1

, r

2

and d

12

from light microscopic images is

limited to the microscope’s optical resolution of 0.42 µm with the
optical setup used and substantially depends on the definition of
the contour in the gray-scale images shown in Fig. 1A. Since the
calculation of absolute values of FZD, A and V is then liable to ex-
hibit systematic and random errors, relative values of all geometri-
cal changes were used to describe the oscillation characteristics.
Analysis of consecutive images provided time-based data for the

pump time constants and the durations of swell times, an example
of which is given in Fig. 1A. The mean values for the doublets’
membrane areas and volumes (see example in Fig. 2B) were
slightly above the ranges given elsewhere for these values [9, 20,
22], which is because of the described problems of optical param-
eter extraction.

The linear connections between the data points of Figs. 3, 5

and 6 do not represent a linear change between those data points,
but are drawn merely for clarity.

Results and discussion

The influence of extracellular colloidosmotic pressure

The time constants of the first pump events do not de-
pend on the colloidosmotic pressure of the suspension
buffer (Fig. 3) and have a mean value of 4.73±2.09 ms.
This value does not differ significantly from the mean
value (4.95±2.12 ms) of the last pump event time con-
stant (data not shown). Since the pump event is driven
by the elastic energy which is stored in the membrane ar-
ea dilatation during the swell phase [1, 6], the buffer

composition and therefore the strength of the colloidos-
motic pressure does not have an influence on membrane
elasticity.

Additionally, the buffers used do not affect the rela-

tive change of the membrane area,

∂

A, during the swell

phase and therefore can be averaged as illustrated in
Fig. 4A. This shows that the drift with time for the first
three swell phases described in this study can be neglect-
ed. Because the geometrical doublet configuration com-
mences every swell phase with a contour shape that re-
sembles an “8” and ends with an oval contour shape like

155

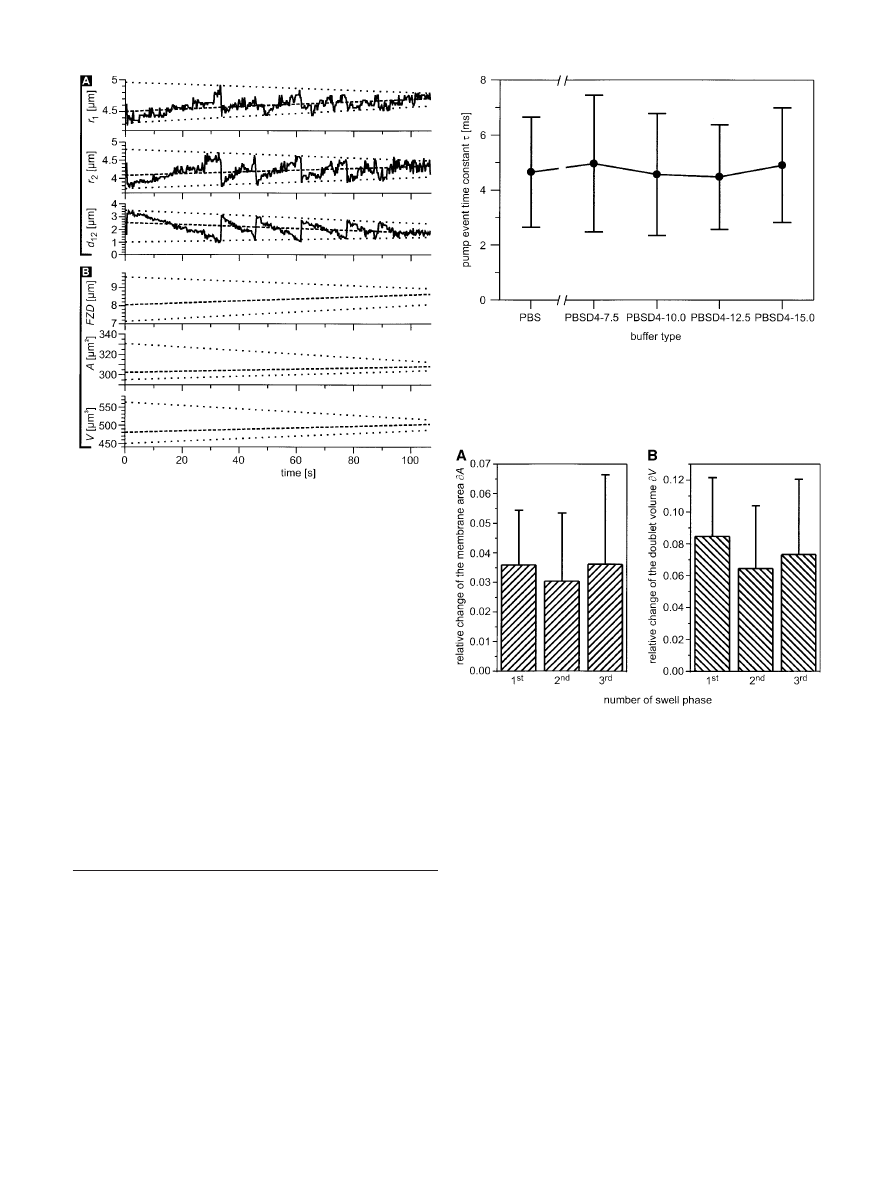
Fig. 2 A Raw data from the automatic image analysis [5] of a rep-
resentative oscillating doublet, starting with the first pump event.
Shown is the development of the radius of the bigger sphere, r

1

, of

the smaller sphere, r

2

, and of the spheres’ centre point distance,

d

12

. The dotted lines above and below the time courses connect the

extrema and show a progressive and almost linear decrease of the
oscillation amplitude. The dashed lines represent the least-squares
linear fits to the oscillation movements. B Starting from the linear
curves in A, the developments of the fusion zone diameter FZD,
the doublet membrane surface A, and the doublet volume V have
been calculated. The amplitudes of the oscillation movements
(distance between dotted lines) also decrease, and all parameters,
FZD, A and V, increase slightly

Fig. 3 The time constants

τ

of the first pump events do not vary

when the colloidosmotic pressure of the buffer rises from 0 Pa
(PBS) to 6460 Pa (PBSD4–15.0). Colloidosmotic pressure values
for the other buffer types are given in Table 1. n=13 for each data
point

Fig. 4 A The relative change of the membrane area

∂

A was aver-

aged for all buffer types used and shows no significant dependen-
cy on the number of the swell phase. B Equally, the relative
change of the doublet volume

∂

V is not affected significantly by

buffer type or by the number of the swell phase. All relative
changes of geometrical doublet characteristics have been calcu-
laed according to the following equation:

∂

M=(M

after

–M

before

)/

M

before

, where M is the magnitude to be evaluated, the index “be-

fore” represents the value of M just before and “after” the value of
M directly after the swell phase. n=64 for each panel

an “O” [1], it is not spherical during the whole swell
phase. Therefore, different volume increase values could
be the reason for the almost identical membrane area
changes observed. To eliminate this possibility, the rela-
tive change of the doublet volume,

∂

V, was measured in

the same set of experiments (Fig. 4B). As shown, differ-
ent colloidosmotic pressure values have no effect on
these values, which are therefore averaged. Again, as in
Fig. 4A, there is no observable drift for the first three
swell phases. Vesiculation processes or membrane invag-
inations that could cause anisotropic tension in the mem-
brane and induce a rupture event were not observed at
any time. Additionally, absolute membrane area in-
creased slightly (Fig. 2B) rather than decreased, which
would accompany vesiculation and invagination process-
es of the doublet membrane.

These findings lead to the conclusion that – for the

time covered by these experiments – the buffer’s colloid-
osmotic pressure influences neither the red blood cell
membrane elasticity nor the generation and configuration
of the membrane hole that is created by the rupture event
after the maximum possible membrane area dilatation.
The combination of these findings justifies the following
investigations.

The influence of the number of swell phases

The swell phase duration rises with increasing extracel-
lular colloidosmotic pressure, because the colloidosmotic
pressure difference drives the swell phase of the oscilla-
tion cycle. On reducing the transmembrane colloidos-
motic pressure gradient, i.e. increasing the extracellular
concentration of Dextran 4, the swell phase duration
must increase, which is shown in Fig. 5. A further in-
crease of the extracellular concentration of Dextran 4
(PBSD4–17.5 and PBSD4 –20.0) results in the ceasing
of the oscillation cycle and therefore swell phase dura-
tion could not be measured.

Another finding from Fig. 5 is that the swell phase du-

ration decreases as the number of swell phases increases.
With every oscillation cycle (i.e. a swell phase in combi-
nation with the subsequent pump event), the intracellular
concentration of colloid-osmotically active solutes is re-
duced to about 91.4±1.2% of the prior value, which was
calculated from doublet volume data taken during the os-
cillation cycle. On the other hand, the extracellular con-
centration of colloid-osmotically active solutes remains
virtually constant. This means that the colloidosmotic
pressure difference decreases stepwise, and this effect
alone would cause a developing increase of the swell
time. Instead, with a rising number of swell phases, a de-
crease of the well times was measured. The results shown
suggest the existence of at least one additional effect
which overcompensates the reduction of the swell-phase-
driving colloidosmotic pressure difference and which is
responsible for membrane rupture at an early stage.

Due to the morphology of the red blood cells, only

the cells’ membranes have additional influence on the

swell time characteristics; therefore, the reason for the
contradictory behaviour is closely related to the mechan-
ical properties of the membrane.

The first result that can be obtained from Fig. 6 is that

the buffer has a negligible influence on the geometrical
changes that occur during the swell phase. This supports
the above-mentioned findings from Figs. 3 and 4. A sec-
ond, more important conclusion to be drawn from Fig. 6
is that, with an increasing number of oscillation cycles,
the relative change of the fusion zone diameter,

∂

FZD,

decreases from 0.17±0.07 (1st swell phase) to 0.13±0.04
(2nd swell phase) and then down to 0.11±0.05 (3rd swell
phase). This means that the amplitude of the doublets’
geometrical alteration is reduced, although no difference

156

Fig. 5 Durations of the first three swell phases as a function of the
buffer type and the number of the swell phase. From the first (●),
to the second (▲) and the third (▼) swell phase, the durations be-
come (although not in every case significant) continuously less.
n=12 except n

PBS

=16

Fig. 6 The relative change of the fusion zone diameter (

∂

FZD)

was calculated according to the equation given in Fig. 4.

∂

FZD

shows no dependency on the buffer type, but decreases with the
number of swell phases (●: first, ▲: second and ▼: third swell
phase). n=12 except n

PBS

=16

in the relative change of the membrane area

∂

A could be

measured (Fig. 4B). The explanation for this takes ac-
count of the fact that the doublet adopts a slightly more
spherical shape at the start of the swell phase [1]. Since
doublets enter the pump event, i.e. their membrane rup-
tures, at a constant FZD to length ratio of 0.89 [3], geo-
metrical changes of FZD must decrease and colloidos-
motic pressure differences must always be high enough
to induce a membrane area dilatation until rupture,
which means that the relative change of the membrane
area

∂

A must stay constant (Fig. 4B).

To summarize, although the driving force for the gen-

eration of a membrane rupture decreases, the membrane
rupture occurs earlier. It is shown that membrane area di-
latation influences do not account for this effect, and that
there are no accompanying effects on the initiation of the
rupture, apart from the rupture itself. It hence must be
concluded that the cell membrane resistance to mechani-
cal ruptures decreases with the rupture events. The ex-
periments performed could not verify whether repetitive
ruptures occur at identical sites;however, this is likely
after the time constants for resealing electroporated
membranes are much greater compared to those ob-
served in this study [12, 42]. Furthermore, local cyto-
skeleton disorders may destabilize the membrane, which
appear either as local destruction or local deformation of
the cytoskeleton [4]. The experimental data and the re-
sults are applicable not only to red blood cells mem-
branes, but also to membranes of different cells because
of similarities in their composition.

References

1. Baumann M (1999) Dynamics of oscillating erythrocyte dou-

blets after electrofusion. Biophys J 77:2602–2611

2. Baumann M (2001) Early stage shape change of human eryth-

rocytes after application of electric field pulses. Mol Membr
Biol 18:153–160

3. Baumann M, Fischer Y (1999) Characterization of the one-di-

mensional fusion zone stress modulus of electrofused mem-
branes. Biophys J 76:A436

4. Baumann M, Grebe R (1998) Characteristics of the osmotical-

ly induced membrane rupture. Mol Membr Biol 15:193–201

5. Baumann M, Grebe R (2000) Automated surface and volume

measurement of fused cells. Anal Quant Cytol Histol 22:247–
257

6. Baumann M, Sowers AE (1996) A mechanical cycling phe-

nomenon in electrofused erythrocytes. Mol Membr Biol
13:113–119

7. Bessis M, Mohandas N (1980) Automated ectacytometry:

a new method of measuring red cell deformability and red
cell indices. Blood Cells 6:315–327

8. Bryant G, Wolfe J (1987) Electromechanical stresses produced

in the plasma membranes of suspended cells by applied elec-
tric fields. J Membr Biol 96:129–139

9. Canham PB, Burton AC (1968) Distribution of size and shape

in populations of human red cells. Circ Res 22:405–422

10. Chien S, Sung KP, Skalak R, Usami S, Tozeren A (1978)

Theoretical and experimental studies on viscoelastic properties
of erythrocyte membrane. Biophys J 24:463–487

11. Deuticke B, Schwister K (1985) Formation and properties of

aqueous leaks induced in human erythrocytes by electrical
breakdown. Biochim Biophys Acta 816:332–348

12. Deuticke B, Schwister K (1989) Leaks induced by electrical

breakdown in erythrocyte membrane, electroporation and elec-
trofusion in cell biology. In: Neumann E, Sowers AE, Jordan
CA (eds) Electroporation and electrofusion in cell biology.
Plenum, New York, pp 127–148

13. Dimitrov DS, Apostolova MA, Sowers AE (1990) Attraction,

deformation and contact of membranes induced by low fre-
quency electric fields. Biochim Biophys Acta 1023:389–397

14. Dimitrov DS, Sowers AE (1990) A delay in membrane fusion:

lag times observed by fluorescence microscopy of individual
fusion events induced by an electric field pulse. Biochemistry
29:8337–8344

15. Dintenfass L (1984) Quantitative study of morphology of

aggregation. Clin Hemorheol 4:223–236

16. Discher DE, Mohandas N, Evans EA (1994) Molecular maps

of red cell deformation: hidden elasticity and in-situ connec-
tivity. Science 266:1023–1035

17. Dormandy J (ed) (1983) Red cell deformability and filtrability.

Nijhoff, Boston

18. Engelhardt H, Gaub H, Sackmann E (1984) Viscoelastic prop-

erties of erythrocyte membrane in high-frequency electric
fields. Nature 307:378–380

19. Engelhardt H, Sackmann E (1988) On the measurement of

shear elastic moduli and viscosities of erythrocyte plasma
membranes by transient deformation in high frequency electric
fields. Biophys J 54:495–508

20. Evans EA, Waugh R, Melnik L (1976) Elasitic area compress-

ibility modulus of red cell membrane. Biophys J 16:585–595

21. Gass GV, Chernomordik LV, Margolis LB (1991) Local defor-

mation of human red blood cells in high frequency electric
fields. Biochim Biophys Acta 1093:162–167

22. Grebe R, Schmid-Schönbein H (1990) Closed fluid quadrilam-

ina model of the erythrocyte membrane. In: Mosora F (ed)
Biomechanical transport processes. Plenum, New York,
pp 223–233.

23. Henszen MMM, Deuticke B (1993) Shape changes accom-

panying electroporation of human erythrocytes (RBC). Biol
Chem Hoppe Seyler 374:144

24. Henszen MMM, Weske M, Schwarz S, Haest CWM, Deuticke

B (1997) Electric field pulses induce reversible shape transfor-
mation of human erythrocytes. Mol Membr Biol 14:195–204

25. Hochmuth RM, Buxbaum KL, Evans EA (1980) Temperature

dependence of the viscoelastic recovery of red cell membrane.
Biophys J 29:177–182

26. Jay AWL, Rowlands S (1975) The stages of osmotic hemoly-

sis. J Physiol (Lond) 252:817–832

27. Kazonori K, Nobuji M, Takeshi S (1987) Erythrocyte defor-

mation in shear flow: influence of internal viscosity, mem-
brane stiffness and hematocrit. Blood 69:727–734

28. Kiesewetter H, Dauer U, Teitel P, Schmid-Schönbein H, Trapp

R (1982) The Single Erythrocyte Rigidometer (SER) as a
reference for RBC deformability. Biorheology 19:737–753

29. Kinosita K, Tsong TY (1977) Voltage-induced pore formation

and hemolysis of human erythrocytes. Biochim Biophys Acta
471: 227–242

30. Kummrow M, Helfrich W (1991) Deformation of giant lipid

vesicles by electric fields. Physiol Rev A 44:8356–8360

31. Markle DR, Evans EA, Hochmuth RM (1983) Force relax-

ation and permanent deformation of erythrocyte membrane.
Biophys J 42:91–98

32. Nash GB, Meiselman HJ (1983) Red cell and ghost viscoelas-

ticity. Biophys J 43:63–73

33. Nash GB, Meiselman HJ (1985) Alteration of red cell mem-

brane viscoelasticity by heat treatment. Biorheology 22:273–
278

34. Neumann E, Sowers AE, Jordan CA (eds) (1989) Electropora-

tion and electrofusion in cell biology. Plenum, New York

35. Potter H (1988) Electroporation in biology: methods, applica-

tion and instrumentation. Anal Biochem 174:361–373

36. Riemann F, Zimmermann U, Pilwat G (1975) Release and

uptake of haemoglobin and ions in red blood cells induced by
dielectric breakdown. Biochim Biophys Acta 394:449–462

157

37. Scheurich P, Zimmermann U, Mischel M, Lamprecht I (1980)

Membrane fusion and deformation of red blood cells by elec-
tric fields. Z Naturforsch 35:1081–1085

38. Schmid-Schönbein H, Heidtmann H, Grebe R (1986) Spectrin,

red cell shape and deformability: II. The antagonistic action of
spectrin and sialic acid residues in determining membrane
curvature in genetic spectrin deficiency in mice. Blut 52:149–
164

39. Schmid-Schönbein H, Heidtmann H, Grebe R (1986) Spectrin,

red cell shape and deformability: I. Membrane curvature in
genetic sprectrin deficiency. Blut 52:131–147

40. Schmid-Schönbein H, Schröder S, Grebe R, Artmann G,

Eschweiler H, Teiltel P (1988) Influence of moxaverine hydro-
chloride on membrane curvature and microsieve filterability of
red cells after exposure to hyperosmolarity and lactacidosis.
Drug Res 38:710–716

41. Schmid-Schönbein H, Teitel P (1987) In vitro assessment of

“convertly abnormal” blood rheology; critical appraisal of

presently available microrheological methology. A review
focusing on diabetic retinopathy as a possible consequence of
rheological occlusion. Clin Hemorheol 7:203–238

42. Serpesu EH, Kinosita K, Tsong TY (1985) Reversible and

irreversible modification of erythrocyte membrane perme-
ability by electric field. Biochim Biophys Acta 812:779–785

43. Sowers AE (1987) The long-lived fusogenic state induced in

erythrocyte ghosts by electric pulses is not laterally mobile.
Biophys J 52:1015–1020

44. Zimmer G, Schirmer H (1974) Viscosity changes of erythro-

cyte membrane and membrane lipids at transition temperature.
Biochim Biophys Acta 345:314–320

45. Zimmermann U (1982) Electric field-mediated fusion and re-

lated electrical phenomena. Biochim Biophys Acta 694:227–
277

46. Zimmermann U (1986) Electrical breakdown, electropermea-

bilisation and electrofusion. Rev Physiol Biochem Pharmacol
105:176–256

158