1.

Pasowania złożone. Przykład liczbowy.

Istnieją przypadki, w których nie mogą być zastosowane ani
pasowania na zasadzie stałego otworu ani pasowania na zasadzie
stałego wałka. Żądane pasowanie może być uzyskane jedynie przez
skojarzenie niepodstawowego otworu z niepodstawowym wałkiem.
Tego rodzaju pasowanie nosi nazwę pasowania złożonego.
Można sie spotkać w praktyce z dwoma rodzajami zagadnień
dotyczących pasowań złożonych.

1.

Określić charakter pasowania – tzn. Znaleźć
pasowanie równoważne na zasadzie stałego otworu
lub stałego wałka, gdy dane są odchyłki graniczne
otworu i wałka niepodstawowego.

2.

Określić odchyłki jednego elementu (wałka lub
otworu), aby w skojarzeniu z danym drugim
elementem niepodstawowym (otworem lub wałkiem)
uzyskać pasowanie o złożonym charakterze.

Sposób rozwiązywania tych zadań przedstawiony zostanie na
przykładach.
1. Określić charakter pasowania fi50 K6/m7

Pasowanie równoważne na zasadzie stałego otworu utworzone
będzie przez otwór podstawowy w 6 klasie dokładności (30 H6 =
30

+0,016

) oraz wałek, którego odchyłki obliczyć można znając luzy

graniczne i odchyłki otworu podstawowego.

Ponieważ Fw>0, będzie to wałek spoczynkowy. Z tablicy
znajdujemy dla D=50, najbliższą obliczonej odchyłkę dolną wałka p
(bardzo lekko wtłaczanego), równą Fp = +26μm. Zatem pasowanie
złożone Ø50 K6/m5 będzie miało charakter zbliżony do pasowania
bardzo lekko wtłaczanego.
2. Dany jest otwór Ø30 F7 =
Należy dobrać wałek, aby uzyskać pasowanie suwliwe równoważne
pasowaniu Ø30 H7/h6.

Odchyłki wałka obliczone z żądanych luzów granicznych i danych
odchyłek otworu Ø30 F7, będą miały wartości następujące:

Ponieważ Fw>0, będzie to wałek spoczynkowy.
Z tablicy dla średnicy D=30 znajdujemy Fw=+8μm dla wałka m
(mocno wciskany). Zatem żądane pasowanie suwliwe uzyskujemy
kojarząc z otworem Ø30 F7 wałek Ø30 m6

2.

Pasowanie łożysk tocznych

tolerancje wykonawcze wymiarów średnic łożysk

tocznych nie są zgodne z układem tolerancji i pasowań ISO. Tworzą
one odrębny układ charakterystyczny tym, że zarówno średnica
zewnętrzna d, jak wewnętrzna D mają górne odchyłki graniczne
równe zeru, natomiast dolne odchyłki graniczne równe zeru,
natomiast dolne odchyłki mniejsze od zera. Zatem średnica
zewnętrzna pierścienia zewnętrznego jest tolerowana jak wałek
podstawowy h, natomiast średnica otworu pierścienia wewnętrznego
jak otwór spoczynkowy pośredni między lekko wciskanym K, a
wciskanym zwykłym M. Wartości tolerancji średnic łożysk tocznych
odpwiadają tolerancjom IT5 do IT7 układu ISO.
Tolerancje średnic łożysk tocznych oznacza się hB dla średnicy
zewnętrznej oraz KB dla średnicy otworu.
Charakter pasowania średnic łożyska tocznego z elementami
współpracującymi (wałkiem i obudową) zależy od charakteru
obciążenia oraz luzów wewnętrznych łożyska.

Charakter obciążenia łożyska określa się w zależności od tego, czy:

–

wałek wiruje a obudowa znajduje się w spoczynku (w
skrócie ruchomy wałek)

–

obudowa wiruje a wałek znajduje się w spoczynku (ruchoma
obudowa),

–

występuje przypadek pośredni, gdyż może wirować wałek i
osłona

W zależności od wartości luzów wewnętrznych, rozróżnia się
łożyska:

–

o luzach zmniejszonych, oznaczonych przez C1 i C2

–

o luzach normalnych (bez oznaczeń)

–

o luzach powiększonych (C3, C4, C5)

Regułą jest, że wirujące pierścienie łożyska pasowane są z
elementami współpracującymi spoczynkowo, natomiast pierścienie
nieruchome – suwliwie lub przylgowo. W przypadku pośrednim oba
pierścienie pasowane są spoczynkowo

4.

Położenie pól tolerancji i odchyłek w gwintach
zewnętrznych i wewnętrznych

5.

Identyfikacja podstawowych parametrów kół
zębatych (z,m,y,x,alfa)

x – współczynnik korekcji, w kołach zębatych niekorygowanych
(zerowych) x = 0, w kołach zębatych korygowanych ≠ 0
y – współczynnik wysokości zęba (y=1 dla zębów normalnych, y>1
dla zębów

wysokich, y<1 dla zębów niskich).

z - liczba zębów
m - moduł nominalny, mierzony w przekroju normalnym do linii
zęba na walcu podziałowym
α - nominalny kąt przyporu, równy 20° lub 15°, określany w
przekroju normalnym do linii zęba

6.

Zasady pomiaru wybranych parametrów kół
zębatych (bicie uzębienia, grubość zęba na cięciwie
pomiarowej, pomiar przez n zębów, pomiar
podziałki zasadniczej).

6.1

Pomiar bicia promieniowego uzębienia

Bicie promieniowe uzębienia Frr określone jest jako największa
różnica odległości od osi koła zębatego linii podziałowej zarysu
odniesienia, przy kojarzeniu tego zarysu z zarysem każdego z zębów
lub wrębów. Sposób pomiaru bicia uzębienia ilustruje rys. 6.1.
Badane koło zębate osadza się bez luzu na trzpieniu, którego błędy
współosiowości powierzchni walcowej względem osi nakiełków są
na tyle małe, że ich wpływ na dokładność pomiaru można pominąć.
Trzpień wraz z kołem zębatym osadza się w kłach przyrządu
kłowego. Jako element pomiarowy powinna być użyta końcówka w
postaci zęba zębatki odniesienia. W zastępstwie może być użyty
wałeczek, dobrany tak aby punkty styku wałeczka z bokami zębów
leżały w pobliżu stałej cięciwy pomiarowej .W górnym położeniu
wałeczka odczytuje się wskazanie czujnika. Czynność tę wykonuje
się dla wszystkich wrębów koła. Bicie promieniowe uzębienia
oblicza się jako różnicę największych i najmniejszych wskazań
czujnika (wzór (12)).

F

rr

= H

r max

− H

r min

W zależności od żądanej dokładności pomiaru, można pomiar
wykonać przy użyciu czujnika z działką elementarną 0,01 lub 0,002
mm

6.2

Pomiar grubości zęba

Pomiar suwmiarką modułową
Korpus narzędzia stanowi kątownik ze stałą szczęką 3. Na
poziomym ramieniu kątownika przesuwa się suwak ze szczęką 4,
przy czym odległość szczęk może być odczytana na podziałce
kreskowej przy pomocy noniusza 5. Wzdłuż pionowego ramienia
kątownika przesuwa się języczek 1, którego dolna krawędź jest
prostopadła do powierzchni mierniczych szczęk 3 i 4. Odległość
krawędzi języczka od dolnych krawędzi szczęk nastawiana jest przy
pomocy podziałki kreskowej z noniuszem 2. Obie podziałki mają
działki elementarne równe 0,5 mm i noniusz o 25 działkach co
pozwala na ustawienie i odczyt z dokładnością 0,02 mm.

Pomiar grubości zęba w kole o prostych zębach pokazano wyżej
Języczek ustawia się w odległości hp od krawędzi szczęk, przy czym
wartość hp dobrana jest tak, żeby szczęki stykały się z zębem na
walcu podziałowym. Odczytana wartość gp, stanowi grubość zęba
zmierzoną wzdłuż koła podziałowego. Wysokość hp oblicza się z
zależności

h

p

=BD=CD BC

gdzie

CD

=h

g

oraz

BC

=OC −OB=

dp

2 

1

−cosφ

stąd

h

p

=h

g



dp

2 

1

−cosφ

podstawiając pod wz.

d

p

=m⋅z

h

p

=m

[

y ± x



z
2 

1

−cosφ

]

grubość pomiarową zęba gp oblicza się z trójkąta OAB:

g

p

=2 ⋅AB

Ponieważ

AB

=

d

p

2 ⋅

sinφ

, uwzględniając wzór

d

p

=m⋅z

otrzymamy

g

p

=m⋅z⋅sinφ

φ – środkowy kąt odpowiadający połowie grubości zęba wyznacza

się z proporcji

φ:

g
2 =

2

⋅⋅d

p

stad

φ:

g

2 =

2

 :⋅d

p

φ

=

g

d

p

w sumie otrzymujemy

Pomiar grubości zęba wykonuje się na wysokości stałej cięciwy
pomiarowej (rys. 41). Stała cięciwa pomiarowa AA' występuje w
miejscu zetknięcia się zębatki odniesienia z zarysem zęba, gdy oś
symetrii zęba koła pokrywa się z osią symetrii wrębu zębatki.
Zębatka odniesienia styka się z bokami zęba w punktach A i A'
powstałych z przecięcia boku zęba linią styczną do koła
zasadniczego i przechodzącą przez punkt centralny C. Dla
wykonania pomiaru należy języczek suwmiarki ustawić w odległości
h

c

od krawędzi szczęk, tak aby szczęki stykały się z zębem na

wysokości stałej cięciwy pomiarowej. Odczytana wartość T

c

jest

grubością zęba zmierzoną na wysokości stałej cięciwy pomiarowej.
Nominalną stałą wysokość pomiarową h

c

(odpowiadającą

nominalnemu położeniu zarysu odniesienia) oblicza się z

6.2

Pomiar przez n zębów

Do pomiaru grubości zęba przez n zębów używa się mikrometrów z
talerzykowymi końcówkami mierniczymi lub innych narzędzi
mierniczych umożliwiających pomiar tą metodą. Zasadę pomiaru
wyjaśnia rys.

Końcówki narzędzia mierniczego obejmują n zębów (w
rozpatrywanym przyp. N=3), stykając się z ewolwentowymi
zarysami skrajnych zębów w punktach A i B, lezących w pobliżu
walca podziałowego. Z zasady powstawania ewolwenty wynika, że
odcinek zmierzony M=AB jest styczny do koła zasadniczego o
promieniu r

g

. Ponieważ zarysy ewolwentowe powstają jako tory

punktów A i B odcinka AB odtaczanego po kole zasadniczym można
napisać : M=Ac+CE+FB=Ab=FK; AC=Fg=t

p

; CE=GH=g

z

;

EB=HK=t

p;

gdzie g

z

grubość zęba mierzona na walcu zasadniczym,

t

p

=m*π*cosα. W ogólnym przypadku można więc napisac:

M=(n-1)*m*π*cosα+g

z

;

gdzie n liczba zębów. Grubość zęba na

walcu zasadniczym można wyznaczyć posługując się rys

Podziękowania dla tych co się choć troszeczkę dołożyli

www.dydaktyka.wm.prv.pl

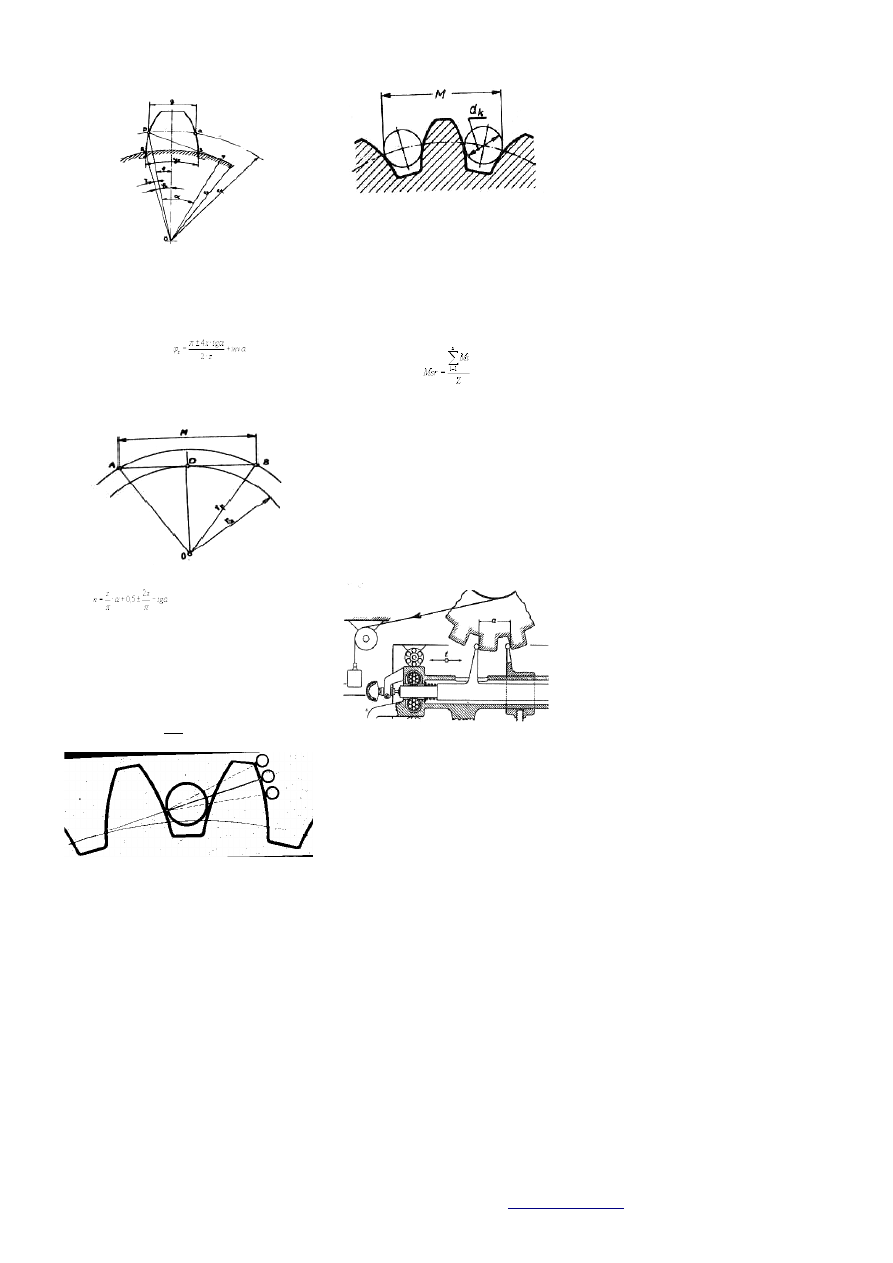
z którego wynika: g

z

/2=r

z

*φ

z

przy czym φ

z

=φ+γ gdzie: φ

z

kąt

środkowy odpowiadający połowie grubości zęba na walcu
podziałowym; γ kąt środkowy zawart między promieniem
początkowym ewolwenty RO=r

z

a promieniem PO=r

p

. Kąt γ

wyznaczać można z następujących zależności: PT=TO*tgα=r

z

*tgα

przy czym PT=TR=r

g

(α+γ) skąd γ= tgα-α. Kąt γ wyrażony w mierze

łukowej określany jest w teorii zazębień jako inwoluta kąta przyporu

(inv α). Ostatecznie mamy:

, podstawiając do

zależności powyżej mamy: M=m*cosα[(9n-0,5)π+z* inv
α]±2mx*sin ilość. Ilość Ilość zębów wziętych do pomiaru określa się
przy założeniu by punkt styku końcówek mierniczych narzędzia z
zarysem zębów leżały na walcu podziaowym lub powyżej. Można
więc na podst. Rys.

napisać DB

2

=OB

2

-OD

2

i korzystając z poprzednich zależności

mamy:

. Wartość n tylko przypadkowo może

być całkowita dlatego zaokrągla się ją do najbliższej całkowitej
górnej wartości.

6.3

Pomiar podziałki zasadniczej

pomiar podziałki przyporu

podzialke przyporu okresla wzor

t

p

=

⋅d

z

z =

m

⋅⋅cos 

jest odległością zarysów ewolwentowych dwóch sąsiednich zębów,
mierzonych wzdłuż linii przyporu stycznej do koła zasadniczego.
Metoda pomiaru: kulista końcówka sztywno związana z korpusem
przyrządu oparta jest we wrębie międzyzębnym , ruchoma
końcówka kulista połączona z czujnikiem którego najmniejsze
wskazanie odpowiada właściwemu położeniu pomiarowemu. Przed
przystąpieniem do pomiaru przyrząd należy ustawić tak, aby zerowe
skazanie czujnika odpowiadalo nominalnej wartości podzialki
przyporu obliczonej według wzoru wcześniejszego. Dobrać należy
końcówki pomiarowe o średnicy D

k

wg. modulu mierzonego koła

zębatego a nastepnie zgodnie ze schematem złożyć stos płytek
wartości poszczególnych płytek i srednice D

k

są zawarte w

tablicach. Błędy podanej metody pomiaru zależą od dokładności
zarysu zębów i przy niewielkich odchyłkach zarysu nie
przekraczających ±0,004mm. Gdy wymagana jest większa
dokładność, pomiar podziałki przyporu może być wykonany na
uniwersalnym przyrządzie firmy C. Zeiss,

pomiar podziałki obwodowej

podziałka obwodowa określana jest wzdłuż łuku koła podziałowego
wobec czego bezpośredni jej pomiar jest praktycznie niemożliwy.
Można dokonywac pomiaru kąta podziałowego, podziałowego
nastepnie obliczyć wartość podziałki. Ten sposób jednak, możliwy
do wykonania przy użyciu teodolitu i kolimatora lub innych bardzo
dokładnych przyrządów do pomiaru kąta, jest trudny i pracochłonny.
Stąd też najczęściej wykonuje się pomiary równomierności
podziałek obwodowych. Najprostszym sposobem pomiaru
równomierności podziałki obwodowej jest pomiar przy użyciu
dwóch wałeczków mierniczych i mikrometru. Po zmierzeniu
odległości M zewnętrznych tworzących wałeczków kolejno dla
wszystkich wrębów koła zębatego oblicz się wartość średnią

z- liczba mierzonych zębów

i- kolejny nr zeba

nastepnie dla poszczególnych zębów koła określa się odchyłki
podziałki obwodowej ze wzoru

f

t1

=M

1

−M

śr

. Gdy dokładnośc pomiaru przy uzyciu mikrometru i wałeczków
mierniczych jest niewystarczająca, pomiar podziałki obwodowej
wykonac można na uniwersalnym przyrządzie firmy C.Ziess do
pomiaru kół zębatych. Schemat pomiaru przedstawiono poniżej.
Mierzone koło zębate 1 osadzone jest na trzpieniu w kłach
przyrządu. Na saniach 2 przyrządu zamocowane są dwie końcówki
miernicze, przy czym końcówka 3 sztywno związana jest z saniami,
końcówka 4 ruchoma powoduje przesuw trzpienia mierniczego
ortotestu 5 w zależności od wartości podziałki obwodowej.

Podziękowania dla tych co się choć troszeczkę dołożyli

www.dydaktyka.wm.prv.pl