Origin i rozkład Gauss’a czyli:

a)

jak narysować histogram

b)

jak dopasować funkcję Gauss’a do histogramu

W poniższej tabelce przedstawiono wyniki 100 pomiarów okresów drgań pewnego wahadła matematycznego
pogrupowane na 7 przedziałów o szerokości 0,1 sekundy.

Okres [s]

Liczba pomiarów

10,20÷10,30

2

10,30÷10,40

3

10,40÷10,50

24

10,50÷10,60

38

10,60÷10,70

27

10,70÷10,80

5

10,90÷11,00

1

a) Aby narysować histogram korzystając z programu Origin należy:

1.

Przygotuj tabelę z dodatkową kolumną, w której będą zamieszczone wartości środków przedziałów.

Okres [s]

Ś

rodek przedziału

Liczba pomiarów

10,20÷10,30

10,25

2

10,30÷10,40

10,35

3

10,40÷10,50

10,45

24

10,50÷10,60

10,55

38

10,60÷10,70

10,65

27

10,70÷10,80

10,75

5

10,90÷11,00

10,25

1

2.

Uruchom Origina.

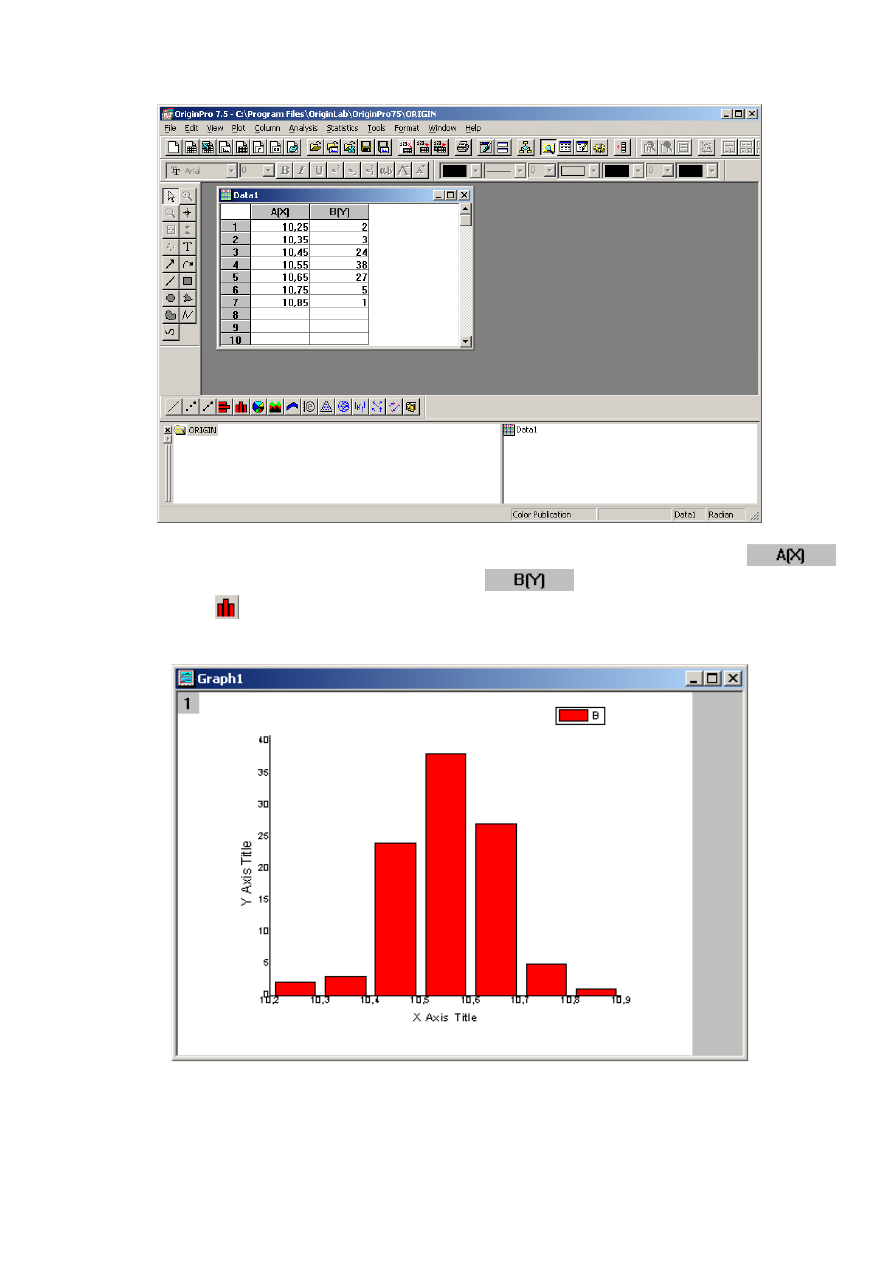
3.

W skoroszyt Data1 w kolumnę A(X) (wartości x) wpisz wartości środków przedziałów, a w kolumnę
B(Y) (wartości y) odpowiadającą danemu przedziałowi liczbę pomiarów.

4.

Zaznacz obie kolumny A(X) i B(Y). Aby to zrobić lewym przyciskiem myszy kliknij w

i

nie puszczając lewego klawisza przeciągnij kursor na

i dopiero teraz puść klawisz.

5.

Kliknij w ikonę

tworzącą pionowy wykres słupkowy.

6.

Pojawi się nowe okienko Graph1 z wykresem.

7.

Aby dostosować szerokość słupków, tak aby przylegały do siebie bokami należy kliknąć dwukrotnie
(lewy klawisz myszy) na dowolnym słupku. Otworzy się okienko o nazwie Plot Details

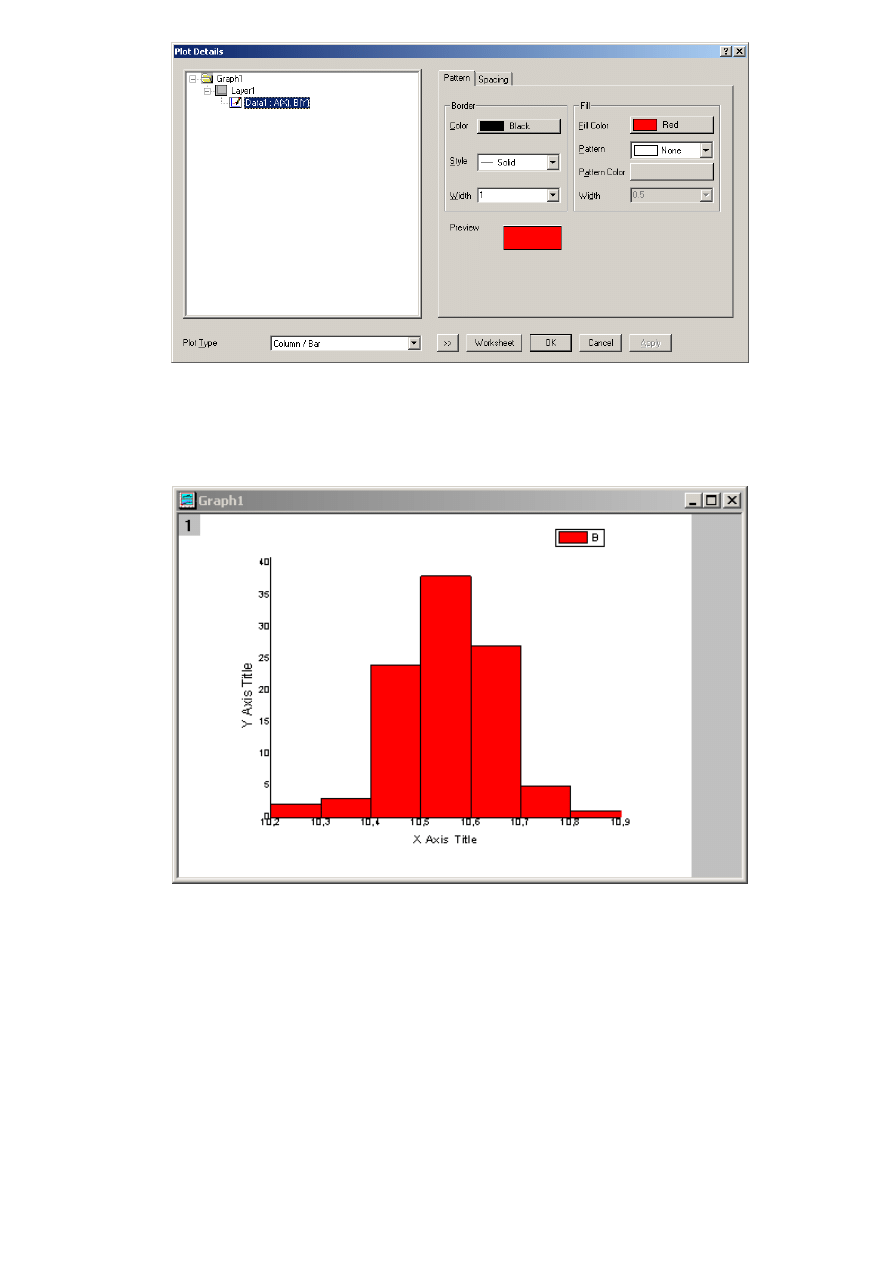
8.

Następnie należy przejść do zakładki Sparing i pole Gap Between Bars (in %) (szerokość odstępu
między słupkami) ustawić na 0.

9.

Zamknij okienko Plot Details klikając na Apply i OK.

10.

Po modyfikacji wykres Graph1 będzie wyglądał tak:

11.

Aby opisać osie wykresu należy dwukrotnie kliknąć na napisy Y Axis Title i X Axis Title.

b) Jak dopasować funkcję Gauss’a do wykresu.

1.

Przejdź do okna skoroszytu Data1.

2.

Z menu głównego wybierz Column | Add New Columns i na pytanie o liczbę nowych kolumn do
utworzenia odpowiedz wpisując 1, następnie kliknij na przycisk OK. Po tej czynności skoroszyt Data1
będzie składał się z trzech kolumn. Kolumna, którą właśnie dodałeś będzie oznaczona symbolem C(Y). „Y”
w nawiasie oznacza, że jest to kolumna wartości y.

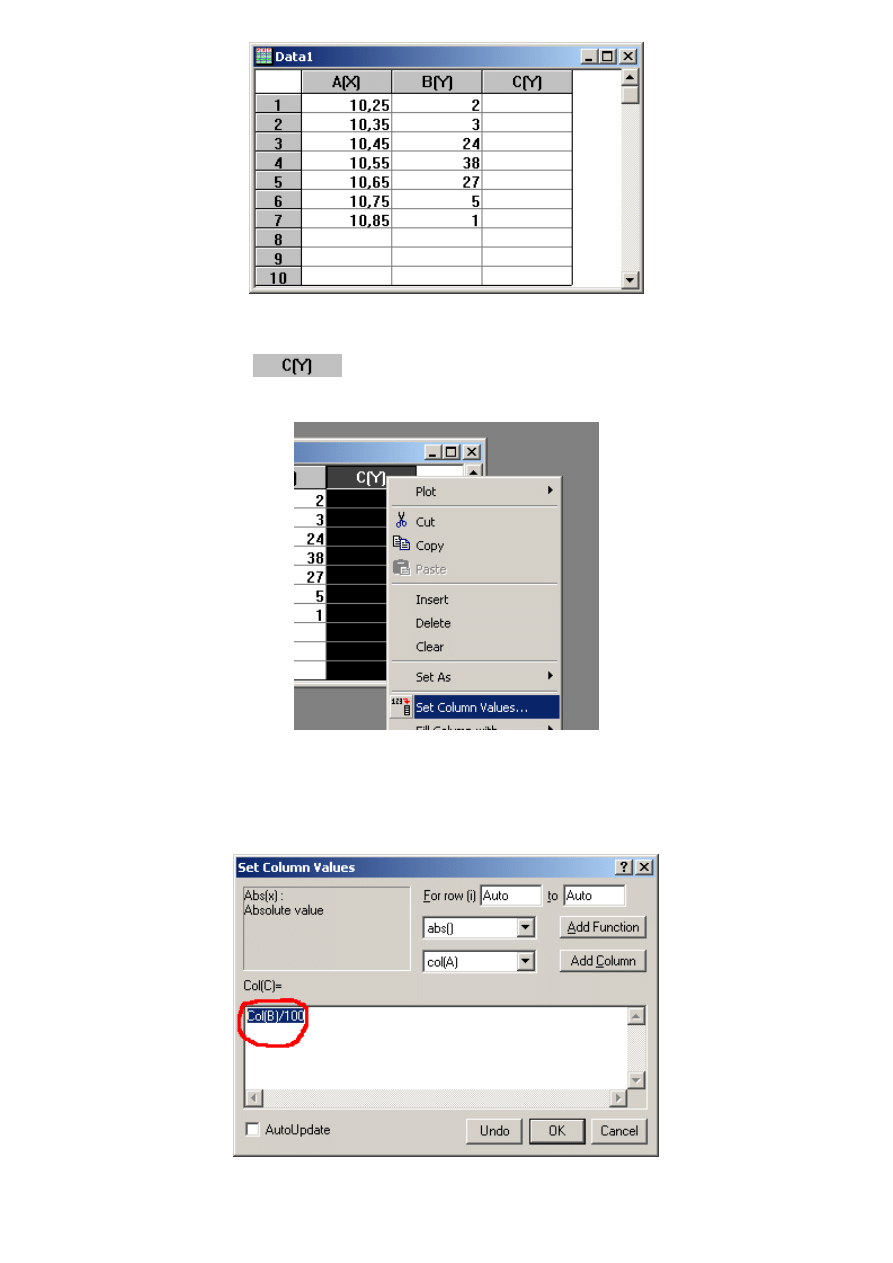
3.

W kolumnie C(Y) należy umieścić ilość wyników w danym przedziale podzieloną przez 100. Origin w
prosty sposób potrafi sam podzielić wartości z kolumny B przez dowolną liczbę, a wynik dzielenia umieścić

w kolumnie C. Kliknij w

i zaznacz całą kolumnę, następnie nie ruszając myszką naciśnij prawy

klawisz myszy i z menu, które się rozwinie wybierz Set Columns Values

4.

Otworzy się okienko o nazwie Set Column Values. W duże białe pole służy do wprowadzenia formuły
(wzoru) według, której zostaną przeprowadzone obliczenia. W miejscu „Col(B)” podstawiane są wartości z
kolumny B. Aby podzielić wartości z kolumny B przez 100 należy użyć wyrażenia Col(B)/100.

Efekt obliczeń będzie wyglądał tak:

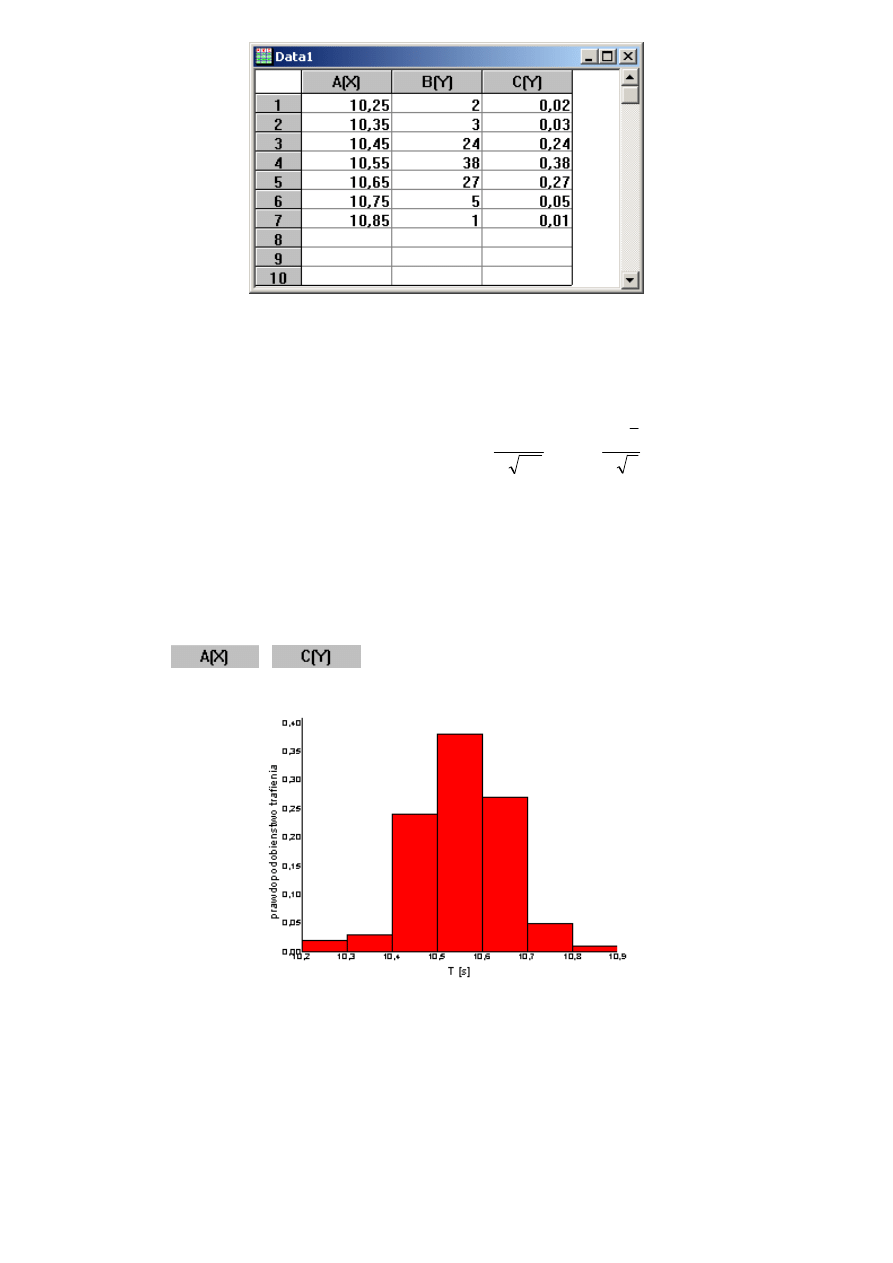
Dzieląc ilość pomiarów w dowolnym przedziale czasu przez liczbę wszystkich pomiarów wyznaczamy
prawdopodobieństwo trafienia z wynikiem pomiaru w dany przedział. Na przykład, jeśli dla pewnego
przedziału prawdopodobieństwo wynosi 0,5 (50%) tzn., że połowa pomiarów, które wykonamy, będzie
zawierała się w tym przedziale.

Ponieważ rozkład Gauss’a, który opisuje wzór





























−

−

=

2

2

exp

2

1

y

σ

π

σ

x

x

, określa takie właśnie

prawdopodobieństwa (przypominam, że cała z

1

ydx

=

∫

∞

∞

−

), aby dopasowa

ć

wykres słupkowy wzorem

opisuj

ą

cym rozkład Gaussa, nale

ż

y na osi y odło

ż

y

ć

prawdopodobie

ń

stwa trafienia w przedział, a nie ilo

ś

ci

trafie

ń

w przedział.

5.

Narysuj wykres słupkowy z kolumn

A(X)

i

C(Y)

post

ę

puj

ą

c analogicznie jak w punkcie a). Uwaga: aby

zaznaczy

ć

kolumn

ę

A(X) i C(Y) nie zaznaczaj

ą

c kolumny B(Y) nale

ż

y wcisn

ąć

klawisz CTRL i trzymaj

ą

c

go klikn

ąć

na

i

.

6.

Upewnij si

ę

,

ż

e okno wykresu

Graph1

jest aktywne (pasek tytułowy pod

ś

wietlony na niebiesko)

7.

Z menu głównego wybierz

Analysis | Fit Gaussian

8.

Po dopasowaniu rozkładem Gaussa okno

Graph1

b

ę

dzie wygl

ą

dało tak:

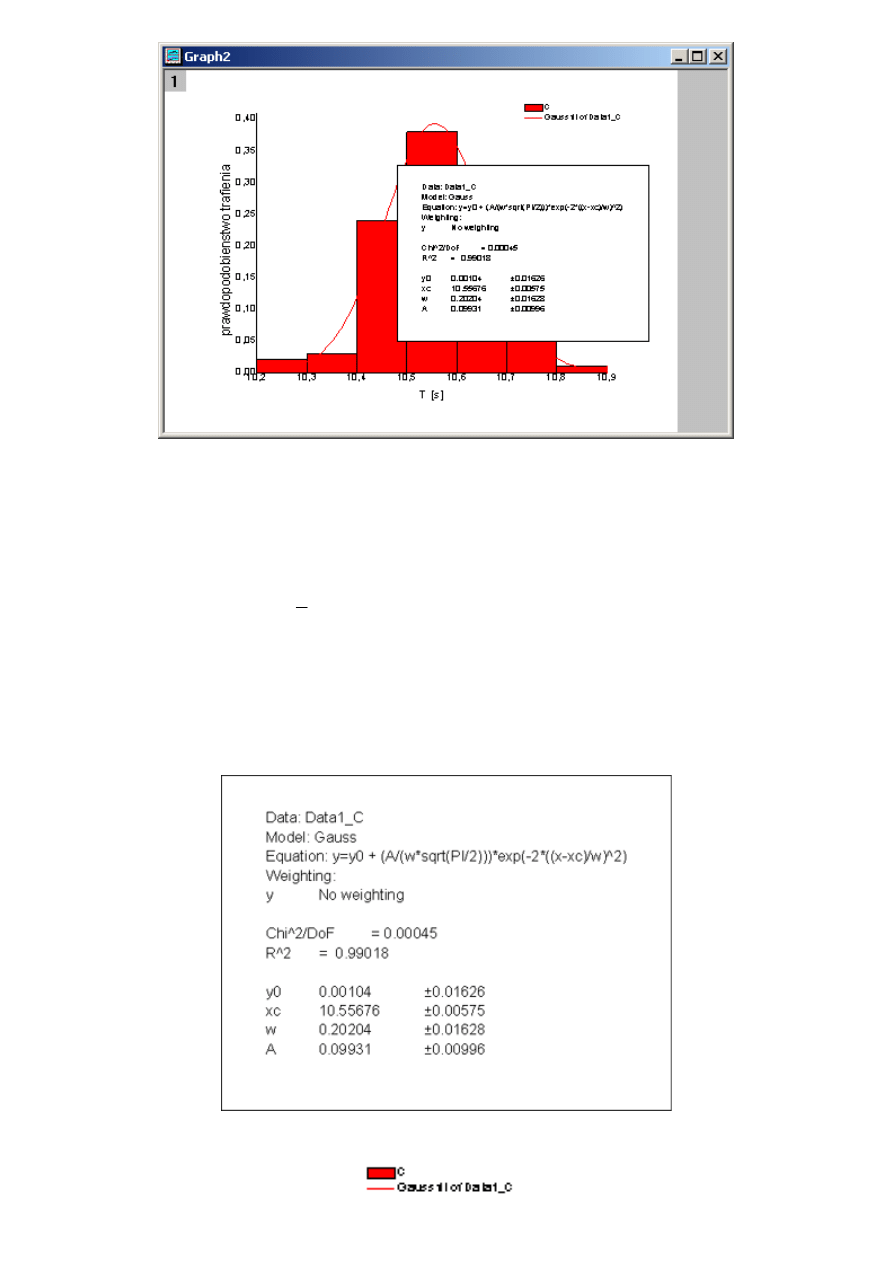
W widocznej na wykresie prostok

ą

tnej ramce zawarte s

ą

wyniki dopasowania. Wiersz zaczynaj

ą

cy si

ę

od słowa

„Equation” przedstawia wzór funkcji jak

ą

wykres został dopasowany. W naszym przypadku jest to rozkład

Gaussa. Uwa

ż

ny student zauwa

ż

y,

ż

e wzór z ramki ró

ż

ni si

ę

nieznacznie od wzoru podanego na poprzedniej

stronie. Mimo, i

ż

wzór z ramki gro

ź

niej wygl

ą

da to ró

ż

nica jest niewielka i polega jedynie na sposobie zapisu.

Mianowicie zamiast

σ

(jak w normalnym wzorze) u

ż

yto literki „

w”

, która jest równa podwojonej warto

ś

ci

σ

,

czyli

w=2 σ

. Je

ś

li do wzoru z ramki podstawimy

σ

2

=

w

to otrzymamy wzór z poprzedniej strony.

Analogicznie podstawiaj

ą

c za

w

2

1

=

σ

do wzoru z poprzedniej strony otrzymamy wzór z ramki.

W wierszach zaczynaj

ą

cych si

ę

od Chi^2 i R^2 podana jest informacja o jako

ś

ci dopasowania.

Warto

ś

ci dopasowanych parametrów i niepewno

ś

ci z jakimi zostały znalezione umieszczone s

ą

w czterech

ostatnich wierszach. Literkami „

xc”

oznaczono warto

ść

ś

redni

ą

. Natomiast przez „

y0”

i „

A”

oznaczono

pomocnicze parametry dopasowania.

Legenda do wykresu wygl

ą

da tak:

Najcz

ęś

ciej po dopasowaniu prostok

ą

tna ramka z wynikami dopasowania i legenda wykresu zasłaniaj

ą

nam

wykres i krzyw

ą

dopasowania. Oba te obiekty mo

ż

na przesun

ąć

. W tym celu nale

ż

y złapa

ć

je myszk

ą

i

trzymaj

ą

c lewy klawisz przesun

ąć

.

Kolor, grubo

ść

krzywej dopasowania i itp. mo

ż

na zmieni

ć

dwukrotnie na ni

ą

klikaj

ą

c

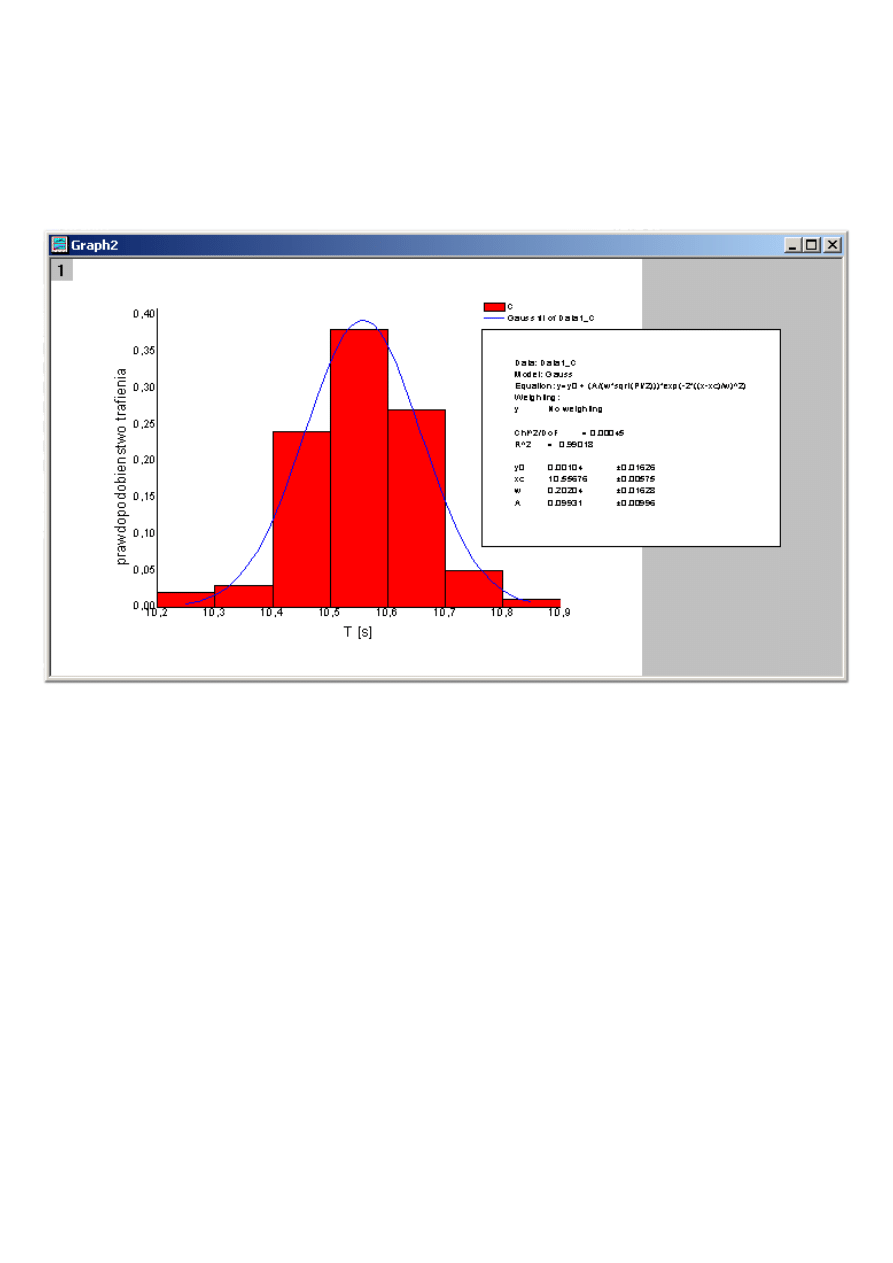
Przykładowy histogram z dopasowanym rozkładem Gaussa powinien wygl

ą

da

ć

tak:

9.

Aby wklei

ć

wykres z Origina do edytora tekstu np. Microsoft Worda nale

ż

y mie

ć

aktywne okno wykresu i z

menu głównego Origina wybra

ć

EDIT | Copy Page

. Wykres zostanie skopiowany do schowka. Teraz

nale

ż

y przej

ść

do Worda i z menu głównego wybra

ć

Edycja | Wklej

lub nacisn

ąć

kombinacj

ę

klawiszy

CTRL V

.

Ewentualnie mo

ż

na wydrukowa

ć

wykres bezpo

ś

rednio z Origina.