Potencjał elektryczny

1a. Elektryczna energia potencjalna

Siła elektrostatyczna jest siłą zachowawczą.

Układowi możemy przypisać

elektryczną

energię potencjalną E

p

.

Elektryczną energię potencjalną uważa się za
rodzaj energii mechanicznej.
Jeśli w układzie izolowanym działają tylko siły
zachowawcze, to energia mechaniczna układu
jest zachowana.

1b. Elektryczna energia potencjalna

Jeśli siła elektrostatyczna działa w jakimś układzie cząstek między dwiema lub
większą liczbą cząstek naładowanych, to możemy przypisać układowi
elektryczną energię potencjalną E

p

.

Jeśli układ zmienia swoją konfigurację ze stanu początkowego do innego stanu
końcowego, to siła elektrostatyczna wykonuje pracę W nad cząstkami.
Odpowiadająca temu procesowi zmiana



E

p

energii potencjalnej spełnia

zależność:

Tak, jak dla innych sił zachowawczych, praca wykonana przez siły
elektrostatyczne jest niezależna od toru cząstek.

Zwykle jako konfigurację odniesienia układu cząstek naładowanych wybieramy
taką, w której cząstki są nieskończenie od siebie oddalone. Przyjmujemy też, że
energia potencjalna odniesienia jest równa zeru. Wówczas:



E

p

= E

p końc

– E

p pocz

= – W

E

p

= – W



2a.

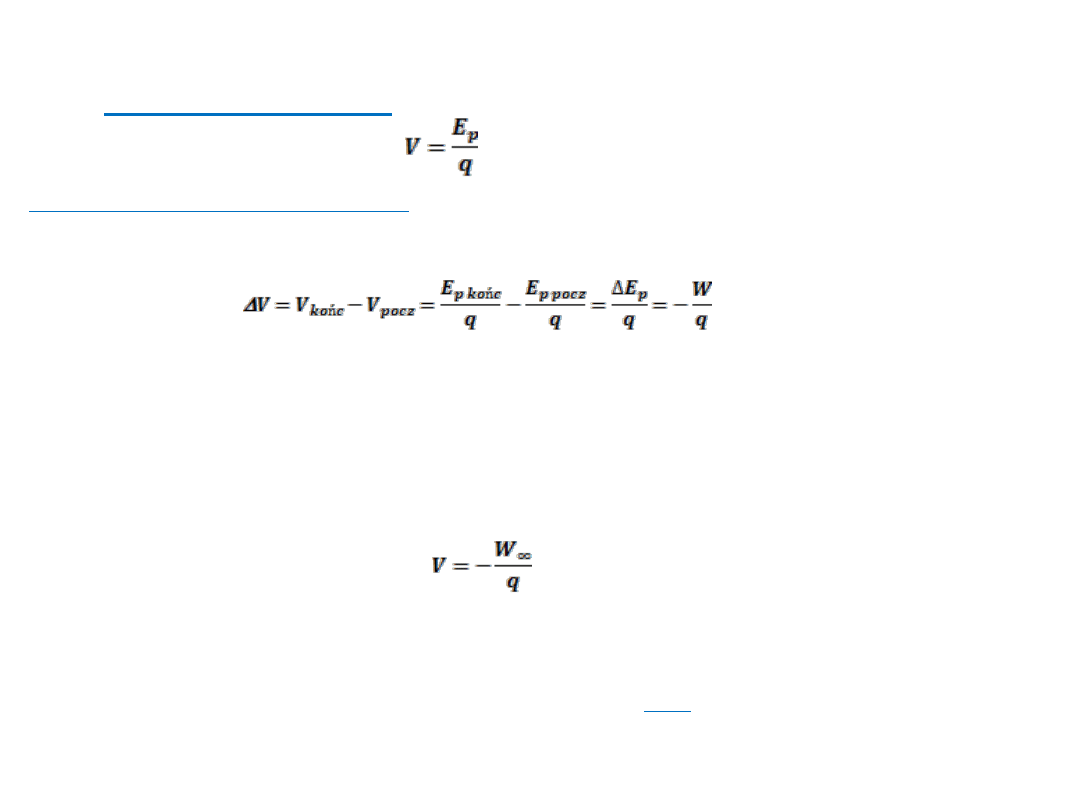
Potencjał elektryczny:

Energia potencjalna na jednostkowy ładunek w wybranym punkcie pola elektrycznego nosi
nazwę potencjału elektrycznego V (lub po prostu potencjału) w tym punkcie. Stąd:

Różnica potencjałów elektrycznych



V między dwoma punktami początkowym i końcowym

w polu elektrycznym jest równa różnicy energii potencjalnej na jednostkowy ładunek między
tymi dwoma punktami:

W – praca wykonana przez siłę elektrostatyczną, przy przesunięciu jednostkowego ładunku z jednego
punktu do drugiego.

Jeśli przyjmiemy E

p pocz

=0 w nieskończoności jako naszą energię potencjalną odniesienia, to

potencjał elektryczny V musi tam być też równy zero. Wówczas, potencjał elektryczny V w
dowolnym punkcie pola elektrycznego definiujemy wzorem:

W

∞

- praca wykonana przez pole elektryczne nad cząstką naładowaną, gdy cząstka przesuwa się z

nieskończoności do punktu końcowego.

Jednostką potencjału w układzie SI jest dżul na kulomb (wolt – V):

(potencjał elektryczny jest skalarem)

(definicja różnicy potencjałów)

(definicja potencjału)

1 wolt = 1 dżul na kulomb

2b. Potencjał elektryczny: jednostki

Jednostka wolt pozwala przyjąć inną jednostkę natężenia pola
elektrycznego E:




Możemy teraz zdefiniować jednostkę energii, która jest wygodna
do pomiarów energii w obszarze atomowym i subatomowym:
Jeden elektronowolt (eV) jest energią równą pracy, potrzebnej do
przesunięcia pojedynczego ładunku elementarnego e (np. elektronu
czy protonu) między punktami o różnicy potencjałów równej
jednemu woltowi. Wartość tej pracy wynosi q



V, czyli:

2c.

Potencjał elektryczny: praca wykonana przez siłę zewnętrzną

Jeśli cząstka o ładunku q jest przesuwana z punktu początkowego do punktu
końcowego w polu elektrycznym, działając na nią siłą, zastosowana siłą wykonuje
pracę W

p

nad ładunkiem, a pole elektryczne wykonuje nad nim pracę W. Zmiana

energii kinetycznej cząstki wynosi:


Jeśli cząstka spoczywa przed wprawieniem w ruch i po jej zatrzymaniu, wówczas
E

k końc

i E

k pocz

są równe zeru:

Wiążąc pracę wykonaną przez przyłożoną siłę ze zmianą energii potencjalnej
cząstki podczas ruchu, otrzymujemy:


Możemy również powiązać W

p

z różnicą potencjałów elektrycznych



V między

początkowym i końcowym położeniem cząstki:



E

k

= E

k końc

-E

k pocz

= W

p

+W

W

p

= - W



E

p

= E

p końc

-E

p pocz

= W

p

W

p

= q



V

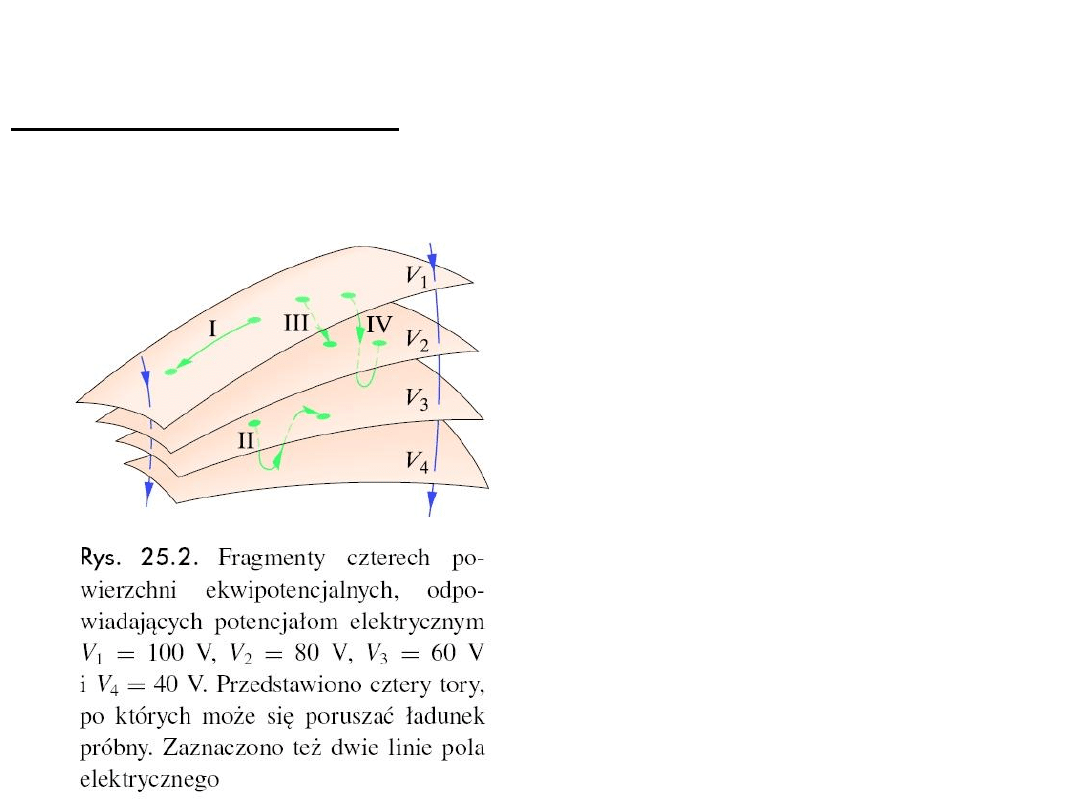
3a. Powierzchnie ekwipotencjalne:

Sąsiadujące ze sobą punkty, które mają taki sam potencjał elektryczny, tworzą
powierzchnię ekwipotencjalną (wyobrażoną albo rzeczywistą powierzchnią fizyczną).
Jeśli cząstka porusza się między dwoma punktami (początkowym i końcowym) po tej
samej powierzchni ekwipotencjalnej, to pole elektryczne nie wykonuje żadnej pracy W.

(praca na torach I i II jest równa zeru – każdy z tych
torów zaczyna się i kończy na tej samej powierzchni
ekwipotencjalnej;
praca na torach III i IV ma taką samą wartość –
początkowe i końcowe potencjały są identyczne dla
tych dwóch torów; tory te łączą tę samą parę
powierzchni ekwipotencjalnych)

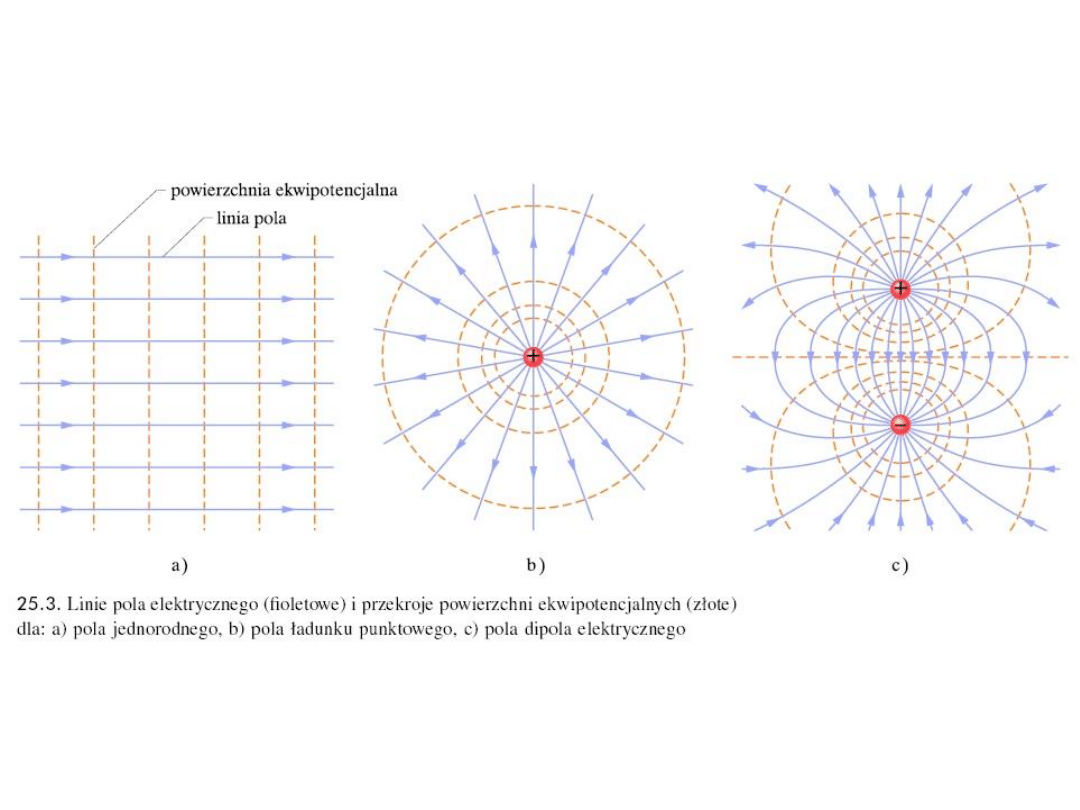
3b. Powierzchnie ekwipotencjalne:

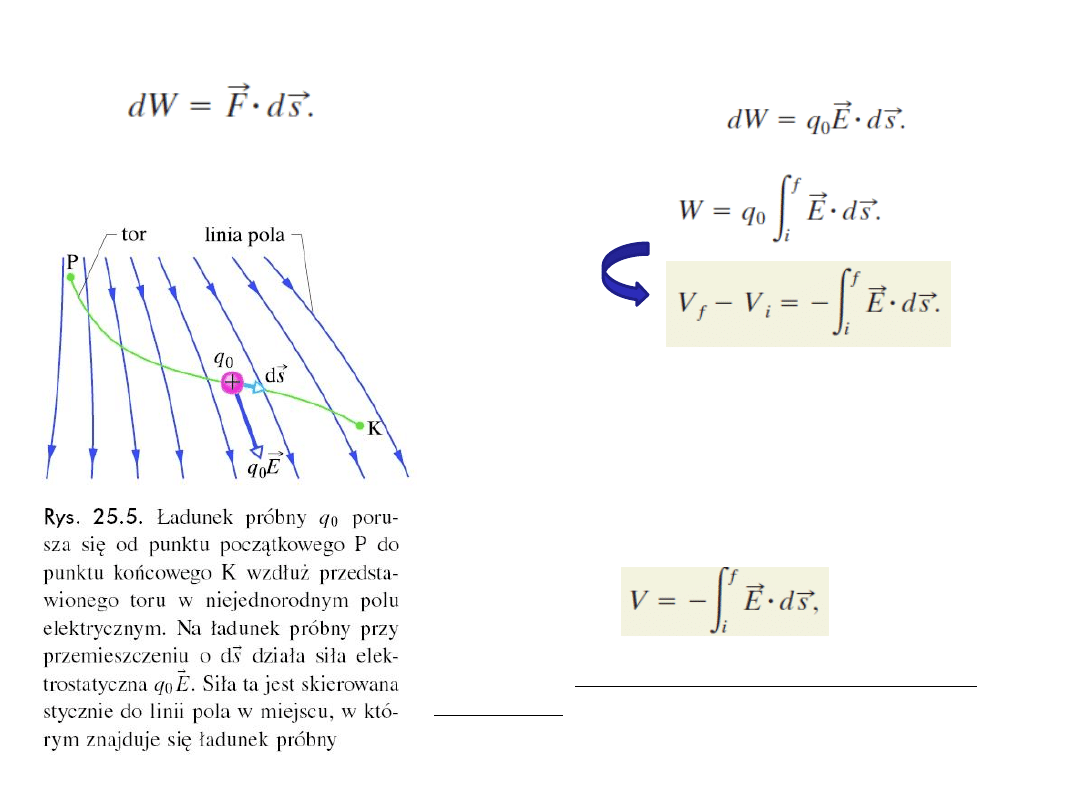
4. Obliczanie potencjału na podstawie natężenia pola:

Dla sytuacji z rys. 25.5:


Całkowita praca:

Zatem różnica potencjałów V

f

-V

i

między dwoma punktami i i f w

polu elektrycznym jest równa wziętej ze znakiem minus całce
krzywoliniowej (wzdłuż toru cząstki) od i do f. Siła
elektrostatyczna jest zachowawcza, dlatego też dla każdego toru
otrzymujemy ten sam wynik.
Jeśli wybierzemy V

i

=0, wówczas:

Jest to potencjał V w dowolnym punkcie końcowym f pola
elektrycznego względem zerowego potencjału w punkcie
poczatkowym i. Jeśli punkt początkowy i jest w nieskończoności,
to V określa potencjał w dowolnym punkcie końcowym f
względem zerowego potencjału w nieskończoności.

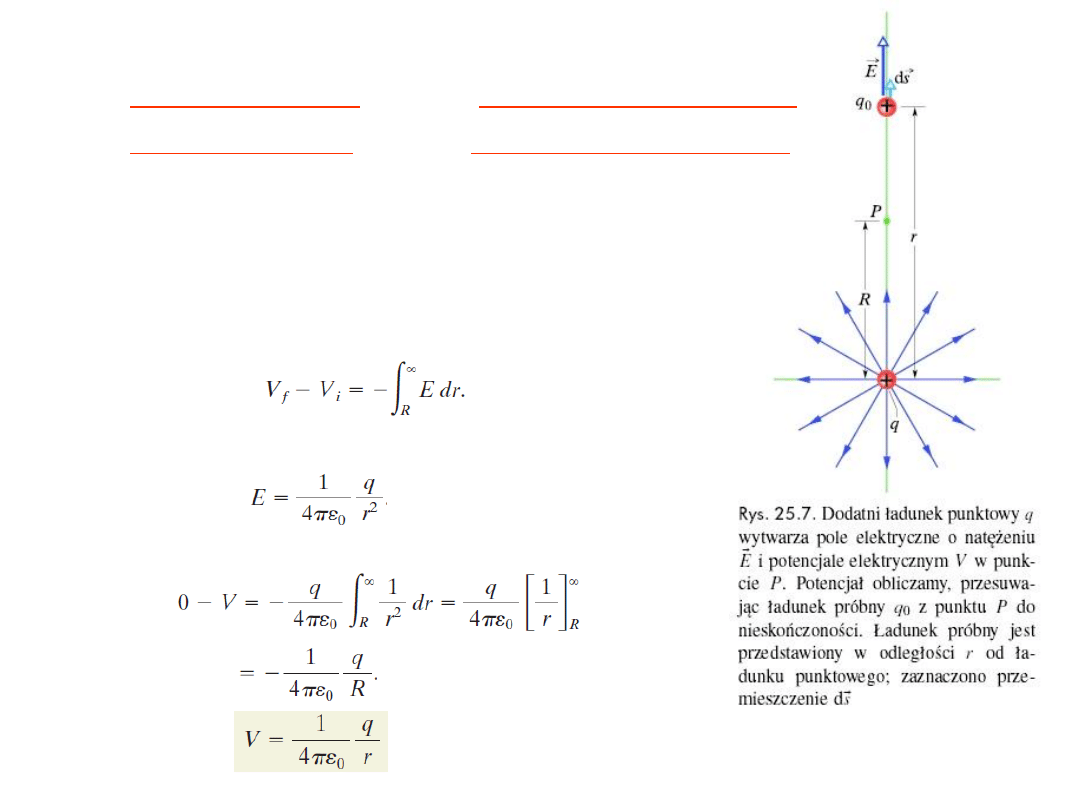
5. Potencjał pola ładunku punktowego:

Rozważmy punkt P w odległości R od nieruchomej cząstki o dodatnim
ładunku q. Wyobraźmy sobie, że przesuwamy dodatni ładunek próbny
q

0

z punktu P do nieskończoności. Tor nie jest istotny — wybieramy

prostą przechodząca przez ładunek q i punkt P .

Załóżmy, że V

f

=0 (w ∞) and V

i

=V (w odległości R). Wówczas

podstawiając

otrzymujemy

Zamieniając R na r:

(potencjał pola wytworzonego przez cząstkę
o ładunku q w odległości r od cząstki)

Cząstka dodatnio naładowana wytwarza dodatni potencjał elektryczny.

Cząstka ujemnie naładowana wytwarza ujemny potencjał elektryczny.

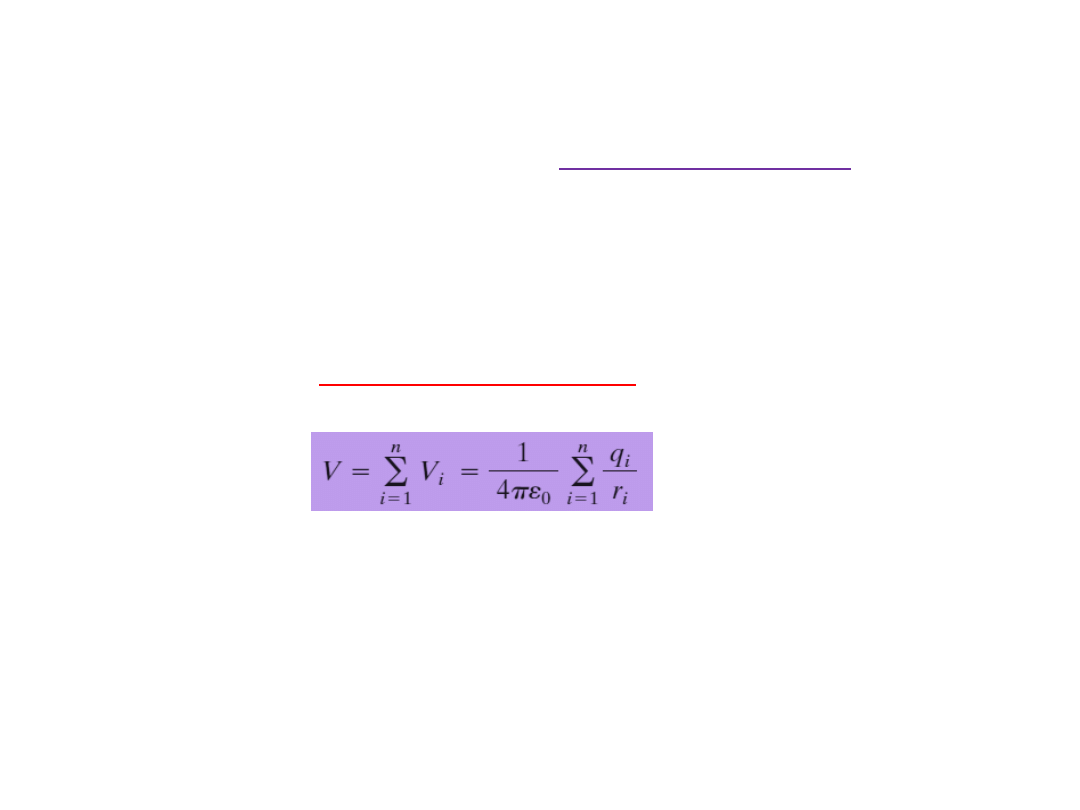
6. Potencjał pola układu ładunków punktowych:

Wypadkowy potencjał układu ładunków punktowych w jakimś
punkcie obliczamy, korzystając z zasady superpozycji:
obliczamy oddzielnie potencjały pochodzące od każdego
ładunku w danym punkcie (uwzględniamy znak ładunku),
a następnie sumujemy te potencjały.

Dla n ładunków,

wypadkowy potencjał

wynosi:

Przykład: potencjał elektryczny w punkcie P, znajdującym się w środku kwadratu

Przykład: potencjał elektryczny nie jest wektorem

7. Elektryczna energia potencjalna układu ładunków punktowych:

Elektryczna energia potencjalna układu nieruchomych
ładunków punktowych, jest równa pracy jaką musi
wykonać siła zewnętrzna, aby utworzyć ten układ
przenosząc każdy ładunek z nieskończonej odległości.

Na rys. przedstawiono dwa ładunki punktowe q

1

and q

2

, znajdujące

się w odległości r. Gdy przeniesiemy q

1

z nieskończoności do

odpowiadającego mu miejsca, nie wykonamy żadnej pracy, bo na
ładunek q

1

nie działa żadna siła. Jeśli następnie przesuniemy q

2

z

nieskończoności do odpowiadającego mu miejsca, to musimy
wykonać pracę, ponieważ q

1

oddziałuje siłą elektrostatyczną na

ładunek q

2

podczas przesuwania.

Wykonana praca jest równa q

2

V, gdzie V jest potencjałem wytworzonym przez ładunek q

1

w punkcie,

w którym umieszczamy q

2

.

E

p

Przykład: elektryczna energia potencjalna układu trzech punktów