
Jacek Kabziński
Automatyka i sterowanie
————————————————————————————————————————
2
Automatyka i sterowanie 17
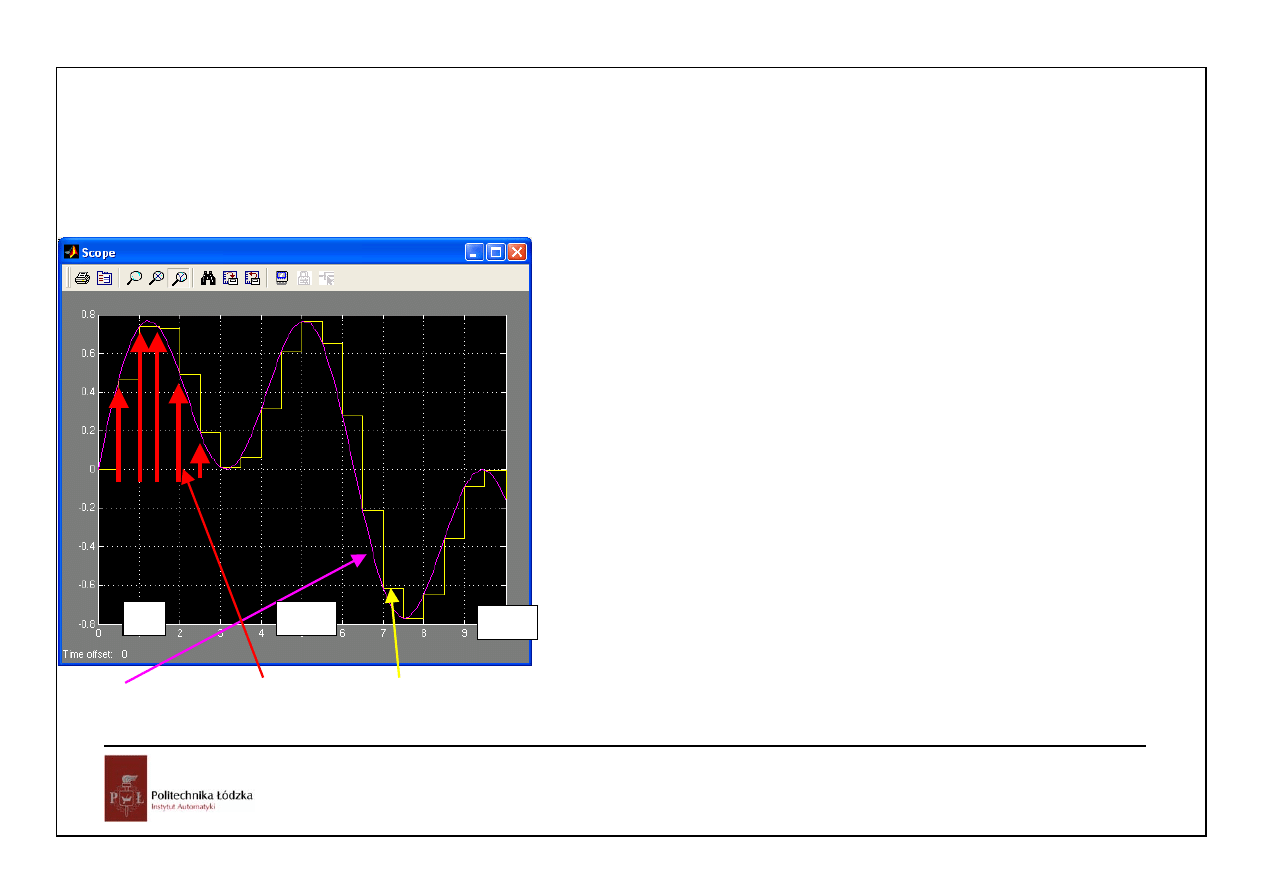
Częstotliwość próbkowania
Częstotliwość próbkowania – wpływ na pracę układu dyskretnego
)
(t
f
)
(
*
t
f
)
(t
x
5
.
0
=
T
2T
10T
20T
3
Automatyka i sterowanie 17
Częstotliwość próbkowania
)
(t
f
)
(
*
t
f
)
(t
x
5
.
0
=
T
1
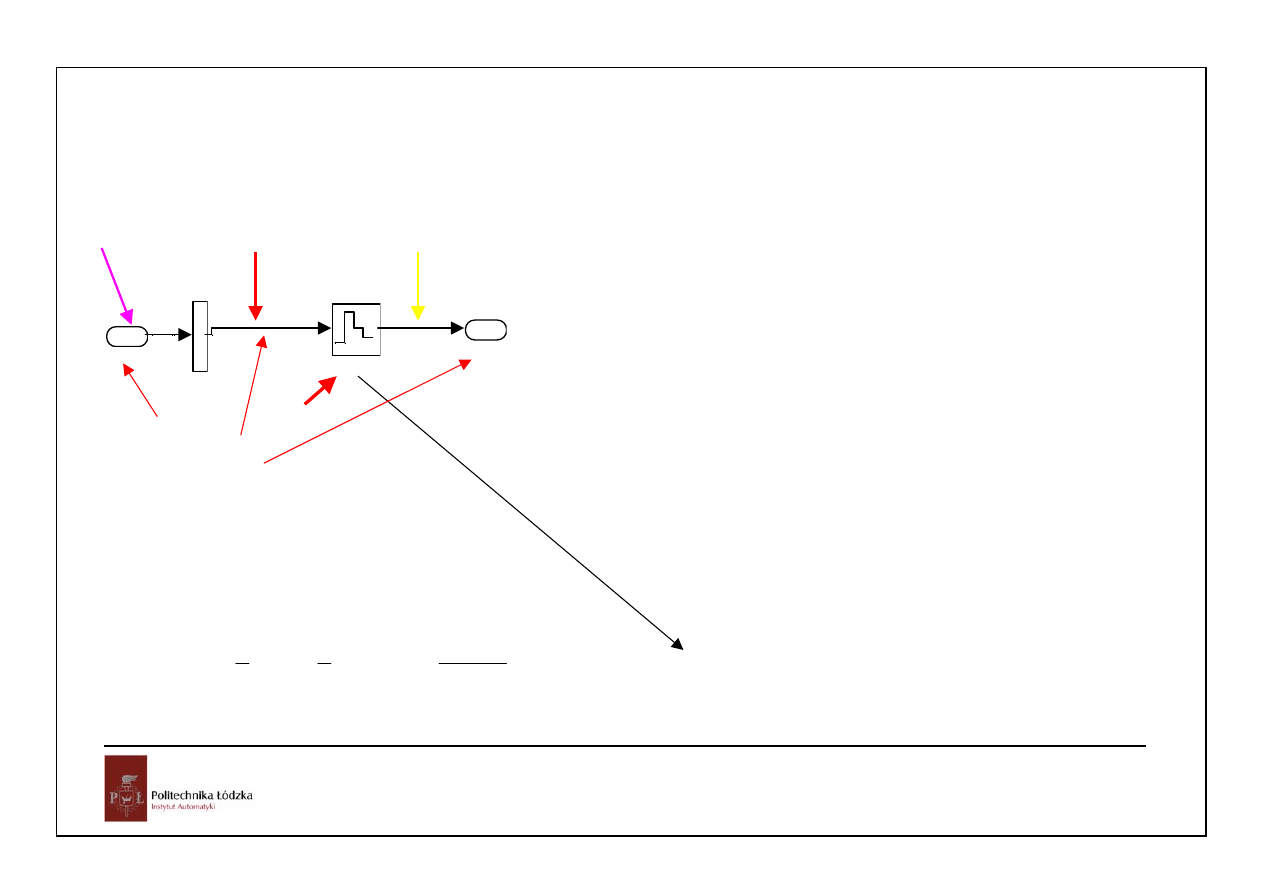
x(t)
f(u)
IMPULSATOR
T
Ekstrapolator
1
f(t)
T
kT
t
kT
kT
f
t
x
+
<
≤
=
)
(
)
(
[
]
)
(
1
)
(
1
)
(
)
(
0
T
kT
t
kT
t
kT
f
t
x
k
−
−
−
−
=
∑
∞
=
)
(
)
(
)
(
1
1
1
)
(
)
(
*
0
)
1
(
0
s
f
s
E
e
kT
f
s
e
e
s
e
s
kT
f
s
x
kTs
k
Ts
Ts
k
kTs
k
=
−
=
⎥⎦
⎤
⎢⎣
⎡
−
=
−
∞
=
−
+
−
−
∞
=
∑
∑
Filtr??
Czy częstotliwości z wejścia są
zniekształcane przez impulsowanie?
Czy będą na wyjściu?

4
Automatyka i sterowanie 17
Częstotliwość próbkowania
)
(
)
(
)
(
)
(
)
(
0
*
kT
t
t
f
kT
t
kT
f
t
f
k
k
−
=
−
=
∑
∑
∞
−∞
=
∞
=
δ
δ
Przeprowadzimy analizę częstotliwościową tej funkcji.
Podstawy częstotliwościowej analizy sygnałów:
Okresową funkcję f(t) o okresie T , spełniającą warunki Dirichleta można przedstawić w postaci sumy
szeregu Fouriera
)
t
n
sin
b
t
n
cos
a
(
a
)
t
(
f
A
n
n
A
n
ω
ω
∑
∞
=
+
+
=
1
0
T
A
π
ω
2
=
∫
+
=
T
t
t
dt
)
t
(
f
T
a
0
0
1
0
,
∫
+
=
T
t
t
A
m
tdt
m
cos
)
t
(
f
T
a
0
0
2
ω
,
∫
+
=
T
t
t
A
m
tdt
m
sin
)
t
(
f
T
b
0
0
2
ω
, m=1,2,....
lub:

5
Automatyka i sterowanie 17
Częstotliwość próbkowania
)
t
n
sin
b
t
n
cos
a
(
a
)
t
(
f
A
n
n
A
n
ω
ω
∑
∞
=
+
+
=
1
0
=
∑
∞
−∞
=
n
t
jn
n
A
e
c
ω
,
n
n
a
b
tan
j
n
n
n
n
n
e
b
a
jb
a
c
1
2
2
2
1
2
−
−
+
=
−
=
=
∫
∫
−
−
−
=
T
t
jn
T
T
t
jn
dt
e
)
t
(
f
T
dt
e
)
t
(
f
T
A
A
0
2
2
1
1
ω
ω
Transformatę Fouriera (nieokresowej) funkcji x(t) określa:
{
}
∫
∞
∞
−
−
=
=
ℑ
dt
e
)
t
(
x
)
j
(
X
)
t
(
x
t
j
ω
ω
a transformatę odwrotną
{
}
∫
∞
∞
−
−
=
=
ℑ
ω
ω
π
ω
ω
d
e
)
j
(
X
)
t
(
x
)
j
(
X
t
j
2
1
1
gdy x(t)=0 dla t<0 to
ω
ω
ω
j
s
t
j
)
s
(
X
dt
e
)
t
(
x
)
j
(
X
=
∞
−
=
=
∫
0

6
Automatyka i sterowanie 17
Częstotliwość próbkowania
Gdy x(t) jest okresowa, to ma rozwinięcie w szereg Fouriera
∑
∞
−∞
=
=
n
t
jn
n
A
e
c
)
t
(
x
ω
wtedy:
{
}
∫
∞
∞
−
−
=
=
ℑ
dt
e
)
t
(
x
)
j
(
X
)
t
(
x
t
j
ω
ω
=
∫ ∑
∞
∞
−
−
∞
−∞
=
dt
e
e
c
t
j
n
t
jn
n
A
ω
ω
=
∫
∑
∞
∞
−
−
∞
−∞
=
dt
e
e
c
t
j
t
jn
n
n
A
ω
ω
=
=
(
)
t
jn
n
n
A
e
c
ω
ℑ
∑
∞
−∞
=
=
)
n
(
c
A
n
n
ω
ω
δ
π
−
∑
∞
−∞
=
2

7
Automatyka i sterowanie 17
Częstotliwość próbkowania
Zastosujmy to do funkcji
)
(
)
(
)
(
)
(
)
(
0
*
kT
t
t
f
kT
t
kT
f
t
f
k
k
−
=
−
=
∑
∑
∞
−∞
=
∞
=
δ
δ
Funkcja
)
kT
t
(
k
−
∑
∞
−∞
=
δ
jest okresowa o kresie T .
Współczynniki jej szeregu Fouriera:
∫
−
−
=
=
2
2
1
1
T
T
t
jn
n
T
dt
e
)
t
(
T
c
A
ω
δ
n=1,2,..
czyli
T
,
e
T
)
kT
t
(
A
t
jk
k
k
A
π
ω
δ
ω
2
1
=
=
−
−
∞
−∞
=
∞
−∞
=
∑
∑
8
Automatyka i sterowanie 17
Częstotliwość próbkowania
t
jk
k
*
A
e
)
t
(
f
T
)
t
(
f
ω
−
∞
−∞
=
∑
=
1
{
}
∫
∞
∞
−
−
=
=
ℑ
dt
e
)
t
(
f
)
j
(
F
)
t
(
f
t
j
*
*
*
ω
ω
(
)
∫
∑
∫
∑
∞
∞
−
+
−
∞
−∞
=
∞
∞
−
−
∞
−∞
=
−
=
=
dt
e
)
t
(
f
T
dt
e
e
)
t
(
f
T
)
j
(
F
t
k
j
k
t
j
k
t
jk
*
A
A
ω
ω
ω
ω
ω
1
1
(
)
(
)
ω
ω
ω
+
=
∑
∞
−∞
=
A
k
*
k
j
F
T
)
j
(
F
1
gdzie
{
}
∫
∞
∞
−
−
=
=
ℑ
dt
e
)
t
(
f
)
j
(
F
)
t
(
f
t
j
ω
ω
przesunięte o wielokrotność
T
A
π
ω
2
=
transformaty Fouriera funkcji
f(t)
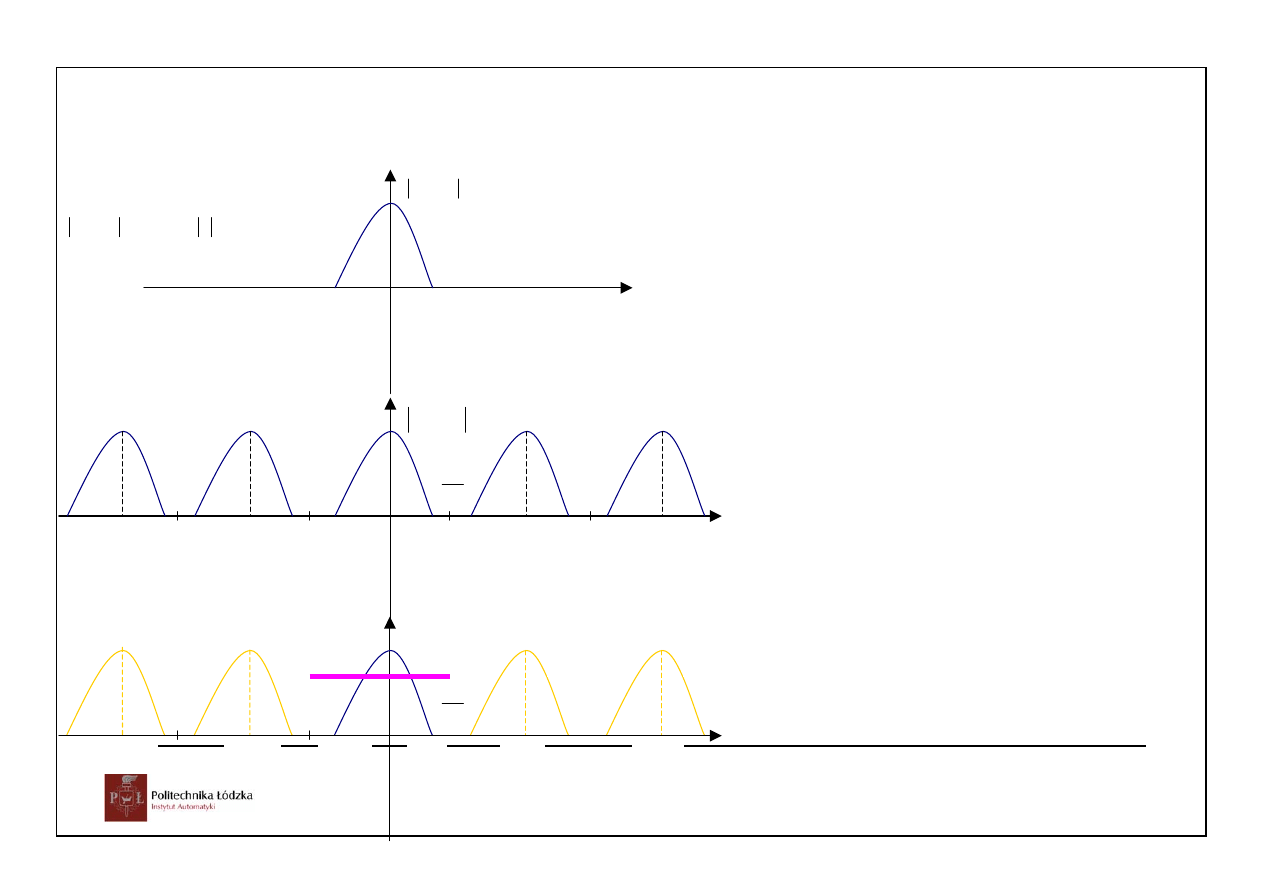
Załóżmy, że
0
=
)
j
(
F
ω
dla
1
ω
ω
>
1
2
ω
ω
>
A
9
Automatyka i sterowanie 17
Częstotliwość próbkowania
0
=
)
j
(
F
ω
dla
1
ω
ω
>
i
1
2
ω
ω
>
A
2
A
ω
2
A
ω
A
ω
)
j
(
G
ω
1
ω
−
1
ω
A
ω
2
A
ω
−
A
ω
2
−
1
−
=
k
2
−
=
k
1
=
k
A
ω
)
j
(
F
ω
1
ω
−
1
ω
)
j
(
F
*
ω
1
ω
−
1
ω
A
ω
2
A
ω
−
A
ω
2
−
1
−
=
k
2
−
=
k
1
=
k
10
Automatyka i sterowanie 17
Częstotliwość próbkowania
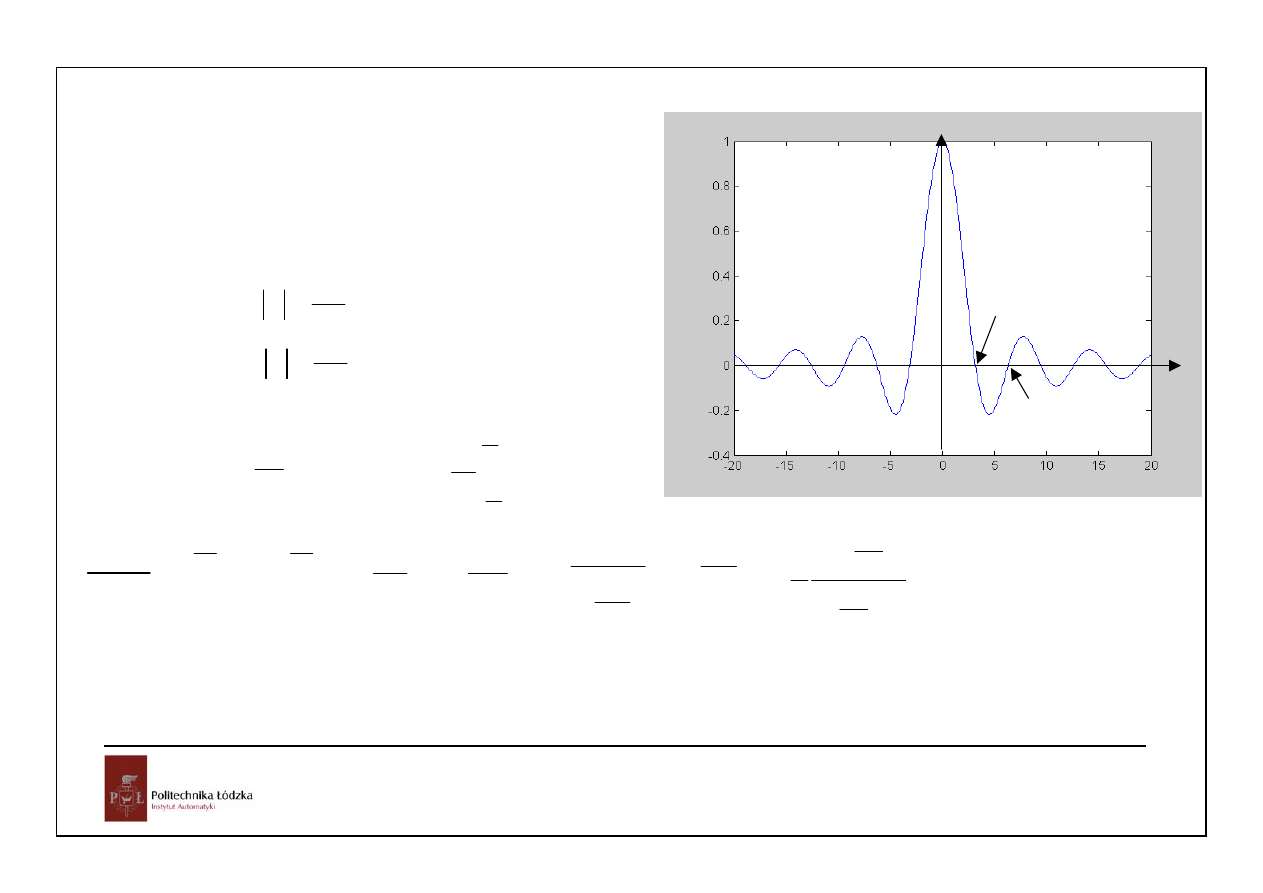
Stosujemy filtr idealny o transmitancji widmowej
⎪
⎩
⎪
⎨
⎧
<
<
=
2
0
2
1
A
A
dla
dla
)
j
(
G
ω
ω
ω
ω
ω
jego odpowiedź impulsowa:
{
}
∫
∞
∞
−
−
=
=
ℑ
ω
ω
π
ω
ω
d
e
)
j
(
G
)
t
(
g
)
j
(
G
t
j
2
1
1
=
∫
−
2
2
2
1
A
A
d
e
t
j
ω
ω
ω
ω
π
=
2
2
1
2
A
A
j
t
j
t
e
e
jt
ω
ω
π
−
⎛
⎞
=
−
⎜
⎟
⎝
⎠
1
2
A
sin
t
t
ω
π
⎛
⎞
=
⎜
⎟
⎝
⎠
1
2
2
A
A
sin
t
T
t
ω
ω
⎛
⎞
=
⎜
⎟
⎝
⎠
1
2
2
A
A
sin
t
T
t
ω
ω
⎛
⎞
⎜
⎟
⎝
⎠
=
T
2T

11
Automatyka i sterowanie 17
Częstotliwość próbkowania
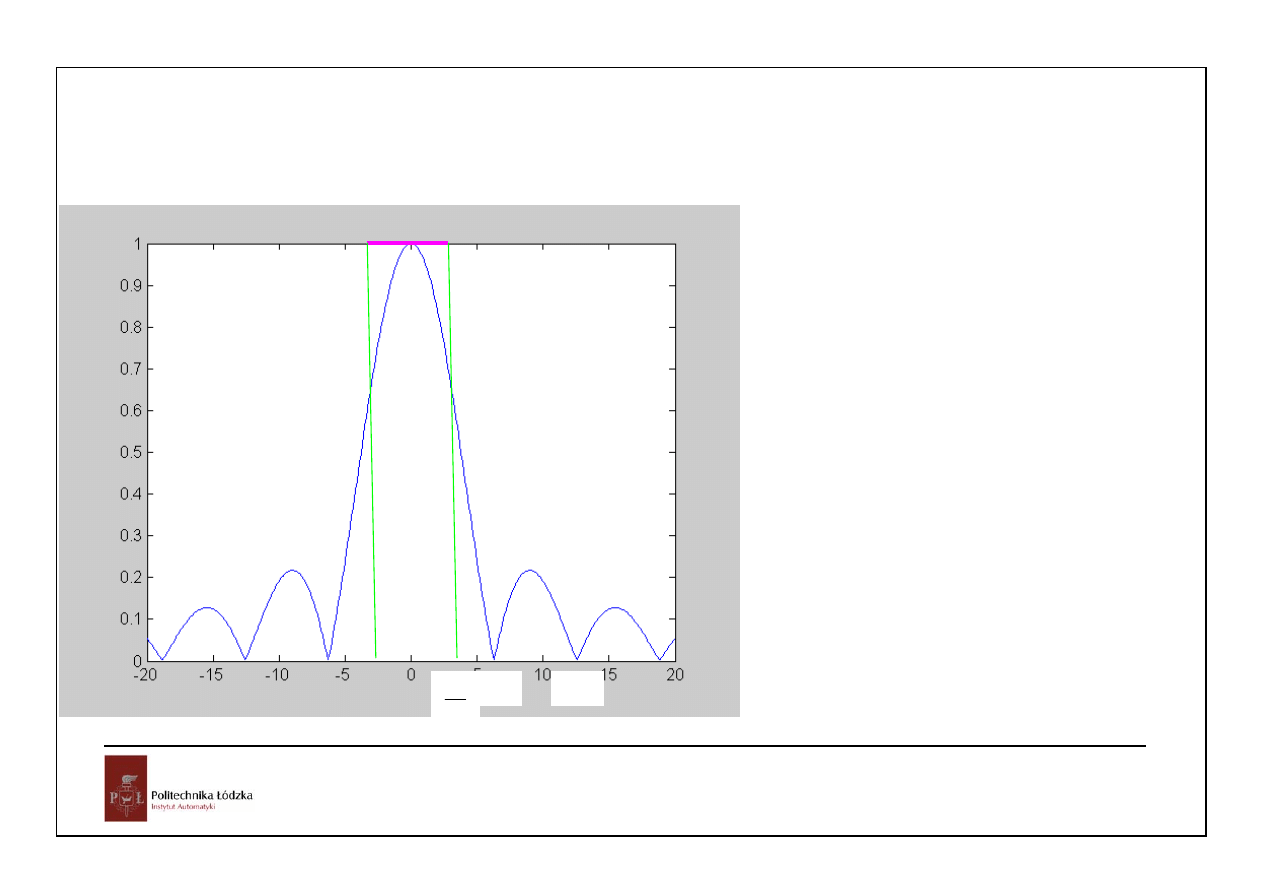
Tw. Shannona
Jeżeli
0
=
)
j
(
F
ω
dla
1
ω
ω
>
to F(j
ω
) jest jednoznacznie określona przez ciąg f(kT) i f(t) jest dana
przez
∑
∞
−∞
=
−
−
=
k
A
A
)
kT
t
(
)
kT
t
(
sin
)
kT
(
f
)
t
(
f
2
2
ω
ω
12
Automatyka i sterowanie 17
Częstotliwość próbkowania
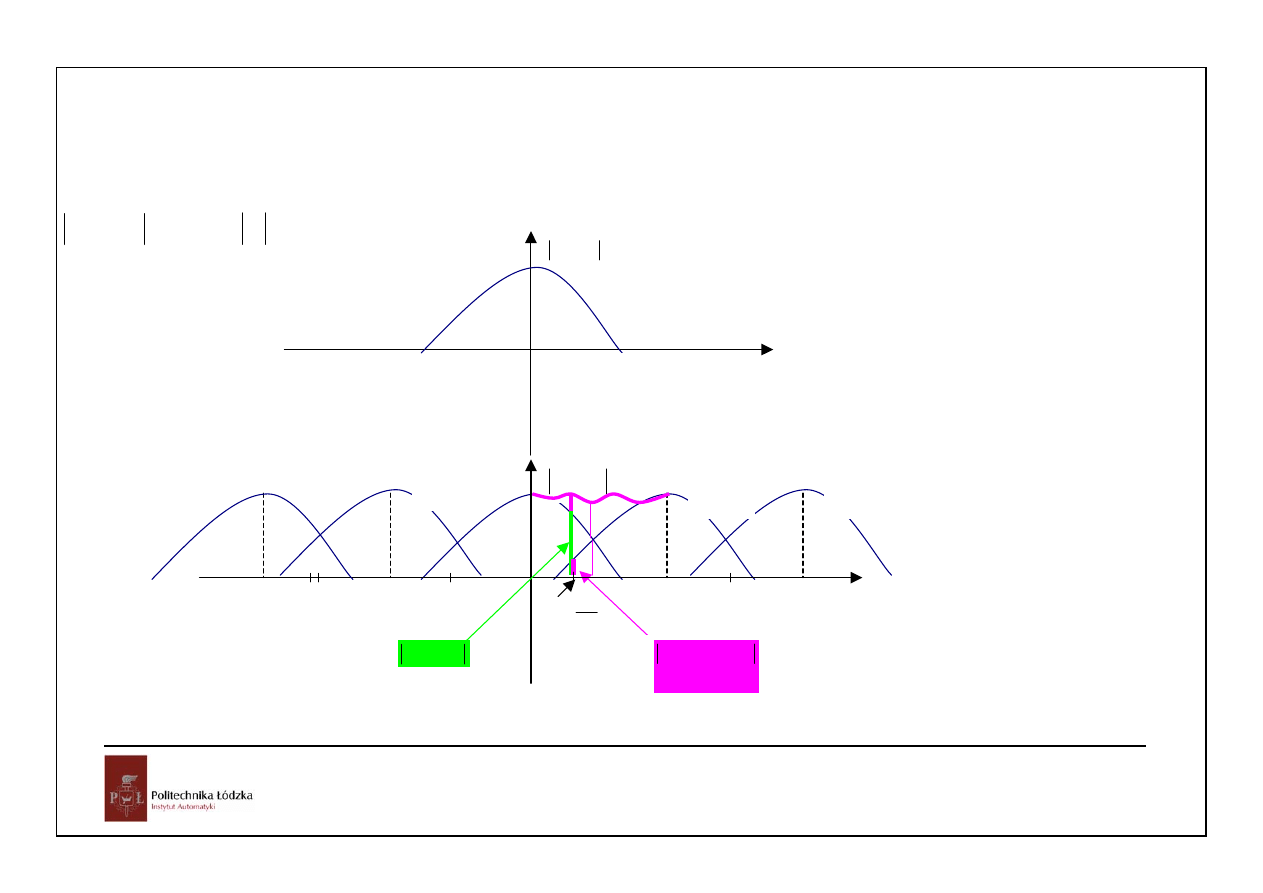
Moduł transmitancji widmowej
ekstrapolatora zerowego rzędu
A
ω
A
ω
2
2
A
ω
0,637
13
Automatyka i sterowanie 17
Częstotliwość próbkowania
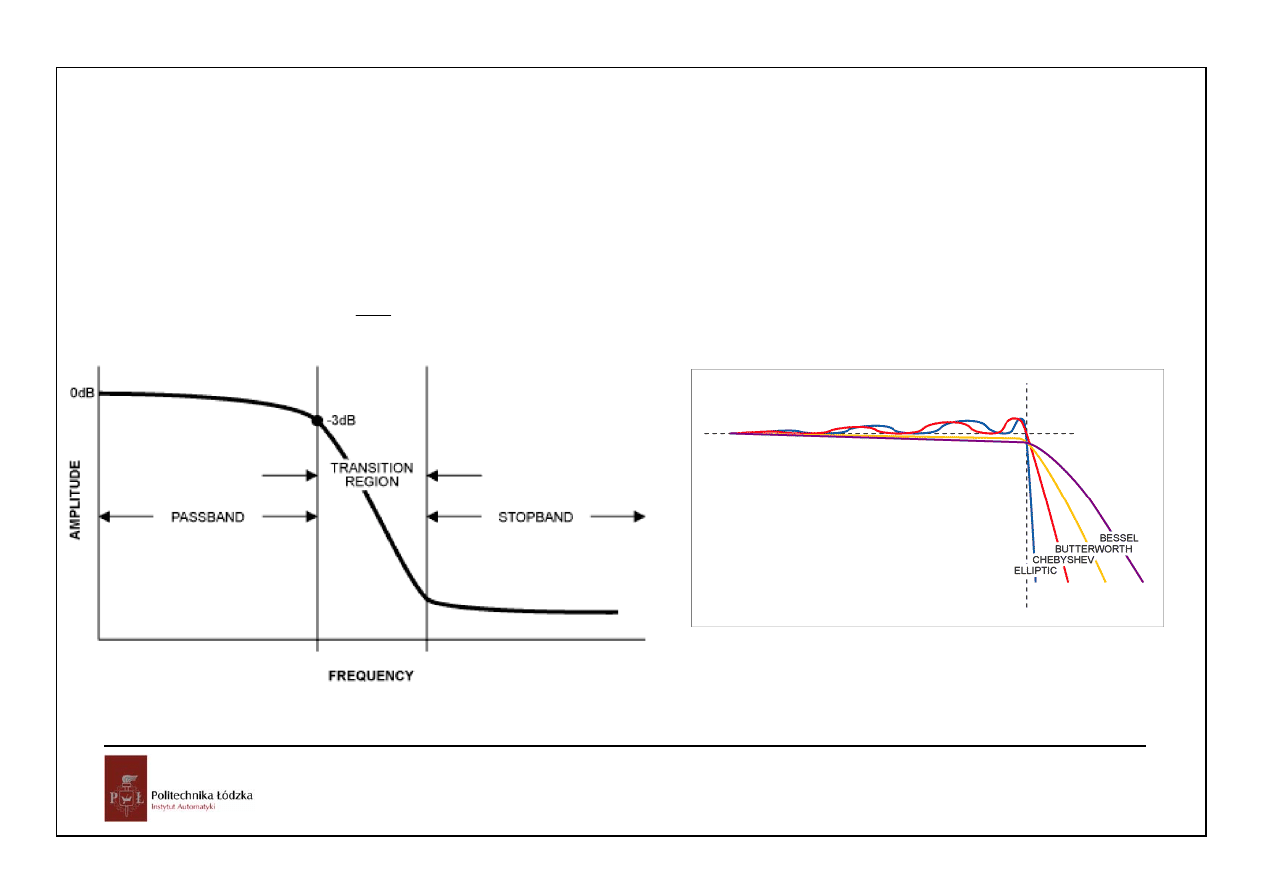
0
=
)
j
(
F
ω
dla
1
ω
ω
>
ale
1
2
ω
ω
<
A
2
A
ω
A
ω
1
ω
2
ω
)
j
(
F
ω
)
j
(
F
*
ω
1
ω
−
A
ω
2
A
ω
−
A
ω
2
−
1
−
=
k
2
−
=
k
1
=
k
1
ω
−
1
ω
2
2
ω
ω
ω
alias
)
(
j
(
F
A
−
)
(
j
(
F
2
ω
14
Automatyka i sterowanie 17
Częstotliwość próbkowania
Środki zaradcze:
1. Podnieść
A
ω
tak by
1
2
ω
ω
>
A
czyli zmniejszyć T. W praktyce
1
10
5
ω
ω
÷
>
A
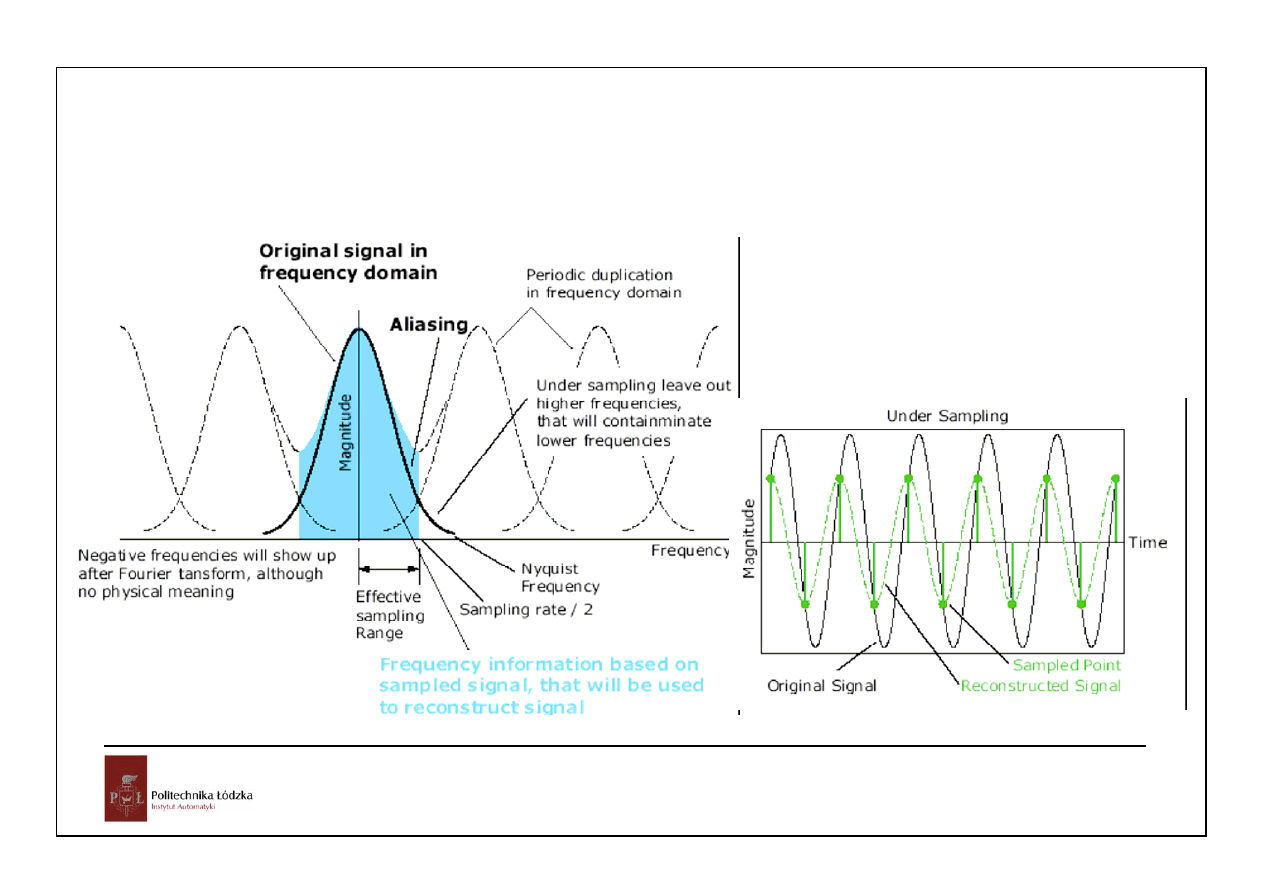
2. Obciąć widmo f(t) do 2
A
ω
przez filtr dolnoprzepustowy przed próbkowaniem
15
Automatyka i sterowanie 17
Częstotliwość próbkowania
16
Automatyka i sterowanie 17
Częstotliwość próbkowania

17
Automatyka i sterowanie 17
Częstotliwość próbkowania
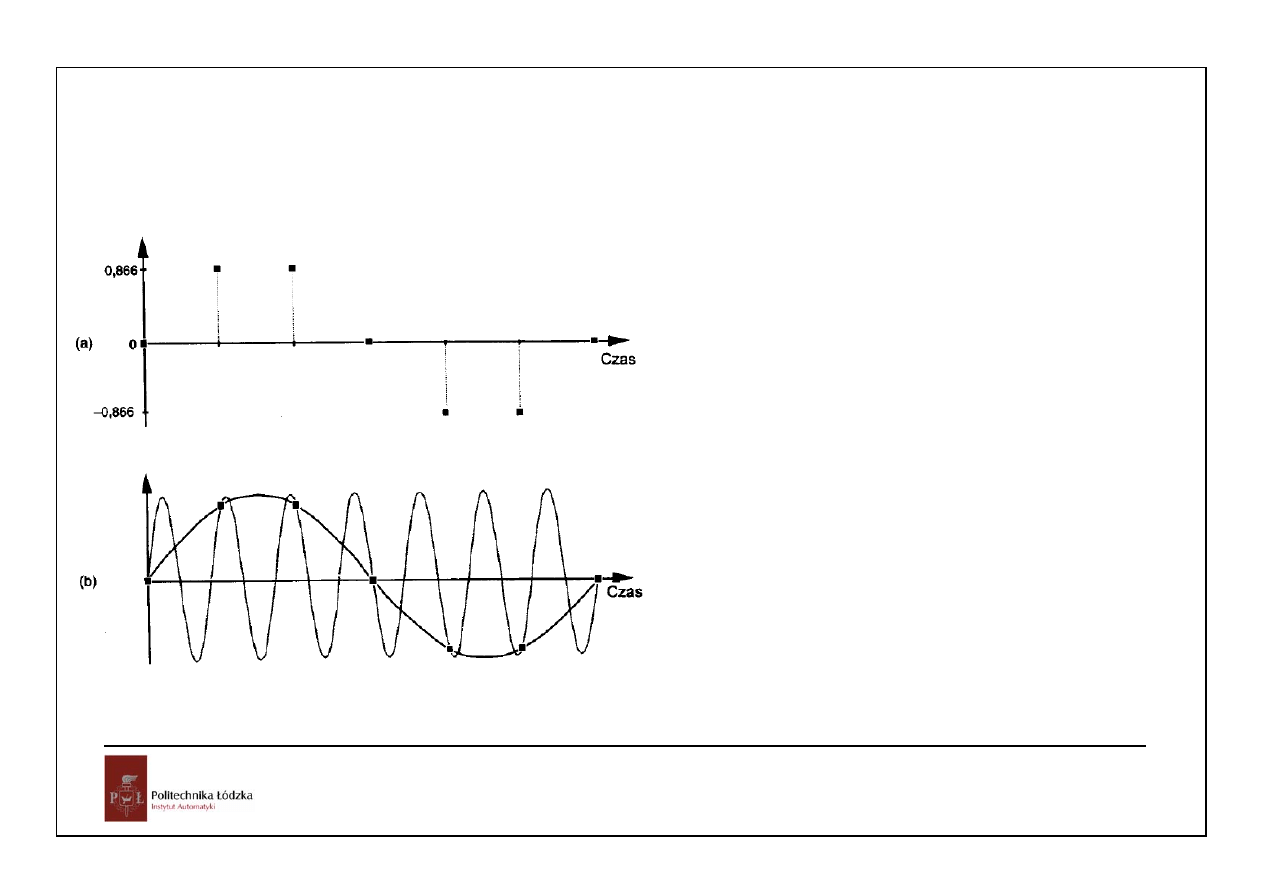
Wolne próbkowanie (undersampling) może być stosowane świadomie. Przetwornik A/C może
przetwarzać informację zakodowana w modulowanym sygnale nośnym o dużej częstotliwości i
wytwarzać sygnał o częstotliwości niższej.
Stosowanie przetwornika próbkującego poniżej częstotliwości Nyquista może być opłacalne finansowo.
Np. Sygnał nośny 10MHz jest modulowany sygnałem o paśmie 100kHz (±50kHz ośrodku 10MHz).
Próbkowanie z częstotliwością 4MHz daje składniki (f1+f2 i f1-f2) o częstotliwości 14MHz i 6Mz, i
składniki (2f1, 2f2, 2f1+f2, f1+2f2, | 2f1-f2 |, | f1-2f2) | o częstotliwości 8MHz, 20MHz, 18MHz, 2MHz,
24MHz i 16MHz. Sygnał o częstotliwości 2MHz jest tym, o który chodzi. Z sygnału 10MHz przez
próbkowanie wytworzono “alias” 2MHz. W sposób cyfrowy można teraz “odzyskać” sygnał o
częstotliwości 50kHz. Nie wymaga to kosztownej obróbki analogowej, wystarczy odpowiednie
oprogramowanie.
Szybkie próbkowanie (oversampling) może być używane do redukcji szumów w przypadku zakłócenia
szumem białym. Zbieramy więcej próbek, niż to konieczne do odtworzenia sygnału, potem filtrując dane
redukujemy poziom zakłóceń.

18
Automatyka i sterowanie 17
Częstotliwość próbkowania
Transmisja sygnałów w układzie regulacji
W układzie regulacji tor główny od sygnału uchybu powinien tłumić częstotliwości
2
A
ω
ω
>
i widmo
sygnału wyjściowego powinno być takie jak wejściowego. Jeżeli widmo to jest ograniczone przez
ω
1
,
to trzeba wybrać
1
2
ω
ω
>
A
, a w praktyce
1
10
5
ω
ω
÷
>
A
Okres próbkowania wpływa na model układu dyskretnego – na transmitancje dyskretne i na macierze
opisu w przestrzeni stanów
„
∫
∫
=
=
=
−
+
T
c
A
t
t
c
T
k
A
T
A
B
d
e
B
d
e
B
e
A
c
c
c
0
)
)
1
((
0
,
τ
τ
τ
τ
gdy
0
det
≠
c
A
[
]
c
T
A
c
T
c
A
B
I
e
A
B
d
e
B
c
c
−
=
=
−
∫
1
0
τ
τ
”
ma więc wpływ na dynamikę układu dyskretnego i nawet na jego stabilność.

19
Automatyka i sterowanie 17
Częstotliwość próbkowania
Sterowalność:
Jeżeli wartościami własnymi układu ciągłego są s
i
, to wartościami własnymi układu po dyskretyzacji są
T
s
i
e
. Jeżeli dwie różne wartości własne przejdą na tą samą wartość własną układu dyskretnego, to układ
dyskretny nie będzie sterowalny, mimo że układ ciągły jest całkowicie sterowalny.
2
2
1
1
ω
σ
ω
σ
j
s
,
j
s
+
=
+
=
(
)
(
)
T
j
T
j
e
e
2
1
ω
σ
ω
σ
+
+
=
(
)
1
2
1
=
−
T
j
e
ω
ω
"
,
,
q
,
q
T
2
1
2
2
1
=
−
±
=
ω
ω
π
gdy
0
2
1
>
=
−
=
ω
ω
ω
"
,
,
q
,
q
T
2
1
=
±
=
ω
π
Jeżeli wartości sterowania są ograniczone to
istotny jest „zakres sterowalności” =obszar w
przestrzeni stanów osiągalny z 0 w N krokach
przy ograniczonym sterowaniu. Dla zwiększenia
„zakresu sterowalności” zaleca się wybierać
częstotliwość próbkowania 3 do 6 razy większą
od częstotliwości dla której następuje utrata
sterowalności czyli
3
6
π
ω
π
<
< T
.
Wyszukiwarka
Podobne podstrony:
automatyka i sterowanie wyklad Nieznany (8)
automatyka i sterowanie wyklad Nieznany (2)
automatyka i sterowanie wyklad Nieznany (7)
automatyka i sterowanie wyklad Nieznany (12)
automatyka i sterowanie wyklad Nieznany (16)
automatyka i sterowanie wyklad Nieznany (5)
automatyka i sterowanie wyklad Nieznany (10)
automatyka i sterowanie wyklad Nieznany (3)
automatyka i sterowanie wyklad Nieznany (8)
automatyka i sterowanie wyklad Nieznany (2)
automatyka i sterowanie wyklad 14
automatyka i sterowanie wyklad 15
automatyka i sterowanie wyklad 3
automatyczny sterownik oswietle Nieznany (2)
automatyka i sterowanie wyklad 16
automatyka i sterowanie wyklad 9
automatyka i sterowanie wyklad 11
automatyka i sterowanie wyklad 4
automatyka i sterowanie wyklad 5
więcej podobnych podstron