
Jacek Kabziński
Automatyka i sterowanie
————————————————————————————————————————

2
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
Sztywne sprzężenie zwrotne:
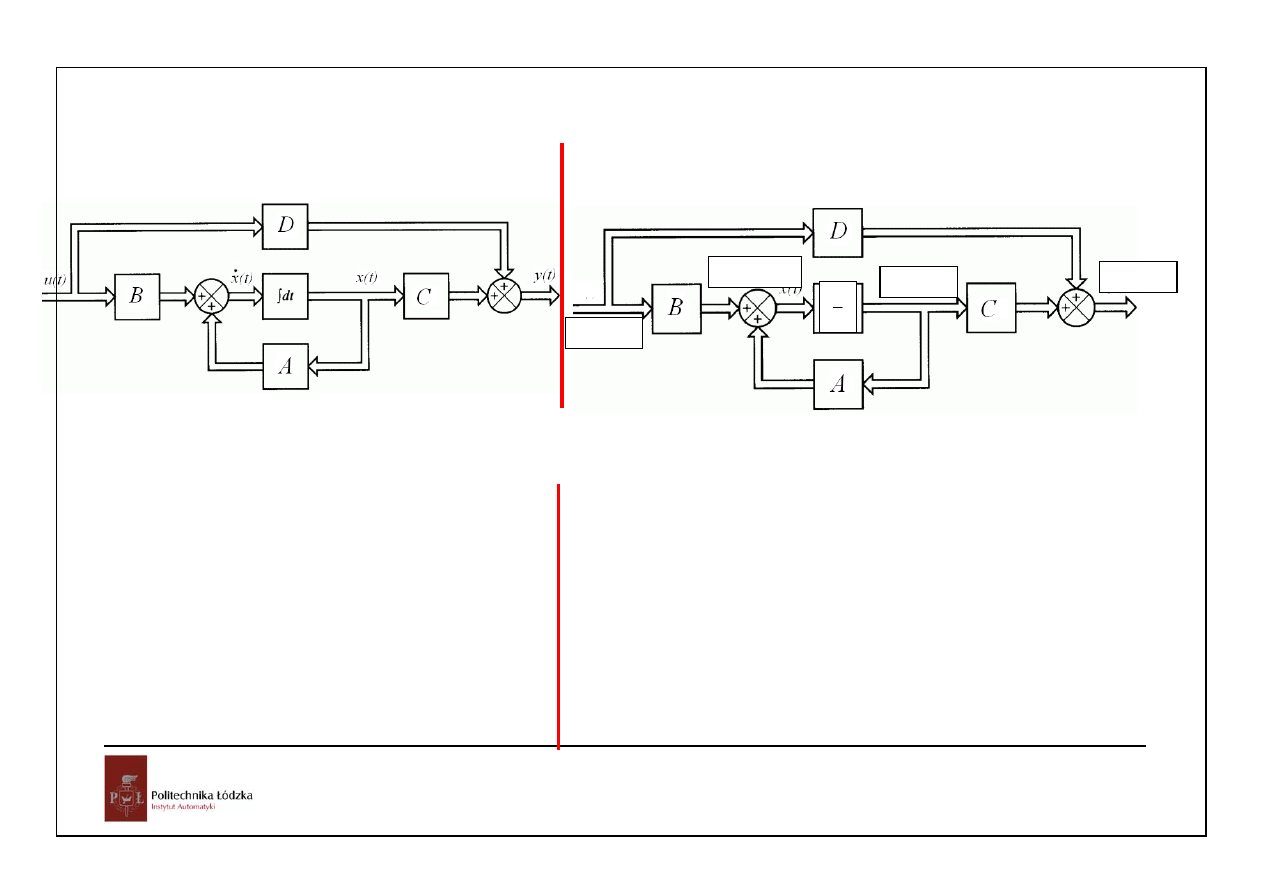
Rozważać będziemy opis układu w postaci:
równanie stanu
d
x( t ) Ax( t ) Bu( t )
dt
y( t ) Cx
równ
(
a
t )
ni
Du(
e wy ś
t )
j cia
=
+
=
+
)
(
)
(
)
(
)
(
)
(
)
)
1
((
kT
Du
kT
Cx
kT
y
kT
Bu
kT
Ax
T
k
x
+
=
+
=
+
x(t) – wektor zmiennych stanu o wymiarze nx1,
u(t) – wektor wejść/sterowań o wymiarze rx1
y(t) – wektor wyjść o wymiarze mx1
z warunkiem początkowym x(0)=x
0
lub bardziej ogólnie x(t
0
)=x
0
3
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
Wpływ proporcjonalnego SZ
(
) (
)
z
z
z
z
u( t ) y
Ky( t ) y
KCx( t )
x( t ) Ax( t ) B y
KCx( t )
A BKC x( t ) By ,
y( t ) Cx( t )
=
−
=
−
=
+
−
=
−
+
=
(
) (
)
)
(
)
(
,
)
(
)
(
)
(
)
)
1
((
)
(
)
(
)
(
kT
Cx
kT
y
By
kT
x
BKC
A
kT
KCx
y
B
kT
Ax
T
k
x
kT
KCx
y
kT
Ky
y
kT
u
z
z
z
z
=
+
−
=
−
+
=
+
−
=
−
=
0
x( t ) Pq( t ), det P
=
≠
0
det
),
(
)
(
≠
=
P
kT
Pq
kT
x
1
z
u(kT)
y(kT)
x(kT)
x((k+1)T

4
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
1
1
1
1
q( t ) P APq( t ) P Bu( t ),
y( t ) CPq( t )
A P AP, B P B, C CP
−
−
−
−
=
+
=
=
=
=
CP
C
B
P
B
AP
P
A
kT
CPq
kT
y
kT
Bu
P
kT
APq
P
T
k
q
=
=
=
=
+
=
+
−
−
−
−
~
,
~
,
~
)
(
)
(
),
(
)
(
)
)
1
((
1
1
1
1
po zamknięciu SZ:
(
)
(
)
1
1
z
z
q( t )
A BKC q( t ) By
P
A BKC Pq( t ) P By ,
y( t ) Cq( t ) CPq( t )
−
−
=
−
+
=
=
−
+
=
=
(
)
(
)
1
1
1
z
z
q(( k
)T )
A BKC q( kT ) By
P
A BKC Pq( kT ) P By ,
y( kT ) Cq( kT ) CPq( kT )
−
−
+
=
−
+
=
=
−
+
=
=
Niech P przekształca do postaci kanonicznej Kalmana:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
0
0
~
0
0
0
0
0
0
0
~
/
/
/
/
/
/
/
/
/
o
s
no
s
o
ns
o
ns
o
ns
no
ns
no
ns
no
ns
o
ns
o
s
o
s
o
s
o
ns
no
s
no
ns
no
s
o
s
no
s
no
s
no
s
B
B
B
A
A
A
A
A
A
A
A
A
A
[
]
o
ns
o
s
C
C
C
−
−
=
0
0
~

5
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
(
)
P
BKC
P
C
K
B
1
~
~
−
=
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
0
0
o
s
no
s
B
B
[
]
o
ns
o
s
C
C
K
−
−
0
0
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
−
−
−
−
−
−
−
−
0
0
0
0
0
0
0
0
0
0
0
0
o
ns
o
s
o
s
o
s
o
ns
no
s
o
s
no
s
C
B
KC
B
C
B
KC
B
=
−
C
K
B
A
~
~
~
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
o
ns
o
ns
o
ns
no
ns
no
ns
no
ns
o
ns
o
s
o
s
o
s
o
ns
no
s
no
ns
no
s
o
s
no
s
no
s
no
s
A
A
A
A
A
A
A
A
A
/
/
/
/
/
/
/
/
/
0
0
0
0
0
0
0
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
−
−
−
0
0
0
0
0
0
0
0
0
0
0
0
o
ns
o
s
o
s
o
s
o
ns
no
s
o
s
no
s
C
B
KC
B
C
B
KC
B
Tylko wartości własne części sterowalnej i obserwowalnej mogą być zmienione przez macierz K w
sprzężeniu zwrotnym!!

6
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
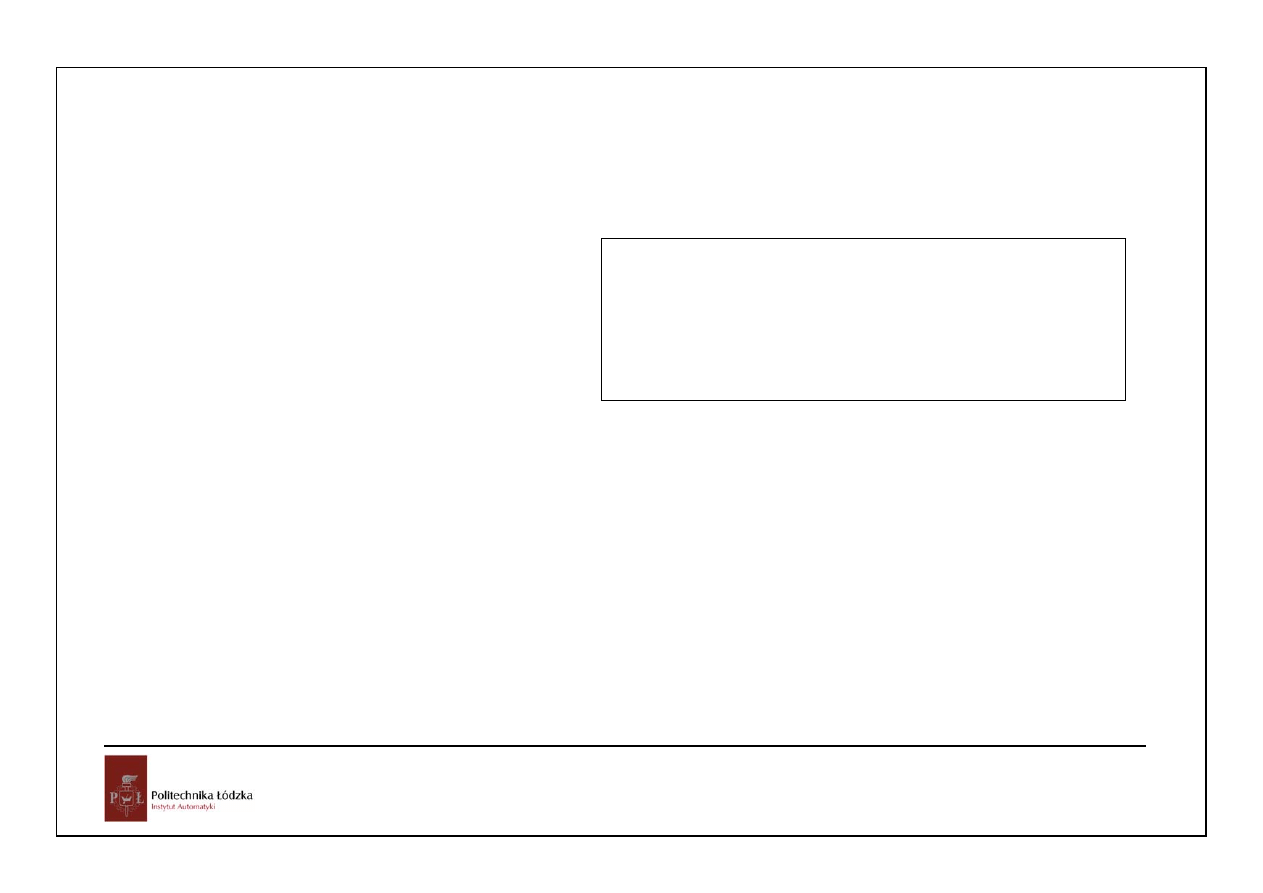
Sprzężenie zwrotne od wektora stanu, układ o jednym wejściu
Problem dowolnego przesuwania/lokowania biegunów:
Dla dowolnego ustalonego zbioru N n liczb zawierających elementy rzeczywiste lub zespolone parami
sprzężone znaleźć taką macierz sprzężenia zwrotnego K by zbiór N był zbiorem wartości własnych
macierzy stanu układu zamkniętego A-BK .
Koniecznym i dostatecznym warunkiem istnienia rozwiązania problemu dowolnego
przesuwania/lokowania biegunów przez sprzężenie od wektora stanu jest całkowita sterowalność pary
macierzy (A,B).
Formuła Ackermana:
Niech żądany wielomian charakterystyczny macierzy stany układu zamkniętego A
c
=A-BK będzie:
(
)
(
) (
)(
)
(
)
1
1
2
1
1
n
n
c
c
n
n
n
M ( s ) det sI A BK
det sI A
s s
s s
s s
s
a s
a s a
−
−
=
− +
=
−
= −
−
−
=
+
+ +
+
"
"
Z tw. Cayley’a-Hamiltona
1
1
1
0
n
n
c
c
c
c
n
c
n
M ( A ) A
a A
a A
a I
−
−
=
+
+ +
+
=
"

7
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
(
)(
)
(
)
(
)
(
)
(
)
2
2
3
2
3
2
2
4
3
2
2
4
3
2
2
3
1
1
2
3
2
1
c
c
c
c
c
c
c
c
c
c
c
c
c
n
n
n
n
n
c
c
c
n
n
n
c
I
I
A
A BK
A
A BK A BK
A
ABK BKA
A
A BK A
ABK BKA
A
A BK ABKA
BKA
A
A BK A
A BK ABKA
BKA
A
A BK A BKA
ABKA
BKA
......................
A
A
A BK
ABKA
BKA
A
A
A B
−
−
−
−
−
−
=
= −
=
−
−
=
−
−
=
−
−
−
=
−
−
−
=
−
−
−
−
=
−
−
−
−
=
−
−
−
−
=
−
"""
2
2
1
n
n
n
c
c
c
K A BKA
ABKA
BKA
−
−
−
−
− −
−
"

8
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
2
2
3
3
2
2
4
4
3
2
2
3
1
1
2
3
2
1
2
2
1
c
c
c
c
c
c
c
c
c
c
n
n
n
n
n
c
c
c
n
n
n
n
n
n
c
c
c
c
I
I
A
A BK
A
A
ABK BKA
A
A
A BK ABKA
BKA
A
A
A BK A BKA
ABKA
BKA
......................
A
A
A BK
ABKA
BKA
A
A
A BK A BKA
ABKA
BKA
−
−
−
−
−
−
−
−
−
=
= −
=
−
−
=
−
−
−
=
−
−
−
−
=
−
−
−
−
=
−
−
− −
−
"""
"

9
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
1
1
1
2
2
2
2
2
2
3
3
2
2
3
3
3
3
3
4
4
3
2
2
3
4
4
4
4
4
4
1
1
2
1
1
1
n
n
n
c
n
n
n
c
n
n
n
c
n
c
n
n
n
c
n
c
n
c
n
n
n
c
n
c
n
c
n
n
n
c
a I
a I
a A
a A a BK
a A
a A
a ABK a BKA
a A
a A
a A BK a ABKA
a BKA
a A
a A
a A BK a A BKA
a ABKA
a BKA
......................
a A
a A
a A BK
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
=
=
−
=
−
−
=
−
−
−
=
−
−
−
−
=
−
3
2
1
1
1
2
2
1
n
n
c
c
n
n
n
n
n
n
c
c
c
c
a ABKA
a BKA
A
A
A BK A BKA
ABKA
BKA
−
−
−
−
−
−
−
−
−
=
−
−
− −
−
"""
"
dodajemy stronami:
(
)
(
)
( )
( )
1
2
2
2
1
1
2
n
n
n
n
c
c
c
n
c
n
c
M ( A ) M ( A ) B a K
KA
AB a K
KA
A B *
A B *
A BK
−
−
−
−
−
−
=
−
+ +
−
+ +
−
− −
−
"
"
"
=0

10
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
1
1
2
1
2
n
n
c
n
n
n
c
c
a K
KA
a K
KA
M ( A)
B AB
A B
K
−
−
−
−
−
⎡
⎤
+ +
⎢
⎥
+ +
⎢
⎥
⎡
⎤
= ⎣
⎦ ⎢
⎥
⎢
⎥
⎣
⎦
"
"
"
#
1
1
2
1
1
2
n
n
c
n
n
n
c
c
a K
KA
a K
KA
B AB
A B
M ( A)
K
−
−
−
−
−
−
⎡
⎤
+ +
⎢
⎥
+ +
⎢
⎥ ⎡
⎤
= ⎣
⎦
⎢
⎥
⎢
⎥
⎣
⎦
"
"
"
#
K jest ostatnim wierszem prawej strony
[
]
1
1
0 0
1
n
c
n
K
B AB
A B
M ( A )
−
−
⎡
⎤
=
⎣
⎦
"
"
Formuła Ackermana
11
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
Szczególnie łatwo:
1
1
0
1
0
0
0
0
1
0
1
n
n
A
B
a
a
a
−
⎡
⎤
⎡ ⎤
⎢
⎥
⎢ ⎥
⎢
⎥
⎢ ⎥
=
=
⎢
⎥
⎢ ⎥
⎢
⎥
⎢ ⎥
−
−
−
⎣ ⎦
⎣
⎦
"
#
%
%
#
#
"
"
[
]
(
) (
)
(
)
1
2
1
1
1
1
2
1
1
1
0
1
0
0
0
0
1
0
1
0
1
0
0
1
0
0
0
1
0
0
1
n
n
n
n
n
n
c ,n
c ,n
c ,
A BK
k
k
k
a
a
a
a
k
a
k
a
k
a
a
a
−
−
−
⎡
⎤ ⎡ ⎤
⎢
⎥ ⎢ ⎥
⎢
⎥ ⎢ ⎥
−
=
−
=
⎢
⎥ ⎢ ⎥
⎢
⎥ ⎢ ⎥
−
−
−
⎣ ⎦
⎣
⎦
⎡
⎤ ⎡
⎤
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
=
=
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
−
+
−
+
−
+
−
−
−
⎣
⎦
⎣
⎦
"
#
%
%
#
#
"
"
"
"
"
#
%
%
#
#
%
%
#
"
"
"
"
1
2
1
1
1
1
c ,n
n
c ,n
n
n
c ,
k
a
a
k
a
a
..............
k
a
a
−
−
=
−
=
−
=
−
Postać będąca wynikiem stosowania
pierwszego wariantu metody bezpośredniej
wyboru zmiennych stanu.
Postać kanoniczna sterowalna
Postać normalna regulatorowa

12
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
Macierzą przekształcenia do postaci kanonicznej sterowalnej jest
1
2
1
2
3
1
1
1 0
1
0 0
1
0
0 0
n
n
n
n
S
a
a
a
a
a
P Q
a
−
−
−
−
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
"
"
#
#
$ #
#
"
"
(
)
(
)
(
)
(
)
1
1
1
1
q( t )
A BK q( t ) P
A BKP
Pq( t )
Pq( t )
A BKP
Pq( t )
x( t )
A BKP
x( t )
−
−
−
−
=
−
=
−
=
−
=
−

13
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
• Nadrzędny jest wybór zadanych położeń biegunów układu zamkniętego.
• Decyduje o właściwościach dynamicznych układu zamkniętego.
• Wpływa na wartości sprzężeń zwrotnych – mogą być zbyt duże.
• Musi być kompromisowy – jeśli zwiększamy szybkość odpowiedzi układu zamkniętego to wpływ
zakłóceń i szumów pomiarowych też rośnie.
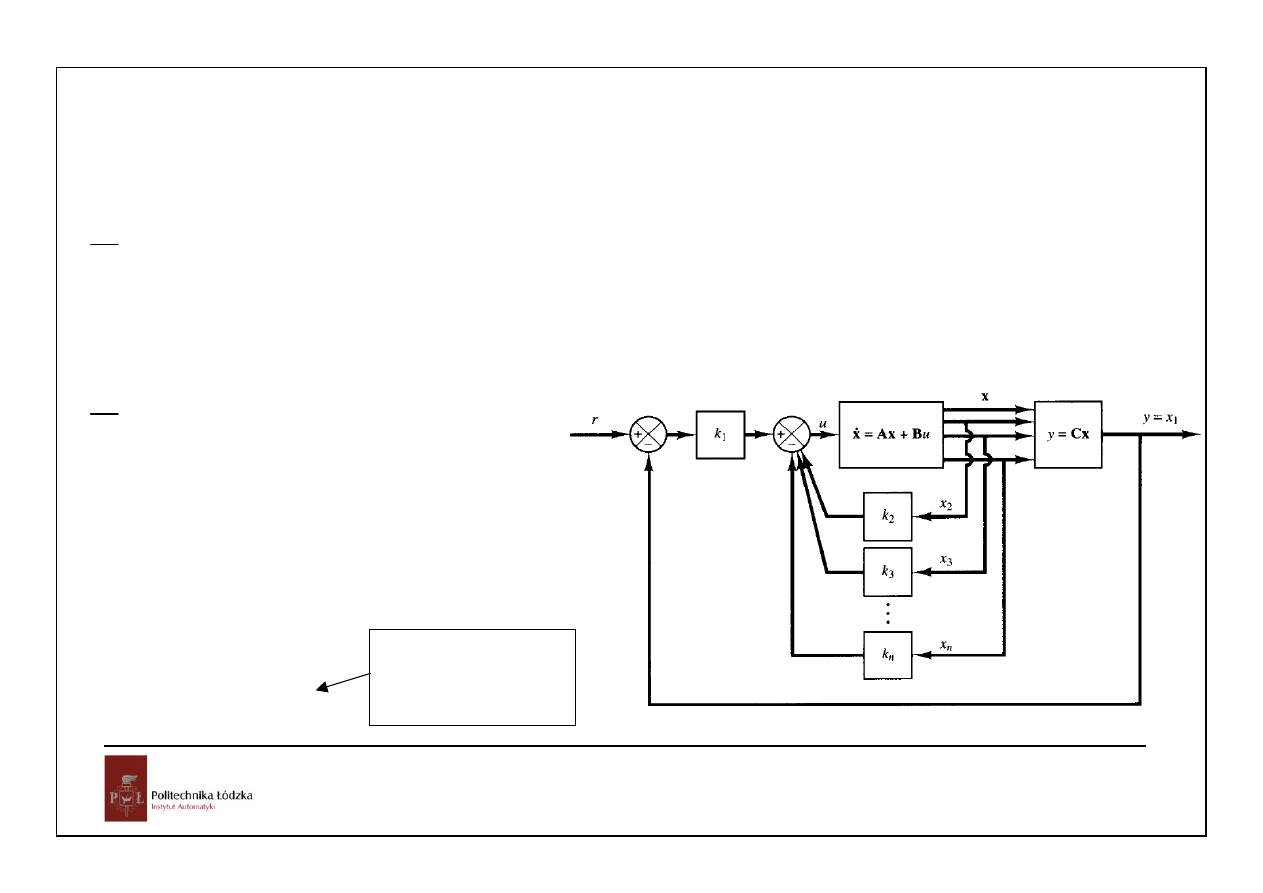
Jak uzyskać astatyzm układu regulacji?
Przyjmijmy:
• wymuszenie skokowe r(t)=r=const
• wielkością regulowaną jest pierwsza zmienna stanu
• obiekt zawiera element całkujący
14
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
[
]
(
)
[
]
2
2
1
1
1
2
2
1
1
0
d
x( t ) Ax( t ) Bu( t )
dt
u( t )
k
k x( t ) k r( t ) x ( t )
k
k
k x( t ) k r( t )
Kx( t ) k r( t )
=
+
= −
+
−
=
= −
+
= −
+
"
"
(
)
1
d
x( t )
A BK x( t ) Bk r( t )
dt
=
−
+
Jeśli zaprojektujemy macierz sprzężeń
tak by wartości własne A-BK były w
lewej półpłaszczyźnie, uzyskamy w
układzie stan ustalony:
(
)
(
)
1
1
1
1
0
0
A BK x
Bk r
x
A BK
Bk r
u
Kx
k r
∞
−
∞
∞
∞
=
−
+
=
−
= −
+
=
z uwagi na
całkowanie w
obiekcie

15
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
Oznaczmy:
e( t ) x( t ) x
∞
=
−
, wtedy
(
)
(
)
(
)
1
1
0
d
x( t )
A BK x( t ) x
Bk r( t ) Bk r( t )
dt
d
e( t )
A BK e( t )
dt
∞
− =
−
−
+
−
=
−
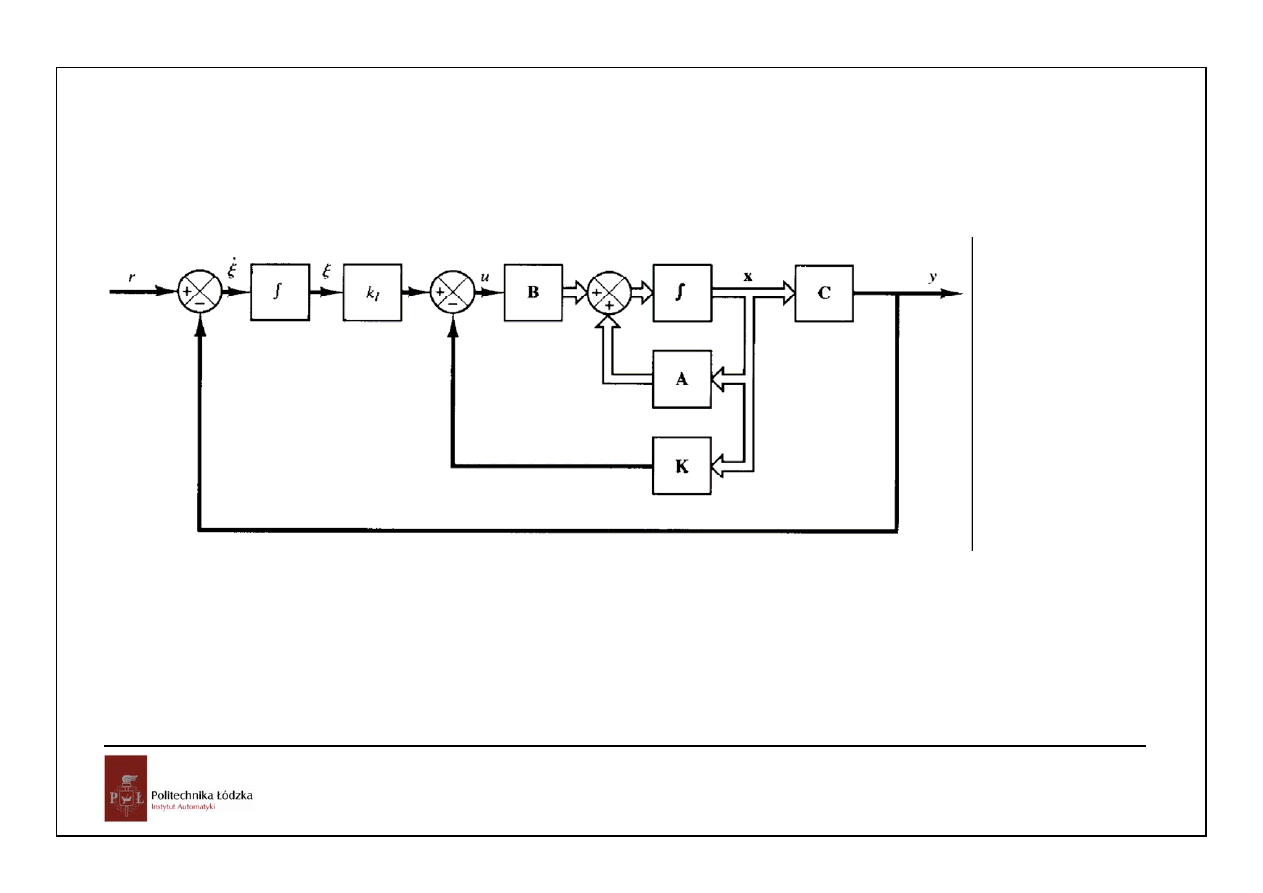
Wystarczy zaprojektować stabilizujące sprzężenie zwrotne dla układu
(A, B) !!
16
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
Jeśli obiekt nie zawiera całkowania:
(
)
i
x
Ax B Kx k
r Cx
ξ
ξ
=
−
+
= −
0
0
1
i
x
A BK k
x
r
C
ξ
ξ
−
⎡ ⎤ ⎡
⎤ ⎡ ⎤ ⎡ ⎤
=
+
⎢ ⎥ ⎢
⎥ ⎢ ⎥ ⎢ ⎥
−
⎣
⎦ ⎣ ⎦ ⎣ ⎦
⎣ ⎦
Jeśli ten układ będzie stabilny, to w stanie równowagi

17
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
0
0
0
0
1
i
x
A BK k
r
C
y
Cx
r
ξ
∞
∞
∞
∞
−
⎡ ⎤
⎡ ⎤ ⎡
⎤
⎡ ⎤
=
+
⎢ ⎥
⎢ ⎥ ⎢
⎥
⎢ ⎥
−
⎣ ⎦ ⎣
⎦
⎣ ⎦
⎣ ⎦
=
=
Trzeba więc ustabilizować macierz
[
]
0
0
0
0
i
i
A BK k
A
B
K k
C
C
−
⎡
⎤ ⎡
⎤ ⎡ ⎤
=
−
⎢
⎥ ⎢
⎥ ⎢ ⎥
−
−
⎣
⎦ ⎣
⎦ ⎣ ⎦
czyli znaleźć stabilizujące sprzężenie zwrotne
[
]
i
K :
K k
=
dla układu opisanego macierzami
0
0
0
A
B
A :
B :
C
⎡
⎤
⎡ ⎤
=
=
⎢
⎥
⎢ ⎥
−
⎣
⎦
⎣ ⎦
. Układ ten będzie całkowicie sterowalny, jeśli macierz
0
A
B
C
⎡
⎤
⎢
⎥
−
⎣
⎦
jest
pełnego rzędu.

18
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
Obliczanie sterowania dead-beat
Układ
)
(
)
(
)
(
)
(
)
)
1
((
kT
cx
kT
y
kT
bu
kT
Ax
T
k
x
=
+
=
+
należy wyposażyć w regulator zapewniający zanikanie przebiegów przejściowych w
N okresach
impulsowania i zerowy uchyb ustalony przy wymuszeniu jednostkowym.
[
]
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
=
−
−
)
0
(
)
(
)
)
1
((
)
(
1
0
u
T
u
T
N
u
b
A
Ab
b
x
A
NT
x
N
N
#
"
1
)
(
)
(
=
=
NT
cx
NT
y
N
k
dla
NT
u
kT
u
kT
x
T
k
x
≥
=
=
+
)
(
)
(
),
(
)
)
1
((

19
Automatyka i sterowanie 14 Przesuwanie/lokowanie biegunów
Układy czasu ciągłego i dyskretnego
)
(
)
(
)
(
NT
bu
NT
Ax
NT
x
+
=
Jeśli
A nie ma wart wł. równych 1, to macierz I-A jest odwracalna i
)
(
)
(
)
(
1
NT
bu
A
I
NT
x
−
−
=
1
)
(
)
(
)
(
1
=
−
=
−
NT
bu
A
I
c
NT
y
)
1
(
1
)
(
1
)
(
1
o
G
b
A
I
c
NT
u
=
−
=
−
Potem wyznacza się
x(NT), potem ciąg sterujący.
Jeśli
A ma wart wł. równą 1, to u(NT)=0 i
(
)
0
)
(
=
−
NT
x
A
I
Równanie to ma wiersze liniowo zależne – jeden z nich należy zastąpić przez
1
)
(
=
NT
cx
Stąd wyznacza się
x(NT), potem ciąg sterujący.
Wyszukiwarka
Podobne podstrony:
automatyka i sterowanie wyklad Nieznany (14)
automatyka i sterowanie wyklad 15
automatyka i sterowanie wyklad Nieznany (8)
automatyka i sterowanie wyklad Nieznany (2)
Teoria sterowania wykład 3 (14 03 2003)
automatyka i sterowanie wyklad 3
automatyka i sterowanie wyklad Nieznany (7)
automatyka i sterowanie wyklad 16
automatyka i sterowanie wyklad Nieznany (12)
automatyka i sterowanie wyklad Nieznany (16)
automatyka i sterowanie wyklad Nieznany (5)
automatyka i sterowanie wyklad 9
automatyka i sterowanie wyklad 11
automatyka i sterowanie wyklad 4
automatyka i sterowanie wyklad 5
automatyka i sterowanie wyklad Nieznany (10)
automatyka i sterowanie wyklad Nieznany (3)
automatyka i sterowanie wyklad 8
automatyka i sterowanie wyklad 2
więcej podobnych podstron