Jacek Kabziński
Automatyka i sterowanie
————————————————————————————————————————
Jacek Kabziński
Automatyka i sterowanie
————————————————————————————————————————
2
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
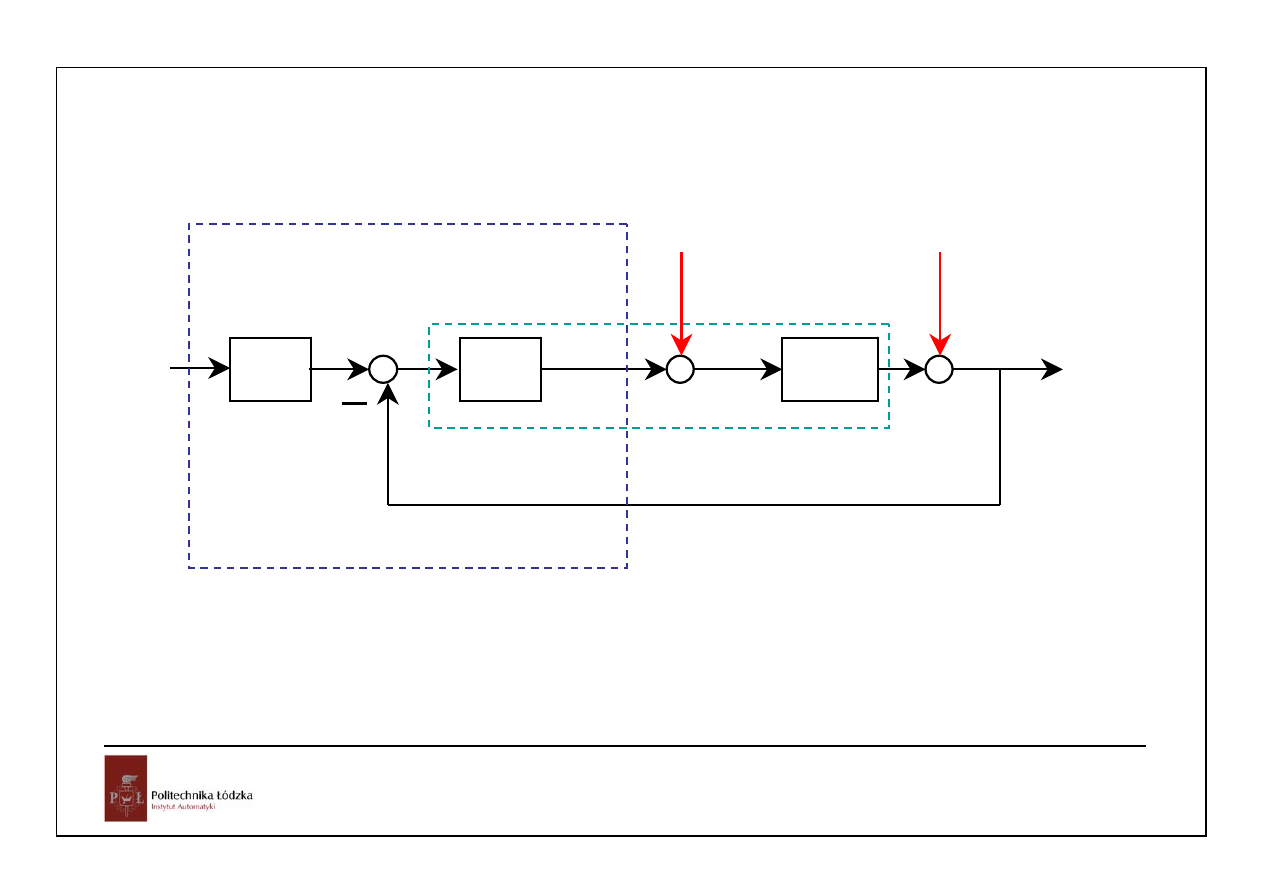
C(s)
P(s)
D(s)
R(s)
Y(s)
E(s)
U(s)
regulator
obiekt
N(s)
F(s)
v(s)
n(s)
F(s)=1 – sprz. od uchybu
3
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
6 transmitancji:
YN
T
,
YD
T
,
YR
T
;
N
PC
D
PC
P
R
PC
FPC
Y
+
+
+
+
+
=
1
1
1
1
,
N
PC
PC
D
PC
P
R
PC
FPC
n
+
−
+
+
+
+
=
1
1
1
,
N
PC
C
D
PC
R
PC
FC
v
+
−
+
+
+
+
=
1
1
1
1
,
UN
T
,
UD
T
,
UR
T
:
N
PC
C
D
PC
PC
R
PC
FC
U
+
−
+
+
−
+
+
=
1
1
1
,
N
PC
D
PC
P
R
PC
F
E
+
−
+
+
−
+
+
=
1
1
1
1
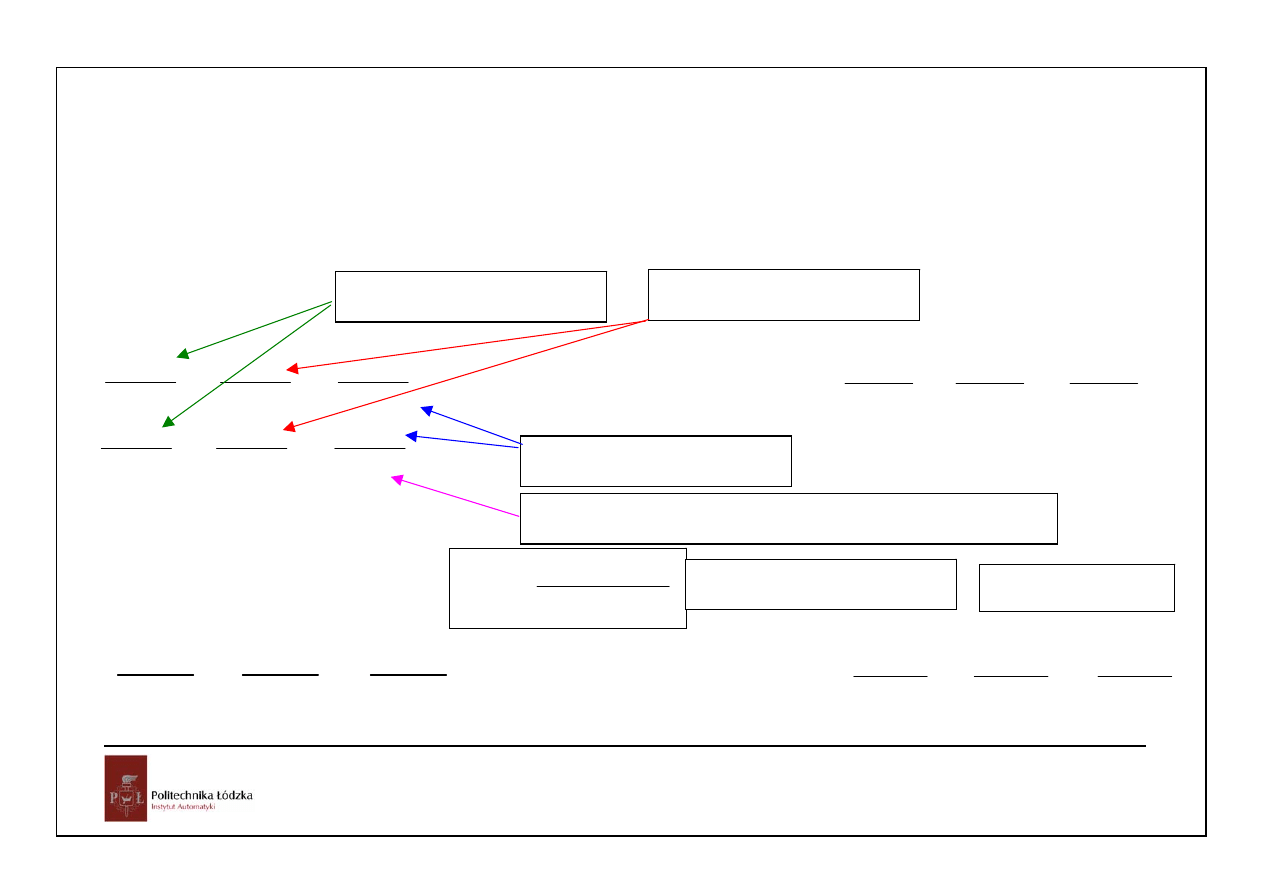
Na sygnał zadający
Na szum pomiarowy
Na zakłócenie
P(s)C(s) Transmitancja układu otwartego
1
1
S( s )
P( s )C( s )
=
+
funkcja wrażliwości
1
YR
S( s ) T ( s )
+
=
4
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
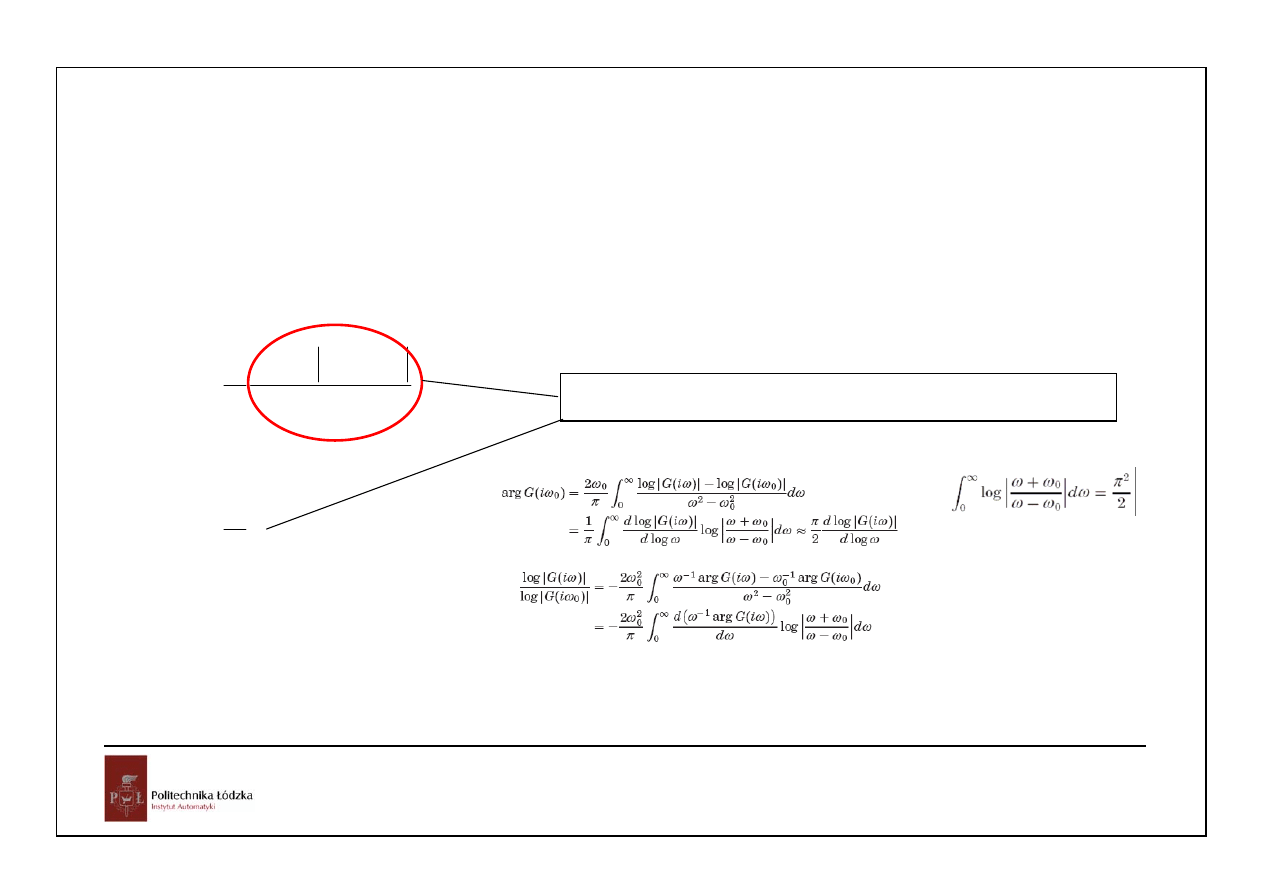
Układy minimalnofazowe – wszystkie bieguny i zera w lewej półpłaszczyźnie.
Obiekty minimalnofazowe nie stwarzają dużych trudności w układach sterowania.
Sztywny związek miedzy charakterystyka modułową a fazową:
2
d log G( j )
arg G( j )
d log
ω
π
ω
ω
≈
2
arg G( j )
n
π
ω
≈
Nachylenie charakterystyki modułowej
5
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
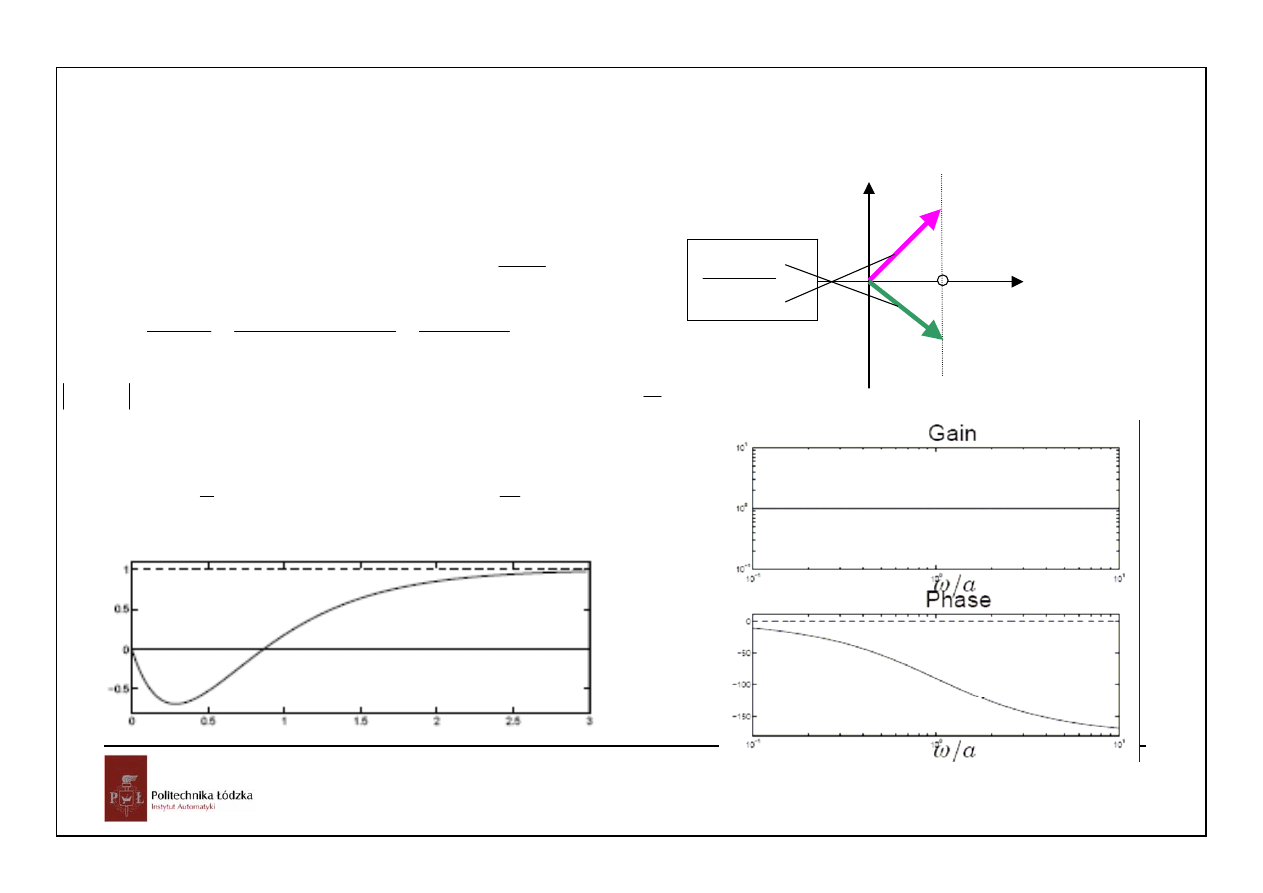
Zero w prawej półpłaszczyźnie:
0
s
G( s )
,
s
α
α
α
−
=
>
+
(
)
(
)(
)
(
)
2
2
2
2
j
j
j
G( j )
j
j
j
α
ω
α
ω
α
ω
ω
ω α
α
ω α
ω
α
ω
−
−
−
=
=
=
+
+
−
+
(
)
(
)
1
2
G( j )
arg G( j ) arg
j
arg
j
arctg
ω
ω
ω
α
ω
α
ω
α
=
=
−
−
+
= −
Odpowiedź jednostkowa h(t):
0
1
st
H( s ) G( s )
e h( t )dt
s
∞
−
=
=
∫
0
1
0
t
G( )
e h( t )dt
α
α
α
∞
−
=
=
∫
j
j
α
ω
ω α
−
+
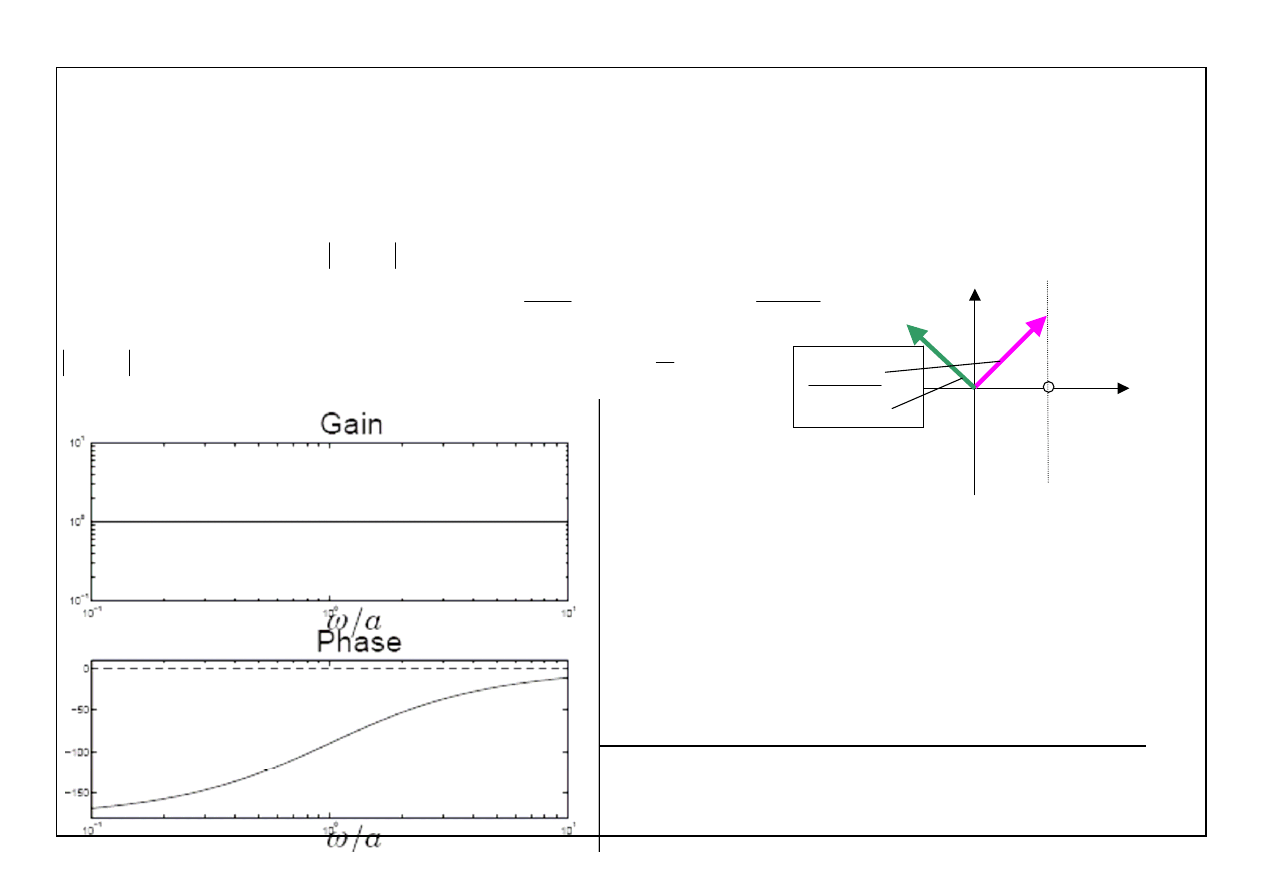
6
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
Opóźnienie
1
sT
G( s ) e
, G( j )
, arg G( j )
T
ω
ω
ω
−
=
=
= −
Biegun w prawej półpłaszczyźnie:
0
s p
j
p
G( s )
, p
, G( j )
,
s p
j
p
ω
ω
ω
+
+
=
>
=
−
−
(
)
(
)
1
2
p
G( j )
arg G( j ) arg p
j
arg
p
j
arctg
ω
ω
ω
ω
ω
=
=
+
−
− +
= −
p
j
j
p
ω
ω
+
−
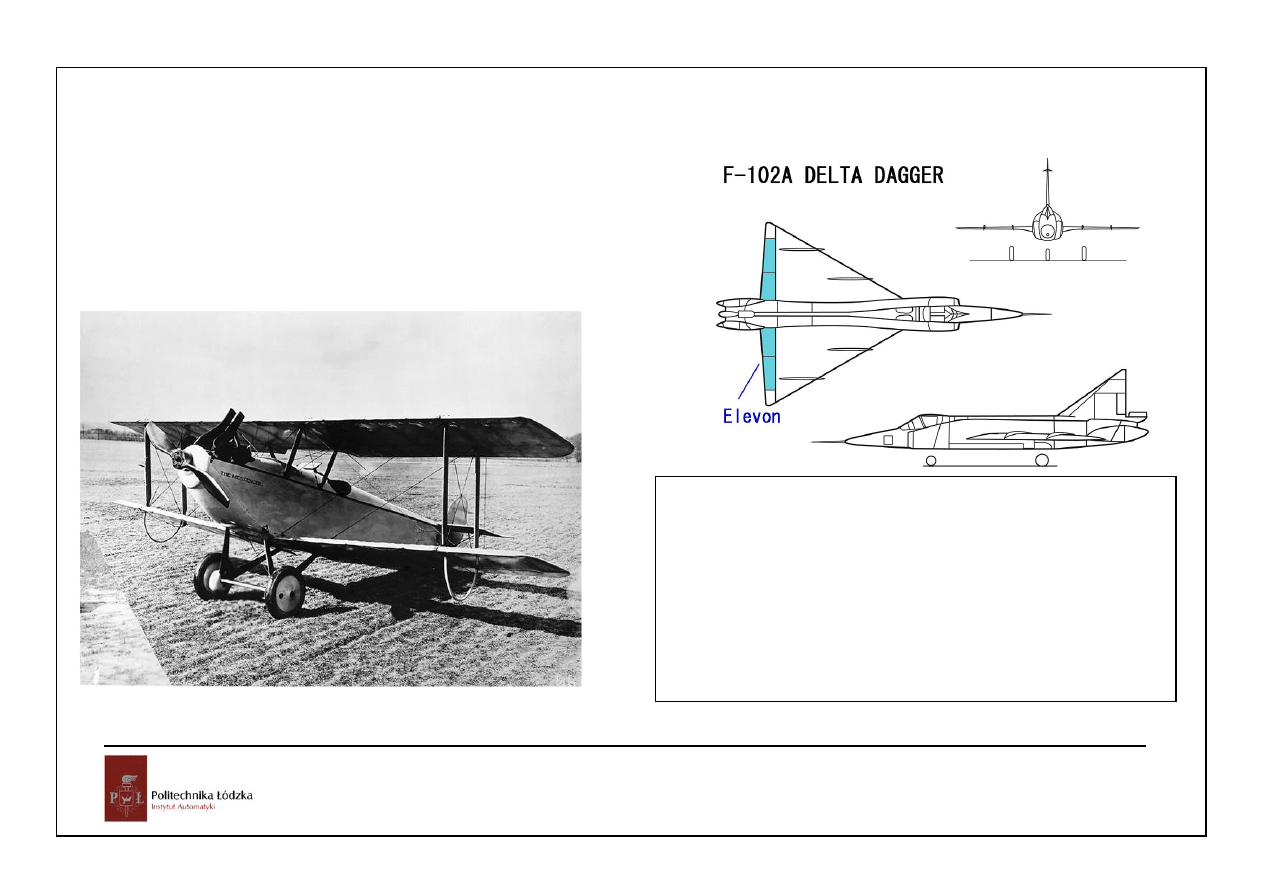
7
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
transmitancja miedzy wychyleniem tylnego statecznika a
wysokością samolotu jest zawsze nieminimalnofazowa
As in their earlier gliders, it had a
variable-camber twin canard in front to
control pitch and a twin rudder in back to
control yaw. Roll was controlled by
warping the wings.
8
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
Regulacja poziomu w zbiorniku z ogrzewana cieczą
Transmitancja miedzy szerokością otwarcia przepływu w moca
hydroelektrowni
9
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
10
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
Podzielmy transmitancję obiektu na część nieminimalnofazową o module równym 1 i część
minimalnofazową:
1
mf
nmf
nmf
P( s ) P ( s )P ( s ), P ( j )
ω
=
=
Niech
0
ω
będzie pulsacją odcięcia:
0
0
0
0
1
L( j
) C( j
)P( j
), L( j
)
ω
ω
ω
ω
=
=
Narzucamy zapas fazy Δφ:
0
0
0
0
0
0
mf
nmf
arg L( j
) arg C( j
) arg P( j
) arg C( j
) arg P ( j
) arg P ( j
)
ω
ω
ω
ω
ω
ω
π
ϕ
=
+
=
+
+
> − + Δ
0
0
0
2
mf
arg C( j
) arg P ( j
)
n
π
ω
ω
+
≈
0
0
d log P( j )
n
d log
ω ω
ω
ω
=
=
- nachylenie charakterystyki modułowej P(s) w okolicy pulsacji odcięcia
0
0
2
nmf
arg P ( j
)
n
π
ω
π
ϕ
> − + Δ −
,
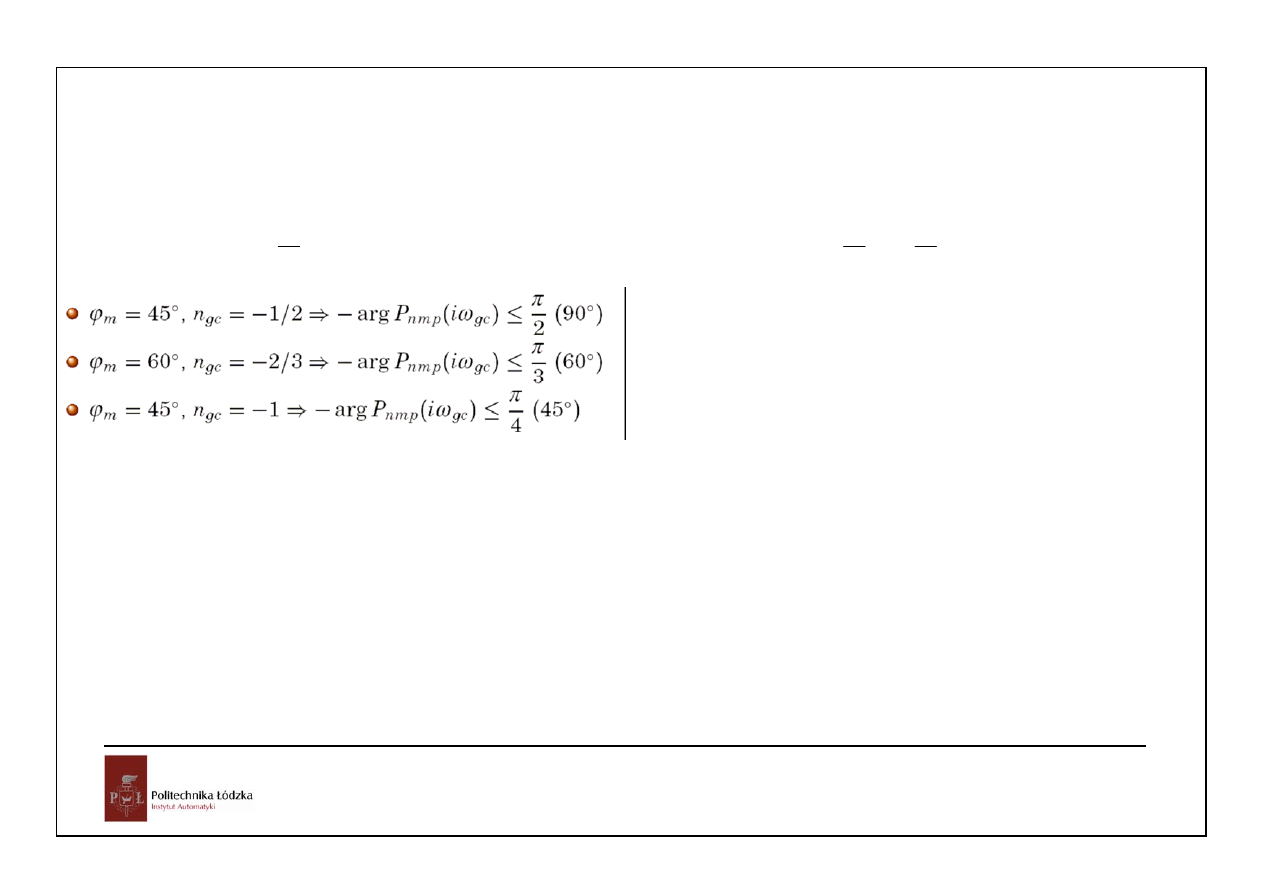
11
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
na przykład
0
0
0
0 5
4
2
2
nmf
, n
.
arg P ( j
)
n
π
π
π
ϕ
ω
π
ϕ
⎛
⎞
Δ =
= −
⇒
> − + Δ −
> −
⎜
⎟
⎝
⎠
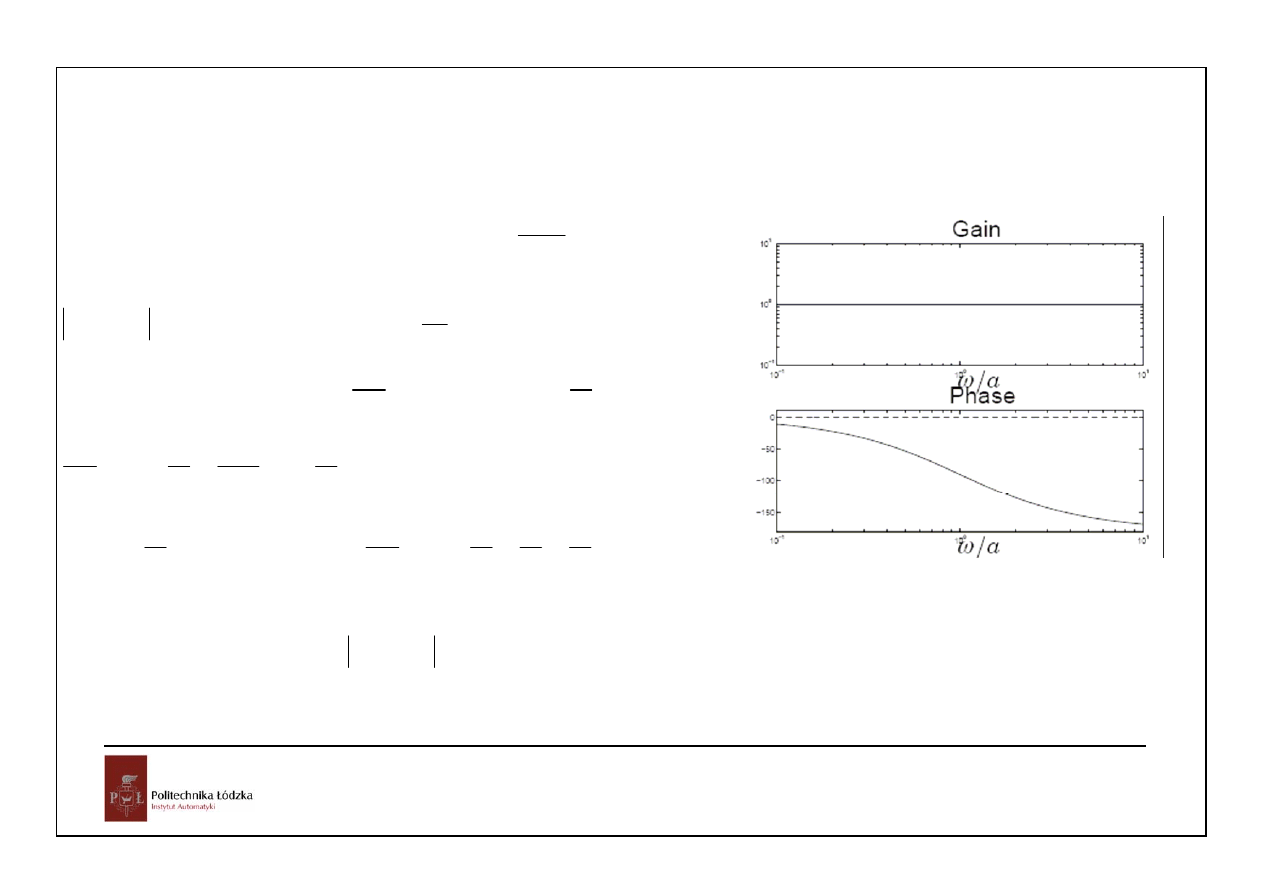
12
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
Zero w prawej półpłaszczyźnie:
0
nmf
s
P ( s )
,
s
α
α
α
−
=
>
+
0
0
1
2
nmf
nmf
P ( j )
arg P ( j
)
arctg
ω
ω
ω
α
=
= −
0
0
0
2
2
nmf
arg P ( j
)
arctg
n
ω
π
ω
π
ϕ
α
= −
> − + Δ −
0
0
2
2
4
tg
n
ω
π
ϕ
π
α
Δ
⎛
⎞
<
−
+
⎜
⎟
⎝
⎠
0
0 5
4
, n
.
π
ϕ
⎛
⎞
Δ =
= −
⇒
⎜
⎟
⎝
⎠
0
2
8
8
tg
ω
π π π
α
⎛
⎞
<
− −
⎜
⎟
⎝
⎠
0
ω
α
<
- zero w prawej półpłaszczyźnie ogranicza pasmo przenoszenia uo, czyli szybkość uz
Opóźnienie
1
sT
nmf
nmf
nmf
P ( s ) e
, P ( j )
, arg P ( j )
T
ω
ω
ω
−
=
=
= −
13
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
0
0
2
T
n
π
ω
π
ϕ
−
> − + Δ −
0
0
2
T
n
π
ω
π
ϕ
< − Δ +
0
0 5
4
, n
.
π
ϕ
⎛
⎞
Δ =
= −
⇒
⎜
⎟
⎝
⎠
0
4
4
2
T
π π π
ω
π
< − −
=
0
2T
π
ω
<
ogranicza pasmo przenoszenia uo, czyli szybkość uz
Biegun w prawej półpłaszczyźnie:
0
nmf
nmf
s p
j
p
P ( s )
, p
, P ( j )
,
s p
j
p
ω
ω
ω
+
+
=
>
=
−
−
1
2
nmf
nmf
p
P ( s )( j )
arg P ( s )( j )
arctg
ω
ω
ω
=
= −
0
0
0
2
2
nmf
p
arg P ( j
)
arctg
n
π
ω
π
ϕ
ω
= −
> − + Δ −
0
0
2
2
4
p
tg
n
π
ϕ
π
ω
Δ
⎛
⎞
<
−
+
⎜
⎟
⎝
⎠
14
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
0
0
2
2
4
p
tg
n
ω
π
ϕ
π
>
Δ
⎛
⎞
−
+
⎜
⎟
⎝
⎠
0
0 5
4
, n
.
π
ϕ
⎛
⎞
Δ =
= −
⇒
⎜
⎟
⎝
⎠
0
2
4
8
p
p
tg
ω
π π π
>
=
⎛
⎞
− −
⎜
⎟
⎝
⎠
WYMAGA dużej pulsacji odcięcia
Biegun w prawej półpłaszczyźnie i opóźnienie:
0
sT
j T
nmf
nmf
s p
j
p
P ( s )
e
, p
, P ( j )
e
,
s p
j
p
ω
ω
ω
ω
−
−
+
+
=
>
=
−
−
0
0
0
0
2
2
nmf
p
arg P ( j
)
arctg
T
n
π
ω
ω
π
ϕ
ω
= −
−
> − + Δ −
po przekształceniach
0
2
2
2
1
1
2
arctg
pT
n
pT
pT
π
ϕ
− −
− > Δ −
czyli pT<2 jest konieczne dla stabilności,
mniejsze dla zapasu fazy
15
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
Zero i biegun w prawej półpłaszczyźnie:
(
)(
)
(
)(
)
(
)(
)
(
)(
)
0
nmf
nmf
z s s p
z
j
j
p
P ( s )
, z, p
, P ( j )
s z s p
j
z j
p
ω
ω
ω
ω
ω
−
+
−
+
=
>
=
+
−
+
−
Niech z>p
2
1
p
z
arg Pnmf ( j )
arctg
p
z
ω
ω
ω
+
= −
−
0
0
0
0
2
2
1
nmf
p
z
arg P ( j
)
arctg
n
p
z
ω
ω
π
ω
π
ϕ
+
= −
> − + Δ −
−
( )
0
0
0
1
2
2
4
p
p
tg
n
z
z
π
ϕ
π
ω
ω
Δ
⎛
⎞
+
< −
−
+
⎜
⎟
⎝
⎠
przekształcając tą zależność można wyprowadzić różnego rodzaju ograniczenia, np.:
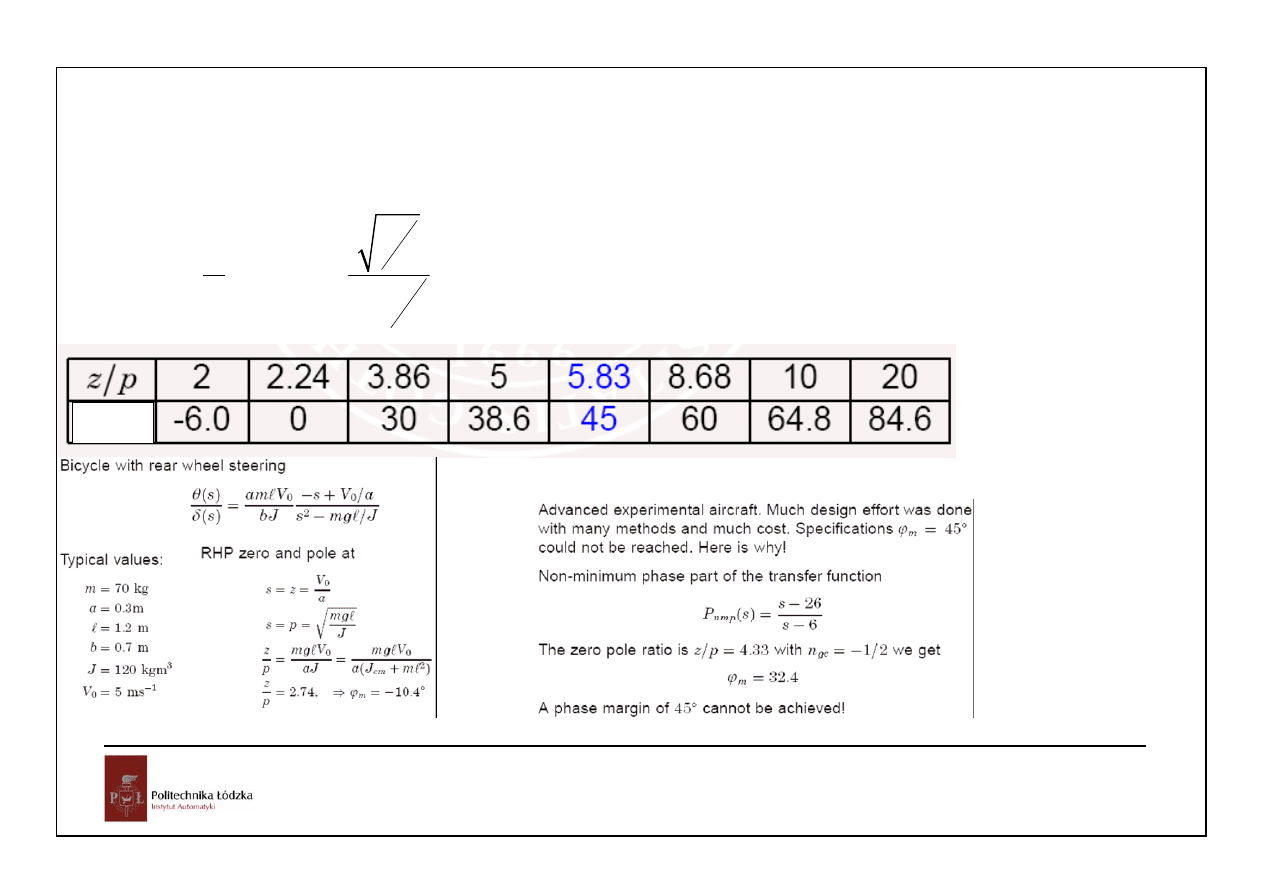
16
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego
0
2
2
1
p
z
n
arctg
p
z
π
ϕ π
⎛
⎞
⎜
⎟
Δ < −
−
⎜
⎟
−
⎜
⎟
⎝
⎠
, co dla n
0
=0.5 daje
Δφ
17
Automatyka i sterowanie 8 Układy minimalnofazowe i nieminimalnofazowe
Układy czasu ciągłego