
Statystyka w analizie i planowaniu eksperymentu
Wykład 11
Zagadnienia klasyfikacji
Przemysław Biecek
Dla 1 roku studentów Biotechnologii

Ogłoszenia
6 czerwca (piątek) w godzinach 8:30 - 11:00 w sali 207 odrabiamy
zaległe zajęcia.
Podczas wykładu będziemy rozwiązywać zadania dotyczące testów.
Powtórka może się przydać przed kolokwiami.
2/23

Klasyfikacja gatunków
Co to za organizmy?
Czy potrafisz wskazać cechy różnicujące te trzy gatunki?
3/23

Klasyfikacja gatunków
Co to za organizmy żywe?
Czy potrafisz wskazać cechy różnicujące te trzy gatunki?
Tak! To są Kosaćce!
Iris setosa
Iris versicolor
Iris virginica
4/23
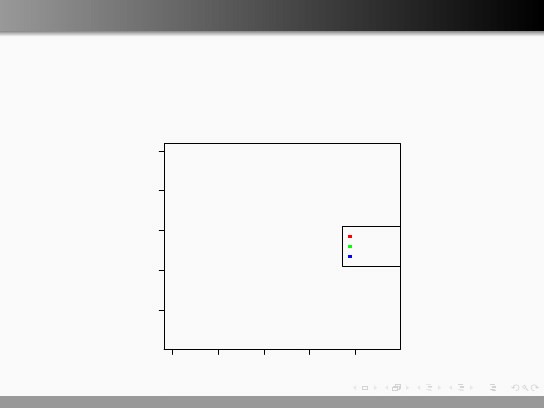
Klasyfikacja gatunków
Botanik Edgar Anderson zebrał dane o długościach i szerokościach petali
i sepali dla 150 irysów. Anderson współpracował z R. Fisherem, który
użył tego zbioru danych jako przykład dla klasyfikacji.
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
2.0
2.5
3.0
3.5
4.0
0.5
1.0
1.5
2.0
2.5
Sepal.Width
Petal.Width
setosa
versicolor
virginica
5/23

Klasyfikacja
Celem klasyfikacji jest zbudowanie reguły, potrafiącej możliwie
dokładnie przypisywać informacje o klasie do nowych obiektów.
Przyjmujemy, że liczba klas jest znana, w przypadku większości
metod możliwe jest klasyfikowanie do więcej niż dwóch klas.
Przykładami zagadnień klasyfikacji są
w medycynie: określenie czy pacjent jest chory, a jeżeli tak to na co,
w analizie kredytowej: określenie czy firma spłaci kredyt czy nie,
w analizie obrazów z fotoradarów: odczytanie numerów rejestracji
samochodów.
w genomice: określenie do których organelli kierowane jest białko.
6/23

Klasyfikacja
Schemat postępowania
1
Określ zbiór klas do których chcesz przypisywać nowe obiekty.
2
Zgromadź dane dotyczące zbioru przedstawicieli tych klas.
3
Wybierz zbiór cech/zmiennych, na bazie których chcesz klasyfikować.
4
Wybierz metodę/regułę klasyfikacji.
5
Oceń jakość/dokładność klasyfikacji.
6
Jeżeli dokładność nie jest wystarczająca to wróć do kroku 1.
7/23
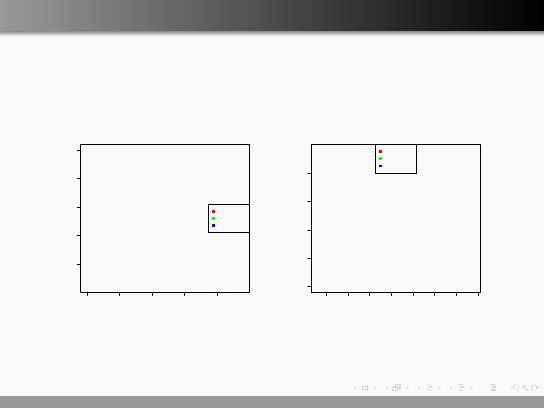
Wybór zmiennych
Nie każde zmienne mają równie dobre właściwości dyskryminujące
(rozróżniające).
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
2.0
2.5
3.0
3.5
4.0
0.5
1.0
1.5
2.0
2.5
Sepal.Width
Petal.Width
setosa
versicolor
virginica
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
4.5
5.0
5.5
6.0
6.5
7.0
7.5
8.0
2.0
2.5
3.0
3.5
4.0
Sepal.Length
Sepal.Width
setosa
versicolor
virginica
8/23
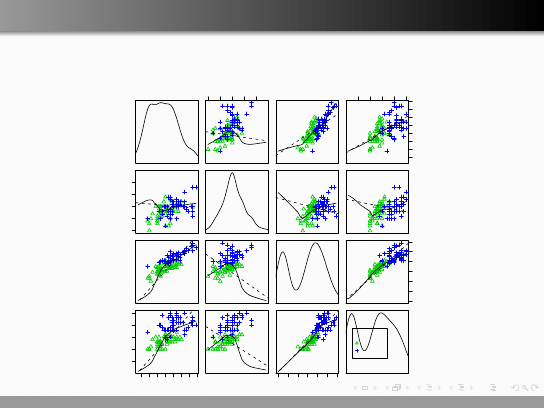
Wybór zmiennych
Wykresy rozrzutu mogą posłużyć do wyboru dobrych zmiennych.
|
|
|
| | |
| |
|
|
|
||
|
|
|
|
|
|
| |
|
|
|
| || ||
||
|
| |
||
|
|
|
|
|
|
|
||
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
| | |
| | | |
| | | |
|
|
|
|| | |
|
|
|
|
|
||
|
|
|
|||
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
||
||
||
|
|
|
|
| |
|
|
| |
| |
|
|
|
|
|
||
|
|
| |
|
|
||
| |
|
|
Sepal.Length
2.0
3.0
4.0
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
0.5
1.5
2.5
4.5
5.5
6.5
7.5
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
2.0
3.0
4.0
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
|
| |
|
| |
||
| |
|
|
||
|
|
|
| ||
| |
|
| |
|
| |
|
|
| |
| |
| | | |
|
| |
|
| | |
|
|
|
|
|
||
|
|
||
|
|
|
|
|
|
|
|| |
|
|
| |
|
|
| | | |
| |
|
|
|| || |
|
|
|
|
| |
|
|
|
| |
||
| |
|
| |
| ||
|
|
|
|
|
| |
| |
|
|
|
|
|
|
||
|
|
|
| |
| |
|
|
||
|
|
|
|
| |||
|
| |
|
|
|
|
|
Sepal.Width
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
||||||
||||||
|
|| |
|| |
||
|
| ||
|||
|||||
||
|||||
||| | |
||
|||
|
| |
| |||
|
|
|
| |
| |
|
||
| |
|
|
|
|
|
|| ||
|
| |||
|
|||
|
|| ||
|
|
||||
|
|
|
|
|
||
|
|
|
| |
|||
||||
||
| |
|
|
|
| |
|| || | |
|
| | |
||
| ||
||
|
|
|
|||
|
Petal.Length
1
2
3
4
5
6
7
●
●
●
●
●
●
●
●
●
●●
●
●
●●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
● ●
●●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
4.5
5.5
6.5
7.5
0.5
1.5
2.5
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
1
2
3
4
5
6
7
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
||||| |
|
||
| ||
|| | ||
|||
| |
| |
|| |
|||| |
| ||||
| || ||
|
|
|
|
||||
| ||
| |
| |
| | |
|
|
|
|
| | |
|
|
|
|
| |
| | || |
|
| |
| |
|
| |
|
|||
| |
|
| |
| ||
| |
|
| |
|
|
|
| ||
|
|
| |
|
|
|
|
| |
|
|
||
| |
||| |
| | | |
|
|
| |
|| | |
|
|
| |
|
| | |
|
Petal.Width
●
setosa
versicolor
virginica
9/23

Dyskryminacja liniowa i kwadratowa
Dyskryminacja liniowa to metoda klasyfikacji w której szuka się
hiperpłaszczyzn najlepiej separujących pary klas. Dla dwóch
zmiennych hiperpłaszczyzna to prosta, dla trzech zmiennych
hiperpłaszczyzna to płaszczyzna, itd.
Klasyfikacja polega na określeniu, po której stronie hiperpłaszczyzny
znajduje się nowy obiekt.
Jest wiele sposobów wyznaczania równań hiperpłaszczyzn, powiemy
o najpopularniejszej klasyfikacji Fishera.
Klasyfikacja kwadratowa tym różni się od liniowej, że klasy rozdziela
się krzywymi stopnia drugiego. Dla dwóch zmiennych są to elipsy,
hiperbole i parabole, dla trzech zmiennych są to elipsoidy,
paraboloidy itp.
10/23
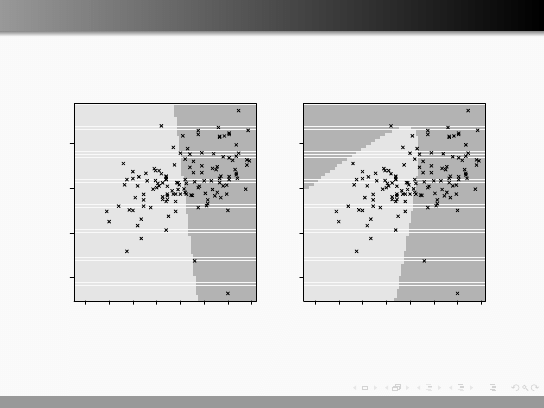
Obszary decyzyjne dla dyskryminacji liniowej i kwadratowej
60
80
100
120
140
160
180
200
3
4
5
6
lda()
glucose
log(insulin)
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
60
80
100
120
140
160
180
200
3
4
5
6
qda()
glucose
log(insulin)
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
11/23

Dyskryminacja liniowa i kwadratowa
> library(MASS)
> data(iris)
> zbior.uczacy
= sample(1:nrow(iris), nrow(iris)/2, F)
> # wywolujemy funkcje lda
> klasyfikatorLDA = lda(iris[,c(2,4)], grouping = iris[,5], subset=zbior.uczacy)
> # uzywajac metody predict wykonujemy klasyfikacje obiektów ze zbioru testowego
> oceny
= predict(klasyfikatorLDA, newdata=iris[-zbior.uczacy,c(2,4)])
> # porównajmy macierz kontyngencji oceny i rzeczywiste etykietki dla kolejnych obiektów
> table(predykcja = oceny$class, prawdziwe = iris[-zbior.uczacy,5])
prawdziwe
predykcja
setosa versicolor virginica
setosa
22
0
0
versicolor
0
26
2
virginica
0
0
25
> # wyniki dla innych zmiennych
> klasyfikatorLDA = lda(iris[,1:2], grouping = iris[,5], subset=zbior.uczacy)
> oceny
= predict(klasyfikatorLDA, newdata=iris[-zbior.uczacy,1:2])
> table(predykcja = oceny$class, prawdziwe = iris[-zbior.uczacy,5])
prawdziwe
predykcja
setosa versicolor virginica
setosa
22
0
0
versicolor
0
22
13
virginica
0
4
14
12/23

Metoda k najbliższych sąsiadów
Metoda k-najbliższych sąsiadów to najbardziej intuicyjna metoda
klasyfikacji.
Dla każdego obiektu, dla którego chcemy określić klasę, szukamy k
najbardziej podobnych obiektów, dla których znamy klasę. Nowemu
obiektowi przypisujmy klasę najczęściej występującą wśród obiektów
mu najbliższych.
Problem: jak wybrać liczbę sąsiadów k? Czy powinna być to duża
liczba czy mała? Od czego zależy ten wybór?
Problem: jak wyznaczyć najbardziej podobne obiekty? Jak określić
odległość?
13/23
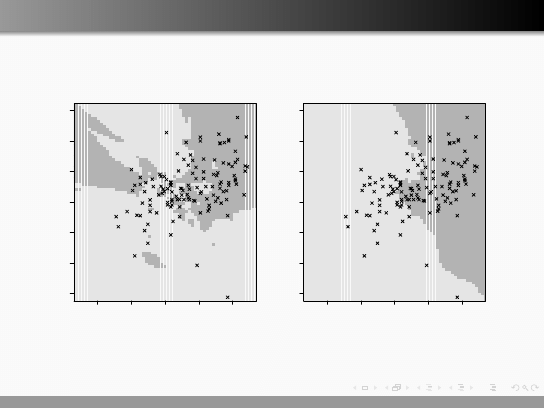
Metoda najbliższych sąsiadów
−2
−1
0
1
2
−3
−2
−1
0
1
2
3
ipredknn(, k=3)
glucose
insulin
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
−2
−1
0
1
2
−3
−2
−1
0
1
2
3
ipredknn(, k=21)
glucose
insulin
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
14/23

Metoda najbliższych sąsiadów
> library(ipred)
> zbior.uczacy
= sample(1:nrow(iris), nrow(iris)/2, F)
> # budujemy klasyfikator k-sasiadów, dla 3 sasiadów
> klasyfikatorKNN = ipredknn(Species~Sepal.Length+Sepal.Width, data=iris,
subset=zbior.uczacy, k=3)
> # wykonujemy predykcje klas
> oceny = predict(klasyfikatorKNN, iris[-zbior.uczacy, ], "class")
> # wyswietlamy macierz kontyngencji
> table(predykcja = oceny, prawdziwe = iris[-zbior.uczacy,5])
prawdziwe
predykcja
setosa versicolor virginica
setosa
21
0
0
versicolor
1
19
10
virginica
0
10
14
15/23

Drzewa decyzyjne
Dla każdego obiektu, dla którego chcemy określić klasę, należy
opowiedzieć na serie pytań dotyczących wartości zmiennych.
Odpowiedzi determinują wybór klasy dla tego obiektu.
Mechanizm klasyfikacji z użyciem drzew decyzyjnych jest łatwy do
weryfikacji przez eksperta.
Problem: jak zbudować drzewo, jakie kryteria podziału węzłów
przyjąć?
Problem: metoda ta uznawana jest za niestabilną.
16/23
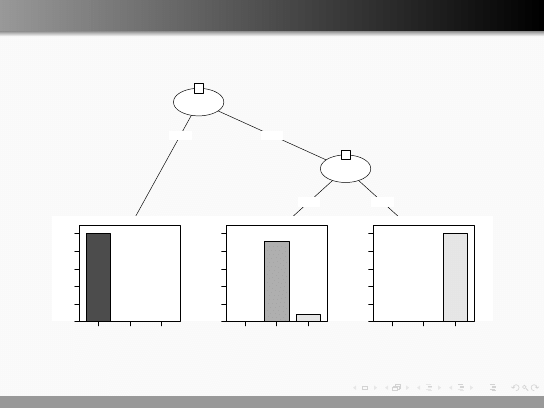
Drzewa decyzyjne
Petal.Width
p < 0.001
1
≤≤
0.6
>>
0.6
Node 2 (n = 28)
setosa versicolor virginica
0
0.2
0.4
0.6
0.8
1
Petal.Width
p < 0.001
3
≤≤
1.6
>>
1.6
Node 4 (n = 23)
setosa versicolor virginica
0
0.2
0.4
0.6
0.8
1
Node 5 (n = 24)
setosa versicolor virginica
0
0.2
0.4
0.6
0.8
1
17/23

Drzewa decyzyjne
>
library(party)
>
# uczymy drzewo
>
drzewo
<- ctree(Species~Petal.Width+Sepal.Width, data=iris, subset = zbior.uczacy)
>
plot(drzewo)
>
# w standardowy sposób przeprowadzamy klasyfikacje
>
oceny = predict(drzewo, iris[-zbior.uczacy,])
>
table(predykcja = oceny, prawdziwe = iris[-zbior.uczacy,5])
prawdziwe
predykcja
setosa versicolor virginica
setosa
22
0
0
versicolor
0
27
2
virginica
0
2
22
18/23
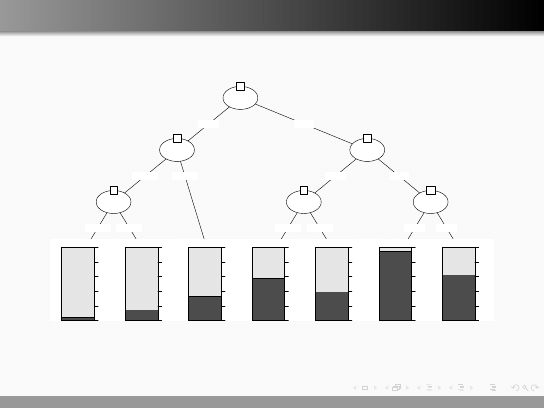
Drzewa decyzyjne, inny przykład
glucose
p < 0.001
1
≤≤
127
>>
127
insulin
p < 0.001
2
≤≤
4.956
>>
4.956
insulin
p = 0.213
3
≤≤
4.466
>>
4.466
Node 4 (n = 107)
pos
neg
0
0.2
0.4
0.6
0.8
1
Node 5 (n = 74)
pos
neg
0
0.2
0.4
0.6
0.8
1
Node 6 (n = 60)
pos
neg
0
0.2
0.4
0.6
0.8
1
glucose
p < 0.001
7
≤≤
165
>>
165
insulin
p = 0.42
8
≤≤
5.204
>>
5.204
Node 9 (n = 62)
pos
neg
0
0.2
0.4
0.6
0.8
1
Node 10 (n = 43)
pos
neg
0
0.2
0.4
0.6
0.8
1
glucose
p = 0.226
11
≤≤
189
>>
189
Node 12 (n = 38)
pos
neg
0
0.2
0.4
0.6
0.8
1
Node 13 (n = 8)
pos
neg
0
0.2
0.4
0.6
0.8
1
19/23
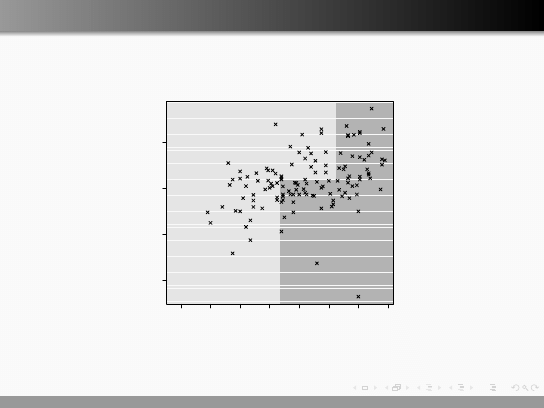
Drzewa decyzyjne
60
80
100
120
140
160
180
200
3
4
5
6
ctree()
insulin
glucose
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
20/23

Błąd klasyfikacji
Przypuśćmy, że otrzymaliśmy następujące wyniki klasyfikacji (dla dwóch
klas).
Ocena klasyfikatora / Prawdziwe klasy
zdrowy
chory
zdrowy
TN
FP
chory
FN
TP
Często używa się następujących ocen jakości klasyfikacji
blad klasyfikacji
=
FN+FP
TP+TN+FP+FN
,
czulosc
=
TP
TP+FN
,
specyficznosc
=
TN
TN+FP
,
gdzie TN = true negative, TP = true positive, FN = false negative, FP
= false positive.
21/23

Uwagi dodatkowe
Nie ma jednego, najlepszego mechanizmu klasyfikacji. Wybór
dobrego klasyfikatora zależy od charakteru danych, liczby
przypadków, liczby klas itp.
Jest wiele klasyfikatorów, te o których mówiliśmy to wybrane
najpopularniejsze.
22/23

Co trzeba zapamiętać?
Co to jest klasyfikacja?
Jakie metody klasyfikacji poznaliśmy i czym się one różnią?
Czy wybór zmiennych ma duży wpływ na wyniki i jak te zmienne
wybierać?
Jak oceniać wynik klasyfikacji?
23/23
Wyszukiwarka
Podobne podstrony:
11. Zagadnienia granic poznania II, Archiwum, Filozofia
11 Zagadnienia granic poznania IIid 12272 ppt
Zagadnienia, 2010-11 zagadnienia
11 Zagadnienia brzegowej teori Nieznany
11 Zagadnienia etyki zawodowej, kompetencji, odpowiedzialności moralnejid 12270 ppt
11 Zagadnienia granic poznania II
eg1 11 zagadnienia
Opinia publiczna zima 2010-11 zagadnienia egzam, Materiały, Opinia publiczna
EUropejska Polityka Społeczna, EPS - 2010.11, Zagadnienia
11. Zagadnienia granic poznania II, Archiwum, Filozofia
11 Zagadnienia etyki zawodowej, kompetencji, odpowiedzialności moralnejid 12271 pptx
11 Główne zanieczyszczenia powietrza atmosferycznego klasyfikacja, źródł
11 Klasyfikacja robotów ze względu na obszar zastosowania
zagadnienia Chemia Ogólna egzamin 10 11
socjologia organizacj do egzaminu SOCJOLOGIA ORGANIZACJI zagadnienia na egzamin WSAP 11
więcej podobnych podstron