METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
1
ROZWI
Ą
ZANIE RAMY PŁASKIEJ METOD
Ą
SIŁ I OBLICZENIE PRZEMIESZCZE
Ń
1
DANE WYJŚCIOWE
Dana jest rama jak na rysunku.
3
,0
0
m
q
=
5
,0
0
k
N
/m
P=20,00kN
M=15,00 kNm
i
k
1
= 0.5 EI
m
3
k
2
=
1
E
I
m
2,00m
2,00m
2,00m
2,00m
2,00m
1
2
-30
o
C
10
o
C
20
o
C
-5
o
C
∆
r =1cm
∆
r = 1.5
o
j
EI
1.3889 EI
Błędy montażu
1.5
o
1
o
1.2
cm
∆
L
2
=1cm
2
∆
L
1
=
-1
.5
cm
1
1.4 cm
Rozwiązać ją metodą sił od danego obciążenia siłami, od zmiany temperatury oraz od błędów montażu
i przemieszczeń podpór. Sporządzić wykresy sił przekrojowych i dokonać kontroli rozwiązania od
jednego z wymienionych wpływów. Obliczyć zaznaczone przemieszczenia.
Uwaga dotycząca oznaczeń.
Aby uniknąć niejednoznaczności oznaczeń wszystkie przemieszczenia obliczane w statycznie
wyznaczalnym układzie podstawowym i dotyczące tylko układu podstawowego oznaczać będziemy
małym symbolem
δ
a przemieszczenia obliczane w statycznie niewyznaczalnym układzie danym lub
obliczane w układzie podstawowym a dotyczące układu danego oznaczać będziemy dużym symbolem
∆
. Siły przekrojowe i reakcje wyznaczane w układzie podstawowym oznaczać będziemy
odpowiednim symbolem z nadkreśleniem (np. M ) a w układzie danym oznaczać będziemy
odpowiednim symbolem bez nadkreślenia (np. M ).
2
WYZNACZENIE STOPNIA STATYCZNEJ NIEWYZNACZALNOŚCI
Aby skorzystać z wzoru
t
e
n
h
⋅
−
=
3
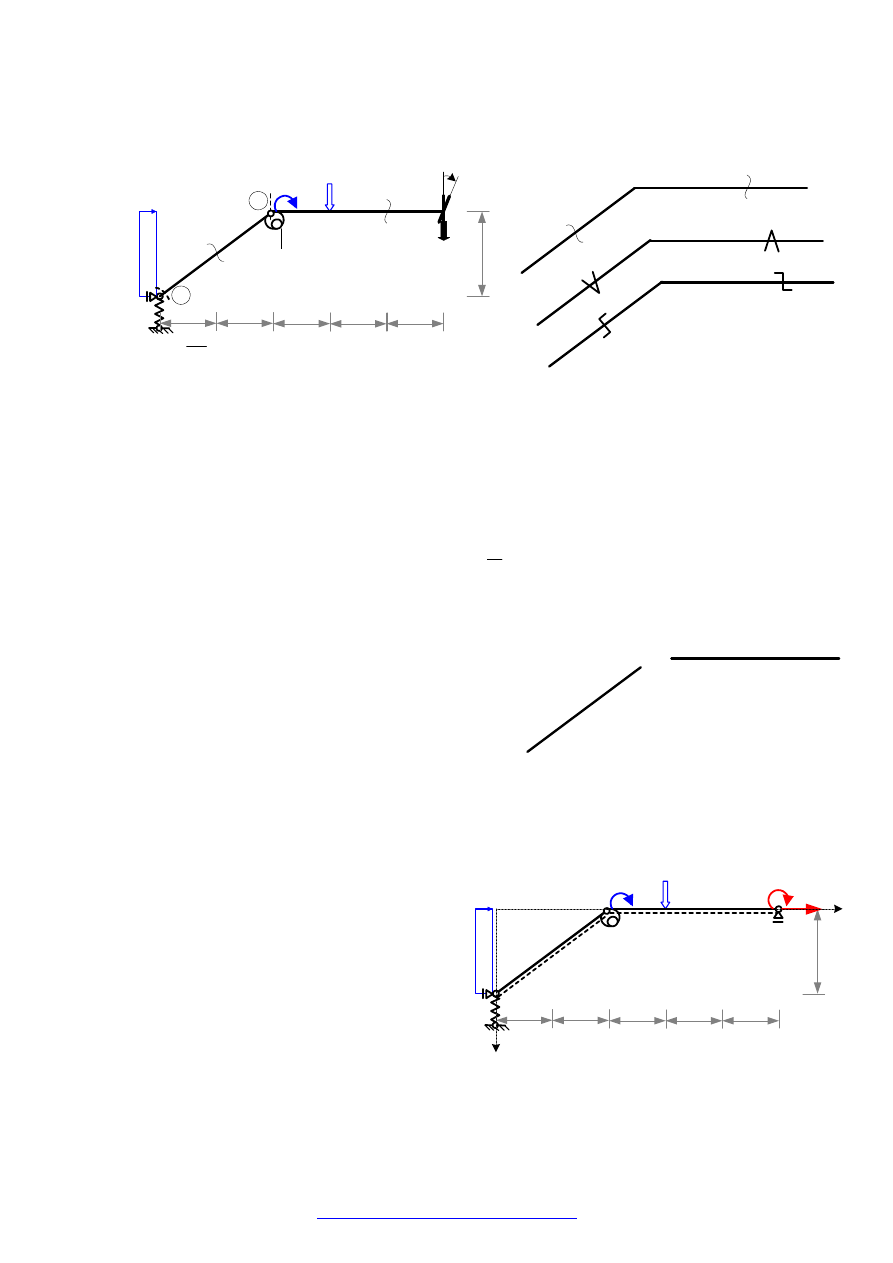
przekształcamy układ dany w zbiór tarcz „sztywnych”
otwartych przez usunięcie więzi podporowych,
dokonanie przecięć wszędzie tam gdzie połączenie nie
jest pełne oraz „otwarcie” tarcz zamkniętych.
Zilustrowano to na rysunku obok. Na rysunku tym w
nawiasach podano liczby usuniętych więzi, których
suma jest liczbą więzi
e
w przytoczonym wzorze.
3
ROZWIĄZANIE RAMY OD OBCIĄŻENIA SIŁAMI
3.1
UKŁAD PODSTAWOWY I ODPOWIADAJĄCY MU UKŁAD RÓWNAŃ
KANONICZNYCH
3.1.1
UKŁAD PODSTAWOWY
Układ podstawowy tworzymy z układu
danego przez zastąpienie
h
n
więzi
niewiadomymi siłami w taki sposób by
powstały układ był geometrycznie
niezmienny.
Uwaga: Liniami przerywanymi wzdłuż osi
prętów wyróżniono włókna do znakowania
momentów zginających
.
3.1.2
UKŁAD RÓWNAŃ KANONICZNYCH
0
1
1
2
12
1
11
=
∆
=
+
⋅
+
⋅
F
rz
F
F
F
X
X
δ
δ
δ
,
0
2
2
2
22
1
21
=
∆
=
+
⋅
+
⋅
F
rz
F
F
F
X
X
δ
δ
δ
.
(e=2)
(e=3)
2
=
t
(e=3)
8
2
3
2
=
+
⋅
=
e
2
2
3
8
=
⋅
−
=
h
n
3
,0
0
m
q
=
5
,0
0
k
N
/m
P=20,00kN
M=15,00 kNm
2,00m
2,00m
2,00m
2,00m
2,00m
EI
1.3889 EI
X
1
X
2
y
x
A
B
C
D
E
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
2
3.2
ROZWIĄZANIA UKŁADU PODSTAWOWEGO
3.2.1
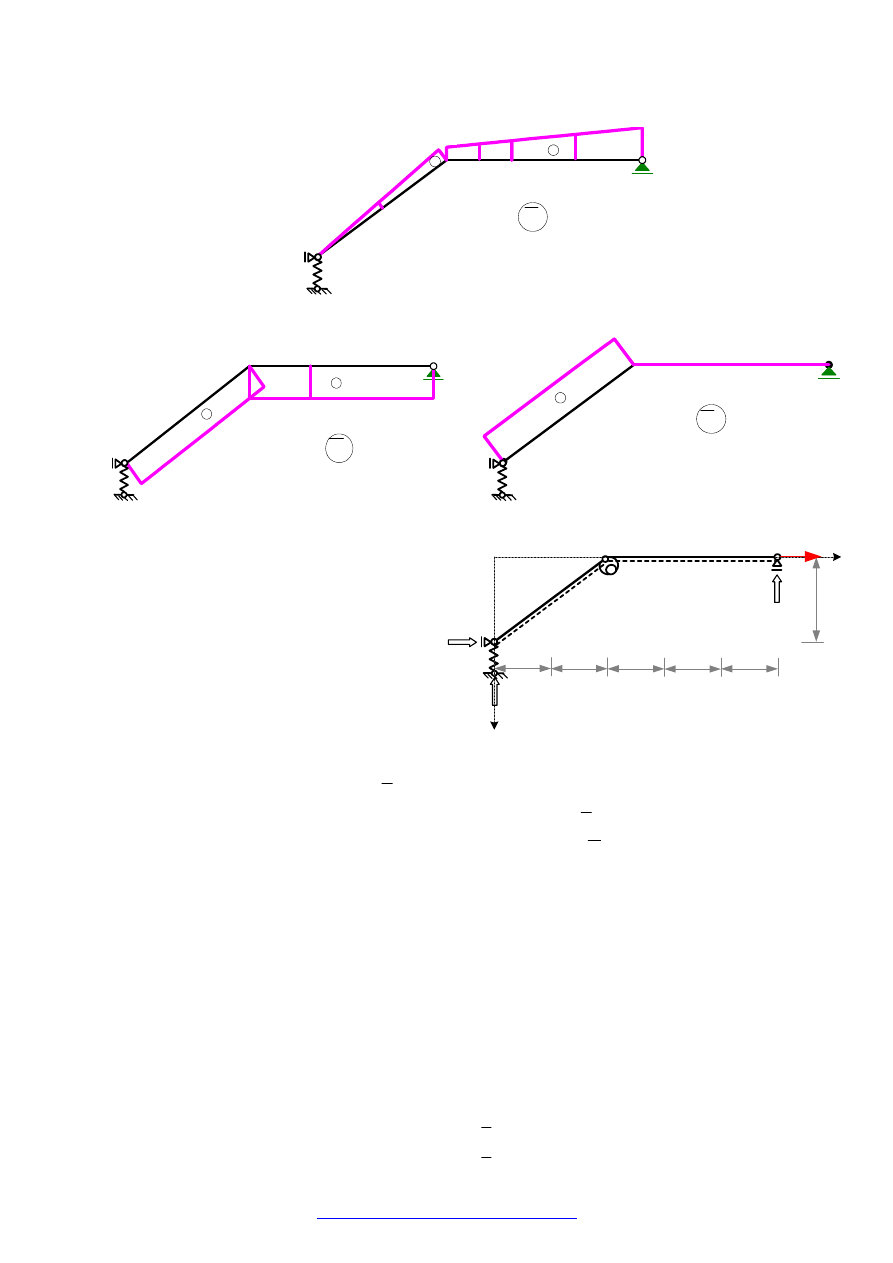
ROZWIĄZANIE UKŁADU PODSTAWOWEGO OD DANEGO OBCIĄŻENIA
F=(M,P,Q)
Uwaga: Wszystkie wielkości
wyznaczane w tym punkcie wyróżniamy
nadkreśleniem i indeksem górnym F.
Dla skrócenia zapisu w obliczeniach
pominiemy te wyróżniki stosując pełne
symbole tylko w oznaczeniach
wielkości, z których korzystać będziemy
w dalszych obliczeniach.
3.2.1.1
WYZNACZENIE REAKCJI PODPÓR
∑
=
⋅
⋅
+
+
⋅
+
⋅
−
=
0
2
/
3
3
6
10
m
m
q
M
m
P
m
V
M
B
A
⇒
0
2
/
3
3
/
5
15
6
20
10
=
⋅
⋅
+
+
⋅
+
⋅
−
m
m
m
kN
kNm
m
kN
m
V
B
⇒
kN
V
V
F
B
B
75
.
15
=
=
,
∑
=
+
−
−
=
0
P
V
V
Y
B
A
⇒
0
20
75
.
15
=
+
−
−
kN
kN
V
A
⇒
kN
V
V
F
A
A
25
.
4
=
=
,
∑
=
⋅
+
=
0
3m
q
H
X
A
⇒
0
3
/
5
=
⋅
+
m
m
kN
H
A
⇒
kN
H
H
F
A
A
00
.
15
−
=
=
.
Kontrola
∑
=
⋅
⋅
−
+
⋅
−
⋅
+
⋅
−
=
2
/
3
3
4
10
3
m
m
q
M
m
P
m
V
m
H
M
A
A
B
0
)
2
/
3
3
5
15
4
20
10
25
.
4
3
15
(
=
⋅
⋅
−
+
⋅
−
⋅
+
⋅
=
kNm
3.2.1.2
OBLICZENIE WARTOŚCI RZĘDNYCH CHARAKTERYSTYCZNYCH SIŁ
PRZEKROJOWYCH.
0
=
A
M
,
=
⋅
⋅
−
⋅
−
⋅
=
2
/
5
.
1
5
.
1
5
.
1
2
m
m
q
m
H
m
V
M
A
A
E
,
375
.
25
2
/
5
.
1
5
.
1
/
5
5
.
1
15
2
25
.
4
kNm
m
m
m
kN
m
kN
m
kN
=
⋅
⋅
−
⋅
+
⋅
=
kNm
m
m
m
kN
m
kN
m
m
m
q
m
H
m
V
M
A
A
CA
50
.
39
2
/
3
3
/
5
3
15
4
25
.
4
2
/
3
3
3
4
=
⋅
⋅
−
⋅
+
⋅
=
⋅
⋅
−
⋅
−
⋅
=
,
kNm
kNm
kNm
M
M
M
CA
CD
50
.
54
15
5
.
39
=
+
=
+
=
,
kNm
m
kN
m
V
M
B
D
00
.
63
4
75
.
15
4
=
⋅
=
⋅
=
,
0
=
B
M
,
(
)
kN
kN
H
V
V
A
A
AC
40
.
12
6
.
0
15
8
.
0
25
.
4
sin
cos
=
⋅
+
⋅
=
⋅
−
⋅
=
α
α
,
(
)
kN
kN
H
V
N
A
A
AC
45
.
9
8
.
0
15
6
.
0
25
.
4
cos
sin
=
⋅
+
⋅
−
=
⋅
−
⋅
−
=
α
α
,
(
)
kN
kN
m
q
H
V
V
A
A
CA
40
.
3
6
.
0
3
5
6
.
0
15
8
.
0
25
.
4
sin
3
sin
cos
=
⋅
⋅
−
⋅
+
⋅
=
⋅
⋅
−
⋅
−
⋅
=
α
α
α
,
(
)
kN
kN
m
q
H
V
N
A
A
CA
55
.
2
8
.
0
3
5
8
.
0
15
6
.
0
25
.
4
cos
3
cos
sin
−
=
⋅
⋅
−
⋅
+
⋅
−
=
⋅
⋅
−
⋅
−
⋅
−
=
α
α
α
,
kN
kN
kN
V
P
V
B
CD
25
.
4
75
.
15
20
=
−
=
−
=
,
kN
V
V
B
DB
75
.
15
−
=
−
=
,
0
=
CB
N
.
Rzędne środkowe momentów zginających dla przedziału CD i DB, wykorzystując ich
prostoliniowy charakter, obliczono jako średnie arytmetyczne z wartości brzegowych.
(
)
(
)
kNm
kNm
M
M
M
D
CD
CD
s
75
.
58
2
/
63
5
.
54
2
/
,
=
⋅
+
=
+
=
,
(
)
(
)
kNm
kNm
M
M
M
B
D
DB
s
50
.
31
2
/
0
63
2
/
,
=
⋅
+
=
+
=
Siła podłużna w więzi sprężystej nr 1:
kN
V
S
A
F
25
.
4
1
−
=
−
=
Moment zginający w więzi sprężystej nr 2:
kNm
M
S
CA
F
50
.
39
2
=
=
3
,0
0
m
q
=
5
,0
0
k
N
/m
P=20,00kN
M=15,00 kNm
2,00m
2,00m
2,00m
2,00m
2,00m
y
x
V
A
H
A
V
B
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
3
3
,0
0
m
2,00m
2,00m
2,00m
2,00m
2,00m
y
x
V
A
H
A
V
B
X
1
3.2.1.3
WYKRESY SIŁ PRZEKROJOWYCH.
39
,5
0k
N
m
5
4
,5
0
k
N
m
6
3
,0
0
k
N
m
25
,3
75
kN
m
M
F
+
+
5
8
,7
5
k
N
m
3
1
,5
0
k
N
m
12
,4
0k
N
3,4
0k
N
4
,2
5
k
N
4
,2
5
k
N
1
5
,7
5
k
N
1
5
,7
5
k
N
V
F
+
+
-
2,5
5k
N
9,4
5k
N
+
-
N
F
3.2.2
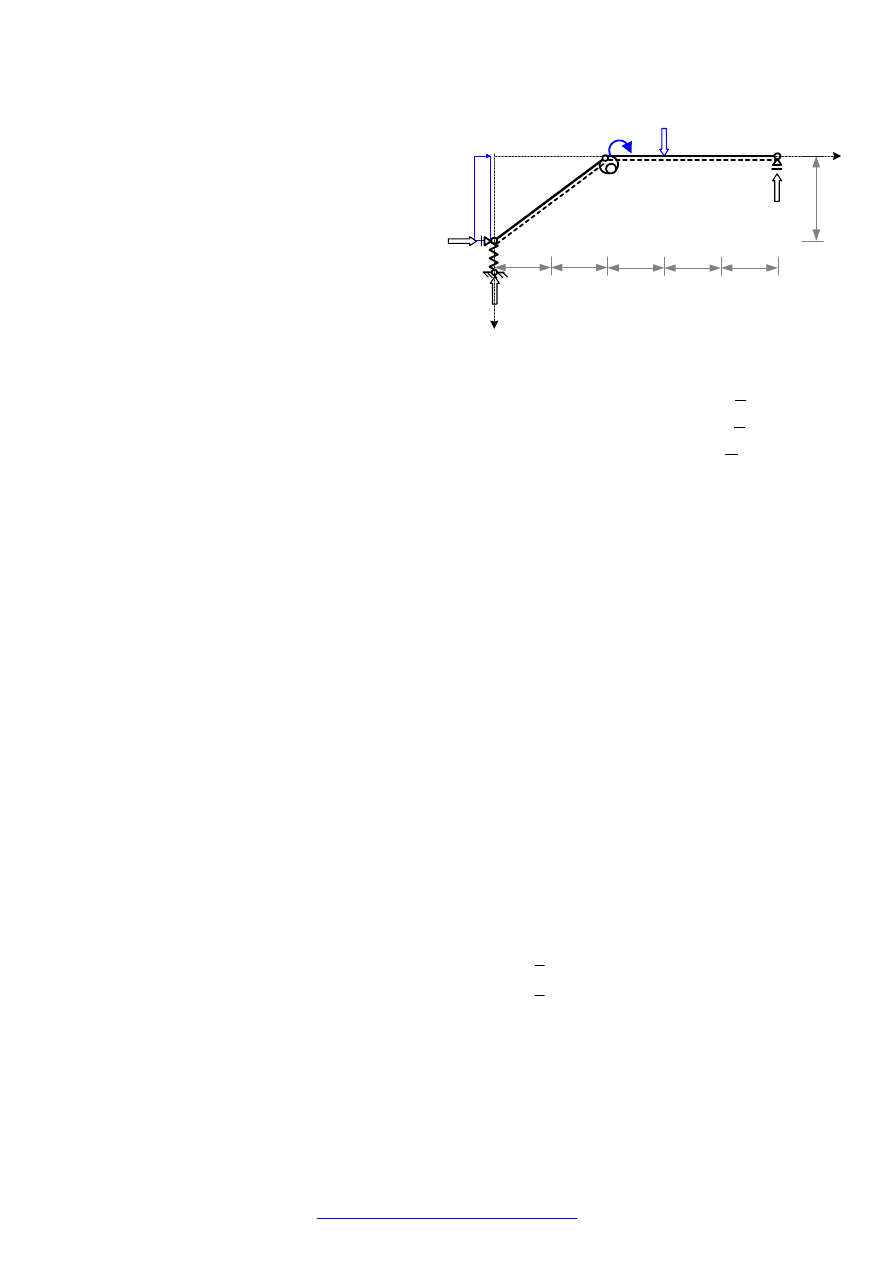
ROZWIĄZANIE UKŁADU PODSTAWOWEGO OD OBCIĄŻENIA X
1
= 1
Uwaga: Wszystkie wielkości wyznaczane w tym
punkcie wyróżniamy nadkreśleniem i indeksem
górnym 1. Dla skrócenia zapisu w obliczeniach
pominiemy te wyróżniki stosując pełne
symbole tylko w oznaczeniach wielkości,
z których korzystać będziemy w dalszych
obliczeniach.
3.2.2.1
WYZNACZENIE REAKCJI PODPÓR
∑
=
+
⋅
−
=
0
1
10m
V
M
B
A
⇒
m
V
V
B
B
/
10
.
0
1
=
=
,
∑
=
−
−
=
0
B
A
V
V
Y
⇒
m
V
V
A
A
/
10
.
0
1
−
=
=
,
∑
=
=
0
A
H
X
⇒
0
1
=
=
A
A
H
H
.
Kontrola
0
1
10
1
.
0
3
0
10
3
1
=
+
⋅
−
⋅
−
=
+
⋅
+
⋅
−
=
∑
X
m
V
m
H
M
A
A
B
3.2.2.2
OBLICZENIE WARTOŚCI RZĘDNYCH CHARAKTERYSTYCZNYCH SIŁ
PRZEKROJOWYCH
0
=
A
M
,
40
.
0
3
4
−
=
⋅
−
⋅
=
m
H
m
V
M
A
A
C
,
60
.
0
1
4
−
=
−
⋅
=
m
V
M
B
D
,
1
−
=
B
M
,
m
H
V
V
A
A
AC
/
08
.
0
sin
cos
−
=
⋅
−
⋅
=
α
α
,
m
H
V
N
A
A
AC
/
06
.
0
cos
sin
=
⋅
−
⋅
−
=
α
α
,
m
V
V
B
CB
/
10
.
0
−
=
−
=
,
0
=
CB
N
.
(
)
(
)
20
.
0
2
/
4
.
0
0
2
/
,
−
=
−
=
+
=
=
C
A
AC
s
E
M
M
M
M
,
(
)
(
)
50
.
0
2
/
6
.
0
4
.
0
2
/
,
−
=
−
−
=
+
=
D
C
CD
s
M
M
M
,
(
)
(
)
80
.
0
2
/
1
6
.
0
2
/
,
−
=
−
−
=
+
=
B
D
DB
s
M
M
M
.
(
)
(
)
70
.
0
2
/
1
4
.
0
2
/
,
−
=
−
−
=
+
=
B
C
CB
s
M
M
M
.
Siła podłużna w więzi sprężystej nr 1:
m
V
S
A
/
10
.
0
1
1
=
−
=
Moment zginający w więzi sprężystej nr 2:
40
.
0
1
2
−
=
=
C
M
S
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
4
3
,0
0
m
2,00m
2,00m
2,00m
2,00m
2,00m
y
x
V
A
H
A
V
B
X
2
3.2.2.3
WYKRESY SIŁ PRZEKROJOWYCH
0
,4
0
0,4
0
0
,6
0
1
,0
0
-
-
M
1
0
,5
0
0
,8
0
0,2
0
0,0
8/m
0
,1
0
/m
-
-
V
1
0
,1
0
/m
0
,1
0
/m
0,0
6/m
0,0
6/m
+
N
1
3.2.3
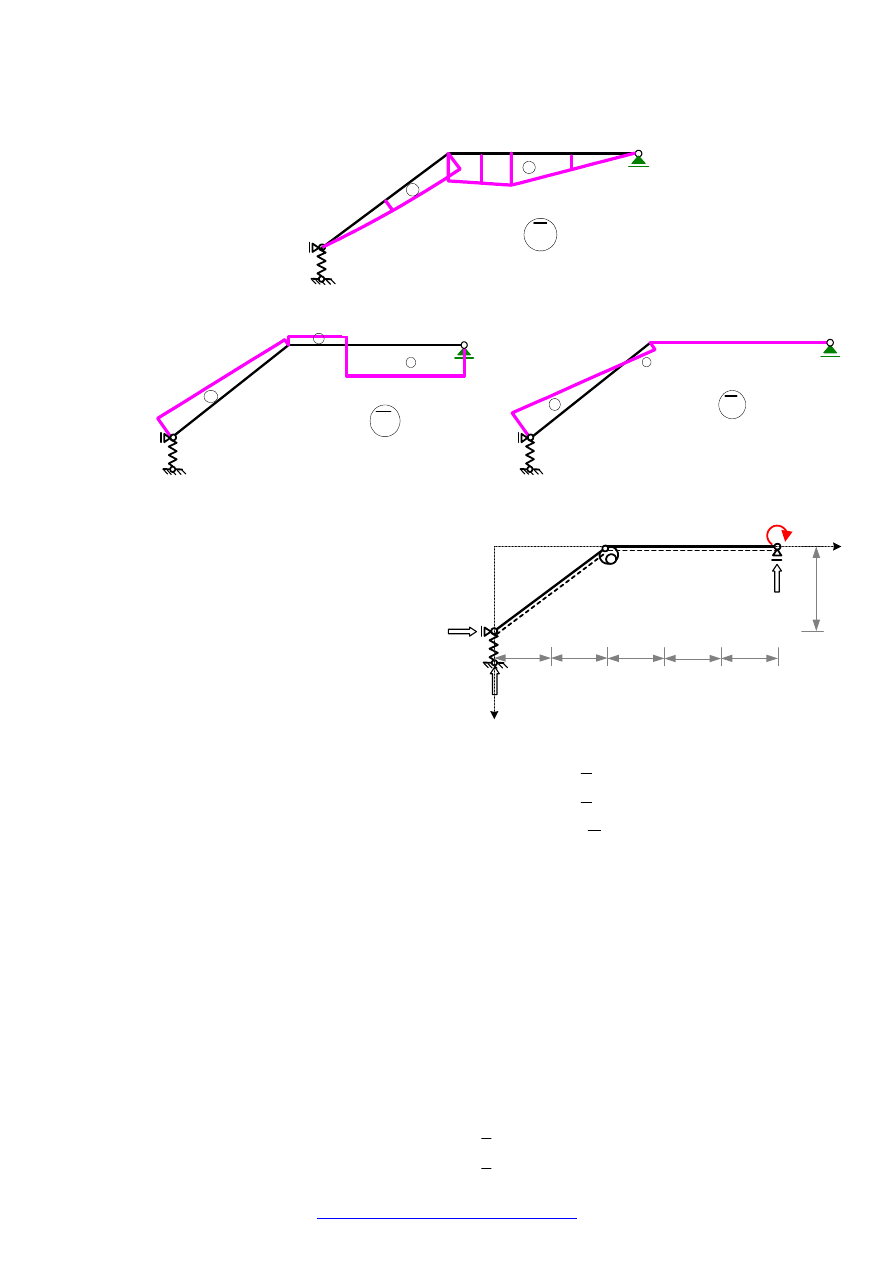
ROZWIĄZANIE UKŁADU PODSTAWOWEGO OD OBCIĄŻENIA X
2
= 1
Uwaga: Wszystkie wielkości wyznaczane w tym
punkcie wyróżniamy nadkreśleniem i indeksem
górnym 2. Dla skrócenia zapisu w obliczeniach
pominiemy te wyróżniki stosując pełne symbole
tylko w oznaczeniach wielkości, z których
korzystać będziemy w dalszych
obliczeniach.
3.2.3.1
WYZNACZENIE REAKCJI PODPÓR
∑
=
⋅
+
⋅
−
=
0
3
1
10
m
m
V
M
B
A
⇒
30
.
0
2
=
=
B
B
V
V
,
∑
=
−
−
=
0
B
A
V
V
Y
⇒
30
.
0
2
−
=
=
A
A
V
V
,
∑
=
+
=
0
1
A
H
X
⇒
1
2
−
=
=
A
A
H
H
.
Kontrola
0
)
10
)
3
.
0
(
3
)
1
(
(
10
3
=
⋅
−
+
⋅
−
−
=
⋅
+
⋅
−
=
∑
m
m
V
m
H
M
A
A
B
3.2.3.2
OBLICZENIE WARTOŚCI RZĘDNYCH CHARAKTERYSTYCZNYCH SIŁ
PRZEKROJOWYCH
0
=
A
M
,
m
m
H
m
V
M
A
A
C
80
.
1
3
4
=
⋅
−
⋅
=
,
m
m
V
M
B
D
20
.
1
4
=
⋅
=
,
0
=
B
M
,
36
.
0
sin
cos
=
⋅
−
⋅
=
α
α
A
A
AC
H
V
V
,
98
.
0
cos
sin
=
⋅
−
⋅
−
=
α
α
A
A
AC
H
V
N
,
30
.
0
−
=
−
=
B
CB
V
V
,
1
=
CB
N
.
(
)
(
)
m
m
M
M
M
M
C
A
AC
s
E
90
.
0
2
/
8
.
1
0
2
/
,
=
⋅
+
=
+
=
=
,
(
)
(
)
m
m
M
M
M
D
C
CD
s
50
.
1
2
/
2
.
1
8
.
1
2
/
,
=
⋅
+
=
+
=
,
(
)
(
)
m
m
M
M
M
B
D
DB
s
60
.
0
2
/
0
2
.
1
2
/
,
=
⋅
+
=
+
=
,
(
)
(
)
m
m
M
M
M
B
C
CB
s
90
.
0
2
/
0
8
.
1
2
/
,
=
⋅
+
=
+
=
.
Siła podłużna w więzi sprężystej nr 1:
30
.
0
2
1
=
−
=
A
V
S
Moment zginający w więzi sprężystej nr 2:
m
M
S
C
80
.
1
2
2
=
=
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
5
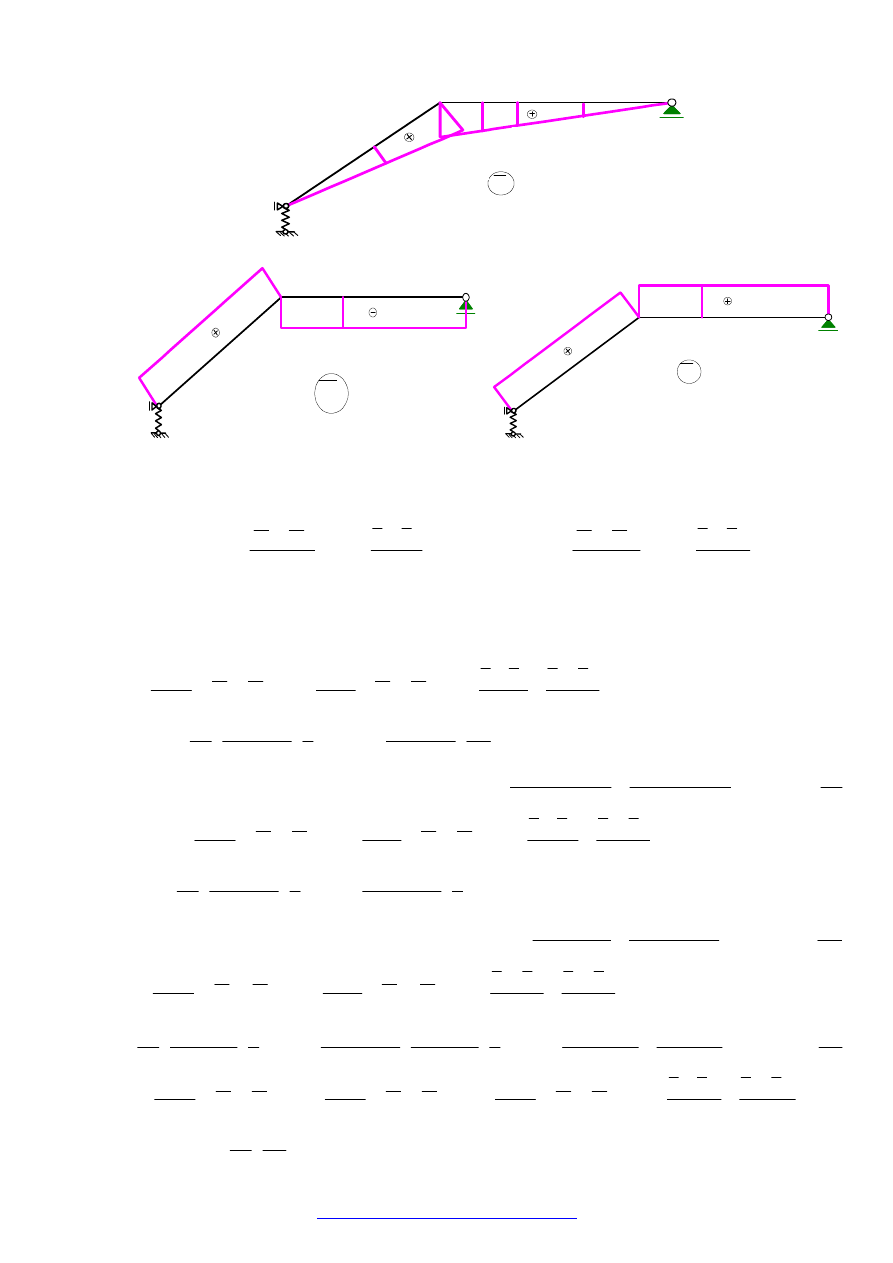
3.2.3.3
WYKRESY SIŁ PRZEKROJOWYCH
1
,8
0
m
1
,2
0
m
1,8
0 m
M
2
1
,5
0
m
0,9
0 m
0
.6
0
m
0,3
60
0,3
60
-0
,3
0
0
-0
,3
0
0
-0
,3
0
0
V
2
0,
98
0
0
,9
8
0
1
,0
0
0
1
,0
0
0
1
,0
0
0
N
2
3.3
OBLICZENIE WSPÓŁCZYNNIKÓW I ROZWIĄZANIE UKŁADU RÓWNAŃ
3.3.1
OBLICZENIE WSPÓŁCZYNNIKÓW UKŁADU RÓWNAŃ
Współczynniki układu równań obliczamy wykorzystując wzory
∑
∫
⋅
+
⋅
=
s
j
s
i
s
j
i
ij
k
S
S
dx
EI
M
M
δ
,
∑
∫
⋅
+
⋅
=
s
F
s
i
s
F
i
iF
k
S
S
dx
EI
M
M
δ
,
Do obliczenia całek w powyższych wzorach zastosowano wzór Simpsona lub Mohra. Ze względu na
charakter wykresów momentów zginających całki w powyższych wzorach przedstawiono w postaci
sum 3 lub 2 całek odpowiadających przedziałom całkowania, w których funkcje podcałkowe spełniają
założenia umożliwiające zastosowanie odpowiedniego wzoru.
=
⋅
+
⋅
+
⋅
⋅
+
⋅
⋅
=
∫
∫
2
1
2
1
2
1
1
1
1
1
1
1
1
1
11
1
1
k
S
S
k
S
S
dx
M
M
EI
dx
M
M
EI
CB
CB
AC
AC
δ
(
)
+
−
⋅
−
+
−
⋅
−
⋅
+
−
⋅
−
⋅
⋅
+
−
⋅
⋅
⋅
−
⋅
=
)
1
(
)
1
(
)
7
.
0
(
)
7
.
0
(
4
)
4
.
0
(
)
4
.
0
(
6
6
3889
.
1
1
)
4
.
0
(
3
2
2
5
4
.
0
1
m
EI
m
EI
EI
m
m
EI
m
EI
m
m
693049
.
2
/
)
4
.
0
(
)
4
.
0
(
/
5
.
0
/
1
.
0
/
1
.
0
3
=
−
⋅
−
+
⋅
+
,
=
⋅
+
⋅
+
⋅
⋅
+
⋅
⋅
=
=
∫
∫
2
2
2
1
2
1
2
1
1
1
2
1
2
1
21
12
1
1
k
S
S
k
S
S
dx
M
M
EI
dx
M
M
EI
CB
CB
AC
AC
δ
δ
(
)
+
⋅
−
+
⋅
−
⋅
+
⋅
−
⋅
⋅
⋅
+
⋅
⋅
⋅
−
⋅
=
2
0
)
1
(
9
.
0
)
7
.
0
(
4
8
.
1
4
.
0
6
6
3889
.
1
1
8
.
1
3
2
2
5
4
.
0
1
m
EI
m
m
EI
EI
m
m
EI
m
m
EI
m
2
3
192781
.
4
/
8
.
1
)
4
.
0
(
/
5
.
0
3
.
0
/
1
.
0
−
=
⋅
−
+
⋅
+
,
=
⋅
+
⋅
+
⋅
⋅
+
⋅
⋅
=
∫
∫
2
2
2
2
2
1
2
1
2
1
2
2
2
2
22
1
1
k
S
S
k
S
S
dx
M
M
EI
dx
M
M
EI
CB
CB
AC
AC
δ
EI
m
m
EI
m
m
EI
m
m
m
EI
m
m
m
EI
3
3
485563
.
13
/
8
.
1
8
.
1
/
5
.
0
3
.
0
3
.
0
8
.
1
3
2
2
6
8
.
1
3889
.
1
1
8
.
1
3
2
2
5
8
.
1
1
=
⋅
+
⋅
+
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
=
,
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
∫
∫
∫
dx
M
M
EI
dx
M
M
EI
dx
M
M
EI
DB
F
DB
CD
F
CD
AC
F
AC
F
1
1
1
1
1
1
1
δ
=
⋅
+
⋅
2
2
1
2
1
1
1
1
k
S
S
k
S
S
F
F
(
)
+
⋅
−
+
⋅
−
⋅
+
⋅
⋅
⋅
=
kNm
kNm
m
EI
5
.
39
)
4
.
0
(
375
.
25
)
2
.
0
(
4
0
0
6
5
1
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
6
(
)
+
⋅
−
+
⋅
−
⋅
+
⋅
−
⋅
⋅
⋅
+
2
63
)
6
.
0
(
75
.
58
)
5
.
0
(
4
5
.
54
4
.
0
6
2
3889
.
1
1
kNm
EI
(
)
=
⋅
−
+
−
⋅
+
⋅
−
+
⋅
−
⋅
+
⋅
−
⋅
⋅
⋅
+
m
EI
kNm
m
EI
kN
m
kNm
EI
/
5
.
39
)
4
.
0
(
/
5
.
0
)
25
.
4
(
/
1
.
0
0
)
1
(
5
.
31
)
8
.
0
(
4
63
6
.
0
6
4
3889
.
1
1
3
2
EI
kNm
2
764461
.
155
−
=
dx
M
M
EI
dx
M
M
EI
dx
M
M
EI
DB
F
DB
CD
F
CD
AC
F
AC
F
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
∫
∫
∫
2
2
2
2
1
1
1
δ
=
⋅
+
⋅
+
2
2
2
2
1
1
2
1
k
S
S
k
S
S
F
F
(
)
+
⋅
+
⋅
⋅
+
⋅
⋅
⋅
=
kNm
m
kNm
m
m
EI
5
.
39
8
.
1
375
.
25
9
.
0
4
0
0
6
5
1
(
)
+
⋅
+
⋅
⋅
+
⋅
⋅
⋅
⋅
+
3
63
2
.
1
75
.
58
5
.
1
4
5
.
54
8
.
1
6
2
3889
.
1
1
kNm
EI
EI
kNm
m
EI
kNm
m
EI
kN
kNm
EI
3
3
3
787409
.
402
/
5
.
39
8
.
1
/
5
.
0
)
25
.
4
(
3
.
0
63
3
2
2
4
2
.
1
3889
.
1
1
=
⋅
+
−
⋅
+
⋅
⋅
⋅
⋅
⋅
+
3.3.2
POSTAĆ SZCZEGÓŁOWA UKŁADU RÓWNAŃ I JEGO ROZWIĄZANIE
0
764461
.
155
192781
.
4
693049
.
2
2
2
2
1
=
−
⋅
−
⋅
EI
kNm
X
EI
m
X
EI
m
F
F
,
0
787409
.
402
485563
.
13
192781
.
4
3
2
3
1
2
=
+
⋅
+
⋅
−
EI
kNm
X
EI
m
X
EI
m
F
F
kNm
X
F
975393
.
21
1
=
,
kN
X
F
035701
.
23
2
−
=
.
3.4
OBLICZENIE WARTOŚCI „RZECZYWISTYCH” REAKCJI I SIŁ PRZEKROJOWYCH
F
r
F
r
F
r
F
r
R
X
R
X
R
R
+
⋅
+
⋅
=
2
2
1
1
,
F
F
F
F
M
X
M
X
M
M
α
α
α
α
+
⋅
+
⋅
=
2
2
1
1
,
F
F
F
F
N
X
N
X
N
N
α
α
α
α
+
⋅
+
⋅
=
2
2
1
1
,
F
F
F
F
V
X
V
X
V
V
α
α
α
α
+
⋅
+
⋅
=
2
2
1
1
,
F
F
F
F
S
X
S
X
S
S
α
α
α
α
+
⋅
+
⋅
=
2
2
1
1
.
kN
kN
kN
kNm
H
X
H
X
H
H
F
A
A
A
F
A
036
.
8
15
)
035701
.
23
(
)
1
(
975393
.
21
0
2
2
1
1
=
−
−
⋅
−
+
⋅
=
+
⋅
+
⋅
=
kN
kN
kN
kNm
m
V
X
V
X
V
V
F
A
A
A
F
A
963
.
8
25
.
4
)
035701
.
23
(
)
3
.
0
(
975393
.
21
/
1
.
0
2
2
1
1
=
+
−
⋅
−
+
⋅
−
=
+
⋅
+
⋅
=
kN
kN
kN
kNm
m
V
X
V
X
V
V
F
B
B
B
F
B
037
.
11
75
.
15
)
035701
.
23
(
3
.
0
975393
.
21
/
1
.
0
2
2
1
1
=
+
−
⋅
+
⋅
=
+
⋅
+
⋅
=
=
+
⋅
+
⋅
=
F
E
E
E
F
E
M
X
M
X
M
M
2
2
1
1
kNm
kNm
kN
m
kNm
2478
.
0
375
.
25
)
035701
.
23
(
9
.
0
975393
.
21
2
.
0
=
+
−
⋅
+
⋅
−
=
=
+
⋅
+
⋅
=
F
CA
CA
CA
F
CA
M
X
M
X
M
M
2
2
1
1
kNm
kNm
kN
m
kNm
7544
.
10
5
.
39
)
035701
.
23
(
8
.
1
975393
.
21
4
.
0
−
=
+
−
⋅
+
⋅
−
=
=
+
⋅
+
⋅
=
F
CD
CD
CD
F
CD
M
X
M
X
M
M
2
2
1
1
kNm
kNm
kN
m
kNm
2456
.
4
5
.
54
)
035701
.
23
(
8
.
1
975393
.
21
4
.
0
=
+
−
⋅
+
⋅
−
=
=
+
⋅
+
⋅
=
F
DC
DC
DC
F
DC
M
X
M
X
M
M
2
2
1
1
kNm
kNm
kN
m
kNm
1719
.
22
63
)
035701
.
23
(
2
.
1
975393
.
21
4
.
0
=
+
−
⋅
+
⋅
−
=
kNm
M
M
F
DC
F
DB
1719
.
22
=
=
kNm
kN
kNm
M
X
M
X
M
M
F
BD
BD
BD
F
BD
9754
.
21
0
)
035701
.
23
(
0
975393
.
21
1
2
2
1
1
−
=
+
−
⋅
+
⋅
−
=
+
⋅
+
⋅
=
kN
kN
kN
kNm
m
V
X
V
X
V
V
F
AC
AC
AC
F
AC
349
.
2
4
.
12
)
035701
.
23
(
36
.
0
975393
.
21
08
.
0
2
2
1
1
=
+
−
⋅
+
⋅
−
=
+
⋅
+
⋅
=
kN
kN
kN
kNm
m
V
X
V
X
V
V
F
CA
CA
CA
F
CA
651
.
6
4
.
3
)
035701
.
23
(
36
.
0
975393
.
21
/
08
.
0
2
2
1
1
−
=
+
−
⋅
+
⋅
−
=
+
⋅
+
⋅
=
kN
kN
kN
kNm
m
V
X
V
X
V
V
F
CD
CD
CD
F
CD
963
.
8
25
.
4
)
0357019
.
23
(
)
3
.
0
(
975393
.
21
1
.
0
2
2
1
1
=
+
−
⋅
−
+
⋅
−
=
+
⋅
+
⋅
=
kN
V
V
F
CD
F
DC
963
.
8
=
=
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
7
=
+
⋅
+
⋅
=
F
DB
DB
DB
F
DB
V
X
V
X
V
V
2
2
1
1
kN
kN
kN
kNm
m
037
.
11
75
.
15
)
035701
.
23
(
)
3
.
0
(
975393
.
21
/
1
.
0
−
=
−
−
⋅
−
+
⋅
−
=
kN
V
V
F
DB
F
BD
037
.
11
−
=
=
=
+
⋅
+
⋅
=
F
AC
AC
AC
F
AC
N
X
N
X
N
N
2
2
1
1
kN
kN
kN
kNm
m
807
.
11
45
.
9
)
035701
.
23
(
98
.
0
975393
.
21
/
06
.
0
−
=
+
−
⋅
+
⋅
−
=
kN
kN
kN
kNm
m
N
X
N
X
N
N
F
CA
CA
CA
F
CA
807
.
23
55
.
2
)
035701
.
23
(
98
.
0
975393
.
21
06
.
0
2
2
1
1
−
=
−
−
⋅
+
⋅
−
=
+
⋅
+
⋅
=
kN
kN
kNm
N
X
N
X
N
N
F
CD
CD
CD
F
CD
036
.
23
0
)
035701
.
23
(
1
975393
.
21
0
2
2
1
1
−
=
+
−
⋅
+
⋅
=
+
⋅
+
⋅
=
kN
N
N
N
N
F
BD
F
DB
F
CD
F
DC
036
.
23
−
=
=
=
=
kN
kN
kN
kNm
m
S
X
S
X
S
S
F
F
9632
.
8
25
.
4
)
035701
.
23
(
3
.
0
975393
.
21
/
1
.
0
1
2
2
1
1
1
1
1
−
=
−
−
⋅
+
⋅
=
+
⋅
+
⋅
=
kNm
kN
kN
m
kNm
S
X
S
X
S
S
F
F
F
F
7544
.
10
5
.
39
)
035701
.
23
(
8
.
1
975393
.
21
4
.
0
1
2
2
2
1
1
2
2
−
=
+
−
⋅
+
⋅
−
=
+
⋅
+
⋅
=
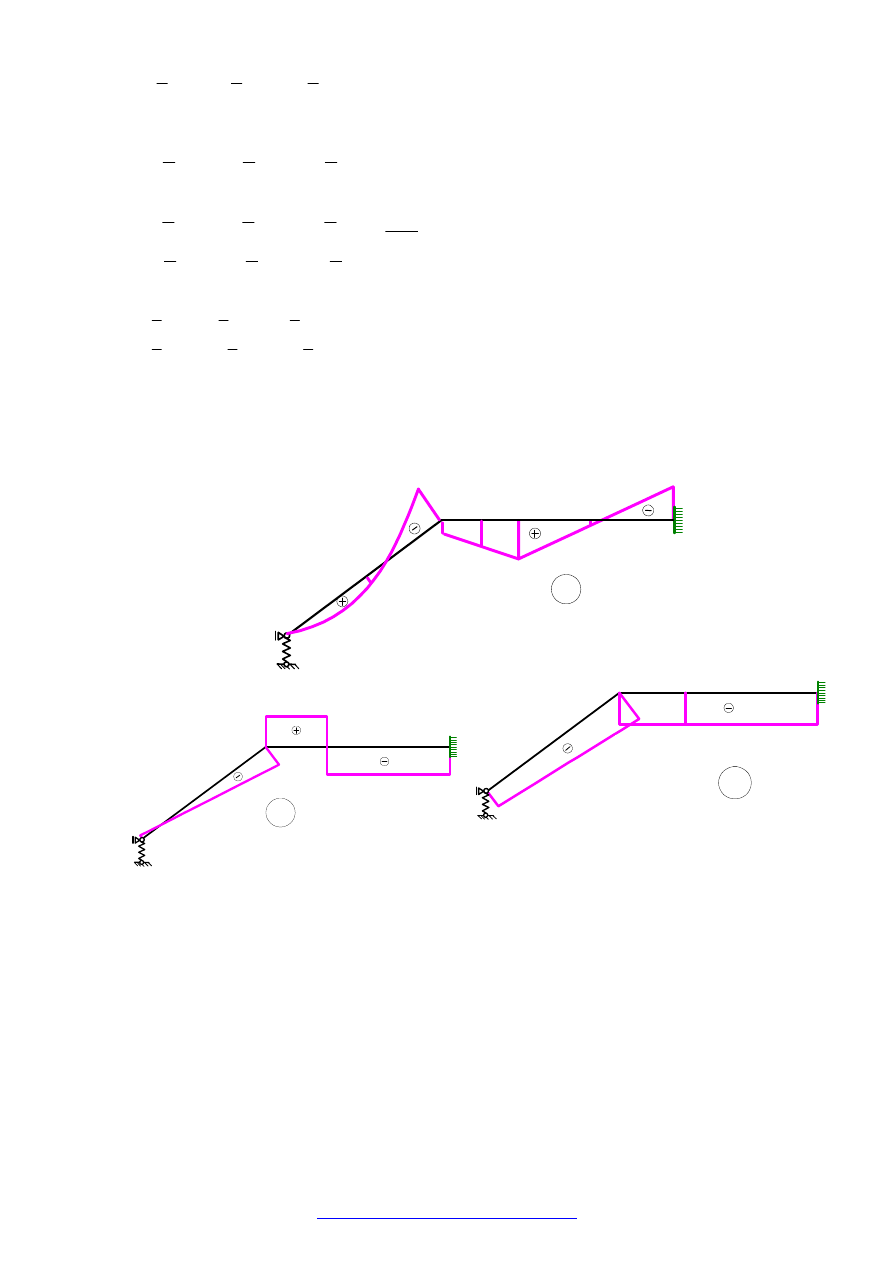
3.5
WYKRESY „RZECZYWISTYCH” SIŁ PRZEKROJOWYCH
-1
0,7
54
k
N
m
0,2
48
k
N
m
4
,2
4
6
k
N
m
2
2
,1
7
2
k
N
m
-2
1
,9
7
5
k
N
m
M
F
1
3
,2
0
9
k
N
m
0
,0
9
8
k
N
m
2,3
49
k
N
-6
,6
51
k
N
8
,9
6
3
k
N
-1
1
,0
3
7
k
N
V F
8
,9
6
3
k
N
-1
1
,0
3
7
k
N
-1
1,8
07
k
N
-2
3,8
08
k
N
-2
3
,0
3
6
k
N
-2
7
,1
9
9
k
N
-2
3
,0
3
6
k
N
NF
Rzeczywiste wartości sił przekrojowych można też policzyć rozwiązując układ podstawowy od
działającego równocześnie obciążenia danego i znanych już sił hiperstatycznych. Wyniki obliczeń
musiałyby być identyczny (w granicach dokładności rachunkowej) jak przedstawione powyżej.
3.6
KONTROLA POPRAWNOŚCI ROZWIĄZANIA.
Kontrola poprawności rozwiązania polega na sprawdzeniu czy otrzymane rozwiązanie jest
statycznie i kinematycznie dopuszczalne, czyli czy siły spełniają równania równowagi a
przemieszczenia są zgodne z warunkami podparcia i ciągłości.
3.6.1
KONTROLA STATYCZNEJ DOPUSZCZALNOŚCI ROZWIĄZANIA
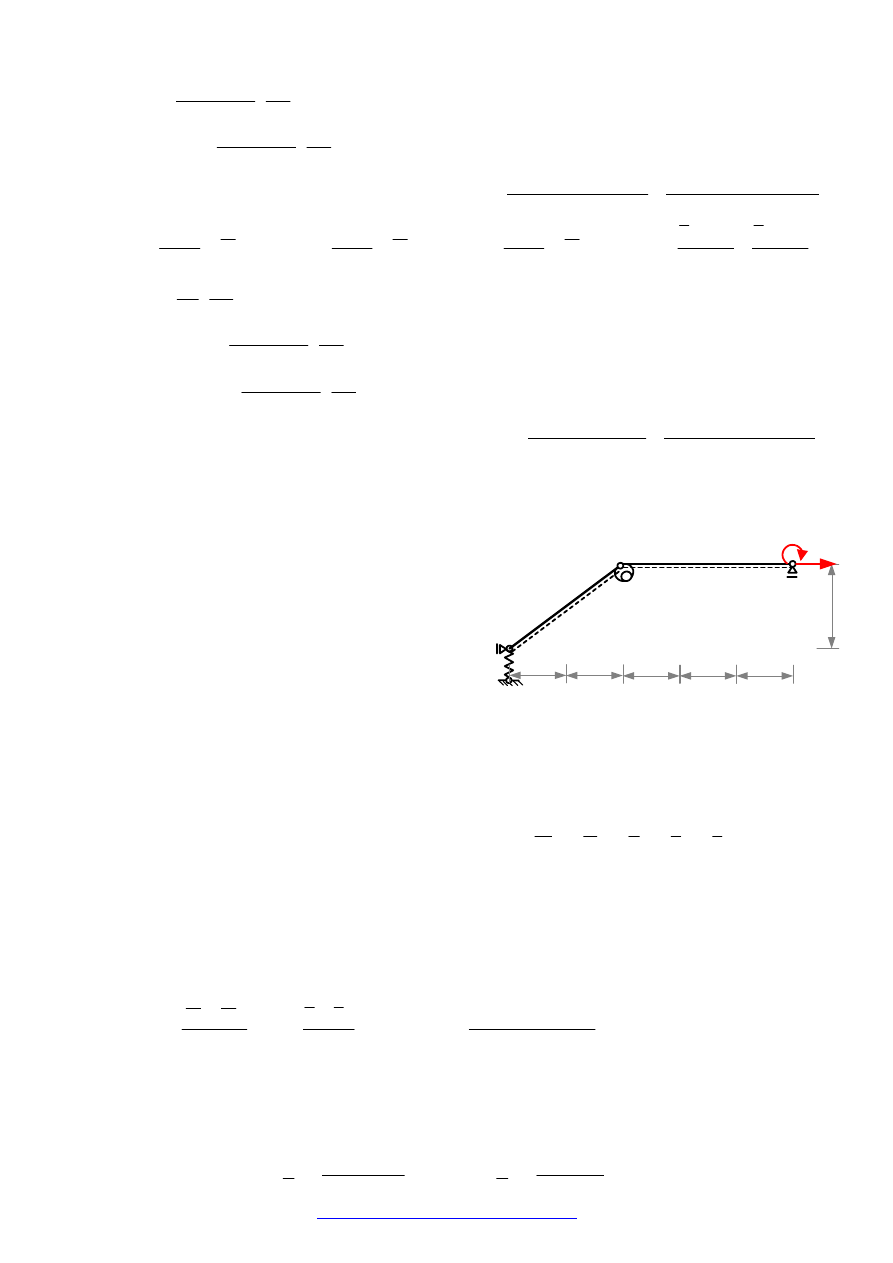
Dokonując kontroli równań równowagi należy pamiętać, że kontroli podlegają tylko te
wartości, które występują w obliczeniach kontrolnych. Zaleca się, więc aby do sprawdzenia równań
równowagi, podzielić układ na pręty i węzły i dla każdego tak wydzielonego elementu napisać 3
równania równowagi. W tym przypadku kontroli podlegają wszystkie wartości brzegowe sił
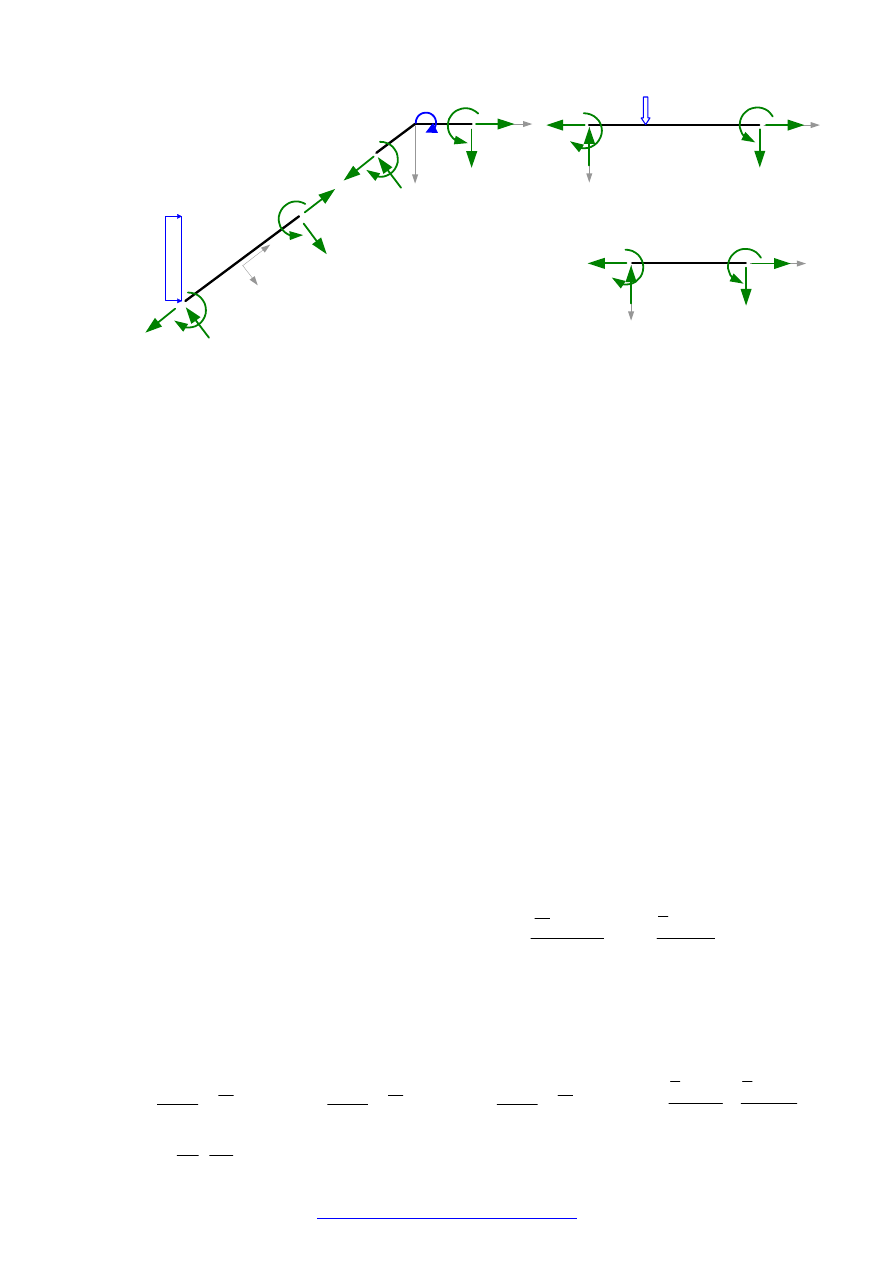
przekrojowych. Na rysunku poniżej pokazano elementy, dla których sprawdzimy równania
równowagi.
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
8
q
=
5
,0
0
k
N
/m
M=15,00 kNm
P=20,00kN
A
B
C
D
x
y
x
y
x
y
N
AC
N
CA
N
CA
M
CA
M
AC
V
CA
V
CA
V
AC
V
CD
V
CD
M
CD
V
BD
N
CD
N
CD
N
BD
B
D
x
y
V
DB
M
DB
M
BD
V
BD
N
DB
N
BD
M
CA
M
CD
M
BD
Dla pręta AC
0
8
.
0
3
5
)
808
.
23
(
)
807
.
11
(
cos
3
≈
⋅
⋅
+
−
+
−
−
=
⋅
⋅
+
+
−
=
∑
α
m
q
N
N
X
CA
AC
,
0
6
.
0
3
5
)
651
.
6
(
349
.
2
sin
3
≈
⋅
⋅
+
−
+
−
=
⋅
⋅
+
+
−
=
∑
α
m
q
V
V
Y
CA
AC
,
0
5
.
1
3
5
5
)
651
.
6
(
)
754
.
10
(
0
5
.
1
3
5
≈
⋅
⋅
+
⋅
−
+
−
−
=
⋅
⋅
+
⋅
+
−
=
∑
m
m
q
m
V
M
M
M
CA
CA
AC
A
Dla węzła C
0
6
.
0
)
651
.
6
(
8
.
0
)
808
.
23
(
036
.
23
sin
cos
≈
⋅
−
−
⋅
−
−
−
=
⋅
−
⋅
−
=
∑
α
α
CA
CA
CD
V
N
N
X
,
0
8
.
0
)
651
.
6
(
6
.
0
)
808
.
23
(
963
.
8
cos
sin
≈
⋅
−
−
⋅
−
+
=
⋅
−
⋅
+
=
∑
α
α
CA
CA
CD
V
N
V
Y
,
0
15
246
.
4
754
.
10
≈
+
−
−
=
+
−
=
∑
M
M
M
M
CD
CA
c
Dla pręta CB
0
036
.
23
)
036
.
23
(
=
−
−
−
=
+
−
=
∑
BD
CD
N
N
X
,
0
20
)
037
.
11
(
963
.
8
=
+
−
+
−
=
+
+
−
=
∑
P
V
V
Y
BD
CD
,
0
2
20
6
)
037
.
11
(
)
975
.
21
(
246
.
4
2
6
≈
⋅
+
⋅
−
+
−
−
=
⋅
+
⋅
+
−
=
∑
m
P
m
V
M
M
M
BD
BD
CD
C
Dla pręta DB
0
036
.
23
)
036
.
23
(
=
−
−
−
=
+
−
=
∑
BD
DB
N
N
X
,
0
)
037
.
11
(
)
037
.
11
(
=
−
+
−
−
=
+
−
=
∑
BD
DB
V
V
Y
,
0
4
)
037
.
11
(
)
975
.
21
(
172
.
22
4
≈
⋅
−
+
−
−
=
⋅
+
−
=
∑
m
V
M
M
M
BD
BD
DB
D
.
3.6.2
KONTROLA KINEMATYCZNEJ ZGODNOŚCI PRZEMIESZCZEŃ.
Kontrola zgodności przemieszczeń polega na sprawdzeniu zgodności przemieszczeń układu
rozwiązanego z przemieszczeniami rzeczywistymi w tylu miejscach ile wynosi stopień statycznej
niewyznaczalności. Można tego dokonać postępując, w fazie początkowej, analogicznie jak buduje się
układ równań kanonicznych, to jest: przyjąć układ podstawowy metody sił i sporządzić wykresy
momentów zginających od jednostkowych wartości sił hiperstatycznych a następnie policzyć
przemieszczenia w układzie danym ze wzoru
∑
∫
⋅
+
⋅
=
∆
s
s
F
s
s
F
F
k
S
S
dx
EI
M
M
α
α
α
w miejscach, w
których przecięto (usunięto) więzi tworząc układ podstawowy. Wartości tych przemieszczeń muszą
być takie, jakie wynikają ze sposobu podparcia układu i połączenia jego elementów. Wystarczające
jest jednak sprawdzenie przemieszczeń w miejscach sił hiperstatycznych przyjętych do rozwiązania
układu. W tym przypadku wykresy momentów zginających od jednostkowych wartości sił
hiperstatycznych są już określone i wystarczy policzyć przemieszczenia
F
1
∆
i
F
2
∆
.
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
∆
∫
∫
∫
dx
M
M
EI
dx
M
M
EI
dx
M
M
EI
DB
F
DB
CD
F
CD
AC
F
AC
F
1
1
1
1
1
1
1
=
⋅
+
⋅
2
2
1
2
1
1
1
1
k
S
S
k
S
S
F
F
(
)
+
−
⋅
−
+
⋅
−
⋅
+
⋅
⋅
⋅
=
kNm
kNm
m
EI
)
754
.
10
(
)
4
.
0
(
248
.
0
)
2
.
0
(
4
0
0
6
5
1
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
9
(
)
+
⋅
−
+
⋅
−
⋅
+
⋅
−
⋅
⋅
⋅
+
kNm
m
EI
172
.
22
)
6
.
0
(
209
.
13
)
5
.
0
(
4
246
.
4
4
.
0
6
2
3889
.
1
1
(
)
+
−
⋅
−
+
⋅
−
⋅
+
⋅
−
⋅
⋅
⋅
+
kNm
m
EI
)
975
.
21
(
)
1
(
098
.
0
)
8
.
0
(
4
172
.
22
6
.
0
6
4
3889
.
1
1
0
/
)
754
.
10
(
4
.
0
/
5
.
0
)
963
.
8
(
/
1
.
0
3
≈
−
⋅
−
+
⋅
−
⋅
+
m
EI
kNm
m
EI
kN
m
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
∆
∫
∫
∫
dx
M
M
EI
dx
M
M
EI
dx
M
M
EI
DB
F
DB
CD
F
CD
AC
F
AC
F
2
2
2
2
1
1
1
=
⋅
+
⋅
2
2
2
2
1
1
2
1
k
S
S
k
S
S
F
F
(
)
+
−
⋅
+
⋅
⋅
+
⋅
⋅
⋅
=
kNm
m
kNm
m
m
EI
)
754
.
10
(
8
.
1
248
.
0
9
.
0
4
0
0
6
5
1
(
)
+
⋅
+
⋅
⋅
+
⋅
⋅
⋅
⋅
+
2
172
.
22
2
.
1
209
.
13
5
.
1
4
246
.
4
8
.
1
6
2
3889
.
1
1
kNm
m
EI
(
)
+
−
⋅
+
⋅
⋅
+
⋅
⋅
⋅
⋅
+
2
)
975
.
21
(
0
098
.
0
6
.
0
4
172
.
22
2
.
1
6
4
3889
.
1
1
kNm
m
EI
0
/
)
754
.
10
(
8
.
1
/
5
.
0
)
963
.
8
(
3
.
0
3
≈
−
⋅
+
⋅
−
⋅
+
m
EI
kNm
m
m
EI
kN
.
4
ROZWIĄZANIE RAMY OD ZMIAN TEMPERATURY
4.1
UKŁAD PODSTAWOWY I ODPOWIADAJĄCY MU UKŁAD RÓWNAŃ
KANONICZNYCH
4.1.1
UKŁAD PODSTAWOWY
Przyjęto układ podstawowy taki jak dla
rozwiązania od obciążeń siłami, aby móc
wykorzystać w obliczeniach wykonane już
rozwiązania od obciążeń hiperstatycznych
4.1.2
UKŁAD RÓWNAŃ KANONICZNYCH
0
1
1
2
12
1
11
=
∆
=
+
⋅
+
⋅
T
rz
T
T
T
X
X
δ
δ
δ
,
0
2
2
2
22
1
21
=
∆
=
+
⋅
+
⋅
T
rz
T
T
T
X
X
δ
δ
δ
.
4.2
ROZWIĄZANIA UKŁADU PODSTAWOWEGO
4.2.1
ROZWIĄZANIE UKŁADU PODSTAWOWEGO OD ZMIAN TEMPERATURY
Ponieważ układ podstawowy jest układem statycznie wyznaczalnym zmiany temperatury
nie wywołują w nim żadnych sił
0
2
1
=
=
=
=
=
T
T
T
T
T
S
S
V
N
M
4.2.2
ROZWIĄZANIE UKŁADU PODSTAWOWEGO OD OBCIĄŻENIA X
1
= 1 I X
2
= 1
Ze względu na to, że przyjęto układ podstawowy analogiczny jak dla rozwiązania od
obciążenia siłami (różne jest tylko obciążenie) rozwiązania układu podstawowego od obciążenia
X
1
= 1 i X
2
= 1 są identyczne jak w punktach 2.3 i 2.4.
4.3
OBLICZENIE WSPÓŁCZYNNIKÓW I ROZWIĄZANIE UKŁADU RÓWNAŃ
4.3.1
OBLICZENIE WSPÓŁCZYNNIKÓW UKŁADU RÓWNAŃ
Współczynniki układu równań obliczamy wykorzystując wzory
∑
∫
⋅
+
⋅
=
s
j
s
i
s
j
i
ij
k
S
S
dx
EI
M
M
δ
,
(
)
∑
∑
Ω
⋅
∆
⋅
+
Ω
⋅
∆
−
∆
⋅
=
p
p
N
T
p
p
M
T
iT
i
i
To
h
Tp
Tw
α
α
δ
)
(
.
Uwzględniając fakt, że rozwiązania układu podstawowego od obciążenia X
1
= 1 i X
2
= 1 są
identyczne jak w punktach 2.3 i 2.4 współczynniki
11
δ
,
21
12
δ
δ
=
i
22
δ
mają wartości takie jak
obliczono w punkcie 2.5.2. Obliczymy więc tylko współczynniki
T
1
δ
i
T
2
δ
.
Określenie składników wzorów dla poszczególnych prętów
Dla pręta AC
m
m
m
M
1
2
5
4
.
0
1
−
=
⋅
−
=
Ω
,
2
5
.
4
2
5
8
.
1
2
m
m
m
M
=
⋅
=
Ω
,
3
,0
0
m
2,00m
2,00m
2,00m
2,00m
2,00m
EI
1.3889 EI
X
1
X
2
-30
o
C
10
o
C
20
o
C
-5
o
C
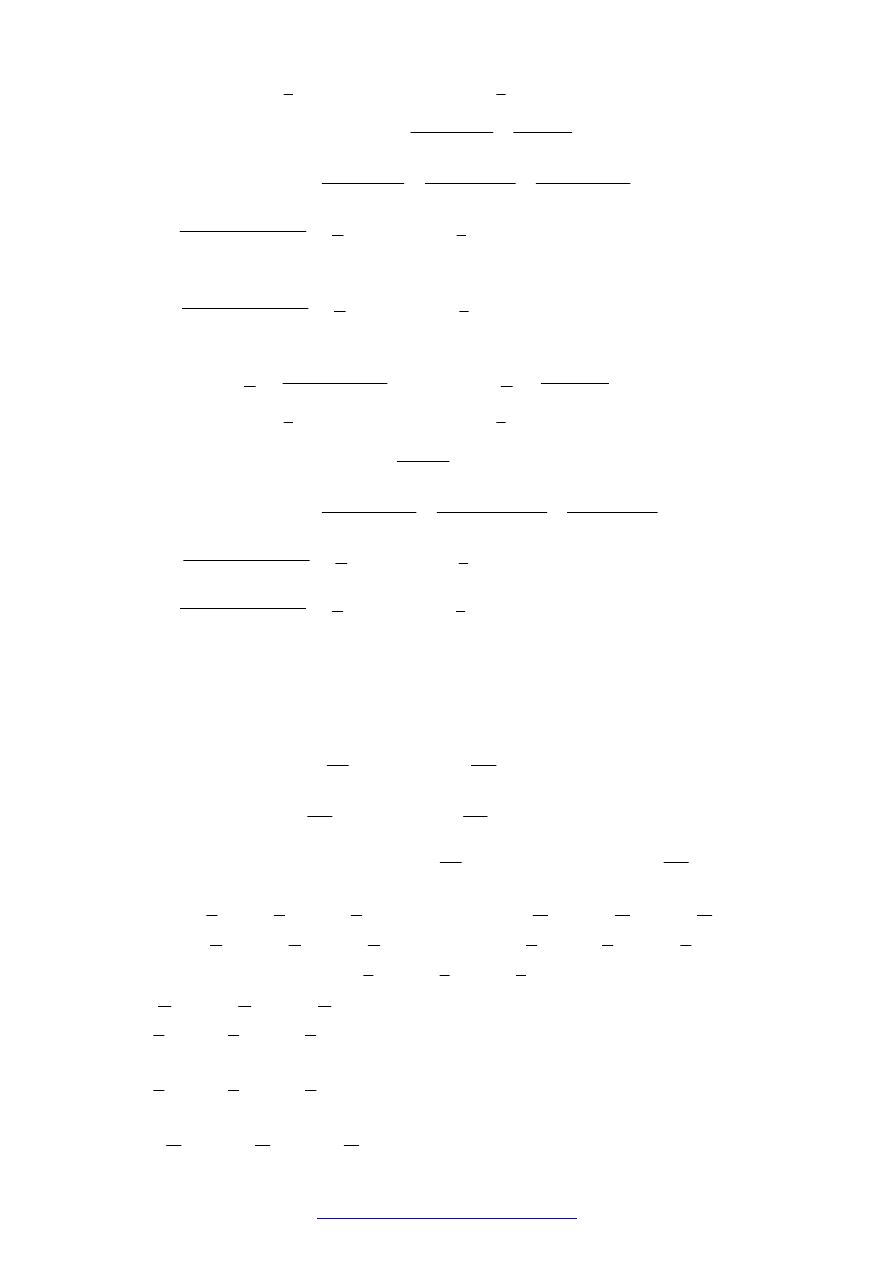
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
10
3
.
0
5
/
06
.
0
1
=
⋅
=
Ω
m
m
N
,
m
m
N
9
.
4
5
98
.
0
2
=
⋅
=
Ω
,
C
Tw
o
5
−
=
∆
,
C
Tp
o
20
=
∆
,
C
Tp
Tw
To
o
5
.
7
2
20
5
2
=
+
−
=
∆
+
∆
=
∆
(przekrój symetryczny),
m
m
h
22
.
0
5
044
.
0
=
⋅
=
,
h
Tp
Tw
∆
−
∆
m
C
m
C
o
o
636
.
113
22
.
0
)
20
5
(
−
=
−
−
=
,
1
)
(
)
(
1
M
T
AC
T
h
Tp
Tw
Ω
⋅
∆
−
∆
⋅
=
α
δ
+
1
N
T
To
Ω
⋅
∆
⋅
α
=
(
)
T
o
o
o
T
C
C
m
m
C
α
α
⋅
=
⋅
+
−
⋅
−
⋅
=
886364
.
115
3
.
0
5
.
7
)
1
(
/
636
.
113
,
2
)
(
)
(
2
M
T
AC
T
h
Tp
Tw
Ω
⋅
∆
−
∆
⋅
=
α
δ
+
2
N
T
To
Ω
⋅
∆
⋅
α
=
(
)
T
o
o
o
T
m
C
m
C
m
m
C
α
α
⋅
⋅
−
=
⋅
+
⋅
−
⋅
=
613636
.
474
9
.
4
5
.
7
5
.
4
/
636
.
113
2
Dla pręta CB
m
m
M
2
.
4
2
6
)
1
4
.
0
(
1
−
=
⋅
+
−
=
Ω
,
2
4
.
5
2
6
8
.
1
2
m
m
m
M
=
⋅
=
Ω
,
0
1
=
Ω
N
,
m
m
N
6
6
1
2
=
⋅
=
Ω
.
C
Tw
o
10
=
∆
,
C
Tp
o
30
−
=
∆
,
C
To
o
10
2
30
10
−
=
−
=
∆
(przekrój symetryczny),
m
m
h
24
.
0
6
04
.
0
=
⋅
=
,
h
Tp
Tw
)
(
∆
−
∆
m
C
m
C
o
o
6667
.
166
24
.
0
))
30
(
10
(
=
−
−
=
,
1
)
(
)
(
1
M
T
CB
T
h
Tp
Tw
Ω
⋅
∆
−
∆
⋅
=
α
δ
+
1
N
T
To
Ω
⋅
∆
⋅
α
=
(
)
T
o
o
T
C
m
m
C
α
α
⋅
−
=
+
−
⋅
⋅
700
0
)
2
.
4
(
/
6667
.
166
,
2
)
(
)
(
2
M
T
CB
T
h
Tp
Tw
Ω
⋅
∆
−
∆
⋅
=
α
δ
+
=
Ω
⋅
∆
⋅
2
N
T
To
α
(
)
m
C
m
C
m
m
C
T
o
o
o
T
⋅
⋅
=
⋅
+
⋅
−
⋅
=
α
α
840
6
5
.
7
4
.
5
/
636
.
113
2
Szukane współczynniki:
T
o
T
o
T
C
C
α
α
δ
⋅
−
=
⋅
−
=
113636
.
584
)
700
8864
.
115
(
1
,
m
C
m
C
T
o
T
o
T
⋅
⋅
=
⋅
⋅
+
−
=
α
α
δ
386363
.
365
)
840
613636
.
474
(
2
.
4.3.2
POSTAĆ SZCZEGÓŁOWA UKŁADU RÓWNAŃ I JEGO ROZWIĄZANIE
0
1136
.
584
192781
.
4
693049
.
2
2
2
1
=
⋅
−
⋅
−
⋅
T
o
T
T
C
X
EI
m
X
EI
m
α
0
386363
.
365
485563
.
13
192781
.
4
2
3
1
2
=
⋅
⋅
+
⋅
+
⋅
−
m
C
X
EI
m
X
EI
m
T
o
T
T
α
m
EI
C
X
T
o
T
⋅
⋅
=
α
6254
.
338
1
,
2
2
1870
.
78
m
EI
C
X
T
o
T
⋅
⋅
=
α
.
4.4
OBLICZENIE WARTOŚCI „RZECZYWISTYCH” REAKCJI I SIŁ PRZEKROJOWYCH
T
r
T
r
T
r
T
r
R
X
R
X
R
R
+
⋅
⋅
⋅
=
2
2
1
1
,
T
T
T
T
M
X
M
X
M
M
α
α
α
α
+
⋅
+
⋅
=
2
2
1
1
,
T
T
T
T
N
X
N
X
N
N
α
α
α
α
+
⋅
+
⋅
=
2
2
1
1
,
T
T
T
T
V
X
V
X
V
V
α
α
α
α
+
⋅
+
⋅
=
2
2
1
1
T
T
T
T
S
X
S
X
S
S
α
α
α
α
+
⋅
+
⋅
=
2
2
1
1
=
+
⋅
+
⋅
=
T
A
T
A
T
A
T
A
H
X
H
X
H
H
2
2
1
1
2
2
/
1870
.
78
0
/
1870
.
78
)
1
(
0
m
EI
C
m
EI
C
T
o
T
o
⋅
⋅
−
=
+
⋅
⋅
⋅
−
+
α
α
=
+
⋅
+
⋅
=
T
A
T
A
T
A
T
A
V
X
V
X
V
V
2
2
1
1
2
2
/
3186
.
57
0
/
1870
.
78
)
3
.
0
(
/
6254
.
338
/
1
.
0
m
EI
C
m
EI
C
m
EI
C
m
T
o
T
o
T
o
⋅
⋅
−
=
+
⋅
⋅
⋅
−
+
⋅
⋅
⋅
−
=
α
α
α
=
+
⋅
+
⋅
=
T
B
T
B
T
B
T
B
V
X
V
X
V
V
2
2
1
1
2
2
/
3186
.
57
0
/
1870
.
78
3
.
0
/
6254
.
338
/
1
.
0
m
EI
C
m
EI
C
m
EI
C
m
T
o
T
o
T
o
⋅
⋅
=
+
⋅
⋅
⋅
+
⋅
⋅
⋅
=
α
α
α
=
+
⋅
+
⋅
=
T
CA
T
CA
T
CA
T
CA
M
X
M
X
M
M
2
2
1
1
m
EI
C
m
EI
C
m
m
EI
C
T
o
T
o
T
o
/
2865
.
5
0
/
1870
.
78
8
.
1
/
6254
.
338
4
.
0
2
⋅
⋅
=
+
⋅
⋅
⋅
+
⋅
⋅
⋅
−
=
α
α
α
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
11
T
CA
T
CB
M
M
=
=
+
⋅
+
⋅
=
T
BC
T
BC
T
BC
T
BC
M
X
M
X
M
M
2
2
1
1
m
EI
C
m
EI
C
m
EI
C
T
o
T
o
T
o
/
6254
.
338
0
/
1870
.
78
0
/
6254
.
338
1
2
⋅
⋅
−
=
+
⋅
⋅
⋅
+
⋅
⋅
⋅
−
=
α
α
α
=
+
⋅
+
⋅
=
T
AC
T
AC
T
AC
T
AC
V
X
V
X
V
V
2
2
1
1
2
2
/
0573
.
1
0
/
1870
.
78
36
.
0
/
6254
.
338
/
08
.
0
m
EI
C
m
EI
C
m
EI
C
m
T
o
T
o
T
o
⋅
⋅
=
+
⋅
⋅
⋅
+
⋅
⋅
⋅
−
=
α
α
α
T
AC
T
CA
V
V
=
=
+
⋅
+
⋅
=
T
CB
T
CB
T
CB
T
CB
V
X
V
X
V
V
2
2
1
1
2
2
/
3186
.
57
0
/
1870
.
78
)
3
.
0
(
/
6254
.
338
/
1
.
0
m
EI
C
m
EI
C
m
EI
C
m
T
o
T
o
T
o
⋅
⋅
−
=
+
⋅
⋅
⋅
−
+
⋅
⋅
⋅
−
=
α
α
α
T
CB
T
BC
V
V
=
=
+
⋅
+
⋅
=
T
AC
T
AC
T
AC
T
AC
N
X
N
X
N
N
2
2
1
1
2
2
/
9408
.
96
0
/
1870
.
78
98
.
0
/
6254
.
338
/
06
.
0
m
EI
C
m
EI
C
m
EI
C
m
T
o
T
o
T
o
⋅
⋅
=
+
⋅
⋅
⋅
+
⋅
⋅
⋅
−
=
α
α
α
T
AC
T
CA
N
N
=
=
+
⋅
+
⋅
=
T
CB
T
CB
T
CB
T
CB
N
X
N
X
N
N
2
2
1
1
2
2
/
1770
.
78
0
/
1870
.
78
1
0
m
EI
C
m
EI
C
T
o
T
o
⋅
⋅
=
+
⋅
⋅
⋅
+
α
α
T
CB
T
BC
N
N
=
=
+
⋅
+
⋅
=
T
T
T
T
S
X
S
X
S
S
1
2
2
1
1
1
1
1
2
2
/
3186
.
57
0
/
1870
.
78
3
.
0
/
6254
.
338
/
1
.
0
m
EI
C
m
EI
C
m
EI
C
m
T
o
T
o
T
o
⋅
⋅
=
+
⋅
⋅
⋅
+
⋅
⋅
⋅
=
α
α
α
=
+
⋅
+
⋅
=
T
T
T
T
S
X
S
X
S
S
2
2
2
2
1
1
2
2
m
EI
C
m
EI
C
m
m
EI
C
T
o
T
o
T
o
/
2865
.
5
0
/
1870
.
78
8
.
1
/
6254
.
338
4
.
0
2
⋅
⋅
=
+
⋅
⋅
⋅
+
⋅
⋅
⋅
−
=
α
α
α
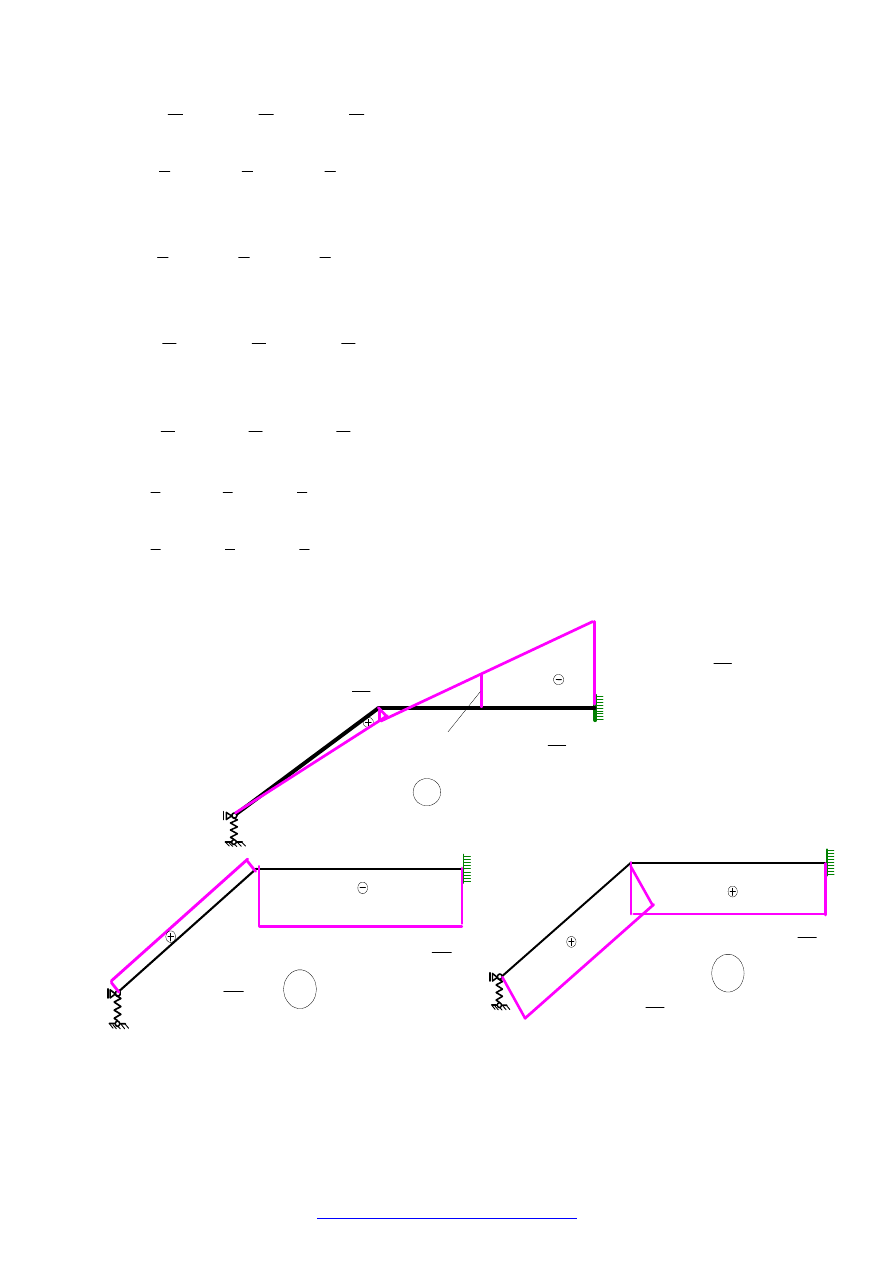
4.5
WYKRESY „RZECZYWISTYCH” SIŁ PRZEKROJOWYCH
m
EI
C
T
o
⋅
⋅
α
2865
.
5
M
T
m
EI
C
T
o
⋅
⋅
−
α
6254
.
338
m
EI
C
T
o
⋅
⋅
−
α
6695
.
166
VT
2
1090
.
1
m
EI
C
T
o
⋅
⋅
α
2
3186
.
57
m
EI
C
T
o
⋅
⋅
−
α
2
9408
.
96
m
EI
C
T
o
⋅
⋅
α
2
1870
.
78
m
EI
C
T
o
⋅
⋅
α
NT
Rzeczywiste wartości sił przekrojowych mogą też być wyznaczone w wyniku rozwiązania układu
podstawowego od działających równocześnie znanych już sił hiperstatycznych. Wyniki obliczeń
musiałyby być identyczny (w granicach dokładności rachunkowej) jak przedstawione powyżej.
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
12
4.6
KONTROLA POPRAWNOŚCI ROZWIĄZANIA.
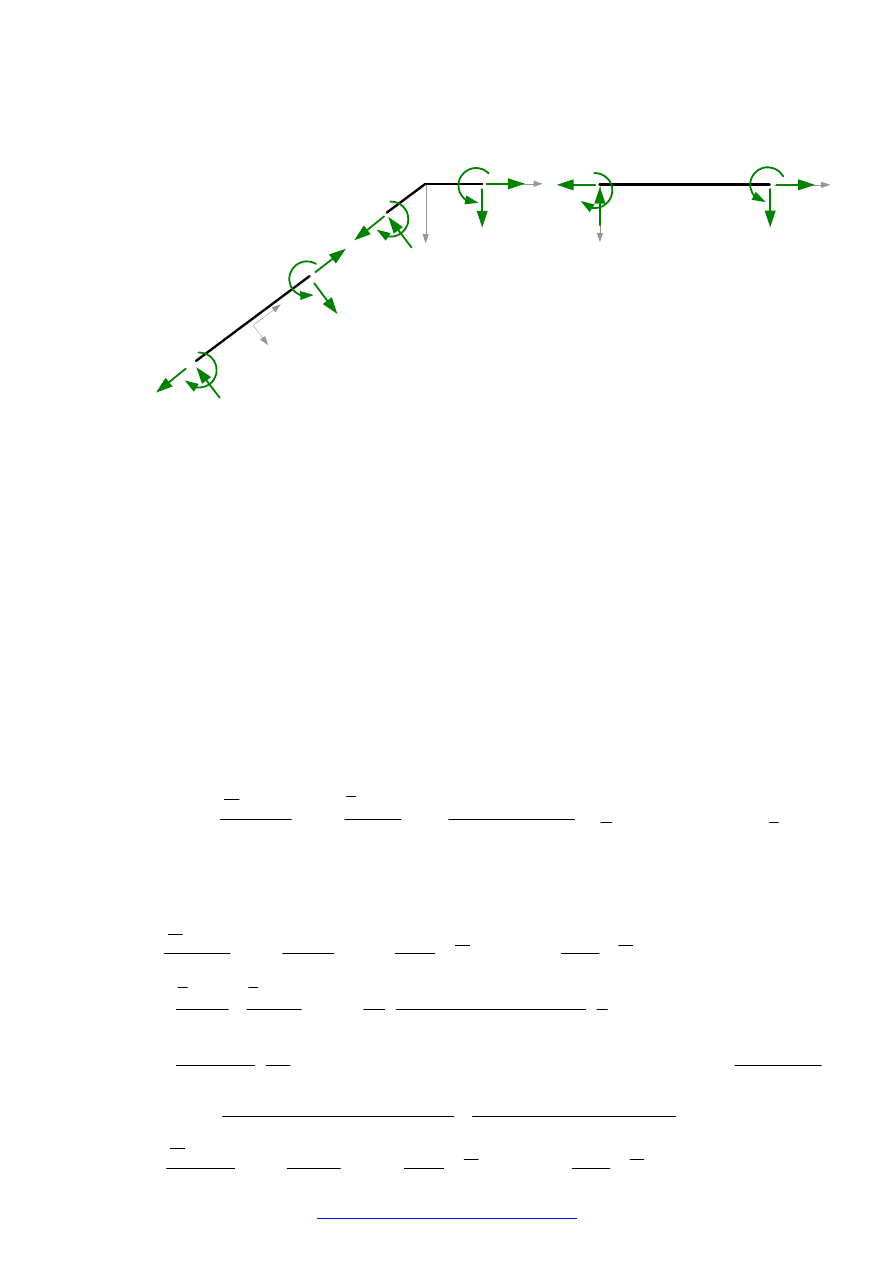
4.6.1
KONTROLA STATYCZNEJ DOPUSZCZALNOŚCI ROZWIĄZANIA
Podział na elementy
Równania równowagi
Dla pręta AC
0
9408
.
96
9408
.
96
=
+
−
=
+
−
=
∑
CA
AC
N
N
X
,
0
0573
.
1
0573
.
1
=
+
−
=
+
−
=
∑
CA
AC
V
V
Y
,
0
5
0573
.
1
2865
.
5
0
5
=
⋅
+
−
=
⋅
+
−
=
∑
m
V
M
M
M
CA
CA
AC
A
Dla węzła C
0
6
.
0
0573
.
1
8
.
0
9408
.
96
1870
.
78
sin
cos
≈
⋅
−
⋅
−
=
⋅
−
⋅
−
=
∑
α
α
CA
CA
CB
V
N
N
X
,
0
8
.
0
0573
.
1
6
.
0
9408
.
96
3186
.
57
cos
sin
≈
⋅
−
⋅
+
−
=
⋅
−
⋅
+
=
∑
α
α
CA
CA
CB
V
N
V
Y
,
0
2865
.
5
2865
.
5
=
−
=
−
=
∑
CD
CA
C
M
M
M
Dla pręta CB
0
1870
.
78
1870
.
78
=
+
−
=
+
−
=
∑
BC
CB
N
N
X
,
0
3186
.
57
3186
.
57
=
+
−
=
+
−
=
∑
BC
CB
V
V
Y
,
0
6
)
3186
.
57
(
)
6254
.
338
(
2865
.
5
6
≈
⋅
−
+
−
−
=
⋅
+
−
=
∑
m
V
M
M
M
BC
BC
CB
C
4.6.2
KONTROLA KINEMATYCZNEJ DOPUSZCZALNOŚCI ROZWIĄZANIA
Wykorzystujemy tu wzór na wyznaczanie przemieszczeń od zmian temperatury
∑
∫
⋅
+
⋅
=
∆
s
s
T
s
s
T
T
k
S
S
dx
EI
M
M
α
α
α
(
)
∑
∑
Ω
⋅
∆
⋅
+
Ω
⋅
∆
−
∆
⋅
+
p
p
N
T
p
p
M
T
To
h
Tp
Tw
α
α
α
α
)
(
Obliczając
T
1
∆
i
T
2
∆
możemy wykorzystać fakt, że suma trzeciego i czwartego członu powyższego
wzoru dla
T
1
∆
wynosi
T
1
δ
a suma trzeciego i czwartego członu powyższego wzoru dla
T
2
∆
wynosi
T
2
δ
, które to wielkości zostały już policzone (p.3.4.2)
+
⋅
⋅
+
⋅
⋅
=
+
⋅
+
⋅
=
∆
∫
∫
∑
∫
dx
M
M
EI
dx
M
M
EI
k
S
S
dx
EI
M
M
CB
T
CB
AC
T
AC
T
s
s
T
s
s
T
T
1
1
1
1
1
1
1
1
δ
+
−
⋅
⋅
⋅
⋅
⋅
=
+
⋅
+
⋅
+
)
4
.
0
(
3
2
2
5
/
2865
.
5
1
1
2
2
1
2
1
1
1
1
m
m
EI
C
EI
k
S
S
k
S
S
T
o
T
T
T
α
δ
(
)
+
⋅
⋅
−
⋅
−
+
−
⋅
−
⋅
+
⋅
−
⋅
⋅
⋅
+
m
EI
C
m
EI
T
o
α
)
6254
.
338
(
)
1
(
)
6695
.
166
(
)
7
.
0
(
4
2865
.
5
4
.
0
6
6
3889
.
1
1
0
1136
.
584
/
1
/
2865
.
5
4
.
0
/
5
.
0
/
3186
.
57
/
1
.
0
3
2
≈
⋅
−
⋅
⋅
⋅
⋅
−
+
⋅
⋅
⋅
⋅
+
T
o
T
o
T
o
C
m
EI
m
EI
C
m
EI
m
EI
C
m
α
α
α
,
+
⋅
⋅
+
⋅
⋅
=
+
⋅
+
⋅
=
∆
∫
∫
∑
∫
dx
M
M
EI
dx
M
M
EI
k
S
S
dx
EI
M
M
CB
T
CB
AC
T
AC
T
s
s
T
s
s
T
T
2
2
2
2
2
2
1
1
δ
A
B
C
D
x
y
x
y
x
y
N
AC
N
CA
N
CA
M
CA
M
AC
V
CA
V
CA
V
AC
V
CD
V
CD
M
CD
V
BD
N
CD
N
CD
N
BD
M
CA
M
CD
M
BD
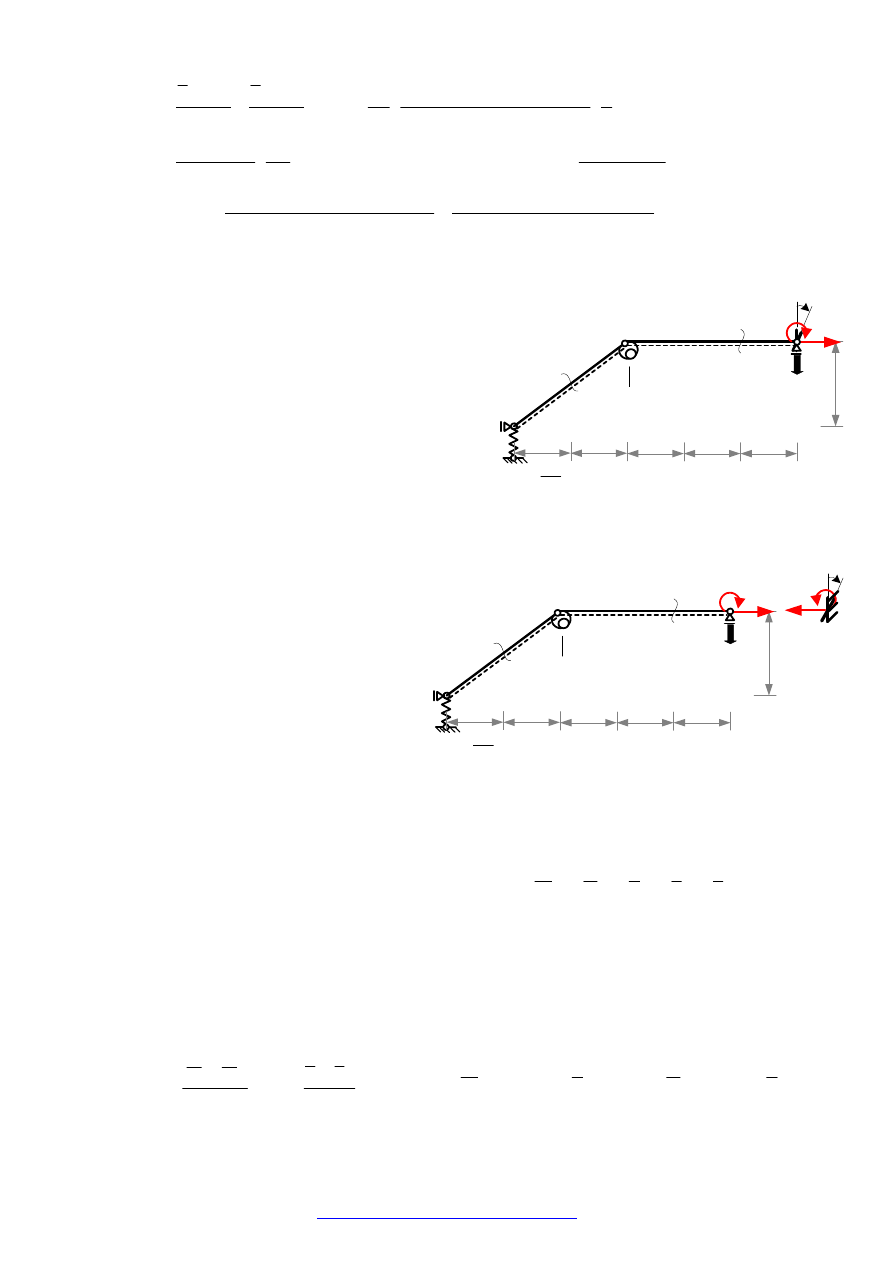
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
13
+
⋅
⋅
⋅
⋅
⋅
⋅
=
+
⋅
+
⋅
+
m
m
m
EI
C
EI
k
S
S
k
S
S
T
o
T
T
T
8
.
1
3
2
2
5
/
2865
.
5
1
2
2
2
2
2
1
1
2
1
α
δ
(
)
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
⋅
⋅
+
m
EI
C
m
m
m
EI
T
o
α
0
6695
.
166
9
.
0
4
2865
.
5
8
.
1
6
6
3889
.
1
1
0
3863
.
365
/
1
/
2865
.
5
8
.
1
/
5
.
0
/
3186
.
57
3
.
0
3
2
≈
⋅
⋅
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
+
T
o
T
o
T
o
m
C
m
EI
m
EI
C
m
m
EI
m
EI
C
α
α
α
.
5
ROZWIĄZANIE RAMY OD PRZEMIESZCZEŃ PODPÓR I BŁĘDÓW MONTAŻU
5.1
UKŁAD PODSTAWOWY I ODPOWIADAJĄCY MU UKŁAD RÓWNAŃ
KANONICZNYCH
5.1.1
UKŁAD PODSTAWOWY
Przyjęto układ podstawowy taki jak dla
rozwiązania od obciążeń siłami, aby móc
wykorzystać w obliczeniach wykonane już
rozwiązania od obciążeń hiperstatycznych
5.1.2
UKŁAD RÓWNAŃ KANONICZNYCH
02618
.
0
180
/
5
.
1
1
1
2
12
1
11
=
⋅
=
∆
=
+
⋅
+
⋅
∆
∆
∆
∆
o
o
rz
X
X
π
δ
δ
δ
,
0
2
2
2
22
1
21
=
∆
=
+
⋅
+
⋅
∆
∆
∆
∆
rz
X
X
δ
δ
δ
UWAGA: Ponieważ usunięto więź podporową (zastępując ją siłą X
1
), w której zadano
przemieszczenie, prawa strona pierwszego równania, to jest przemieszczenie
rzeczywiste w tym miejscu równe jest temu przemieszczeniu.
Jeśli chciałoby się mieć
0
1
=
∆
∆
rz
to należałoby przyjąć układ podstawowy dokonując
przecięcia odpowiednich więzi tak jak na rysunku
obok. W tym przypadku równanie pierwsze
opisywałoby zmianę kąta między przekrojami,
w których przyłożono siły X
1
.
Dalsze obliczenia będą
wykonywane dla układu przyjętego
w punkcie 5.1.1.
5.2
ROZWIĄZANIA UKŁADU PODSTAWOWEGO
5.2.1
ROZWIĄZANIE UKŁADU PODSTAWOWEGO OD PRZEMIESZCZEŃ PODPÓR I
BŁĘDÓW MONTAŻU
Ponieważ układ podstawowy jest układem statycznie wyznaczalnym przemieszczenia podpór i błędy
montażu nie wywołują w nim żadnych sił
0
2
1
=
=
=
=
=
∆
∆
∆
∆
∆
S
S
V
N
M
5.2.2
ROZWIĄZANIE UKŁADU PODSTAWOWEGO OD OBCIĄŻENIA X
1
= 1 I X
2
= 1
Ze względu na to, że przyjęto układ podstawowy analogiczny jak dla rozwiązania od
obciążenia siłami (różne jest tylko obciążenie) rozwiązania układu podstawowego od obciążenia
X
1
= 1 i X
2
= 1 są identyczne jak w punktach 2.3 i 2.4.
5.3
OBLICZENIE WSPÓŁCZYNNIKÓW I ROZWIĄZANIE UKŁADU RÓWNAŃ
5.3.1
OBLICZENIE WSPÓŁCZYNNIKÓW UKŁADU RÓWNAŃ
Współczynniki układu równań obliczamy wykorzystując wzory
∑
∫
⋅
+
⋅
=
s
j
s
i
s
j
i
ij
k
S
S
dx
EI
M
M
δ
,
∑
∑
∑
∑
∆
⋅
−
∆
⋅
+
∆
⋅
+
∆
⋅
=
∆
r
r
i
r
n
n
i
n
v
v
i
v
m
m
i
m
i
R
L
N
h
V
M
ϕ
δ
.
Uwzględniając fakt, że rozwiązania układu podstawowego od obciążenia X
1
= 1 i X
2
= 1 są
identyczne jak w punktach 2.3 i 2.4 współczynniki
11
δ
,
21
12
δ
δ
=
i
22
δ
mają wartości takie jak
obliczono w punkcie 2.5.2. Obliczymy więc tylko współczynniki
∆
1
δ
i
∆
2
δ
.
3
,0
0
m
k
1
= 0.5 EI
L
3
2,00m
2,00m
2,00m
2,00m
2,00m
1
2
∆
r =1cm
∆
r
1
= 1.5
o
EI
1.3889 EI
X
1
X
2
=
1
E
I
m
k
2
3
,0
0
m
k
1
= 0.5 EI
L
3
2,00m
2,00m
2,00m
2,00m
2,00m
1
2
∆
r =1cm
∆
r
1
= 1.5
o
EI
1.3889 EI
X
1
X
2
=
1
E
I
m
k
2
X
1
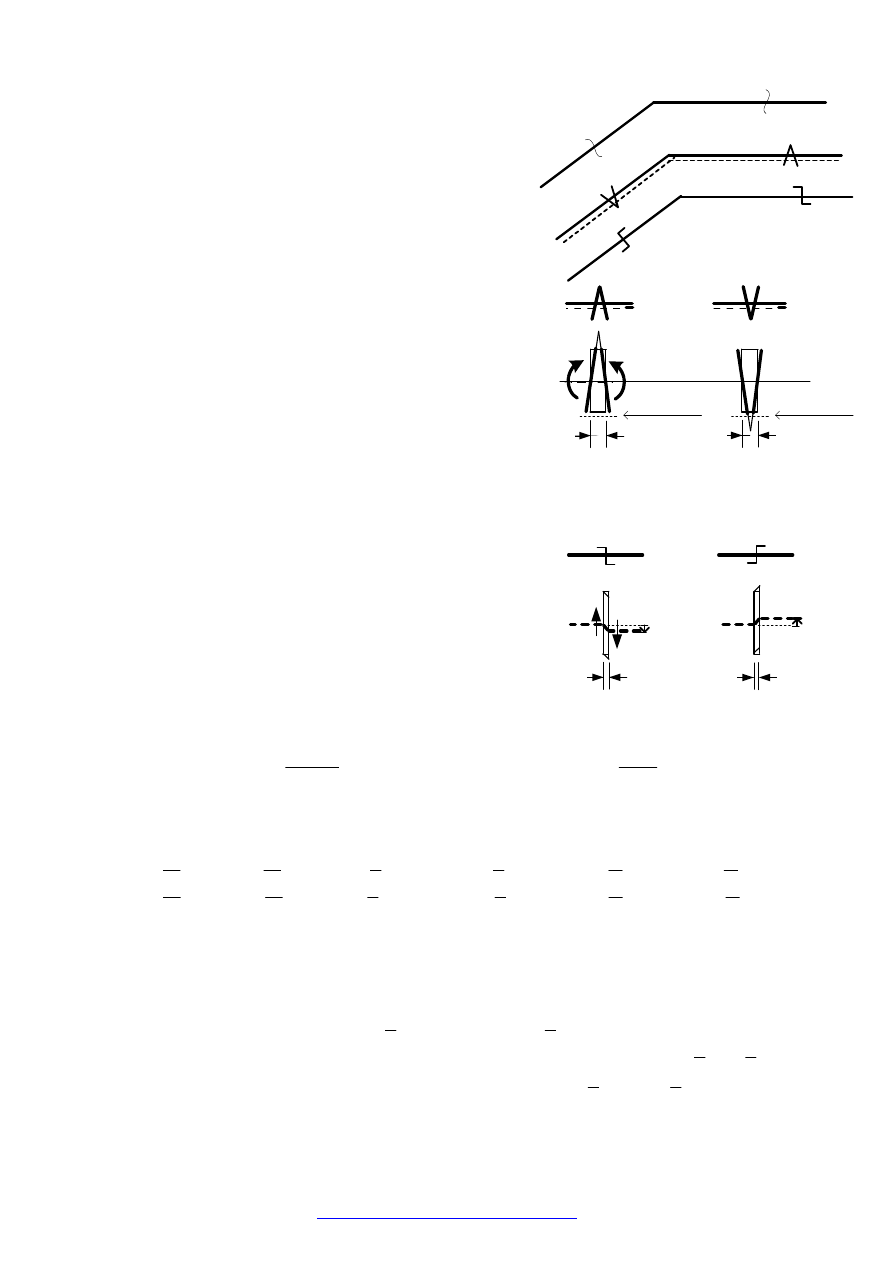
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
14
Błędy montażu wystąpiły w dwóch przekrojach, co
symbolicznie zilustrowano na rysunku obok.
Błędy montażu znakuje się analogicznie jak
odpowiednie siły przekrojowe tzn. zmiany kąta jak
momenty zginające, przesunięcia poprzeczne jak siły
tnące a odkształcenia podłużne jak siły osiowe.
Odkształceniom podłużnym
1
L
∆
i
2
L
∆
przypisano
znaki zgodnie z zasadą: wydłużenie i siła osiowa
rozciągająca „+”, skrócenie i siła osiowa ściskająca „-„.
Symbole odkształceń kątowych ilustrują zmiany kąta
między przekrojami równoległymi, co symbolicznie na osi
pręta i dla elementu odkształconego przedstawiono na
rysunku obok.
Jeśli tej zmianie kąta towarzyszy wydłużenie włókien
wyróżnionych (symbol lewy) to takiej zmianie kąta
przypisujemy znak „+” w przeciwnym przypadku (symbol
prawy) znak „-„.
Wynika stąd, że odkształceniu kątowemu w przekroju „1” należy przypisać znak „-„
a odkształceniu kątowemu w przekroju „2” znak „+”.
Symbole odkształceń postaciowych ilustrują wzajemne poprzeczne przesunięcie osi pręta, co
symbolicznie na osi pręta i dla elementu odkształconego
przedstawiono na rysunku obok
Symbol lewy oznacza deformację h
∆
o zwrocie
zgodnym z dodatnimi zwrotami siły poprzecznej (znak „+”) a
symbol prawy oznacza deformację h
∆
o zwrocie prze-
ciwnym do dodatnich zwrotów siły poprzecznej (znak „-”).
Wynika stąd, że odkształceniu postaciowemu w przekroju
„1” należy przypisać znak „-„
a odkształceniu postaciowemu w przekroju „2” znak „+”.
Wartości błędów montażu są, więc następujące:
02618
.
0
180
5
.
1
5
.
1
1
−
=
⋅
−
=
−
=
∆
o
o
o
π
ϕ
,
0175
.
0
180
1
1
2
=
⋅
=
=
∆
o
o
o
π
ϕ
,
m
cm
h
012
.
0
2
.
1
1
−
=
−
=
∆
,
m
cm
h
014
.
0
4
.
1
2
=
=
∆
,
m
cm
L
015
.
0
5
.
1
1
−
=
−
=
∆
,
m
cm
L
01
.
0
1
2
=
=
∆
Siły przekrojowe od obciążeń jednostkowych, w miejscach błędów, mają wartości
2
.
0
1
1
−
=
M
,
8
.
0
1
2
−
=
M
,
m
V
/
08
.
0
1
1
−
=
,
m
V
/
1
.
0
1
2
−
=
,
m
N
/
06
.
0
1
1
=
,
0
1
2
=
N
,
m
M
9
.
0
2
1
=
,
m
M
6
.
0
2
2
=
,
36
.
0
2
1
=
V
,
3
.
0
2
2
−
=
V
,
98
.
0
2
1
=
N
,
1
2
2
=
N
,
Przemieszczenia podpór wystąpiły w kierunku reakcji
B
V
i kąt obrotu podpory B.
Wynoszą one
m
cm
B
V
01
.
0
1
=
=
∆
,
02618
.
0
180
/
5
.
1
5
.
1
=
⋅
=
=
∆
π
ϕ
o
R
B
.
Zwroty reakcji
B
V
w rozwiązaniach od obciążeń jednostkowych przyjęto przeciwnie do zwrotu
przemieszczenia podpory, więc do obliczania przemieszczeń zmieniamy znaki tej reakcji
m
V
B
/
1
.
0
1
−
=
,
3
.
0
2
−
=
B
V
.
Przyjmując układ podstawowy usunięto więź rotacyjną podpory B, więc
0
2
1
=
=
ϕ
ϕ
B
B
R
R
.
(
Gdyby przyjąć układ podstawowy przytoczony w punkcie 4.1.2 byłoby
1
1
=
ϕ
B
R
,
0
2
=
ϕ
B
R
).
Szukane współczynniki:
+
+
−
⋅
+
⋅
−
−
⋅
−
⋅
−
−
⋅
−
=
∆
0
)
015
.
0
(
/
06
.
0
014
.
0
/
1
.
0
)
012
.
0
(
/
08
.
0
0175
.
0
8
.
0
)
02618
.
0
(
2
.
0
1
m
m
m
m
m
m
δ
009104
.
0
0
01
.
0
)
/
1
.
0
(
−
=
−
⋅
−
−
m
m
,
1.5
o
1
o
1.2
cm
∆
L
2
=1cm
2
∆
L
1
=
-1
.5
cm
1
1.4 cm
dx
włókna
wyró
ż
nione
dx
włókna
wyró
ż
nione
0
<
∆
ϕ
0
>
∆
ϕ
M
M
dx
dx
V
V
0
>
∆
h
0
<
∆
h
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
15
+
⋅
+
−
⋅
+
⋅
−
−
⋅
+
⋅
+
−
⋅
=
∆
m
m
m
m
m
m
01
.
0
1
)
015
.
0
(
98
.
0
014
.
0
3
.
0
)
012
.
0
(
36
.
0
0175
.
0
6
.
0
)
02618
.
0
(
9
.
0
2
δ
m
m
023282
.
0
0
01
.
0
)
3
.
0
(
−
=
−
⋅
−
−
.
(
Gdyby przyjąć układ podstawowy przytoczony w punkcie 4.1.2 byłoby
+
+
−
⋅
+
⋅
−
−
⋅
−
⋅
−
−
⋅
−
=
∆
0
)
015
.
0
(
/
06
.
0
014
.
0
/
1
.
0
)
012
.
0
(
/
08
.
0
0175
.
0
8
.
0
)
02618
.
0
(
2
.
0
1
m
m
m
m
m
m
δ
035284
.
0
02618
.
0
1
01
.
0
)
/
1
.
0
(
−
=
⋅
−
⋅
−
−
m
m
).
5.3.2
POSTAĆ SZCZEGÓŁOWA UKŁADU RÓWNAŃ I JEGO ROZWIĄZANIE
Równanie pierwsze
02618
.
0
009104
.
0
192781
.
4
693049
.
2
2
2
1
=
−
⋅
−
⋅
∆
∆
X
EI
m
X
EI
m
po przekształceniu ma postać
0
035284
.
0
192781
.
4
693049
.
2
2
2
1
=
−
⋅
−
⋅
∆
∆
X
EI
m
X
EI
m
Równanie drugie
0
023282
.
0
485563
.
13
192781
.
4
2
3
1
2
=
−
⋅
+
⋅
−
∆
∆
m
X
EI
m
X
EI
m
Rozwiązanie układu równań
m
EI
X
/
030603
.
0
1
=
∆
,
2
2
/
011241
.
0
m
EI
X
=
∆
.
5.4
OBLICZENIE WARTOŚCI „RZECZYWISTYCH” REAKCJI I SIŁ PRZEKROJOWYCH
∆
∆
∆
∆
+
⋅
+
⋅
=
r
r
r
r
R
X
R
X
R
R
2
2
1
1
,
∆
∆
∆
∆
+
⋅
+
⋅
=
α
α
α
α
M
X
M
X
M
M
2
2
1
1
,
∆
∆
∆
∆
+
⋅
+
⋅
=
α
α
α
α
N
X
N
X
N
N
2
2
1
1
,
∆
∆
∆
∆
+
⋅
+
⋅
=
α
α
α
α
V
X
V
X
V
V
2
2
1
1
∆
∆
∆
∆
+
⋅
+
⋅
=
α
α
α
α
S
X
S
X
S
S
2
2
1
1
=
+
⋅
+
⋅
=
∆
∆
∆
∆
A
A
A
A
H
X
H
X
H
H
2
2
1
1
2
2
/
01124
.
0
0
/
011241
.
0
)
1
(
0
m
EI
m
EI
−
=
+
⋅
−
+
=
+
⋅
+
⋅
=
∆
∆
∆
∆
A
A
A
A
V
X
V
X
V
V
2
2
1
1
2
2
006433
.
0
0
011241
.
0
)
3
.
0
(
030603
.
0
1
.
0
m
EI
m
EI
m
EI
m
−
=
+
⋅
−
+
⋅
−
=
+
⋅
+
⋅
=
∆
∆
∆
∆
B
B
B
B
V
X
V
X
V
V
2
2
1
1
2
2
/
006433
.
0
0
/
011241
.
0
3
.
0
/
030603
.
0
/
1
.
0
m
EI
m
EI
m
EI
m
=
+
⋅
+
⋅
=
+
⋅
+
⋅
=
∆
∆
∆
∆
CA
CA
CA
CA
M
X
M
X
M
M
2
2
1
1
m
EI
m
EI
m
m
EI
007993
.
0
0
011241
.
0
8
.
1
030603
.
0
4
.
0
2
=
+
⋅
+
⋅
−
∆
∆
=
CA
CB
M
M
=
+
⋅
+
⋅
=
∆
∆
∆
∆
BC
BC
BC
BC
M
X
M
X
M
M
2
2
1
1
m
EI
m
EI
/
03060
.
0
0
0
/
030603
.
0
1
−
=
+
+
⋅
−
=
+
⋅
+
⋅
=
∆
∆
∆
∆
AC
AC
AC
AC
V
X
V
X
V
V
2
2
1
1
2
2
001599
.
0
0
011241
.
0
36
.
0
030603
.
0
08
.
0
m
EI
m
EI
m
EI
m
=
+
⋅
+
⋅
−
∆
∆
=
AC
CA
V
V
=
+
⋅
+
⋅
=
∆
∆
∆
∆
CB
CB
CB
CB
V
X
V
X
V
V
2
2
1
1
2
2
006433
.
0
0
011241
.
0
)
3
.
0
(
030603
.
0
1
.
0
m
EI
m
EI
m
EI
m
−
=
+
⋅
−
+
⋅
−
∆
∆
=
CB
BC
V
V
=
+
⋅
+
⋅
=
∆
∆
∆
∆
AC
AC
AC
AC
N
X
N
X
N
N
2
2
1
1
2
2
01285
.
0
0
011241
.
0
98
.
0
030603
.
0
06
.
0
m
EI
m
EI
m
EI
m
=
+
⋅
+
⋅
−
∆
∆
=
AC
CA
N
N
=
+
⋅
+
⋅
=
∆
∆
∆
∆
CB
CB
CB
CB
N
X
N
X
N
N
2
2
1
1
2
2
/
01124
.
0
0
/
011241
.
0
1
0
m
EI
m
EI
=
+
⋅
+
∆
∆
=
CB
BC
N
N
=
+
⋅
+
⋅
=
∆
∆
∆
∆
1
2
2
1
1
1
1
1
S
X
S
X
S
S
2
2
/
006433
.
0
0
/
011241
.
0
3
.
0
/
030603
.
0
/
1
.
0
m
EI
m
EI
m
EI
m
=
+
⋅
+
⋅
=
+
⋅
+
⋅
=
∆
∆
∆
∆
2
2
2
2
1
1
2
2
S
X
S
X
S
S
m
EI
m
EI
m
m
EI
/
007993
.
0
0
/
011241
.
0
8
.
1
/
030603
.
0
4
.
0
2
=
+
⋅
+
⋅
−
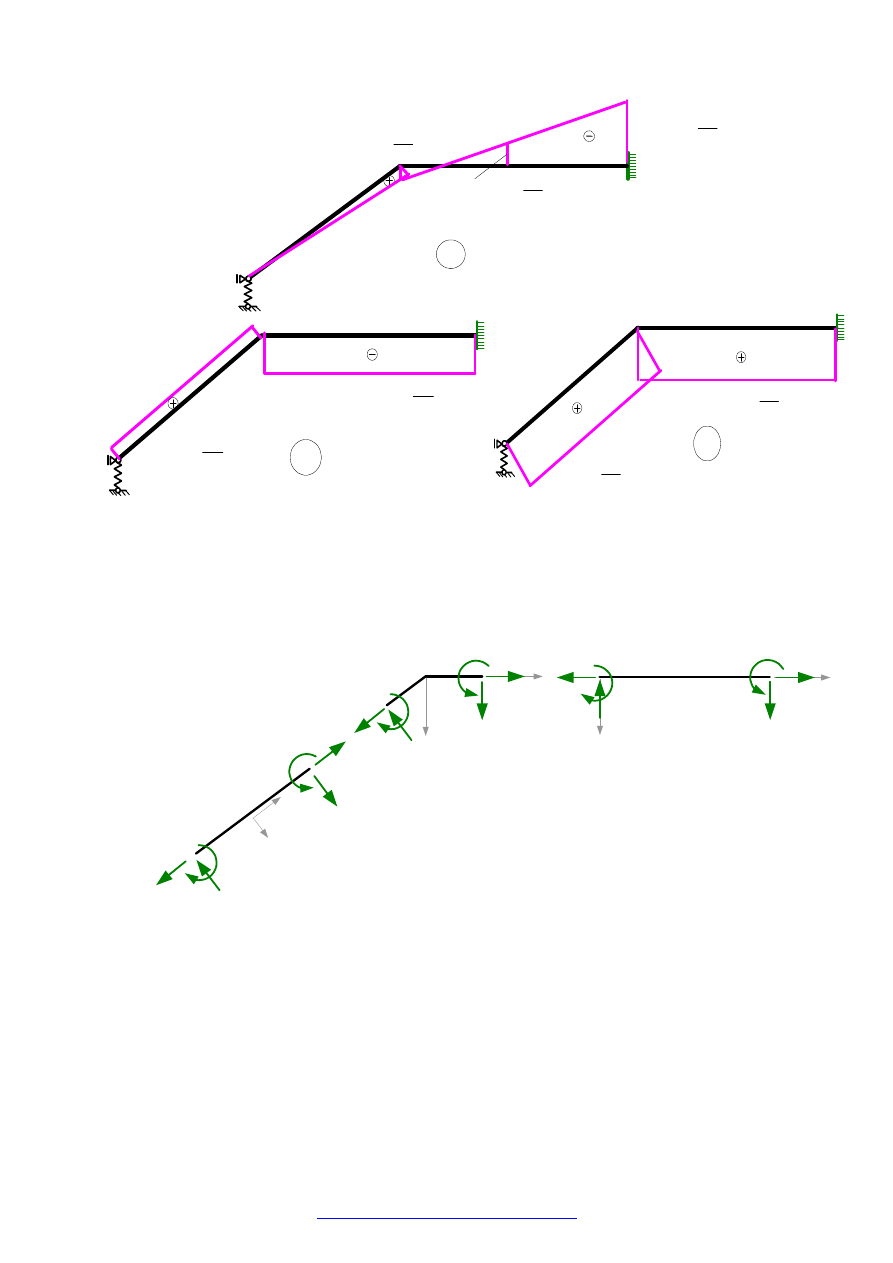
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
16
5.5
WYKRESY „RZECZYWISTYCH” SIŁ PRZEKROJOWYCH
m
EI
007993
.
0
M
∆∆∆∆
m
EI
03060
.
0
−
m
EI
01131
.
0
−
V
∆∆∆∆
2
001599
.
0
m
EI
2
006433
.
0
m
EI
−
N
∆∆∆∆
2
01285
.
0
m
EI
2
01124
.
0
m
EI
Rzeczywiste wartości sił przekrojowych mogą też być wyznaczone w wyniku rozwiązania układu
podstawowego od działających równocześnie znanych już sił hiperstatycznych. Wyniki obliczeń
musiałyby być identyczny (w granicach dokładności rachunkowej) jak przedstawione powyżej.
5.6
KONTROLA POPRAWNOŚCI ROZWIĄZANIA.
5.6.1
KONTROLA STATYCZNEJ DOPUSZCZALNOŚCI ROZWIĄZANIA
Podział na elementy
Równania równowagi
Dla pręta AC
0
011285
.
0
01285
.
0
=
+
−
=
+
−
=
∑
CA
AC
N
N
X
,
0
001599
.
0
001599
.
0
=
+
−
=
+
−
=
∑
CA
AC
V
V
Y
,
0
5
001599
.
0
007993
.
0
0
5
≈
⋅
+
−
=
⋅
+
−
=
∑
m
V
M
M
M
CA
CA
AC
A
Dla węzła C
0
6
.
0
001599
.
0
8
.
0
01285
.
0
01124
.
0
sin
cos
≈
⋅
−
⋅
−
=
⋅
−
⋅
−
=
∑
α
α
CA
CA
CB
V
N
N
X
,
0
8
.
0
01285
.
0
6
.
0
01124
.
0
006433
.
0
cos
sin
≈
⋅
−
⋅
+
−
=
⋅
−
⋅
+
=
∑
α
α
CA
CA
CB
V
N
V
Y
,
0
007993
.
0
007993
.
0
=
−
=
−
=
∑
CD
CA
C
M
M
M
Dla pręta CB
0
01124
.
0
01124
.
0
=
+
−
=
+
−
=
∑
BC
CB
N
N
X
,
A
B
C
D
x
y
x
y
x
y
N
AC
N
CA
N
CA
M
CA
M
AC
V
CA
V
CA
V
AC
V
CD
V
CD
M
CD
V
BD
N
CD
N
CD
N
BD
M
CA
M
CD
M
BD
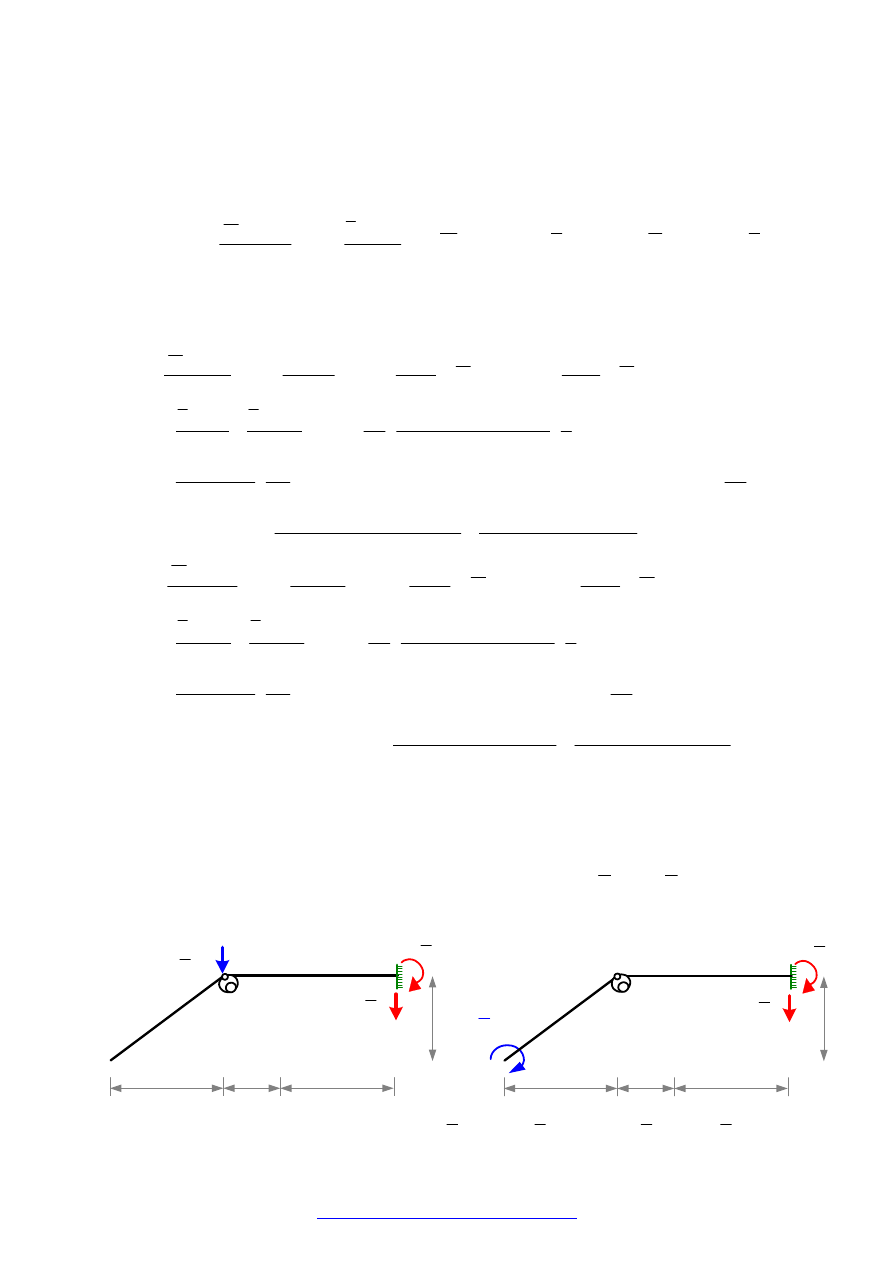
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
17
0
006433
.
0
)
006433
.
0
(
=
−
−
−
=
+
−
=
∑
BC
CB
V
V
Y
,
0
6
)
006433
.
0
(
)
03060
.
0
(
007993
.
0
6
≈
⋅
−
+
−
−
=
⋅
+
−
=
∑
m
V
M
M
M
BC
BC
CB
C
5.6.2
KONTROLA KINEMATYCZNEJ ZGODNOŚCI ROZWIĄZANIA
Wykorzystujemy tu wzór na wyznaczanie przemieszczeń od przemieszczeń podpór i błędów
montażu.
∑
∫
∆
∆
∆
⋅
+
⋅
=
∆
s
s
s
s
k
S
S
dx
EI
M
M
α
α
α
∑
∑
∑
∑
∆
⋅
−
∆
⋅
+
∆
⋅
+
∆
⋅
+
r
r
r
n
n
v
v
v
m
m
m
R
L
N
h
V
M
α
α
α
α
ϕ
.
Obliczając
∆
∆
1
i
∆
∆
2
możemy wykorzystać fakt, że człony: trzeci, czwarty, piąty i szósty powyższego
wzoru dla
∆
∆
1
równe są razem
∆
1
δ
a człony trzeci, czwarty, piąty i szósty powyższego wzoru dla
∆
∆
2
równe są razem
∆
2
δ
, które to wielkości zostały już policzone (p.4.4.1)
+
⋅
⋅
+
⋅
⋅
=
+
⋅
+
⋅
=
∆
∫
∫
∑
∫
∆
∆
∆
∆
∆
∆
dx
M
M
EI
dx
M
M
EI
k
S
S
dx
EI
M
M
CB
CB
AC
AC
s
s
s
s
1
1
1
1
1
1
1
1
δ
+
−
⋅
⋅
⋅
⋅
=
+
⋅
+
⋅
+
∆
∆
)
4
.
0
(
3
2
2
5
/
007993
.
0
1
1
2
2
1
2
1
1
1
1
m
m
EI
EI
k
S
S
k
S
S
T
δ
(
)
+
−
⋅
−
+
−
⋅
−
⋅
+
⋅
−
⋅
⋅
⋅
+
m
EI
m
EI
)
0306
.
0
(
)
1
(
)
01131
.
0
(
)
7
.
0
(
4
007993
.
0
4
.
0
6
6
3889
.
1
1
02618
.
0
009104
.
0
/
1
/
007993
.
0
4
.
0
/
5
.
0
/
006433
.
0
/
1
.
0
1
3
2
=
∆
≈
−
⋅
⋅
−
+
⋅
⋅
⋅
+
∆
rz
m
EI
m
EI
m
EI
m
EI
m
+
⋅
⋅
+
⋅
⋅
=
+
⋅
+
⋅
=
∆
∫
∫
∑
∫
∆
∆
∆
∆
∆
∆
dx
M
M
EI
dx
M
M
EI
k
S
S
dx
EI
M
M
CB
CB
AC
AC
s
s
s
s
2
2
2
2
2
2
1
1
δ
+
⋅
⋅
⋅
⋅
⋅
=
+
⋅
+
⋅
+
∆
∆
∆
m
m
m
EI
EI
k
S
S
k
S
S
8
.
1
3
2
2
5
/
007993
.
0
1
2
2
2
2
2
1
1
2
1
δ
(
)
+
+
−
⋅
⋅
+
⋅
⋅
⋅
⋅
+
m
EI
m
m
m
EI
0
)
01131
.
0
(
9
.
0
4
007993
.
0
8
.
1
6
6
3889
.
1
1
0
02328
.
0
/
1
/
007993
.
0
8
.
1
/
5
.
0
/
006433
.
0
3
.
0
3
2
≈
−
⋅
⋅
+
⋅
⋅
⋅
+
m
m
EI
m
EI
m
m
EI
m
EI
6
WYZNACZENIE SZUKANYCH PRZEMIESZCZEŃ
6.1
ROZWIĄZANIA WIRTUALNE OD OBCIĄŻEŃ JEDNOSTKOWYCH
Uwzględniając fakt, że układy zostały rozwiązane od danych obciążeń, w celu obliczenia
szukanych przemieszczeń należy uzyskać rozwiązania wirtualne od obciążeń jednostkowych
przyłożonych w miejscach i kierunkach szukanych przemieszczeń. Rozwiązania te otrzymamy
rozwiązując dowolne układy podstawowe danej ramy od obciążeń
1
=
i
F
i
1
=
j
F
. Może to być taki
sam układ, jaki był przyjęty do rozwiązania ramy od obciążenia danego. Mogą też być dowolne inne
układy. Tu przyjęto układy jak na rysunkach poniżej.
4,00m
2,00m
4,00m
3
,0
0
m
EI
1.3889 EI
F
i
=1
V
B
i
R
B
i
ϕ
4,00m
2,00m
4,00m
3
,0
0
m
EI
1.3889 EI
F
j
=1
V
B
j
R
B
j
ϕ
Reakcje w miejscach przemieszczeń podpór :
1
−
=
i
B
V
,
m
R
i
B
6
=
ϕ
,
0
=
i
B
V
,
1
−
=
i
B
R
ϕ
.
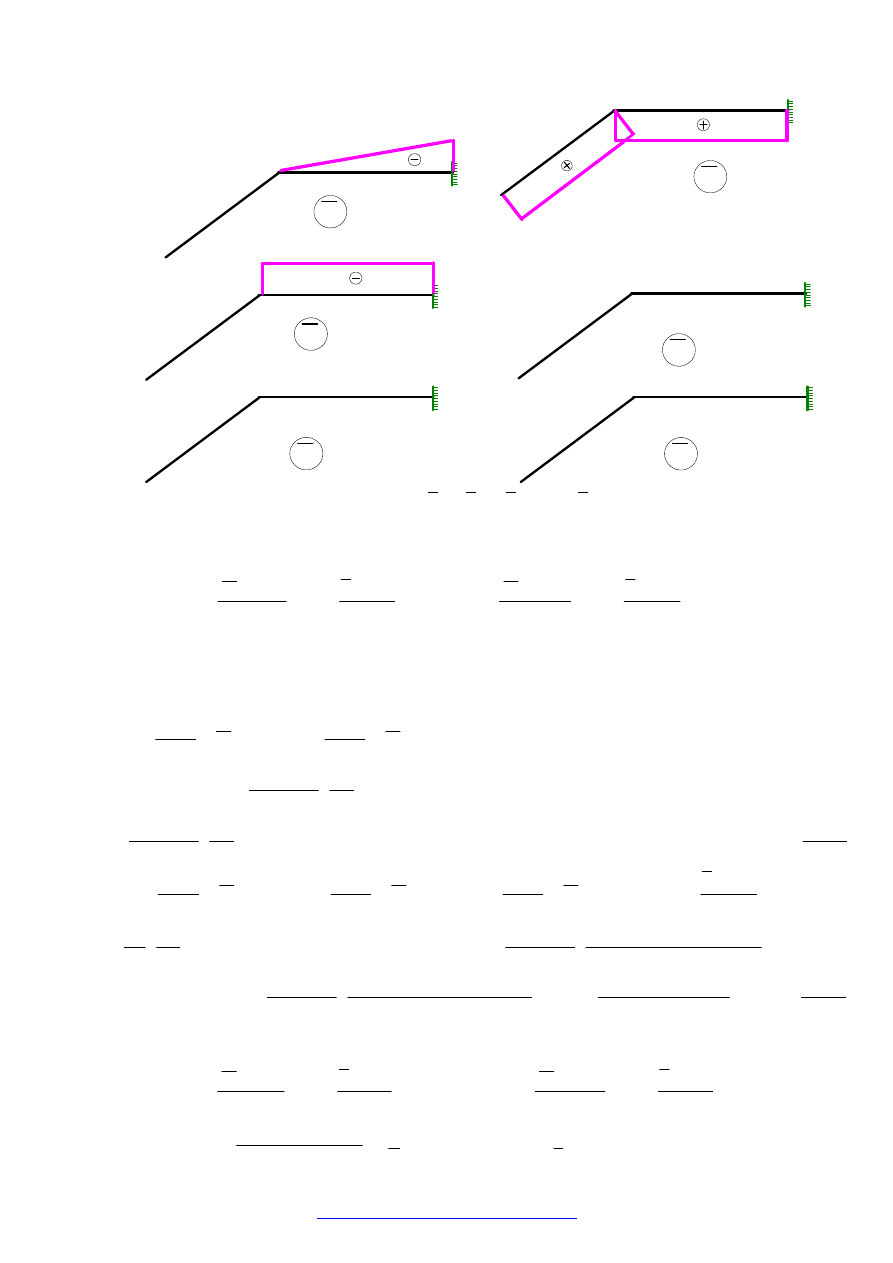
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
18
Wykresy sił przekrojowych
6
m
M
i
1,0
00
M
j
1,0
00
1
,0
0
0
1
,0
0
0
1
V
i
N
i
V
j
N
j
Siły w więziach sprężystych
0
2
1
1
=
=
=
i
j
i
S
S
S
,
1
2
=
j
S
.
6.2
PRZEMIESZCZENIA OD OBCIĄŻEŃ SIŁAMI
Szukane przemieszczenia obliczymy na podstawie wzorów
∑
∫
⋅
+
⋅
=
∆
s
s
F
s
i
s
F
i
iF
k
S
S
dx
EI
M
M
,
∑
∫
⋅
+
⋅
=
∆
s
s
F
s
j
s
F
j
jF
k
S
S
dx
EI
M
M
.
Do obliczenia całek w powyższych wzorach zastosowano wzór Simpsona lub Mohra. Ze względu na
charakter wykresów momentów zginających całki w powyższych wzorach przedstawiono w postaci
sum 3 całek odpowiadających przedziałom całkowania, w których funkcje podcałkowe spełniają
założenia umożliwiające zastosowanie odpowiedniego wzoru.
=
+
⋅
⋅
+
⋅
⋅
=
∆
∫
∫
0
1
1
dx
M
M
EI
dx
M
M
EI
DB
F
i
DB
CD
F
i
CD
iF
(
)
+
⋅
−
+
⋅
−
⋅
+
⋅
⋅
=
kNm
m
kNm
m
m
EI
172
.
22
)
2
(
209
.
13
)
1
(
4
0
6
2
3889
.
1
1
(
)
EI
kNm
kNm
m
kNm
m
kNm
m
m
EI
3
9264
.
17
)
975
.
21
(
)
6
(
098
.
0
)
4
(
4
172
.
22
2
6
4
3889
.
1
1
=
−
⋅
−
+
⋅
−
⋅
+
⋅
−
⋅
⋅
+
(
)
+
⋅
⋅
+
⋅
+
−
⋅
+
⋅
⋅
+
⋅
⋅
⋅
=
=
⋅
+
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
∆
∫
∫
∫
1
2
2
172
.
22
246
.
4
3889
.
1
1
)
754
.
10
(
1
248
.
0
1
4
0
1
6
5
1
0
1
1
1
2
2
2
m
kNm
kNm
EI
kNm
kNm
m
EI
k
S
S
dx
M
M
EI
dx
M
M
EI
dx
M
M
EI
F
j
DB
F
j
DB
CD
F
j
CD
AC
F
j
AC
jF
EI
kNm
m
EI
kNm
m
kNm
kNm
EI
2
4130
.
0
/
1
)
7544
.
10
(
1
1
4
2
975
.
21
172
.
22
3889
.
1
1
=
−
⋅
+
⋅
⋅
−
⋅
+
6.3
PRZEMIESZCZENIA OD ZMIAN TEMPERATURY
Szukane przemieszczenia policzymy na podstawie wzorów
iT
s
s
T
s
i
s
T
i
iT
k
S
S
dx
EI
M
M
δ
+
⋅
+
⋅
=
∆
∑
∫
,
jT
s
s
T
s
j
s
T
j
jT
k
S
S
dx
EI
M
M
δ
+
⋅
+
⋅
=
∆
∑
∫
gdzie
(
)
∑
∑
Ω
⋅
∆
⋅
+
Ω
⋅
∆
−
∆
⋅
=
p
p
N
T
p
p
M
T
iT
i
i
To
h
Tp
Tw
α
α
δ
)
(
,

METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
19
(
)
∑
∑
Ω
⋅
∆
⋅
+
Ω
⋅
∆
−
∆
⋅
=
p
p
N
T
p
p
M
T
jT
j
j
To
h
Tp
Tw
α
α
δ
)
(
.
Ze względu na charakter wykresów momentów zginających całki w powyższych wzorach
przedstawiono w postaci sum 2 całek odpowiadających przedziałom całkowania, w których funkcje
podcałkowe spełniają założenia umożliwiające zastosowanie odpowiedniego wzoru.
Obliczenia rozpoczniemy od wyznaczenia składników
iT
δ
,
jT
δ
Pręt AC
0
=
Ω
i
M
,
m
m
j
M
5
5
1
=
⋅
=
Ω
,
0
=
Ω
i
N
,
0
=
Ω
j
N
,
C
Tw
o
5
−
=
∆
,
C
Tp
o
20
=
∆
,
C
Tp
Tw
To
o
5
.
7
2
20
5
2
=
+
−
=
∆
+
∆
=
∆
(przekrój symetryczny),
m
m
h
22
.
0
5
044
.
0
=
⋅
=
,
h
Tp
Tw
∆
−
∆
m
C
m
C
o
o
636
.
113
22
.
0
)
20
5
(
−
=
−
−
=
,
i
M
T
AC
iT
h
Tp
Tw
Ω
⋅
∆
−
∆
⋅
=
)
(
)
(
α
δ
+
0
=
Ω
⋅
∆
⋅
i
N
T
To
α
,
j
M
T
AC
jT
h
Tp
Tw
Ω
⋅
∆
−
∆
⋅
=
)
(
)
(
α
δ
+
=
Ω
⋅
∆
⋅
j
N
T
To
α
(
)
T
o
o
T
C
m
m
C
α
α
⋅
−
=
+
⋅
−
⋅
1818
.
568
0
5
/
636
.
113
Dla pręta CB
2
18
2
/
6
6
m
m
m
i
M
−
=
⋅
−
=
Ω
,
m
m
j
M
6
6
1
=
⋅
=
Ω
,
0
=
Ω
i
N
,
0
=
Ω
j
N
,
C
Tw
o
10
=
∆
,
C
Tp
o
30
−
=
∆
,
C
To
o
10
2
30
10
−
=
−
=
∆
(przekrój symetryczny),
m
m
h
24
.
0
6
04
.
0
=
⋅
=
,
h
Tp
Tw
)
(
∆
−
∆
m
C
m
C
o
o
6667
.
166
24
.
0
))
30
(
10
(
=
−
−
=
,
i
M
T
CB
iT
h
Tp
Tw
Ω
⋅
∆
−
∆
⋅
=
)
(
)
(
α
δ
+
i
N
T
To
Ω
⋅
∆
⋅
α
=
(
)
T
o
o
T
m
C
m
m
C
α
α
⋅
⋅
−
=
+
−
⋅
⋅
=
3000
0
)
18
(
/
6667
.
166
2
,
j
M
T
CB
jT
h
Tp
Tw
Ω
⋅
∆
−
∆
⋅
=
)
(
)
(
α
δ
+
=
Ω
⋅
∆
⋅
j
N
T
To
α
(
)
T
o
o
T
C
m
m
C
α
α
⋅
=
+
⋅
⋅
1000
0
6
/
6667
.
166
T
o
T
o
iT
m
C
m
C
α
α
δ
⋅
⋅
−
=
⋅
⋅
−
=
3000
)
3000
0
(
,
T
o
T
o
jT
C
C
α
α
δ
⋅
=
⋅
+
−
=
8182
.
431
)
1000
1818
.
568
(
.
Szukane przemieszczenia
+
⋅
⋅
+
⋅
⋅
=
+
⋅
+
⋅
=
∆
∫
∫
∑
∫
dx
M
M
EI
dx
M
M
EI
k
S
S
dx
EI
M
M
CB
T
i
CB
AC
T
i
AC
T
s
s
T
s
i
s
T
i
iT
1
1
1
δ
=
+
⋅
+
⋅
+
iT
T
i
T
i
k
S
S
k
S
S
δ
2
2
2
1
1
1
(
)
+
+
⋅
⋅
−
⋅
−
+
−
⋅
−
⋅
+
⋅
⋅
⋅
+
=
0
)
6254
.
338
(
)
6
(
)
6695
.
166
(
)
3
(
4
0
6
6
3889
.
1
1
0
m
EI
C
m
m
m
EI
T
o
α
m
C
m
C
T
o
T
o
⋅
⋅
−
=
⋅
⋅
−
α
α
1373
.
97
3000
,
+
⋅
⋅
+
⋅
⋅
=
+
⋅
+
⋅
=
∆
∫
∫
∑
∫
dx
M
M
EI
dx
M
M
EI
k
S
S
dx
EI
M
M
CB
T
j
CB
AC
T
j
AC
T
s
s
T
s
j
s
T
j
jT
1
1
2
δ
+
⋅
⋅
⋅
⋅
⋅
=
+
⋅
+
⋅
+
1
2
5
/
2865
.
5
1
2
2
1
1
1
m
m
EI
C
EI
k
S
j
S
k
S
S
T
o
jT
T
T
j
α
δ
(
)
+
+
⋅
⋅
−
⋅
+
−
⋅
⋅
+
⋅
⋅
⋅
⋅
+
0
)
6254
.
338
(
1
)
6695
.
166
(
1
4
2865
.
5
1
6
6
3889
.
1
1
m
EI
C
m
EI
T
o
α
T
o
T
o
T
o
C
C
m
EI
m
EI
C
α
α
α
⋅
−
=
⋅
+
⋅
⋅
⋅
+
6855
.
269
8182
.
431
/
1
/
2865
.
5
1
METODA SIŁ - przykład 2-siły, zmiany temperatury, przemieszczenia podpór i błędy montażu 26-03-09
http://www.iil.pwr.wroc.pl/zukowski
20
6.4
PRZEMIESZCZENIA OD PRZEMIESZCZEŃ PODPÓR I BŁĘDÓW MONTAŻU
Szukane przemieszczenia policzymy na podstawie wzorów
∑
∫
∆
∆
∆
∆
+
⋅
+
⋅
=
∆
s
i
s
s
i
s
i
i
k
S
S
dx
EI
M
M
δ
,
∆
∆
∆
∆
+
⋅
+
⋅
=
∆
∑
∫
j
s
s
s
j
s
j
j
k
S
S
dx
EI
M
M
δ
gdzie
∑
∑
∑
∑
∆
⋅
−
∆
⋅
+
∆
⋅
+
∆
⋅
=
∆
r
r
i
r
n
n
i
n
v
v
i
v
m
m
i
m
i
R
L
N
h
V
M
ϕ
δ
,
∑
∑
∑
∑
∆
⋅
−
∆
⋅
+
∆
⋅
+
∆
⋅
=
∆
r
r
j
r
n
n
j
n
v
v
j
v
m
m
j
m
j
R
L
N
h
V
M
ϕ
δ
Ze względu na charakter wykresów momentów zginających całki w powyższych wzorach
przedstawiono w postaci sum 2 całek odpowiadających przedziałom całkowania, w których funkcje
podcałkowe spełniają założenia umożliwiające zastosowanie odpowiedniego wzoru.
Błędy montażu scharakteryzowane w punkcie 4.4.1 wynoszą:
02618
.
0
180
5
.
1
5
.
1
1
−
=
⋅
−
=
−
=
∆
o
o
o
π
ϕ
,
0175
.
0
180
1
1
2
=
⋅
=
=
∆
o
o
o
π
ϕ
,
m
cm
h
012
.
0
2
.
1
1
−
=
−
=
∆
,
m
cm
h
014
.
0
4
.
1
2
=
=
∆
,
m
cm
L
015
.
0
5
.
1
1
−
=
−
=
∆
,
m
cm
L
01
.
0
1
2
=
=
∆
Siły przekrojowe od obciążeń jednostkowych, w miejscach błędów, mają wartości
0
1
=
i
M
,
m
M
i
4
2
−
=
,
0
1
=
i
V
,
1
2
−
=
i
V
,
0
1
=
i
N
,
0
2
=
i
N
,
1
1
=
j
M
,
1
1
2
=
M
,
0
2
1
=
V
,
0
2
2
=
V
,
0
2
1
=
N
,
0
2
2
=
N
,
Przemieszczenia podpór wystąpiły w kierunku reakcji
B
V
i kąt obrotu podpory B.
Wynoszą one
m
cm
B
V
01
.
0
1
=
=
∆
,
02618
.
0
180
/
5
.
1
5
.
1
1
=
⋅
=
=
∆
π
o
r
.
Wartości reakcji odpowiadających tym przemieszczeniom wywołane obciążeniami jednostkowymi
wynoszą
1
−
=
i
B
V
,
m
R
i
B
6
=
ϕ
,
0
=
j
B
V
,
1
−
=
j
B
R
ϕ
.
m
m
m
m
i
23108
.
0
02618
.
0
6
01
.
0
)
1
(
0
0
014
.
0
1
0
0175
.
0
4
0
−
=
⋅
−
⋅
−
−
+
+
⋅
−
+
⋅
−
=
∆
δ
,
0175
.
0
02618
.
0
)
1
(
0
0
0
0
0
0175
.
0
1
)
02618
.
0
(
1
=
⋅
−
−
−
+
+
+
+
⋅
+
−
⋅
=
∆
j
δ
.
+
⋅
⋅
+
⋅
⋅
=
+
⋅
+
⋅
=
∆
∫
∫
∑
∫
∆
∆
∆
∆
∆
∆
dx
M
M
EI
dx
M
M
EI
k
S
S
dx
EI
M
M
CB
i
CB
AC
i
AC
i
s
s
s
i
s
i
i
1
1
δ
=
+
⋅
+
⋅
+
∆
∆
∆
i
i
i
k
S
S
k
S
S
δ
2
2
2
1
1
1
(
)
m
m
m
EI
m
m
m
EI
0012
.
0
23108
.
0
0
)
0306
.
0
(
)
6
(
)
01131
.
0
(
)
3
(
4
0
6
6
3889
.
1
1
0
−
=
−
+
−
⋅
−
+
−
⋅
−
⋅
+
⋅
⋅
⋅
+
=
,
+
⋅
⋅
+
⋅
⋅
=
+
⋅
+
⋅
=
∆
∫
∫
∑
∫
∆
∆
∆
∆
∆
∆
dx
M
M
EI
dx
M
M
EI
k
S
S
dx
EI
M
M
CB
j
CB
AC
j
AC
s
s
s
j
s
j
j
1
1
2
δ
+
⋅
⋅
⋅
⋅
=
+
⋅
+
⋅
+
∆
∆
∆
1
2
5
/
007993
.
0
1
2
2
1
1
1
m
m
EI
EI
k
S
j
S
k
S
S
T
j
δ
(
)
=
+
⋅
+
+
−
⋅
+
−
⋅
⋅
+
⋅
⋅
⋅
⋅
+
0175
.
0
/
1
/
007993
.
0
1
0
)
0306
.
0
(
1
)
01131
.
0
(
1
4
007993
.
0
1
6
6
3889
.
1
1
m
EI
m
EI
m
EI
m
EI
o
o
19
.
0
/
180
*
003363
.
0
003363
.
0
−
=
−
=
−
=
π
.
Wyszukiwarka
Podobne podstrony:
NiSHiP spr lab2 MS i MT id 3201 Nieznany
Projekty LW przyk2 id 661366 Nieznany
Belka MS id 82485 Nieznany (2)
4 MS lect5 mo id 37217 Nieznany (2)
MS lect6 mo id 309495 Nieznany
LC MS Lek a srodowisko id 26394 Nieznany
MS powerpoint2007 cz3 id 309477 Nieznany
Belka MS id 82485 Nieznany (2)
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
więcej podobnych podstron