1

MATLAB – Podstawowe informacje

Wersja nr: 1
Przygotował: Łukasz Hirt

Uwagi wstępne



Jeżeli nie chcemy żeby struktura zawarta w danej zmiennej nie wyświetliła się w Command Window, na końcu
linii w naszym skrypcie wstawiamy średnik ;

A = 3

Zostanie wyświetlone

A = 3;

Nie zostanie wyświetlone

Kiedy nasz skrypt będzie już w pełni gotowy i jego celem samym w sobie nie jest wyświetlanie żadnych
informacji, zaleca się komentowanie wszystkich linii. Możemy ich nie komentować w trakcie tworzenia skryptu,
kiedy chcemy na bieżąco sprawdzać przepływ informacji w naszym kodzie.



Wszystkie słowa kluczowe (tj. takie słowa, które są zarezerwowane dla Matlaba i nie możemy ich używać) mają
kolor niebieski. Należ do nich m.in. nazwy typu: if, end, function itp.



Jeżeli kiedykolwiek zdarzy się, że nasz kod/skrypt się „zawiesi” – co możemy stwierdzić poprzez brak aktywnego
znaku w Command Window, to naciskając (czasami do skutku) połączenie klawiszy powinniśmy
przerwać działanie kodu.



Komentarz wstawiamy po znaku %, skomentowane zostanie wszystko od znaku do końca linii. Jeżeli szybko
chcemy skomentować większą część kodu możemy użyć skrótu klawiszowego , żeby w podobny sposób
pozbyć się komentarza używamy skrótu .

A = 3;

% to jest komentarz

Komentarz za definicją zmiennej

% To też jest komentarz

A = 3;

Komentarz zdeklarowany sam w linii



Możemy kontynuować definicję zmiennej w nowej linii używając operatora przejścia, którym w Matlabie są trzy
kropki. W oknie Matlaba powinny one automatycznie zmienić kolor na niebieski.

A = [1 2 3 4 5 6]

Te dwa polecenia są sobie równoważne!

Kropki nie muszą być podane bezpośrednio po ostatnim znaku linii!

A = [1 2 3

...

4 5 6]



W niniejszym opisie nazwy tablica oraz macierz będą oznaczały tą samą strukturę. Wektorem będziemy nazywali
tablicę jednowymiarową. Wniosek stąd taki, że wszystkie operacje, które możemy wykonać na macierzach
możemy wykonać też na wektorach.



Nie możemy się odwoływać do elementu tablicy, który nie istnieje, tj. jeżeli tablica ma wymiar 2x4 to nie
możemy posłużyć się odwołaniem ponieważ tablica ma tylko dwa wiersze.



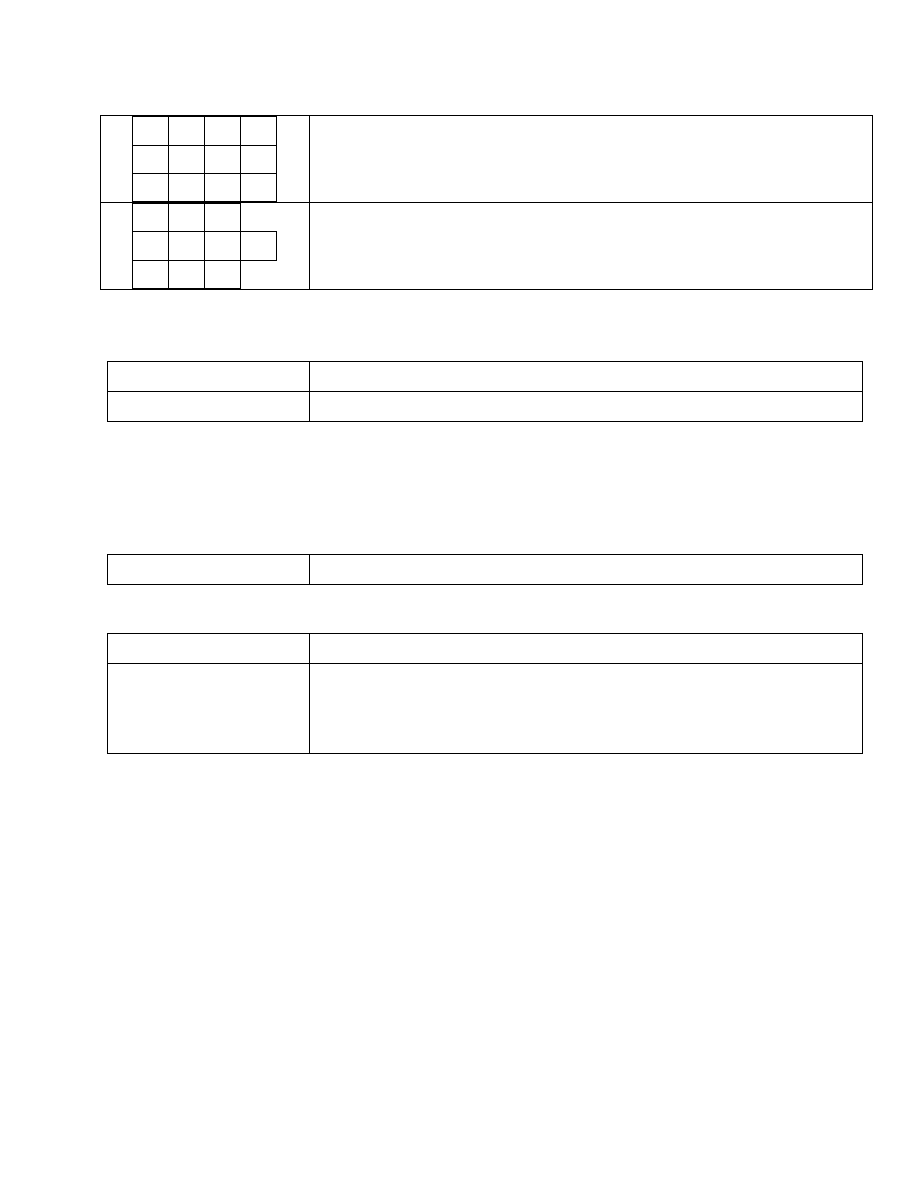
Dla łatwiejszego zrozumienia macierzy proszę je potraktować jako pewnego rodzaju kontenery stworzone z
pudełek tego samego rozmiaru, ułożonymi w taki sposób, że tworzą geometrycznie prostokąty czy też w

2

trójwymiarze prostopadłościany. Należy zapamiętać, że w każdym wierszu znajduje się tyle samo elementów. To
samo można powiedzieć o kolumnach.

1 2 3 4

5 6 7 8

9 10 11 12

M = [1 2 3 4; 5 6 7 8; 9 10 11 12];

DOBRZE!!

1 2 3

5 6 7 8

9 10 12

M = [1 2 3; 5 6 7 8; 9 10 12];

ŹLE!!



Zachęcam do niestosowania małej litery l (mała litera L) na początku nazwy zmiennej gdyż może się ona mylić z
jedynką!!!

1

Jedynka

l

Mała litera L



Kiedy definiujemy nowe macierze wygodnie jest na początku zdefiniować dla nich swego rodzaju pojemnik.
Dzięki temu damy znać MATLABOWI na jaką macierz ma się przygotować (ile pamięci zarezerwować). UWAGA:
Krok ten nie jest konieczny, ale zwiększa efektywność działania kodu i należy do dobrych praktyk.

Miejsce rezerwujemy tworząc tzw. macierz zerową, musimy znać rozmiar naszej macierzy.

M=

zeros

(2000,50);

Funkcja zeros jest wbudowaną funkcją MATLABA



Z każdego wektora oraz z każdej tablicy możemy stworzyć wektor kolumnowy

MC = M(:)

Kolejne kolumny macierzy M ustawiane są pod sobą

VC1 = VW(:)

VC2 = VC(:)

Dla wektora wierszowego operacja analogiczna do transponowania, ale
jeżeli nie wiemy czy wektor ma jest aktualnie wierszowy, czy kolumnowy, a
chcemy żeby był kolumnowy, to ta operacja zadziała zarówno na wektor
kolumnowy (pozostanie kolumnowym) jak i wierszowy .

3

CO CHCEMY UZYSKAĆ?

JAK TO ZROBIĆ W MATLABIE?

Tworzenie zmiennej skalarnej

A = 4

Tworzenie wektora wierszowego

RV = [1,2,3,-3]
RV = [1 2 3 -3]

Tworzenie wektora kolumnowego

CV = [1;2;3;-3]

Tworzenie wektora o wartościach
różniących się o jeden

V_EQS = 1:5

Tworzenie wektora z przedziału
podzielonego na N wartości (N-1
podprzedziałów)

Start=0
Koniec = 3
Liczba = 40
V_LINS =

linspace

(Start, Koniec, Liczba)

Tworzenie tablicy/macierzy

o

wymiarze 2 (liczba wierszy) na 3 (liczba
kolumn)

M23 = [1 1 1; 2 2 2]
M23 = [1 1 1;…
2 2 2]

Transponowanie tablicy

M_transponowana = M’

Pobieranie części tablicy

M_2_2to4 = M(2,2:3)

Modyfikacja części tablicy

M_2_2to4_new = [-1 1]
M(2,2:3) = M_2_2to4_new

Dodawanie nowego wiersza do tablicy

(na jej koniec)

nowy_wiersz = [0 – 1 -2]
M = [M; nowy_wiersz]

Dodawanie nowej kolumny do tablicy

(na jej koniec)

nowa_kolumna = [0;–1;-2]
M = [M, nowa_kolumna]

Zamiana całego wiersza tablicy

M(3,:)=[1 3 4 5]

Zamiana całej kolumny tablicy

M(:,1) = [3;4;5]

Zamiana elementów w drugim wierszu od
3 do ostatniego tablicy

M(2,3:end) = [3 4 5]

Wektor odwołania nie musi być sekwencją
rosnącą

M(2,[3 1 2]) = [3 4 5]

Pobieranie rozmiaru tablicy

Size_M =

size

(M)

Liczba_wierszy = size_M(1)
Liczba_kolumn = size_M(2)

Pobieranie liczby elementów w tablicy

Liczba_elementow =

length

(M(:);

% Dla tablicy 2D

Size_M =

size

(M)

Liczba_wierszy = size_M(1)
Liczba_kolumn = size_M(2)
Liczba_elementow = Liczba_wierszy*Liczba_kolumn

4

Pobieranie liczby elementów w wektorze

Liczba_elementow = length(V)

% Nie trzeba używać V(:)

Podstawowe funkcje matematyczne

Y_sin_radiany =

sin

(pi)

Y_cos_radiany =

cos

(pi/2)

Y_sin_stopnie =

sind

(180)

Y_cos_stopnie =

cosd

(90)

Y_eDO5 =

exp

(5)

Y_lnZ5 =

log

(5)

% logarytm naturalny

Podstawowe operacje matematyczne na
zmiennych skalarnych

a = 4
b = 5
YD = a+b

% dodawanie

YO = a-b

% odejmowanie

YM = a*b

% mnozenie

YD = a/b

% dzielenie

YP = a^b

% potęgowanie

YZ = (a-b)+a^2

% operacja zlozona

Operacje matematyczne na macierzach.
Chcemy wykonać operacje na każdym z
elementów macierzy A i B. W przypadku
dodawania operacje mają spełniać
zależności:
A(1)+B(1)
A(2)+B(2)
…
A(N)+B(N)

a = [1 2 3 4; 5 6 7 8]
b = [8 7 6 5; 4 3 2 1]
YD = a+b

% dodawanie

YO = a-b

% odejmowanie

YM = a.*b

% mnozenie

YD = a./b

% dzielenie

YP = a.^b

% potęgowanie

% Dla operacji MNOZENIE, DZIELENIE, POTEGOWANIE
% dodajemy przed operatorem kropkę.
% KOLEJNOŚĆ ZMIENNCYH NIE MA ZNACZENIA

Mnożenie macierzowe
Mnożenie macierzy

oraz

Musi być spełniony warunek

A_2NA3 = [2 3 4; 2 3 4];
B_3NA1 = [3;4;5];
C_2NA1 = A*B

Operacje logiczne

a = 4;
b = -4;
c = 0.45;
L1 = a==3

% RÓWNE

L2 = b~=5

% ROZNE OD

L3 = c>0

% WIEKSZE OD

L4 = a<5

% MNIEJSZE OD

L5 = c>=3

% WIEKSZE ROWNE

L6 = b<=11

% MNIEJSZE ROWNE

Łącznie operacji logicznych
Operatory: I, LUB (ang. AND, OR)
Kilka warunków spełnionych jednocześnie

a = 4;
b = -4;
c = 0.45;
L1 = (a>0) & (b == 4)

% OPERATOR: I

L2 = (a<0) | (c ~= 9)

% OPERATOR: LUB

L3 = (a<0) | ((c ~= 9)&(b>-2))

% MIESZANIE TYPÓW

5

Struktura warunkowa

if

Wykonaj jeżeli spełniony jest warunek
Instrukcje znajdujące się niżej zostaną
wykonane tylko wtedy jeżeli warunki
znajdujące się nad nimi nie zostały
spełnione.

if

(warunek0)

% Cos tu zrob

elseif

(warunek1)

%Jezeli powyższe nieprawdziwe zrob cos

%innego

elseif

(warunek2)

%Zrob jeszcze cos innego

else

%Zrob to domyślnie jeżeli żaden z powyższych

%warunkow nie będzie spelniony

end

% Wszystkie zmienne warunek0, warunek1, warunek2
% sa zmiennymi typu logicznego
% np.
% warunek0 = (a>6)

Pętla

for

for z = wektorA
Zmienna przyjmuje kolejne wartości z
wektora , więc wykona się tyle
razy jaka będzie długość
wektora

for

i=1:10

% W tej petli ponizsza operacja zostanie

% wykonana 10 razy

g = i^2;

end

num_el = 4;
G =

zeros

(num_el,1);

for

k=

linspace

(1,5,num_el)

% W tej petli ponizsza operacja zostanie

% wykonana num_el razy. Dodatkowo wynik
% każdej kolejnej operacji staje się
% elementem wektora G

G(k) = i^2;

end

Pętla

while

while (warunek)
Wykonuj dopóki spełniony jest warunek

a = 5;

while

(a > 0)

a = a – 1;

end

Przydatne funkcje
– macierz 2D
- wektor

minM =

min

(M)

% wartosc minimalna z kazdej

% kolumny

minV =

min

(V)

% wartosc minimalna w calym

% wektorze

maxM =

max

(M)

% wartosc maksymalna z kazdej

% kolumny

maxV =

max

(V)

% wartosc maksymalna w calym

% wektorze

meanM =

mean

(M)

% wartosc srednia z kazdej

% kolumny

meanV =

mean

(V)

% wartosc srednia w calym

% wektorze

minM_all =

min

(M(:));

% wartosc minimalna w

% calej macierzy

6

Tworzenie szczególnych macierzy

% Macierz zerowa o wymiarze 5x3

M0 =

zeros

(5,3);

% Macierz wypełniona samymi jedynkami

M1 =

ones

(5,3)

% Macierz wartości losowych z zakresu [0,1]

MR =

rand

(5,3)

% Umieszcza wektor na diagonalnej macierzy
% wymiar macierzy – kwadratowa, liczba kolumn i
% wierszy równa długości wektora, np.
1 0
0 2

MDIAG =

diag

([1 2])

Inne przydatne funkcje

% Roznica pomiedzy kolejymi elementami wektora
% np. v = [1 4 5] , wówczas
% diff(v) = [3,1]

ROZNICA_V =

diff

(v)

% Suma wszystkich elementow w wektorze

SUMA_V =

sum

(v)