
Adam Kucharski
Metoda DEA w ocenie efektywności gospodarczej
Wydanie 2
Łódź 2014
ISBN 978-83-934591-2-4

Spis treści
1. Podstawowe pojęcia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
Czym jest efektywność i jak ją mierzyć? . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
Programowanie ilorazowe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2. Metoda DEA – charakterystyka i podział modeli . . . . . . . . . . . . . . . . . . . . . .
10
Model CCR . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
Inne typy modeli DEA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
3. Wybrane typy analiz w metodzie DEA . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
Analizy wynikające bezpośrednio z optymalizacji . . . . . . . . . . . . . . . . . . . . . . .
26
Ranking obiektów a superefektywność . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
29
Dynamika zmian w modelach DEA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
32
Wpływ własności danych empirycznych na wyniki modelu CCR
. . . . . . . . . . . . . .
38
4. Uwzględnianie luzów nakładów i efektów . . . . . . . . . . . . . . . . . . . . . . . . . . .
40
Nadwyżki efektów i niedobory nakładów w zadaniu standardowym . . . . . . . . . . . . .
40
Model z karami za luzy nakładów i efektów . . . . . . . . . . . . . . . . . . . . . . . . . .
42
5. Model wykorzystujący efektywność nieradialną . . . . . . . . . . . . . . . . . . . . . . .
46
Model efektywności nieradialnej
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
46
Wybrane analizy modelu z efektywnością nieradialną . . . . . . . . . . . . . . . . . . . . .
47
6. Wykorzystanie komputera do obliczeń w metodzie DEA
. . . . . . . . . . . . . . . . .
51
Arkusz kalkulacyjny . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
51
Pakiet EMS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
52
DEA w środowisku R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
55

1. Podstawowe pojęcia
1.1. Czym jest efektywność i jak ją mierzyć?
Badania dotyczące efektywności obejmują zazwyczaj efekty działalności osiągane przy usta-
lonych nakładach lub zajmują się wykorzystaniem nakładów pozwalających na osiągnięcie zakła-
danych efektów. Samuelson i Nordhaus głoszą pogląd, że „efektywność jest być może głównym
przedmiotem ekonomii – najogólniej rzecz ujmując – jest ona brakiem marnotrawstwa”. Zgod-
nie z tym gospodarka działa efektywnie, jeżeli nie można zwiększyć wielkości produkcji danego
dobra bez zmniejszenia produkcji innego, co jest tożsame z osiągnięciem krawędzi możliwości
produkcyjnych.
Podstawowe relacje efektywnościowe to: wydajność pracy, produktywność majątku trwałego,
efektywność inwestycji, materiałochłonność i energochłonność produkcji. Wyrazem poprawy efek-
tywności ekonomicznej jest wzrost 3 pierwszych relacji i obniżenie się 2 pozostałych. Efektywność
ekonomiczną można rozpatrywać w mikroskali – w odniesieniu do całego przedsiębiorstwa lub do
jednego z czynników produkcji zaangażowanych w jednym przedsiębiorstwie, albo w makroskali,
tzn. w odniesieniu do całej gospodarki narodowej.
Efektywność obiektów funkcjonujących w gospodarce bada się rożnymi metodami zaliczanymi
do jednej z trzech grup:
— metod klasycznych np. wykorzystanie wskaźników finansowych;
— metod parametrycznych np. modeli ekonometrycznych;
— metod nieparametrycznych np. DEA.
Ostatnie z wymienionych nie wymagają wcześniejszej znajomości parametrów, które wyrażają
związek między efektami a nakładami. Nakłady umożliwiają osiągnięcie pewnych efektów
z
prowadzonej działalności przy czym ani jedne, ani drugie nie muszą być wyrażone w jednostkach
pieniężnych czy fizycznych. Co więcej, już wkrótce okaże się, że poszczególne nakłady i efekty mo-
gą zostać wyrażone w dowolnych, odpowiadających nam jednostkach. W przypadku problemów z
odróżnieniem nakładów od efektów należy sprawdzić czy zwiększenie danej wielkości doprowadzi
do zwiększenia efektów. Jeśli tak, mamy do czynienia z nakładem.
Przez efektywność technologiczną rozumieć będziemy sprawność z jaką nakłady przekształca-
ne są w efekty zaś przez technologię danego obiektu rozumiemy wektor empirycznych nakładów
i efektów. Jeden obiekt jest bardziej efektywny od drugiego jeśli przy nie większych od drugiego
nakładach uzyskuje nie mniejsze efekty.
Postuluje się, aby wskaźnik efektywności spełniał następujące założenia:
1. powinien zawierać się w przedziale h0,1i;
2. wyższa wartość powinna oznaczać wyższą efektywność;
1
Guzik w swojej książce w miejsce terminu efekty używa rezultaty. Jest jednak w swych poglądach odosob-
niony i w pozostałej polskojęzycznej literaturze pisze się o efektach. Tak też i my będziemy czynić.
4
1. Podstawowe pojęcia
3. powinien określać przynajmniej efektywność względną w danym zbiorze obiektów.
Są oczywiście sytuacje kiedy powyższe postulaty trudno spełnić. Na przykład stopa zwrotu może
być ujemna lub wyższa niż 1. Zwykle jednak odpowiednie przekształcenia pozwalają doprowadzić
wskaźnik do postaci zgodnej z naszymi oczekiwaniami. Sam wskaźnik to po prostu iloraz efektów
podzielonych przez nakłady. W swojej najbardziej klasycznej formie jest to jeden efekt podzielony
przez jeden nakład. Metoda DEA pozwala znieść to ograniczenie i włączyć do wskaźnika kilka
efektów oraz kilka nakładów jednocześnie. Wtedy wskaźnik efektywności jest ilorazem łącznej
wartości efektów przez sumę wartości nakładów. Aby jednak ustalić wartość licznika i mianownika
należy wycenić jednostkę efektu oraz jednostkę nakładu. Tym właśnie zajmuje się metoda DEA.
Jeżeli mamy do czynienia z jednym efektem i kilkoma nakładami (lub jednym nakładem i kil-
koma efektami) możemy zbudować model ekonometryczny. Wykorzystywanie jednocześnie wielu
efektów i nakładów, zwłaszcza jeśli te same nakłady wykorzystuje się do osiągnięcia kilku efektów,
uniemożliwia analizę ekonometryczną ponieważ nie możemy jednoznacznie ustalić bezpośrednie-
go wpływu danego cząstkowego nakładu na osiągnięcie danego efektu. Zawodzi też tradycyjna
analiza wskaźnikowa bo przyjęte standardy rachunkowości nie są wystarczająco szczegółowe.
Guzik podaje następujący przykład. Chcemy ustalić efektywność uczelni wyższej. Dysponu-
jemy danymi na temat majątku trwałego uczelni, liczby studentów stacjonarnych, liczby dokto-
rantów oraz profesorów. Jeżeli podzielimy wartość majątku np. przez liczbę studentów nie uzy-
skujemy wcale wskaźnika efektywności ponieważ ten sam majątek wykorzystywany jest również
na obsługę doktorantów i profesorów. Aby policzyć wskaźnik efektywności w sensie jaki opisali-
śmy go powyżej należałoby wiedzieć jaka część majątku trwałego przypada tylko i wyłącznie na
obsługę studentów czego po prostu nie jesteśmy w stanie określić. Jedyne czym dysponujemy to
całkowite wielkości efektów i nakładów i to nam musi wystarczyć.
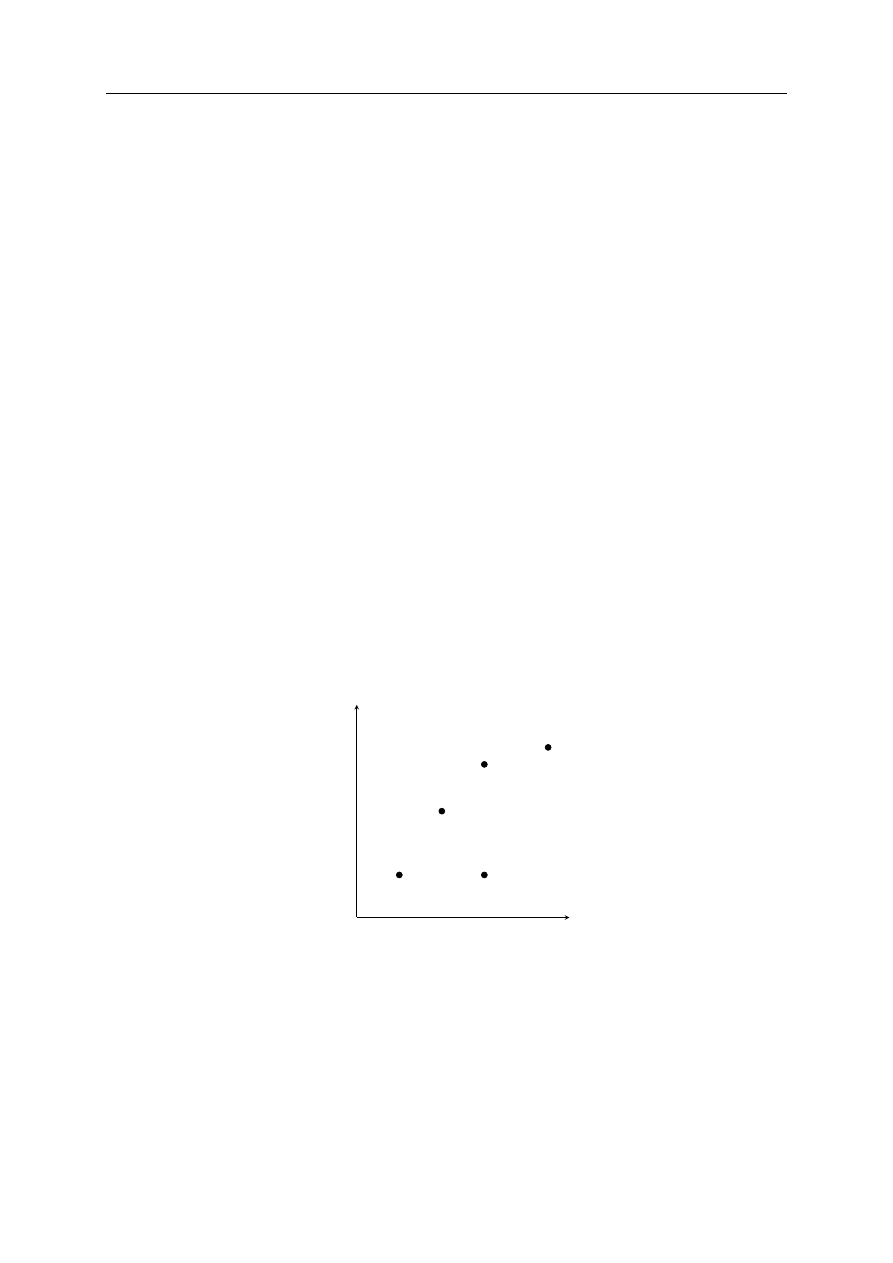
Nakład (X)
Efekt (Y)
O1
O2
O4
O3
O5
Rysunek 1.1. Nakłady i efekty w sensie Pareto
Podstawy teorii efektywności ekonomicznej w warunkach konkurencji doskonałej sformuło-
wał włoski ekonomista Pareto. Głosi ona, iż warunki efektywności są spełnione tylko wtedy,
gdy nie można zwiększyć użyteczności jednego podmiotu (obiektu), nie obniżając jednocześnie
użyteczności innego. Załóżmy, że mamy do czynienia z dwoma obiektami O1 i O2 opisanymi
technologiami t
1
=
h
x
1
y
1
i
i t
2
=
h
x
2
y
2
i
. Obiekt O1 jest w sensie Pareto bardziej efektyw-
ny od obiektu O2 jeżeli przy nie większych nakładach (x
1
6 x
2
) uzyskuje nie mniejsze efekty

1.1. Czym jest efektywność i jak ją mierzyć?
5
(y
1
> y
2
) przy czym jeżeli wszystkie nakłady są równe to przynajmniej jeden efekt w obiekcie O1
jest większy lub jeśli wszystkie efekty są równe to przynajmniej jeden nakład w O2 jest mniejszy.
Choć efektywność Pareto pozwala wskazać, które obiekty są efektywne to nie pozwala zmierzyć
skali ich efektywności.
Na rysunku 1.1 znalazło się pięć obiektów różniących się nakładami i efektami. Obiekt O2
jest mniej efektywny od O1 ponieważ osiąga ten sam efekt wykorzystując do tego wyższy nakład.
Jest też mniej efektywny względem O4 gdyż przy tym samym nakładzie jego efekt jest niższy.
Z kolei obiekt O4 jest efektywny względem O3. Pomimo, że zużywa on większą ilość nakładu
wytwarza też większy efekt. Spośród obiektów na rysunku 1.1 efektywne w sensie Pareto są: O1,
O3, O4 i O5.
Debreu i Farell sformułowali definicję produktywności p jako stosunek pojedynczego efektu
Y do pojedynczego nakładu X, czyli:
p =
Y
X
Propozycja Farrella przedstawia czystą efektywność techniczną odpowiadającą na pytanie czy
dany obiekt znajduje się na krzywej możliwości produkcyjnych czy nie. Możliwe więc stawało się
wyznaczenie maksymalnej wartości efektów osiąganych przy określonych kombinacjach nakładów
lub minimalnej ilości tychże nakładów koniecznej do osiągnięcia zakładanych z góry efektów.
Był tylko jeden problem, a mianowicie brak znajomości postaci funkcji. Tu z pomocą przychodzi
metoda DEA.
Niech T =
h
x
y
i
oznacza technologię ze zbioru technologii dopuszczalnych, zaś ˆ
T =
h
ˆ
x
ˆ
y
i
technologię dopuszczalną za pomocą której można uzyskać efekt ˆ
y > y przy możliwie najmniej-
szych nakładach nieprzekraczających nakładów proporcjonalnych do x czyli ˆ
x 6 θx (θ ∈ (0,1i).
Przynajmniej dla jednej składowych obu wektorów zachodzi ostra nierówność.
Efektywnością Farrella-Debreu dla technologii T =
h
x
y
i
nazywamy taki wskaźnik θ ∈
(0,1i, dla którego nakłady technologii dopuszczalnej ˆ
T =
h
ˆ
x
y
i
minimalizującej nakłady dla
osiągnięcia efektu y wynoszą ˆ
x 6 θx. Wyznaczony wskaźnik efektywności Farrella ˆ
θ można
interpretować jako krotność do jakiej obiekt powinien zmniejszyć obecne nakłady, aby uzy-
skać 100-procentową efektywność. Przykładowo jeżeli ˆ
θ = 0,8 to oznacza to iż dla uzyskania
100-procentowej efektywności dany obiekt powinien zmniejszyć ponoszone nakłady proporcjo-
nalnie do 20% ich obecnego poziomu a więc do 0,7x.
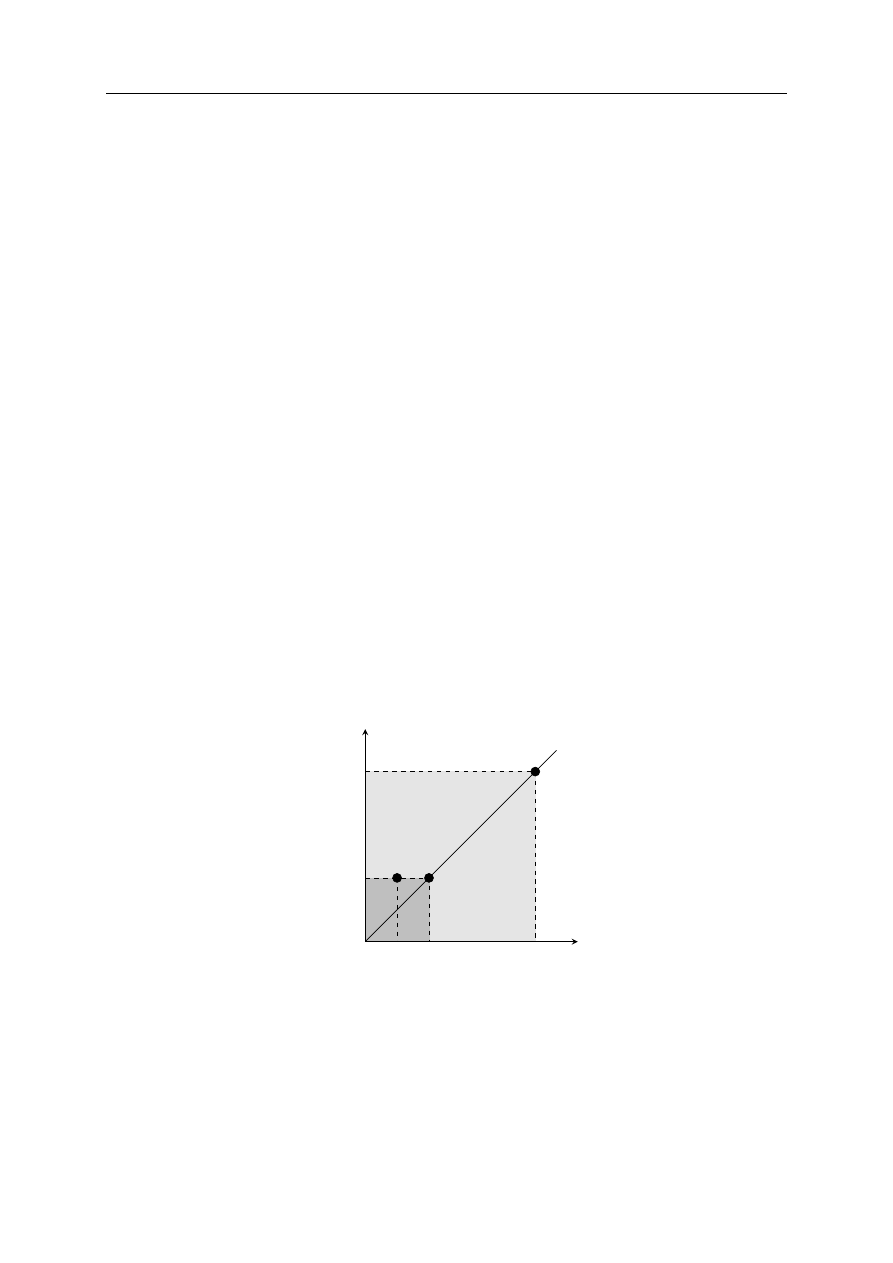
Efektywność Farrella-Debreu jest efektywnością radialną – opiera się na tzw. liniowym pro-
mieniu technologicznym. Promieniem technologicznym technologii
h
x
y
i
nazywamy półprostą
wychodzącą z początku układu współrzędnych i przechodzącą przez punkt x. Promień techno-
logiczny określa zbiór relacji między nakładami niezbędnych do uzyskania efektów y. Wykres
na rysunku 1.2 ilustruje zmiany efektywności dokonujące się proporcjonalnie wzdłuż promienia
technologicznego.
Technologia obiektu znajdującego się w punkcie A wykorzystuje nakłady empiryczne (fak-
tycznie zaobserwowane). Z kolei w punkcie B występują minimalne (optymalne) nakłady, które
wystarczyłoby wykorzystać, aby osiągnąć dotychczasowy efekt.Strzałka narysowana przerywaną
linią pokazuje kierunek proporcjonalnych zmian nakładów dokonujący się właśnie wzdłuż pro-
mienia technologicznego. Przyjmijmy, że współrzędne obu punktów (czyli poziomy nakładów X
1
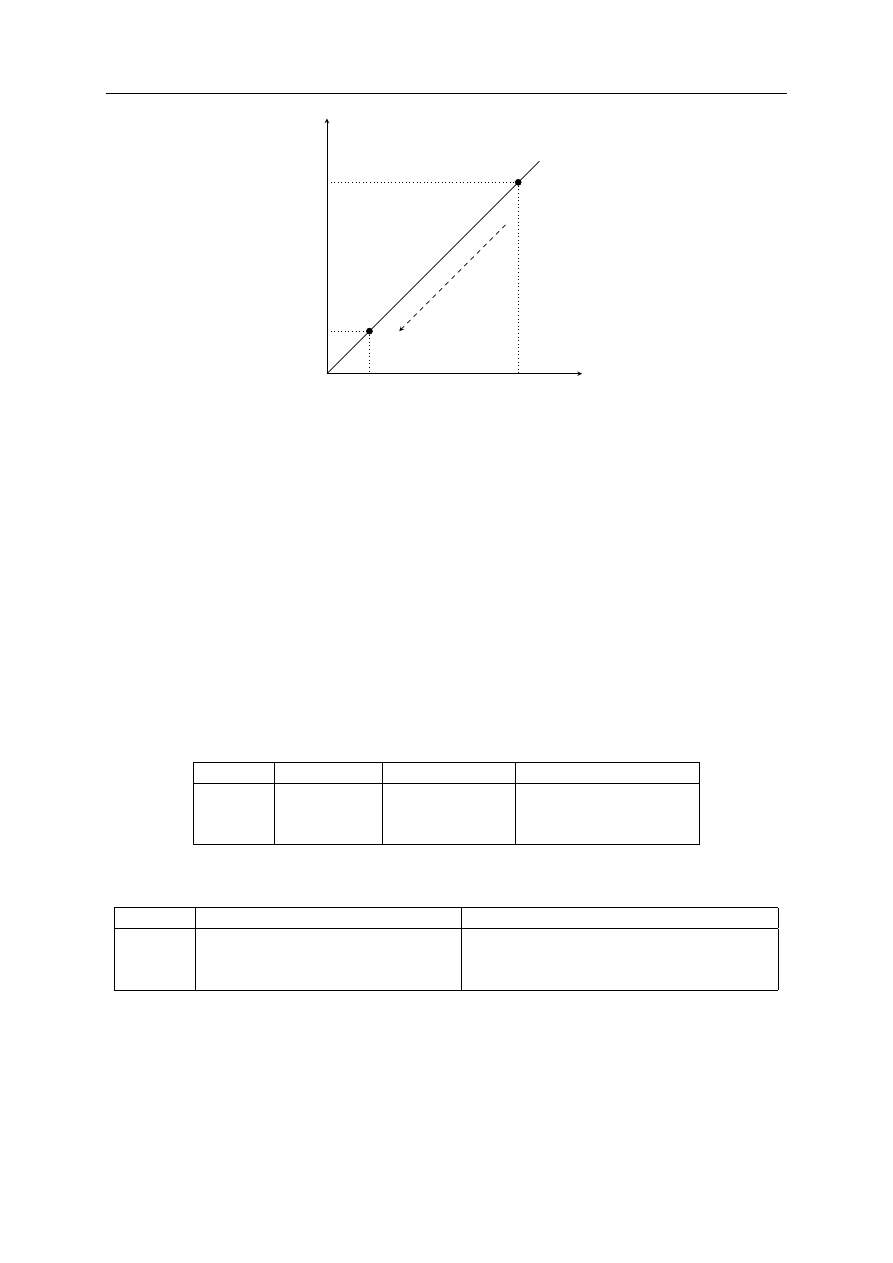
6
1. Podstawowe pojęcia
X
1
X
2
A
B
x
x
∗
x
1
x
∗
1
x
2
x
∗
2
Rysunek 1.2. Zmiany efektywności dla promienia technologicznego
i X
2
) są następujące: A=(25,50) zaś B=(5,10). Wówczas współczynnik efektywności Farrella
wynosi θ
∗
= 5/25 = 0,2. Oznacza to, że technologia z punktu B pozwala na osiągnięcie bie-
żącego efektu przy pomocy 20% aktualnych nakładów tego obiektu. Tym samym powiemy, że
efektywność technologii z punktu A wynosi tylko 20%.
Przykład oceny efektywności.
Pewne przedsiębiorstwo tworzą trzy zakłady. Postanowiono zbadać jak efektywnie wykorzy-
stywany jest w nich nakład siły roboczej i porównać zakłady między sobą. Fikcyjne dane zebrane
zostały w tabeli 1.1. Na tej podstawie obliczyliśmy efektywność wykorzystania zatrudnionych dla
każdego z zakładów. Wyniki przedstawia tabela 1.2.
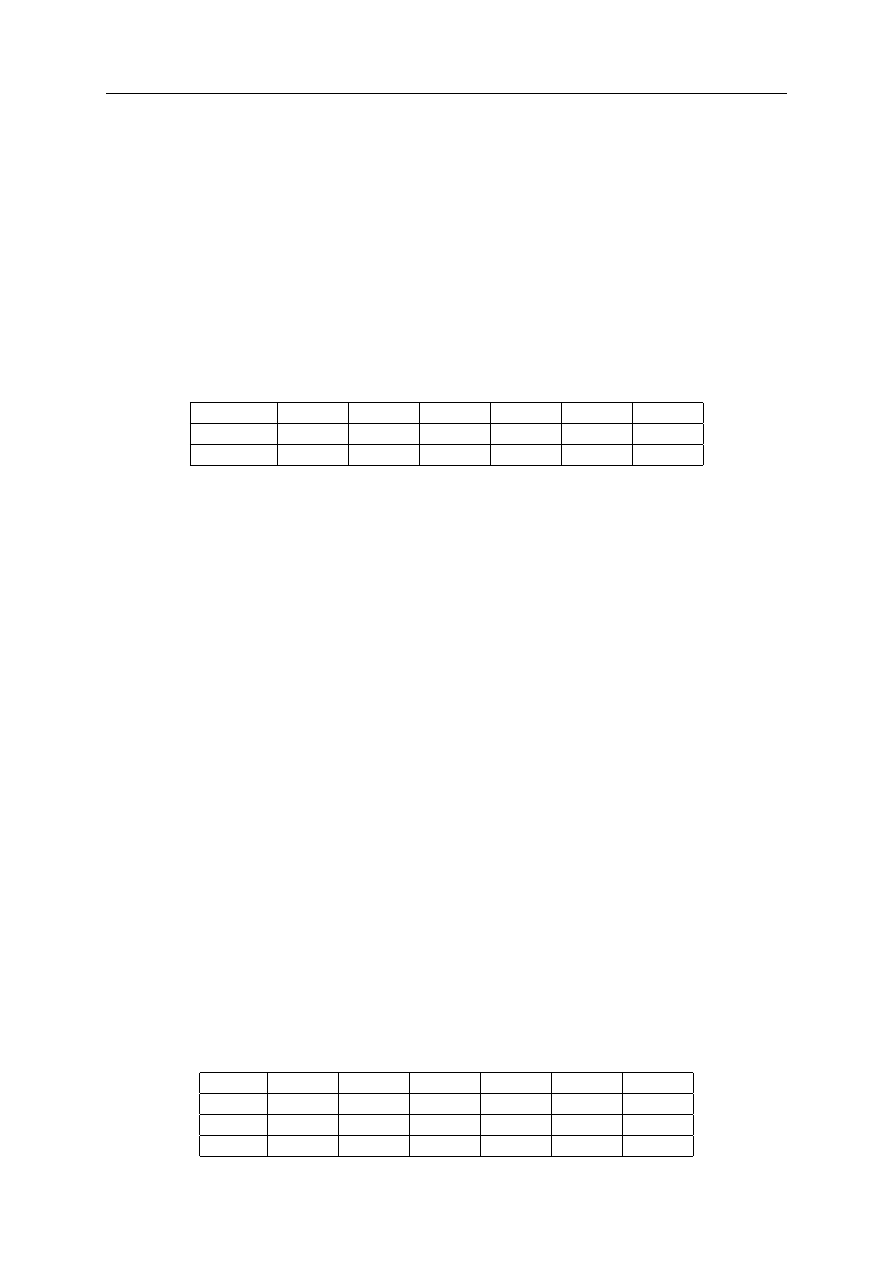
Tabela 1.1. Dane na temat wykorzystania siły roboczej
Zatrudnienie
Liczba wyrobów
Przepracowane godziny
Zakład 1
120
600
2400
Zakład 2
160
1600
2000
Zakład 3
250
1500
2500
Tabela 1.2. Efektywność siły roboczej
Liczba wyrobów / 1 zatrudnionego
Przepracowane godziny / 1 zatrudnionego
Zakład 1
5
20
Zakład 2
10
12,5
Zakład 3
6
10
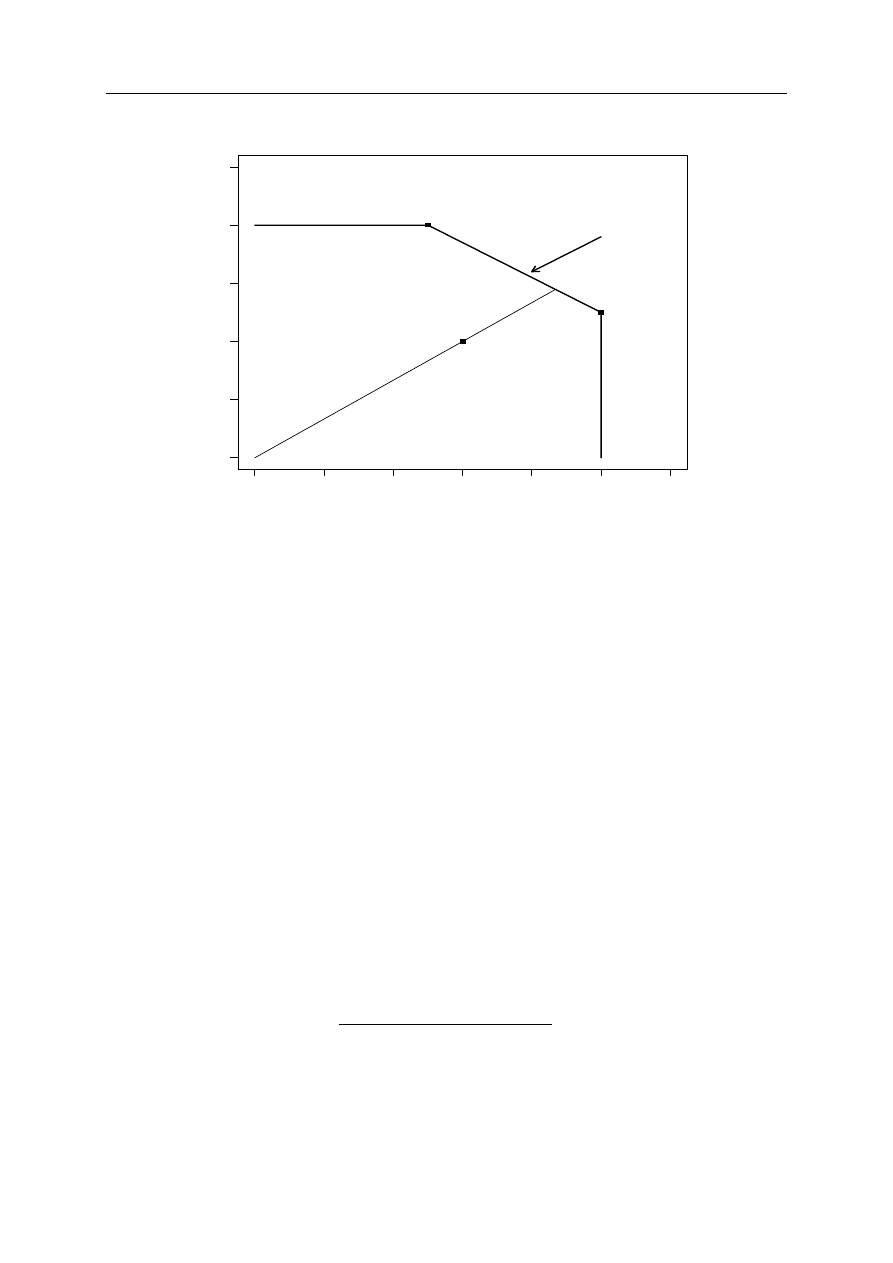
Dane z tabeli 1.2 dadzą się przedstawić na wykresie (patrz rysunek 1.3). Obiekty efektyw-
ne to te, które leżą na tzw. granicy efektywności (u nas są to Zakład 1 i Zakład 2), o której
więcej powiemy później. W ich przypadku osiągnięto maksymalne możliwe efekty wykorzystując
dostępne nakłady. Przypomnijmy, że utworzona miara efektywności porównuje obiekty między
sobą. Dołączenie kolejnego zakładu do przeprowadzanej analizy prawdopodobnie doprowadziłoby
do innych wniosków.
1.2. Programowanie ilorazowe
7
0
2
4
6
8
10
12
0
5
10
15
20
25
Liczba wyrobów/1 zatrudnionego
Liczba godzin/1 zatr
udnionego
Zaklad 1
Zaklad 2
Zaklad 3
A
B
C
granica efektywnosci
Rysunek 1.3. Granica efektywności dla przykładu 1
Zakład 3 znalazł się poniżej granicy efektywności. W jego przypadku można wyznaczyć
półprostą (promień technologiczny) wychodzącą z początku układu współrzędnych i przecho-
dzącą przez współrzędne odpowiadające Zakładowi 3 (czyli zaznaczony na wykresie punkt B).
Punkt C prezentuje zmiany wartości efektów dla Zakładu 3 pod warunkiem zmniejszenia liczby
zatrudnionych. Wyznaczenie efektywności dla Zakładu 3 sprowadza się do obliczenia ilorazu
długości odcinka |AB| do długości odcinka |BC|. W ten sposób otrzymamy wskaźnik w sensie
Farrella-Debreu.
1.2. Programowanie ilorazowe
Zadania tego rodzaju mogą być stosowane do poszukiwania rozwiązania kompromisowego
problemów dwukryterialnych na przykład wskaźnika efektywności nakładów rozumianego jako
iloraz nakładów do efektów. Ilorazowa funkcja celu wyrażać będzie pewien wskaźnik efektywności
nakładów. Zadanie programowania ilorazowego ma postać:
h(x) =
c
1
x
1
+ c
2
x
2
+ . . . + c
n
x
n
+ c
0
d
1
x
1
+ d
2
x
2
+ . . . + d
n
x
n
+ d
0
→ max
(1.1)
a
11
x
1
+
a
12
x
2
+
. . .
+
a
1n
x
n
=
b
1
a
12
x
1
+
a
22
x
2
+
. . .
+
a
2n
x
n
=
b
2
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
a
m1
x
1
+
a
m2
x
2
+
. . .
+
a
mn
x
n
=
b
n
(1.2)

8
1. Podstawowe pojęcia
x
1
> 0,x
2
> 0, . . . ,x
n
> 0
(1.3)
Zapis macierzowy:
h(x) =
c
T
x + c
0
d
T
x + d
0
(1.4)
Ax = b
(1.5)
x > 0
(1.6)
Elementy: c
0
i d
0
są wyrazami wolnymi w liczniku i mianowniku funkcji celu. Zadanie
(1.4)-(1.6) można, posługując się tzw. transformacją Charnesa-Coopera, przekształcić do zadania
PL. Zastępujemy w niej powyższe zadanie następującym:
g(u,u
0
) = c
T
u + c
0
u
0
→ max
(1.7)
Au − bu
0
= 0
(1.8)
d
T
u + d
0
u
0
= 1
(1.9)
u > 0,u
0
> 0
(1.10)
Po osłabieniu warunku dotyczącego u
0
otrzymamy:
u
0
> 0
(1.11)
Ponadto:
u =
x
d
T
x + d
0
(1.12)
u
0
=
1
d
T
x + d
0
(1.13)
Metodę (transformację) Charnesa-Coopera opisują twierdzenia:
Twierdzenie 1. Jeżeli zadanie (1.4)-(1.6) jest niesprzeczne i istnieje dla niego skończone rozwią-
zanie optymalne, to ilorazowa funkcja celu (1.4) osiąga swoją wartość największą w wierzchołku
zbioru rozwiązań dopuszczalnych.
Twierdzenie 2. Rozwiązanie optymalne zadania (1.4)-(1.6) istnieje wtedy i tylko wtedy, gdy
istnieje rozwiązanie optymalne zadania (1.7)-(1.11) takie, że u
o
0
> 0.
Twierdzenie 3. Jeżeli zadanie PL (1.7)-(1.11) jest sprzeczne to, sprzeczne jest również wyjścio-
we zadanie programowania ilorazowego.

1.2. Programowanie ilorazowe
9
Twierdzenie 4. Jeżeli zadanie PL (1.7)-(1.11) nie posiada skończonego rozwiązania optymalne-
go, to również wyjściowe zadanie programowania ilorazowego nie posiada skończonego rozwiązania
optymalnego.
Twierdzenie 5. Jeżeli istnieje skończone rozwiązanie optymalne zadania (1.7)-(1.11) [u
o
,u
o
0
]
takie, że u
o
0
> 0, to rozwiązanie zadania programowania ilorazowego wyznacza się:
x
o
=
u
o
u
o
0
(1.14)
zaś optymalna wartość ilorazowej funkcji celu jest równa:
h(x
o
) = g(u
o
,u
o
0
)
(1.15)

2. Metoda DEA – charakterystyka i podział modeli
2.1. Model CCR
Pod koniec lat 70-tych trójka Amerykanów: Charnes, Cooper i Rhodes zwróciła uwagę na
kwestię porównywania między sobą efektywności różnych systemów. Efektywność oznaczała tu
stosunek osiąganych efektów do wielkości ponoszonych nakładów. Amerykanie postanowili zde-
finiować efektywność jako stosunek sumy ważonych efektów do sumy ważonych nakładów. Tak
narodziła się Data Envelopment Analysis (w skrócie DEA) czyli metoda analizy danych granicz-
nych.
Wspomniane podejście nie wymaga znajomości postaci funkcji efektywności. Wykorzystując
empiryczne wielkości nakładów i efektów poszukuje się (dla danego obiektu, który w anglojęzycz-
nej literaturze określa się zwykle skrótem DMU – Decision Making Unit ) wag maksymalizujących
efektywność. W ten sposób otrzymujemy zadanie programowania matematycznego, w którym
chodzi o wyznaczanie efektywności konkretnych obiektów względem całej ich grupy.
Metoda DEA w języku polskim jest określana również jako: metoda analizy danych granicz-
nych, metoda granicznej analizy danych lub metoda analizy efektywności granicznej. Nie spotyka
się polskiego odpowiednika dla angielskiego skrótu nazwy.
Metoda DEA opiera się na analizach granicznych, a jej ilustracją graficzną jest częściowo
liniowa funkcja łącząca najbardziej efektywne jednostki decyzyjne. Krzywa efektywności (ang.
best practice frontier ) jest estymowana na podstawie danych empirycznych dotyczących nakładów
i efektów. Jednostki, które znajdą się na krzywej uznajemy za efektywne, a ich efektywność
θ = 1. DMU leżące poniżej efektywności są zdominowane przez obiekty leżące na krzywej, a
więc nieefektywne. Stopień ich nieefektywności wynosi 1 − θ. Samego pomiaru dokonujemy bez
konieczności jakiegokolwiek uśredniania danych.
Model opracowany przez Charnesa, Coopera i Rhodesa jest obecnie nazywany modelem CCR i
historycznie powstał jako pierwszy. Występuje w nim efektywność w sensie Farrella czyli zmiany
nakładów (lub efektów) są proporcjonalne. Dla każdego obiektu ustalamy czy jego aktualna
technologia pozwala na najbardziej korzystną realizację stawianych mu zadań.
Załóżmy, że bierzemy pod uwagę n obiektów, z których każdy konsumuje R różnych nakładów
w celu otrzymania P różnych efektów. Obiekt h
i
zużywa tym samym x
pi
nakładu p i produkuje
y
ri
efektu r. Dodatkowo zakładamy, że wartości nakładów i efektów nie mogą być wielkościami
ujemnymi oraz, że dla każdego analizowanego obiektu przynajmniej jeden nakład i przynajmniej
jeden efekt są różne od zera. Odpowiedni model programowania matematycznego został opisany
zależnościami (2.1)-(2.3). Zadanie to można sprowadzić do postaci liniowej przy pomocy znanej
nam już transformacji Charnesa-Coopera.
Przejście na postać liniową ułatwia nie tylko obliczenia, ale również interpretacje wyników.
Własności klasycznych modeli liniowych są bowiem dobrze zbadane.

2.1. Model CCR
11
θ = h
i
(µ,ν) =
R
X
r=1
µ
r
y
ri
P
X
p=1
ν
p
x
pi
→ max
(2.1)
R
X
r=1
µ
r
y
ri
P
X
p=1
ν
p
x
pi
6 1
(2.2)
µ
r
> 0,ν
p
> 0
(2.3)
gdzie:
h
i
– efektywność obiektu i (i = 1, . . . ,n)
µ
r
– wagi odpowiadające poszczególnym efektom (r = 1, . . . ,R)
ν
p
– wagi odpowiadające poszczególnym nakładom (p = 1, . . . ,P )
Model po transformacji:
g
i
=
R
X
r=1
µ
r
y
ri
→ max
(2.4)
P
X
p=1
ν
p
x
pi
= 1
(2.5)
R
X
r=1
µ
r
y
ri
−
P
X
p=1
ν
p
x
pi
6 0
(2.6)
µ
r
> 0, ν
p
> 0
(2.7)
W literaturze można również spotkać uogólniony przypadek warunków opisanych przez (2.7),
a mianowicie:
µ
r
> ε, ν
p
> ε
(2.8)
gdzie ε jest dowolnie małą liczbą dodatnią.
Wiemy już, że optymalizacja efektywności może być rozumiana dwojako: jako zmniejszanie
nakładów w celu osiągnięcia dotychczasowych efektów lub zwiększanie efektów przy wykorzysta-
niu nakładów na dotychczasowym poziomie. Model (2.4)-(2.7) zalicza się do pierwszego typu i
dlatego będzie w dalszych rozważaniach nazywany modelem CCR zorientowanym na nakłady.
Jego odpowiednik czyli model CCR zorientowany na efekty przedstawia się następująco:
g
i
=
R
X
r=1
µ
r
y
ri
→ min
(2.9)
12
2. Metoda DEA – charakterystyka i podział modeli
P
X
p=1
ν
p
x
pi
= 1
(2.10)
R
X
r=1
µ
r
y
ri
−
P
X
p=1
ν
p
x
pi
> 0
(2.11)
µ
r
> 0, ν
p
> 0
(2.12)
Oba modele można przekształcić do postaci dualnej:
Model dualny zorientowany na nakłady:
θ
∗
= θ → min
(2.13)
n
X
j=1
x
pj
λ
j
6 θx
pi
(2.14)
n
X
j=1
y
rj
λ
j
> y
ri
(2.15)
λ
j
> 0
(2.16)
Model dualny zorientowany na efekty:
θ
∗
= θ → max
(2.17)
n
X
j=1
x
pj
λ
j
6 x
pi
(2.18)
n
X
j=1
y
rj
λ
j
> θy
ri
(2.19)
λ
j
> 0
(2.20)
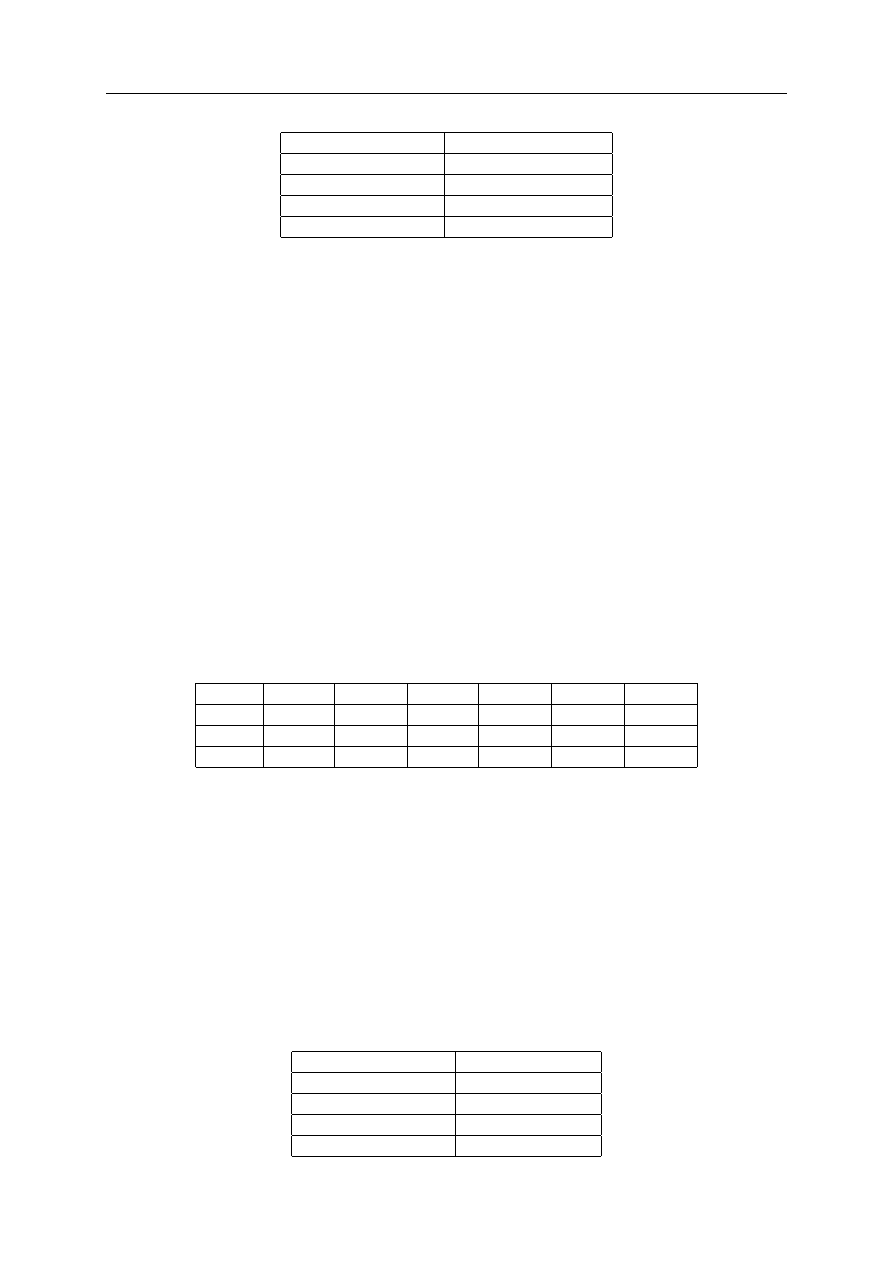
Przykład wyznaczania granicy efektywności (dwa nakłady i dwa efekty)
Dokonajmy rozszerzenia pierwszego przykładu o dodatkowy nakład obrazujący wykorzystanie
w produkcji pewnego surowca. Zmodyfikowane dane do zadania znalazły się w tabeli 2.1.
Tabela 2.1. Zmodyfikowane dane do przykładu 2
Surowiec
Zatrudnienie
Liczba wyrobów
Przeprac. godziny
Zakład 1
50
120
600
2400
Zakład 2
60
160
1600
2000
Zakład 3
70
250
1500
2500
Rozważymy model CCR zorientowany na nakłady. W tym celu dla każdego zakładu nale-
ży zbudować i rozwiązać oddzielne zadanie optymalizacyjne opisane wzorami (2.9)-(2.12). Na
przykład dla Zakładu 1 ma ono postać:
g
1
= µ
1
600 + µ
2
2400 → max
(2.21)
ν
1
50 + ν
2
120 = 1
(2.22)
µ
1
600 + µ
2
2400 − ν
1
50 − ν
2
120 6 0
(2.23)
µ
1
1600 + µ
2
2000 − ν
1
60 − ν
2
160 6 0
(2.24)
µ
1
1500 + µ
2
2500 − ν
1
70 − ν
2
250 6 0
(2.25)
µ
1
> 0,µ
2
> 0,ν
1
> 0,ν
2
> 0
(2.26)
Rezultaty pochodzące z rozwiązania wszystkich trzech zadań znalazły się w tabeli 2.2. Opty-
malna wartość funkcji celu dla zakładów 1 i 2 wyniosła 1. Znalazły się one zatem na granicy

2.1. Model CCR
13
Tabela 2.2. Wyniki modelu CCR dla przykładu 2
g
opt
i
µ
opt
1
µ
opt
2
ν
opt
1
ν
opt
2
Zakład 1
1
0,0003
0,0003
0,02
0
Zakład 2
1
0,0003
0,0003
0,0167
0
Zakład 3
0,9524
0,0002
0,0002
0,0143
0
efektywności
. Z kolei Zakład 3 okazał się nieefektywny ponieważ w jego wypadku optymalna
wartość funkcji celu jest mniejsza od jedności. Na tle pozostałych dwóch zakładów odznacza się
ono około 5-procentową nieefektywnością.
Skoro Zakład 3 okazał się nieefektywny można wyznaczyć dla niego liniową kombinację zło-
żoną z efektywnych obiektów, która przy nie większych nakładach pozwoli na osiągnięcie co
najmniej takich samych efektów. Współczynnikami tej kombinacji są wyceny dualne rozwiązania
zadania dla Zakładu 3 dla ograniczeń dotyczących łącznej wartości poniesionych nakładów i
łącznej wartości uzyskanych efektów w zakładach 1 i 2. Współczynniki te wynoszą (po zaokrą-
gleniu) 0,3788 dla Zakładu 1 i 0,7955 dla Zakładu 2. Jeżeli obliczymy kombinacje liniowe efektów
osiąganych przez obiekty efektywne (np. dla liczby wyrobów: 0,3788 · 600 + 0,7955 · 1600) to okaże
się, że otrzymamy liczby wyrobów i przepracowane godziny o wartościach odpowiadających tym
dla Zakładu 3. Podobne działanie dla nakładów da następujący rezultat:
0,3788 · 50 + 0,7955 · 60 = 66,67
0,3788 · 120 + 0,7955 · 160 = 172,736
Otrzymane wartości kombinacji nakładów zakładów pierwszego i drugiego znajdują się po-
niżej wielkości odpowiadających Zakładowi 3 (odpowiednio 70 i 250). Możliwe więc było lepsze
wykorzystanie nakładów przez Zakład 3 pozwalające na osiągnięcie dotychczasowych efektów.
Na podstawie powyższych informacji jesteśmy w stanie sformułować przesłanki stosowania
modeli DEA. Po pierwsze oczekujemy, że zbiór obiektów będzie jednorodny lub prawie jedno-
rodny. Które jednak obiekty można uznać za jednorodne to temat na oddzielną dyskusję. Po
drugie nakłady i efekty winny być nieujemne. W razie konieczności można je doprowadzić do
nieujemności stosownymi przekształceniami.
Trzecim warunkiem stosowania DEA jest jednolitość jednostek pomiaru nakładów i efektów
we wszystkich obiektach. Innymi słowy nakład wyrażony w jednym DMU w tys. zł nie może w
innym zostać wyrażony w mln zł. Efekt musi mieć taką definicję, aby jego wzrost był ocenia-
ny pozytywnie. Z kolei wzrost nakładu (przy założeniu ceteris paribus) powinien być oceniany
negatywnie.
Pewien problem stanowi ustalenie liczby obiektów włączonych do analizy. Generalnie zakłada
się, że ilość DMU będzie znacznie większa od łącznej liczby nakładów i efektów. Sugeruje się, żeby
była ona wyższa od max {P R,3(P + R)}, ale wynika to z chęci zapewnienia stabilnych wartości
współczynników efektywności. Model DEA da się rozwiązać nawet wtedy gdy liczba obiektów
jest niewielka w porównaniu z liczbą nakładów i efektów.
Podsumowując rozważania w tej części opracowania do zalet metody DEA zaliczymy:
1
Są efektywne w sensie Farrella.

14
2. Metoda DEA – charakterystyka i podział modeli
1. Możliwość jednoczesnego uwzględnienia wielu nakładów i efektów.
2. Brak wymagań co do postaci funkcji wyrażającej zawiązek między nakładami a efektami.
3. Zmienne opisujące nakłady i efekty mogą posiadać różne miana.
4. Metoda wychwytuje wielkości skrajne zamiast je uśredniać jak to dzieje się na przykład w
przypadku linii regresji.
Metoda ta posiada też wady, wśród których wymienimy:
1. Efektywność mierzona jest względem pozostałych obiektów, co uwrażliwia metodę na usuwa-
nie bądź dołączanie do zbioru obiektów.
2. Duża wrażliwość na błędne dane (szczególnie w obiektach uznanych za wzorcowe).
3. Konieczność oddzielnego rozwiązywania zadania dla każdego obiektu.
4. W podstawowych modelach np. CCR pojawia się duża liczba obiektów efektywnych w sto-
sunku do całkowitej liczby obiektów.
2.2. Inne typy modeli DEA
Model CCR nie wyczerpuje puli modeli stosowanych w analizach DEA. Modele tego typu
dzielone są zwykle według dwóch podstawowych kryteriów. Pierwsze z nich wyróżnia:
— modele zorientowane na efekty;
— modele zorientowane na nakłady;
— modele niezorientowane.
W modelach zorientowanych na efekty celem optymalizacji jest uzyskanie jak najwyższych efek-
tów przy zachowaniu stałych i zrównoważonych nakładów. W drugim z wymienionych przypad-
ków minimalizujemy nakłady w taki sposób, aby efekty pozostały na ustalonym poziomie. Istnieje
też trzecia kategoria, w której nie określamy orientacji na efekty bądź nakłady, lecz rzadko się ją
wykorzystuje z uwagi na kłopoty z interpretacją.
Drugim ważnym podziałem jest podejście od strony efektów skali. Z tego punktu widzenia
wyróżniamy:
— model ze stałymi efektami skali (od nazwisk autorów: Charnes, Cooper, Rhodes oznaczany
jako CCR);
— model ze zmiennymi efektami skali (od nazwisk autorów: Banker, Charnes, Cooper oznaczany
jako BCC);
— model z nierosnącymi efektami skali (ang. Non Increasing Return to Scale – NIRS);
— model z niemalejącymi efektami skali (ang. Non Decreasing Return to Scale – NDRS).
Oba podziały nakładają się na siebie (z wyłączeniem modeli niezorientowanych). Zanim przed-
stawimy szczegółowo interesujące nas modele wyjaśnienia wymaga kwestia nazewnictwa. W li-
teraturze przedmiotu wykorzystuje się bowiem modele dualne zamiast pierwotnych. Praktyka ta
jest tak powszechna, że doprowadziła do odwrócenia terminologii. Model pierwotny staje się w
tej sytuacji dualnym zaś dualny – pierwotnym.
Postać modelu CCR została przedstawiona w poprzednim podrozdziale. Rozwiązując ten
model otrzymujemy całkowitą efektywność techniczną danej jednostki (e_crs). W modelu zo-
rientowanym na nakłady równa się ona θ
∗
zaś w modelu zorientowanym na efekty: 1/θ
∗
. Jeśli
θ
∗
= 1 wówczas dany obiekt określamy mianem efektywnego. Całkowita efektywność techniczna
2.2. Inne typy modeli DEA
15
obiektu w modelu zorientowanym na nakłady określa o ile (proporcjonalnie) należy zredukować
nakłady, aby osiągnąć efekty na tym samym co dotychczas poziomie. Rozważymy teraz przykład
analizy metodą DEA wykorzystującą zorientowany na nakłady model CCR przy czym rozwią-
zywać będziemy model (2.13)-(2.16) czyli wariant dualny (a od teraz pierwotny).
Przykład wyznaczania efektywności w modelu CCR
Rozważamy sześć jednostek decyzyjnych (DMU) reprezentujących firmy o podobnym profilu
działalności opisanych przy pomocy jednego nakładu oraz jednego efektu. Ograniczenie to pozwoli
dokonać graficznej ilustracji idei wyznaczania efektywności poszczególnych obiektów. Dane do
przykładu znalazły się w tabeli 2.3.
Tabela 2.3. Przykładowe nakłady i efekty dla sześciu firm
DMU 1
DMU 2
DMU 3
DMU 4
DMU 5
DMU 6
Nakład X
4
3
6
7
4
5
Efekt Y
10
4
15
16
7
10
Poniżej prezentujemy model CCR zorientowany na nakłady oraz jego rozwiązanie. Wartość
θ
∗
wyraża tu miarę efektywności technicznej. Sam model należy rozwiązać 6 razy, za każdym z
nich zmieniając wartości x
i
a także y
i
, wstawiając w te miejsca nakłady i efekty odpowiadające
obiektowi, dla którego obliczamy efektywność.
θ → min
(2.27)
4λ
1
+ 3λ
2
+ 6λ
3
+ 7λ
4
+ 4λ
5
+ 5λ
6
6 θx
i
(2.28)
10λ
1
+ 4λ
2
+ 15λ
3
+ 16λ
4
+ 7λ
5
+ 10λ
6
> y
i
(2.29)
λ
1
> 0,λ
2
> 0,λ
3
> 0,λ
4
> 0,λ
5
> 0,λ
6
> 0
(2.30)
Wyniki z tabeli 2.4 wskazują, że efektywne okazały się firmy oznaczone jako DMU1 i DMU3.
Oznacza to, że znalazły się one na krzywej efektywności. Firma DMU2, aby stać się efektyw-
ną powinna zużywać 1-0,5333=0,4667 jednostek mniej nakładu dla uzyskania tego samego co
dotychczas efektu. Na tej podstawie możemy wyznaczyć nowe, mniejsze wielkości nakładów, któ-
re pozwoliłyby na osiągnięcie niezmienionych efektów dla wszystkich nieefektywnych jednostek
decyzyjnych (czyli znalezienie się na krzywej efektywności). Stosowne obliczenia znalazły się w
tabeli 2.5.
Optymalna wartość parametru λ informuje jaką wielkość nakładu powinien zużyć dany obiekt
w porównaniu z jednostkami efektywnymi. Numer w nawiasie w wierszu λ
j
tabeli 2.4 podaje,
które spośród obiektów efektywnych stały się punktami odniesienia (tzw. benchmarkami) dla
Tabela 2.4. Wyniki dla modelu CCR zorientowanego na nakłady
DMU 1
DMU 2
DMU 3
DMU 4
DMU 5
DMU 6
e_crs
j
1
0,5333
1
0,9143
0,7
0,8
θ
∗
1
0,5333
1
0,9143
0,7
0,8
λ
j
0,4 (1)
0,6 (1)
0,7 (1)
1 (1)
16
2. Metoda DEA – charakterystyka i podział modeli
Tabela 2.5. Nowe wielkości nakładów w modelu CCR przy ustalonych efektach
Obiekt nieefektywny
Zmniejszone nakłady
DMU 2
0,5333 · 3 = 1,6
DMU 4
0,9143 · 7 = 6,4
DMU5
0,7 · 4 = 2,8
DMU 6
0,8 · 5 = 4
obiektów nieefektywnych. Tak się składa, że w naszym przykładzie porównywać będziemy wszyst-
kie nieefektywne jednostki decyzyjne jedynie z DMU1. DMU2 powinien więc zużyć 0,4 tego co
zużywa DMU1, czyli 0,4 · 4 = 1,6 jednostki w celu osiągnięcia efektu równego 4 jednostki.
Model CCR zorientowany na efekty, który podlega optymalizacji zapiszemy następująco:
θ → max
(2.31)
4λ
1
+ 3λ
2
+ 6λ
3
+ 7λ
4
+ 4λ
5
+ 5λ
6
6 x
i
(2.32)
10λ
1
+ 4λ
2
+ 15λ
3
+ 16λ
4
+ 7λ
5
+ 10λ
6
> θy
i
(2.33)
λ
1
> 0,λ
2
> 0,λ
3
> 0,λ
4
> 0,λ
5
> 0,λ
6
> 0
(2.34)
Współczynniki efektywności technicznej są w tym przypadku takie same jak dla modelu
zorientowanego na nakłady, ale powstały jako odwrotność wskaźnika efektywności θ
∗
. Siłą rzeczy
zachowany został podział na jednostki efektywne i nieefektywne technicznie. Należy przez to
rozumieć, że DMU1 i DMU3 w optymalny sposób wykorzystują posiadane nakłady.
Tabela 2.6. Wyniki dla modelu CCR zorientowanego na efekty
DMU 1
DMU 2
DMU 3
DMU 4
DMU 5
DMU 6
e_crs
j
1
0,5333
1
0,9143
0,7
0,8
1/θ
1
1,875
1
1,0938
1,4286
1,25
λ
j
0,75 (1)
1,75 (1)
0,67 (3)
1,25 (1)
Wybierzmy do analizy, podobnie jak poprzednio, obiekt DMU2. Zgodnie z danymi z tabeli
2.6, aby osiągnąć stuprocentową efektywność powinien on wytwarzać 1,875 raza większy efekt
(czyli 1,875 · 4 = 7,5 jednostki) wykorzystując do tego celu dotychczasową, niezmienioną wielkość
nakładu. Znalazłby się wtedy na krzywej efektywności. W tabeli 2.7 podajemy nowe, wyższe
wielkości efektów, które powinny być osiągnięte przez firmy nieefektywne, gdyby te optymalnie
wykorzystały posiadane nakłady.
Parametr lambda podaje jaki efekt osiąga dana jednostka decyzyjna w porównaniu z wzor-
cowymi jednostkami efektywnymi. DMU2 porównywać będziemy z DMU1. Wynika z tego, że
Tabela 2.7. Nowe wielkości efektów osiągane przy ustalonych nakładach w modelu CCR
Obiekt nieefektywny
Zwiększone efekty
DMU 2
1,875 · 4 = 7,5
DMU 4
1,0938 · 16 = 17,5
DMU 5
1,4286 · 7 = 10
DMU 6
1,25 · 10 = 12,5
2.2. Inne typy modeli DEA
17
●
●
●
●
●
●
0
2
4
6
8
0
5
10
15
20
Naklady
Ef
ekty
CRS
DMU1
DMU2
DMU3
DMU4
DMU5
DMU6
A1
A2
C1
C2
B1
B2
D2
D1
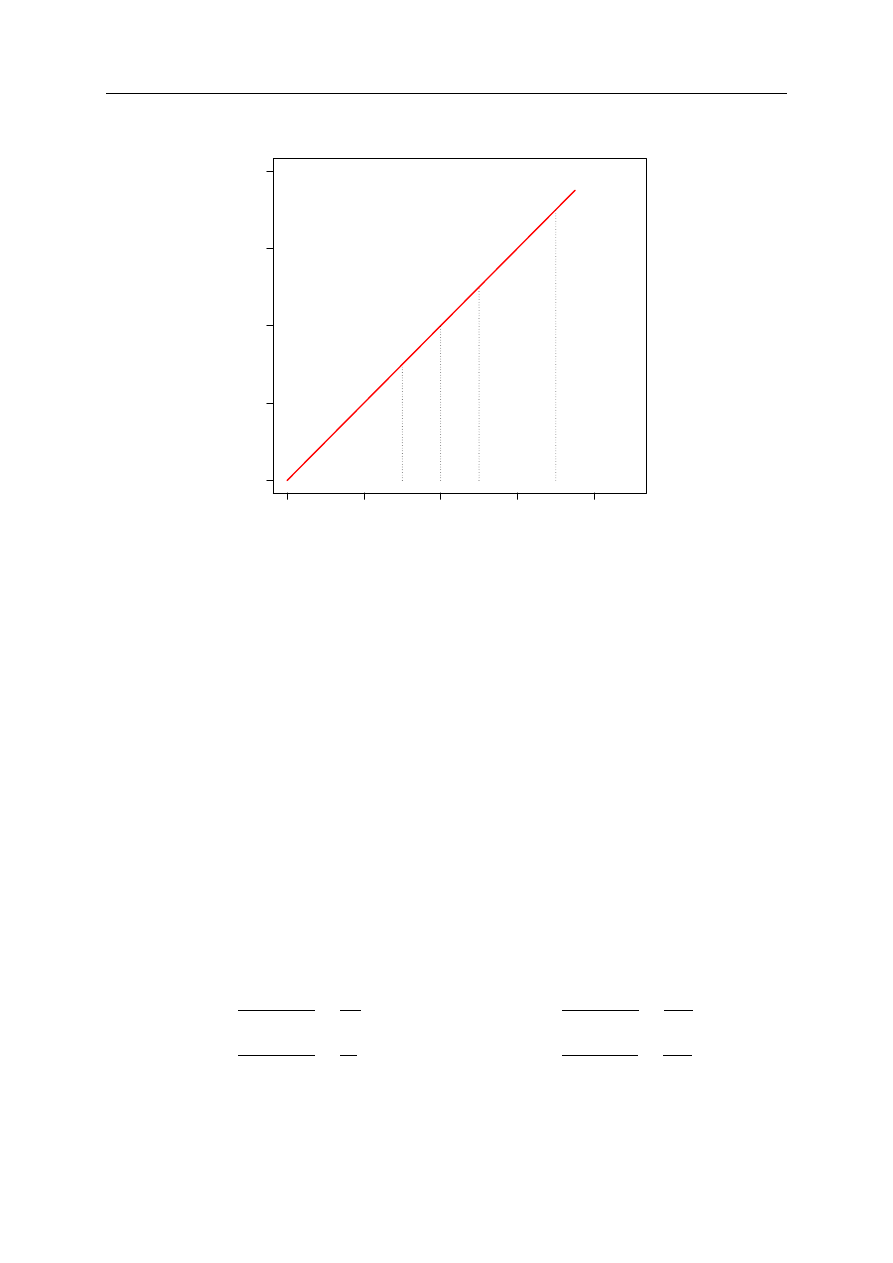
Rysunek 2.1. Krzywa całkowitej efektywności technicznej
nieefektywny obiekt, przy wykorzystaniu nakładów firmy efektywnej osiągałby efekt równy
0,75 ∗ 10 = 7,5 jednostki.
Wartości nakładów i efektów wykorzystamy jako współrzędne punktów odpowiadających
obiektom. Na rysunku 2.1 oprócz jednostek decyzyjnych znalazła się, wychodząca z początku
układu współrzędnych i oznaczona jako CRS, krzywa efektywności przy stałych efektach skali,
która dla modelu CCR wyznacza poziom całkowitej efektywności technicznej. Jednostki leżące na
krzywej w optymalny sposób wykorzystują nakłady czyli nie istnieje lepsza kombinacja efektów
osiąganych przy tych samych wielkościach nakładów. Dominują one nad jednostkami znajdują-
cymi się pod krzywą, dla których istnieje bardziej optymalna kombinacja efektów możliwa do
otrzymania przy wykorzystaniu tej samej wielkości nakładów.
Na krzywej CRS znalazły się dwa, znane nam już obiekty efektywne: DMU1 i DMU3 co
oznacza, że w ich przypadku θ
∗
= 1. Efektywność techniczną dla pozostałych jednostek graficznie
da się wyznaczyć następująco:
e_crs
DM U 2
=
|DMU2A
2
|
|A
1
A
2
|
=
4
7,5
= 0,5333
e_crs
DM U 4
=
|DMU4B
2
|
|D
1
D
2
|
=
16
17,5
= 0,9143
e_crs
DM U 5
=
|DMU5B
2
|
|B
1
B
2
|
=
7
10
= 0,7
e_crs
DM U 6
=
|DMU6C
2
|
|C
1
C
2
|
=
10
12,5
= 0,8
Przyjrzyjmy się obiektowi DMU2 w tym kontekście. Ma on współczynnik efektywności równy
0,5333. W kategoriach modelu zorientowanego na efekty oznacza to, że firma ta produkuje średnio
53,33% tego, co produkowałaby firma efektywnie wykorzystująca tą samą ilość nakładów. Przy

18
2. Metoda DEA – charakterystyka i podział modeli
obecnym nakładzie efekt powinien zatem wzrosnąć o 46,67% do 7,5 jednostki co spowodowałoby
znalezienie się na krzywej CRS.
Wykres na rysunku 2.1 da się również zinterpretować w kontekście modelu zorientowanego
na nakłady. DMU2 znalazłby się również na krzywej CRS zmniejszając nakłady o 46,67% do 1,6
jednostki.
W modelu CCR o stałych efektach skali określamy możliwą, proporcjonalną redukcję nakła-
dów przy zachowaniu co najmniej tej samej ilości efektów. Jeżeli chcemy analizować o ile mniej
nakładów można by wykorzystać do wyprodukowania tej samej ilości efektów musimy sięgnąć po
model BCC. Różni się on od modelu CCR założeniem zmiennych efektów skali. Wprowadzamy
w nim dodatkowe ograniczenie wypukłości, które oznaczyliśmy (2.38) oraz (2.43) w modelach
zorientowanych odpowiednio na nakłady i na efekty.
Model BCC zorientowany na nakłady:
θ
∗
= θ → min
(2.35)
n
X
j=1
x
pj
λ
j
6 θx
pi
(2.36)
n
X
j=1
y
rj
λ
j
> y
ri
(2.37)
n
X
j=1
λ
j
= 1
(2.38)
λ
j
> 0
(2.39)
Model BCC zorientowany na efekty:
θ
∗
= θ → max
(2.40)
n
X
j=1
x
pj
λ
j
6 x
pi
(2.41)
n
X
j=1
y
rj
λ
j
> θy
ri
(2.42)
n
X
j=1
λ
j
= 1
(2.43)
λ
j
> 0
(2.44)
Rozwiązaniem modelu BCC jest tzw. czysta efektywność techniczna (e_vrs). Podobnie jak
miało to miejsce w przypadku poprzednio omówionego modelu, efektywność ta jest równa θ
∗
w modelu zorientowanym na nakłady i 1/θ
∗
tej wielkości w modelu zorientowanym na efekty.
W odróżnieniu jednak od modelu CCR optymalne optymalne wartości funkcji celu z modelu
zorientowanego na nakłady oraz na efekty nie muszą być swoimi odwrotnościami.
Wyznaczona krzywa efektywności przy zmiennych efektach skali (VRS) opiera się na trzech
następujących aksjomatach:
1. nie ma darmowego lunchu – nie można produkować przy zerowych nakładach;
2. mogą istnieć koszty utopione – przy niskim poziomie nakładów produkcja nie jest możliwa;
3. zbiór możliwości produkcyjnych jest zwarty i wypukły.
Jeżeli efektywności przy stałych (model CCR) i zmiennych (model BCC) efektach skali istotnie
się od siebie różnią, to możemy określić efektywność skali zgodnie ze wzorem:
e_s_vrs =
e_crs
e_vrs
(2.45)
Efektywność skali dana wzorem (2.45) informuje o tym, o ile mniej nakładów można by
wykorzystać, gdyby wielkość efektów była optymalna. Interpretując ten wzór powiemy, że przy
e_s_vrs = 1 dana jednostka decyzyjna jest efektywna względem skali zaangażowanych czynni-
ków produkcji zaś e_s_vrs < 1 oznacza, że jest nieefektywna względem skali zaangażowanych
czynników produkcji choć nie wiadomo w jakim obszarze efektów skali dokładnie się znajduje.
2.2. Inne typy modeli DEA
19
Przykład wyznaczania efektywności w modelu BCC
Przyjrzyjmy się teraz, jak wygląda rozwiązanie modelu BCC dla danych z poprzedniego
przykładu. Zaczniemy od modelu zorientowanego na nakłady, który prezentujemy poniżej:
θ → min
4λ
1
+ 3λ
2
+ 6λ
3
+ 7λ
4
+ 4λ
5
+ 5λ
6
6 θx
i
10λ
1
+ 4λ
2
+ 15λ
3
+ 16λ
4
+ 7λ
5
+ 10λ
6
> y
i
λ
1
+ λ
2
+ λ
3
+ λ
4
+ λ
5
+ λ
6
= 1
λ
1
> 0,λ
2
> 0,λ
3
> 0,λ
4
> 0,λ
5
> 0,λ
6
> 0
Na podstawie wyników znajdujących się w tabeli 2.8 możemy stwierdzić, że przy założeniu
zmiennych efektów skali, efektywne okazały się nie tylko DMU1 i DMU3, ale również DMU2 i
DMU4. Obiekt DMU5 powinien zużywać 1 − 0,875 = 0,125 mniej nakładu, aby osiągnąć efekt
ten sam co do tej pory. Nowe, mniejsze wielkości nakładów dla obu nieefektywnych jednostek
decyzyjnych znalazły się w tabeli 2.9.
Tabela 2.8. Wyniki dla modelu BCC zorientowanego na nakłady
DMU 1
DMU 2
DMU 3
DMU 4
DMU 5
DMU 6
e_vrs
j
1
1
1
1
0,875
0,8
θ
∗
1
1
1
1
0,875
0,8
λ
j
0,5 (1)
1 (1)
0,5 (2)
Tabela 2.9. Nowe wielkości nakładów przy ustalonych efektach w modelu BCC
Obiekt nieefektywny
Zmniejszone nakłady
DMU5
0,875 · 4 = 3,5
DMU6
0,8 · 5 = 4
Parametry λ
j
podają wielkości nakładów, które winna zużyć jednostka nieefektywna w porów-
naniu z jednostkami wzorcowymi przy założeniu zmiennych efektów skali. Dla DMU5 benchmark
wyznaczają DMU1 i DMU2 więc firma DMU5 powinna zużywać połowę nakładu DMU1 oraz
połowę nakładu DMU2 czyli 0,5 · 4 + 0,5 · 3 = 3,5 jednostki, aby osiągnąć wymagany efekt.
W przypadku modelu zorientowanego na efekty optymalizowany model BCC ma postać:
θ → max
4λ
1
+ 3λ
2
+ 6λ
3
+ 7λ
4
+ 4λ
5
+ 5λ
6
6 x
i
10λ
1
+ 4λ
2
+ 15λ
3
+ 16λ
4
+ 7λ
5
+ 10λ
6
> θy
i
λ
1
+ λ
2
+ λ
3
+ λ
4
+ λ
5
+ λ
6
= 1
λ
1
> 0,λ
2
> 0,λ
3
> 0,λ
4
> 0,λ
5
> 0,λ
6
> 0
20
2. Metoda DEA – charakterystyka i podział modeli
Jego rozwiązanie znalazło się w tabeli 2.10. Wynika z niej, że w przypadku DMU5, przy
założeniu zmiennych efektów skali, aby osiągnąć stuprocentową efektywność powinien on wy-
twarzać 1,4286 · 7 = 10 jednostek wykorzystując do tego celu dotychczasową wielkość nakładu.
W tabeli 2.11 znalazły się efekty, które powinny osiągnąć firmy nieefektywne, gdyby optymalnie
wykorzystały posiadane nakłady.
Parametr lambda podaje jaki efekt osiąga dana jednostka decyzyjna w porównaniu z wzorco-
wymi jednostkami efektywnymi. DMU5 porównywać będziemy tylko z DMU1. Wynika z tego, że
przy wykorzystaniu nakładu firmy efektywnej DMU5 osiągałby efekt równy 1 · 10 = 10 jednostek.
Tabela 2.10. Wyniki dla modelu BCC zorientowanego na efekty
DMU 1
DMU 2
DMU 3
DMU 4
DMU 5
DMU 6
e_vrs
j
1
1
1
1
0,7
0,8
1/θ
∗
1
1
1
1
1,4286
1,25
λ
j
1 (1)
0,5 (1)
0,5 (3)
Tabela 2.11. Nowe wielkości efektów osiągane przy ustalonych nakładach w modelu BCC
Obiekt nieefektywny
Zwiększone efekty
DMU5
1,4286 · 7 = 10
DMU6
1,25 · 10 = 12,5
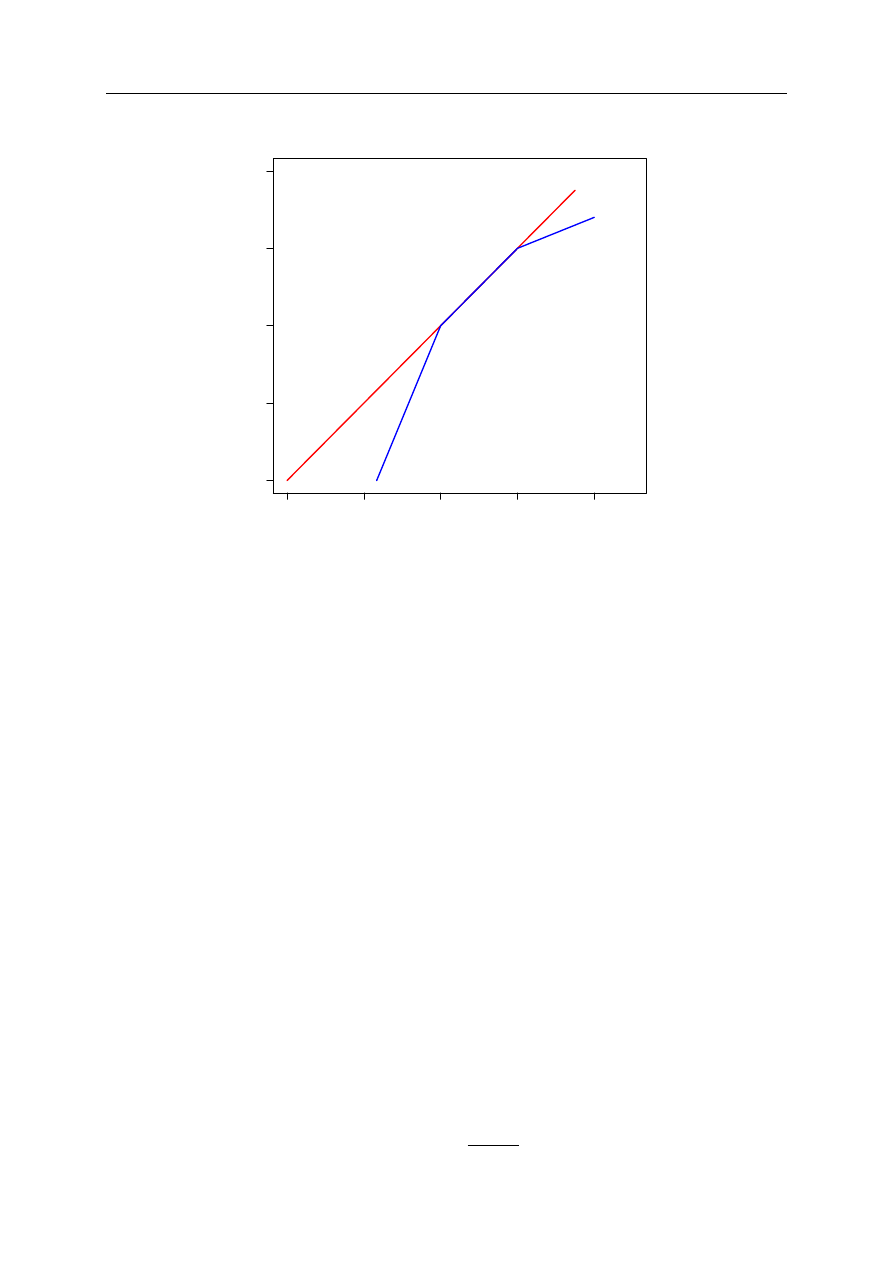
Na rysunku 2.2 oprócz krzywej CRS (stałe efekty skali) znalazła się krzywa VRS dla zmien-
nych efektów skali. Na mocy aksjomatu 2 nie przechodzi ona przez początek układu współrzęd-
nych. Widać wyraźnie, że jest ona odcinkami liniowa oraz to, że DMU5 i DMU6 wyraźnie znalazły
się poza samą krzywą (zostały zdominowane przez jednostki na krzywej).
Na podstawie efektywności zorientowanych na nakłady modeli CCR i BCC możemy sprawdzić
czy poszczególne jednostki decyzyjne są efektywne względem skali zaangażowanych czynników
produkcji. Wskaźniki e_crs (efektywności technicznej) oraz e_vrs (czystej efektywności tech-
nicznej) wraz z ich ilorazami obliczonymi na podstawie wzoru (2.45) podaje tabela 2.12. Wynika z
niej, że DMU2, DMU4 i DMU5 działają w obszarze zmiennych efektów skali. Nie wiemy natomiast
nic o rodzaju tych efektów.
Tabela 2.12. Miary efektywności i efekty skali modeli CCR i BCC
DMU1
DMU2
DMU3
DMU4
DMU5
DMU6
e_crs
1
0,5333
1
0,9143
0,7
0,8
e_vrs
1
1
1
1
0,875
0,8
e_s_vrs
1
0,5333
1
0,9143
0,8
1
Rozwiązując model BCC dowiadujemy się, czy dany obiekt znalazł się w obszarze zmiennych
efektów skali. Nie uzyskujemy jednak informacji, czy chodzi o rosnące, czy też malejące efek-
ty skali. Odpowiedź na to pytanie uzyskujemy dzięki rozwiązaniu modelu NIRS. Różni się on
od modelu BCC poluzowaniem ograniczenia dotyczącego współczynnik kombinacji liniowej. W
2.2. Inne typy modeli DEA
21
●
●
●
●
●
●
0
2
4
6
8
0
5
10
15
20
Naklady
Ef
ekty
CRS
VRS
DMU1
DMU2
DMU3
DMU4
DMU5
DMU6
Rysunek 2.2. Krzywe: całkowitej i czystej efektywności technicznej
Model NIRS zorientowany na nakłady:
θ
∗
= θ → min
(2.46)
n
X
j=1
x
pj
λ
j
6 θx
pi
(2.47)
n
X
j=1
y
rj
λ
j
> y
ri
(2.48)
n
X
j=1
λ
j
6 1
(2.49)
λ
j
> 0
(2.50)
Model NIRS zorientowany na efekty:
θ
∗
= θ → max
(2.51)
n
X
j=1
x
pj
λ
j
6 x
pi
(2.52)
n
X
j=1
y
rj
λ
j
> θy
ri
(2.53)
n
X
j=1
λ
j
6 1
(2.54)
λ
j
> 0
(2.55)
Niech e_nirs oznacza rozwiązanie tego modelu zorientowanego na nakłady. Posłuży ono
do określenia rejonu efektów skali, w którym operuje jednostka decyzyjna charakteryzująca się
zmiennymi efektami skali.
Wyznaczając wartość e_s_nirs zgodnie ze wzorem (2.56) dla każdego obiektu dowiadujemy
się, czy mamy do czynienia z rosnącymi czy malejącymi efektami skali. Jeżeli e_s_nirs = 1
wówczas jednostka decyzyjna działa w obszarze rosnących efektów skali. Wartość e_s_nirs < 1
świadczy o znalezieniu się w obszarze malejących efektów skali.
e_s_nirs =
e_crs
e_nirs
(2.56)
22
2. Metoda DEA – charakterystyka i podział modeli
Wyznaczymy teraz rozwiązanie modelu NIRS zorientowanego na nakłady dla danych z nasze-
go przykładu. Następnie poszerzymy tabelę 2.12 o nowe wskaźniki efektywności oraz wyznaczymy
efekty skali zgodnie ze wzorem (2.56).
Tabela 2.13. Wyniki dla modelu NIRS zorientowanego na nakłady
DMU1
DMU2
DMU3
DMU4
DMU5
DMU6
e_nirs
j
1
0,5333
1
1
0,7
0,8
θ
∗
1
0,5333
1
1
0,7
0,8
λ
j
0,1 (1)
0,26 (1)
0,43 (1)
0,2 (3)
0,29 (3)
0,38 (3)
●
●
●
●
●
●
0
2
4
6
8
0
5
10
15
20
Naklady
Ef
ekty
CRS
VRS
NIRS
DMU1
DMU2
DMU3
DMU4
DMU5
DMU6
Rysunek 2.3. Porównanie krzywych CRS, VRS i NIRS
DMU1 oraz DMU3 wypadły najlepiej zarówno pod względem stałych jak i zmiennych efek-
tów skali. Są więc jednostkami wzorcowymi dla pozostałych czterech firm. DMU2 i DMU4 są
wśród nich efektywne jedynie przy założeniu zmiennych efektów skali (jak informują nas warto-
ści e_vrs = 1), natomiast DMU6 jako jedyna okazała się spośród wspomnianych czterech firm
efektywna względem skali zaangażowanych środków (e_s_vrs = 1).
Spośród obiektów, które znalazły się w obszarze zmiennych efektów skali tylko DMU4 cha-
rakteryzował się malejącymi efektami skali. Pozostałe jednostki decyzyjne czyli: DMU2 i DMU5
odznaczają się rosnącymi efektami skali.
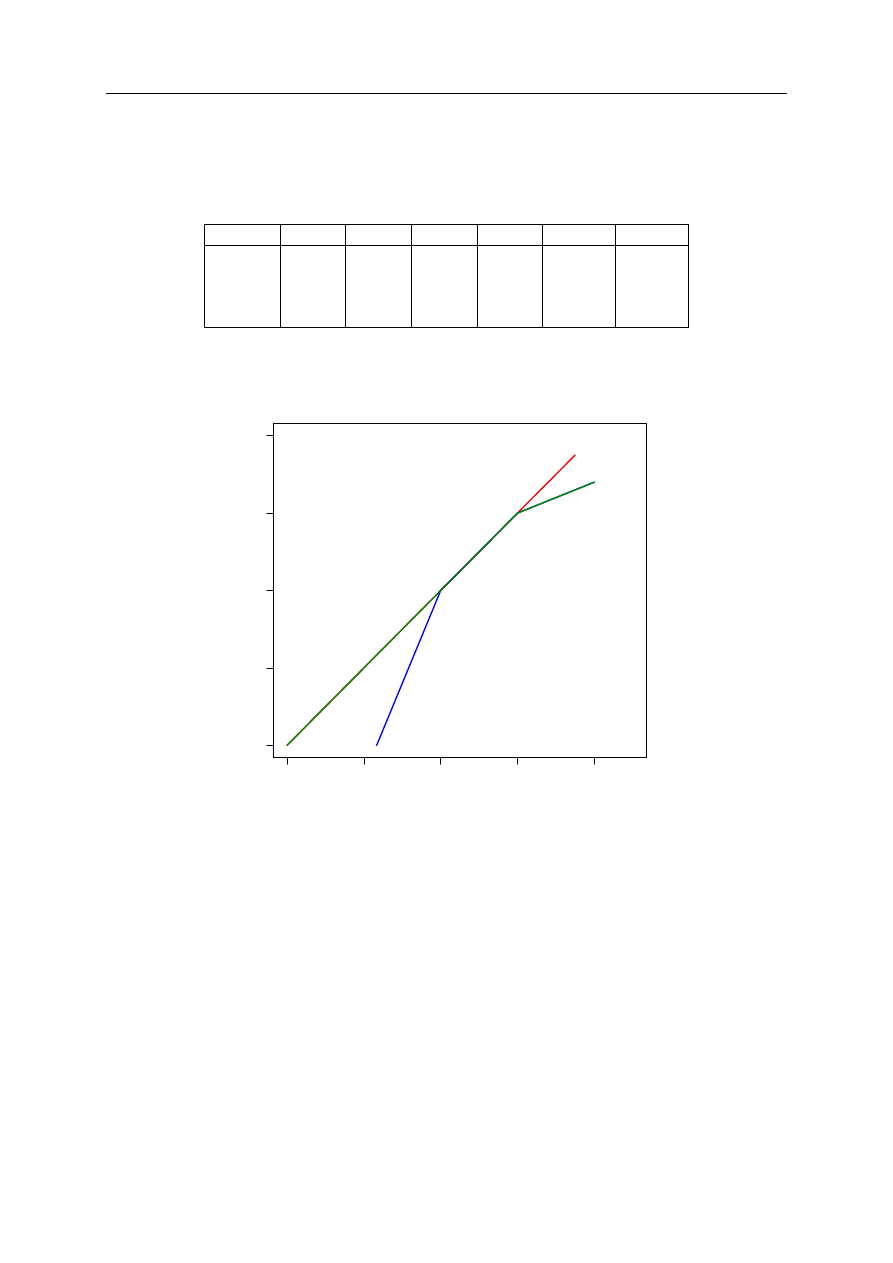
Krzywa efektywności NIRS pozwala określić gdzie na krzywej VRS znajdują się rosnące, a
gdzie malejące efekty skali. Ponieważ VRS nie przechodzi przez punkt (0,0) relacja efektów do
nakładów jest tu gorsza niż w przypadku krzywej CRS. Wzrost nakładów powoduje poprawę
2.2. Inne typy modeli DEA
23
Tabela 2.14. Miary efektywności i efekty skali modeli CCR, BCC i NIRS
DMU1
DMU2
DMU3
DMU4
DMU5
DMU6
e_crs
1
0,5333
1
0,9143
0,7
0,8
e_vrs
1
1
1
1
0,875
0,8
e_s_vrs
1
0,5333
1
0,9143
0,8
1
e_nirs
1
0,5333
1
1
0,7
0,8
e_s_nirs
1
1
1
0,9143
1
1
tej relacji co interpretujemy jako rosnące efekty skali. Na rysunku 2.3 krzywą NIRS oznaczono
zielonym kolorem.

3. Wybrane typy analiz w metodzie DEA
3.1. Technologia w modelach DEA
Każdy obiekt w metodzie DEA charakteryzuje się określoną technologią wynikającą z zestawu
posiadanych nakładów i osiąganych efektów. Połączony wektor nakładów i efektów wybranego
obiektu j nazywamy technologią empiryczną i zapisujemy go następująco:
t
j
=
"
x
j
y
j
#
(3.1)
Liniową kombinację technologii wszystkich obiektów uznajemy za technologię wspólną całego
ich zbioru. Technologia taka ma charakter teoretyczny. Znany nam już współczynnik λ
j
dla
DMU
j
staje się wagą określającą intensywność wykorzystania technologii empirycznej danego
obiektu w technologii wspólnej. Z tego powodu możemy spotkać się z określeniami takimi jak:
waga intensywności lub po prostu intensywność. Współczynniki te są parametrami kombinacji
liniowej wyznaczającej technologię wspólną całego zbioru obiektów (T):
T =
n
X
j=1
λ
j
t
j
(3.2)
Wspominaliśmy już o obiektach wzorcowych, z którymi porównywaliśmy obiekty nieefektyw-
ne. Obliczaliśmy m.in. ważone wielkości nakładów obiektów efektywnych, które powinien zużywać
obiekt nieefektywny, aby osiągnąć ustalone efekty. Było to nic innego jak właśnie wyznaczenie
technologii wspólnej na podstawie technologii empirycznych efektywnych jednostek decyzyjnych.
Nie nakładamy przy tym warunku, aby suma wag dawała 1, wymagamy jedynie ich nieujemności.
Zbiór technologii wspólnych dla wszystkich dopuszczalnych kombinacji parametrów lambda
nazywamy przestrzenią produkcyjną. Oczywiście zawierają się w niej również technologie empi-
ryczne samych obiektów, nie tylko ich kombinacje. Wzór (3.2) opisuje więc przestrzeń rozpiętą
na technologiach empirycznych danego zbioru obiektów. Jeżeli posiadamy informacje o innych
technologiach np. wzorcowych wówczas można do zadania wprowadzić dodatkowe obiekty. Nie
oceniamy ich efektywności, ale posłużą one do oceny efektywności pozostałych obiektów. Ważne
jest, aby brać pod uwagę technologie wiarygodne z punktu widzenia ich zastosowania, które na
przykład pojawiały się w praktyce. Rzecz jasna zaliczają się do nich technologie empiryczne.
Podsumowując, w metodzie DEA mamy do czynienia z trzema rodzajami technologii:
1. empiryczną;
2. dopuszczalną, za pomocą której możemy uzyskać dany wektor y
∗
> y efektów przy pomocy
możliwie najmniejszych nakładów x
∗
proporcjonalnych do nakładów x czyli x
∗
= θx;
3.1. Technologia w modelach DEA
25
3. optymalną, za pomocą której możemy uzyskać dany wektor ˆ
y > y efektów przy pomocy
możliwie najmniejszych nakładów x
∗
nieprzekraczających nakładów proporcjonalnych do x
czyli x
∗
6 θx.
Po raz kolejny mówimy o nakładach proporcjonalnych co nie znaczy, że nie mogą istnieć tech-
nologie, w których nie są one proporcjonalne do x. Rozpatrujemy efektywność Farrella-Debreu,
w której wskaźnik efektywności ˆ
θ interpretujemy jako proporcjonalne zmniejszenie nakładów
(krotność) do poziomu, który zapewni jednostce decyzyjnej stuprocentową efektywność co poka-
zywaliśmy we wcześniejszych przykładach.
Wartość współczynnika ˆ
θ w tym kontekście wyraża największe proporcjonalne zmniejszenie
nakładów potrzebnych do osiągnięcia założonych efektów. Geometrycznie oznacza to przesuwanie
się wzdłuż promienia technologicznego w stronę początku układu współrzędnych. Na rysunku 3.1
odpowiada to przesunięciu się z punktu A do punktu B (w obu punktach proporcja między nakła-
dami jest taka sama), w którym osiągamy największe dopuszczalne, proporcjonalne zmniejszenie
nakładów, aby osiągnąć efekty dane wektorem y. Przypomnijmy, że półprosta przechodząca przez
te punkty to promień technologiczny.
Dla modelu zorientowanego na nakłady efektywność radialna w ścisłym sensie oznacza pełną
komplementarność oraz zerową substytucję nakładów. W praktyce zdarza się przeważnie, że
przynajmniej jedna składowa optymalnego wektora nakładów bądź efektów może być mniej niż
proporcjonalna do składowej odpowiedniego wektora empirycznego oraz przynajmniej jedna taka
składowa jest proporcjonalna. Wówczas poza promieniem technologicznym znajdą się technologie
dopuszczalne, dla których efektywność również równa się ˆ
θ. W ich przypadku nie możemy mówić o
proporcjonalności nakładów (efektów) zaś sama technologia oddala się od promienia. Na rysunku
3.1 ilustruje to położenie punktu ˆ
x wyrażającego rozwiązanie optymalne. Wynika z tego, że
niekoniecznie musi ono znajdować się na promieniu technologicznym.
B
A
x
2
x
1
x
∗
2
= ˆ
x
2
x
∗
1
ˆ
x
ˆ
x
1
X
2
X
1
Rysunek 3.1. Graficzna ilustracja zmian proporcji nakładów dla technologii dopuszczalnych
Przy efektywności Farrella równej 1 i optymalnej technologii znajdującej się poza promieniem
technologicznym przynajmniej jeden nakład (dla tych samych efektów) jest większy niż nakład
minimalny – orientacja na nakłady lub przynajmniej jeden efekt jest mniejszy niż maksymalny
(przy założeniu stałych nakładów) – orientacja modelu na efekty. Technologie te nie są efektyw-
ne w sensie Pareto. Skutkuje to pojawieniem się luzów nakładów bądź efektów dla technologii z

26
3. Wybrane typy analiz w metodzie DEA
promienia i optymalnej. Tylko w sytuacji kiedy technologia optymalna leży na promieniu tech-
nologicznym luzy owe są równe zero. W przeciwnym wypadku dostosowanie się do rozwiązania
optymalnego oznacza zejście z promienia technologicznego.
Przez optymalne luzy nakładów w metodzie DEA należy rozumieć różnice między nakładami
technologii z promienia technologicznego o efektywności ˆ
θ = 1 a nakładami optymalnymi.
3.2. Analizy wynikające bezpośrednio z optymalizacji
Modele DEA dają możliwość różnorodnej analizy wyników. Na podstawie przykładu przed-
stawimy niektóre, wybrane przez nas jej rodzaje. Posłużymy się w tym celu danymi z rynku
Otwartych Funduszy Emerytalnych. Naszym zamiarem będzie ocena efektywności OFE z punk-
tu widzenia prowadzonej przez nie polityki inwestycyjnej. Należy w tym miejscu podkreślić,
ze jest to tylko jeden z możliwych kierunków analizy tego typu podmiotów, ponieważ można
rozpatrywać takie aspekty ich działalności jak choćby efektywność prowadzonej akwizycji. Rzecz
jasna wiązałoby się to z doborem innych nakładów i efektów.
Jako nakłady wybrane zostały następujące wielkości:
1. liczba martwych rachunków;
2. liczba członków, którzy opuścili fundusz;
3. koszty operacyjne (mln zł).
Zestaw efektów składał się zaś z wielkości jak poniżej:
1. liczba członków, którzy przystąpili do funduszu;
2. wartość składek przekazanych przez ZUS (mln zł, uwzględnia również należne i przekazane
odsetki);
3. średnia wartość jednostki rozrachunkowej (zł);
4. przychody z lokat (mln zł).
Dane pochodzą z oficjalnych raportów publikowanych przez Komisję Nadzoru Finansowego i
obejmują sprawozdania kwartalne oraz roczne za rok 2009 a zawarte zostały w tabeli 3.1.
Tabela 3.1. Dane na temat OFE w 2009 r.
Fundusz
Martwe
Opuściło
Koszty
Przystąpiło
Składki
Jednostka
Przychody
rach.
rozr.
AEGON
75610
54907
19,91
33402
832,46
25,19
278,3
Allianz
35635
41314
20,64
25355
1135,66
24,02
182,7
Amplico
39525
34994
41,98
28464
1098,99
24,42
475,59
Aviva
71122
79939
175,69
54819
4246,26
25,07
1624,85
AXA
23309
38033
37,39
93829
984,16
25,37
336,26
Generali
64614
41091
14,94
38727
1666,73
26,75
273,54
ING
118072
35989
134,83
53752
1979,4
26,97
1561,9
Nordea
85452
65597
31,41
82719
4434,78
25,94
249,3
Pekao
28484
34401
13,69
35997
761,53
24,29
109,49
Bankowy
39024
18415
23,15
7099
443,4
24,51
187,66
Pocztylion
79347
26411
16,73
6810
491,59
23,85
128,91
Polsat
13829
16056
7,69
280
285,68
27,5
47,12
PZU
110709
62210
103,49
91041
2821,96
25,6
937,89
WARTA
37397
19727
12,1
16790
335,55
25,79
98,41
3.2. Analizy wynikające bezpośrednio z optymalizacji
27
Jako pierwsze podamy wyniki optymalizacji zorientowanego na nakłady modelu CCR dla 2009
roku. Znalazły się one w tabeli 3.2. Liczby w nawiasach w kolumnie „lambda” jak poprzednio,
oznaczają numery obiektów wzorcowych. Na podstawie zawartych tam wyników stwierdzamy,
że brakiem efektywności przy założeniu stałych efektów skali charakteryzowały się następujące
fundusze emerytalne: AEGON, Allianz, Bankowy, Pocztylion i PZU, przy czym najmniej efek-
tywny okazał się OFE Pocztylion (współczynnik równy 0,7194). Pozostałe fundusze znalazły
się na krzywej efektywności CRS. Fakt, że większość funduszy solidarnie na niej się ulokowała
świadczy o prowadzeniu podobnej polityki inwestycyjnej.
Najmniej efektywny fundusz emerytalny powinien zużywać średnio 28,06% mniej nakładów,
aby osiągnąć te same efekty. Innymi słowy, gdyby OFE Pocztylion skonstruował swoją technologię
na wzór tych funduszy efektywnych, które wyznaczają dla niego benchmark (czyli Generali, ING
i Polsat) wykorzystałby 71,94% swoich nakładów.
Wartości parametrów lambda pozwalają określić jakie wielkości nakładów powinien zużyć
nieefektywny fundusz gdyby stosował optymalną technologię wzorowaną na technologiach trzech
wzorcowych funduszy. Jeżeli przez t
6
,t
7
,t
12
oznaczymy technologie empiryczne odpowiednio:
Generali, ING i OFE Polsat wtedy ogólna formuła optymalnej technologii zorientowanej na OFE
Pocztylion ( ˆ
T
11
) ma postać daną wzorem (3.3) Składa się więc ona z 17% technologii stosowanej
w funduszu Generali, 3% technologii stosowanej w funduszu ING oraz 67% technologii używanej
w OFE Polsat. Podstawiając nakłady i efekty wzorcowych funduszy do wzoru (3.3) otrzymamy
nowe wartości technologii optymalnej dla OFE Pocztylion.
ˆ
T
11
= 0,17t
6
+ 0,03t
7
+ 0,67t
12
(3.3)
W tym miejscu należy zwrócić uwagę na różnice wartości współczynników lambda w kombina-
cji obiektów wzorcowych. Najniższy z nich ma wartość 0,03 zaś najwyższy 0,67. Przypominamy,
że jest to krotność wykorzystania nakładów wzorcowego DMU. Wartość λ
ij
zależy od skali na-
kładów i efektów obiektu ocenianego oraz wzorcowego. Tym samym jeśli na przykład DMU
podlegający ocenie okaże się dużo mniejszy od DMU wzorcowego wówczas współczynnik lambda
musi być niewielki.
Tabela 3.2. Wyniki optymalizacji zorientowanego na nakłady modelu CCR dla 2009 roku
Lp
Nazwa OFE
e_crs
λ
j
(benchmark)
1
AEGON
0,8096
0,02 (3); 0,91 (6); 0,01 (7)
2
Allianz
0,8999
0,17 (3); 0,06 (5); 0,09 (6); 0,14 (8); 0,45 (12)
3
Amplico
1
4
Aviva
1
5
AXA
1
6
Generali
1
7
ING
1
8
Nordea
1
9
Pekao
1
10
Bankowy
0,9094
0,01 (5); 0,11 (7); 0,78 (12)
11
Pocztylion
0,7194
0,17 (6); 0,03 (7); 0,67 (12)
12
Polsat
1
13
PZU
0,8739
0,41 (5); 0,46 (7); 0,34 (8)
14
WARTA
1
28
3. Wybrane typy analiz w metodzie DEA
Tabela 3.3. Wyznaczenie technologii optymalnej dla OFE Pocztylion za 2009 rok
Benchmark
Generali
ING
Polsat
Pocztylion
λ
11j
0,17
0,03
0,67
technologia
udział w techn.
×
×
×
optymalna
empirycznej
Martwe rach.
64614
118072
13829
23791,97
29,98%
Opuściło
41091
35989
16056
18822,66
71,27%
Koszty oper.
14,94
134,83
7,69
11,74
70,16%
Przystąpiło
38727
53752
280
8383,75
123,11%
Składki
1666,73
1979,4
285,68
534,13
108,65%
Jednostka rozr.
26,75
26,97
27,5
23,78
99,71%
Przychody
273,54
1561,9
47,12
124,93
96,91%
Z tabeli 3.3 wynika, że wzorcowe fundusze emerytalne uczestniczące w optymalnej technolo-
gii zorientowanej na fundusz Pocztylion potrafiłyby osiągnąć jego efekty wykorzystując do tego
znacznie mniejsze nakłady. Szczególnie mocno widać to w przypadku liczby martwych rachunków,
których liczba spadłaby w takiej sytuacji do około 30% liczby martwych rachunków faktycznie
odnotowanych przez fundusz nieefektywny. Zdecydowanie ma on tu wiele do zrobienia. Pozostałe
nakłady nie są aż tak radykalnie mniejsze, ale oscylują w okolicach 70% tego czym w rzeczywi-
stości dysponuje OFE Pocztylion przez co należy rozumieć, że angażuje on mniej więcej o 30%
nakładów za dużo osiągając podane powyżej efekty.
Widać chyba wyraźnie jak nieefektywna była technologia wspomnianego OFE w 2009 roku.
Zwróćmy również uwagę na fakt, że wartość jednostki rozrachunkowej oraz wartość przychodów
operacyjnych są nieco niższe od tych osiąganych przez analizowany fundusz. Może to świadczyć
o oddaleniu się od promienia technologicznego. Tak się bowiem składa, że dla liczby martwych
rachunków oraz dwóch efektów: liczby osób, które przystąpiły do funduszu i kwoty składek prze-
kazanych przez ZUS wystąpiły luzy, które w celu dostosowania się do rozwiązania optymalnego
wymusiły zejście z promienia technologicznego.
W tabeli 3.4 prezentujemy wyniki dla zorientowanego na nakłady modelu BCC. Okazało się,
że przy założeniu zmiennych efektów skali liczba nieefektywnych obiektów spada o jeden. Zbiór
powiększył się o OFE PZU „Złota Jesień”, który w modelu CCR znalazł się pod krzywą efektyw-
ności okazując teraz się efektywnym względem skali zaangażowanych czynników produkcji.
Dla modelu BCC również można przeprowadzić analizy nakładów bądź efektów podobne
do tych, które wykonaliśmy dla modelu CCR. Zostawiamy to zainteresowanym czytelnikom. My
natomiast, po zoptymalizowaniu zorientowanego na nakłady modelu NIRS przystąpimy do oceny
efektów skali. W tabeli 3.5 porównujemy wyniki trzech trzech wspomnianych modeli.
Analizując wartości e_s_vrs zauważamy, że pięć funduszy emerytalnych: AEGON, Allianz,
Bankowy, Pocztylion i OFE PZU w 2009 roku działały w obszarze zmiennych efektów skali.
Ostatnia kolumna tabeli zawierająca wskaźnik e_s_nirs informuje nas, że tylko ostatni spośród
wymienionych funduszy odznaczał się malejącymi efektami skali. Pozostałe cztery znalazły się w
obszarze rosnących efektów skali. Trzeba jednak zwrócić uwagę na fakt, że są one nieefektywne
tak przy stałych, jak i przy zmiennych efektach skali. Są więc nieefektywne technologicznie (nie
wykorzystują posiadanych nakładów w dostatecznym stopniu).
3.3. Ranking obiektów a superefektywność
29
Tabela 3.4. Wyniki optymalizacji zorientowanego na nakłady modelu BCC dla 2009 roku
Lp
Nazwa OFE
e_vrs
λ
j
(benchmark)
1
AEGON
0,8162
0,06 (3); 0,91 (6); 0,03 (12)
2
Allianz
0,9181
0,16 (3); 0,07 (5); 0,09 (6); 0,13 (8); 0,55 (12)
3
Amplico
1
4
Aviva
1
5
AXA
1
6
Generali
1
7
ING
1
8
Nordea
1
9
Pekao
1
10
Bankowy
0,9931
0,00 (5); 0,09 (7); 0,8 (12); 0,11 (14)
11
Pocztylion
0,7689
0,14 (6); 0,03 (7); 0,82 (12)
12
Polsat
1
13
PZU
1
14
WARTA
1
Tabela 3.5. Efekty skali OFE w 2009 roku
Lp
Nazwa OFE
e_crs
e_vrs
e_nirs
e_s_vrs
e_s_nirs
1
AEGON
0,8096
0,8162
0,8096
0,9919
1
2
Allianz
0,8999
0,9181
0,8999
0,9802
1
3
Amplico
1
1
1
1
1
4
Aviva
1
1
1
1
1
5
AXA
1
1
1
1
1
6
Generali
1
1
1
1
1
7
ING
1
1
1
1
1
8
Nordea
1
1
1
1
1
9
Pekao
1
1
1
1
1
10
Bankowy
0,9094
0,9931
0,9094
0,9157
1
11
Pocztylion
0,7194
0,7689
0,7194
0,9356
1
12
Polsat
1
1
1
1
1
13
PZU
0,8739
1
1
0,8739
0,8739
14
WARTA
1
1
1
1
1
3.3. Ranking obiektów a superefektywność
Wskaźnik efektywności ˆ
θ dobrze nadaje się do porządkowania jednostek decyzyjnych. Intu-
icyjnie zrozumiałe jest, że w tak utworzonym rankingu obiekty o niższym wskaźniku efektywności
zajmować będą dalsze pozycje. Problem stanowią jednak obiekty efektywne, ponieważ dla każ-
dego z nich ˆ
θ = 1. Pojawia się więc nadmiar liderów rankingu. Taka sytuacja nie wystąpi jedynie
wtedy, gdy w pełni efektywny okaże się tylko jeden obiekt. Rozwiązanie problemu stanowi wy-
korzystanie pojęcia tzw. superefektywności.
W modelu DEA z superefektywnością nadal oceniamy DMU na tle wszystkich pozostałych
obiektów, ale po tym razem następuje to wyłączeniu go ze zbioru. Sama nazwa wzięła stąd, że
wskaźnik efektywności może przyjmować wartości większe od 1, a model możemy traktować jako
uogólnienie klasycznych modeli DEA. Do wyznaczenia superefektywności używa się modeli CCR
(tak zorientowanych na nakłady, jak i na efekty).

30
3. Wybrane typy analiz w metodzie DEA
Punkt wyjścia modeli z superefektywnością jest następujący: jeżeli inne obiekty radzą sobie
z zadaniami danego DMU gorzej od niego, to jest on efektywny.
Założenia dla modelu zorientowanego na nakłady sformułowane przez Bankera, Gilforda,
Andersena i Petersena brzmią jak poniżej:
1. model CCR rozszerzamy o warunek, że własny (tj. dla analizowanego obiektu) współczynnik
λ jest równy zero;
2. współczynnik ˆ
θ nie musi być mniejszy lub równy 1.
Pomijając powyższe założenia, w modelu zorientowanym na nakłady nadal minimalizujemy
współczynnik efektywności. Poszukujemy więc takich wartości λ
ij
, których kombinacja wyznacza-
jąca technologię wspólną zapewni przynajmniej efekty osiągane przez DMU
i
przy czym nakłady
technologii wspólnej są proporcjonalne do nakładów obiektu DMU
i
, lecz nie występuje w niej
technologia tego obiektu. Rozpatrujemy więc daną jednostkę decyzyjną na tle zbioru wszyst-
kich pozostałych jednostek, które traktować należy jako konkurencyjne wobec niej. Optymalną
wartość funkcji celu w zorientowanym na nakłady modelu z superefektywnością interpretuje-
my jako minimalne nakłady konkurentów wymagane do zrealizowania efektów danego obiektu
decyzyjnego.
Wartość współczynnika ˆ
θ < 1 modelu z superefektywnością oznacza, że obiekt jest nieefek-
tywny, a więc konkurencja uporałaby się z jego zadaniami wykorzystując mniejsze nakłady. Z
kolei dla obiektu efektywnego zachodzi ˆ
θ > 1, przy czym:
1. ˆ
θ > 1 oznacza, że dla osiągnięcia efektów danej jednostki decyzyjnej konkurenci potrzebowa-
liby więcej nakładów niż te, które badana jednostka faktycznie poniosła;
2. ˆ
θ = 1 oznacza, że dana jednostka decyzyjna jest nie gorsza od konkurentów.
Pomiędzy efektywnościami e_crs z modeli klasycznych a takimi, w których wprowadzono super-
efektywność występują pewne różnice:
1. w przypadku obiektów nieefektywnych wartość współczynnika efektywności jest w obu typach
modeli taka sama;
2. w przypadku obiektów efektywnych z punktu widzenia klasycznego modelu CCR superefek-
tywność jest różna dla tych jednostek i pozwala na określenie, który DMU jest bardziej
efektywny.
Dzięki drugiej z wymienionych różnic otrzymujemy możliwość uporządkowania obiektów od naj-
bardziej do najmniej efektywnego. Warto przy tym pamiętać, że tak wyznaczony ranking będzie
identyczny dla modelu zorientowanego na nakłady i zorientowanego na efekty.
Przypomnijmy, że w klasycznym modelu DEA obiekty efektywne lokowały się na granicy
efektywności. Jednak wykluczenie jednego z obiektów przy ustalaniu rozwiązania optymalnego
powoduje, że tworzy się odmienna od dotychczasowej, lokalna granica efektywności o następują-
cych własnościach:
1. każdemu obiektowi efektywnemu odpowiada inna lokalna granica efektywności pod warun-
kiem, że każdy z nich ma inną technologię. W przeciwnym wypadku kilku obiektom może
odpowiadać jedna granica lokalna;
2. dla obiektu nieefektywnego lokalna i globalna granica efektywności jest taka sama;
3. jeśli obiekt nieefektywny leży na lokalnej granicy efektywności innego obiektu jego efektyw-
ność nie jest równa 1.
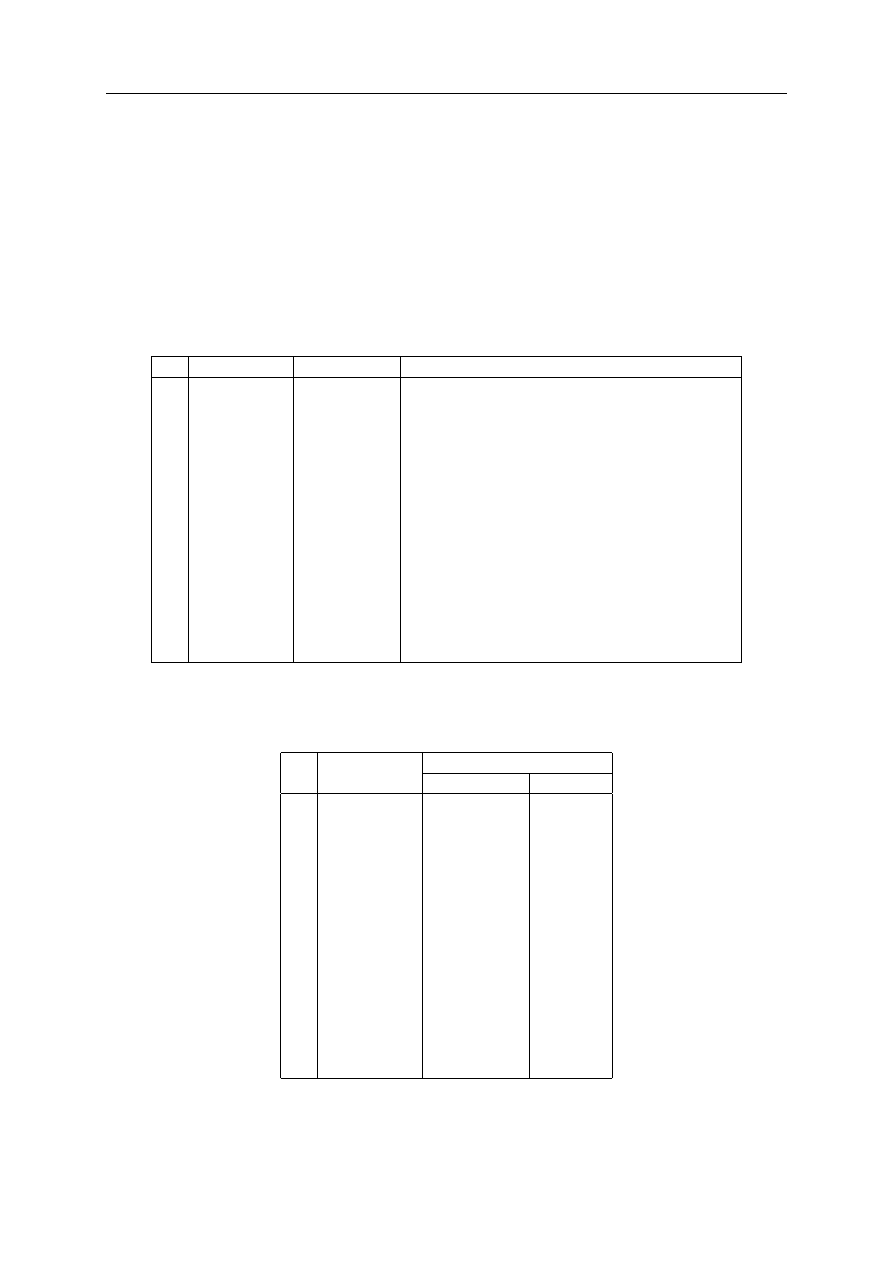
3.3. Ranking obiektów a superefektywność
31
Przykład wyznaczania superefektywności
Powyższe rozważania zilustrujemy przykładem bazującym na danych dotyczących rynku fun-
duszy emerytalnych w 2009 roku. Obliczenia wykonaliśmy dla zorientowanego na nakłady modelu
CCR, w którym uwzględniliśmy występowanie superefektywności a wyniki umieściliśmy w tabeli
3.6. Oczywiście fundusze, które były nieefektywne w tabeli 3.2 nadal pozostają nieefektywne z
tymi samymi wartościami współczynników. Z kolei tabela 3.7 zawiera ranking OFE z punktu
widzenia osiąganej przez nie efektywności. Przez superefektywność względną należy rozumieć
podzielenie wartości każdego ze wskaźników efektywności przez najwyższy otrzymany wynik ˆ
θ.
Tabela 3.6. Wyniki optymalizacji zorientowanego na nakłady modelu CCR z superefektywnością
Lp
Nazwa OFE
Efektywność
λ
j
(benchmark)
1
AEGON
0,8096
0,02 (3); 0,91 (6); 0,01 (7)
2
Allianz
0,8999
0,17 (3); 0,06 (5); 0,09 (6); 0,14 (8); 0,45 (12)
3
Amplico
1,0631
4
Aviva
1,7343
5
AXA
3,2268
6
Generali
1,5322
7
ING
2,1732
8
Nordea
1,8506
9
Pekao
1,2016
10
Bankowy
0,9094
0,01 (5); 0,11 (7); 0,78 (12)
11
Pocztylion
0,7194
0,17 (6); 0,03 (7); 0,67 (12)
12
Polsat
2,3317
13
PZU
0,8739
0,41 (5); 0,46 (7); 0,34 (8)
14
WARTA
1,0140
Tabela 3.7. Ranking OFE na podst. modelu z superefektywnością
Superefektywność
Lp
Nazwa OFE
bezwzględna
względna
1
AXA
3,2268
1
2
Polsat
2,3317
0,7226
3
ING
2,1732
0,6735
4
Nordea
1,8506
0,5735
5
Aviva
1,7343
0,5375
6
Generali
1,5322
0,4748
7
Pekao
1,2016
0,3724
8
Amplico
1,0631
0,3295
9
WARTA
1,0140
0,3142
10
Bankowy
0,9094
0,2818
11
Allianz
0,8999
0,2789
12
PZU
0,8739
0,2708
13
AEGON
0,8096
0,2509
14
Pocztylion
0,7194
0,2229
Najbardziej efektywnym funduszem emerytalnym w 2009 roku okazał OFE AXA (por. tabela
3.7). Aby osiągnąć swoje efekty potrzebował on ponad trzy razy mniej nakładów niż musiałyby

32
3. Wybrane typy analiz w metodzie DEA
ich zużyć pozostałe fundusze w ramach optymalnej technologii wspólnej. Konkurenci najsłab-
szego z funduszy efektywnych – OFE WARTA dla osiągnięcia jego efektów musieliby ponieść
nakłady zaledwie o 1,4% większe od tych jakie empirycznie zastosował OFE WARTA.
Analizując względną superefektywność zauważamy, że efektywność drugiego na liście OFE
Polsat stanowi niewiele ponad 70% efektywności najlepszego funduszu. Najmniej efektywny –
Pocztylion charakteryzuje się jeszcze mniej korzystnym stosunkiem, bo wynoszącym nieco ponad
20%. Świadczy to o dużym zróżnicowaniu efektywności poszczególnych funduszy emerytalnych.
Wyznaczając technologie optymalne obiektów efektywnych w sensie modelu CCR musimy
pamiętać, że w tym wypadku otrzymujemy technologie optymalne konkurentów danego obiektu.
W przypadku nieefektywnych jednostek decyzyjnych postępowanie mające na celu otrzymanie
technologii optymalnej nie różni się od tego z klasycznego modelu CCR.
Z uwagi na to, że w modelu z superefektywnością współczynnik ˆ
θ
i
może być większy od 1, ale
nie określamy jego górnej wartości istnieje niebezpieczeństwo, że przyjmie on bardzo duże war-
tości. Mówimy wtedy o braku jednorodności zbioru obiektów wybranych do badania. Zwróćmy
uwagę, że dla zwykłych modeli DEA takiego wniosku nie jesteśmy w stanie wyciągnąć.
Za nietypowe uznajemy te obiekty, dla których superefektywność znalazła się poza pewną,
założoną z góry granicą. W tym celu ustalamy progi górny (θ
G
) i dolny (θ
D
) po czym porów-
nujemy z nimi efektywności uzyskane w toku obliczeń. Jeżeli ˆ
θ
i
> θ
G
lub ˆ
θ
i
< θ
D
obiekt taki
uznajemy za nietypowy i usuwamy ze zbioru. Całe postępowanie da się ująć w ramy następującej
procedury:
1. Rozwiązujemy zadanie dla wszystkich obiektów.
2. Odrzucamy te obiekty, dla których zachodzi ˆ
θ
i
> θ
G
.
3. Rozwiązujemy zadanie ponownie, już dla nowego zbioru obiektów.
4. Jeżeli nadal występują obiekty o ˆ
θ
i
> θ
G
wracamy do etapu 2. W przeciwnym przypadku
przechodzimy dalej.
5. Odrzucamy obiekty, dla których zachodzi ˆ
θ
i
< θ
D
.
6. Tak otrzymany zbiór możemy uznać za jednorodny.
Etap odrzucania obiektów o zbyt małej wartości ˆ
θ
i
przeprowadzamy na końcu ponieważ po
ponownym obliczeniu wskaźniki efektywności będą nie mniejsze od poprzednich. Zatem tak w
pełnym, jak i w zredukowanym zbiorze obiektów cały czas będzie zachodzić ˆ
θ
i
< θ
D
.
3.4. Dynamika zmian w modelach DEA
Modele DEA oparte na efektywności Farrella nie muszą ograniczać się do analiz o charakte-
rze statycznym. Istnieje również możliwość badania zmian dynamiki efektywności. Jako punkt
wyjścia potraktujemy tzw. odległość Shepharda (D
•
(x
•
,y
•
)). Jest to odwrotność optymalnej efek-
tywności z modelu zorientowanego na nakłady czyli 1/ˆ
θ. Pochodzić więc może bezpośrednio z
modelu CCR zorientowanego na efekty (taką właśnie interpretację ma tam wartość funkcjis celu)
lub może zostać obliczona na podstawie wyników optymalizacji modelu CCR zorientowanego na
nakłady. Zapiszemy zatem:
D
•
(x
•
,y
•
) =
1
ˆ
θ
(3.4)

3.4. Dynamika zmian w modelach DEA
33
Tabela 3.8. Sposoby wyznaczania odległości Shepharda
LHS
RHS
D
•
(x
•
,y
•
)
technologia
obiekt
D
t
(x
t
,y
t
)
z okresu t
z okresu t
D
t+1
(x
t+1
,y
t+1
)
z okresu t + 1
z okresu t + 1
D
t
(x
t+1
,y
t+1
)
z okresu t
z okresu t + 1
D
t+1
(x
t
,y
t
)
z okresu t + 1
z okresu t
Symbol • przy D oznacza technologię w okresie t lub t + 1 (przy założeniu, że porównujemy
dwa sąsiednie okresy) zaś przy zmiennych (x,y) okres z którego pochodzą nakłady i efekty.
Odległości Shepharda obliczamy określając w odpowiedni sposób parametry lewych oraz prawych
stron ograniczeń obecnych w modelu DEA co ilustruje tabela 3.8.
W związku z zależnościami podanymi w tabeli 3.8 odległości D
t
(x
t
,y
t
) oraz D
t+1
(x
t+1
,y
t+1
)
otrzymujemy na przykład poprzez rozwiązanie zorientowanych na efekty modeli CCR dla danych
dotyczących nakładów i efektów pochodzących z okresów odpowiednio t i t + 1. Model zorien-
towany na efekty pozwalający wyznaczyć odległości Shepharda D
t
(x
t+1
,y
t+1
) prezentuje się jak
poniżej:
θ
∗
= θ → max
(3.5)
n
X
j=1
x
t
pj
λ
j
6 x
t+1
pi
(3.6)
n
X
j=1
y
t
rj
λ
j
> θy
t+1
ri
(3.7)
λ
j
> 0
(3.8)
Odległości dane jako D
t+1
(x
t
,y
t
) wyznaczymy z następującego modelu:
θ
∗
= θ → max
(3.9)
n
X
j=1
x
t+1
pj
λ
j
6 x
t
pi
(3.10)
n
X
j=1
y
t+1
rj
λ
j
> θy
t
ri
(3.11)
λ
j
> 0
(3.12)
Zmiany efektywności (zwanej w literaturze w tym przypadku również produktywnością) po-
między okresami t oraz t + 1 możemy oceniać wykorzystując tzw. indeksy Malmquista. Opierają
się one na modelach CCR a więc nie informują o zmianach efektów skali. Warto przy tym dodać,
że niezależnie od tego czy wyznaczymy je na podstawie modelu zorientowanego na nakłady czy
na efekty ich wartość liczbowa będzie taka sama.
Indeks Malmquista dla okresu t ma postać:

34
3. Wybrane typy analiz w metodzie DEA
M
t
(x
t
,y
t
,x
t+1
,y
t+1
) =
D
t
(x
t+1
,y
t+1
)
D
t
(x
t
,y
t
)
(3.13)
Z kolei indeks Malmquista dla okresu t + 1 obliczamy następująco:
M
t+1
(x
t
,y
t
,x
t+1
,y
t+1
) =
D
t+1
(x
t+1
,y
t+1
)
D
t+1
(x
t
,y
t
)
(3.14)
Wzór (3.13) porównuje efektywność (produktywność) obiektu w okresie t + 1 z jego efektyw-
nością w okresie t, wykorzystując jako punkt odniesienia technologię z okresu t. Natomiast wzór
(3.14) pozwala na porównywanie efektywności) obiektu w okresie t + 1 z jego efektywnością w
okresie t, wykorzystując jako punkt odniesienia technologię z okresu t + 1.
Indeksy Malmquista uśredniamy przy pomocy średniej geometrycznej w celu określenia zmian
w efektywności działania obiektu pomiędzy okresami t i t + 1 (wzór (3.15)).
M
t,t+1
(x
t
,y
t
,x
t+1
,y
t+1
) =
s
D
t
(x
t+1
,y
t+1
)
D
t
(x
t
,y
t
)
·
D
t+1
(x
t+1
,y
t+1
)
D
t+1
(x
t
,y
t
)
(3.15)
Po przekształceniach średniej geometrycznej uzyskamy:
M
t,t+1
(x
t
,y
t
,x
t+1
,y
t+1
) = T E(x
t
,y
t
,x
t+1
,y
t+1
) · T C(x
t
,y
t
,x
t+1
,y
t+1
)
(3.16)
gdzie:
T E(x
t
,y
t
,x
t+1
,y
t+1
) =
D
t+1
(x
t+1
,y
t+1
)
D
t
(x
t
,y
t
)
(3.17)
T C(x
t
,y
t
,x
t+1
,y
t+1
) =
s
D
t
(x
t+1
,y
t+1
)
D
t+1
(x
t+1
,y
t+1
)
·
D
t
(x
t
,y
t
)
D
t+1
(x
t
,y
t
)
(3.18)
TE wyraża zmianę efektywności technicznej, która określa relatywną zmianę efektywności
obiektu pomiędzy okresami t i t + 1 bez uwzględnienia zmiany położenia krzywej efektywności
(efektywność jest mierzona względem krzywej z odpowiedniego okresu t albo t + 1).
TC zaś jest miernikiem zmiany technicznej (związanej z postępem technologicznym), która
określa relatywną (w rozumieniu zmiany położenia krzywej efektywności) zmianę efektywności,
mierzoną osobno względem technologii z dwóch różnych okresów, tzn. efektywność obiektu w
okresie t jest mierzona względem technologii z okresu t + 1, a efektywność obiektu w okresie
t + 1 jest mierzona względem technologii z okresu t (następuje przesunięcie krzywej efektywności
między okresem t a t + 1).
Jeżeli jesteśmy zainteresowani oceną dynamiki zmian efektywności w czasie z uwzględnieniem
wpływu efektów skali obliczamy indeksy oparte na modelu CCR (krzywa CRS) i modelu BCC
(krzywa VRS). Indeks zmiany czystej efektywności technicznej (PTE) oraz indeks zmiany skali
efektywności (SE) dla modelu zorientowanego na efekty opisują równania:
P T E(x
t
,y
t
,x
t+1
,y
t+1
) =
D
t+1
V RS
(x
t+1
,y
t+1
)
D
t
V RS
(x
t
,y
t
)
(3.19)
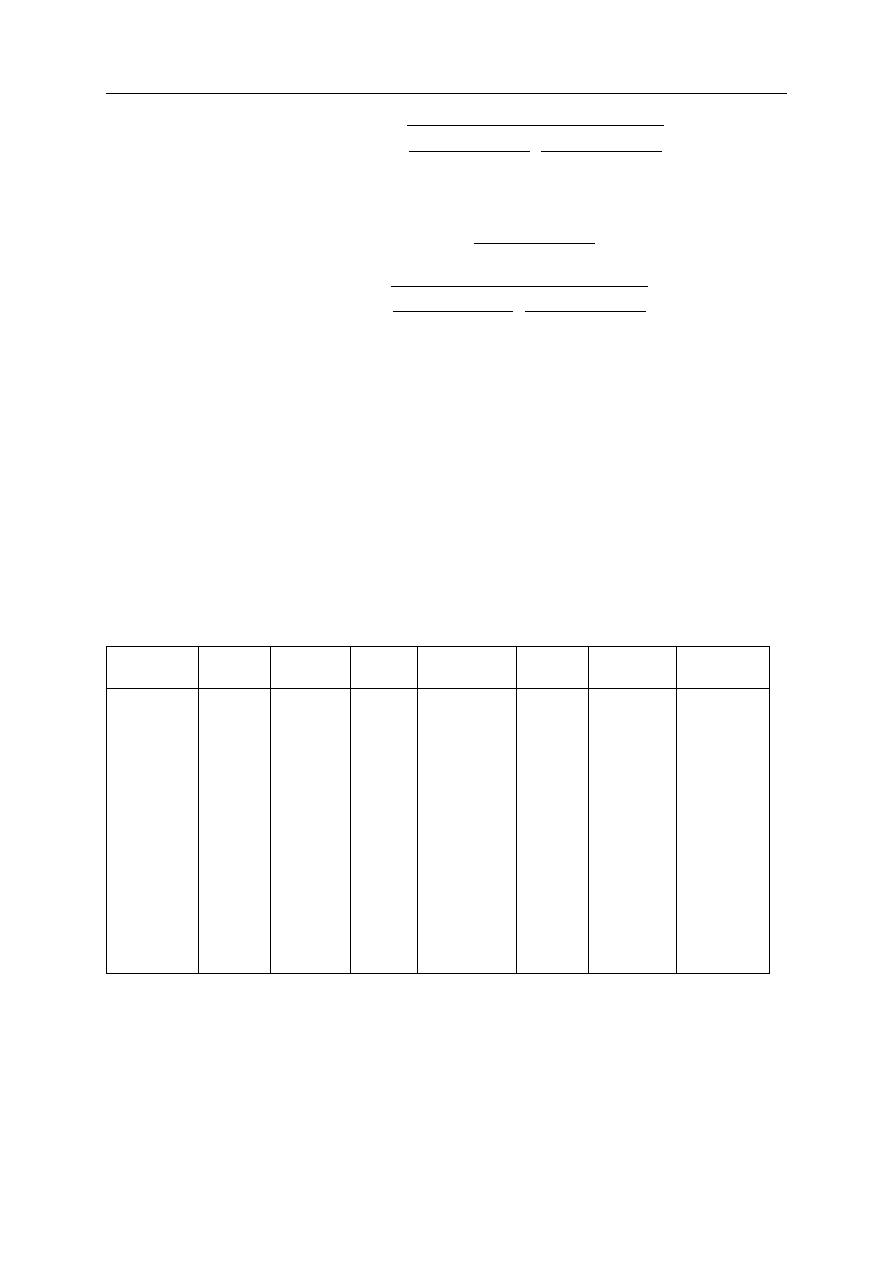
3.4. Dynamika zmian w modelach DEA
35
SE(x
t
,y
t
,x
t+1
,y
t+1
) =
s
D
t+1
CRS
(x
t+1
,y
t+1
)
D
t
CRS
(x
t
,y
t
)
/
D
t+1
V RS
(x
t+1
,y
t+1
)
D
t
V RS
(x
t
,y
t
)
(3.20)
Dla modelu zorientowanego na nakłady odpowiednie równania mają postać:
P T E(x
t
,y
t
,x
t+1
,y
t+1
) =
D
t
V RS
(x
t
,y
t
)
D
t+1
V RS
(x
t+1
,y
t+1
)
(3.21)
SE(x
t
,y
t
,x
t
,y
t
) =
s
D
t
CRS
(x
t
,y
t
)
D
t+1
CRS
(x
t+1
,y
t+1
)
/
D
t
V RS
(x
t
,y
t
)
D
t+1
V RS
(x
t+1
,y
t+1
)
(3.22)
Odległość obliczona na podstawie modelu BCC zorientowanego na nakłady nie jest odwrot-
nością odległości wyliczonej z modelu zorientowanego na efekty. Dlatego indeksy PTE i SE w
przypadku orientacji na nakłady i na efekty nie muszą być jednakowe.
Przykłady analizy dynamiki w metodzie DEA
Na początek wyznaczymy odległości Shepharda wymienione w tabeli 3.8. Ponownie wykorzy-
stamy znane nam już informacje na temat OFE. Rozszerzymy je dodatkowo o kolejny 2010 rok,
z którego pochodzą dane zawarte w tabeli 3.9. Same odległości D
•
(x
•
,y
•
) znalazły się w tabeli
3.10. Przyjmujemy, że t oznacza rok 2009 zaś t + 1 rok 2010. W tabeli tej zamieściliśmy wyniki
optymalizacji modeli CCR zorientowanych na efekty.
Tabela 3.9. Dane na temat OFE w 2010 r.
Fundusz
Martwe
Opuściło
Koszty
Przystąpiło
Składki
Jednostka
Przychody
rach.
rozr.
AEGON
83303
41602
48,21
60705
923,37
28,59
295,65
Allianz
30570
16845
35,31
21681
697,76
27,4
211,04
Amplico
35299
45485
93,18
43437
1717,88
28,12
528,41
Aviva
55125
142638
247,48
17727
5192,85
28,72
1755,71
AXA
34264
36151
65,28
136196
1375,03
28,92
422,72
Generali
70397
21506
55,4
56479
1140,52
30,52
338,91
ING
101347
101319
223,65
50042
5836,23
31,07
1761,14
Nordea
56665
41375
48,26
60425
1005,26
29,55
302,89
Pekao
26923
13589
18,11
19835
410,67
27,8
118,56
Bankowy
58087
23535
34,24
60039
624
28,17
197,29
Pocztylion
48147
19692
23,42
5941
527,15
27,16
137,54
Polsat
13279
12878
10,51
1310
287,8
31,97
55,47
PZU
92117
65508
142,41
53809
3076,12
29,38
978,47
WARTA
29316
21385
16,54
15882
343,17
29,48
101,58
Przypomnijmy, że odległość Shepharda możemy otrzymać bezpośrednio rozwiązując model
zorientowany na efekty. Zgodnie z zasadami przedstawionymi w tabeli 3.8 wartość D
t
(x
t
,y
t
)
to nic innego jak model CCR dla 2009 roku. Dlatego nie powinno nas dziwić, że nieefektywne
okazały się te same fundusze co w modelu CCR zorientowanym na nakłady. Na przykład OFE
Pocztylion, aby osiągnąć stuprocentową efektywność powinien (przy niezmienionych nakładach)
wytwarzać efekty średnio o 39% większe od dotychczasowych.
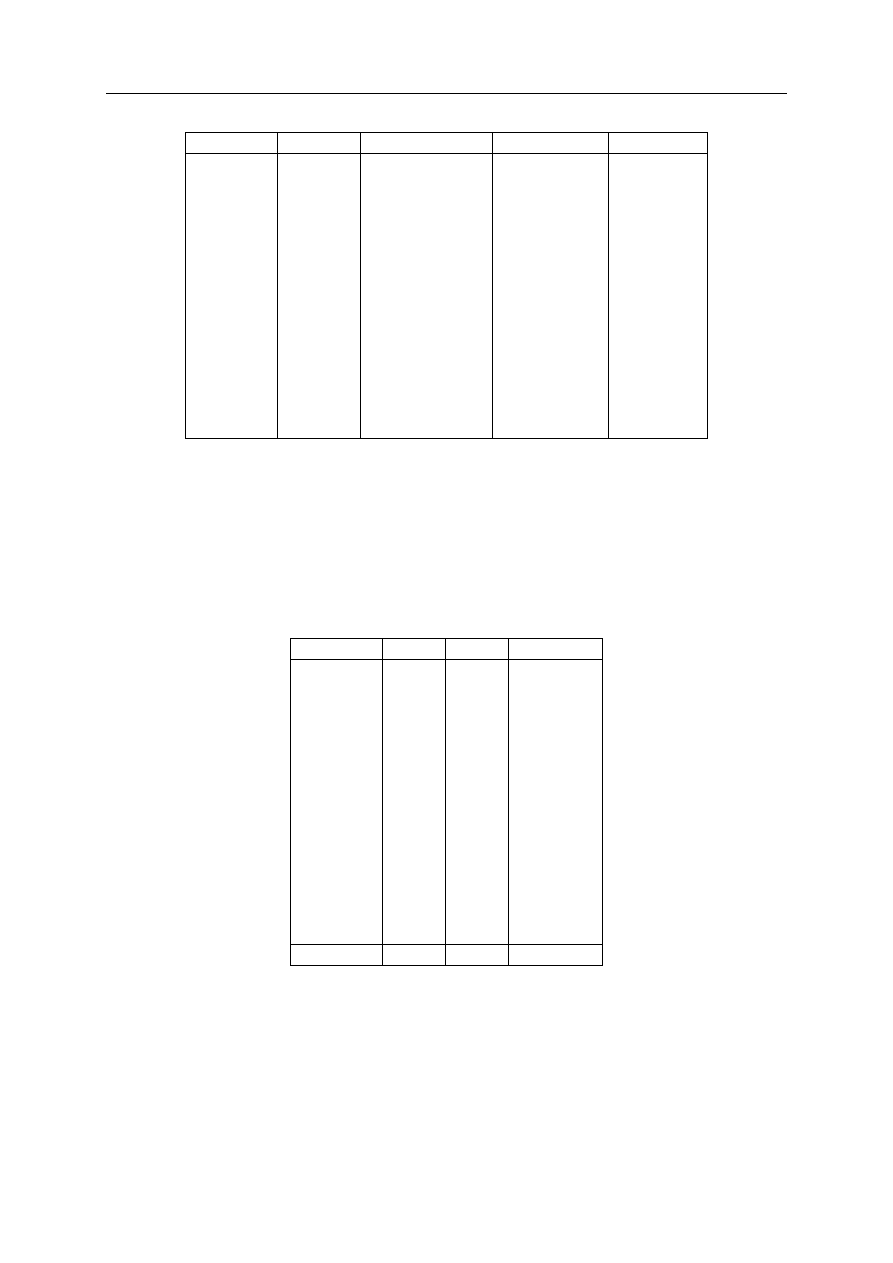
36
3. Wybrane typy analiz w metodzie DEA
Tabela 3.10. Odległości Shepharda dla OFE w latach 2009-2010
Fundusz
D
t
(x
t
,y
t
)
D
t+1
(x
t+1
,y
t+1
)
D
t
(x
t+1
,y
t+1
)
D
t+1
(x
t
,y
t
)
AEGON
1,2351
1,1113
1,2730
1
Allianz
1,1112
1
1
1
Amplico
1
1,0832
1,0069
1
Aviva
1
1
1
1
AXA
1
1
1
1
Generali
1
1
1
1
ING
1
1
1
1
Nordea
1
1,0890
1,2259
1
Pekao
1
1
1
1
Bankowy
1,0996
1,0195
1
1
Pocztylion
1,3900
1,1562
1,0482
1
Polsat
1
1
1
1
PZU
1,1443
1,1069
1,1695
1
WARTA
1
1,0076
1,0139
1
Kolumna D
t+1
(x
t+1
,y
t+1
) zawiera wyniki optymalizacji zorientowanego na efekty modelu
CCR dla 2010 roku. Zmienił się w tym wypadku zbiór funduszy nieefektywnych. Znalazły się
w nim: AEGON, Amplico, Nordea, Bankowy, Pocztylion, PZU i WARTA. Najsłabiej ponownie
wypadł Pocztylion, który w 2010 roku powinien zwiększyć stopień osiąganych efektów średnio
rzec biorąc około 1,16 razy.
Tabela 3.11. Indeks dynamiki Malmquista i jego składowe dla OFE w latach 2009-2010
Fundusz
TE
TC
Malmquist
AEGON
0,8998
1,1895
1,0702
Allianz
0,8999
1,0541
0,9486
Amplico
1,0832
0,9641
1,0444
Aviva
1
1
1
AXA
1
1
1
Generali
1
1
1
ING
1
1
1
Nordea
1,0890
1,0610
1,1554
Pekao
1
1
1
Bankowy
0,9272
1,0385
0,9629
Pocztylion
0,8318
1,1226
0,9338
Polsat
1
1
1
PZU
0,9673
1,0996
1,0636
WARTA
1,0076
1,0031
1,0107
Średnia
0,9790
1,0380
1,0135
Na podstawie wyników, które znalazły się w tabeli 3.11 możemy stwierdzić, że bez uwzględ-
niania efektów skali (tj. interpretując jej ostatnią kolumnę) największy wzrost produktywności
w 2010 roku w porównaniu do roku 2009 odnotował OFE Nordea. Zwiększyła się ona o 15,54%.
Fundusz ten miał również jeden z większych wzrostów efektywności technicznej o czym poniżej.
Z kolei największy spadek zaobserwowaliśmy w przypadku OFE Pocztylion a wyniósł on 6,62%.
Warto zwrócić również uwagę na to, że sześć funduszy nie odnotowało zmian produktywności
w analizowanym okresie w związku z czym średnia produktywność dla całego rynku wzrosła

3.4. Dynamika zmian w modelach DEA
37
Tabela 3.12. Indeksy dynamiki uwzględniające wpływ efektów skali dla OFE w latach 2009-2010
Orientacja na
efekty
nakłady
Fundusz
PTE
SE
PTE
SE
AEGON
1,0028
0,8972
1,1046
1,0061
Allianz
0,9020
0,9977
1,0892
1,0202
Amplico
1,0812
1,0018
0,9438
0,9782
Aviva
1
1
1
1
AXA
1
1
1
1
Generali
1
1
1
1
ING
1
1
1
1
Nordea
1,0355
1,0517
0,9265
0,9911
Pekao
1
1
1
1
Bankowy
0,9631
0,9627
1,0069
1,0712
Pocztylion
1,0057
0,8270
1,1479
1,0474
Polsat
1
1
1
1
PZU
1,0494
0,9218
0,9045
1,1430
WARTA
1,0068
1,0008
0,9956
0,9968
zaledwie o 1,35%. Ponadto, żaden z owych sześciu funduszy nie charakteryzował się zmianami
składników TE oraz TC.
Analizując zmianę efektywności technicznej bez uwzględniania zmiany położenia krzywej efek-
tywności (kolumna TE tabeli 3.11) możemy powiedzieć, że największy wzrost (o 8,9%) wystąpił
również w przypadku OFE Nordea oraz Amplico (8,32%). Największy spadek obserwujemy po-
nownie u OFE Pocztylion, dla którego wyniósł on 16,82%. Rynek OFE jako całość zanotował
średnio rzecz biorąc spadek efektywności technicznej rzędu 2,1%.
Zmiana techniczna (związana z postępem technologicznym), uwzględniająca zmianę położenia
krzywej efektywności zaprezentowana w kolumnie TC naszej tabeli najsilniej zaznaczyła swoją
obecność w przypadku OFE AEGON (wzrost o 18,95%) oraz Pocztylion (wzrost o 12,26%).
Obecność drugiego z wymienionych funduszy jest tu sporym zaskoczeniem, ponieważ w dotych-
czasowych analizach plasował się on w grupie najsłabszych obiektów. Jak widać duży wzrost w
dziedzinie postępu technicznego nie zrównoważył w jego przypadku spadku efektywności tech-
nicznej w dostatecznym stopniu. Największy spadek wielkości TC wystąpił dla OFE Amplico i
wyniósł 3,59%. Fundusz ten był wymieniony wcześniej w gronie OFE o największym wzroście
efektywności technicznej. Średnia wartość TC dla wszystkich funduszy wskazuje, że nastąpił
3,8% wzrost efektywności związany z postępem technicznym.
W tabeli 3.12 zawarliśmy wyniki obliczeń indeksów PTE i SE uwzględniających zmianę efek-
tów skali. Indeks zmian czystej efektywności technicznej (PTE) dla modelu zorientowanego na
efekty przyjął największą wartość OFE Amplico, który w 2010 roku w porównaniu do roku 2009
zanotował wzrost wynoszący 8,12%. Z kolei w modelu zorientowanym na nakłady największy
wzrost na poziomie 14,79% obserwujemy w przypadku OFE Pocztylion. Najniższe wartości tego
indeksu to odpowiednio: spadek o 9,8% dla OFE Allianz oraz 9,55% dla OFE PZU „Złota Jesień".
Interpretując indeks zmiany skali efektywności (SE) dla modelu zorientowanego na efekty
zauważamy, że największy wzrost efektów skali (o 5,17%) wystąpił w przypadku OFE Nordea.
Za to największy spadek (o 17,3%) odnotował OFE Pocztylion. Jeśli chodzi o model zorientowany

38
3. Wybrane typy analiz w metodzie DEA
na nakłady, to analogiczne wielkości są następujące: OFE PZU – wzrost o 14,3% i Amplico –
spadek o 2,18%.
3.5. Wpływ własności danych empirycznych na wyniki modelu CCR
Efektywność wyznaczana z modelu CCR i innych zależy nie tylko od różnic między obiektami.
Zależy ona również od pewnych własności związanych ze zgromadzonym materiałem empirycz-
nym. Mamy tu na myśli zmiany liczby nakładów i efektów, dodawanie nowych obiektów czy
występowanie korelacji między składowymi modelu.
Jeżeli na przykład zwiększamy liczbę nakładów i/lub efektów efektywność obiektów zwykle
rośnie a przynajmniej nie maleje. Różnice wskaźników efektywności między obiektami ulegają
zmniejszeniu. Efektywność DMU nieefektywnego nie pogarsza się a może nawet wzrosnąć zaś jed-
nostki decyzyjne, które były do tej pory efektywne pozostają efektywnymi. Z drugiej strony duży
wzrost ilości nakładów/efektów powoduje (zwłaszcza w modelu CCR) pojawienie się dużej liczby
obiektów efektywnych. W modelu CCR wyniki są bardziej zróżnicowane przy niewielkiej liczbie
nakładów/efektów. Ponadto zmiana liczby nakładów i/lub efektów wywołuje zmiany wartości
współczynników lambda.
We wcześniejszych rozważaniach poświęciliśmy nieco uwagi kwestii liczby obiektów analizo-
wanych metodą DEA. Nie były to rozważania bezpodstawne. Na dołączenie kolejnego obiektu do
już istniejącego zbioru należy patrzeć z punktu widzenia jego efektywności. Pojawienie się DMU
nieefektywnego nie zmienia wskaźnika efektywności już uwzględnionego obiektu. Jednakże dołą-
czenie obiektu w pełni efektywnego powoduje, że efektywność pozostałych obiektów spada lub
co najwyżej pozostaje na dotychczasowym poziomie. Tym samym liczba obiektów efektywnych
zmienia się w miarę dodawania kolejnych DMU.
Niekiedy decydujemy się na wprowadzenie nakładów i efektów w postaci wskaźników natęże-
nia zamiast jednostek naturalnych. Przechodzimy więc przykładowo z przychodów w mln zł na
przychody w przeliczeniu na 10 tys. mieszkańców. Operacja taka nie pozostaje bez wpływu na
wyniki optymalizacji w metodzie DEA. Wprowadzenie wskaźników natężenia sprawia, że wskaź-
nik efektywności obiektu może ulec zmianie. W konsekwencji zmienić się może liczba obiektów
efektywnych.
Inną operacją często wykonywaną na danych jest ich przeskalowanie czyli pomnożenie zmien-
nej przez pewną liczbę dodatnią. Okazuje się, że taka operacja nie zmienia wskaźnika efektywności
obiektu. Innym rodzajem jest przesunięcie zmiennej czyli powiększenie jej o pewną stałą. W takim
wypadku dodawanie wartości do zmiennej nie wpływa na obiekty efektywne, ale może wpłynąć
na obiekty nieefektywne.
Kolejną sytuacją z jaką się stykamy, szczególnie gdy korzystamy ze zmiennych ekonomicznych,
jest występowanie korelacji między nimi. Zaznaczmy, że w przypadku metody DEA rozpatrujemy
wyłącznie korelację dodatnią, ponieważ wzrost nakładów powinien powodować wzrost efektów.
Po pierwsze należy podkreślić, że wysoka korelacja między nakładami a efektami oznacza de-
generację rozwiązania. Jeżeli przynajmniej jeden efekt jest skorelowany (współczynnik korelacji
równy 1) z przynajmniej jednym nakładem wtedy wszystkie obiekty są efektywne w sensie Far-
rela. W związku z tym na liście nakładów i efektów nie może występować ta sama zmienna. Jeśli

3.5. Wpływ własności danych empirycznych na wyniki modelu CCR
39
między nakładami a efektami korelacja występuje jako funkcja liniowa z wyrazem wolnym wtedy
efektywność może odchylać się od 1 szczególnie jeśli wyraz wolny jest ujemny.
Związki korelacyjne można również rozpatrywać w ograniczeniu wyłącznie do grupy nakładów
lub efektów. Rozszerzenie modelu o nakład (efekt) będący liniową kombinacją innych nakładów
(efektów) bez wyrazu wolnego nie powoduje zmiany rozwiązania. Jeżeli wyraz wolny jest różny
od 0 wtedy rozwiązanie ulega zmianie przy czym najsilniejsze zmiany powoduje wyraz wolny
dużo mniejszy od 0.

4. Uwzględnianie luzów nakładów i efektów
4.1. Nadwyżki efektów i niedobory nakładów w zadaniu standardowym
Oryginalne modele DEA w jawny sposób uwzględniają w funkcji celu i ograniczeniach luzy
nakładów i efektów rozumianych jako nadwyżki pierwszych i niedobory drugich dla technologii
empirycznej w stosunku do technologii optymalnej. Mają one podobne znaczenie jak zmienne
swobodne znane z badań operacyjnych z tym, że luzy w funkcji celu modelu DEA mogą pojawiać
się z wagami różnymi od zera. Jednak w przeważającej liczbie zastosowań praktycznych nie
uwzględnia się luzów w w modelach.
Zacząć należy od tego, że po rozwiązaniu na przykład zadania CCR jesteśmy w stanie wyzna-
czyć kilka różnic o odmiennej interpretacji. Przez optymalne luzy nakładów rozumiemy różnice
między nakładami technologii z promienia technologicznego, dla której ˆ
θ
o
= 1 a nakładami opty-
malnymi. Wiąże się to z istnieniem technologii dopuszczalnych poza promieniem technologicznym
o czym pisaliśmy już wcześniej. Technologia optymalna najczęściej nie leży bowiem na promieniu,
ale na krawędzi kostki określającej rzut punktu leżącego na promieniu technologicznym na od-
powiednią oś. Różnicę tę możemy zapisać następująco: D
o
= ˆ
θ
o
x
o
− ˆ
x
o
. Jej odjemna to nakłady
ˆ
θ
o
-proporcjonalne a odjemnik to nakłady optymalne optymalne.
Tylko gdy technologia optymalna leży bezpośrednio na promieniu technologicznym luzy są
równe zero. Ich pojawienie się sygnalizuje, że utrzymywanie dotychczasowych nakładów poprzez
przemieszczanie się po promieniu jest nieefektywne w sensie Pareto. Rozwiązanie dowolnego
modelu DEA pozwala jednak wyznaczyć kilka innych zależności. Możemy określić nadwyżkę
nakładów empirycznych nad optymalnymi czyli ∆
o
= x
o
− ˆ
x
o
oraz różnicę między nakładami
empirycznymi a tymi z promienia technologicznego: δ
o
= x
o
− ˆ
θ
o
x
o
.
Przyjmijmy jednak definicję luzu analogiczną do definicji zmiennej swobodnej z badań ope-
racyjnych czyli jest to różnica między lewą a prawą stroną danego ograniczenia. Dla nakładu n
w obiekcie o otrzymamy wówczas:
D
on
= θ
n
x
no
−
J
X
j=1
λ
oj
x
nj
(4.1)
Z kolei dla efektu r w obiekcie o różnica owa wyrażać się będzie wzorem:
S
or
=
J
X
j=1
λ
oj
y
rj
− y
ro
(4.2)
Luzy wprowadzamy do modelu z wagami ε, które są dowolnie małymi liczbami dodatnimi.
Uzyskamy w ten sposób model w postaci kanonicznej zapisany jak poniżej (dla przypadku modelu
CCR zorientowanego na nakłady):

4.1. Nadwyżki efektów i niedobory nakładów w zadaniu standardowym
41
θ
o
− ε
N
X
n=1
D
on
+
R
X
r=1
S
or
!
→ min
(4.3)
J
X
j=1
x
nj
λ
oj
+ D
on
= θ
o
x
no
(4.4)
J
X
j=1
y
rj
λ
oj
− S
or
= y
ro
(4.5)
θ
o
6 1
(4.6)
θ
o
; λ
o1
, . . . ,λ
oJ
; S
o1
, . . . ,S
oR
; D
o1
, . . . ,D
oN
> 0
(4.7)
Wprowadzenie luzów do funkcji celu służy zasygnalizowaniu obniżenia efektywności obiektu z
powodu deficytu efektów lub nadmiaru nakładów. Stąd założenie, że wagi ε są małymi liczbami
dodatnimi. W ograniczeniach spełniają one podobną rolę jak zmienne swobodne.
Zadania w postaci kanonicznej nie rozwiązuje się bezpośrednio, ale stosując specyficzną dla
niego procedurę. Przechodzi ona następujące etapy:
1. Rozwiązujemy zadanie CCR w postaci standardowej i określamy optymalny mnożnik nakła-
dów ˆ
θ
o
.
2. Jeżeli obiekt jest w pełni efektywny (ˆ
θ
o
= 1, ˆ
λ
o,o
= 1, λ
oj
= 0) to nie ma żadnych luzów i na-
stępuje koniec postępowania. Jeżeli jednak jego efektywność jest mniejsza od 1 przechodzimy
do kroku 3.
3. Obliczamy prawe strony ograniczeń dla nakładów przy mnożniku ˆ
θ
o
: ˆ
x
no
= ˆ
θ
o
x
no
.
4. Rozwiązujemy model CCR(II), w którym ustala się nowe współczynniki λ
oj
maksymalizujące
sumę luzów przy warunkach z zadania w postaci kanonicznej. Prawe strony warunków doty-
czących nakładów równe są wartościom danym w kroku 3 zaś te dotyczące efektów zawierają
efekty empiryczne.
Model CCR(II) ma następującą postać:
N
X
n=1
D
on
+
R
X
r=1
S
or
→ max
(4.8)
J
X
j=1
x
nj
λ
oj
+ D
on
= ˆ
x
no
(4.9)
J
X
j=1
y
rj
λ
oj
− S
or
= y
ro
(4.10)
θ
o
; λ
o1
, . . . ,λ
oJ
; S
o1
, . . . ,S
oR
; D
o1
, . . . ,D
oN
> 0
(4.11)
Ze względu na uwarunkowania metody DEA model (4.8)-(4.11) podlega istotnym ogranicze-
niom. Załóżmy najpierw, że interesuje nas maksymalizacja jedynie luzów dla nakładów. Mini-
malizacja θ w standardowym modelu zorientowanym na nakłady oznacza maksymalizację luzów
dla nakładów. Nie ma więc sensu rozpatrywać zadania, w którym maksymalizuje się tylko luzy

42
4. Uwzględnianie luzów nakładów i efektów
związane z nakładami. W szczególności mija się to z celem gdy w standardowym modelu CCR
zorientowanym na nakłady luzy dla efektów i tak są zerowe.
Po drugie różnice lambd pojawiają się między modelem standardowym a kanonicznym kiedy
występują luzy dla efektów (efekt technologii optymalnej jest większy od efektu empirycznego).
Wprowadzenie do modelu CCR(II) efektów empirycznych (y
ro
) doprowadzi do tego, że przy
nowych parametrach lambda otrzymana technologia nie będzie optymalna w sensie Pareto.
Z powyższych powodów za bardziej właściwe należy uznać korzystanie z modelu standardo-
wego.
4.2. Model z karami za luzy nakładów i efektów
Wiemy już, że optymalne nakłady i efekty wyznaczone po rozwiązaniu na przykład zadania
CCR różnią się od faktycznie poniesionych. W przypadku nakładów mówić będziemy o nadwyż-
ce zaś w przypadku efektów o niedoborze tychże w stosunku do wielkości empirycznych. Stąd
nadwyżkę nakładów możemy zdefiniować następująco:
S
no
= x
∗
no
− ˆ
x
no
(4.12)
Wzór (4.12) można rozumieć trojako:
1. Jako oszczędność nakładów optymalnych ˆ
x
no
technologii wspólnej w stosunku do nakładów
ˆ
θ
o
-proporcjonalnych stanowiących ˆ
θ
o
krotność nakładów empirycznych.
2. Jako nadwyżkę nakładów ˆ
θ
o
-proporcjonalnych w stosunku do nakładów optymalnych.
3. Jako rozrzutność obiektu w wydatkowaniu nakładów (nakłady ponad miarę).
Deficyt efektów w sensie ekonomicznym zapiszemy:
D
ro
= ˆ
y
ro
− y
ro
(4.13)
W jego wypadku interpretacja również ma potrójne znaczenie:
1. Uzyskana przy nakładach ˆ
x
no
nadwyżka efektu optymalnej technologii ponad poziom efektu
danego obiektu.
2. Niedobór rezultatu w stosunku do tego jaki ten obiekt mógłby uzyskać przy swoich nakładach
ˆ
x
no
w technologii optymalnej.
3. Niewykorzystane możliwości generowania wyższych efektów przez dany obiekt.
Obecność luzów nakładów i efektów wpływa na poziom efektywności danego obiektu. Ponoszenie
nakładów ponad miarę lub osiąganie efektów niższych niż to możliwe obniża wartość ˆ
θ
o
i rodzi
chęć skorygowania efektywności poprzez zmniejszenie pojawiających się luzów. Odbywa się to po-
przez wprowadzanie do modelu kar za nadwyżki nakładów i/lub niedobory efektów. Wspomniana
korekta może odbywać się albo poprzez zmniejszenie początkowej wartości ˆ
θ
o
o karę związaną z
nadwyżką nakładów lub niedoborem efektów, albo rozwiązanie zadanie DEA, w którym kary za
nadwyżkę nakładów lub niedobór efektów wprowadza się do funkcji celu.
Zajmiemy się tym drugim przypadkiem. Poniżej prezentujemy model CCR zorientowany na
nakłady, w którym funkcja celu została powiększona o kary nakładane na luzy nakładów i efek-
tów:

4.2. Model z karami za luzy nakładów i efektów
43
θ
o
+ K
o
→ min
(4.14)
J
X
j=1
y
rj
λ
oj
− D
ro
= y
ro
(4.15)
J
X
j=1
x
nj
λ
oj
+ S
no
= θ
o
x
no
(4.16)
θ
o
6 1
(4.17)
K
o
6 θ
o
(4.18)
θ
o
; λ
o1
, . . . ,λ
oJ
; S
o1
, . . . ,S
oR
; D
o1
, . . . ,D
oN
> 0
(4.19)
Wartość kar obecnych w funkcji celu obliczamy następująco:
K
o
=
N
X
n=1
S
no
s
no
+
R
X
r=1
D
ro
d
ro
(4.20)
gdzie:
s
no
=
1
N + R
1
x
no
(4.21)
d
ro
=
1
N + R
1
y
ro
(4.22)
Wprowadzenie kar do modelu zwiększa zróżnicowanie efektywności zbioru obiektów. Ponad-
to parametry lambda w stosunku do modelu bez kar będą inne. Rozpatrzmy teraz ponownie
przykład badania efektywności otwartych funduszy emerytalnych w 2009 roku. Dane do tego
modelu znajdowały się w tabeli 3.1. Model dla OFE AEGON czyli obiektu nr 1 prezentuje się
θ
o
+ K
o
→ min
33402λ
o1
+ 25355λ
o2
+ . . . + 16790λ
o14
− D
1o
= 33402
832,46λ
o1
+ 1135,66λ + . . . + 335,55λ
o14
− D
2o
= 832,46
25,19λ
o1
+ 24,02λ
o2
+ . . . + 25,79λ
o14
− D
3o
= 25,19
278,3λ
o1
+ 182,7λ
o2
+ . . . + 98,41λ
o14
− D
4o
= 278,3
75610λ
o1
+ 35635λ
o2
+ . . . + 37397λ
o14
+ S
1o
= 75610θ
o
54907λ
o1
+ 41314λ
o2
+ . . . + 19727λ
o14
+ S
2o
= 54907θ
o
19,91λ
o1
+ 20,64λ
o2
+ . . . + 12,1λ
o14
+ S
3o
= 19,91θ
o
1
Dla łatwiejszego porównania z modelem (4.14)-(4.19) pozostawiamy symbol o w miejscu przeznaczonym na
numer obiektu.
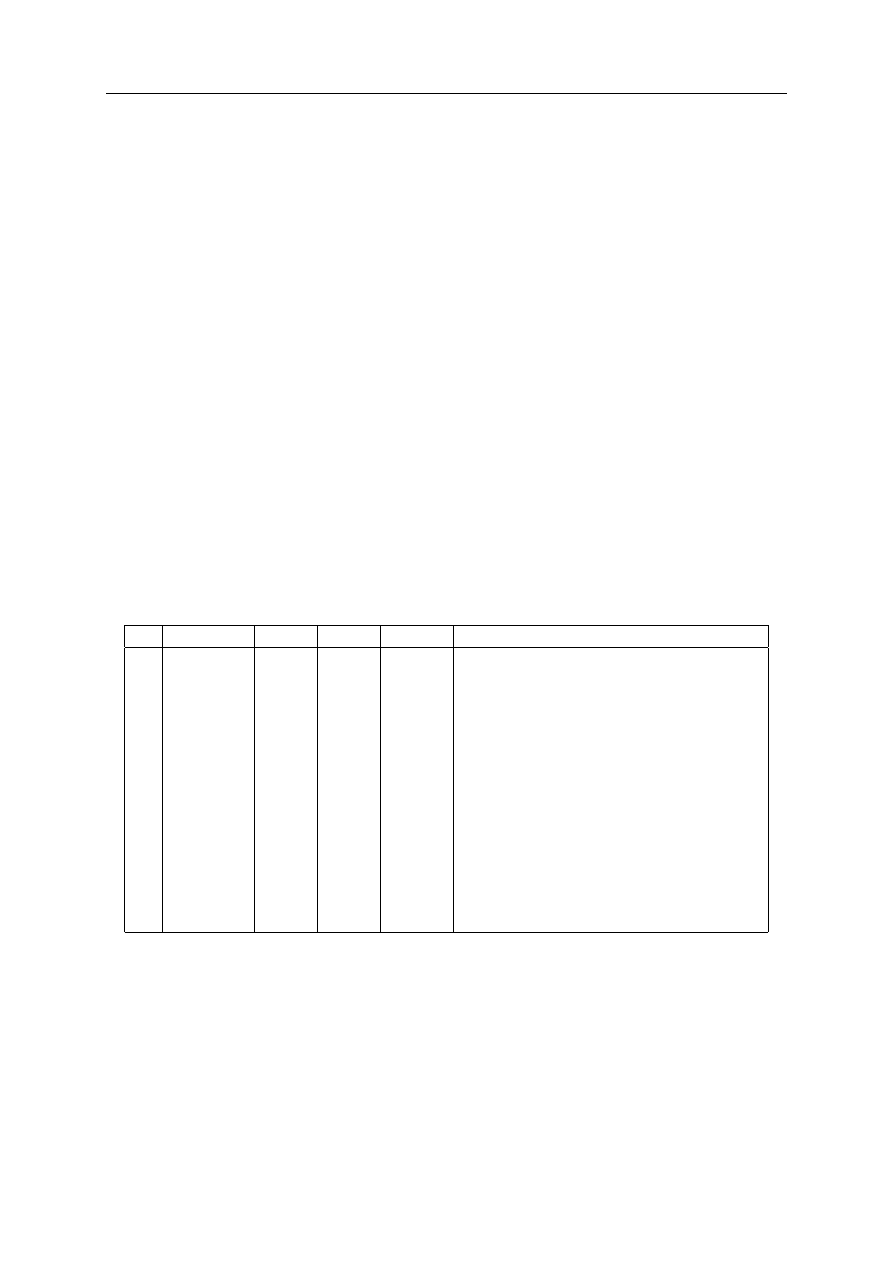
44
4. Uwzględnianie luzów nakładów i efektów
θ
o
6 1
K
o
6 θ
o
θ
o
; λ
o1
, . . . ,λ
oJ
; S
o1
, . . . ,S
oR
; D
o1
, . . . ,D
oN
> 0
Kary jednostkowe dla luzów nakładów i efektów obliczone zostały według formuł (4.22) i
(4.22). W tabeli 4.1 prezentujemy wyniki obliczeń dla modelu CCR z karami za luzy nakładów i
efektów. Dodanie wartości kary powoduje podwyższenie wartości funkcji celu co sugeruje wyższą
niż rzeczywista efektywność obiektu. Dlatego należy ją zmniejszyć o wartość K
o
i różnica ta
również znalazła się w tabeli. Jest to zatem faktyczny poziom efektywności obiektu. Nie zmienia
się jednak interpretacja wskaźnika efektywności ani wag intensywności wykorzystania techno-
logii obiektów efektywnych. Poza tym obiekty efektywne wg klasycznego modelu CCR nadal
pozostają efektywne. Dlatego najsłabiej nakłady na efekty przekładają się wciąż w przypadku
OFE Pocztylion tak jak to miało miejsce we wcześniejszym przykładzie. W tym modelu tech-
nologię zorientowaną na ten fundusz tworzą technologie czterech innych funduszy efektywnych
a mianowicie: OFE AEGON, OFE Generali, OFE ING i OFE POLSAT z wagami podanymi
w ostatniej kolumnie tabeli 4.1. Ponadto zwiększa się zróżnicowanie wskaźników efektywności
pomiędzy funduszami nieefektywnymi.
Tabela 4.1. Wyniki modelu CCR z karami za luzy nakładów i efektów
Lp
OFE
ˆ
θ
o
K
o
ˆ
θ
o
− K
o
Parametry ˆ
λ
oj
1
AEGON
0,9641
0,1536
0,8104
0,91(6), 0,02(7), 0,01(12)
2
Allianz
0,9309
0,0310
0,8999
0,17(3), 0,06(5), 0,09(6), 0,14(8), 0,45(12)
3
Amplico
1
0
1
4
Aviva
1
0
1
5
AXA
1
0
1
6
Generali
1
0
1
7
ING
1
0
1
8
Nordea
1
0
1
9
PEKAO
1
0
1
10
Bankowy
0,9684
0,0559
0,9125
0,11(7), 0,73(12)
11
Pocztylion
0,8285
0,0884
0,7401
0,05(1), 0,11(6), 0,03(7), 0,68(12)
12
POLSAT
1
0
1
13
PZU
0,9158
0,0420
0,8739
0,41(5), 0,46(7), 0,34(8)
14
Warta
1
0
1
To jednak nie wszystko. Uwzględnienie w modelu optymalizacyjnym kar za luzy nie oznacza
jeszcze, że automatycznie będą one równe zero dla wszystkich obiektów. Jak można przekonać
się na podstawie tabeli 4.2 dzieje się tak dla obiektów w pełni efektywnych. W pozostałych
przypadkach pojawiają się nadwyżki niektórych nakładów oraz niedobory części efektów. Na
przykład dla wymienionego wcześniej OFE Pocztylion liczba martwych rachunków powinna być
o ponad 34 tysiące mniejsza zaś w stosunku do osiąganej przez niego efektywności liczba nowych
członków winna być większa o prawie 1300 osób. W podobny sposób da się przeanalizować
pozostałe wartości luzów z tabeli 4.2.
4.2. Model z karami za luzy nakładów i efektów
45
Tabela 4.2. Obliczone luzy nakładów i efektów
Nakład/efekt
Martwe
Opuściło
Koszty
Przystąpiło
Składki
Jedn.
Przychody
Lp
OFE
rach.
oper.
rozr.
1
AEGON
0
6158
0
2942,47
728,44
0
0
2
Allianz
0
8955,93
0
0
0
0
0
3
Amplico
0
0
0
0
0
0
0
4
Aviva
0
0
0
0
0
0
0
5
AXA
0
0
0
0
0
0
0
6
Generali
0
0
0
0
0
0
0
7
ING
0
0
0
0
0
0
0
8
Nordea
0
0
0
0
0
0
0
9
PEKAO
0
0
0
0
0
0
0
10
Bankowy
10393,04
0
0
0
0
0
22,34
11
Pocztylion
34232,55
0
0
1277,05
0
0
0
12
POLSAT
0
0
0
0
0
0
0
13
PZU
3959,11
0
2,7
0
0
5,94
0
14
Warta
0
0
0
0
0
0
0
Jeżeli jednostkowe kary za luzy ulegają zwiększeniu wówczas rośnie wskaźnik efektywności i
przy odpowiednio wysokich karach wszystkie luzy mogą się wyzerować. Tylko technologia własna
obiektu pozbawiona jest bowiem luzów. Z kolei zmniejszanie kar za luzy powoduje, że rozwiązanie
zbliża się do tego z klasycznej metody (na przykład CCR). Tak więc odpowiednio małe kary nie
wpłyną na rozwiązanie zwykłego modelu. Mnożnik w modelu z karami za luzy jest nie mniejszy od
mnożnika z modelu klasycznego. Wynika to po pierwsze z dwóch przed chwilą podanych własności
a po drugie z faktu dołączenia do modelu dodatkowego ograniczenia. Wagi intensywności lambda
zmieniają się ponieważ lista zmiennych decyzyjnych uległa rozszerzeniu właśnie o luzy .

5. Model wykorzystujący efektywność nieradialną
5.1. Model efektywności nieradialnej
Klasyczne podejście do metody DEA zakłada jednolitą efektywność wszystkich nakładów lub
efektów. Założenie to da się jednak uchylić. Punktem wyjścia jest tzw. efektywność Russella, którą
można potraktować jako uogólnienie efektywności Farrella-Debreu. W modelu zorientowanym na
nakłady bada się w niej efektywność względem poszczególnych nakładów natomiast w modelu
zorientowanym na efekty bada się efektywność względem poszczególnych efektów. Wskaźnikiem
efektywności Russella w modelu zorientowanym na nakłady staje się średnia efektywności cząst-
kowych względem poszczególnych nakładów.
¯
θ =
1
N
N
X
n=1
θ
n
(5.1)
Z tego powodu ten sam poziom wskaźnika efektywności Russella może być osiągany przy
różnych kompensujących się efektywnościach cząstkowych. W modelu zorientowanym na efekty
efektywność Russella wyznacza się jako odwrotność średniej arytmetycznej optymalnych efek-
tywności cząstkowych.
W modelu efektywności radialnej (Farrella) zmiany efektywności dokonują się poprzez propor-
cjonalne zmiany wszystkich nakładów lub efektów. W rezultacie przesuwamy się wzdłuż półpro-
stej wychodzącej z początku układu współrzędnych. Punkty na tej półprostej określają zmiany
nakładów lub efektów co w konsekwencji przekłada się na ich całkowitą komplementarność czyli
zerową substytucyjność.
Efektywność nieradialna zakłada, że efektywność cząstkowa ze względu na dany nakład lub
efekt może być inna dla każdego nakładu (efektu) przy czym sama efektywność cząstkowa jest
wciąż radialna. Jeżeli cząstkowe wskaźniki efektywności nie są identyczne to kombinacje nakładów
i efektów nie układają się na promieniu technologicznym. W konsekwencji możliwa jest substytu-
cyjność nakładów lub efektów. Możliwe jest także uwzględnienie zmian struktury nakładów czy
efektów oraz zróżnicowanie ich efektywności.
Nieradialny zorientowany na nakłady model CCR opisany został równaniami (5.2)-(5.7). W
literaturze można niekiedy spotkać model, w którym minimalizuje się nie średnią a po prostu
sumę cząstkowych wskaźników efektywności. Istnieje możliwość zastąpienia funkcji celu (5.2)
średnią ważoną jeżeli z jakiegoś powodu niektóre nakłady są ważniejsze od innych. Ograniczenie
(5.6) wyraża pożądane relacje między mnożnikami efektywności różnych nakładów. Mogą to być
relacje typu równy, mniejszy lub równy albo większy lub równy.
1
N
N
X
n=1
θ
no
→ min
(5.2)

5.2. Wybrane analizy modelu z efektywnością nieradialną
47
J
X
j=1
λ
oj
y
rj
> y
ro
(5.3)
J
X
j=1
λ
oj
x
nj
6 θ
no
x
no
(5.4)
θ
no
6 1
(5.5)
θ
no
Rθ
mo
(5.6)
θ
1o
, . . . ,θ
N o
; λ
o1
, . . . ,λ
oJ
> 0
(5.7)
Optymalny wskaźnik ˆ
θ
no
wyraża po pierwsze efektywność obiektu o ze względu na nakład
n. Po drugie określa procent do jakiego należałoby zmniejszyć nakład n aby obiekt o uzyskał
stuprocentową efektywność ze względu na ten nakład. Mnożniki optymalne dla poszczególnych
nakładów wskazują przy jakich krotnościach nakładów obiektu o optymalna technologia wspólna
pozwoli uzyskać efekt analogiczny do efektu tego obiektu przy minimalnych nakładach. Średnia
wartości optymalnych cząstkowych wskaźników efektywności dla wszystkich nakładów jest wspo-
mnianą wcześniej efektywnością Russella.
5.2. Wybrane analizy modelu z efektywnością nieradialną
Rozważmy teraz model CCR dla otwartych funduszy emerytalnych jako zadanie z niera-
dialną efektywnością Russella. Jako empiryczne nakłady i efekty wykorzystamy dane dla OFE
obejmujące 2009 rok.
Tabela 5.1. Wyniki nieradialnego modelu CCR dla OFE z 2009 r.
Martwe
Opuściło
Koszty
Lp
OFE
¯
θ
rach. ˆ
θ
1
ˆ
θ
2
oper. ˆ
θ
3
Parametry ˆ
λ
oj
1
AEGON
0,7569
0,6659
0,6049
1
0,07(5), 0,62(6), 0,05(7), 0,2(12)
2
Allianz
0,8252
0,8404
0,6748
0,9604
0,21(3), 0,07(5), 0,16(8), 0,48(12)
3
Amplico
1
4
Aviva
1
5
AXA
1
6
Generali
1
7
ING
1
8
Nordea
1
9
PEKAO
1
10
Bankowy
0,7729
0,5765
0,9123
0,8299
0,02(5), 0,09(7), 0,78(12)
11
Pocztylion
0,5723
0,2849
0,6805
0,7514
0,13(6), 0,04(7) 0,7(12)
12
POLSAT
1
13
PZU
0,8373
0,5522
1
0,9596
0,34(4), 0,6(5), 0,1(7), 0,14(8)
14
Warta
1
Oczywiście efektywność Russella w tabeli 5.1 nie przekracza 1 gdyż jest ona średnią liczb
zawierających się w przedziale od 0 do 1. Fundusze, które były efektywne w klasycznym modelu
CCR w modelu z nieradialną efektywnością nadal są efektywne przy czym w tym wypadku

48
5. Model wykorzystujący efektywność nieradialną
interpretujemy to jako pełną efektywność ze względu na każdy z nakładów. Obiekty nieefek-
tywne w sensie nieradialnym są nieefektywne ze względu na przynajmniej jeden nakład choć
mogą być (jak na przykład OFE Pocztylion) nieefektywne ze względu na wszystkie nakłady.
Wskaźnik efektywności zwykłego modelu CCR jest nie mniejszy od wskaźnika efektywności Rus-
sella. Wskaźnik efektywności klasycznego modelu CCR na ogól zawiera się między minimum a
maksimum wskaźników dla nakładów nieradialnej CCR.
Gdy liczba nakładów jest mała wskaźnik efektywności CCR jest często równy maksymalnemu
cząstkowemu wskaźnikowi efektywności.
Analizując cząstkowe efektywności funduszy nieefektywnych dowiadujemy się jaka jest efek-
tywność obiektu z punktu widzenia poszczególnych nakładów. I tak na przykład OFE PZU jest
bardzo nieefektywny jeśli chodzi o liczbę martwych rachunków, ale wykazuje się stuprocentową
efektywnością w przypadku liczby członków, którzy opuścili w 2009 roku fundusz (opuścili go ci,
którzy powinni). Jego technologia wykorzystania tego nakładu jest zatem w pełni efektywna. Dla
kosztów operacyjnych efektywność znalazła się dość blisko 1. Analizując efektywności (czy raczej
nieefektywności) cząstkowe funduszy gdzie ¯
θ < 1 możemy zaobserwować duże zróżnicowanie
poziomów wskaźnika efektywności.
Jeśli chodzi o efektywność wykorzystania martwych rachunków to fundusze nieefektywne
generalnie nie radzą sobie z tym zjawiskiem przy czym najgorszą sytuację obserwujemy w OFE
Pocztylion.
Dysponując cząstkowymi efektywnościami możemy przygotować rankingi obiektów z punktu
widzenia poszczególnych nakładów. Gdyby taką listę utworzyć dla liczby osób, które opuściły
fundusz to liczba obiektów efektywnych byłaby o 1 większa od liczby obiektów efektywnych w
sensie Russella gdyż znalazłby się na niej OFE PZU. Poza tym może dojść do zmian pozycji
DMU na różnych listach rankingowych w zależności od rozpatrywanego nakładu.
Formuły benchmarkingowe w modelu z nieradialną efektywnością są inne niż te z radial-
nego modelu CCR. Niektóre fundusze (np. Pocztylion) zachowały niezmienioną listę obiektów
wzorcowych, ale występują one z innymi wagami. Z kolei inne mogą mieć bardzo różniące się for-
muły benchamrkingowe (por. np. PZU). Zresztą poprawa technologii może być teraz rozumiana
dwojako:
1. jako poprawę wykorzystania tych nakładów, dla których cząstkowa efektywność jest mniejsza
od 1;
2. jako poprawę efektywności wybranych nakładów, które wypadły pod tym względem najsła-
biej.
Model nieradialny pozwala również przeprowadzić analizę dysproporcji nakładów i efektów. Jeżeli
wszystkie nakłady i efekty charakteryzują się taką samą efektywnością uznajemy je za zharmoni-
zowane. Jeżeli przynajmniej jedna para nakładów lub para efektów ma różne cząstkowe wskaźniki
efektywności to mówimy o pojawieniu się dysproporcji tym większej im większa jest wspomniana
różnica efektywności. Stopień braku zharmonizowania można określić na przykład przy pomocy
odchylenia standardowego lub po prostu obliczając rozstęp.
Dla danych z tabeli 5.1 obliczyliśmy odchylenia standardowe współczynników efektywności
poszczególnych funduszy. Dodatkowo tabelę 5.2 wzbogaciliśmy o współczynniki zmienności. Na
jej podstawie stwierdzamy ogólnie spore niezharmonizowanie nakładów przy czym zdecydowanie
5.2. Wybrane analizy modelu z efektywnością nieradialną
49
najwyższe jest ono w przypadku OFE Pocztylion. Spośród funduszy nieefektywnych najbardziej
zharmonizowane nakłady obserwujemy w OFE Allianz (najniższy współczynnik zmienności).
Tabela 5.2. Ocena stopnia zharmonizowania efektywności funduszy
Odchylenie
Wsp.
Lp
OFE
¯
θ
stand.
zmienności
1
AEGON
0,7569
0,1737
0,2294
2
Allianz
0,8252
0,1171
0,1419
3
Amplico
1
0
0
4
Aviva
1
0
0
5
AXA
1
0
0
6
Generali
1
0
0
7
ING
1
0
0
8
Nordea
1
0
0
9
PEKAO
1
0
0
10
Bankowy
0,7729
0,1429
0,1849
11
Pocztylion
0,5723
0,2053
0,3587
12
POLSAT
1
0
0
13
PZU
0,8373
0,2022
0,2415
14
Warta
1
0
0
Gdy efektywność obiektu w modelu nieradialnym jest mniejsza od 1 możemy określić roz-
rzutność nakładu, której stopień wyraża zależność:
β
no
= 1 − ˆ
θ
no
(5.8)
W tabeli 5.3 przedstawiona została rozrzutność nakładów nieefektywnych funduszy emery-
talnych. Jak widać mamy w ich przypadku do czynienia z dużym niewykorzystaniem nakładów
rzędu średnio 70-80%. Jak to już miało miejsce wcześniej ponownie zwraca uwagę liczba martwych
rachunków. Najgorszy pod tym względem OFE Pocztylion ma ich aż ponad 70% za dużo.
Tabela 5.3. Wskaźniki rozrzutności nakładów dla funduszy nieefektywnych
Martwe
Opuściło
Koszty
OFE
rachunki
oper.
AEGON
0,3341
0,3951
0
Allianz
0,1596
0,3252
0,0396
Bankowy
0,4235
0,0877
0,1701
Pocztylion
0,7151
0,3195
0,2486
PZU
0,4471
0
0,0404
średnia
0,7914
0,7234
0,6785
Dla modelu z nieradialną efektywnością można również wyznaczyć luzy nakładów i efektów,
ale należy pamiętać, że w modelu zorientowanym na nakłady luzy nakładów będą równe zero. Po-
nieważ wzrost liczby nakładów i/lub efektów powoduje wzrost wskaźnika efektywności wskaźnik
z modelu nieradialnego może być traktowany jako sposób na dokładniejsze oszacowanie efektyw-
ności obiektu. Wiąże się to również z poglądem, że obecność luzów przyczynia się do obniżenia
efektywności.

50
5. Model wykorzystujący efektywność nieradialną
Izokwanty efektywności nieradialnego modelu CCR są nieliniowe co przekłada się na stabil-
ność rozwiązań. Może się bowiem zdarzyć, że nawet niewielka zmiana nakładów spowoduje dużą
zmianę efektywności oraz wag lambda. Ta sama zmiana efektywności wymagać będzie różnej
skali nakładów a przecież model nieradialny zakłada możliwą substytucję nakładów.

6. Wykorzystanie komputera do obliczeń w metodzie
DEA
6.1. Arkusz kalkulacyjny
Z formalnego punktu widzenia metoda DEA jest zadaniem programowania ilorazowego, ale
dzięki transformacji Charnesa-Coopera można dokonać przekształcenia w zadanie programowa-
nia liniowego, które dużo łatwiej rozwiązać. Problem polega na tym, że zadanie optymalizacyjne
należy rozwiązać oddzielnie dla każdego obiektu. Gdy jest ich kilka nie stanowi to dużego proble-
mu, lecz przy kilkudziesięciu lub kilkuset jednostkach decyzyjnych konieczne staje się sięgnięcie
po oprogramowanie komputerowe.
Celem tego dodatku jest zaprezentowanie możliwości wybranych narzędzi do poszukiwania
rozwiązań modeli DEA. Istniejące komercyjne pakiety są dość kosztowne w zakupie dlatego
ograniczymy się do narzędzi dostępnych za darmo.
Na początek omówimy możliwości, które dają arkusze kalkulacyjne. Będziemy posługiwać
się zrzutami ekranu z arkusza MS Excel, ale wykorzystane funkcje i formuły równie dobrze
można zastosować na przykład w arkuszu Calc będącym częścią darmowego pakietu biurowego
LibreOffice.
Rysunek 6.1 przedstawia arkusz przygotowany do rozwiązania zorientowanego na nakłady
modelu CCR. W kolumnie A znalazły się etykiety obiektów. Zakres B3:H16 zawiera empirycz-
ne efekty i nakłady. Komórki J3:J17 przedstawiają zmienne decyzyjne modelu czyli parametry
lambda. Zwróćmy uwagę na ostatnią komórkę wspomnianego zakresu. Jest ona opisana jako
„theta”. Jest ona jednocześnie obecna w ograniczeniach i stanowi funkcję celu. Dlatego celowo
wyróżniliśmy ją ossdzielnym odwołaniem pod adresem L3.
Poniżej znajdują się formuły konieczne do rozwiązania zadania. Zakres B18:H18 zawiera lewą
stronę ograniczeń odpowiadających poszczególnym nakładom i efektom. Powstaje ona prze po-
mnożenie wektora lambd przez odpowiednią kolumnę zakresu danych. Wykorzystaliśmy do tego
celu funkcję SUMA.ILOCZYNÓW. Znaki nierówności w wierszu 19 pełnią jedynie informacyjny
charakter.
Przygotowany arkusz pozwala na rozwiązanie modelu DEA tylko dla jednego obiektu naraz.
Postanowiliśmy ułatwić zmianę parametrów zadania wynikającą ze zmiany jednostki decyzyj-
nej. W tej chwili optymalizacja dokonywana jest dla OFE1. Wpisanie w komórce A21 etykiety
innego funduszu spowoduje automatyczną zmianę parametrów zadania. Służy do tego funkcja
WYSZUKAJ.PIONOWO, która pobiera nazwę aktualnie rozpatrywanego funduszu z komórki
A21 a potem wyszukuje ją na liście znajdującej się w kolumnie A. Drugi argument tej funk-
cji przechowuje cały zakres włącznie z wartościami nakładów i efektów. Po znalezieniu wiersza
odpowiadającego danemu obiektowi trzeci argument pobrany z wiersza 20 wskazuje który efekt
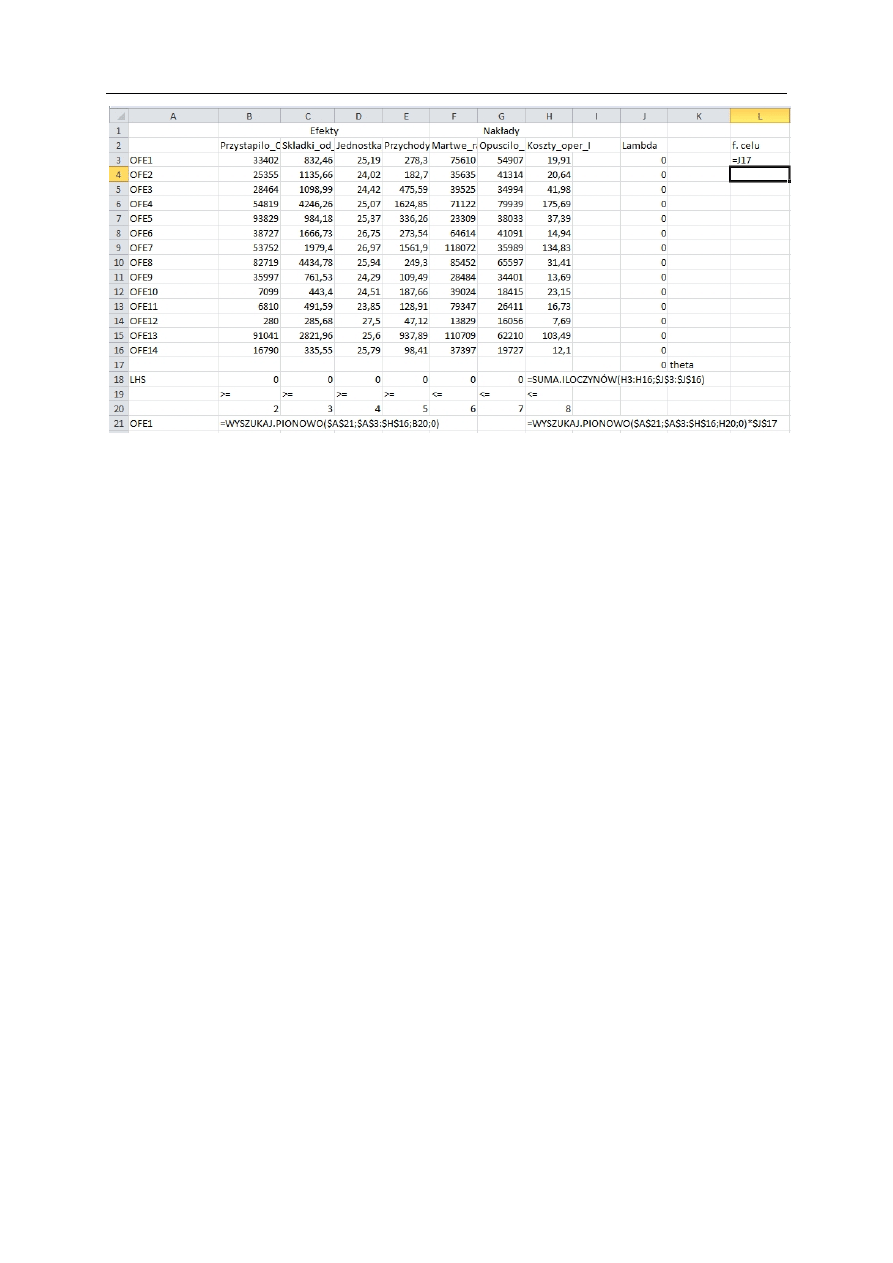
52
6. Wykorzystanie komputera do obliczeń w metodzie DEA
Rysunek 6.1. Arkusz przygotowany do modelu CCR zorientowanego na nakłady
lub nakład staje się prawą stroną ograniczenia. Formułę z komórki B21 należy skopiować dla
wszystkich efektów czyli do komórki E21 włącznie.
Jako że nasz model jest zorientowany na nakłady, prawe strony ograniczeń dotyczących na-
kładów właśnie są mnożone przez krotność wyrażoną parametrem theta. Z tego powodu wynik
działania funkcji WYSZUKAJ.PIONOWO dla nakładów jest dodatkowo mnożony przez zawar-
tość komórki J17. Taka formuła znalazła się w komórkach zakresu F21:H21.
Po przygotowaniu arkusza uruchamiamy dodatek Solver arkusza MS Excel (w arkuszu Calc
występuje on pod podobną nazwą). Sposób wprowadzenia parametrów zadania ilustruje zrzut na
rysunku 6.2. Zwracamy uwagę żeby jako metodę rozwiązywania wybrać „LP simpleks” w miejsce
domyślnej „Nieliniowej GRG”. Po rozwiązaniu otrzymujemy wskaźnik efektywności danego obiek-
tu. Jeżeli będzie on nieefektywny wówczas w kolumnie J pojawią się wartości wag intensywności
lambda, które ponadto wskażą obiekty efektywne wyznaczające benchmark.
Oczywiście przedstawiony sposób wykorzystania arkusza kalkulacyjnego nie eliminuje ko-
nieczności ręcznego rozwiązywania modelu dla każdego obiektu oddzielnie. Jedynie czyni to mniej
uciążliwym. Czytelnik obeznany z językiem VBA może jednak na bazie takiego arkusza napisać
program, który w pełni zautomatyzuje procedury obliczeniowe. Nie taki jest wszakże cel niniej-
szego opracowania więc zostawiamy to zainteresowanym. Warto przy tym podkreślić, że arkusz o
opisanej strukturze łatwo modyfikuje się do pozostałych typów modeli: zorientowanych na efekty,
BCC, NIRS i innych.
6.2. Pakiet EMS
Na potrzeby DEA powstaje również dedykowane oprogramowanie. Duża jego część jest płat-
na, ale istnieje darmowa alternatywa. Jest nią program EMS autorstwa Holgera Scheela. Program
można pobrać ze strony www.holger-scheel.de/ems/. Od razu trzeba podkreślić, że najnowsza
dostępna wersja pochodzi z 2000 roku. Program najwyraźniej nie jest już rozwijany, ale wciąż
6.2. Pakiet EMS
53
Rysunek 6.2. Parametry dodatku Solver dla modelu CCR
zachowuje swoją funkcjonalność choć należy się spodziewać, że z upływem czasu i zmianami w
systemach operacyjnych uruchomienie go będzie stwarzało coraz większe problemy.
Sam program obsługuje się bardzo prosto. Dane wczytuje się z z plików .csv lub .xls
. Arkusz
musi nazywać się Data i zawierać wyłącznie dane do wczytania. Nazwę (pozbawioną polskich
znaków) każdego nakładu należy opatrzyć symbolem {I} zaś efektu {O}. Ilustracja na rysunku
6.3 zawiera fragment arkusza przygotowany do wczytania.
Rysunek 6.3. Arkusz z danymi do programu EMS
Po wczytani danych wybieramy z menu DEA->Run model i przechodzimy do okna, w którym
ustawiamy parametry rozwiązywanego modelu. Okno to znalazło się na rysunku 6.4. W zakładce
Model wybieramy takie opcje jak rodzaj efektów skali, orientację czy superefektywność. Przy-
kładowo na naszym rysunku obliczone zostaną wskaźniki efektywności dla zorientowanego na
nakłady modelu CCR z uwzględnieniem superefektywności. Po wybraniu parametrów naciskamy
Start i otrzymujemy wyniki obliczeń. Przykład wyników dla zorientowanego na nakłady modelu
CCR prezentuje rysunek 6.5.
Kolumna DMU zawiera etykiety jednostek decyzyjnych (o ile zostały jakieś przyjęte). W
kolumnie Score znajdują się wartości wskaźników efektywności. Obiekty w pełni efektywne mają
wyróżnione całe wiersze. Informacje w kolumnie Benchmarks różnią się w zależności od tego czy
dany obiekt okazał się efektywny czy nie. W pierwszym przypadku podawana jest ilość obiektów
1
Z uwagi na zaawansowany „wiek” programu obsługiwany jest jedynie format MS Excel 97-2003.
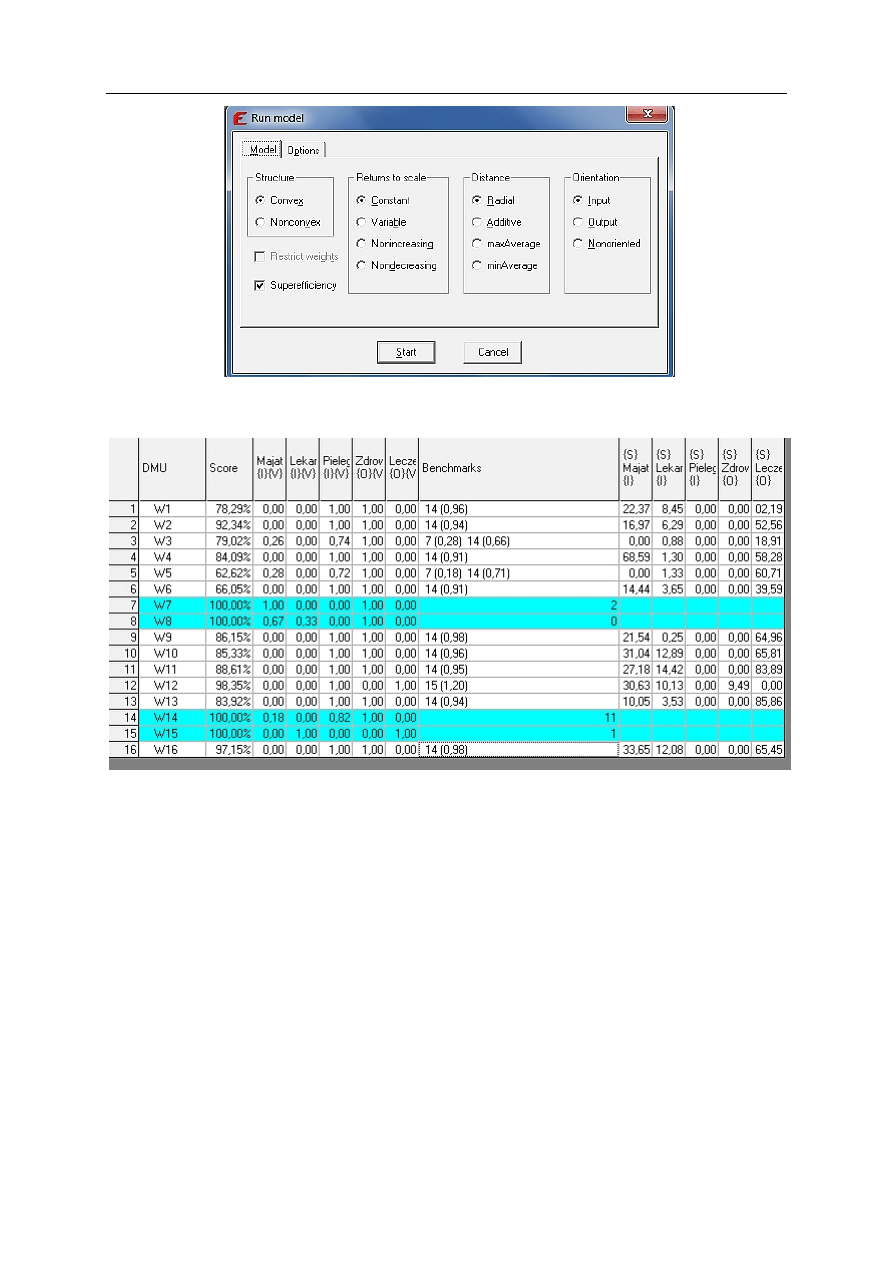
54
6. Wykorzystanie komputera do obliczeń w metodzie DEA
Rysunek 6.4. Okno wyboru modelu w programie EMS
Rysunek 6.5. Okno wyników dla modelu CCR w EMS
nieefektywnych, w których dana jednostka służy jako wzorzec. W drugim program informuje,
które jednostki decyzyjne i z jakimi wagami (lambda) należy wykorzystać do utworzenia techno-
logii mającej poprawić efektywność obiektu. Ostatnie kolumny oznaczone jako {S} podają luzy
dla odpowiednich nakładów i efektów. Otrzymane wyniki mogą zostać wyeksportowane do plików
.csv lub .xls.
Zakładkę Options w oknie wyboru modelu możemy wykorzystać podczas wyznaczania in-
deksów Malmquista. Podręcznik użytkownika podpowiada inne rozwiązanie, ale jest ono dość
skomplikowane. Rysunek 6.6 ilustruje jak przygotować opcje, w którym lewa i prawa strona
ograniczeń pochodzą z tego samego okresu. Mamy do czynienia z trzema jednostkami decyzyjny-
mi o nakładach i efektach pochodzących z dwóch okresów. Dane w arkuszu zostały pogrupowane
właśnie według okresów. Najpierw wszystkie obiekty z okresu t potem te same obiekty z okresu
t +1. Na rysunku 6.6 widzimy ustawienia właśnie dla okresu t. Z kolei rysunek 6.7 obrazuje
w jaki sposób przygotować program do obliczenia odległości Shepharda D
t+1
(x
t
,y
t
), w której
6.3. DEA w środowisku R
55
Rysunek 6.6. Odległość D
t
(x
t
,y
t
) w EMS
Rysunek 6.7. Odległość D
t+1
(x
t
,y
t
) w EMS
lewa strona ograniczeń pochodzi z okresu wcześniejszego zaś prawa z późniejszego. Należy zatem
czterokrotnie użyć EMS zmieniając opcje modelu po czym na przykład w arkuszu kalkulacyjnym
obliczyć indeksy Malmquista według podanych wcześniej wzorów.
6.3. DEA w środowisku R
Program EMS jest wygodny w użyciu, ale wobec zaniechania jego rozwoju przyjdzie moment,
w którym nie będzie dało się go uruchomić bez karkołomnych operacji w systemie operacyjnym.
Dlatego zaprezentujemy jeszcze jedno narzędzie a jest nim pakiet benchmarking napisany dla śro-
dowiska obliczeniowego R. Samo środowisko to zbiór funkcji i pakietów przeznaczonych głównie
do analiz statystycznych i prognozowania udostępniane na licencji Open Source. Jednak ciągle
powiększająca się społeczność zaowocowała wieloma interesującymi pakietami napisanymi przez
użytkowników, które znacząco rozszerzają możliwości środowiska.
Wersję instalacyjną R można pobrać ze strony www.cran.r-project.org. Tam również znaj-
dziemy interesujący nas pakiet, ale można go zainstalować z poziomu konsoli programu (tzw.

56
6. Wykorzystanie komputera do obliczeń w metodzie DEA
0
2
4
6
8
0
5
10
15
X
Y
A
B
C
D
E
F
Rysunek 6.8. Granica efektywności graficznie – pakiet benchmarking
RGui ). W tym celu wybieramy w menu Pakiety->Zainstaluj pakiet(y), wybieramy jeden z ser-
werów po czym na liście znajdujemy benchmarking
. Po zainstalowaniu przy pomocy poleceń
Pakiety->Załaduj pakiet... uruchamiamy nasz pakiet.
Typową cechą R i podobnych pakietów jest obsługa przy pomocy wiersza poleceń. Dlatego
właśnie podamy wybrane zestawy poleceń. Jako pierwszy rozważymy przypadek przedstawienia
metoda DEA graficznie co jest możliwe przy jednym nakładzie i jednym efekcie. Przyjrzyjmy się
następującym poleceniom:
x <− m a t r i x ( c ( 4 , 3 , 6 , 7 , 4 , 5 ) , n c o l =1 , dimnames= l i s t (LETTERS [ 1 : 6 ] , " x " ) )
y <− m a t r i x ( c ( 1 0 , 4 , 1 5 , 1 6 , 7 , 1 0 ) , n c o l =1 , dimnames= l i s t (LETTERS [ 1 : 6 ] , " y " ) )
dea . p l o t ( x , y , RTS=" v r s " ,ORIENTATION="i n −o u t " , t x t=rownames ( x ) )
dea . p l o t ( x , y , RTS=" d r s " ,ORIENTATION="i n −o u t " , add=TRUE, l t y ="dashed " , lwd =2)
dea . p l o t ( x , y , RTS=" c r s " ,ORIENTATION="i n −o u t " , add=TRUE, l t y ="d o t t e d " )
Pierwsze dwa tworzą dwie zmienne x i y, które przechowują odpowiednio poziom nakładu
oraz efektu dla sześciu obiektów. Wykorzystaliśmy w tym celu standardowe polecenia R. Funkcja
dea.plot pochodzi już jednak z pakietu benchmarking. Jako jej argumenty podajemy macie-
rze nakładów i efektów, rodzaj efektów skali i orientację. Pozostałe argumenty dotyczą efektów
graficznych. Jak widać wywołaliśmy funkcję trzykrotnie za każdym razem podając inny rodzaj
efektów skali. Efekty jej działania czyli granicę efektywności ilustruje wykres na rysunku 6.8.
Zwykle jednak nie będziemy ręcznie wprowadzać danych. R posiada duże możliwości importu
z różnych formatów, ale my ograniczymy się do plików typu .csv jako najbardziej uniwersalnych.
Następne przykłady będą bazowały na danych z książki Guzika a dotyczących oceny efektywności
funkcjonowania służby zdrowia w poszczególnych województwach. Znajdujący się poniżej listing
przedstawia polecenia służące wczytaniu danych zebranych w pliku dane_guzik97.csv. Zmienna
DaneDEA przechowuje wczytane dane. Kolejne polecenia tworzą macierze nakładów i efektów a
następnie przypisują odpowiednie nazwy kolumnom i wierszom.
DaneDEA<−r e a d . c s v 2 ( f i l e ="dane_guzik97 . c s v " , row . names =1 , h e a d e r=TRUE)
2
Uwaga! Na liście znajduje się również pakiet benchmark, ale służy on do innych celów.
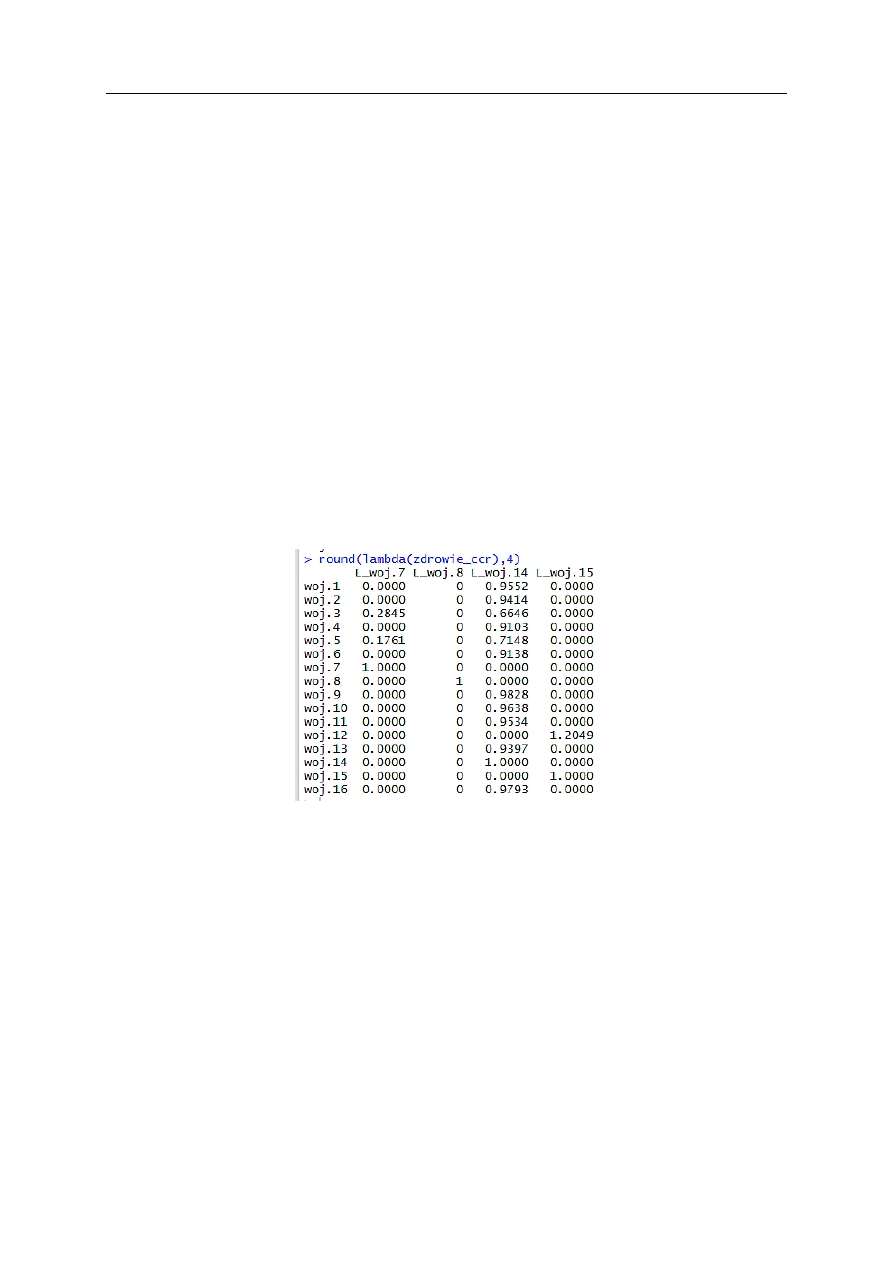
6.3. DEA w środowisku R
57
x<−c b i n d ( DaneDEA$Majatek_I , DaneDEA$Lekarze_I , DaneDEA$Pielegniarki_I )
y<−c b i n d ( DaneDEA$Zdrowi_O , DaneDEA$Leczeni_O )
naklady<−c ( " Majatek " , " L e k a r z e " , " P i e l e g n i a r k i " )
e f e k t y <−c ( " Zdrowi " , " L e c z e n i " )
dimnames ( x)<− l i s t ( rownames ( x , do . NULL=FALSE, p r e f i x ="woj . " ) , n a k l a d y )
dimnames ( y)<− l i s t ( rownames ( y , do . NULL=FALSE, p r e f i x ="woj . " ) , e f e k t y )
Kolejny ciąg poleceń pozwala obliczyć zorientowany na nakłady model CCR. Służy do tego
funkcja dea, której rezultaty zostały zapamiętane w zmiennej zdrowie_ccr. Jej argumenty są
następujące: macierz nakładów, macierz efektów, RTS – rodzaj efektów skali, ORIENTATION –
orientacja modelu. Szczegółowe informacje na temat możliwych wartości tych parametrów za-
wiera podręcznik użytkownika.
z d r o w i e _ c c r <−dea ( x , y , RTS=" c r s " , ORIENTATION=" i n " )
e f f ( z d r o w i e _ c c r )
lambda ( z d r o w i e _ c c r )
p r i n t ( p e e r s ( z d r o w i e _ c c r , NAMES=TRUE) , q u o t e=FALSE)
summary ( z d r o w i e _ c c r )
Rysunek 6.9. Wartości lambd z pakietu benchmarking
Poszczególne olecenia służą wyświetlaniu poszczególnych składowych zapamiętanego rozwią-
zania. Wywołanie eff z argumentem w postaci zmiennej przechowującej wyniki optymalizacji
wyświetli wskaźniki efektywności. Jak nietrudno się domyślić komenda lambda wywoła wartości
wag intensywności. Kolumny odpowiadają obiektom efektywnym. Wiersze podają wagi inten-
sywności wykorzystania technologii dla danej jednostki decyzyjnej. Jak możemy zauważyć na
rysunku 6.9 na przykład dla województwa 5 benchmark wyznaczają województwa 7 i 14 z wagami
odpowiednio 0,1761 oraz 0,7148.
Nieco podobną funkcje pełni polecenie peers. Podaje ono po prostu listę obiektów tworzących
benchmark dla danej jednostki decyzyjnej. Z kolei summary wyświetla krótkie podsumowanie
wyników jako zestaw miar statystycznych.
Na zakończenie warto dodać, że benchmarking pozwala na obliczenie superefektywności dzięki
funkcji sdea. Jego składnia jest podobna jak przed chwilą opisanej funkcji dea.

58
6. Wykorzystanie komputera do obliczeń w metodzie DEA
Bibliografia
1. Feruś A. Zastosowanie metody DEA do określania poziomu ryzyka kredytowego przedsię-
biorstw, Bank i Kredyt, lipiec 2006
2. Guzik B. (2009) Podstawowe modele DEA w badaniu efektywności gospodarczej i społecznej,
Wydawnictwo Uniwersytetu Ekonomicznego w Poznaniu, Poznań
3. Mielnik M., Ławrynowicz M. Badanie efektywności technicznej banków komercyjnych w Polsce
metodą DEA, Bank i Kredyt, maj 2002
4. Miszczyńska D., Miszczyński M. Analiza danych granicznych (DEA), www.kbo.uni.lodz.pl
5. Rogowski G. (1998) Metody analizy i oceny działalności banku na potrzeby zarządzania stra-
tegicznego, wyd. Wyższa Szkoła Bankowa, Poznań
Document Outline
- Podstawowe pojęcia
- Metoda DEA – charakterystyka i podział modeli
- Wybrane typy analiz w metodzie DEA
- Uwzględnianie luzów nakładów i efektów
- Model wykorzystujący efektywność nieradialną
- Wykorzystanie komputera do obliczeń w metodzie DEA
Wyszukiwarka
Podobne podstrony:
Macierzowa metoda przemieszczeń przykład 2014
cwiczenie 5 amylaza oznaczanie aktywnosci enzymu metoda kolorymetryczna 05 05 2014
Metoda magnetyczna MT 14
Metoda animacji społecznej (Animacja społeczno kulturalna)
Metoda Weroniki Sherborne[1]
Metoda Ruchu Rozwijajacego Sherborne
Postmodernity and Postmodernism ppt May 2014(3)
Projet metoda projektu
Wyklad 04 2014 2015
Norma ISO 9001 2008 ZUT sem 3 2014
9 ćwiczenie 2014
METODA DENNISONA
więcej podobnych podstron