ASYMPTOTY
Asymptotą wykresu funkcji nazywamy styczną do wykresu funkcji w nieskończenie
oddalonym punkcie tego wykresu.
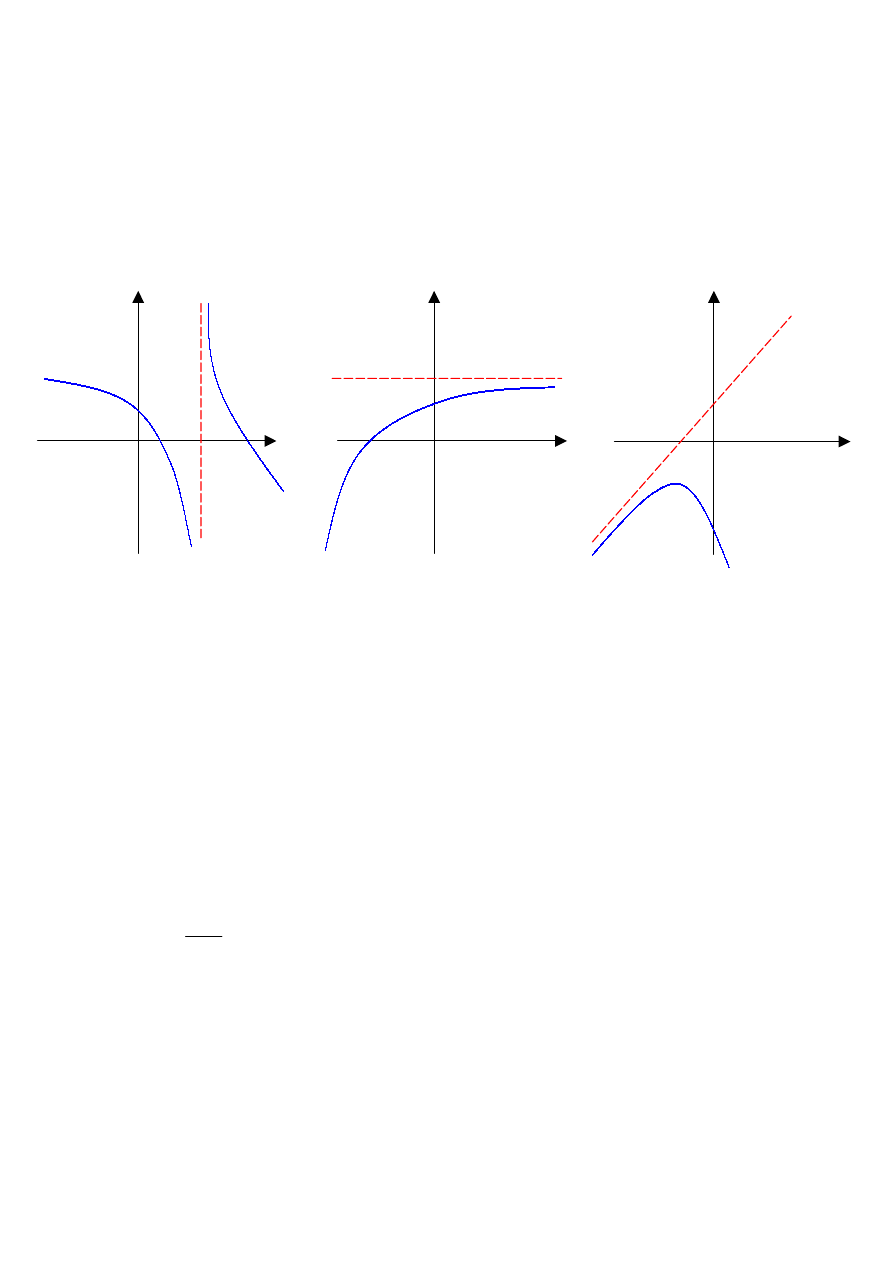
Asymptota pionowa
Asymptota pozioma
Asymptota ukośna
Asymptoty pionowe mogą istnieć tylko w punktach nieciągłości lub nieokreśloności
funkcji f(x), Jeśli wartość funkcji z lewej lub z prawej strony takiego punktu (np. x
0
) dąży
do nieskończoności, tzn.
, to prosta x=x
( )
∞
=
→
x
f
x
x
0
lim
0
jest asymptotą pionową.
Jeżeli x dąży do nieskończoności (plus lub minus) i wykres funkcji f(x) dąży do pewnego
punktu c, tzn.
, to y=c jest asymptotą poziomą funkcji f(x).
( )
c
x
f
x
=
∞
→
lim
Jeżeli x dąży do nieskończoności i wykres funkcji f(x) dąży do pewnej prostej y=ax+b,
gdzie
x
x
f
a
x
)
(
lim
∞
→
=
i
, to prosta y=ax+b jest asymptotą ukośną funkcji
f(x) (oczywiście
a
,
a
,
b
).
[
ax
x
f
b
x
−
=
∞
→
)
(
lim
0
∞
≠
∞
≠
]
≠
Arkadiusz Lisak
1

Przykład.
1.
1
1
+
=
x
y
, x
.
1
−
≠
0
1
1
lim
=
+
−∞
→
x
x
,
0
1
1
lim
=
+
+∞
→
x
x
,
−∞
=
+
−
−
→
1
1
lim
1
x
x
,
+∞
=
+
+
−
→
1
1
lim
1
x
x
Asymptota pozioma:
y=0
Asymptota
pionowa:
x=-1
2.
2
2
3
1
5
3
x
x
x
y
+
−
=
,
0
≠
x
3
1
5
3
lim
3
2
3
=
+
−
=
∞
→
x
x
x
a
x
,
5
1
5
lim
3
1
5
3
lim
3
1
5
3
lim
2
2
2
3
2
3
2
2
3
−
=
+
−
=
−
+
−
=
−
+
−
=
∞
→
∞
→
∞
→
x
x
x
x
x
x
x
x
x
x
x
x
x
b
Asymptota ukośna:
y=3x-5.
OBLICZANIE POCHODNEJ Z DEFINICJI
x
x
f
x
x
f
x
f
x
∆
−
∆
+
=
→
∆
)
(
)
(
lim
)
(
'
0
Przykład.
2
)
(
x
x
f
=
=
∆
−
∆
+
∆
+
=
∆
−
∆
+
=
∆
−
∆
+
=
→
∆
→
∆
→
∆
x
x
x
x
x
x
x
x
x
x
x
x
f
x
x
f
x
f
x
x
x
2
2
2
0
2
2
0
0
2
lim
)
(
lim
)
(
)
(
lim
)
(
'
(
)
x
x
x
x
x
x
x
x
x
x
x
x
x
x
2
2
lim
)
2
(
lim
2
lim
0
0
2
0
=
∆
+
=
∆
∆
∆
+
=
∆
∆
+
∆
=
→
∆
→
∆
→
∆
,
czyli
( )
x
x
2
'
2
=
Arkadiusz Lisak
2
Wyszukiwarka
Podobne podstrony:
Pochodne z definicji Zadanie Zadanie domowe id 810247
obliczanie pochodnych z definicji
Pochodne z definicji Zadanie Rozwiazanie zadania domowego id
obliczanie pochodnych z definicji
AMI 17 3 Pochodne zrozumieć definicję pochodnej
12. Definicja pochodnej funkcji jednej zmiennej w punkcie i przykład jej interpretacji, Studia, Seme
9 Zadania do wykladu Asymptoty funkcji pochodna funkcji
Definicji pochodnej funkcji, Notatki
AMI 17 3 Pochodne zrozumieć definicję pochodnej
pochodne de l Hospitala asymptoty ekstrema
AMI 17 3 Pochodne zrozumieć definicję pochodnej
Definicja i podzia skazy krwotocznej
Ewolucja marketingu era produkcyjna, sprzedazowa, marketingowa Rynek definicja
2 Pochodna calkaid 21156 ppt
INTER 1 DEFINICJA
DEFINICJA STRESU
więcej podobnych podstron